华东师大版2024—2025学年八年级下册数学期末考试素养检测卷(含答案)
文档属性
| 名称 | 华东师大版2024—2025学年八年级下册数学期末考试素养检测卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1013.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
华东师大版2024—2025学年八年级下册数学期末考试素养检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.数字0.000000193用科学记数法表示为( )
A. B. C. D.
2.下列式子从左到右变形正确的是( )
A. B. C. D.
3.将分式中的,同时扩大为原来的3倍,则分式的值( )
A.扩大为原来的6倍 B.扩大为原来的9倍
C.扩大为原来的3倍 D.不变
4.下列不能表示y是x的函数的是( )
A. B. C. D.
5.下列关于函数的性质说法正确的是( )
A.图象不经过第二象限 B.图象与y轴交于点
C.图象与x轴交于点 D.y随x的增大而减小
6.已知反比例函数 的图象经过点,则下列说法正确的是( )
A.图象位于第一、三象限 B.图象经过点
C.图象关于y轴对称 D.y随x的增大而增大
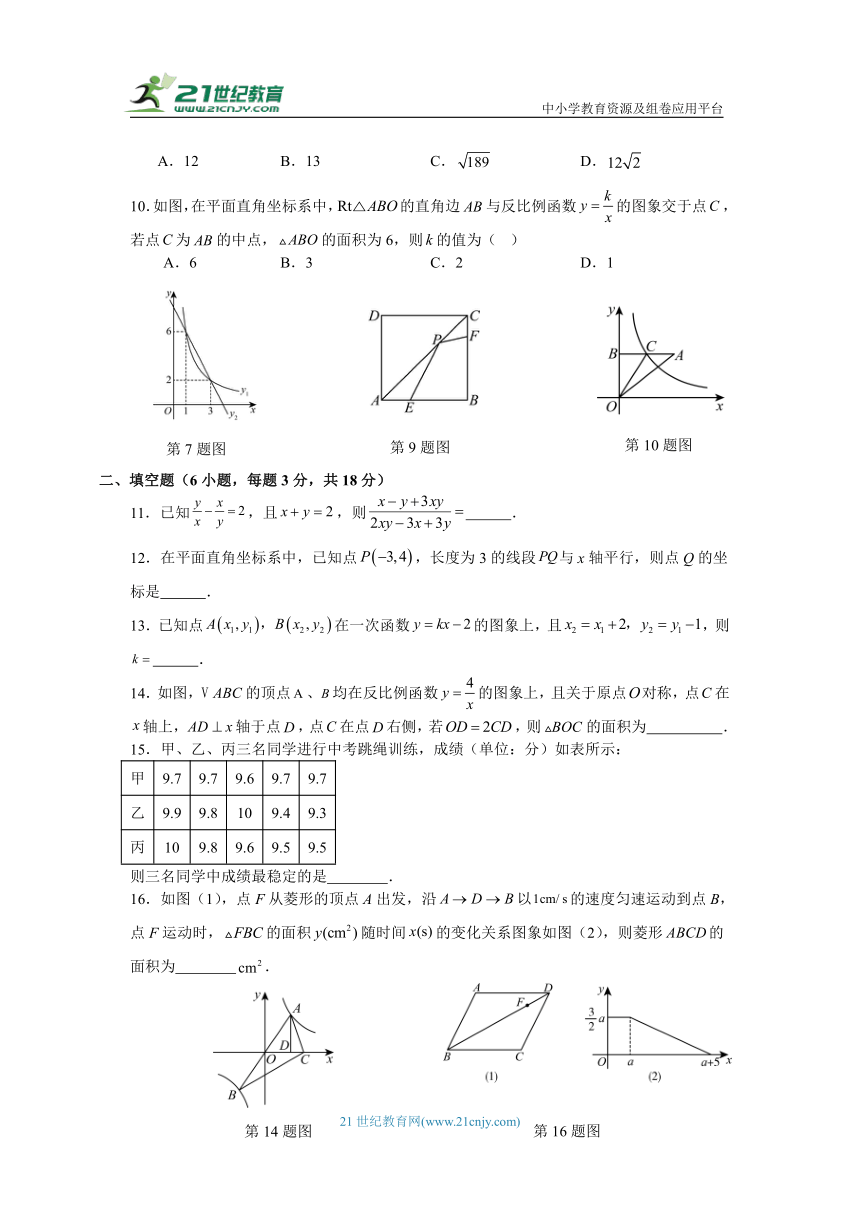
7.若函数与函数的图象如图所示,则不等式的解集是( )
A. B. C. D.
8.一次体质健康检测中,某班体育委员对该班20名男生在一分钟内“引体向上”的个数进行了统计,并制作如下统计表:
个数 6 9 11 12 15
人数 2 5 8 3 2
则这20名男生在一分钟内“引体向上”的个数的众数是( )
A.6 B.9 C.11 D.15
9.如图,正方形的边长为12,点E、F分别为、上动点(E、F均不与端点重合),且,P是对角线上的一个动点,则的最小值是( )
A.12 B.13 C. D.
10.如图,在平面直角坐标系中,的直角边与反比例函数的图象交于点,若点为的中点,的面积为6,则的值为( )
A.6 B.3 C.2 D.1
二、填空题(6小题,每题3分,共18分)
11.已知,且,则 .
12.在平面直角坐标系中,已知点,长度为3的线段与x轴平行,则点Q的坐标是 .
13.已知点在一次函数的图象上,且,则 .
14.如图,的顶点、均在反比例函数的图象上,且关于原点对称,点在轴上,轴于点,点在点右侧,若,则的面积为 .
15.甲、乙、丙三名同学进行中考跳绳训练,成绩(单位:分)如表所示:
甲 9.7 9.7 9.6 9.7 9.7
乙 9.9 9.8 10 9.4 9.3
丙 10 9.8 9.6 9.5 9.5
则三名同学中成绩最稳定的是 .
16.如图(1),点F从菱形的顶点A出发,沿以的速度匀速运动到点B,点F运动时,的面积随时间的变化关系图象如图(2),则菱形的面积为 .
华东师大版2024—2025学年八年级下册数学期末考试素养检测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解分式方程:
(1); (2).
18.先化简,再求值:,其中是不等式组的整数解.
19.某农业试验基地在相同环境条件下,研究甲、乙两种小麦的苗高分布,以评估其生长稳定性和产量潜力,为优化种植方案提供依据.从两种小麦试验田各随机抽取16株麦苗,测量苗高(单位:),将数据分组整理,分别得到了如下统计表(表内方差保留整数)和不完整的统计图.(注:将苗高共分为,,,四组,分别用A,,,表示)
其中甲种小麦苗高的具体数据如下:12,11,10,13,8,15,10,14,11,10,18,16,9,13,12,8.
甲、乙两种小麦苗高情况统计表
统计量 中位数 众数 方差
甲种小麦 8
乙种小麦 13.5 15 10
根据以上信息解答下列问题:
(1)将条形统计图补充完整;
(2)______,______;
(3)请结合稳定性优先和产量潜力(优质麦苗()占比更高的品种潜力大)两个要求,给出种植建议并说明理由.
20.为了更好的服务各云计算中心,某科技公司计划购进两类服务器升级后再销售.高性能服务器每台的进价是普通服务器每台进价的倍.花费480万元购进高性能服务器的台数比花费560万元购进普通服务器的台数少6台.
(1)高性能服务器和普通服务器每台的进价各是多少万元?
(2)若该科技公司采购这两种服务器共100台,且购买的总费用不超过5400万元.高性能服务器每台售价80万元,普通服务器按进价的2倍标价后再打7折销售,请你帮该科技公司设计利润最大的进货方案,并求出最大利润.
21.在平面直角坐标系中,点是坐标原点,定义点和点的相关系数如下:若点在一条直线上,则;若点不在一条直线上,则.如图,已知点的坐标为,点的坐标为,点为平面直角坐标系内一动点,
请回答下列问题:
(1)______.
(2)若,,求点的坐标.
(3)点在第二象限,若,且点的纵坐标为2,求点的坐标.
(4)当时,直接写出点的横坐标.
22.如图,在中,E为的中点,延长交的延长线于点F,连接、.
(1)求证:;
(2)若,,,求的长.
23.如图①,四边形为正方形,E为对角线上一点,连接.
(1)求证:;
(2)如图②,过点E作,交边于点F,以为邻边作矩形,连接.
①求证:矩形是正方形;
②若,探究:的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
24.定义:我们把一次函数的图象与正比例函数的图象的交点称为一次函数图象的“亮点”.例如:求一次函数图象的“亮点”时,联立方程得,解得,则一次函数图象的“亮点”为.
(1)求一次函数图象的“亮点”;
(2)一次函数图象的“亮点”为,求,的值;
(3)若一次函数的图象分别与轴,轴交于点,,且一次函数的图象上没有“亮点”,点在轴上,,求满足条件的点的坐标.
25.如图,在平面直角坐标系中,反比例函数的图象与一次函数的图象相交于、两点.
(1)求反比例函数和一次函数的表达式;
(2)当时,请根据函数图象,直接写出关于x的不等式的解集;
(3)过直线上的点C作轴,交反比例函数的图象于点.若点横坐标为,求的面积.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C B A B A C B A
二填空题
11.【解】解:∵,
,
,
,
,
原式
,
故答案为:.
12.【解】解:点的坐标为,且轴,
点和点的纵坐标相同,为4,
,
当点在点的左边时,横坐标为,此时点Q的坐标是,
当点在点的右边时,横坐标为,此时点Q的坐标是,
综上所述,点的坐标为或,
故答案为:或.
13.【解】解:点在一次函数的图象上,
∴,,
∵,
∴,
∵,
∴,
解得,
故答案为:.
14.【解】解:根据反比例函数的性质可得:的面积为,
即,
故,
∵,
∴的面积为,
∴的面积为,
∵、均在反比例函数的图象上,且关于原点对称,
∴与的面积相等,
即的面积为.
故答案为:.
15.【解】解:∵甲的成绩在9.6和9.7之间波动;乙的成绩在9.3和10之间波动;丙的成绩在9.5和10之间波动,成绩最稳定的是甲.
故答案为:甲.
16.【解】解:设点A到的距离为h,
由点F的运动轨迹和速度可知,,且,
解得:,
过点D作交的延长线与点E,
则,
∴,
∵四边形是菱形,
∴,
∴,
在中,,
即,
解得:,
∴,
故答案为:
三、解答题
17.【解】(1)解:;
两边同时乘,得,
去括号,得,
移项、合并同类项,得,
系数化为1,得,
经检验,是分式方程的解.
(2)解:.
两边同时乘,得,
去括号,得,
移项、合并同类项,得,
系数化为1,得,
经检验,是分式方程的解.
18.【解】解:
.
解,
解得,
解得,
∴不等式组的解集为.
∵为整数,
∴或3,
∵,,
∴,0,
∴,
∴原式.
19.【解】(1)解:甲种小麦苗高在内的7个,内的4个,
∴补全条形统计图,
(2)解:甲种小麦苗高的数据按从小到大的顺序排列:8,8,9,10,10,10,11,11,12,12,13,13,14,15,16,18.
∴,,
故答案为:11.5,12;
(3)解:∵甲种小麦的方差小于乙种小麦的方差,
∴甲种小麦的稳定性更优,
∵甲种小麦的优质麦苗占比为,
乙种小麦的优质麦苗占比为,
∴甲种小麦的产量潜力更高,
故建议种植甲种小麦.
20.【解】(1)解:设普通服务器每台进价为万元,则高性能服务器每台进价为万元.
根据题意列方程得:,
解得:,
经检验,是原方程的解,则高性能服务器每台进价为:万元;
答:高性能服务器每台的进价是50万元,普通服务器每台的进价是30万元;
(2)解:设购进高性能服务器台,则购进普通服务器台.
可列出不等式:,
解得:,且m的整数,
高性能服务器每台利润为:(万元),
普通服务器每台利润为:(万元),
设总利润为万元,则,化简得:,
∵,
∴随的增大而增大,
又∵,
∴当时,有最大值,(万元),此时购进普通服务器:(台).
答:购进高性能服务器70台,普通服务器30台时利润最大,最大利润是1880万元.
21.【解】(1)解:∵点的坐标为,点的坐标为,
∴,,
∴,
故答案为:;
(2)解:∵,点的坐标为,
∴点在一条直线上,即点在轴上,
设,
∵,
∴,
∴,
∴点的坐标为或;
(3)解:∵点的纵坐标为,
∴设,
∵,
∴,
∴,
∴,
∵点在第二象限,
∴,
∴点的坐标为;
(4)解:设点的横坐标为,
∵,
∴,
∴,
∴,
∴点的横坐标.
22.【解】(1)证明:∵为的中点,
∴,
∵四边形为平行四边形,
∴,,
∴,
在和中,
,
∴;
(2)解:∵,四边形为平行四边形,,
∴,
又∵,
∴,
∵,
∴,
∵,
∴,
∵且,
∴四边形为平行四边形,
∴.
23.【解】(1)证明:∵四边形是正方形,
∴,
∵是正方形的对角线,
∴,
在和中,
,
∴,
∴;
(2)证明:过E作于M点,过E作于N点,如图所示:
∵四边形是正方形,
∴,且平分,
∴,
∵,
∴,
∴,
∵四边形DEFG是矩形,
∴,
∴,
∴
∴
又,
在和中,
,
∴,
∴,
∴矩形为正方形;
解:的值为定值6,
理由如下:
∵矩形为正方形,
∴,,
∵四边形是正方形,
∴,,
∴
∴,
在和中,
,
∴,
∴,
∴
又,
∴是定值.
24.【解】(1)解:由定义可知,一次函数的“亮点”为一次函数解析式与正比例函数的交点,
联立,
解得,
一次函数的“亮点”为;
(2)解:根据定义可得,点在上,
,
解得,
∴点的坐标为,
∵点在直线上,
,
解得.
(3)解:∵直线上没有“亮点”,
∴直线与直线没有交点,即直线与平行,
∴,
∴直线的解析式为,
在中,当时,,当时,,
,
,
∵,
∴,
∴,
∵,
∴点P的坐标为或.
25.【解】(1)解:∵反比例函数的图象过点
∴,
故反比例函数的表达式为
把点代入反比例函数得,,解得
∴点的坐标为
∵一次函数的图象经过、两点
∴,解得
故一次函数的表达式为;
(2)∵
∴,即一次函数图象在反比例函数图象的上方
∴;
(3)∵点横坐标为,代入
解得:
∴
当时,代入,得
解得:
∴
如图,过点分别作轴的垂线,垂足分别为,
∵,
∴,
∵,
∴.
21世纪教育网(www.21cnjy.com)
华东师大版2024—2025学年八年级下册数学期末考试素养检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.数字0.000000193用科学记数法表示为( )
A. B. C. D.
2.下列式子从左到右变形正确的是( )
A. B. C. D.
3.将分式中的,同时扩大为原来的3倍,则分式的值( )
A.扩大为原来的6倍 B.扩大为原来的9倍
C.扩大为原来的3倍 D.不变
4.下列不能表示y是x的函数的是( )
A. B. C. D.
5.下列关于函数的性质说法正确的是( )
A.图象不经过第二象限 B.图象与y轴交于点
C.图象与x轴交于点 D.y随x的增大而减小
6.已知反比例函数 的图象经过点,则下列说法正确的是( )
A.图象位于第一、三象限 B.图象经过点
C.图象关于y轴对称 D.y随x的增大而增大
7.若函数与函数的图象如图所示,则不等式的解集是( )
A. B. C. D.
8.一次体质健康检测中,某班体育委员对该班20名男生在一分钟内“引体向上”的个数进行了统计,并制作如下统计表:
个数 6 9 11 12 15
人数 2 5 8 3 2
则这20名男生在一分钟内“引体向上”的个数的众数是( )
A.6 B.9 C.11 D.15
9.如图,正方形的边长为12,点E、F分别为、上动点(E、F均不与端点重合),且,P是对角线上的一个动点,则的最小值是( )
A.12 B.13 C. D.
10.如图,在平面直角坐标系中,的直角边与反比例函数的图象交于点,若点为的中点,的面积为6,则的值为( )
A.6 B.3 C.2 D.1
二、填空题(6小题,每题3分,共18分)
11.已知,且,则 .
12.在平面直角坐标系中,已知点,长度为3的线段与x轴平行,则点Q的坐标是 .
13.已知点在一次函数的图象上,且,则 .
14.如图,的顶点、均在反比例函数的图象上,且关于原点对称,点在轴上,轴于点,点在点右侧,若,则的面积为 .
15.甲、乙、丙三名同学进行中考跳绳训练,成绩(单位:分)如表所示:
甲 9.7 9.7 9.6 9.7 9.7
乙 9.9 9.8 10 9.4 9.3
丙 10 9.8 9.6 9.5 9.5
则三名同学中成绩最稳定的是 .
16.如图(1),点F从菱形的顶点A出发,沿以的速度匀速运动到点B,点F运动时,的面积随时间的变化关系图象如图(2),则菱形的面积为 .
华东师大版2024—2025学年八年级下册数学期末考试素养检测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解分式方程:
(1); (2).
18.先化简,再求值:,其中是不等式组的整数解.
19.某农业试验基地在相同环境条件下,研究甲、乙两种小麦的苗高分布,以评估其生长稳定性和产量潜力,为优化种植方案提供依据.从两种小麦试验田各随机抽取16株麦苗,测量苗高(单位:),将数据分组整理,分别得到了如下统计表(表内方差保留整数)和不完整的统计图.(注:将苗高共分为,,,四组,分别用A,,,表示)
其中甲种小麦苗高的具体数据如下:12,11,10,13,8,15,10,14,11,10,18,16,9,13,12,8.
甲、乙两种小麦苗高情况统计表
统计量 中位数 众数 方差
甲种小麦 8
乙种小麦 13.5 15 10
根据以上信息解答下列问题:
(1)将条形统计图补充完整;
(2)______,______;
(3)请结合稳定性优先和产量潜力(优质麦苗()占比更高的品种潜力大)两个要求,给出种植建议并说明理由.
20.为了更好的服务各云计算中心,某科技公司计划购进两类服务器升级后再销售.高性能服务器每台的进价是普通服务器每台进价的倍.花费480万元购进高性能服务器的台数比花费560万元购进普通服务器的台数少6台.
(1)高性能服务器和普通服务器每台的进价各是多少万元?
(2)若该科技公司采购这两种服务器共100台,且购买的总费用不超过5400万元.高性能服务器每台售价80万元,普通服务器按进价的2倍标价后再打7折销售,请你帮该科技公司设计利润最大的进货方案,并求出最大利润.
21.在平面直角坐标系中,点是坐标原点,定义点和点的相关系数如下:若点在一条直线上,则;若点不在一条直线上,则.如图,已知点的坐标为,点的坐标为,点为平面直角坐标系内一动点,
请回答下列问题:
(1)______.
(2)若,,求点的坐标.
(3)点在第二象限,若,且点的纵坐标为2,求点的坐标.
(4)当时,直接写出点的横坐标.
22.如图,在中,E为的中点,延长交的延长线于点F,连接、.
(1)求证:;
(2)若,,,求的长.
23.如图①,四边形为正方形,E为对角线上一点,连接.
(1)求证:;
(2)如图②,过点E作,交边于点F,以为邻边作矩形,连接.
①求证:矩形是正方形;
②若,探究:的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
24.定义:我们把一次函数的图象与正比例函数的图象的交点称为一次函数图象的“亮点”.例如:求一次函数图象的“亮点”时,联立方程得,解得,则一次函数图象的“亮点”为.
(1)求一次函数图象的“亮点”;
(2)一次函数图象的“亮点”为,求,的值;
(3)若一次函数的图象分别与轴,轴交于点,,且一次函数的图象上没有“亮点”,点在轴上,,求满足条件的点的坐标.
25.如图,在平面直角坐标系中,反比例函数的图象与一次函数的图象相交于、两点.
(1)求反比例函数和一次函数的表达式;
(2)当时,请根据函数图象,直接写出关于x的不等式的解集;
(3)过直线上的点C作轴,交反比例函数的图象于点.若点横坐标为,求的面积.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C B A B A C B A
二填空题
11.【解】解:∵,
,
,
,
,
原式
,
故答案为:.
12.【解】解:点的坐标为,且轴,
点和点的纵坐标相同,为4,
,
当点在点的左边时,横坐标为,此时点Q的坐标是,
当点在点的右边时,横坐标为,此时点Q的坐标是,
综上所述,点的坐标为或,
故答案为:或.
13.【解】解:点在一次函数的图象上,
∴,,
∵,
∴,
∵,
∴,
解得,
故答案为:.
14.【解】解:根据反比例函数的性质可得:的面积为,
即,
故,
∵,
∴的面积为,
∴的面积为,
∵、均在反比例函数的图象上,且关于原点对称,
∴与的面积相等,
即的面积为.
故答案为:.
15.【解】解:∵甲的成绩在9.6和9.7之间波动;乙的成绩在9.3和10之间波动;丙的成绩在9.5和10之间波动,成绩最稳定的是甲.
故答案为:甲.
16.【解】解:设点A到的距离为h,
由点F的运动轨迹和速度可知,,且,
解得:,
过点D作交的延长线与点E,
则,
∴,
∵四边形是菱形,
∴,
∴,
在中,,
即,
解得:,
∴,
故答案为:
三、解答题
17.【解】(1)解:;
两边同时乘,得,
去括号,得,
移项、合并同类项,得,
系数化为1,得,
经检验,是分式方程的解.
(2)解:.
两边同时乘,得,
去括号,得,
移项、合并同类项,得,
系数化为1,得,
经检验,是分式方程的解.
18.【解】解:
.
解,
解得,
解得,
∴不等式组的解集为.
∵为整数,
∴或3,
∵,,
∴,0,
∴,
∴原式.
19.【解】(1)解:甲种小麦苗高在内的7个,内的4个,
∴补全条形统计图,
(2)解:甲种小麦苗高的数据按从小到大的顺序排列:8,8,9,10,10,10,11,11,12,12,13,13,14,15,16,18.
∴,,
故答案为:11.5,12;
(3)解:∵甲种小麦的方差小于乙种小麦的方差,
∴甲种小麦的稳定性更优,
∵甲种小麦的优质麦苗占比为,
乙种小麦的优质麦苗占比为,
∴甲种小麦的产量潜力更高,
故建议种植甲种小麦.
20.【解】(1)解:设普通服务器每台进价为万元,则高性能服务器每台进价为万元.
根据题意列方程得:,
解得:,
经检验,是原方程的解,则高性能服务器每台进价为:万元;
答:高性能服务器每台的进价是50万元,普通服务器每台的进价是30万元;
(2)解:设购进高性能服务器台,则购进普通服务器台.
可列出不等式:,
解得:,且m的整数,
高性能服务器每台利润为:(万元),
普通服务器每台利润为:(万元),
设总利润为万元,则,化简得:,
∵,
∴随的增大而增大,
又∵,
∴当时,有最大值,(万元),此时购进普通服务器:(台).
答:购进高性能服务器70台,普通服务器30台时利润最大,最大利润是1880万元.
21.【解】(1)解:∵点的坐标为,点的坐标为,
∴,,
∴,
故答案为:;
(2)解:∵,点的坐标为,
∴点在一条直线上,即点在轴上,
设,
∵,
∴,
∴,
∴点的坐标为或;
(3)解:∵点的纵坐标为,
∴设,
∵,
∴,
∴,
∴,
∵点在第二象限,
∴,
∴点的坐标为;
(4)解:设点的横坐标为,
∵,
∴,
∴,
∴,
∴点的横坐标.
22.【解】(1)证明:∵为的中点,
∴,
∵四边形为平行四边形,
∴,,
∴,
在和中,
,
∴;
(2)解:∵,四边形为平行四边形,,
∴,
又∵,
∴,
∵,
∴,
∵,
∴,
∵且,
∴四边形为平行四边形,
∴.
23.【解】(1)证明:∵四边形是正方形,
∴,
∵是正方形的对角线,
∴,
在和中,
,
∴,
∴;
(2)证明:过E作于M点,过E作于N点,如图所示:
∵四边形是正方形,
∴,且平分,
∴,
∵,
∴,
∴,
∵四边形DEFG是矩形,
∴,
∴,
∴
∴
又,
在和中,
,
∴,
∴,
∴矩形为正方形;
解:的值为定值6,
理由如下:
∵矩形为正方形,
∴,,
∵四边形是正方形,
∴,,
∴
∴,
在和中,
,
∴,
∴,
∴
又,
∴是定值.
24.【解】(1)解:由定义可知,一次函数的“亮点”为一次函数解析式与正比例函数的交点,
联立,
解得,
一次函数的“亮点”为;
(2)解:根据定义可得,点在上,
,
解得,
∴点的坐标为,
∵点在直线上,
,
解得.
(3)解:∵直线上没有“亮点”,
∴直线与直线没有交点,即直线与平行,
∴,
∴直线的解析式为,
在中,当时,,当时,,
,
,
∵,
∴,
∴,
∵,
∴点P的坐标为或.
25.【解】(1)解:∵反比例函数的图象过点
∴,
故反比例函数的表达式为
把点代入反比例函数得,,解得
∴点的坐标为
∵一次函数的图象经过、两点
∴,解得
故一次函数的表达式为;
(2)∵
∴,即一次函数图象在反比例函数图象的上方
∴;
(3)∵点横坐标为,代入
解得:
∴
当时,代入,得
解得:
∴
如图,过点分别作轴的垂线,垂足分别为,
∵,
∴,
∵,
∴.
21世纪教育网(www.21cnjy.com)
同课章节目录
