华东师大版2024—2025学年八年级下册数学期末教学质量监测试卷(含答案)
文档属性
| 名称 | 华东师大版2024—2025学年八年级下册数学期末教学质量监测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
华东师大版2024—2025学年八年级下册数学期末教学质量监测试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图象中,不能表示y是x的函数的是( )
A. B. C. D.
2.下列运算正确的是( )
A. B. C. D.
3.量子计算原型机“九章三号”,在百万分之一秒时间内所处理的最高复杂度的样本,需要当前最强的超级计算机花费超过二百亿年的时间.将“百万分之一”用科学记数法表示为( )
A. B. C. D.
4.若关于x的方程的解为正数,则m的值可以为( )
A.1 B.2 C.3 D.4
5.点在直线上,坐标(x,y)是二元一次方程的解,则点的位置在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.对于反比例函数,下列结论正确的是( )
A.在在该函数的图象上
B.该函数的图象分别位于第二、第四象限
C.当时,随的增大而增大
D.当时,随的增大而减小
7.如图,在中,,,的平分线,分别与直线交于点,.当点,,,相邻两点间的距离相等时,则的长为( )
A. B. C.或 D.或或
8.九年级中10名男生身高数据为(单位:厘米):175、170、175、178、169、180、174、173、175、180.上数据中的众数、极差、中位数分别为________.
A.175、11、175 B.180、11、175 C.175、11、180 D.180、169、175
9.如图1,在正方形中,动点从点出发,在正方形的边上以的速度沿运动.设运动的时间为,的面积为,与的函数图象如图2所示,则图2中的值为( )
A. B. C. D.
10.如图,正方形的边长为4,在上,且,是上一动点.则周长的最小值为( )
A. B. C.7 D.6
二、填空题(6小题,每题3分,共18分)
11.关于的分式方程的解为非负数,则的取值范围是 .
12.点在轴上,则点的坐标是 .
13.已知一次函数的图象经过点和点,那么关于x的方程的解为 .
14.在平面直角坐标系中,若函数的图象经过点和,则的值是 .
15.已知下列一组数据23,25,20,18,x,12,若中位数是20,则众数是 .
16.正方形中,点在上,,,点在上,的最小值 .
第II卷
华东师大版2024—2025学年八年级下册数学期末教学质量监测试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值:,其中.
18.解方程:
(1); (2)
19.在甲、乙两公司全体员工捐款活动中,甲公司共捐款元,乙公司共捐款元.下面是甲、乙两公司员工的一段对话:
甲公司员工:我们公司的人数比你们公司少人
乙公司员工:我们公司的人均捐款数是你们公司的倍
(1)甲、乙两公司各有多少人?
(2)现甲、乙两公司共同使用这笔捐款购买两种物资,种物资每箱元,种物资每箱元.若购买种物资不少于箱,并恰好将捐款用完,有几种购买方案?请设计出来.(注: 两种物资均需购买,并按整箱配送.)
20.在平面直角坐标系中,已知点.
(1)若点在轴上,求的值;
(2)若点到轴的距离为1,求的值;
(3)若轴,点,求的值.
21.如图,在直角坐标系中,
(1)请写出各点的坐标.
(2)若把向上平移3个单位,再向右平移2个单位得,在 图 中 画 出 变化位置,并 写 出 的坐标.
(3)求出
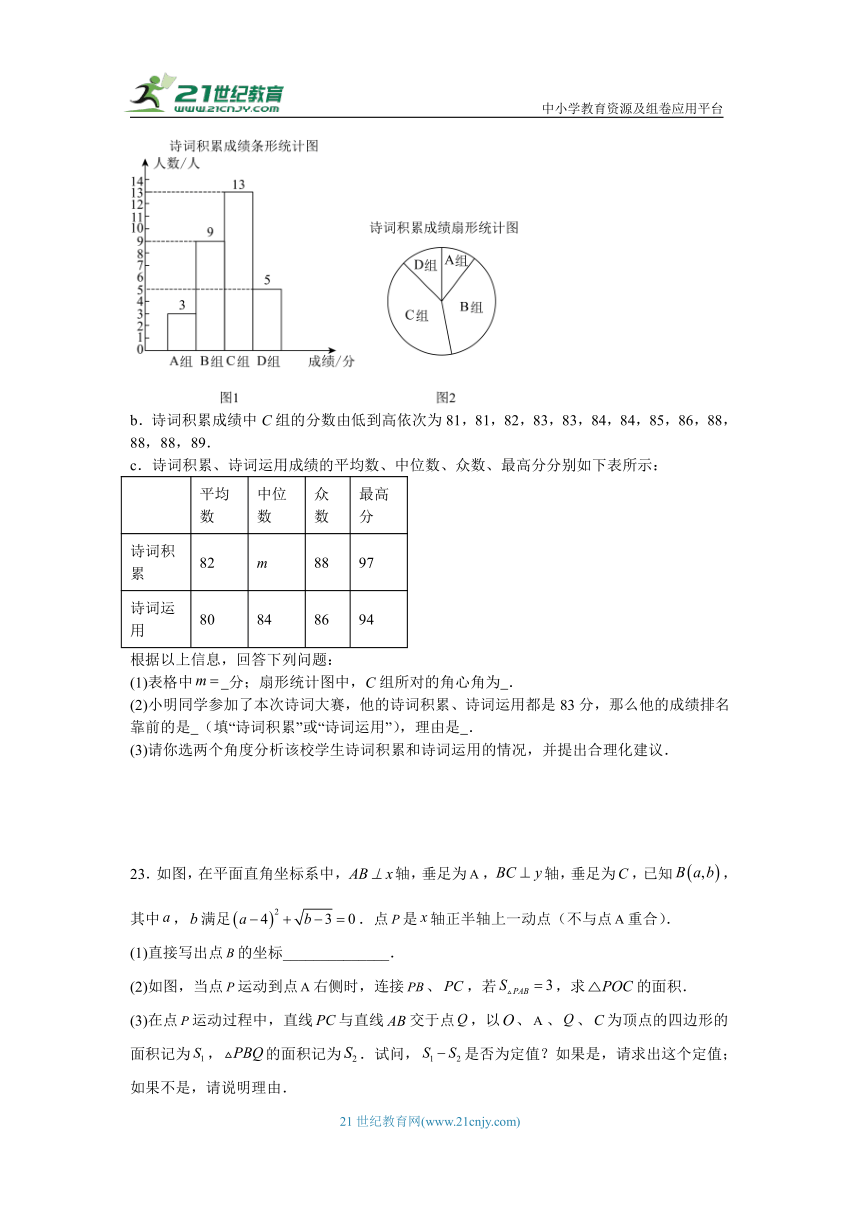
22.为弘扬中华优秀传统文化,某校举办了诗词大赛,本次比赛随机抽取了30名学生参加了诗词积累和诗词运用比赛,该校对他们的这两项成绩(百分制)分别进行了整理和分析.(A组:,B组:,C组:,D组:),部分信息如下:
a.诗词积累成绩频数分布直方图和诗词积累成绩扇形统计图分别如图1和图2所示.
b.诗词积累成绩中C组的分数由低到高依次为81,81,82,83,83,84,84,85,86,88,88,88,89.
c.诗词积累、诗词运用成绩的平均数、中位数、众数、最高分分别如下表所示:
平均数 中位数 众数 最高分
诗词积累 82 m 88 97
诗词运用 80 84 86 94
根据以上信息,回答下列问题:
(1)表格中 分;扇形统计图中,C组所对的角心角为 .
(2)小明同学参加了本次诗词大赛,他的诗词积累、诗词运用都是83分,那么他的成绩排名靠前的是 (填“诗词积累”或“诗词运用”),理由是 .
(3)请你选两个角度分析该校学生诗词积累和诗词运用的情况,并提出合理化建议.
23.如图,在平面直角坐标系中,轴,垂足为,轴,垂足为,已知,其中,满足.点是轴正半轴上一动点(不与点重合).
(1)直接写出点的坐标______________.
(2)如图,当点运动到点右侧时,连接、,若,求的面积.
(3)在点运动过程中,直线与直线交于点,以、、、为顶点的四边形的面积记为,的面积记为.试问,是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
24.如图1,矩形的顶点、分别在轴,轴的正半轴,已知点,且,满足.若点为矩形的对角线的中点,过点作的垂线分别交,于点,,交轴于点.
(1)求,的值;
(2)求线段的长度;
(3)如图2,连接,若点P为射线上的点,在平面直角坐标系中,是否存在点Q,使得以为边,点O,D,P,Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标,若不存在,请说明理由.
25.如图,一次函数的图象与反比例函数的图象交于点和点.
(1)求a,b的值和反比例函数解析式;
(2)若点在该反比例函数图象上,且它到x轴距离大于3,请根据图象直接写出m的取值范围;
(3)在y轴上有一点C,且,求点C的坐标.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B C A D D A C D
二、填空题
11.【解】解:去分母得:,
解得:,
由分式方程的解为非负数,得到且,
解得:且.
故答案为:且.
12.【解】解:∵点在轴上,
∴,
∴,
即点P的坐标为;
故答案为:.
13.【解】解:函数的图象经过,即当时,,
∴关于的方程的解为.
故答案为:.
14.【解】解:把和代入解析式得:,,
∴,
故答案为:.
15.【解】解:∵一组数据23,25,20,18,x,12的中位数是20,,
∴,
∴,
则这组数据的众数为20,
故答案为:20.
16.【详解】如图,连接交于点,连接与交于点P,连接,
∵四边形是正方形,
∴,且,
∴,则,此时最短,
∵,,
∴根据勾股定理得,
∴,
即的最小值为:,
故答案为:.
三、解答题
17.【解】解:
,
当时,原式.
18.【解】(1)解:,
去分母得到,
解得:,
检验:当时,,
是分式方程的解;
(2)解:,
去分母得到,,
解得:,
检验:当时,,
∴是增根,分式方程无解.
19.【解】(1)解:设甲公司有人,则乙公司有人,根据题意得
解得:
检验:把代入
故是所列方程的解.
则(人)
答:甲公司有人,乙公司有人;
(2)解:设购买种物资箱,购买种物资箱,且,,都是正整数,
根据题意得
∴,
∴,
当时, 符合题意;
当时, 符合题意;
当时, 不符合题意;
综上所述,购买方案有种:一种物资买箱,物资买箱;另一种是物资买箱,物资买箱.
20.【解】(1)解:∵点,
∴,
解得:;
(2)解:∵点到轴的距离为1,
∴,
解得:或;
(3)解:轴,点,
∴,
∴.
21.【解】(1)解:由题意得,;
(2)解:如图所示,即为所求,则;
(3)解:.
22.【解】(1)解;把这30名学生的诗词积累成绩按照从低到高的顺序排列,中位数为第15名的成绩和第16名成绩的中位数,
∵,
∴诗词积累成绩的中位数为,即;
扇形统计图中,C组所对的角心角为;
(2)解:诗词积累排名靠前,理由是:诗词积累成绩83大于其中位数,说明成绩在中等水平之上;诗词运用成绩小于其中位数,说明成绩在中等水平之下.
(3)解:从平均数看,诗词积累略好于诗词运用;从中位数看诗词运用处于中间的人数的成绩略好于诗词积累;建议学校活动策划侧重于诗词运用的学习.
23.【解】(1)解:∵,
∴,
∴,
∴点的坐标为,
故答案为:;
(2)解:轴,轴,
,,
又,即,
,
,
(3)解:是为定值,如图,当点在点右侧时,
如图,当点在点左侧时,
,
,
,
,
,
,
综上所述,为定值,.
24.【解】(1)解:∵,,
,,
∴,
,;
故答案为:8,6;
(2)解:如图1,连接,
,,
,,
∵四边形是矩形,
∴,
,
又∵,
,
,
,
四边形是菱形,
由(1)得,
∴,
在中,,
,
设,,
在中,,,
,
解得,
,
,
,
.
(3)解:存在点Q,使得以为边,点O,D,P,Q为顶点的四边形是菱形;
分两种情况,①当P在线段上时,取的中点M,连接并延长,过点P作于点N,如图4,
由题可得:,,为的中位线,
∴,,
∴,
当为边,四边形为菱形时,则,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
在和中,
∴,
∴,
∴,
∵,
∴点D向下平移3个单位,向左平移4个单位得到点O,
∴点P向下平移3个单位,向左平移4个单位得到点Q,
∴;
②当P在射线上时,当P在线段延长线上时,取的中点M,连接,过点P作于点N,如图5,
当为边,四边形为菱形时,则,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
在和中,
∴,
∴,
∴,
∵,
∴点D向下平移3个单位,向左平移4个单位得到点O,
∴点P向下平移3个单位,向左平移4个单位得到点Q,
∴;
综上所述,或.
25.【解】(1)解:把代入,得,
解得.
把代入,得,
解得.
把代入,得,
∴反比例函数解析式为;
(2)解:由(1)知,反比例函数的解析式是,
当时,则;当时,,
由图象可知,若点在反比例函数图象上,且它到轴距离大于3,
则的取值范围是或.
(3)解:设与轴交于点,
当时,,
∴点为,
∵,
∴,
∴,
∴,
∵点在轴上,点为.
∴点坐标为或.
21世纪教育网(www.21cnjy.com)
华东师大版2024—2025学年八年级下册数学期末教学质量监测试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图象中,不能表示y是x的函数的是( )
A. B. C. D.
2.下列运算正确的是( )
A. B. C. D.
3.量子计算原型机“九章三号”,在百万分之一秒时间内所处理的最高复杂度的样本,需要当前最强的超级计算机花费超过二百亿年的时间.将“百万分之一”用科学记数法表示为( )
A. B. C. D.
4.若关于x的方程的解为正数,则m的值可以为( )
A.1 B.2 C.3 D.4
5.点在直线上,坐标(x,y)是二元一次方程的解,则点的位置在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.对于反比例函数,下列结论正确的是( )
A.在在该函数的图象上
B.该函数的图象分别位于第二、第四象限
C.当时,随的增大而增大
D.当时,随的增大而减小
7.如图,在中,,,的平分线,分别与直线交于点,.当点,,,相邻两点间的距离相等时,则的长为( )
A. B. C.或 D.或或
8.九年级中10名男生身高数据为(单位:厘米):175、170、175、178、169、180、174、173、175、180.上数据中的众数、极差、中位数分别为________.
A.175、11、175 B.180、11、175 C.175、11、180 D.180、169、175
9.如图1,在正方形中,动点从点出发,在正方形的边上以的速度沿运动.设运动的时间为,的面积为,与的函数图象如图2所示,则图2中的值为( )
A. B. C. D.
10.如图,正方形的边长为4,在上,且,是上一动点.则周长的最小值为( )
A. B. C.7 D.6
二、填空题(6小题,每题3分,共18分)
11.关于的分式方程的解为非负数,则的取值范围是 .
12.点在轴上,则点的坐标是 .
13.已知一次函数的图象经过点和点,那么关于x的方程的解为 .
14.在平面直角坐标系中,若函数的图象经过点和,则的值是 .
15.已知下列一组数据23,25,20,18,x,12,若中位数是20,则众数是 .
16.正方形中,点在上,,,点在上,的最小值 .
第II卷
华东师大版2024—2025学年八年级下册数学期末教学质量监测试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值:,其中.
18.解方程:
(1); (2)
19.在甲、乙两公司全体员工捐款活动中,甲公司共捐款元,乙公司共捐款元.下面是甲、乙两公司员工的一段对话:
甲公司员工:我们公司的人数比你们公司少人
乙公司员工:我们公司的人均捐款数是你们公司的倍
(1)甲、乙两公司各有多少人?
(2)现甲、乙两公司共同使用这笔捐款购买两种物资,种物资每箱元,种物资每箱元.若购买种物资不少于箱,并恰好将捐款用完,有几种购买方案?请设计出来.(注: 两种物资均需购买,并按整箱配送.)
20.在平面直角坐标系中,已知点.
(1)若点在轴上,求的值;
(2)若点到轴的距离为1,求的值;
(3)若轴,点,求的值.
21.如图,在直角坐标系中,
(1)请写出各点的坐标.
(2)若把向上平移3个单位,再向右平移2个单位得,在 图 中 画 出 变化位置,并 写 出 的坐标.
(3)求出
22.为弘扬中华优秀传统文化,某校举办了诗词大赛,本次比赛随机抽取了30名学生参加了诗词积累和诗词运用比赛,该校对他们的这两项成绩(百分制)分别进行了整理和分析.(A组:,B组:,C组:,D组:),部分信息如下:
a.诗词积累成绩频数分布直方图和诗词积累成绩扇形统计图分别如图1和图2所示.
b.诗词积累成绩中C组的分数由低到高依次为81,81,82,83,83,84,84,85,86,88,88,88,89.
c.诗词积累、诗词运用成绩的平均数、中位数、众数、最高分分别如下表所示:
平均数 中位数 众数 最高分
诗词积累 82 m 88 97
诗词运用 80 84 86 94
根据以上信息,回答下列问题:
(1)表格中 分;扇形统计图中,C组所对的角心角为 .
(2)小明同学参加了本次诗词大赛,他的诗词积累、诗词运用都是83分,那么他的成绩排名靠前的是 (填“诗词积累”或“诗词运用”),理由是 .
(3)请你选两个角度分析该校学生诗词积累和诗词运用的情况,并提出合理化建议.
23.如图,在平面直角坐标系中,轴,垂足为,轴,垂足为,已知,其中,满足.点是轴正半轴上一动点(不与点重合).
(1)直接写出点的坐标______________.
(2)如图,当点运动到点右侧时,连接、,若,求的面积.
(3)在点运动过程中,直线与直线交于点,以、、、为顶点的四边形的面积记为,的面积记为.试问,是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
24.如图1,矩形的顶点、分别在轴,轴的正半轴,已知点,且,满足.若点为矩形的对角线的中点,过点作的垂线分别交,于点,,交轴于点.
(1)求,的值;
(2)求线段的长度;
(3)如图2,连接,若点P为射线上的点,在平面直角坐标系中,是否存在点Q,使得以为边,点O,D,P,Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标,若不存在,请说明理由.
25.如图,一次函数的图象与反比例函数的图象交于点和点.
(1)求a,b的值和反比例函数解析式;
(2)若点在该反比例函数图象上,且它到x轴距离大于3,请根据图象直接写出m的取值范围;
(3)在y轴上有一点C,且,求点C的坐标.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B C A D D A C D
二、填空题
11.【解】解:去分母得:,
解得:,
由分式方程的解为非负数,得到且,
解得:且.
故答案为:且.
12.【解】解:∵点在轴上,
∴,
∴,
即点P的坐标为;
故答案为:.
13.【解】解:函数的图象经过,即当时,,
∴关于的方程的解为.
故答案为:.
14.【解】解:把和代入解析式得:,,
∴,
故答案为:.
15.【解】解:∵一组数据23,25,20,18,x,12的中位数是20,,
∴,
∴,
则这组数据的众数为20,
故答案为:20.
16.【详解】如图,连接交于点,连接与交于点P,连接,
∵四边形是正方形,
∴,且,
∴,则,此时最短,
∵,,
∴根据勾股定理得,
∴,
即的最小值为:,
故答案为:.
三、解答题
17.【解】解:
,
当时,原式.
18.【解】(1)解:,
去分母得到,
解得:,
检验:当时,,
是分式方程的解;
(2)解:,
去分母得到,,
解得:,
检验:当时,,
∴是增根,分式方程无解.
19.【解】(1)解:设甲公司有人,则乙公司有人,根据题意得
解得:
检验:把代入
故是所列方程的解.
则(人)
答:甲公司有人,乙公司有人;
(2)解:设购买种物资箱,购买种物资箱,且,,都是正整数,
根据题意得
∴,
∴,
当时, 符合题意;
当时, 符合题意;
当时, 不符合题意;
综上所述,购买方案有种:一种物资买箱,物资买箱;另一种是物资买箱,物资买箱.
20.【解】(1)解:∵点,
∴,
解得:;
(2)解:∵点到轴的距离为1,
∴,
解得:或;
(3)解:轴,点,
∴,
∴.
21.【解】(1)解:由题意得,;
(2)解:如图所示,即为所求,则;
(3)解:.
22.【解】(1)解;把这30名学生的诗词积累成绩按照从低到高的顺序排列,中位数为第15名的成绩和第16名成绩的中位数,
∵,
∴诗词积累成绩的中位数为,即;
扇形统计图中,C组所对的角心角为;
(2)解:诗词积累排名靠前,理由是:诗词积累成绩83大于其中位数,说明成绩在中等水平之上;诗词运用成绩小于其中位数,说明成绩在中等水平之下.
(3)解:从平均数看,诗词积累略好于诗词运用;从中位数看诗词运用处于中间的人数的成绩略好于诗词积累;建议学校活动策划侧重于诗词运用的学习.
23.【解】(1)解:∵,
∴,
∴,
∴点的坐标为,
故答案为:;
(2)解:轴,轴,
,,
又,即,
,
,
(3)解:是为定值,如图,当点在点右侧时,
如图,当点在点左侧时,
,
,
,
,
,
,
综上所述,为定值,.
24.【解】(1)解:∵,,
,,
∴,
,;
故答案为:8,6;
(2)解:如图1,连接,
,,
,,
∵四边形是矩形,
∴,
,
又∵,
,
,
,
四边形是菱形,
由(1)得,
∴,
在中,,
,
设,,
在中,,,
,
解得,
,
,
,
.
(3)解:存在点Q,使得以为边,点O,D,P,Q为顶点的四边形是菱形;
分两种情况,①当P在线段上时,取的中点M,连接并延长,过点P作于点N,如图4,
由题可得:,,为的中位线,
∴,,
∴,
当为边,四边形为菱形时,则,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
在和中,
∴,
∴,
∴,
∵,
∴点D向下平移3个单位,向左平移4个单位得到点O,
∴点P向下平移3个单位,向左平移4个单位得到点Q,
∴;
②当P在射线上时,当P在线段延长线上时,取的中点M,连接,过点P作于点N,如图5,
当为边,四边形为菱形时,则,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
在和中,
∴,
∴,
∴,
∵,
∴点D向下平移3个单位,向左平移4个单位得到点O,
∴点P向下平移3个单位,向左平移4个单位得到点Q,
∴;
综上所述,或.
25.【解】(1)解:把代入,得,
解得.
把代入,得,
解得.
把代入,得,
∴反比例函数解析式为;
(2)解:由(1)知,反比例函数的解析式是,
当时,则;当时,,
由图象可知,若点在反比例函数图象上,且它到轴距离大于3,
则的取值范围是或.
(3)解:设与轴交于点,
当时,,
∴点为,
∵,
∴,
∴,
∴,
∵点在轴上,点为.
∴点坐标为或.
21世纪教育网(www.21cnjy.com)
同课章节目录
