华东师大版2024—2025学年八年级下册数学期末调研检测卷(含答案)
文档属性
| 名称 | 华东师大版2024—2025学年八年级下册数学期末调研检测卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 22:29:04 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
华东师大版2024—2025学年八年级下册数学期末调研检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列各式中最简分式是( )
A. B. C. D.
2.“宝剑锋从磨砺出,梅花香自苦寒来.”已知某种梅花的花粉直径约为0.000028m,将0.000028用科学记数法表示为( )
A. B. C. D.
3.在平面直角坐标系中,如果点在y轴上,则点P的坐标为( )
A. B. C. D.
4.关于一次函数的性质及其图象,下列说法正确的是( )
A.的值随值的增大而减小
B.该函数的图象经过第一、三、四象限
C.点一定在函数图象上
D.和是图象上两点,则
5.关于反比例函数,下列说法正确的是( )
A.图象在第一、三象限 B.图象与轴有一个交点
C.当时,随的增大而减小
D.如果点和点均在该函数的图象上,那么
6.在中,的值可以是( )
A. B. C. D.
7.如图,在正方形中,点是上一动点(不与,重合),对角线,相交于点,过点分别作,的垂线,分别交,于点与点,交,于点与点,若正方形的边长是2,则四边形的周长是( )
A.2 B. C.4 D.
8.学校准备准备购买一款校服,对全校同学喜欢的颜色进行了问卷调查,统计结果如表所示(第8题图):学校最终决定购买红色校服,其参考的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
颜色 白色 红色 蓝色
学生人数 100 820 180
9.下列条件中不能确定一个四边形一定是菱形的是( )
A.一组邻边相等的平行四边形 B.对角线互相垂直且相等的四边形
C.对角线平分一组内角的平行四边形 D.对角线垂直且互相平分的四边形
10.如图,在中,对角线,点从点出发,以的速度沿匀速运动,点同时从点出发,以的速度沿匀速运动,当其中一个点到达终点时,另一点也随之停止运动,图是的面积随时间变化的函数图象(图中为线段),当点运动到点处时,的面积为( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.要使分式有意义,则x的取值应满足的条件为 .
12.如图,直线y=﹣x+3与y=mx+n交点的横坐标为1,则关于x,y的二元一次方程组的解为 .
13.一次函数y=(2m﹣3)x+3﹣m的图象经过第一、二、三象限,则m的取值范围是 .
14.如图,点A是反比例函数y在第四象限上的点,AB⊥x轴,若S△AOB=1,则k的值为 .
15.如图,平行四边形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点F、E,若设该平行四边形的面积为16,则图中阴影部分的面积为 .
16.如图,在平面直角坐标系xOy中,点A、B分别在函数y(x>0)和y(x<0)的图象上,AB∥x轴,点C是y轴上一点,线段AC与x轴的正半轴交于点D,若△ABC的面积为18,,则k的值为 .
第II卷
华东师大版2024—2025学年八年级下册数学期末调研检测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解方程:
(1) (2)
18.先化简,再求值:,从,1,3这三个数中选取一个你认为合适的数作为x的值代入求值.
19.某公司计划购买,两种型号的货车搬运货物.每台型货车比每台型货车的载重量少15吨,且载重量60吨货物所需型货车的台数与载重量90吨货物所需型货车的台数相同.
(1)求型和型货车每台的载重量;
(2)该公司共采购21台这两种型号货车来搬运一批货物.若一半的货运量用型货车搬运,则剩余5吨;另一半的货运量用型货车搬运,则最后一台型货车不满也不空.求该公司采购的型和型货车数量.
20.为深入实施科教兴国战略,加快提升广大青少年科技素养,某区市开展了科技素养测评活动,内容包括知识测试和实践创新两部分.所有参赛学生的总成绩均不低于70分;总成绩x(单位:分)分为三个等级:优秀,良好,一般;总成绩80分及以上人数占总人数的百分比是优良率.
阳光中学为了解本校参赛学生科技素养测评情况,整理了这次活动本校及所在区市参赛学生测评总成绩的相关数据,部分信息如下:
测评总成绩统计表
平均数 中位数 优秀率 优良率
阳光中学 84.6 88 a
区市 85.3 87
请根据所给信息,解答下列问题:
(1)求阳光中学参赛人数及a的值,并补全统计图;
(2)请你对比区市测评总成绩,选择两个角度,对阳光中学参赛学生科技素养测评情况做出评价:
(3)每位参赛学生的总成绩是由知识测试和实践创新成绩按一定的百分比折合而成.小红同学知识测试成绩为80分,实践创新成绩为90分,她的总成绩为87分,求知识测试成绩和实践创新成绩各占自百分比.
21.如图,已知四边形是平行四边形,为边的中点,连接并延长,交的延长线于点.
(1)求证:;
(2)若,,,求点到的距离.
22.如图,在平行四边形中,,分别是边,的中点,对角线,连接,.
(1)求证:四边形是菱形;
(2)若的周长为24,,求四边形的面积.
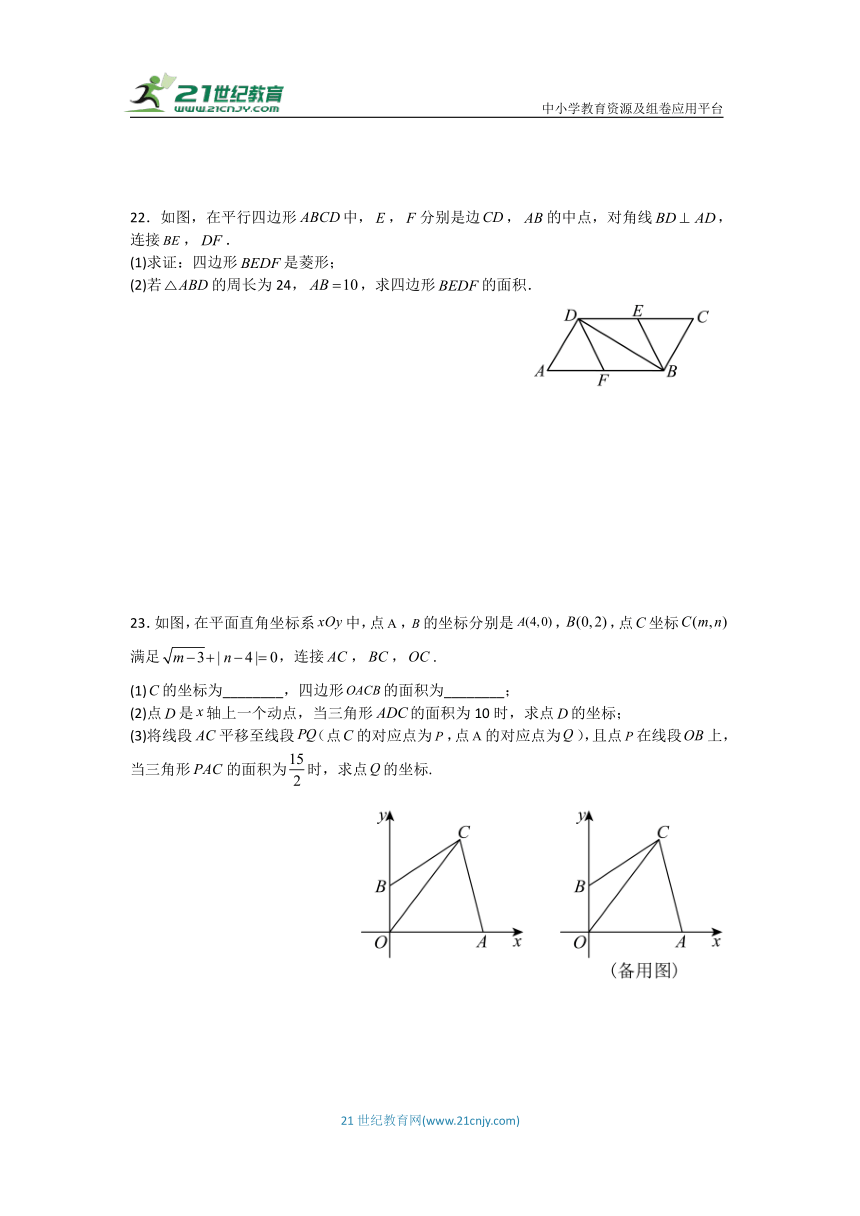
23.如图,在平面直角坐标系中,点,的坐标分别是,,点坐标满足,连接,,.
(1)的坐标为________,四边形的面积为________;
(2)点是轴上一个动点,当三角形的面积为10时,求点的坐标;
(3)将线段平移至线段(点的对应点为,点的对应点为),且点在线段上,当三角形的面积为时,求点的坐标.
24.如图,在平面直角坐标系中,直线与x轴相交于点A,与y轴相交于点B,且与直线相交于点.直线与x轴相交于点C,与y轴相交于点K.
(1)求k的值及点A,B的坐标.
(2)若,求直线的函数表达式.
(3)在(2)的条件下,如图2,过点D作y轴的垂线段,垂足为E,M为y轴上的一点,且,请直接写出直线的函数表达式.
18.如图,一次函数与反比例函数的图象交于,两点.
(1)求反比例函数和一次函数的表达式;
(2)根据图象,直接写出不等式的解集;
(3)连接和,求的面积;
(4)在轴上找一点,使的值最大,求满足条件的点的坐标及的最大值.
(5)点M是轴上一点,是否存在点M,使点M、O、B为顶点的三角形是等腰三角形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B C D D B C B A
二、填空题
11.【解答】解:由题意可得:x+1≠0,
解得x≠﹣1,
故答案为:x≠﹣1.
12.【解答】解:∵直线y=﹣x+3与y=mx+n交点的横坐标为1,
∴纵坐标为y=﹣1+3=2,
∴两直线交点坐标(1,2),
∴x,y的方程组的解为,
故答案为:.
13.【解答】解:∵函数y=(2m﹣3)x+3﹣m的图象经过第一、二、三象限,
∴,
∴1.5<m<3.
故答案为:1.5<m<3.
14.【解答】解:设A(x,y),
则OB=x,AB=﹣y,
∵S△AOB=1,
∴OB×AB=1,
∴﹣xy=2,
∴xy=﹣2,
∵点A在y上,
∴k=xy=﹣2,
故答案为:﹣2.
15.【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,OA=OC,OB=OD,AD∥BC,
∴∠FAO=∠ECO,∠FDO=∠EBO,
在△AOB和△COD中,
,
∴△AOB≌△COD(SSS),
∴S△AOB=S△COD,
在△AFO和△CEO中,
,
∴△AFO≌△CEO(ASA),
同理,△BOE≌△DOF(ASA),
∴S△AFO=S△CEO,S△BOE=S△DOF,
∴阴影部分的面积=S四边形ABEFS平行四边形ABCD16=8.
故答案为:8.
16.【解答】解:如图,设AB与y轴交于点E,过点A、点B分别作AM⊥x轴,BN⊥x轴,垂足分别为M、N,
∵点A、点B分别在两个反比例函数的图象上,
∴反比例函数系数k的几何意义可知,S矩形AEOM=14,S矩形OEBN=|k|=﹣k,
∵△ABC的面积为18,,
∴,
∴S△ADB=12,
∵,
∴S矩形ABNM=2S△ADB=24,
∴S矩形OEBN=24﹣14=10=﹣k,
∴k=﹣10,
故答案为:﹣10.
三、解答题
17.【解】(1)解:
去分母得:,
解得:,
检验:把代入得:,
是原方程的解.
故原分式方程的解为;
(2)解:
去分母得:
去括号得:
即
解得,
检验:把代入得:,
是原方程的解.
故原分式方程的解为.
18.【解】解:
,
要使原分式有意义,则
,
∴且,
∴当时,原式.
19.【解】(1)解:设A型货车每台的载重量为x吨,则B型货车每台的载重量为吨,
由题意得:,
解得:,
经检验,是原方程的解,且符合题意,
∴,
答:A型货车每台的载重量为30吨,则B型货车每台的载重量为45吨;
(2)解:设该公司采购A型货车a台,则采购B型货车台,
由题意得:,
解得:,
∵a为正整数,
∴,
∴,
答:该公司采购A型货车12台,B型货车9台.
20.【解】(1)∵阳光中学的优秀率
∴阳光中学参赛人数为(人)
∴∴阳光中学良好的人数为
∴阳光中学的优良率;
补全统计图如下:
(2)从中位数看,阳光中学的中位数大于区市的中位数
∴阳光中学参赛学生科技素养测评情况更好;
从优良率看,阳光中学的优良率大于区市的优良
∴阳光中学参赛学生科技素养测评情况更好;
(3)设知识测试成绩占的百分比为,则实践创新成绩占的百分比为
根据题意得,
解得,
∴知识测试成绩占的百分比为,实践创新成绩占的百分比为.
21.【解】(1)证明:为边的中点,
.
四边形是平行四边形,
,
.
,
.
(2)解:,
.
四边形是平行四边形,
.
.
,,
,
点到的距离.
22.【解】(1)证明:∵四边形为平行四边形,
∴,,
∵,分别是边,的中点,
∴,,
∴,,
∴四边形为平行四边形,
∵对角线,
∴,
∵是的中点,
∴,
∴四边形为菱形;
(2)解:设,,
∵的周长为24,,
∴,
∴,即,
∵,
∴在中,根据勾股定理得,即.
∵,即,
∴,
∵,
∴,
∴四边形的面积为24.
23.【解】(1)解:∵,上
∴,
解得,
∴点C的坐标为.
∴四边形的面积为.
故答案为:11.
(2)解:设点D的坐标为,
∵三角形的面积为10,
∴,
解得或,
∴点D的坐标为或.
(3)解:如图,
∵点P在线段上,
∴设点P的坐标为,
∴三角形的面积为,
解得,
∴点P的坐标为,
∴线段是向左平移3个单位长度,向下平移3个单位长度得到线段,
∴点A的对应点Q的坐标为.
24.【解】(1)解:把点代入,
得,
解得,
直线的函数表达式为.
当时,
点的坐标为;
当时,
点的坐标为.
(2)解:,
,即,
解得,
点的坐标为.
设直线的函数表达式为,
把点代入,
得
解得
直线的函数表达式为.
(3)解:或.
①当点在点的上方时,
如图,过点作,交的延长线于点,过点作轴的平行线,分别交过点作轴的平行线于点,交的延长线于点.
由,,
故,
故,
即.
,
,
为等腰直角三角形,
.
设点.
,
.
,
,
,即且,
解得,即点,
设直线的函数表达式为,
根据题意,得,
解得,
故直线的函数表达式为.
②当点在点的下方时,设为点,
则直线和直线关于直线即对称,
所以直线的函数表达式为.
综上所述,直线的函数表达式为或.
25.【解】(1)解:将点代入,得:,
∴这个反比例函数的解析式为,
在中,当时,,
∴,
将、代入,得:,
解得,
∴这个一次函数的表达式为;
(2)解:由函数图象可得,不等式的解集为或;
(3)解;如图,设直线与轴交于点C,
令,则,解得:
∴,
∴
;
(4)解:如图2,作点关于轴的对称点,连接并延长交轴于点,
则点即为所求.此时.
设直线的关系式为.
∴,
解得:,
∴直线的关系式为,
令,则,
∴满足条件的点的坐标,
此时,的最大值为;
(5)解:,
.
设点M的坐标为,则,,
当时,则,解得,
∴点M的坐标为或;
当时,则,解得或(舍去),
∴点M的坐标为;
当时,则,解得,
∴点M的坐标为;
综上所述,点M的坐标为或或或.
21世纪教育网(www.21cnjy.com)
华东师大版2024—2025学年八年级下册数学期末调研检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列各式中最简分式是( )
A. B. C. D.
2.“宝剑锋从磨砺出,梅花香自苦寒来.”已知某种梅花的花粉直径约为0.000028m,将0.000028用科学记数法表示为( )
A. B. C. D.
3.在平面直角坐标系中,如果点在y轴上,则点P的坐标为( )
A. B. C. D.
4.关于一次函数的性质及其图象,下列说法正确的是( )
A.的值随值的增大而减小
B.该函数的图象经过第一、三、四象限
C.点一定在函数图象上
D.和是图象上两点,则
5.关于反比例函数,下列说法正确的是( )
A.图象在第一、三象限 B.图象与轴有一个交点
C.当时,随的增大而减小
D.如果点和点均在该函数的图象上,那么
6.在中,的值可以是( )
A. B. C. D.
7.如图,在正方形中,点是上一动点(不与,重合),对角线,相交于点,过点分别作,的垂线,分别交,于点与点,交,于点与点,若正方形的边长是2,则四边形的周长是( )
A.2 B. C.4 D.
8.学校准备准备购买一款校服,对全校同学喜欢的颜色进行了问卷调查,统计结果如表所示(第8题图):学校最终决定购买红色校服,其参考的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
颜色 白色 红色 蓝色
学生人数 100 820 180
9.下列条件中不能确定一个四边形一定是菱形的是( )
A.一组邻边相等的平行四边形 B.对角线互相垂直且相等的四边形
C.对角线平分一组内角的平行四边形 D.对角线垂直且互相平分的四边形
10.如图,在中,对角线,点从点出发,以的速度沿匀速运动,点同时从点出发,以的速度沿匀速运动,当其中一个点到达终点时,另一点也随之停止运动,图是的面积随时间变化的函数图象(图中为线段),当点运动到点处时,的面积为( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.要使分式有意义,则x的取值应满足的条件为 .
12.如图,直线y=﹣x+3与y=mx+n交点的横坐标为1,则关于x,y的二元一次方程组的解为 .
13.一次函数y=(2m﹣3)x+3﹣m的图象经过第一、二、三象限,则m的取值范围是 .
14.如图,点A是反比例函数y在第四象限上的点,AB⊥x轴,若S△AOB=1,则k的值为 .
15.如图,平行四边形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点F、E,若设该平行四边形的面积为16,则图中阴影部分的面积为 .
16.如图,在平面直角坐标系xOy中,点A、B分别在函数y(x>0)和y(x<0)的图象上,AB∥x轴,点C是y轴上一点,线段AC与x轴的正半轴交于点D,若△ABC的面积为18,,则k的值为 .
第II卷
华东师大版2024—2025学年八年级下册数学期末调研检测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解方程:
(1) (2)
18.先化简,再求值:,从,1,3这三个数中选取一个你认为合适的数作为x的值代入求值.
19.某公司计划购买,两种型号的货车搬运货物.每台型货车比每台型货车的载重量少15吨,且载重量60吨货物所需型货车的台数与载重量90吨货物所需型货车的台数相同.
(1)求型和型货车每台的载重量;
(2)该公司共采购21台这两种型号货车来搬运一批货物.若一半的货运量用型货车搬运,则剩余5吨;另一半的货运量用型货车搬运,则最后一台型货车不满也不空.求该公司采购的型和型货车数量.
20.为深入实施科教兴国战略,加快提升广大青少年科技素养,某区市开展了科技素养测评活动,内容包括知识测试和实践创新两部分.所有参赛学生的总成绩均不低于70分;总成绩x(单位:分)分为三个等级:优秀,良好,一般;总成绩80分及以上人数占总人数的百分比是优良率.
阳光中学为了解本校参赛学生科技素养测评情况,整理了这次活动本校及所在区市参赛学生测评总成绩的相关数据,部分信息如下:
测评总成绩统计表
平均数 中位数 优秀率 优良率
阳光中学 84.6 88 a
区市 85.3 87
请根据所给信息,解答下列问题:
(1)求阳光中学参赛人数及a的值,并补全统计图;
(2)请你对比区市测评总成绩,选择两个角度,对阳光中学参赛学生科技素养测评情况做出评价:
(3)每位参赛学生的总成绩是由知识测试和实践创新成绩按一定的百分比折合而成.小红同学知识测试成绩为80分,实践创新成绩为90分,她的总成绩为87分,求知识测试成绩和实践创新成绩各占自百分比.
21.如图,已知四边形是平行四边形,为边的中点,连接并延长,交的延长线于点.
(1)求证:;
(2)若,,,求点到的距离.
22.如图,在平行四边形中,,分别是边,的中点,对角线,连接,.
(1)求证:四边形是菱形;
(2)若的周长为24,,求四边形的面积.
23.如图,在平面直角坐标系中,点,的坐标分别是,,点坐标满足,连接,,.
(1)的坐标为________,四边形的面积为________;
(2)点是轴上一个动点,当三角形的面积为10时,求点的坐标;
(3)将线段平移至线段(点的对应点为,点的对应点为),且点在线段上,当三角形的面积为时,求点的坐标.
24.如图,在平面直角坐标系中,直线与x轴相交于点A,与y轴相交于点B,且与直线相交于点.直线与x轴相交于点C,与y轴相交于点K.
(1)求k的值及点A,B的坐标.
(2)若,求直线的函数表达式.
(3)在(2)的条件下,如图2,过点D作y轴的垂线段,垂足为E,M为y轴上的一点,且,请直接写出直线的函数表达式.
18.如图,一次函数与反比例函数的图象交于,两点.
(1)求反比例函数和一次函数的表达式;
(2)根据图象,直接写出不等式的解集;
(3)连接和,求的面积;
(4)在轴上找一点,使的值最大,求满足条件的点的坐标及的最大值.
(5)点M是轴上一点,是否存在点M,使点M、O、B为顶点的三角形是等腰三角形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B C D D B C B A
二、填空题
11.【解答】解:由题意可得:x+1≠0,
解得x≠﹣1,
故答案为:x≠﹣1.
12.【解答】解:∵直线y=﹣x+3与y=mx+n交点的横坐标为1,
∴纵坐标为y=﹣1+3=2,
∴两直线交点坐标(1,2),
∴x,y的方程组的解为,
故答案为:.
13.【解答】解:∵函数y=(2m﹣3)x+3﹣m的图象经过第一、二、三象限,
∴,
∴1.5<m<3.
故答案为:1.5<m<3.
14.【解答】解:设A(x,y),
则OB=x,AB=﹣y,
∵S△AOB=1,
∴OB×AB=1,
∴﹣xy=2,
∴xy=﹣2,
∵点A在y上,
∴k=xy=﹣2,
故答案为:﹣2.
15.【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,OA=OC,OB=OD,AD∥BC,
∴∠FAO=∠ECO,∠FDO=∠EBO,
在△AOB和△COD中,
,
∴△AOB≌△COD(SSS),
∴S△AOB=S△COD,
在△AFO和△CEO中,
,
∴△AFO≌△CEO(ASA),
同理,△BOE≌△DOF(ASA),
∴S△AFO=S△CEO,S△BOE=S△DOF,
∴阴影部分的面积=S四边形ABEFS平行四边形ABCD16=8.
故答案为:8.
16.【解答】解:如图,设AB与y轴交于点E,过点A、点B分别作AM⊥x轴,BN⊥x轴,垂足分别为M、N,
∵点A、点B分别在两个反比例函数的图象上,
∴反比例函数系数k的几何意义可知,S矩形AEOM=14,S矩形OEBN=|k|=﹣k,
∵△ABC的面积为18,,
∴,
∴S△ADB=12,
∵,
∴S矩形ABNM=2S△ADB=24,
∴S矩形OEBN=24﹣14=10=﹣k,
∴k=﹣10,
故答案为:﹣10.
三、解答题
17.【解】(1)解:
去分母得:,
解得:,
检验:把代入得:,
是原方程的解.
故原分式方程的解为;
(2)解:
去分母得:
去括号得:
即
解得,
检验:把代入得:,
是原方程的解.
故原分式方程的解为.
18.【解】解:
,
要使原分式有意义,则
,
∴且,
∴当时,原式.
19.【解】(1)解:设A型货车每台的载重量为x吨,则B型货车每台的载重量为吨,
由题意得:,
解得:,
经检验,是原方程的解,且符合题意,
∴,
答:A型货车每台的载重量为30吨,则B型货车每台的载重量为45吨;
(2)解:设该公司采购A型货车a台,则采购B型货车台,
由题意得:,
解得:,
∵a为正整数,
∴,
∴,
答:该公司采购A型货车12台,B型货车9台.
20.【解】(1)∵阳光中学的优秀率
∴阳光中学参赛人数为(人)
∴∴阳光中学良好的人数为
∴阳光中学的优良率;
补全统计图如下:
(2)从中位数看,阳光中学的中位数大于区市的中位数
∴阳光中学参赛学生科技素养测评情况更好;
从优良率看,阳光中学的优良率大于区市的优良
∴阳光中学参赛学生科技素养测评情况更好;
(3)设知识测试成绩占的百分比为,则实践创新成绩占的百分比为
根据题意得,
解得,
∴知识测试成绩占的百分比为,实践创新成绩占的百分比为.
21.【解】(1)证明:为边的中点,
.
四边形是平行四边形,
,
.
,
.
(2)解:,
.
四边形是平行四边形,
.
.
,,
,
点到的距离.
22.【解】(1)证明:∵四边形为平行四边形,
∴,,
∵,分别是边,的中点,
∴,,
∴,,
∴四边形为平行四边形,
∵对角线,
∴,
∵是的中点,
∴,
∴四边形为菱形;
(2)解:设,,
∵的周长为24,,
∴,
∴,即,
∵,
∴在中,根据勾股定理得,即.
∵,即,
∴,
∵,
∴,
∴四边形的面积为24.
23.【解】(1)解:∵,上
∴,
解得,
∴点C的坐标为.
∴四边形的面积为.
故答案为:11.
(2)解:设点D的坐标为,
∵三角形的面积为10,
∴,
解得或,
∴点D的坐标为或.
(3)解:如图,
∵点P在线段上,
∴设点P的坐标为,
∴三角形的面积为,
解得,
∴点P的坐标为,
∴线段是向左平移3个单位长度,向下平移3个单位长度得到线段,
∴点A的对应点Q的坐标为.
24.【解】(1)解:把点代入,
得,
解得,
直线的函数表达式为.
当时,
点的坐标为;
当时,
点的坐标为.
(2)解:,
,即,
解得,
点的坐标为.
设直线的函数表达式为,
把点代入,
得
解得
直线的函数表达式为.
(3)解:或.
①当点在点的上方时,
如图,过点作,交的延长线于点,过点作轴的平行线,分别交过点作轴的平行线于点,交的延长线于点.
由,,
故,
故,
即.
,
,
为等腰直角三角形,
.
设点.
,
.
,
,
,即且,
解得,即点,
设直线的函数表达式为,
根据题意,得,
解得,
故直线的函数表达式为.
②当点在点的下方时,设为点,
则直线和直线关于直线即对称,
所以直线的函数表达式为.
综上所述,直线的函数表达式为或.
25.【解】(1)解:将点代入,得:,
∴这个反比例函数的解析式为,
在中,当时,,
∴,
将、代入,得:,
解得,
∴这个一次函数的表达式为;
(2)解:由函数图象可得,不等式的解集为或;
(3)解;如图,设直线与轴交于点C,
令,则,解得:
∴,
∴
;
(4)解:如图2,作点关于轴的对称点,连接并延长交轴于点,
则点即为所求.此时.
设直线的关系式为.
∴,
解得:,
∴直线的关系式为,
令,则,
∴满足条件的点的坐标,
此时,的最大值为;
(5)解:,
.
设点M的坐标为,则,,
当时,则,解得,
∴点M的坐标为或;
当时,则,解得或(舍去),
∴点M的坐标为;
当时,则,解得,
∴点M的坐标为;
综上所述,点M的坐标为或或或.
21世纪教育网(www.21cnjy.com)
同课章节目录
