华东师大版2024—2025学年八年级下册数学期末复习提分强化训练(含答案)
文档属性
| 名称 | 华东师大版2024—2025学年八年级下册数学期末复习提分强化训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 883.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-24 22:30:02 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
华东师大版2024—2025学年八年级下册数学期末复习提分强化训练
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.红细胞的平均直径约是,将数据0.000008用科学记数法表示为( )
A. B. C. D.
2.在同一平面直角坐标系中,直线与的交点坐标为( )
A. B. C. D.
众数 中位数 平均数 方差
3.在“百善孝为先”朗诵比赛中,晓晴根据七位评委所给的某位参赛选手的分数制作了如下表格:
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是( )
A.平均数 B.中位数 C.众数 D.方差
4.根据所标数据,不能判断下列四边形是平行四边形的是( )
A.B.C.D.
5.下列条件不能判定平行四边形是正方形的是( )
A.且 B.且
C.且 D.且
6.若将分式中的m和n都变为原来的2倍,则分式的值( ).
A.变为原来的2倍 B.变为原来的4倍
C.变为原来的 D.不变
7.已知平面直角坐标系中有点,过点作直线轴,如果,则点的坐标为( )
A.或 B.或 C.或 D.
8.已知某函数图象经过,,三个点,则该函数图象可能为( )
A.B.C.D.
9.如图1,在矩形中,对角线,相交于点,一动点从点出发,沿的边逆时针匀速运动一周后回到点,线段的长与点运动的路程之间的关系如图2,则矩形的面积是( )
A.1 B.2 C. D.
10.如图,将矩形沿折叠,使点D落在点B处,点C落在点处,P为折痕上的任意一点,过点P作,,垂足分别为G,H,若,,则的值为( )
A.6 B.8
C.10 D.16
二、填空题(6小题,每题3分,共18分)
11.要使分式有意义,则x的取值应满足的条件为 .
12.如图,直线y=﹣x+3与y=mx+n交点的横坐标为1,则关于x,y的二元一次方程组的解为 .
13.一次函数y=(2m﹣3)x+3﹣m的图象经过第一、二、三象限,则m的取值范围是 .
14.如图,点A是反比例函数y在第四象限上的点,AB⊥x轴,若S△AOB=1,则k的值为 .
15.如图,平行四边形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点F、E,若设该平行四边形的面积为16,则图中阴影部分的面积为 .
16.如图,在矩形ABCD中,E为对角线AC上与A,C不重合的一个动点,过点E作EF⊥AB与点F,EG⊥BC于点G,连接DE,FG,若AB=3,BC=4,则FG的最小值 .
第II卷
华东师大版2024—2025学年八年级下册数学期末复习提分强化训练
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解方程:
(1); (2).
18.先化简,再从,0,3这三个数中取一个合适的数作为的值代入求值.
19.某校八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(单位:分):
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是_______分,乙队成绩的众数是________分.
(2)计算乙队的平均成绩和方差.
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是_______队.
20.某中学为落实教育部办公厅发布的《关于进一步加强中小学生体质管理工作的通知》文件要求,决定增设篮球、足球两门选修课程,需要购进一批篮球和足球.已知一个篮球的价格比一个足球的价格多30元,花1800元购买的篮球个数和花1350 元购买的足球个数相同.
(1)一个篮球和一个足球的价格分别是多少元?
(2)学校计划采购篮球、足球共30个,且总费用不超过3200元,那么需采购篮球最多多少个?
21.如图,在中,是直线上两点,且.
(1)证明:;
(2)证明:.
22.如图所示,正方形的边长为4,点为边上的一动点,设.
(1)的面积与之间的函数关系为_____;
(2)当时,求的值;
(3)当的面积为5时,求的长.
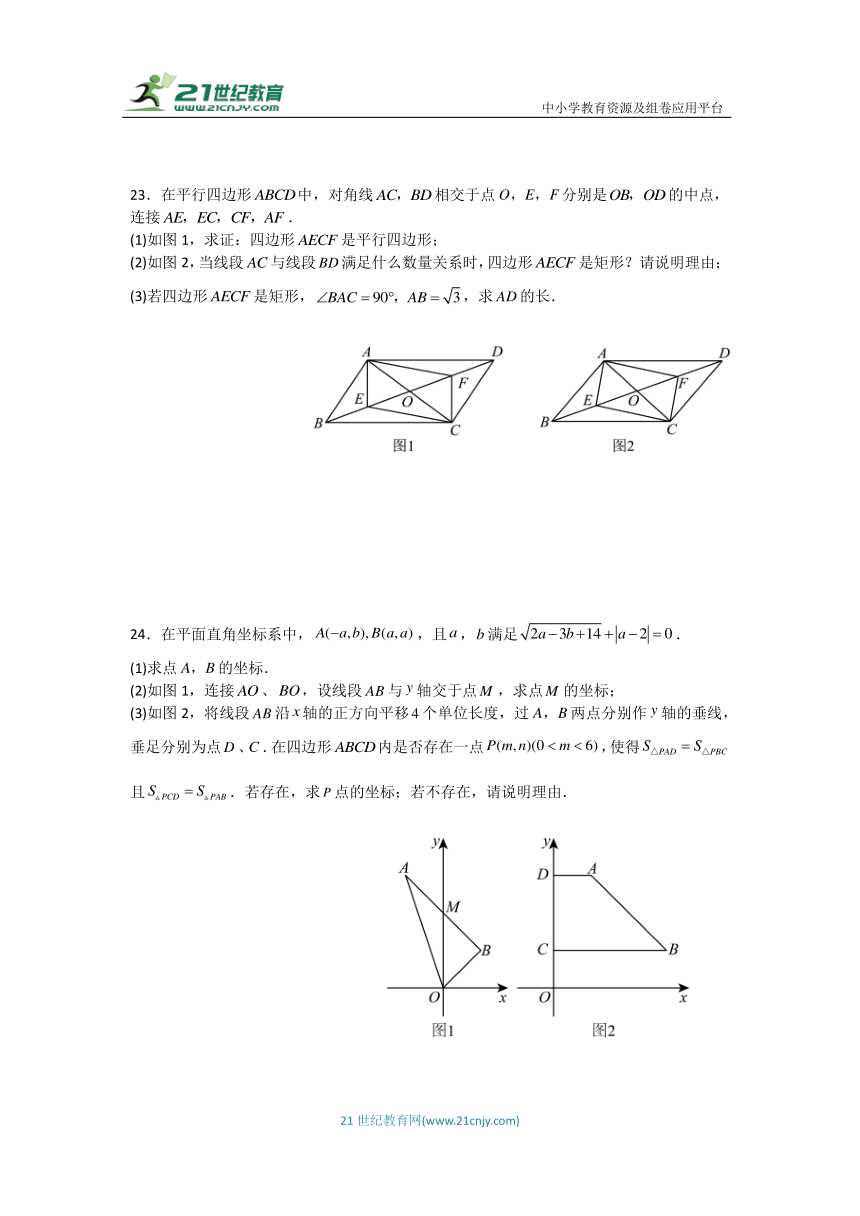
23.在平行四边形中,对角线相交于点O,E,F分别是的中点,连接.
(1)如图1,求证:四边形是平行四边形;
(2)如图2,当线段与线段满足什么数量关系时,四边形是矩形?请说明理由;
(3)若四边形是矩形,,求的长.
24.在平面直角坐标系中,,且,满足.
(1)求点A,B的坐标.
(2)如图1,连接、,设线段与轴交于点,求点的坐标;
(3)如图2,将线段沿轴的正方向平移个单位长度,过A,B两点分别作轴的垂线,垂足分别为点、.在四边形内是否存在一点,使得且.若存在,求点的坐标;若不存在,请说明理由.
25.已知,一次函数的图象交反比例函数图象于点A,B,交x轴于点C,点B为.
(1)求反比例函数的解析式;
(2)如图1,点M为反比例函数在第一象限图象上的一点,过点M作x轴垂线,交一次函数图象于点N,连接,若是以为底边的等腰三角形,求的面积;
(3)如图2,一次函数交y轴于点F,将一次函数绕C顺时针旋转交反比例函数图象于点D,E,求点E的坐标.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B C B A A D C B
二、填空题
11.【解答】解:由题意可得:x+1≠0,
解得x≠﹣1,
故答案为:x≠﹣1.
12.【解答】解:∵直线y=﹣x+3与y=mx+n交点的横坐标为1,
∴纵坐标为y=﹣1+3=2,
∴两直线交点坐标(1,2),
∴x,y的方程组的解为,
故答案为:.
13.【解答】解:∵函数y=(2m﹣3)x+3﹣m的图象经过第一、二、三象限,
∴,
∴1.5<m<3.
故答案为:1.5<m<3.
14.【解答】解:设A(x,y),
则OB=x,AB=﹣y,
∵S△AOB=1,
∴OB×AB=1,
∴﹣xy=2,
∴xy=﹣2,
∵点A在y上,
∴k=xy=﹣2,
故答案为:﹣2.
15.【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,OA=OC,OB=OD,AD∥BC,
∴∠FAO=∠ECO,∠FDO=∠EBO,
在△AOB和△COD中,
,
∴△AOB≌△COD(SSS),
∴S△AOB=S△COD,
在△AFO和△CEO中,
,
∴△AFO≌△CEO(ASA),
同理,△BOE≌△DOF(ASA),
∴S△AFO=S△CEO,S△BOE=S△DOF,
∴阴影部分的面积=S四边形ABEFS平行四边形ABCD16=8.
故答案为:8.
16.【解答】解:如图,连接BE,
∵四边形ABCD是矩形,
∴∠B=90°,
∴AC5,
∵EF⊥AB,EG⊥BC,
∴∠EFB=∠EGB=90°.
∵∠ABC=90°,
∴四边形EFBG为矩形,
∴FG=BE,
当BE⊥AC时,BE最小,
此时,△ABC的面积AC BEAC BC,
∴5BE=3×4,
∴BE,
∴FG的最小值是,
故答案为:.
三、解答题
17.【解】(1)解:,
去分母得:,
去括号得:,
移项得:,
合并同类项得:,
系数化为得:,
检验:当时,,,
是原分式方程的根;
(2)解:,
去分母得:,
去括号得:,
移项得:,
系数化为得:,
检验:当时,,
∴是原分式方程的增根,
原分式方程无解.
18.【解】解:
,
∵,
∴,
∴当时,原式.
19.【解】(1)解:将甲队数据排序后,位于中间的2个数据是9和10,
∴中位数为(分);
乙队数据中出现次数最多的是10,故众数为10分;
故答案为:9.5;10
(2)(分);
;
(3)∵,甲队成绩的方差是1.4,;
故成绩较为整齐的是乙队;
故答案为:乙.
20.【解】(1)解:设篮球的单价为元,足球的单价为元,
根据题意,得,
解得,
经检验,符合题意
∴足球的单价为元
答:篮球的单价为120元,足球的单价为90元;
(2)设采购篮球个,则采购足球个,
根据题意,得,解得,
∵为整数,
∴最大取16.
答:最多采购篮球16个.
21.【解】(1)证明:四边形是平行四边形,
,
,
∴
.
,
,
(2)解:,
,
.
22.【解】(1)解:∵正方形的边长为4,
∴,
∵,
∴的面积;
(2)解:当时,;
(3)解:由题意可知
则,
解得,
即,
.
23.【解】(1)证明:∵四边形是平行四边形,
∴,
∵E,F分别是的中点,
∴,
∴,
∴四边形是平行四边形;
(2)解:当时,四边形是矩形,证明如下:
∵四边形是平行四边形,
∴,
∵E,F分别是的中点,
∴,
∴,
∵,即,
∴
∵四边形是平行四边形;
∴四边形是矩形;
(3)解:∵四边形是矩形,
∴由(2)可知,
∵,
∴,
在中,由勾股定理得,
∴,
∴或(舍去),
∴,
∴,
∴由平行四边形的性质可得.
24.【解】(1)解:∵.
∴,,
∴,
解得,
∴;
(2)解:设的解析式为,代入得:
,解得:,
∴的解析式为,
令,则,
∴;
(3)解:假设存在点,则,,
∵,
∴,
解得不合题意,舍去或,
当时,如图所示:
,,,
,
∴,,
解得,
∴,
∴存在点,点坐标为.
25.【解】(1)解:对于一次函数,
当时,可有,
∴点,
将点的坐标代入反比例函数表达式,
可得 ,
即反比例函数表达式为;
(2)设点的坐标为,则点,
若是以为底边的等腰三角形,则点在的垂直平分线上,
则有 ,
解得(舍去)或,
∴,,
则;
(3)设一次函数的图像与轴交于点,过点作于,过作轴于,过点作,交延长线于点,如下图,
对于一次函数,
令,可有,即的坐标为,
令,可有,解得,即的坐标为,
由题意可知,一次函数的图像绕点顺时针旋转交反比例函数图像于点,,
∴,
∵,
∴,
∴,
∵,,轴,
∴,
∴,
又∵,
∴,
∴,,
设,
∵ ,,
∴,,,,
∴可有,解得,
∴,
设直线的解析式为,
将点,代入,
可得,解得,
∴直线的解析式为,
联立直线的解析式与反比例函数解析式,
可得,可得,
整理可得,
解得,(不合题意,舍去),
∴,
∴.
21世纪教育网(www.21cnjy.com)
华东师大版2024—2025学年八年级下册数学期末复习提分强化训练
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.红细胞的平均直径约是,将数据0.000008用科学记数法表示为( )
A. B. C. D.
2.在同一平面直角坐标系中,直线与的交点坐标为( )
A. B. C. D.
众数 中位数 平均数 方差
3.在“百善孝为先”朗诵比赛中,晓晴根据七位评委所给的某位参赛选手的分数制作了如下表格:
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是( )
A.平均数 B.中位数 C.众数 D.方差
4.根据所标数据,不能判断下列四边形是平行四边形的是( )
A.B.C.D.
5.下列条件不能判定平行四边形是正方形的是( )
A.且 B.且
C.且 D.且
6.若将分式中的m和n都变为原来的2倍,则分式的值( ).
A.变为原来的2倍 B.变为原来的4倍
C.变为原来的 D.不变
7.已知平面直角坐标系中有点,过点作直线轴,如果,则点的坐标为( )
A.或 B.或 C.或 D.
8.已知某函数图象经过,,三个点,则该函数图象可能为( )
A.B.C.D.
9.如图1,在矩形中,对角线,相交于点,一动点从点出发,沿的边逆时针匀速运动一周后回到点,线段的长与点运动的路程之间的关系如图2,则矩形的面积是( )
A.1 B.2 C. D.
10.如图,将矩形沿折叠,使点D落在点B处,点C落在点处,P为折痕上的任意一点,过点P作,,垂足分别为G,H,若,,则的值为( )
A.6 B.8
C.10 D.16
二、填空题(6小题,每题3分,共18分)
11.要使分式有意义,则x的取值应满足的条件为 .
12.如图,直线y=﹣x+3与y=mx+n交点的横坐标为1,则关于x,y的二元一次方程组的解为 .
13.一次函数y=(2m﹣3)x+3﹣m的图象经过第一、二、三象限,则m的取值范围是 .
14.如图,点A是反比例函数y在第四象限上的点,AB⊥x轴,若S△AOB=1,则k的值为 .
15.如图,平行四边形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点F、E,若设该平行四边形的面积为16,则图中阴影部分的面积为 .
16.如图,在矩形ABCD中,E为对角线AC上与A,C不重合的一个动点,过点E作EF⊥AB与点F,EG⊥BC于点G,连接DE,FG,若AB=3,BC=4,则FG的最小值 .
第II卷
华东师大版2024—2025学年八年级下册数学期末复习提分强化训练
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解方程:
(1); (2).
18.先化简,再从,0,3这三个数中取一个合适的数作为的值代入求值.
19.某校八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(单位:分):
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是_______分,乙队成绩的众数是________分.
(2)计算乙队的平均成绩和方差.
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是_______队.
20.某中学为落实教育部办公厅发布的《关于进一步加强中小学生体质管理工作的通知》文件要求,决定增设篮球、足球两门选修课程,需要购进一批篮球和足球.已知一个篮球的价格比一个足球的价格多30元,花1800元购买的篮球个数和花1350 元购买的足球个数相同.
(1)一个篮球和一个足球的价格分别是多少元?
(2)学校计划采购篮球、足球共30个,且总费用不超过3200元,那么需采购篮球最多多少个?
21.如图,在中,是直线上两点,且.
(1)证明:;
(2)证明:.
22.如图所示,正方形的边长为4,点为边上的一动点,设.
(1)的面积与之间的函数关系为_____;
(2)当时,求的值;
(3)当的面积为5时,求的长.
23.在平行四边形中,对角线相交于点O,E,F分别是的中点,连接.
(1)如图1,求证:四边形是平行四边形;
(2)如图2,当线段与线段满足什么数量关系时,四边形是矩形?请说明理由;
(3)若四边形是矩形,,求的长.
24.在平面直角坐标系中,,且,满足.
(1)求点A,B的坐标.
(2)如图1,连接、,设线段与轴交于点,求点的坐标;
(3)如图2,将线段沿轴的正方向平移个单位长度,过A,B两点分别作轴的垂线,垂足分别为点、.在四边形内是否存在一点,使得且.若存在,求点的坐标;若不存在,请说明理由.
25.已知,一次函数的图象交反比例函数图象于点A,B,交x轴于点C,点B为.
(1)求反比例函数的解析式;
(2)如图1,点M为反比例函数在第一象限图象上的一点,过点M作x轴垂线,交一次函数图象于点N,连接,若是以为底边的等腰三角形,求的面积;
(3)如图2,一次函数交y轴于点F,将一次函数绕C顺时针旋转交反比例函数图象于点D,E,求点E的坐标.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B C B A A D C B
二、填空题
11.【解答】解:由题意可得:x+1≠0,
解得x≠﹣1,
故答案为:x≠﹣1.
12.【解答】解:∵直线y=﹣x+3与y=mx+n交点的横坐标为1,
∴纵坐标为y=﹣1+3=2,
∴两直线交点坐标(1,2),
∴x,y的方程组的解为,
故答案为:.
13.【解答】解:∵函数y=(2m﹣3)x+3﹣m的图象经过第一、二、三象限,
∴,
∴1.5<m<3.
故答案为:1.5<m<3.
14.【解答】解:设A(x,y),
则OB=x,AB=﹣y,
∵S△AOB=1,
∴OB×AB=1,
∴﹣xy=2,
∴xy=﹣2,
∵点A在y上,
∴k=xy=﹣2,
故答案为:﹣2.
15.【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,OA=OC,OB=OD,AD∥BC,
∴∠FAO=∠ECO,∠FDO=∠EBO,
在△AOB和△COD中,
,
∴△AOB≌△COD(SSS),
∴S△AOB=S△COD,
在△AFO和△CEO中,
,
∴△AFO≌△CEO(ASA),
同理,△BOE≌△DOF(ASA),
∴S△AFO=S△CEO,S△BOE=S△DOF,
∴阴影部分的面积=S四边形ABEFS平行四边形ABCD16=8.
故答案为:8.
16.【解答】解:如图,连接BE,
∵四边形ABCD是矩形,
∴∠B=90°,
∴AC5,
∵EF⊥AB,EG⊥BC,
∴∠EFB=∠EGB=90°.
∵∠ABC=90°,
∴四边形EFBG为矩形,
∴FG=BE,
当BE⊥AC时,BE最小,
此时,△ABC的面积AC BEAC BC,
∴5BE=3×4,
∴BE,
∴FG的最小值是,
故答案为:.
三、解答题
17.【解】(1)解:,
去分母得:,
去括号得:,
移项得:,
合并同类项得:,
系数化为得:,
检验:当时,,,
是原分式方程的根;
(2)解:,
去分母得:,
去括号得:,
移项得:,
系数化为得:,
检验:当时,,
∴是原分式方程的增根,
原分式方程无解.
18.【解】解:
,
∵,
∴,
∴当时,原式.
19.【解】(1)解:将甲队数据排序后,位于中间的2个数据是9和10,
∴中位数为(分);
乙队数据中出现次数最多的是10,故众数为10分;
故答案为:9.5;10
(2)(分);
;
(3)∵,甲队成绩的方差是1.4,;
故成绩较为整齐的是乙队;
故答案为:乙.
20.【解】(1)解:设篮球的单价为元,足球的单价为元,
根据题意,得,
解得,
经检验,符合题意
∴足球的单价为元
答:篮球的单价为120元,足球的单价为90元;
(2)设采购篮球个,则采购足球个,
根据题意,得,解得,
∵为整数,
∴最大取16.
答:最多采购篮球16个.
21.【解】(1)证明:四边形是平行四边形,
,
,
∴
.
,
,
(2)解:,
,
.
22.【解】(1)解:∵正方形的边长为4,
∴,
∵,
∴的面积;
(2)解:当时,;
(3)解:由题意可知
则,
解得,
即,
.
23.【解】(1)证明:∵四边形是平行四边形,
∴,
∵E,F分别是的中点,
∴,
∴,
∴四边形是平行四边形;
(2)解:当时,四边形是矩形,证明如下:
∵四边形是平行四边形,
∴,
∵E,F分别是的中点,
∴,
∴,
∵,即,
∴
∵四边形是平行四边形;
∴四边形是矩形;
(3)解:∵四边形是矩形,
∴由(2)可知,
∵,
∴,
在中,由勾股定理得,
∴,
∴或(舍去),
∴,
∴,
∴由平行四边形的性质可得.
24.【解】(1)解:∵.
∴,,
∴,
解得,
∴;
(2)解:设的解析式为,代入得:
,解得:,
∴的解析式为,
令,则,
∴;
(3)解:假设存在点,则,,
∵,
∴,
解得不合题意,舍去或,
当时,如图所示:
,,,
,
∴,,
解得,
∴,
∴存在点,点坐标为.
25.【解】(1)解:对于一次函数,
当时,可有,
∴点,
将点的坐标代入反比例函数表达式,
可得 ,
即反比例函数表达式为;
(2)设点的坐标为,则点,
若是以为底边的等腰三角形,则点在的垂直平分线上,
则有 ,
解得(舍去)或,
∴,,
则;
(3)设一次函数的图像与轴交于点,过点作于,过作轴于,过点作,交延长线于点,如下图,
对于一次函数,
令,可有,即的坐标为,
令,可有,解得,即的坐标为,
由题意可知,一次函数的图像绕点顺时针旋转交反比例函数图像于点,,
∴,
∵,
∴,
∴,
∵,,轴,
∴,
∴,
又∵,
∴,
∴,,
设,
∵ ,,
∴,,,,
∴可有,解得,
∴,
设直线的解析式为,
将点,代入,
可得,解得,
∴直线的解析式为,
联立直线的解析式与反比例函数解析式,
可得,可得,
整理可得,
解得,(不合题意,舍去),
∴,
∴.
21世纪教育网(www.21cnjy.com)
同课章节目录
