数学:第二章二次函数复习教案(鲁教版九年级上)
文档属性
| 名称 | 数学:第二章二次函数复习教案(鲁教版九年级上) | 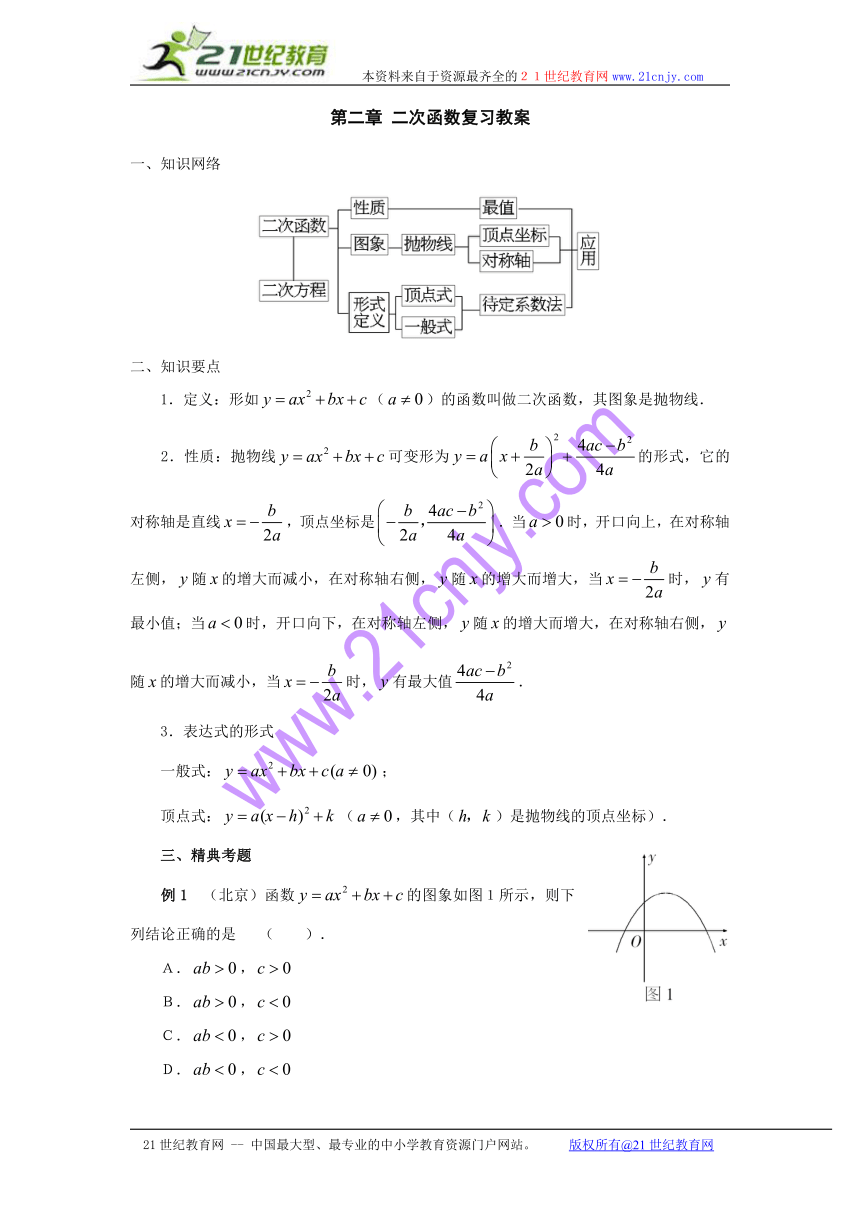 | |
| 格式 | rar | ||
| 文件大小 | 70.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-30 14:32:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第二章 二次函数复习教案
一、知识网络
二、知识要点
1.定义:形如()的函数叫做二次函数,其图象是抛物线.
2.性质:抛物线可变形为的形式,它的对称轴是直线,顶点坐标是.当时,开口向上,在对称轴左侧,随的增大而减小,在对称轴右侧,随的增大而增大,当时,有最小值;当时,开口向下,在对称轴左侧,随的增大而增大,在对称轴右侧,随的增大而减小,当时,有最大值.
3.表达式的形式
一般式:;
顶点式:(,其中()是抛物线的顶点坐标).
三、精典考题
例1 (北京)函数的图象如图1所示,则下列结论正确的是 ( ).
A.,
B.,
C.,
D.,
析解:由抛物线开口向下知,由抛物线与轴的交点在轴的正半轴上知,又由抛物线的对称轴及知,所以,.故选C.
点评:抛物线的系数与图象间的关系如下表:
几何意义 时,开口向下;时,开口向上;越大,开口越小. 同号时,对称轴在y轴左侧;a,b异号时,对称轴在y轴右侧. 时,抛物线交于y轴的正半轴;时,抛物线交于y轴的负半轴.
例2 (台洲、温州市)将抛物线向左平移1个单位,再向上平移3个单位得到的抛物线的表达式是( ).
A. B.
C. D.
析解:将抛物线向左平移1个单位得到的抛物线表达式是,再向上平移3个单位得到的抛物线表达式是.故选A.
点评:随着抛物线的平移对应的函数表达式将发生一定的变化,其规律如下:
;;
;.
说明:可以根据以上变化规律,求平移后的函数表达式.
例3 (济南课改实验区)小明代表班级参加校运动会的铅球项目,他想:“怎样才能将铅球推的更远呢?”,于是找来小刚做了如下探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°,45°,60°方向推了三次.铅球推出后沿抛物线形运动.如图2,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为轴,地平线为轴建立直角坐标系,分别得到的有关数据如下表:
推铅球的方向与水平线的夹角
铅球运动所得到的抛物线表达式
估测铅球在最高点的坐标
铅球落点到小明站立处的水平距离 _______
(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.
析解:(1)因为三条抛物线都经过点,所以抛物线也经过(0,2),则把(0,2)代入可得,则抛物线的表达式为.另外,铅球落地点到小明站立处的水平距离,也就是当时的值,解方程得或(舍去),所以铅球落点到小明站立处的水平距离为10m.
(2)根据以上分析可知在挚铅球时运动的方向与水平线的夹角是45°时挚的最远,因此挚铅球时最好沿与水平线的夹角是45°的方向挚出.
综观近几年的中考试卷发现:二次函数在中考中出题的比重越来越大,所占分数值约为15分-25分之间,并且题型向多元化、生活化、整合化和动态性、实践性、创新性、应用性等方向发展.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第二章 二次函数复习教案
一、知识网络
二、知识要点
1.定义:形如()的函数叫做二次函数,其图象是抛物线.
2.性质:抛物线可变形为的形式,它的对称轴是直线,顶点坐标是.当时,开口向上,在对称轴左侧,随的增大而减小,在对称轴右侧,随的增大而增大,当时,有最小值;当时,开口向下,在对称轴左侧,随的增大而增大,在对称轴右侧,随的增大而减小,当时,有最大值.
3.表达式的形式
一般式:;
顶点式:(,其中()是抛物线的顶点坐标).
三、精典考题
例1 (北京)函数的图象如图1所示,则下列结论正确的是 ( ).
A.,
B.,
C.,
D.,
析解:由抛物线开口向下知,由抛物线与轴的交点在轴的正半轴上知,又由抛物线的对称轴及知,所以,.故选C.
点评:抛物线的系数与图象间的关系如下表:
几何意义 时,开口向下;时,开口向上;越大,开口越小. 同号时,对称轴在y轴左侧;a,b异号时,对称轴在y轴右侧. 时,抛物线交于y轴的正半轴;时,抛物线交于y轴的负半轴.
例2 (台洲、温州市)将抛物线向左平移1个单位,再向上平移3个单位得到的抛物线的表达式是( ).
A. B.
C. D.
析解:将抛物线向左平移1个单位得到的抛物线表达式是,再向上平移3个单位得到的抛物线表达式是.故选A.
点评:随着抛物线的平移对应的函数表达式将发生一定的变化,其规律如下:
;;
;.
说明:可以根据以上变化规律,求平移后的函数表达式.
例3 (济南课改实验区)小明代表班级参加校运动会的铅球项目,他想:“怎样才能将铅球推的更远呢?”,于是找来小刚做了如下探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°,45°,60°方向推了三次.铅球推出后沿抛物线形运动.如图2,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为轴,地平线为轴建立直角坐标系,分别得到的有关数据如下表:
推铅球的方向与水平线的夹角
铅球运动所得到的抛物线表达式
估测铅球在最高点的坐标
铅球落点到小明站立处的水平距离 _______
(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.
析解:(1)因为三条抛物线都经过点,所以抛物线也经过(0,2),则把(0,2)代入可得,则抛物线的表达式为.另外,铅球落地点到小明站立处的水平距离,也就是当时的值,解方程得或(舍去),所以铅球落点到小明站立处的水平距离为10m.
(2)根据以上分析可知在挚铅球时运动的方向与水平线的夹角是45°时挚的最远,因此挚铅球时最好沿与水平线的夹角是45°的方向挚出.
综观近几年的中考试卷发现:二次函数在中考中出题的比重越来越大,所占分数值约为15分-25分之间,并且题型向多元化、生活化、整合化和动态性、实践性、创新性、应用性等方向发展.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
