数学:第二章二次函数复习课件(鲁教版九年级上)
文档属性
| 名称 | 数学:第二章二次函数复习课件(鲁教版九年级上) |

|
|
| 格式 | rar | ||
| 文件大小 | 793.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-30 00:00:00 | ||
图片预览







文档简介
课件21张PPT。九年级数学(上)第二章 二次函数回顾与思考----
二次函数小结回顾与思考 1.你在哪些情况下见到过抛物线的“身影”?用语言或图形进行描述.
2.你能用二次函数的知识解决哪些实际问题?与同伴交流.
3.小结一下作二次函数图象的方法.
4.二次函数的图象有哪些性质?如何确定它的开口方向,对称轴和顶点坐标?请用具体例子进行说明.
5.用具体例子说明如何更恰当或更有效地利用二次函数的表达式,表格和图象刻画变量之间的关系.
6.用自己的语言描述二次函数y=ax2+bx+c的图象与方程ax2+bx+c=0的根之间的关系.驶向胜利的彼岸例.求次函数y=ax2+bx+c的对称轴和顶点坐标. 函数y=ax2+bx+c的顶点式 一般地,对于二次函数y=ax2+bx+c,我们可以利用配方法推导出它的对称轴和顶点坐标. 1.配方:提取二次项系数配方:加上再减去一次项系数绝对值一半的平方整理:前三项化为平方形式,后两项合并同类项化简:去掉中括号老师提示:
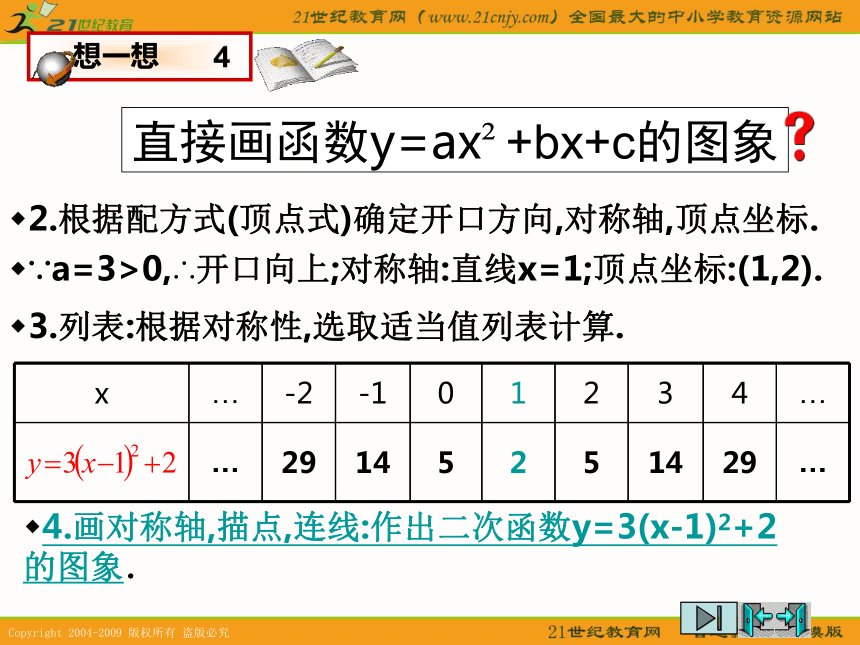
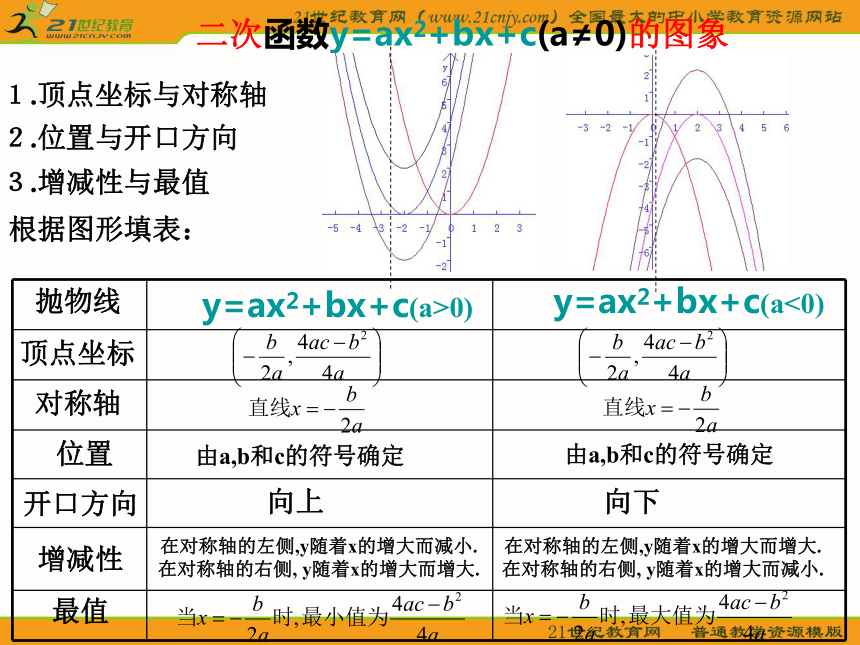
这个结果通常称为求顶点坐标公式.怎样直接作出函数y=3x2-6x+5的图象?函数y=ax2+bx+c的图象 我们知道,作出二次函数y=3x2的图象,通过平移抛物线y=3x2可以得到二次函数y=3x2-6x+5的图象. 1.配方:提取二次项系数配方:加上再减去一次项系数绝对值一半的平方整理:前三项化为平方形式,后两项合并同类项化简:去掉中括号直接画函数y=ax2+bx+c的图象4.画对称轴,描点,连线:作出二次函数y=3(x-1)2+2的图象. 2.根据配方式(顶点式)确定开口方向,对称轴,顶点坐标.3.列表:根据对称性,选取适当值列表计算.∵a=3>0,∴开口向上;对称轴:直线x=1;顶点坐标:(1,2).顶点坐标公式因此,二次函数y=ax2+bx+c的图象是一条抛物线.根据公式确定下列二次函数图象的对称轴和顶点坐标: ?二次函数y=ax2+bx+c(a≠0)的图象和性质1.顶点坐标与对称轴2.位置与开口方向3.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c的符号确定由a,b和c的符号确定向上向下在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 根据图形填表:1.相同点:
(1)形状相同(图像都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最(大或小)值.
(4)a>0时, 开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大. a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随 x的增大而减小 . 回味无穷函数y=ax2+bx+c(a≠0)与y=ax2的关系2.不同点:
(1)位置不同(2)顶点不同:分别是 和(0,0).
(3)对称轴不同:分别是 和y轴.
(4)最值不同:分别是 和0.
3.联系:
函数y=ax2+bx+c(a≠0) 的图象可以看成y=ax2的图象先沿x轴整体左(右)平移| |个单位(当 >0时,向左平移;当 <0时,向右平移),再沿对称轴整体上(下)平移| |个单位 (当 >0时向上平移;当 <0时,向下平移)得到的.回味无穷函数y=ax2+bx+c(a≠0)与y=ax2的关系二次函数与一元二次方程二次函数y=ax2+bx+c的图象和x轴交点有三种情况:有两个交点,有一个交点,没有交点.当二次函数y=ax2+bx+c的图象和x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.有两个交点有两个相异的实数根b2-4ac > 0有一个交点有两个相等的实数根b2-4ac = 0没有交点没有实数根b2-4ac < 01.理解问题;“二次函数应用” 的思路 解决“最值问题”如:“最大利润”和“最大面积” 此类问题的基本思路:2.分析问题中的变量和常量,以及它们之间的关系,建立好平面直角坐标系;3.把现实中的数转化为坐标.用数学的方式表示出它们之间的关系;4.做数学求解;5.检验结果的合理性,拓展,注重逆向思维,提高能力等.知识的升华复习题A组, 3~7题,
B组1~6题.
祝你成功!驶向胜利的彼岸2. (P73A组第3,4,5,7题,P75B组第2,3,5题)确定函数的解析式,作函数图象,求指定的对应值.
3. (P74A组第4,5,6,7题,P75B组第4,5,6题,P77C组第1,2,3,4,5,6题)二次函数的应用求最大值或最小值.
4.(P73A组第2题,P75B组第1题)二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根的关系.二次函数的图象和性质 1.(P73A组第1题)确定下列二次函数的开口方向,对称轴和顶点.驶向胜利的彼岸解:如图,设矩形的一边AB=xm,那么另一边BC=(15-x)cm,面积为Scm2,则二次函数的应用A组: 6题6.如图,假设篱笆(虚线部分)的长度是15m,如何围篱笆才能使其所围成矩形的面积最大?驶向胜利的彼岸解法1:(用公式)根据题意,y=-5t2+v0t顶点的纵坐标为15m.二次函数的应用B组: 6题6.竖直向上发射物体的h(m)满足关系式y=-5t2+v0t,其中t(s)是物体运动的时间,v0(m/s)是物体被发射时的速度.某公园计划设计园内喷泉,喷水的最大高度要求达到15m,那么喷水的速度应该达到多少?(结果精确到0.01m/s).解法1:(用顶点式)根据题意,y=-5t2+v0t顶点的纵坐标为15m.解:建立如图所示的坐标系二次函数的应用C组: 2题2.一座抛物线型拱桥如图所示,桥下水面宽度是4m,拱高是2m.当水面下降1m后,水面的宽度是多少?(结果精确到0.1m).●A(2,-2)●B(X,-3)二次函数的应用C组: 3题3.(1)如图,第n个图形中有多少个小正方形?你是如何计算的?
(2)求1+3,1+3+5,1+3+5+7,
1+3+5+7+9,…,1+3+5+7+9+…+(2n-1).驶向胜利的彼岸二次函数的应用C组: 3题3.(1)如图,第n个图形中有多少个小正方形?你是如何计算的?
(2)求1+3,1+3+5,1+3+5+7,
1+3+5+7+9,…,1+3+5+7+9+…+(2n-1).二次函数的应用C组: 5题5.(1)如图,下面每个图形中有多少个小圆圈?第5个图形中有多少个小圆圈?你是如何计算的?
(2)完成下表:二次函数的应用C组: 5题5.(1)如图,下面每个图形中有多少个小圆圈?第5个图形中有多少个小圆圈?你是如何计算的?
(2)完成下表:结束寄语形成天才的决定因素应该是勤奋.再见
二次函数小结回顾与思考 1.你在哪些情况下见到过抛物线的“身影”?用语言或图形进行描述.
2.你能用二次函数的知识解决哪些实际问题?与同伴交流.
3.小结一下作二次函数图象的方法.
4.二次函数的图象有哪些性质?如何确定它的开口方向,对称轴和顶点坐标?请用具体例子进行说明.
5.用具体例子说明如何更恰当或更有效地利用二次函数的表达式,表格和图象刻画变量之间的关系.
6.用自己的语言描述二次函数y=ax2+bx+c的图象与方程ax2+bx+c=0的根之间的关系.驶向胜利的彼岸例.求次函数y=ax2+bx+c的对称轴和顶点坐标. 函数y=ax2+bx+c的顶点式 一般地,对于二次函数y=ax2+bx+c,我们可以利用配方法推导出它的对称轴和顶点坐标. 1.配方:提取二次项系数配方:加上再减去一次项系数绝对值一半的平方整理:前三项化为平方形式,后两项合并同类项化简:去掉中括号老师提示:
这个结果通常称为求顶点坐标公式.怎样直接作出函数y=3x2-6x+5的图象?函数y=ax2+bx+c的图象 我们知道,作出二次函数y=3x2的图象,通过平移抛物线y=3x2可以得到二次函数y=3x2-6x+5的图象. 1.配方:提取二次项系数配方:加上再减去一次项系数绝对值一半的平方整理:前三项化为平方形式,后两项合并同类项化简:去掉中括号直接画函数y=ax2+bx+c的图象4.画对称轴,描点,连线:作出二次函数y=3(x-1)2+2的图象. 2.根据配方式(顶点式)确定开口方向,对称轴,顶点坐标.3.列表:根据对称性,选取适当值列表计算.∵a=3>0,∴开口向上;对称轴:直线x=1;顶点坐标:(1,2).顶点坐标公式因此,二次函数y=ax2+bx+c的图象是一条抛物线.根据公式确定下列二次函数图象的对称轴和顶点坐标: ?二次函数y=ax2+bx+c(a≠0)的图象和性质1.顶点坐标与对称轴2.位置与开口方向3.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c的符号确定由a,b和c的符号确定向上向下在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 根据图形填表:1.相同点:
(1)形状相同(图像都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最(大或小)值.
(4)a>0时, 开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大. a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随 x的增大而减小 . 回味无穷函数y=ax2+bx+c(a≠0)与y=ax2的关系2.不同点:
(1)位置不同(2)顶点不同:分别是 和(0,0).
(3)对称轴不同:分别是 和y轴.
(4)最值不同:分别是 和0.
3.联系:
函数y=ax2+bx+c(a≠0) 的图象可以看成y=ax2的图象先沿x轴整体左(右)平移| |个单位(当 >0时,向左平移;当 <0时,向右平移),再沿对称轴整体上(下)平移| |个单位 (当 >0时向上平移;当 <0时,向下平移)得到的.回味无穷函数y=ax2+bx+c(a≠0)与y=ax2的关系二次函数与一元二次方程二次函数y=ax2+bx+c的图象和x轴交点有三种情况:有两个交点,有一个交点,没有交点.当二次函数y=ax2+bx+c的图象和x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.有两个交点有两个相异的实数根b2-4ac > 0有一个交点有两个相等的实数根b2-4ac = 0没有交点没有实数根b2-4ac < 01.理解问题;“二次函数应用” 的思路 解决“最值问题”如:“最大利润”和“最大面积” 此类问题的基本思路:2.分析问题中的变量和常量,以及它们之间的关系,建立好平面直角坐标系;3.把现实中的数转化为坐标.用数学的方式表示出它们之间的关系;4.做数学求解;5.检验结果的合理性,拓展,注重逆向思维,提高能力等.知识的升华复习题A组, 3~7题,
B组1~6题.
祝你成功!驶向胜利的彼岸2. (P73A组第3,4,5,7题,P75B组第2,3,5题)确定函数的解析式,作函数图象,求指定的对应值.
3. (P74A组第4,5,6,7题,P75B组第4,5,6题,P77C组第1,2,3,4,5,6题)二次函数的应用求最大值或最小值.
4.(P73A组第2题,P75B组第1题)二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根的关系.二次函数的图象和性质 1.(P73A组第1题)确定下列二次函数的开口方向,对称轴和顶点.驶向胜利的彼岸解:如图,设矩形的一边AB=xm,那么另一边BC=(15-x)cm,面积为Scm2,则二次函数的应用A组: 6题6.如图,假设篱笆(虚线部分)的长度是15m,如何围篱笆才能使其所围成矩形的面积最大?驶向胜利的彼岸解法1:(用公式)根据题意,y=-5t2+v0t顶点的纵坐标为15m.二次函数的应用B组: 6题6.竖直向上发射物体的h(m)满足关系式y=-5t2+v0t,其中t(s)是物体运动的时间,v0(m/s)是物体被发射时的速度.某公园计划设计园内喷泉,喷水的最大高度要求达到15m,那么喷水的速度应该达到多少?(结果精确到0.01m/s).解法1:(用顶点式)根据题意,y=-5t2+v0t顶点的纵坐标为15m.解:建立如图所示的坐标系二次函数的应用C组: 2题2.一座抛物线型拱桥如图所示,桥下水面宽度是4m,拱高是2m.当水面下降1m后,水面的宽度是多少?(结果精确到0.1m).●A(2,-2)●B(X,-3)二次函数的应用C组: 3题3.(1)如图,第n个图形中有多少个小正方形?你是如何计算的?
(2)求1+3,1+3+5,1+3+5+7,
1+3+5+7+9,…,1+3+5+7+9+…+(2n-1).驶向胜利的彼岸二次函数的应用C组: 3题3.(1)如图,第n个图形中有多少个小正方形?你是如何计算的?
(2)求1+3,1+3+5,1+3+5+7,
1+3+5+7+9,…,1+3+5+7+9+…+(2n-1).二次函数的应用C组: 5题5.(1)如图,下面每个图形中有多少个小圆圈?第5个图形中有多少个小圆圈?你是如何计算的?
(2)完成下表:二次函数的应用C组: 5题5.(1)如图,下面每个图形中有多少个小圆圈?第5个图形中有多少个小圆圈?你是如何计算的?
(2)完成下表:结束寄语形成天才的决定因素应该是勤奋.再见
