数学:第三章圆复习课件(鲁教版九年级上)
文档属性
| 名称 | 数学:第三章圆复习课件(鲁教版九年级上) |  | |
| 格式 | rar | ||
| 文件大小 | 118.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-30 14:33:00 | ||
图片预览



文档简介
课件13张PPT。第三章 圆回顾与思考确定圆的方法:ABO1、确定圆心和半径
2、不在同一直线上的三个点C1、圆的定义:
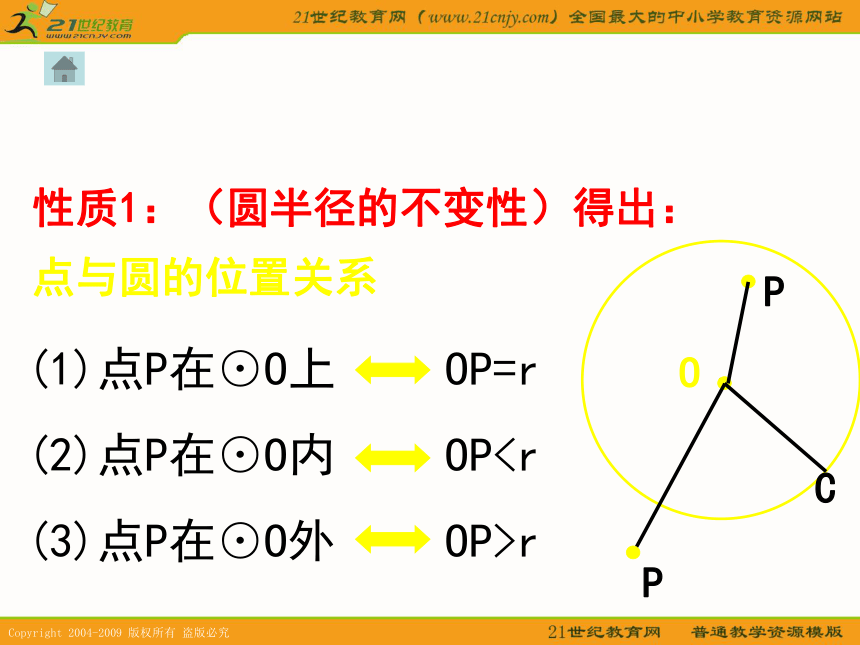
圆是到定点的距离等于定长的点的集合.PCPO性质1:(圆半径的不变性)得出:
点与圆的位置关系(1)点P在⊙O上
(2)点P在⊙O内
(3)点P在⊙O外OP=r
OPOP>r圆有关概念弦
直径
弧
半圆
优弧劣弧
弓形
同心圆
等圆
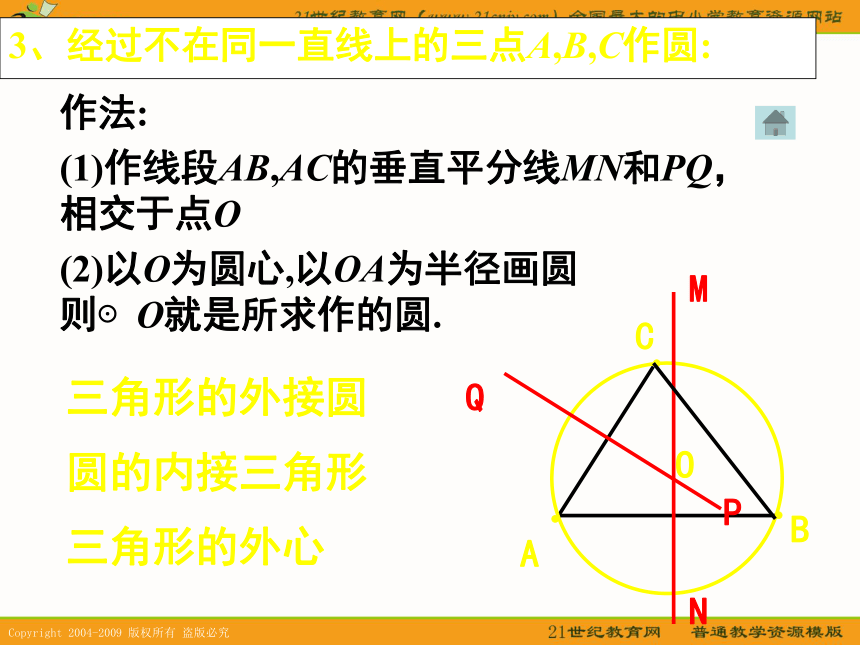
等弧3、经过不在同一直线上的三点A,B,C作圆:作法:
(1)作线段AB,AC的垂直平分线MN和PQ, 相交于点O
(2)以O为圆心,以OA为半径画圆 则⊙O就是所求作的圆.BACOMNPQ三角形的外接圆
圆的内接三角形
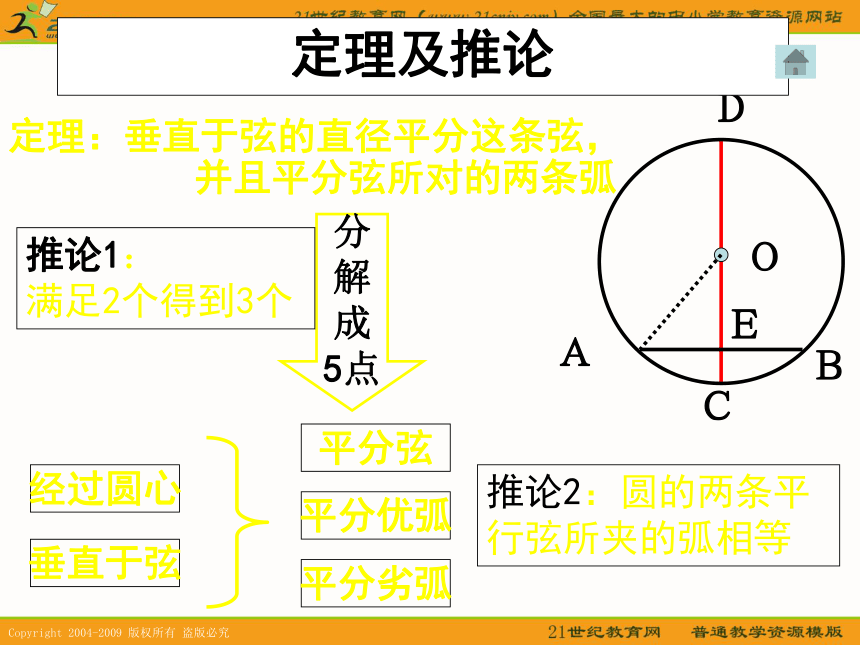
三角形的外心定理及推论定理:垂直于弦的直径平分这条弦, 并且平分弦所对的两条弧E分 解 成 5点经过圆心垂直于弦平分弦平分优弧平分劣弧推论1: 满足2个得到3个推论2:圆的两条平行弦所夹的弧相等圆心角、圆心角所对的弦、弧及弦心距之间的关系AB定理: 在同圆或等圆中,相等的圆心角 所对的弧相等, 所对的弦相等, 所对的弦的弦心距相等推论: 在同圆或等圆中,如果 两个圆心角 两条弧, 两条弦 两条弦的弦心距中有一组量相等, 那么它们所对应的其余各组量都相等推论1:
同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等.AC1BC2C31、直线和圆的三种位置关系:PL(1)直线 L 和⊙O相交
(2)直线 L 和⊙O相切
(3)直线 L和⊙O相离OP=r
OPOP>rLLPP返回2、切线的判定定理:
经过直径的一端,并且垂直于这条直径的 直线是圆的切线LA∵OA是半径,L⊥OA
∴直线 L是⊙O的半径3、切线的性质定理推论:
lA垂直于切线的直线:
(1)过圆心必过切点
(2)过切点必过圆心已知条件为:
切线和垂直于切线的直线如图:AC=12cm,BC=5cm,求:CD,BD.OADCB如图:⊙O是Rt ABC的内切圆,且AB=6,AC=8,BC=10。求⊙O的半径。BACODEF
2、不在同一直线上的三个点C1、圆的定义:
圆是到定点的距离等于定长的点的集合.PCPO性质1:(圆半径的不变性)得出:
点与圆的位置关系(1)点P在⊙O上
(2)点P在⊙O内
(3)点P在⊙O外OP=r
OP
直径
弧
半圆
优弧劣弧
弓形
同心圆
等圆
等弧3、经过不在同一直线上的三点A,B,C作圆:作法:
(1)作线段AB,AC的垂直平分线MN和PQ, 相交于点O
(2)以O为圆心,以OA为半径画圆 则⊙O就是所求作的圆.BACOMNPQ三角形的外接圆
圆的内接三角形
三角形的外心定理及推论定理:垂直于弦的直径平分这条弦, 并且平分弦所对的两条弧E分 解 成 5点经过圆心垂直于弦平分弦平分优弧平分劣弧推论1: 满足2个得到3个推论2:圆的两条平行弦所夹的弧相等圆心角、圆心角所对的弦、弧及弦心距之间的关系AB定理: 在同圆或等圆中,相等的圆心角 所对的弧相等, 所对的弦相等, 所对的弦的弦心距相等推论: 在同圆或等圆中,如果 两个圆心角 两条弧, 两条弦 两条弦的弦心距中有一组量相等, 那么它们所对应的其余各组量都相等推论1:
同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等.AC1BC2C31、直线和圆的三种位置关系:PL(1)直线 L 和⊙O相交
(2)直线 L 和⊙O相切
(3)直线 L和⊙O相离OP=r
OP
经过直径的一端,并且垂直于这条直径的 直线是圆的切线LA∵OA是半径,L⊥OA
∴直线 L是⊙O的半径3、切线的性质定理推论:
lA垂直于切线的直线:
(1)过圆心必过切点
(2)过切点必过圆心已知条件为:
切线和垂直于切线的直线如图:AC=12cm,BC=5cm,求:CD,BD.OADCB如图:⊙O是Rt ABC的内切圆,且AB=6,AC=8,BC=10。求⊙O的半径。BACODEF
