北师大版七年级数学下册第4—5章选择题常考热点专题提升训练 (含详解)
文档属性
| 名称 | 北师大版七年级数学下册第4—5章选择题常考热点专题提升训练 (含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 567.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-26 08:42:09 | ||
图片预览

文档简介
北师大版七年级数学下册期末复习《第4—5章》
选择题常考热点专题提升训练
1.汉字作为中华优秀传统文化的根脉和重要载体,在发展过程中演变出多种字体,给人以美的享受.下面是“遂宁之美”四个字的篆书,能看作是轴对称图形的是( )
A. B. C. D.
2.下列轴对称图形中,有两条对称轴的是( ).
A.B.C. D.
3.昆明市打算在某条街道新建一所中学,为了方便居民区A、B的学生上学,要使A、B两小区到学校的距离之和最小,则学校C的位置应该在( )
A. B.
C. D.
4.按如图的方法折纸,下列说法不正确的是( )
A.与互余 B.
C.平分 D.与互补
5.如图,在中,,平分,交于点,于点.若,则的面积为( )
A.30 B.15 C.20 D.10
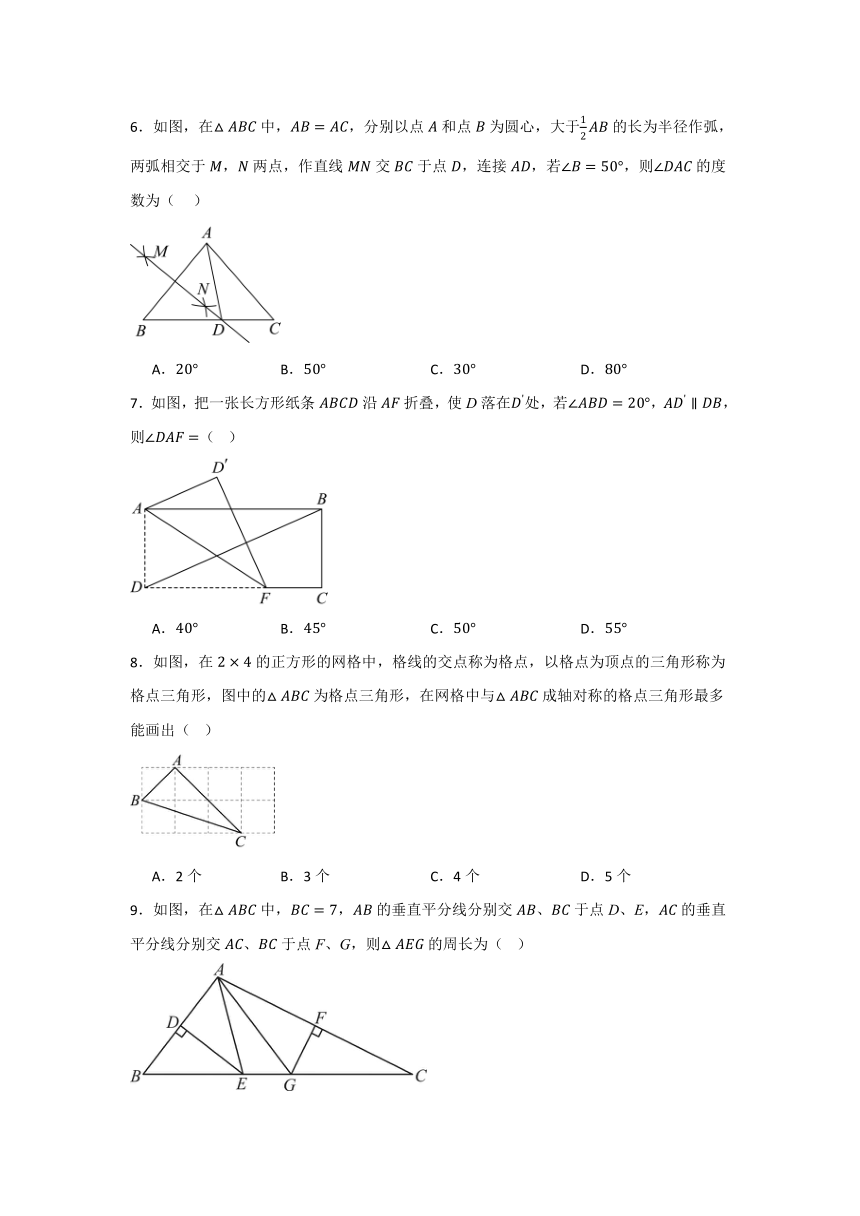
6.如图,在中,,分别以点和点为圆心,大于的长为半径作弧,两弧相交于,两点,作直线交于点,连接,若,则的度数为( )
A. B. C. D.
7.如图,把一张长方形纸条沿折叠,使D落在处,若,,则( )
A. B. C. D.
8.如图,在的正方形的网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的为格点三角形,在网格中与成轴对称的格点三角形最多能画出( )
A.2个 B.3个 C.4个 D.5个
9.如图,在中,,的垂直平分线分别交、于点D、E,的垂直平分线分别交、于点F、G,则的周长为( )
A.5 B.6 C.7 D.8
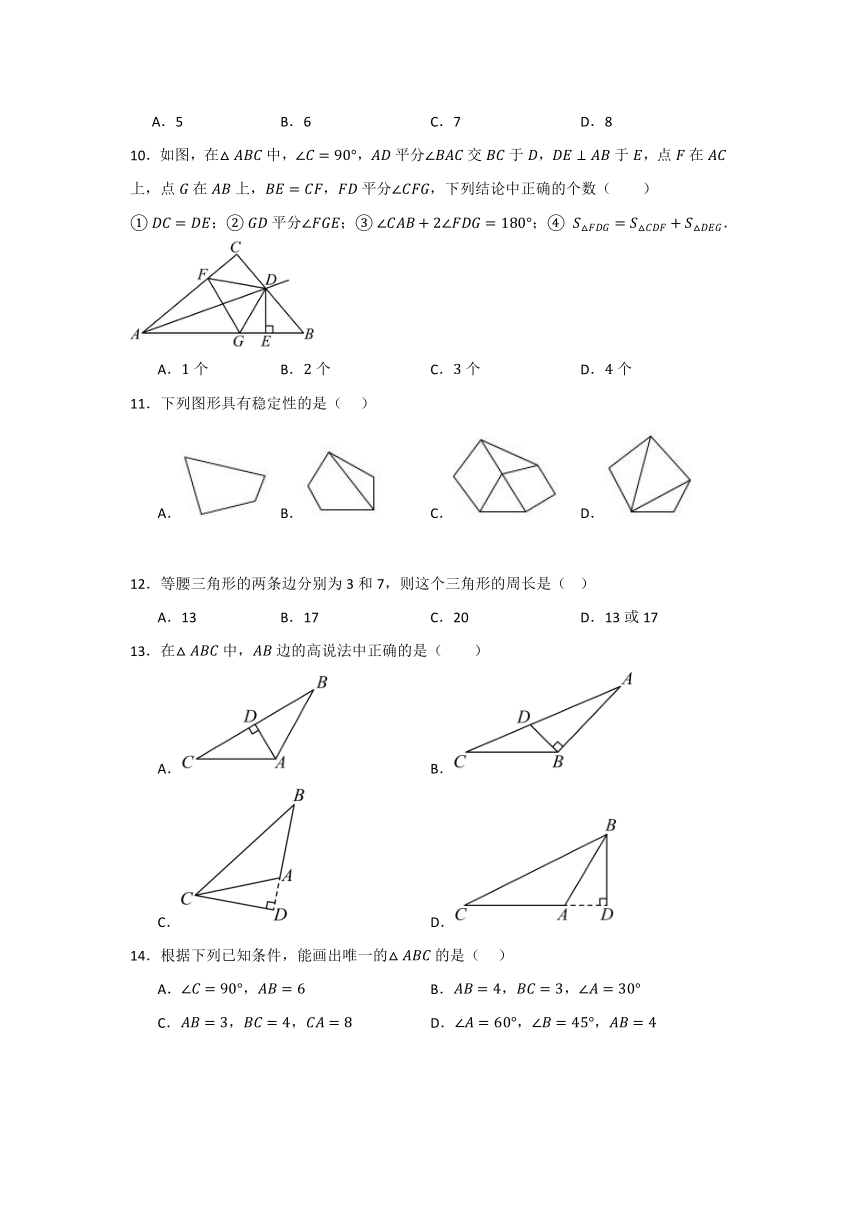
10.如图,在中,,平分交于,于,点在上,点在上,,平分,下列结论中正确的个数( )
; 平分; ; .
A.个 B.个 C.个 D.个
11.下列图形具有稳定性的是( )
A. B. C. D.
12.等腰三角形的两条边分别为3和7,则这个三角形的周长是( )
A.13 B.17 C.20 D.13或17
13.在中,边的高说法中正确的是( )
A. B.
C. D.
14.根据下列已知条件,能画出唯一的的是( )
A., B.,,
C.,, D.,,
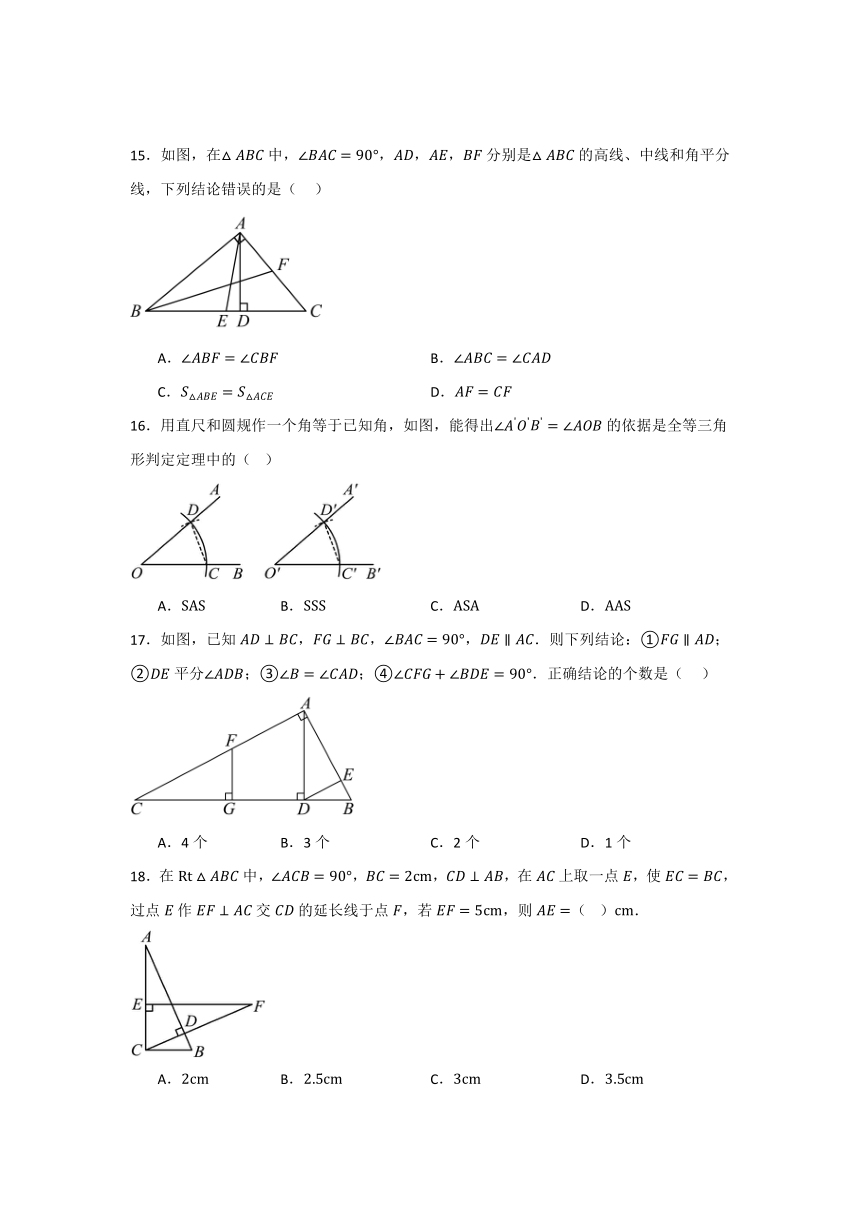
15.如图,在中,,,,分别是的高线、中线和角平分线,下列结论错误的是( )
A. B.
C. D.
16.用直尺和圆规作一个角等于已知角,如图,能得出的依据是全等三角形判定定理中的( )
A. B. C. D.
17.如图,已知,,,.则下列结论:①;②平分;③;④.正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
18.在中,,,,在上取一点,使,过点作交的延长线于点,若,则( ).
A. B. C. D.
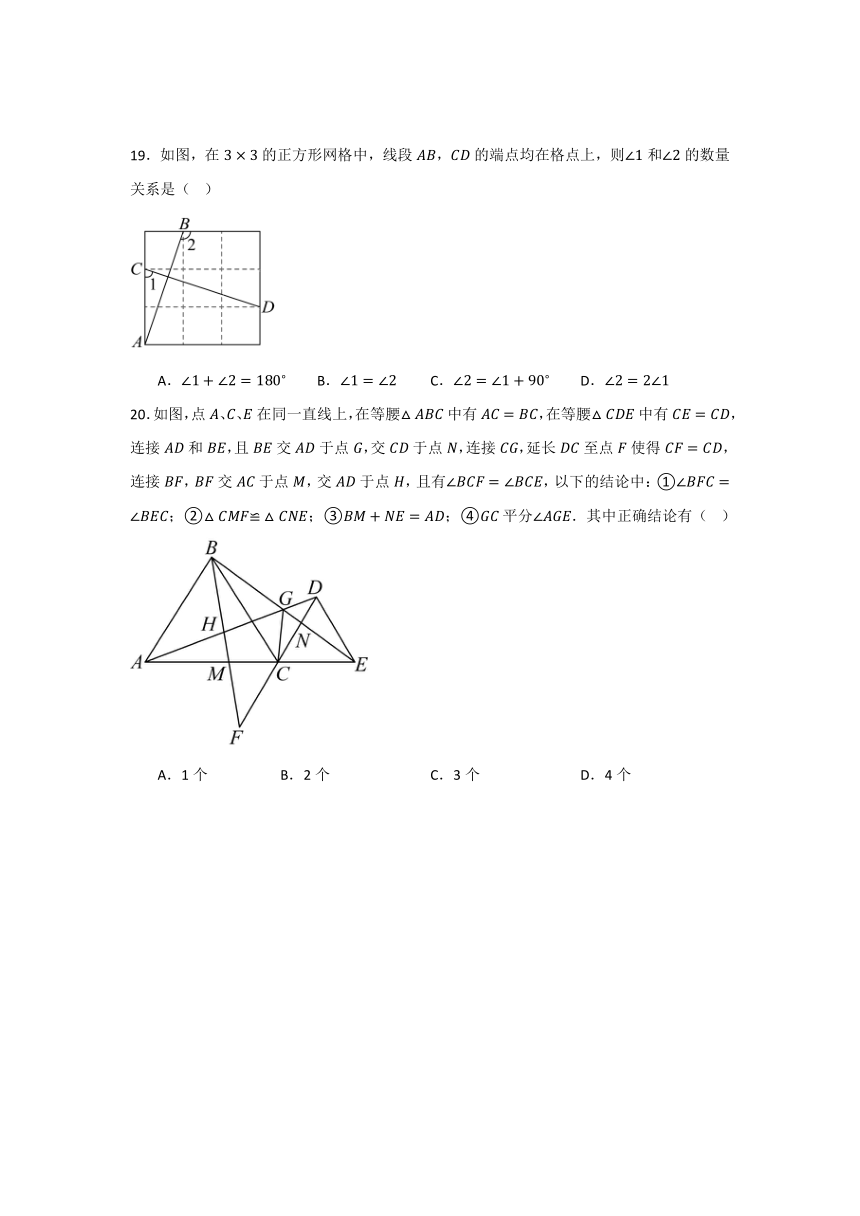
19.如图,在的正方形网格中,线段,的端点均在格点上,则和的数量关系是( )
A. B. C. D.
20.如图,点、、在同一直线上,在等腰中有,在等腰中有,连接和,且交于点,交于点,连接,延长至点使得,连接,交于点,交于点,且有,以下的结论中:①;②;③;④平分.其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
参考答案
1.解:A、不能看作是轴对称图形,故本选项不符合题意;
B、不能看作是轴对称图形,故本选项不符合题意;
C、不能看作是轴对称图形,故本选项不符合题意;
D、能看作是轴对称图形,故本选项符合题意;
故选:D.
2.解:A、图形有两条对称轴,故此选项符合题意;
B、图形有一条对称轴,故此选项不符合题意;
C、图形有一条对称轴,故此选项不符合题意;
D、图形有六条对称轴,故此选项不符合题意;
故选:A.
3.解:∵要使A、B两小区到学校的距离之和最小,
∴先作点A关于街道的对称点,再连接,与街道的所在直线的交点即为点,学校C的位置如图所示:
∴此时,
故选:C.
4.解:由折叠的性质可得,
∴,
∴与互余,故A正确,不符合题意;
∴,故B正确,不符合题意;
∵,
∴不平分,故C错误,符合题意;
∵,
∴与互补,故D正确,不符合题意;
故选:C.
5.解:如图所示,过点作于,
∵,平分,
∴,
∴,
故选:B.
6.解:由作图过程可得,直线为线段的垂直平分线,
∴,
∴.
∵,,
∴.
∴,
∴.
故选:C.
7.解:∵,
∴,
∴,
∴由折叠的性质可得,
故选;D.
8.解:在网格中与△成轴对称的格点三角形最多能画出3个.
故选:B.
9.解:∵垂直平分,垂直平分,
∴,,
∴的周长为,
故选:C.
10.解:∵,
∴,
∵平分交于,,
∴,故正确;
如图,过作于点,
∵平分,,
∴,
∵,
∴,
∴点在角平分线上,
∴平分,故正确;
∵平分,平分,
∴,,
∵,
∴,,
∴,,
∴,
∵,
∴,故正确;
由上得,,
∴,,
∴,
∴,故正确,
综上可知,正确,共个正确,
故选:.
11.解:选项中只有选项D是三角形组成,故具有稳定性.
故选:D.
12.解:当3是腰时,则,不能组成三角形,应舍去;
当7是腰时,则三角形的周长是.
故选:B.
13.
解:根据题意,
是符合题意的,A,B,D都不符合题意,
故选C.
14.解:A、已知一角和一边,不能判定三角形全等,故该选项不能画出唯一,不合题意;
B、已知两边及一边的对角相等,不能判定三角形全等,故该选项不能画出唯一,不合题意;
C、因为,所以三条线段不能构成三角形,故该选项不能画出唯一,不合题意;
D、已知两角及夹边相等,由能判定三角形全等,故该选项能画出唯一,符合题意;
故选:D.
15.解:∵是的角平分线,
∴,
故选项A结论正确,不符合题意;
∵是的高线,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
故选项B结论正确,不符合题意;
∵是的中线,
∴,
∴,
即,
故选项C结论正确,不符合题意;
∵是的角平分线,无法判定是的中线,
∴选项D结论错误,符合题意;
故选:D.
16.解:由作图可知:,
∴(),
∴,即
故选:B.
17.解:∵,
∴,故①正确;
∵,
∴,
∵与的数量无法确定,即与不一定相等,
∴不能判定平分,故②错误;
∵,
∴,
∵,
∴,故③正确;
∵,
∴,
∵,
∴,
∴,故④正确;
综上所述,正确的有①③④,共3个,
故选:B .
18.解: ,
,
,
,
,
,
,
,
,
,
,,
,,
,
故选:C.
19.解:如图
在和中
,
∴,
∴,
∵,
∵,
故选:A.
20.解:∵,,
∴,
∵,,
∴,
∴,故①正确;
∵,,,
∴,故②正确;
∵,
∴,
∵,
∴,
∴,
∵与不一定相等,
∴,
∴,
∴与不一定全等,
∴,
∴,
∴,故③不正确;
∵与不一定全等,,
∴点C到、的距离不一定相等,
∴不一定平分,故④不正确;
综上分析可知:正确的有2个.
故选:B.
选择题常考热点专题提升训练
1.汉字作为中华优秀传统文化的根脉和重要载体,在发展过程中演变出多种字体,给人以美的享受.下面是“遂宁之美”四个字的篆书,能看作是轴对称图形的是( )
A. B. C. D.
2.下列轴对称图形中,有两条对称轴的是( ).
A.B.C. D.
3.昆明市打算在某条街道新建一所中学,为了方便居民区A、B的学生上学,要使A、B两小区到学校的距离之和最小,则学校C的位置应该在( )
A. B.
C. D.
4.按如图的方法折纸,下列说法不正确的是( )
A.与互余 B.
C.平分 D.与互补
5.如图,在中,,平分,交于点,于点.若,则的面积为( )
A.30 B.15 C.20 D.10
6.如图,在中,,分别以点和点为圆心,大于的长为半径作弧,两弧相交于,两点,作直线交于点,连接,若,则的度数为( )
A. B. C. D.
7.如图,把一张长方形纸条沿折叠,使D落在处,若,,则( )
A. B. C. D.
8.如图,在的正方形的网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的为格点三角形,在网格中与成轴对称的格点三角形最多能画出( )
A.2个 B.3个 C.4个 D.5个
9.如图,在中,,的垂直平分线分别交、于点D、E,的垂直平分线分别交、于点F、G,则的周长为( )
A.5 B.6 C.7 D.8
10.如图,在中,,平分交于,于,点在上,点在上,,平分,下列结论中正确的个数( )
; 平分; ; .
A.个 B.个 C.个 D.个
11.下列图形具有稳定性的是( )
A. B. C. D.
12.等腰三角形的两条边分别为3和7,则这个三角形的周长是( )
A.13 B.17 C.20 D.13或17
13.在中,边的高说法中正确的是( )
A. B.
C. D.
14.根据下列已知条件,能画出唯一的的是( )
A., B.,,
C.,, D.,,
15.如图,在中,,,,分别是的高线、中线和角平分线,下列结论错误的是( )
A. B.
C. D.
16.用直尺和圆规作一个角等于已知角,如图,能得出的依据是全等三角形判定定理中的( )
A. B. C. D.
17.如图,已知,,,.则下列结论:①;②平分;③;④.正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
18.在中,,,,在上取一点,使,过点作交的延长线于点,若,则( ).
A. B. C. D.
19.如图,在的正方形网格中,线段,的端点均在格点上,则和的数量关系是( )
A. B. C. D.
20.如图,点、、在同一直线上,在等腰中有,在等腰中有,连接和,且交于点,交于点,连接,延长至点使得,连接,交于点,交于点,且有,以下的结论中:①;②;③;④平分.其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
参考答案
1.解:A、不能看作是轴对称图形,故本选项不符合题意;
B、不能看作是轴对称图形,故本选项不符合题意;
C、不能看作是轴对称图形,故本选项不符合题意;
D、能看作是轴对称图形,故本选项符合题意;
故选:D.
2.解:A、图形有两条对称轴,故此选项符合题意;
B、图形有一条对称轴,故此选项不符合题意;
C、图形有一条对称轴,故此选项不符合题意;
D、图形有六条对称轴,故此选项不符合题意;
故选:A.
3.解:∵要使A、B两小区到学校的距离之和最小,
∴先作点A关于街道的对称点,再连接,与街道的所在直线的交点即为点,学校C的位置如图所示:
∴此时,
故选:C.
4.解:由折叠的性质可得,
∴,
∴与互余,故A正确,不符合题意;
∴,故B正确,不符合题意;
∵,
∴不平分,故C错误,符合题意;
∵,
∴与互补,故D正确,不符合题意;
故选:C.
5.解:如图所示,过点作于,
∵,平分,
∴,
∴,
故选:B.
6.解:由作图过程可得,直线为线段的垂直平分线,
∴,
∴.
∵,,
∴.
∴,
∴.
故选:C.
7.解:∵,
∴,
∴,
∴由折叠的性质可得,
故选;D.
8.解:在网格中与△成轴对称的格点三角形最多能画出3个.
故选:B.
9.解:∵垂直平分,垂直平分,
∴,,
∴的周长为,
故选:C.
10.解:∵,
∴,
∵平分交于,,
∴,故正确;
如图,过作于点,
∵平分,,
∴,
∵,
∴,
∴点在角平分线上,
∴平分,故正确;
∵平分,平分,
∴,,
∵,
∴,,
∴,,
∴,
∵,
∴,故正确;
由上得,,
∴,,
∴,
∴,故正确,
综上可知,正确,共个正确,
故选:.
11.解:选项中只有选项D是三角形组成,故具有稳定性.
故选:D.
12.解:当3是腰时,则,不能组成三角形,应舍去;
当7是腰时,则三角形的周长是.
故选:B.
13.
解:根据题意,
是符合题意的,A,B,D都不符合题意,
故选C.
14.解:A、已知一角和一边,不能判定三角形全等,故该选项不能画出唯一,不合题意;
B、已知两边及一边的对角相等,不能判定三角形全等,故该选项不能画出唯一,不合题意;
C、因为,所以三条线段不能构成三角形,故该选项不能画出唯一,不合题意;
D、已知两角及夹边相等,由能判定三角形全等,故该选项能画出唯一,符合题意;
故选:D.
15.解:∵是的角平分线,
∴,
故选项A结论正确,不符合题意;
∵是的高线,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
故选项B结论正确,不符合题意;
∵是的中线,
∴,
∴,
即,
故选项C结论正确,不符合题意;
∵是的角平分线,无法判定是的中线,
∴选项D结论错误,符合题意;
故选:D.
16.解:由作图可知:,
∴(),
∴,即
故选:B.
17.解:∵,
∴,故①正确;
∵,
∴,
∵与的数量无法确定,即与不一定相等,
∴不能判定平分,故②错误;
∵,
∴,
∵,
∴,故③正确;
∵,
∴,
∵,
∴,
∴,故④正确;
综上所述,正确的有①③④,共3个,
故选:B .
18.解: ,
,
,
,
,
,
,
,
,
,
,,
,,
,
故选:C.
19.解:如图
在和中
,
∴,
∴,
∵,
∵,
故选:A.
20.解:∵,,
∴,
∵,,
∴,
∴,故①正确;
∵,,,
∴,故②正确;
∵,
∴,
∵,
∴,
∴,
∵与不一定相等,
∴,
∴,
∴与不一定全等,
∴,
∴,
∴,故③不正确;
∵与不一定全等,,
∴点C到、的距离不一定相等,
∴不一定平分,故④不正确;
综上分析可知:正确的有2个.
故选:B.
同课章节目录
