辽宁省丹东市凤城市第二中学2024-2025学年高二下学期6月教学质量检测数学试卷(PDF版、含答案)
文档属性
| 名称 | 辽宁省丹东市凤城市第二中学2024-2025学年高二下学期6月教学质量检测数学试卷(PDF版、含答案) |

|
|
| 格式 | |||
| 文件大小 | 548.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-25 00:00:00 | ||
图片预览




文档简介
凤城二中高二学年 2025年 6月考教学质量检测
高二数学
考试时间:120分钟满分 150分
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
2.答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂
黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案
写在答题卡上.写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、单项选择题:共 8小题,每小题 5分,共 40分.
f x f x f x
1. 已知函数 的图象如图所示, 是 的导函数,则下列数值排序正确
的是( )
A. 0 f 4 f 4 f 3 f 3
B. 0 f 3 f 4 f 4 f 3
C. 0 f 4 f 3 f 4 f 3
D. 0 f 4 f 3 f 4 f 3
2. 随着我国铁路的发展,列车的正点率有了显著的提高.据统计,途经某车站的只有和谐
号和复兴号列车,且和谐号列车的列次为复兴号列车的列次的 3 倍,和谐号列车的正点率为
0.98,复兴号列车的正点率为 0.99,则一列车能正点到达该车站的概率为( )
A. 0.9825 B. 0.9833 C. 0.9867 D. 0.9875
3. 随机变量 X N (110,92 ),Y N (100,192 ) ,若 P X A P Y A ,那么实数 A
的值为( )
第 1页/共 24页
A. 119 B. 120 C. 121 D. 122
1
4. 2若函数 f x lnx x ax在 0, 上单调递增,则实数 a的取值范围是( )
2
A. 2, B. 2, C. , 2 D.
, 2
5. 某种植基地统计出花卉种植面积 y与年份 x的数据如下:
x 1 2 3 4 5
y 5 7 9 10 14
根据上表数据得到 y关于 x的线性回归方程为 y 2.1x a ,则第 6 年的花卉种植面积约为
( )
A. 17 B. 16 C. 15.3 D. 15
6. 已知函数 f x x 1 x 2 x 3 x 4 ,则 f x 的图象在 x 2处的切线方程为
( )
A. 2x y 4 0 B. 2x y 4 0
C. x y 2 0 D. x y 2 0
7. 已知 f (x)是函数 f (x) 的导函数,对于任意实数 x都有 f (x) f (x) ex (2x 3),
f (0) 4,则不等式 f (x) 4ex的解集为( )
A. ( ,0) (3, ) B. ( , 1) (4, ) C. (0,3) D. ( 1,4)
8. 已知定义在 (0, )的函数 f (x) ,满足 f (x 1) 2 f (x) 2x,且 f (1) 0,则 f (100)
的值为( )
A. 99 299 B. 99 299 C. 100 2100 D.
100 2100
二、多项选择题:共 3小题,每小题 6分,共 18分.
9. 已知随机事件 A,B发生的概率分别为 P(A) 0.3,P(B) 0.6 ,下列说法正确的有( )
A. 若 P(AB) 0.18,则 A,B相互独立 B. 若 A,B相互独立,则
P B A 0.6
第 2页/共 24页
C. 若P B A 0.4 ,则 P(AB) 0.12 D. 若 A B,则 P A B 0.3
10. 已知数列 an 的首项为 4,且满足 2 n 1 an nan 1 n N* ,则( )
a
A. n 为等差数列 B. an 为递增数列
n
2
C. a n 2n 的前 n项和 Sn n 1 2 4
a
D. n n n n
2n 1
的前 项和T
n 2
11. f x xex已知函数 a,则( )
A. f x 在区间 0,2 上单调递增
B. f x 1有最大值 a
e
C. 当 a 0 时, y f x 的图象过 1,0 的切线有且仅有 2 条
1
D. 关于 x的方程 f x 0有两个不等实根,则 a的取值范围是 ,
e
三、填空题:共 3小题,每小题 5分,共 15分.
12. 已知数列 an 满足 an+1=3an 4, a1 1,则 an __________.
13. 已知 a,b,c,d 成等差数列,函数 f (x) x3 3bx2 cx b2 在 x 1时有极值 0,则
d a ______.
14. x x
b 1
已知函数 f x xe ax be ab a 0 ,若 f x 0,则 的最大值为
a
__________.
四、解答题
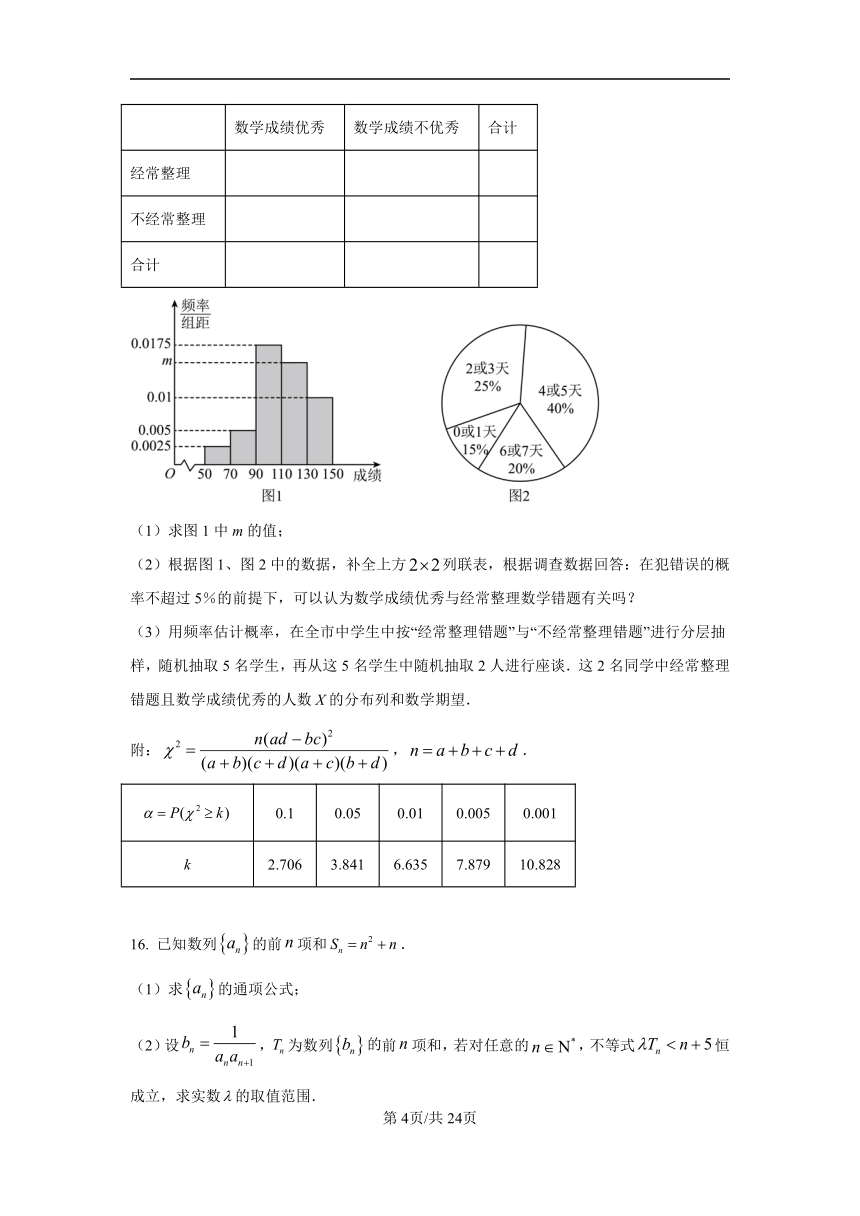
15. 为了研究学生每天整理数学错题情况,某课题组在某市中学生中随机抽取了 100 名学生
调查了他们期中考试的数学成绩和平时整理数学错题情况,并绘制了下列两个统计图表,图
1 为学生期中考试数学成绩的频率分布直方图,图 2 为学生一个星期内整理数学错题天数的
扇形图.若本次数学成绩在 110 分及以上视为优秀,将一个星期有 4 天及以上整理数学错题
视为“经常整理”,少于 4 天视为“不经常整理”.已知数学成绩优秀的学生中,经常整理错题
的学生占 70%.
第 3页/共 24页
数学成绩优秀 数学成绩不优秀 合计
经常整理
不经常整理
合计
(1)求图 1 中 m的值;
(2)根据图 1、图 2 中的数据,补全上方2 2列联表,根据调查数据回答:在犯错误的概
率不超过 5%的前提下,可以认为数学成绩优秀与经常整理数学错题有关吗?
(3)用频率估计概率,在全市中学生中按“经常整理错题”与“不经常整理错题”进行分层抽
样,随机抽取 5 名学生,再从这 5 名学生中随机抽取 2 人进行座谈.这 2 名同学中经常整理
错题且数学成绩优秀的人数 X的分布列和数学期望.
n(ad bc)2 2附: , n a b c d .
(a b)(c d )(a c)(b d )
P( 2 k ) 0.1 0.05 0.01 0.005 0.001
k 2.706 3.841 6.635 7.879 10.828
16. 已知数列 an 的前 n项和 Sn n2 n.
(1)求 an 的通项公式;
b 1(2)设 n ,T ba a n 为数列 n 的前 n项和,若对任意的 n N
*,不等式 Tn n 5恒
n n 1
成立,求实数 的取值范围.
第 4页/共 24页
17. 已知 f x 1 4 x3 bx2 cx bc, 在 x 1处取得极值 ,
3 3
(1)求b,c的值.
(2) f x 在区间 4,4 上的最值.
18. 已知等比数列 an 的前 n项和为 Sn,且 an 1 3 Sn 1 .
(1)求数列 an 的通项公式;
(2)令bn nan,求 bn 的前 n项和Tn ;
1 1 1 8
(3)令 cn an 1,证明: c .1 c2 cn 9
19. 设函数 f x ln x ax, x R.
(1)若 a 1,求 f x 在 e, e 1 处的切线方程;
(2)讨论函数 f x 的单调性;
(3)若 f x x 1恒成立,求实数 a的取值范围.
第 5页/共 24页
凤城二中高二学年 2025年 6月考教学质量检测
高二数学
考试时间:120分钟满分 150分
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
2.答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂
黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案
写在答题卡上.写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、单项选择题:共 8小题,每小题 5分,共 40分.
f x f 1. x f x 已知函数 的图象如图所示, 是 的导函数,则下列数值排序正确
的是( )
A. 0 f 4 f 4 f 3 f 3
B. 0 f 3 f 4 f 4 f 3
C. 0 f 4 f 3 f 4 f 3
D. 0 f 4 f 3 f 4 f 3
【答案】A
【解析】
【分析】根据图象判断函数增长速度即可得解.
【详解】由图可知, f x 的增长速度越来越慢,所以0 f 4 f 3 ,
f
f 4 f 3
4 f 3
表示在 3, 4 上的平均变化率,
4 3
第 6页/共 24页
由图可知0 f 4 f 4 f 3 f 3 .
故选:A
2. 随着我国铁路的发展,列车的正点率有了显著的提高.据统计,途经某车站的只有和谐
号和复兴号列车,且和谐号列车的列次为复兴号列车的列次的 3 倍,和谐号列车的正点率为
0.98,复兴号列车的正点率为 0.99,则一列车能正点到达该车站的概率为( )
A. 0.9825 B. 0.9833 C. 0.9867 D. 0.9875
【答案】A
【解析】
【分析】利用全概率公式可得答案.
3 1
【详解】依题意,设到达该车站列车为和谐号列车的概率为 ,为复兴号列车的概率为 ,
4 4
3 1
则一列车能正点到达该车站的概率为 0.98 0.99 0.9825 .
4 4
故选:A.
3. 随机变量 X N (110,92 ),Y N (100,192 ) ,若 P X A P Y A ,那么实数 A
的值为( )
A. 119 B. 120 C. 121 D. 122
【答案】A
【解析】
【分析】利用正态分布3 原则来研究概率,即可判断各选项.
【详解】当 A 119时,由于 P X 119 P X 110 9 P X ,
P Y 119 P Y 100 19 P Y ,
所以 P X 119 P Y 119 ,故 A 正确,
当 A 120,121,122 时,此时 A 2 ,故无法判断是否相等,故 BCD 都不正确,
故选:A.
1
4. 2若函数 f x lnx x ax在 0, 上单调递增,则实数 a的取值范围是( )
2
A. 2, B. 2, C. , 2 D.
第 7页/共 24页
, 2
【答案】C
【解析】
1 1
【分析】由题意可得 a≤ x对 x 0, 恒成立,利用基本不等式求得 y x的最
x x
小值即可.
【详解】因为函数 f x lnx 1 x2 ax在 0, 上单调递增,
2
所以 f x 1 x a 0对 x 0, a 1恒成立,所以 ≤ x对 x 0, 恒成立,
x x
即 a
1
x 1 ,又 y
1 1
x 2 x 2,当且仅当 x,即 x 1时取等号,
x min x x x
所以 a 2,得到实数 a的取值范围是 , 2 .
故选:C.
5. 某种植基地统计出花卉种植面积 y与年份 x的数据如下:
x 1 2 3 4 5
y 5 7 9 10 14
根据上表数据得到 y关于 x的线性回归方程为 y 2.1x a ,则第 6 年的花卉种植面积约为
( )
A. 17 B. 16 C. 15.3 D. 15
【答案】C
【解析】
【分析】计算平均数可得样本中心,代入回归方程求解 a 2.7,最后将 x 6 代入回归方
程计算即可.
1 2 3 4 5 5 7 9 10 14
【详解】由表中数据可得 x 3, y 9,故样本中心
5 5
为 (3,9),
将 (3,9)代入 y 2.1x a 可得 a 2.7,所以线性回归方程为 y 2.1x 2.7 ,
当 x 6 时, y 2.1 6 2.7 15.3,故第 6 年的花卉种植面积约为15.3 .
第 8页/共 24页
故选:C
6. 已知函数 f x x 1 x 2 x 3 x 4 ,则 f x 的图象在 x 2处的切线方程为
( )
A. 2x y 4 0 B. 2x y 4 0
C. x y 2 0 D. x y 2 0
【答案】A
【解析】
【分析】构建 g x x 1 x 3 x 4 ,可得 f x x 2 g x ,求导,结合导数
的几何意义求切线方程.
【详解】构建 g x x 1 x 3 x 4 ,
则 f x x 2 g x , f x g x x 2 g x ,
可得 f 2 0 , f 2 g 2 2 ,可知切线坐标为 2,0 ,切线斜率 k 2,
所以切线方程为 y 2 x 2 ,即 2x y 4 0 .
故选:A.
7. 已知 f (x)是函数 f (x) 的导函数,对于任意实数 x都有 f (x) f (x) ex (2x 3),
f (0) 4,则不等式 f (x) 4ex的解集为( )
A. ( ,0) (3, ) B. ( , 1) (4, ) C. (0,3) D. ( 1,4)
【答案】A
【解析】
f (x) f (x)
【分析】根据要求解的不等式可变形为 x 4,构造函数 g(x) x ,并结合已知e e
f (x) f (x) ex (2x 3)可得 g(x) x2 3x c,从而得 f (x) e x(x 2 3x c) ,利用
f 0 4 求得参数 c的值,由此可将不等式 f (x) 4ex 化为 x2 3x 4 4 ,即可求得答
案.
g(x) f (x) , f
(x) f (x)
【详解】令 x ① 则 g
(x) ,
e ex
第 9页/共 24页
∵ f (x) f (x) ex (2x 3),
f (x) f (x)
∴ x 2x 3,e
即 g x 2x 3 ,
∴ g(x) x2 3x c(c为常数)②,
f (x)
由①②知, x x
2 3x c ,
e
∴ f (x) e x(x 2 3x c) ,又 f 0 4 ,
∴ e0 c 4 ,即 c 4 ,
f (x)
x x
2 3x 4 ,
e
f (x) 2
不等式 f (x) 4ex 即 x x 3x 4 4,e
∴ x 0 或 x 3,
即不等式 f (x) 4ex的解集为 ,0 3, ,
故选:A.
8. 已知定义在 (0, )的函数 f (x) ,满足 f (x 1) 2 f (x) 2x,且 f (1) 0,则 f (100)
的值为( )
A. 99 299 B. 99 299 C. 100 2100 D.
100 2100
【答案】B
【解析】
x
【分析】通过已知的递推公式 f x 1 2 f x 2 ,逐步推导出 f x 的表达式,进而
求出 f 100 的值.首先对递推公式进行变形,构造出一个新的数列,求出新数列的通项公式,
再得到 f x 的通项公式,最后代入 x 100 求值.
【详解】因为 f x 1 2 f x 2x ,等式两边同时除以 2x 1 ,
f x 1 f x 1
得到 .
2x 1
2x 2
第 10页/共 24页
f xg x 设 ,则 g x 1
f 1
1 g x ,且x g 1 1 0 .2 2 2
所以 g x 1是以 0 为首项, 为公差的等差数列.
2
1 x 1
所以该数列的通项公式为 g x 0 x 1 .
2 2
f x 2x g x 2x x 1 x 1 2x 1所以 .
2
所以 f 100 100 1 2100 1 99 299 .
故选:B.
二、多项选择题:共 3小题,每小题 6分,共 18分.
9. 已知随机事件 A,B发生的概率分别为 P(A) 0.3,P(B) 0.6 ,下列说法正确的有( )
A. 若 P(AB) 0.18,则 A,B相互独立 B. 若 A,B相互独立,则
P B A 0.6
C. 若P B A 0.4 ,则 P(AB) 0.12 D. 若 A B,则 P A B 0.3
【答案】ABC
【解析】
【分析】利用条件概率公式及独立事件的定义逐项分析即得.
【详解】因为随机事件 A,B发生的概率分别为 P(A) 0.3,P(B) 0.6 ,
对于 A,因为 P(AB) 0.18 P(A)P(B) 0.3 0.6 ,所以 A,B相互独立,故 A 正确;
对于 B,若 A,B相互独立,则 P B A P(B) 0.6,故 B 正确;
P AB P AB对于 C,若 P B A 0.4 ,则 P(AB) 0.12,故 C 正确;P A 0.3
P A
对于 D,若 A B,则 P A B 0.3 0.5,故 D 错误.
P B 0.6
故选:ABC
10. 已知数列 an 的首项为 4,且满足 2 n 1 an nan 1 n N* ,则( )
an A. 为等差数列 B. an 为递增数列
n
第 11页/共 24页
2
C. an 的前 n n 2
a
项和 Sn n 1 2 4 D. n n nn 1 的前 n项和T 2 n 2
【答案】BCD
【解析】
a a an
【分析】由 2(n 1)an nan 1得 n 1 2 n ,所以可知数列 是以首项为 4,公比为n 1 n n
2 的等比数列,从而可求出 an n 2
n 1
,可得数列 an 为递增数列,利用错位相减法可求
n 1
得 an 的前 n a n 2项和,由于 nn 1 n,从而利用等差数列的求和公式可求出数列2 2n 1
an
2n 1
的前 n项和Tn .
【详解】对于选项 A:由 2(n 1)an na
a
,得 n 1
a
n 1 2 n ,n 1 n
an a
所以 是以 1 a1 4 为首项,2 为公比的等比数列,故 A 错误; n 1
a
B n 4 2n 1 2n 1 a n 2n 1对于选项 :因为 ,即
n n
,
a 0 an 1 n 1 2
n 2
1
显然 n ,且 n 1 2 1 1,即 an 1 aa n
,
n n 2 n
所以 an 为递增数列,故 B 正确;
C S 1 22 2 23 n 2n 1对于选项 :因为 n ,
2S 3 4 n 2则 n 1 2 2 2 n 2 ,
22 1 2n
两式相减得 S 1 22 23 L 2n 1
n n 2
n 2 n 2n 2 1 n 2n 2 4 ,
1 2
所以 Sn (n 1) 2
n 2 4,故 C 正确;
a n 2n 1
对于选项 D:因为 n ,
2n 1
2n 1
n
an n(1 n) n2 n
所以
2n 1
的前 n项和Tn ,故 D 正确. 2 2
第 12页/共 24页
故选:BCD.
【点睛】方法点睛:错位相减法的关注点
1.适用题型:等差数列 an 与等比数列 bn 对应项相乘 an bn 型数列求和;
2.步骤:①求和时先乘以数列 bn 的公比;②把两个和的形式错位相减.③整理结果形式.
11. 已知函数 f x xex a,则( )
A. f x 在区间 0,2 上单调递增
f x 1B. 有最大值 a
e
C. 当 a 0 时, y f x 的图象过 1,0 的切线有且仅有 2 条
1
D. 关于 x的方程 f x 0有两个不等实根,则 a的取值范围是 ,
e
【答案】AC
【解析】
【分析】利用函数的单调性与导数的关系可判断 A 选项;分析函数 f x 的单调性,利用函
t
数的最值与导数的关系可判断 B 选项;设切点坐标为 t, te ,利用导数求出切线方程,再
将点 1,0 x的坐标代入切线方程,判断关于 t的方程解的个数,可判断 C 选项;令 g x xe ,
求导得到其单调性和最值,数形结合可判断 D 选项.
【详解】对于 A x选项,对任意的 x 0, 2 , f x x 1 e 0恒成立,
所以, f x 在区间 0,2 上单调递增,A 对;
对于 B 选项,当 x 1时, f x 0,当 x 1时, f x 0 .
所以在区间 , 1 上 f x 单调递减,在区间 1, 上 f x 单调递增,
所以 f x 有最小值 f 1 1 a,无最大值,B 错;
e
对于 C 选项,当 a 0 时, f x xe x,设切点为 t, tet ,
f x x 1 ex,则切线斜率为 t 1 et ,
y f x t, tet t t所以曲线 在点 的切线方程为 y te t 1 e x t ,
第 13页/共 24页
将点 1,0 t的坐标代入切线方程为 te 1 t t 1 et,整理可得 t 2 t 1 0,
1 4 5 0 ,即方程 t 2 t 1 0有两个不等的实根,
所以,当 a 0 时, y f x 的图象过 1,0 的切线有且仅有 2 条,C 对;
对于 D 选项,方程 f x 0 ,即 xex a 0 xex a ,
令 g x xe x,而 g x ex xex ex x 1 ,
当 x 1时, g x 0,当 x 1时, g x 0 .
所以在区间 , 1 上 g x 单调递减,在区间 1, 上 g x 单调递增,
当 x 0 时 g x 0 ,且 g 0 0 ,如图,
要使方程 f x 1 0 有两个不等实根, a的范围是 ,0 ,D 错.
e
故选:AC.
三、填空题:共 3小题,每小题 5分,共 15分.
12. 已知数列 an 满足 an+1=3an 4, a1 1,则 an __________.
【答案】3n 2
【解析】
【分析】利用构造法,构造等比数列求通项公式.
【详解】∵ an+1=3an 4,由 an 1 p a an p ,解得 a 3, p 2,
∴有 an 1 2 3 an 2 ,
an 2 是首项为 a1 2 3,公比为 3 的等比数列,
所以 an 2=3
n a =3n,∴ n 2 .
故答案为:3n 2 .
第 14页/共 24页
13. 已知 a,b,c,d 成等差数列,函数 f (x) x3 3bx2 cx b2 在 x 1时有极值 0,则
d a ______.
【答案】21
【解析】
【分析】由 f ( 1) 0, f 1 0,求得b,c,并验证,再结合等差数列概念即可求解.
【详解】 f (x) 3x2 6bx c,
由题意 f ( 1) 0, f 1 0,
1 3b c b2 0 b 2 b 1
即 ,解得: 或 ,
3 6b c 0 c 9 c 3
b 1
当 时, f (x) x3c 3 3x
2 3x 1, f (x) 3x2 6x 3 0,
此时函数单调递增无极值,舍去,
b 2
经验证 符合题意,
c 9
因 a,b,c,d 成等差数列,所以 d a 3 c b 21 .
故答案为: 21
14. 已知函数 f x xex ax bex ab a 0 b 1,若 f x 0,则 的最大值为
a
__________.
【答案】1
【解析】
【分析】由函数不等式恒成立可得a eb,再构造函数 g a ,求导分析单调性,得到最值
即可.
f x xex ax bex【详解】 ab x b ex a ,
因为 f x 0 x恒成立,所以 x b e a 0恒成立,所以 a eb,
b 1 ln a 1
所以 ,
a a
第 15页/共 24页
令 g a ln a 1 ln a , a 0 ,则 g a 2 ,令 g a 0 a 1,a a
所以当 a 0,1 时,g a 0 ,g a 为增函数;当 a 1, 时,g a 0 ,g a 为
减函数;
所以 g a g 1 1,
b 1
所以 的最大值为 1.
a
故答案为:1
四、解答题
15. 为了研究学生每天整理数学错题情况,某课题组在某市中学生中随机抽取了 100 名学生
调查了他们期中考试的数学成绩和平时整理数学错题情况,并绘制了下列两个统计图表,图
1 为学生期中考试数学成绩的频率分布直方图,图 2 为学生一个星期内整理数学错题天数的
扇形图.若本次数学成绩在 110 分及以上视为优秀,将一个星期有 4 天及以上整理数学错题
视为“经常整理”,少于 4 天视为“不经常整理”.已知数学成绩优秀的学生中,经常整理错题
的学生占 70%.
数学成绩优秀 数学成绩不优秀 合计
经常整理
不经常整理
合计
(1)求图 1 中 m的值;
(2)根据图 1、图 2 中的数据,补全上方2 2列联表,根据调查数据回答:在犯错误的概
第 16页/共 24页
率不超过 5%的前提下,可以认为数学成绩优秀与经常整理数学错题有关吗?
(3)用频率估计概率,在全市中学生中按“经常整理错题”与“不经常整理错题”进行分层抽
样,随机抽取 5 名学生,再从这 5 名学生中随机抽取 2 人进行座谈.这 2 名同学中经常整理
错题且数学成绩优秀的人数 X的分布列和数学期望.
n(ad bc)2
附: 2 , n a b c d .
(a b)(c d )(a c)(b d )
P( 2 k ) 0.1 0.05 0.01 0.005 0.001
k 2.706 3.841 6.635 7.879 10.828
【答案】(1)m 0.015
(2)表格见解析,有 (3)分布列见解析, 0.7
【解析】
【分析】(1)利用频率分布直方图各个小矩形的面积和为 1,求出m的值;
(2)先求出数学优秀和不优秀的人,常整理错题和不经常整理错题的人,得到2 2列联表,
根据2 2列联表求出 2 值,从而得出判断;
(3)先求出 X 的可能取值,并求出相应取值的概率,从而求出分布列和期望.
【小问 1 详解】
由题意可得 0.0025 0.005 0.0175 m 0.01 20 1,
解得m 0.015;
【小问 2 详解】
数学成绩优秀的有100 50% 50人,不优秀的人100 50% 50人,
经常整理错题的有100 40% 20% 60 人,不经常整理错题的是100 60 40人,
经常整理错题且成绩优秀的有 50 70% 35人,则
数学成绩优秀 数学成绩不优秀 合计
经常整理 35 25 60
第 17页/共 24页
不经常整理 15 25 40
合计 50 50 100
零假设为H0 :数学成绩优秀与经常整理数学错题无关,
2 100(35 25 15 25)
2 25
根据列联表中的数据,经计算得到可得 4.167 3.841,
50 50 60 40 6
由于 4.167 3.841,所以在犯错误的概率不超过 5%的前提下,
可以认为数学成绩优秀与经常整理数学错题有关联;
【小问 3 详解】
由分层抽样知,随机抽取的 5 名学生中经常整理错题的有 3 人,
不经常整理错题的有 2 人,则 X 可能取为 0,1,2,
经常整理错题的 3 名学生中,恰抽到 k人记为事件 Ak k 0,1,2 ,
Ck C2 k
则 P A 3 2k C2 (k 0,1,2,3)5
参与座谈的 2 名学生中经常整理错题且数学成绩优秀的恰好抽到m人记为事件
Bm m 0,1,2
则 P(B0 | A0 ) 1, P(B | A )
5
0 1 ,P(B0 | A2 ) (
5 )2 25 , P(B | A ) 7 ,
12 12 144 1 1 12
P(B 1 5 7 35 7 2 491 | A2 ) C2 ,P(B2 | A2 ) ( ) ,12 12 72 12 144
P X 0 P A0 P(B0 A0 ) P A1 P(B0 A1) P A2 P(B0 | A2 )
C2 1 12 1 C3C2 5 C
2
3 25 193 2 2 2 ,C5 C5 12 C5 144 480
P X 1 P A1 P(B1 A1) P A2 P(B1 A2 )
C1C1 7 C23 2 3 35 238 2 ,C5 12 C
2
5 72 480
2
P X 2 P A2 P(B
C3 49 49
2 | A2) ,C25 144 480
故 X的分布列如下:
第 18页/共 24页
X 0 1 2
193 238 49
P
480 480 480
193 238 49
则可得 X的数学期望为 E X 0 1 2 0.7.
480 480 480
16. 已知数列 an 的前 n项和 Sn n2 n.
(1)求 an 的通项公式;
1
(2)设b *n ,Tn 为数列 bn 的前 na a 项和,若对任意的 n N ,不等式 Tn n 5恒n n 1
成立,求实数 的取值范围.
【答案】(1) an 2n, n N
(2) , 42
【解析】
【分析】(1)利用 Sn与 an 的关系求出数列 an 的通项公式,
(2)由(1)的结论,用裂项相消法求得Tn ,再根据不等式的恒成立问题以及函数的单调
性与最值,求实数的取值范围.
【小问 1 详解】
当 n 1时, a1 S1 2,
2
当 n 2 时, an Sn Sn 1 n n n 1
2 n 1 2n,
当 n 1时, a1 2成立,
所以 an 2n, n N
【小问 2 详解】
b 1 1 1 1 1由(1)得 n
a a ,n n 1 2n 2n 2 4 n n 1
T 1 1 1 1 1 1 1 1 n所以 n
,
4 2
2 3 n n 1 4 n 1
第 19页/共 24页
T n 5 1 n
n 5 n 1
则 n n 5 4
4 n 5 6 ,
4 n 1 n n
5
由函数 y x 6在 0, 5 上单调递减,在 5, 上单调递增,x
当 x 1时, y 12
21
;当 x 2时, y ;
2
5 32
当 x 3时, y 3 6 ,
3 3
5
所以当 x 2时, 4 n 6 取最小值为 42,所以 42 ,
n
所以实数 的取值范围为 , 42 .
f x 117. 已知 x3 bx2 cx bc 4, 在 x 1处取得极值 ,
3 3
(1)求b,c的值.
(2) f x 在区间 4,4 上的最值.
【答案】(1)b 1,c 3
4 85
(2)最大值为 ,最小值为
3 3
【解析】
4
【分析】(1)求导,利用在 x 1处的导数值为 0,并且 f (1) ,解之检验即可求解;
3
(2)结合(1)的结果,列出在 x [ 4,4]时,随 x的变化, f (x), f (x)的变化情况,进而
即可求解.
【小问 1 详解】
1 3 2
因为函数 f x x bx cx bc,所以 f (x) x 2 2bx c,
3
4
又函数 f (x) 在 x 1处取得极值 .
3
f 1 1 2b c 0 1 2b c
b 1
则有 ,即 1 4 1
,解得:
f 1 b c bc b 1 2b b 1 2b
4
c 3
3 3 3 3
b 1
或
c 1
第 20页/共 24页
经检验,b 1,c 1时, f x x2 2x 1 x 1 2 0, f x 单调递减,无极值不
符合题意,
经检验,b 1,c 3时,符合题意,故b 1,c 3 .
【小问 2 详解】
1
由(1 3 2 2)知:函数 f x x x 3x 3,则 f x x 2x 3,
3
令 f (x) 0,解得: x1 3, x2 1,
在 x [ 4,4]时,随 x的变化, f (x), f (x)的变化情况如下表所示:
x 4 ( 4, 3) 3 ( 1,1) 1 (1, 4) 4
f (x) 0 0
单调递 单调递 单调递
f (x) 29 4 85 12
3 减 增 3 减 3
由表可知:当 x 1时,函数 f (x) 有极大值 f (1)
4
;
3
当 x 3时,函数 f (x) 有极小值 f ( 3) 12;
因为 f ( 4) 29 , f (4) 85 ,
3 3
故函数 f (x) 在[ 4,4] 85上的最小值为 f (4) ,最大值为 f (1) 4 .
3 3
18. 已知等比数列 an 的前 n项和为 Sn,且 an 1 3 Sn 1 .
(1)求数列 an 的通项公式;
(2)令bn nan,求 bn 的前 n项和Tn ;
1 1 1 8
(3)令 cn an 1,证明: c1 c2 c
.
n 9
n- 1
【答案】(1) an = 3 4
第 21页/共 24页
T n 1 n 1(2) n 4
3 3
(3)证明见解析
【解析】
【分析】(1)根据 an 和 Sn关系求得 an 1 4an n 2 ,即可求出公比 q 4,再利用条件
求出 a1 3,即可求解通项公式.
(2)利用错位相减法求和即可.
1 1 2
(3)通过变形得 n 1 dc 3 4 1 3 4n 1 n,结合等比数列求和公式及数列的有界性证n
明即可.
【小问 1 详解】
由 an 1 3 Sn 1 ,得 an 3 Sn 1 1 n 2 ,
两式相减,得 an 1 an 3an n 2 ,
即 an 1 4an n 2 ,又 an 是等比数列,故公比q 4,
由 a n- 12 3 a1 1 4a1,知 a1 3,则 an = 3 4 .
【小问 2 详解】
n 1
由题bn nan 3n 4 ,
则Tn 3 4
0 6 41 3n 4n 1,
4Tn 3 4
1 6 42 3n 4n,
两式相减,得
3 1 4n
3Tn 3 1 41 42 4n 1 3n 4n 3n 4n 1 3n 4n 1,1 4
T 1 n 1即 n n 4 .
3 3
【小问 3 详解】
第 22页/共 24页
2 1 3 4n 1 1 1cn an 1 3 4n 1 1,由 3 4n 1 0,3 4n 1 1 3 4n 1 3 4n 1 1
1 1 2
得: n 1 dcn 3 4 1 3 4
n 1 n
2 n 1
1
1 1 1 3 4
则 d1 d2 d
8 1 1 8 .
c c c n n 1 2 n 1 1 9 4 9
4
19. 设函数 f x ln x ax, x R.
(1)若 a 1,求 f x 在 e, e 1 处的切线方程;
(2)讨论函数 f x 的单调性;
(3)若 f x x 1恒成立,求实数 a的取值范围.
1
【答案】(1) y 1e
x
,1 1 (2)答案见解析 (3)
e2
【解析】
'
【分析】(1)先求 f x ,进而求切线斜率,再用点斜式求方程即可;
2 a 0 a 0 f '( )分 和 两种情况,分别研究 x 的正负性即可;
x 1 ln x
(3)利用参变分离,构造函数 g x ,求其最小值即可.
x
【小问 1 详解】
由题意 f x ln x x f ',得 x 1 1 1,所以切线的斜率为 k 1,
x e
y 1 1e, e 1 所以曲线在 处的切线方程为 1 x e e 1,即 y 1 x,
e e
则 f x 1在 e, e 1 处的切线方程为 y 1 x .
e
【小问 2 详解】
第 23页/共 24页
由 f x ln x ax ' 1,则 f x a, x 0 ,
x
a 0 f '当 时, x 0恒成立,则 f x 在 0, 上单调递增;
a 0 '
1 ' 1
当 时, f x 0得0 x ; f x 0得 x ,
a a
则 f x 在 0,
1 1 上单调递增,在 ,
上单调递减.
a a
综上,当 a 0时, f x 在 0, 上单调递增;
1 1
当 a 0 时, f x 在 0, 上单调递增,在 , 上单调递减.
a a
【小问 3 详解】
由题意 ln x ax x 1恒成立,
a x 1 ln x a
x 1 ln x
因为 x 0 ,即得 恒成立,即 x
, x 0 ,
x min
g x x 1 ln x
1 1 x 0 x x 1 ln x 记 , ,则 g ' x x ln x 2 ,x 2 x x2
令 g ' x 0 '得 0 x e2 ; g x 0 可得 x e2 ,
则 g x 在 0,e2 2上单调递减,在 e , 上单调递增,
2 1 1
所以 g x gmin e 1 2 ,所以a 1 e e2 ,
1
则实数 a的取值范围为 ,1 2 . e
第 24页/共 24页
高二数学
考试时间:120分钟满分 150分
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
2.答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂
黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案
写在答题卡上.写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、单项选择题:共 8小题,每小题 5分,共 40分.
f x f x f x
1. 已知函数 的图象如图所示, 是 的导函数,则下列数值排序正确
的是( )
A. 0 f 4 f 4 f 3 f 3
B. 0 f 3 f 4 f 4 f 3
C. 0 f 4 f 3 f 4 f 3
D. 0 f 4 f 3 f 4 f 3
2. 随着我国铁路的发展,列车的正点率有了显著的提高.据统计,途经某车站的只有和谐
号和复兴号列车,且和谐号列车的列次为复兴号列车的列次的 3 倍,和谐号列车的正点率为
0.98,复兴号列车的正点率为 0.99,则一列车能正点到达该车站的概率为( )
A. 0.9825 B. 0.9833 C. 0.9867 D. 0.9875
3. 随机变量 X N (110,92 ),Y N (100,192 ) ,若 P X A P Y A ,那么实数 A
的值为( )
第 1页/共 24页
A. 119 B. 120 C. 121 D. 122
1
4. 2若函数 f x lnx x ax在 0, 上单调递增,则实数 a的取值范围是( )
2
A. 2, B. 2, C. , 2 D.
, 2
5. 某种植基地统计出花卉种植面积 y与年份 x的数据如下:
x 1 2 3 4 5
y 5 7 9 10 14
根据上表数据得到 y关于 x的线性回归方程为 y 2.1x a ,则第 6 年的花卉种植面积约为
( )
A. 17 B. 16 C. 15.3 D. 15
6. 已知函数 f x x 1 x 2 x 3 x 4 ,则 f x 的图象在 x 2处的切线方程为
( )
A. 2x y 4 0 B. 2x y 4 0
C. x y 2 0 D. x y 2 0
7. 已知 f (x)是函数 f (x) 的导函数,对于任意实数 x都有 f (x) f (x) ex (2x 3),
f (0) 4,则不等式 f (x) 4ex的解集为( )
A. ( ,0) (3, ) B. ( , 1) (4, ) C. (0,3) D. ( 1,4)
8. 已知定义在 (0, )的函数 f (x) ,满足 f (x 1) 2 f (x) 2x,且 f (1) 0,则 f (100)
的值为( )
A. 99 299 B. 99 299 C. 100 2100 D.
100 2100
二、多项选择题:共 3小题,每小题 6分,共 18分.
9. 已知随机事件 A,B发生的概率分别为 P(A) 0.3,P(B) 0.6 ,下列说法正确的有( )
A. 若 P(AB) 0.18,则 A,B相互独立 B. 若 A,B相互独立,则
P B A 0.6
第 2页/共 24页
C. 若P B A 0.4 ,则 P(AB) 0.12 D. 若 A B,则 P A B 0.3
10. 已知数列 an 的首项为 4,且满足 2 n 1 an nan 1 n N* ,则( )
a
A. n 为等差数列 B. an 为递增数列
n
2
C. a n 2n 的前 n项和 Sn n 1 2 4
a
D. n n n n
2n 1
的前 项和T
n 2
11. f x xex已知函数 a,则( )
A. f x 在区间 0,2 上单调递增
B. f x 1有最大值 a
e
C. 当 a 0 时, y f x 的图象过 1,0 的切线有且仅有 2 条
1
D. 关于 x的方程 f x 0有两个不等实根,则 a的取值范围是 ,
e
三、填空题:共 3小题,每小题 5分,共 15分.
12. 已知数列 an 满足 an+1=3an 4, a1 1,则 an __________.
13. 已知 a,b,c,d 成等差数列,函数 f (x) x3 3bx2 cx b2 在 x 1时有极值 0,则
d a ______.
14. x x
b 1
已知函数 f x xe ax be ab a 0 ,若 f x 0,则 的最大值为
a
__________.
四、解答题
15. 为了研究学生每天整理数学错题情况,某课题组在某市中学生中随机抽取了 100 名学生
调查了他们期中考试的数学成绩和平时整理数学错题情况,并绘制了下列两个统计图表,图
1 为学生期中考试数学成绩的频率分布直方图,图 2 为学生一个星期内整理数学错题天数的
扇形图.若本次数学成绩在 110 分及以上视为优秀,将一个星期有 4 天及以上整理数学错题
视为“经常整理”,少于 4 天视为“不经常整理”.已知数学成绩优秀的学生中,经常整理错题
的学生占 70%.
第 3页/共 24页
数学成绩优秀 数学成绩不优秀 合计
经常整理
不经常整理
合计
(1)求图 1 中 m的值;
(2)根据图 1、图 2 中的数据,补全上方2 2列联表,根据调查数据回答:在犯错误的概
率不超过 5%的前提下,可以认为数学成绩优秀与经常整理数学错题有关吗?
(3)用频率估计概率,在全市中学生中按“经常整理错题”与“不经常整理错题”进行分层抽
样,随机抽取 5 名学生,再从这 5 名学生中随机抽取 2 人进行座谈.这 2 名同学中经常整理
错题且数学成绩优秀的人数 X的分布列和数学期望.
n(ad bc)2 2附: , n a b c d .
(a b)(c d )(a c)(b d )
P( 2 k ) 0.1 0.05 0.01 0.005 0.001
k 2.706 3.841 6.635 7.879 10.828
16. 已知数列 an 的前 n项和 Sn n2 n.
(1)求 an 的通项公式;
b 1(2)设 n ,T ba a n 为数列 n 的前 n项和,若对任意的 n N
*,不等式 Tn n 5恒
n n 1
成立,求实数 的取值范围.
第 4页/共 24页
17. 已知 f x 1 4 x3 bx2 cx bc, 在 x 1处取得极值 ,
3 3
(1)求b,c的值.
(2) f x 在区间 4,4 上的最值.
18. 已知等比数列 an 的前 n项和为 Sn,且 an 1 3 Sn 1 .
(1)求数列 an 的通项公式;
(2)令bn nan,求 bn 的前 n项和Tn ;
1 1 1 8
(3)令 cn an 1,证明: c .1 c2 cn 9
19. 设函数 f x ln x ax, x R.
(1)若 a 1,求 f x 在 e, e 1 处的切线方程;
(2)讨论函数 f x 的单调性;
(3)若 f x x 1恒成立,求实数 a的取值范围.
第 5页/共 24页
凤城二中高二学年 2025年 6月考教学质量检测
高二数学
考试时间:120分钟满分 150分
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
2.答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂
黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案
写在答题卡上.写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、单项选择题:共 8小题,每小题 5分,共 40分.
f x f 1. x f x 已知函数 的图象如图所示, 是 的导函数,则下列数值排序正确
的是( )
A. 0 f 4 f 4 f 3 f 3
B. 0 f 3 f 4 f 4 f 3
C. 0 f 4 f 3 f 4 f 3
D. 0 f 4 f 3 f 4 f 3
【答案】A
【解析】
【分析】根据图象判断函数增长速度即可得解.
【详解】由图可知, f x 的增长速度越来越慢,所以0 f 4 f 3 ,
f
f 4 f 3
4 f 3
表示在 3, 4 上的平均变化率,
4 3
第 6页/共 24页
由图可知0 f 4 f 4 f 3 f 3 .
故选:A
2. 随着我国铁路的发展,列车的正点率有了显著的提高.据统计,途经某车站的只有和谐
号和复兴号列车,且和谐号列车的列次为复兴号列车的列次的 3 倍,和谐号列车的正点率为
0.98,复兴号列车的正点率为 0.99,则一列车能正点到达该车站的概率为( )
A. 0.9825 B. 0.9833 C. 0.9867 D. 0.9875
【答案】A
【解析】
【分析】利用全概率公式可得答案.
3 1
【详解】依题意,设到达该车站列车为和谐号列车的概率为 ,为复兴号列车的概率为 ,
4 4
3 1
则一列车能正点到达该车站的概率为 0.98 0.99 0.9825 .
4 4
故选:A.
3. 随机变量 X N (110,92 ),Y N (100,192 ) ,若 P X A P Y A ,那么实数 A
的值为( )
A. 119 B. 120 C. 121 D. 122
【答案】A
【解析】
【分析】利用正态分布3 原则来研究概率,即可判断各选项.
【详解】当 A 119时,由于 P X 119 P X 110 9 P X ,
P Y 119 P Y 100 19 P Y ,
所以 P X 119 P Y 119 ,故 A 正确,
当 A 120,121,122 时,此时 A 2 ,故无法判断是否相等,故 BCD 都不正确,
故选:A.
1
4. 2若函数 f x lnx x ax在 0, 上单调递增,则实数 a的取值范围是( )
2
A. 2, B. 2, C. , 2 D.
第 7页/共 24页
, 2
【答案】C
【解析】
1 1
【分析】由题意可得 a≤ x对 x 0, 恒成立,利用基本不等式求得 y x的最
x x
小值即可.
【详解】因为函数 f x lnx 1 x2 ax在 0, 上单调递增,
2
所以 f x 1 x a 0对 x 0, a 1恒成立,所以 ≤ x对 x 0, 恒成立,
x x
即 a
1
x 1 ,又 y
1 1
x 2 x 2,当且仅当 x,即 x 1时取等号,
x min x x x
所以 a 2,得到实数 a的取值范围是 , 2 .
故选:C.
5. 某种植基地统计出花卉种植面积 y与年份 x的数据如下:
x 1 2 3 4 5
y 5 7 9 10 14
根据上表数据得到 y关于 x的线性回归方程为 y 2.1x a ,则第 6 年的花卉种植面积约为
( )
A. 17 B. 16 C. 15.3 D. 15
【答案】C
【解析】
【分析】计算平均数可得样本中心,代入回归方程求解 a 2.7,最后将 x 6 代入回归方
程计算即可.
1 2 3 4 5 5 7 9 10 14
【详解】由表中数据可得 x 3, y 9,故样本中心
5 5
为 (3,9),
将 (3,9)代入 y 2.1x a 可得 a 2.7,所以线性回归方程为 y 2.1x 2.7 ,
当 x 6 时, y 2.1 6 2.7 15.3,故第 6 年的花卉种植面积约为15.3 .
第 8页/共 24页
故选:C
6. 已知函数 f x x 1 x 2 x 3 x 4 ,则 f x 的图象在 x 2处的切线方程为
( )
A. 2x y 4 0 B. 2x y 4 0
C. x y 2 0 D. x y 2 0
【答案】A
【解析】
【分析】构建 g x x 1 x 3 x 4 ,可得 f x x 2 g x ,求导,结合导数
的几何意义求切线方程.
【详解】构建 g x x 1 x 3 x 4 ,
则 f x x 2 g x , f x g x x 2 g x ,
可得 f 2 0 , f 2 g 2 2 ,可知切线坐标为 2,0 ,切线斜率 k 2,
所以切线方程为 y 2 x 2 ,即 2x y 4 0 .
故选:A.
7. 已知 f (x)是函数 f (x) 的导函数,对于任意实数 x都有 f (x) f (x) ex (2x 3),
f (0) 4,则不等式 f (x) 4ex的解集为( )
A. ( ,0) (3, ) B. ( , 1) (4, ) C. (0,3) D. ( 1,4)
【答案】A
【解析】
f (x) f (x)
【分析】根据要求解的不等式可变形为 x 4,构造函数 g(x) x ,并结合已知e e
f (x) f (x) ex (2x 3)可得 g(x) x2 3x c,从而得 f (x) e x(x 2 3x c) ,利用
f 0 4 求得参数 c的值,由此可将不等式 f (x) 4ex 化为 x2 3x 4 4 ,即可求得答
案.
g(x) f (x) , f
(x) f (x)
【详解】令 x ① 则 g
(x) ,
e ex
第 9页/共 24页
∵ f (x) f (x) ex (2x 3),
f (x) f (x)
∴ x 2x 3,e
即 g x 2x 3 ,
∴ g(x) x2 3x c(c为常数)②,
f (x)
由①②知, x x
2 3x c ,
e
∴ f (x) e x(x 2 3x c) ,又 f 0 4 ,
∴ e0 c 4 ,即 c 4 ,
f (x)
x x
2 3x 4 ,
e
f (x) 2
不等式 f (x) 4ex 即 x x 3x 4 4,e
∴ x 0 或 x 3,
即不等式 f (x) 4ex的解集为 ,0 3, ,
故选:A.
8. 已知定义在 (0, )的函数 f (x) ,满足 f (x 1) 2 f (x) 2x,且 f (1) 0,则 f (100)
的值为( )
A. 99 299 B. 99 299 C. 100 2100 D.
100 2100
【答案】B
【解析】
x
【分析】通过已知的递推公式 f x 1 2 f x 2 ,逐步推导出 f x 的表达式,进而
求出 f 100 的值.首先对递推公式进行变形,构造出一个新的数列,求出新数列的通项公式,
再得到 f x 的通项公式,最后代入 x 100 求值.
【详解】因为 f x 1 2 f x 2x ,等式两边同时除以 2x 1 ,
f x 1 f x 1
得到 .
2x 1
2x 2
第 10页/共 24页
f xg x 设 ,则 g x 1
f 1
1 g x ,且x g 1 1 0 .2 2 2
所以 g x 1是以 0 为首项, 为公差的等差数列.
2
1 x 1
所以该数列的通项公式为 g x 0 x 1 .
2 2
f x 2x g x 2x x 1 x 1 2x 1所以 .
2
所以 f 100 100 1 2100 1 99 299 .
故选:B.
二、多项选择题:共 3小题,每小题 6分,共 18分.
9. 已知随机事件 A,B发生的概率分别为 P(A) 0.3,P(B) 0.6 ,下列说法正确的有( )
A. 若 P(AB) 0.18,则 A,B相互独立 B. 若 A,B相互独立,则
P B A 0.6
C. 若P B A 0.4 ,则 P(AB) 0.12 D. 若 A B,则 P A B 0.3
【答案】ABC
【解析】
【分析】利用条件概率公式及独立事件的定义逐项分析即得.
【详解】因为随机事件 A,B发生的概率分别为 P(A) 0.3,P(B) 0.6 ,
对于 A,因为 P(AB) 0.18 P(A)P(B) 0.3 0.6 ,所以 A,B相互独立,故 A 正确;
对于 B,若 A,B相互独立,则 P B A P(B) 0.6,故 B 正确;
P AB P AB对于 C,若 P B A 0.4 ,则 P(AB) 0.12,故 C 正确;P A 0.3
P A
对于 D,若 A B,则 P A B 0.3 0.5,故 D 错误.
P B 0.6
故选:ABC
10. 已知数列 an 的首项为 4,且满足 2 n 1 an nan 1 n N* ,则( )
an A. 为等差数列 B. an 为递增数列
n
第 11页/共 24页
2
C. an 的前 n n 2
a
项和 Sn n 1 2 4 D. n n nn 1 的前 n项和T 2 n 2
【答案】BCD
【解析】
a a an
【分析】由 2(n 1)an nan 1得 n 1 2 n ,所以可知数列 是以首项为 4,公比为n 1 n n
2 的等比数列,从而可求出 an n 2
n 1
,可得数列 an 为递增数列,利用错位相减法可求
n 1
得 an 的前 n a n 2项和,由于 nn 1 n,从而利用等差数列的求和公式可求出数列2 2n 1
an
2n 1
的前 n项和Tn .
【详解】对于选项 A:由 2(n 1)an na
a
,得 n 1
a
n 1 2 n ,n 1 n
an a
所以 是以 1 a1 4 为首项,2 为公比的等比数列,故 A 错误; n 1
a
B n 4 2n 1 2n 1 a n 2n 1对于选项 :因为 ,即
n n
,
a 0 an 1 n 1 2
n 2
1
显然 n ,且 n 1 2 1 1,即 an 1 aa n
,
n n 2 n
所以 an 为递增数列,故 B 正确;
C S 1 22 2 23 n 2n 1对于选项 :因为 n ,
2S 3 4 n 2则 n 1 2 2 2 n 2 ,
22 1 2n
两式相减得 S 1 22 23 L 2n 1
n n 2
n 2 n 2n 2 1 n 2n 2 4 ,
1 2
所以 Sn (n 1) 2
n 2 4,故 C 正确;
a n 2n 1
对于选项 D:因为 n ,
2n 1
2n 1
n
an n(1 n) n2 n
所以
2n 1
的前 n项和Tn ,故 D 正确. 2 2
第 12页/共 24页
故选:BCD.
【点睛】方法点睛:错位相减法的关注点
1.适用题型:等差数列 an 与等比数列 bn 对应项相乘 an bn 型数列求和;
2.步骤:①求和时先乘以数列 bn 的公比;②把两个和的形式错位相减.③整理结果形式.
11. 已知函数 f x xex a,则( )
A. f x 在区间 0,2 上单调递增
f x 1B. 有最大值 a
e
C. 当 a 0 时, y f x 的图象过 1,0 的切线有且仅有 2 条
1
D. 关于 x的方程 f x 0有两个不等实根,则 a的取值范围是 ,
e
【答案】AC
【解析】
【分析】利用函数的单调性与导数的关系可判断 A 选项;分析函数 f x 的单调性,利用函
t
数的最值与导数的关系可判断 B 选项;设切点坐标为 t, te ,利用导数求出切线方程,再
将点 1,0 x的坐标代入切线方程,判断关于 t的方程解的个数,可判断 C 选项;令 g x xe ,
求导得到其单调性和最值,数形结合可判断 D 选项.
【详解】对于 A x选项,对任意的 x 0, 2 , f x x 1 e 0恒成立,
所以, f x 在区间 0,2 上单调递增,A 对;
对于 B 选项,当 x 1时, f x 0,当 x 1时, f x 0 .
所以在区间 , 1 上 f x 单调递减,在区间 1, 上 f x 单调递增,
所以 f x 有最小值 f 1 1 a,无最大值,B 错;
e
对于 C 选项,当 a 0 时, f x xe x,设切点为 t, tet ,
f x x 1 ex,则切线斜率为 t 1 et ,
y f x t, tet t t所以曲线 在点 的切线方程为 y te t 1 e x t ,
第 13页/共 24页
将点 1,0 t的坐标代入切线方程为 te 1 t t 1 et,整理可得 t 2 t 1 0,
1 4 5 0 ,即方程 t 2 t 1 0有两个不等的实根,
所以,当 a 0 时, y f x 的图象过 1,0 的切线有且仅有 2 条,C 对;
对于 D 选项,方程 f x 0 ,即 xex a 0 xex a ,
令 g x xe x,而 g x ex xex ex x 1 ,
当 x 1时, g x 0,当 x 1时, g x 0 .
所以在区间 , 1 上 g x 单调递减,在区间 1, 上 g x 单调递增,
当 x 0 时 g x 0 ,且 g 0 0 ,如图,
要使方程 f x 1 0 有两个不等实根, a的范围是 ,0 ,D 错.
e
故选:AC.
三、填空题:共 3小题,每小题 5分,共 15分.
12. 已知数列 an 满足 an+1=3an 4, a1 1,则 an __________.
【答案】3n 2
【解析】
【分析】利用构造法,构造等比数列求通项公式.
【详解】∵ an+1=3an 4,由 an 1 p a an p ,解得 a 3, p 2,
∴有 an 1 2 3 an 2 ,
an 2 是首项为 a1 2 3,公比为 3 的等比数列,
所以 an 2=3
n a =3n,∴ n 2 .
故答案为:3n 2 .
第 14页/共 24页
13. 已知 a,b,c,d 成等差数列,函数 f (x) x3 3bx2 cx b2 在 x 1时有极值 0,则
d a ______.
【答案】21
【解析】
【分析】由 f ( 1) 0, f 1 0,求得b,c,并验证,再结合等差数列概念即可求解.
【详解】 f (x) 3x2 6bx c,
由题意 f ( 1) 0, f 1 0,
1 3b c b2 0 b 2 b 1
即 ,解得: 或 ,
3 6b c 0 c 9 c 3
b 1
当 时, f (x) x3c 3 3x
2 3x 1, f (x) 3x2 6x 3 0,
此时函数单调递增无极值,舍去,
b 2
经验证 符合题意,
c 9
因 a,b,c,d 成等差数列,所以 d a 3 c b 21 .
故答案为: 21
14. 已知函数 f x xex ax bex ab a 0 b 1,若 f x 0,则 的最大值为
a
__________.
【答案】1
【解析】
【分析】由函数不等式恒成立可得a eb,再构造函数 g a ,求导分析单调性,得到最值
即可.
f x xex ax bex【详解】 ab x b ex a ,
因为 f x 0 x恒成立,所以 x b e a 0恒成立,所以 a eb,
b 1 ln a 1
所以 ,
a a
第 15页/共 24页
令 g a ln a 1 ln a , a 0 ,则 g a 2 ,令 g a 0 a 1,a a
所以当 a 0,1 时,g a 0 ,g a 为增函数;当 a 1, 时,g a 0 ,g a 为
减函数;
所以 g a g 1 1,
b 1
所以 的最大值为 1.
a
故答案为:1
四、解答题
15. 为了研究学生每天整理数学错题情况,某课题组在某市中学生中随机抽取了 100 名学生
调查了他们期中考试的数学成绩和平时整理数学错题情况,并绘制了下列两个统计图表,图
1 为学生期中考试数学成绩的频率分布直方图,图 2 为学生一个星期内整理数学错题天数的
扇形图.若本次数学成绩在 110 分及以上视为优秀,将一个星期有 4 天及以上整理数学错题
视为“经常整理”,少于 4 天视为“不经常整理”.已知数学成绩优秀的学生中,经常整理错题
的学生占 70%.
数学成绩优秀 数学成绩不优秀 合计
经常整理
不经常整理
合计
(1)求图 1 中 m的值;
(2)根据图 1、图 2 中的数据,补全上方2 2列联表,根据调查数据回答:在犯错误的概
第 16页/共 24页
率不超过 5%的前提下,可以认为数学成绩优秀与经常整理数学错题有关吗?
(3)用频率估计概率,在全市中学生中按“经常整理错题”与“不经常整理错题”进行分层抽
样,随机抽取 5 名学生,再从这 5 名学生中随机抽取 2 人进行座谈.这 2 名同学中经常整理
错题且数学成绩优秀的人数 X的分布列和数学期望.
n(ad bc)2
附: 2 , n a b c d .
(a b)(c d )(a c)(b d )
P( 2 k ) 0.1 0.05 0.01 0.005 0.001
k 2.706 3.841 6.635 7.879 10.828
【答案】(1)m 0.015
(2)表格见解析,有 (3)分布列见解析, 0.7
【解析】
【分析】(1)利用频率分布直方图各个小矩形的面积和为 1,求出m的值;
(2)先求出数学优秀和不优秀的人,常整理错题和不经常整理错题的人,得到2 2列联表,
根据2 2列联表求出 2 值,从而得出判断;
(3)先求出 X 的可能取值,并求出相应取值的概率,从而求出分布列和期望.
【小问 1 详解】
由题意可得 0.0025 0.005 0.0175 m 0.01 20 1,
解得m 0.015;
【小问 2 详解】
数学成绩优秀的有100 50% 50人,不优秀的人100 50% 50人,
经常整理错题的有100 40% 20% 60 人,不经常整理错题的是100 60 40人,
经常整理错题且成绩优秀的有 50 70% 35人,则
数学成绩优秀 数学成绩不优秀 合计
经常整理 35 25 60
第 17页/共 24页
不经常整理 15 25 40
合计 50 50 100
零假设为H0 :数学成绩优秀与经常整理数学错题无关,
2 100(35 25 15 25)
2 25
根据列联表中的数据,经计算得到可得 4.167 3.841,
50 50 60 40 6
由于 4.167 3.841,所以在犯错误的概率不超过 5%的前提下,
可以认为数学成绩优秀与经常整理数学错题有关联;
【小问 3 详解】
由分层抽样知,随机抽取的 5 名学生中经常整理错题的有 3 人,
不经常整理错题的有 2 人,则 X 可能取为 0,1,2,
经常整理错题的 3 名学生中,恰抽到 k人记为事件 Ak k 0,1,2 ,
Ck C2 k
则 P A 3 2k C2 (k 0,1,2,3)5
参与座谈的 2 名学生中经常整理错题且数学成绩优秀的恰好抽到m人记为事件
Bm m 0,1,2
则 P(B0 | A0 ) 1, P(B | A )
5
0 1 ,P(B0 | A2 ) (
5 )2 25 , P(B | A ) 7 ,
12 12 144 1 1 12
P(B 1 5 7 35 7 2 491 | A2 ) C2 ,P(B2 | A2 ) ( ) ,12 12 72 12 144
P X 0 P A0 P(B0 A0 ) P A1 P(B0 A1) P A2 P(B0 | A2 )
C2 1 12 1 C3C2 5 C
2
3 25 193 2 2 2 ,C5 C5 12 C5 144 480
P X 1 P A1 P(B1 A1) P A2 P(B1 A2 )
C1C1 7 C23 2 3 35 238 2 ,C5 12 C
2
5 72 480
2
P X 2 P A2 P(B
C3 49 49
2 | A2) ,C25 144 480
故 X的分布列如下:
第 18页/共 24页
X 0 1 2
193 238 49
P
480 480 480
193 238 49
则可得 X的数学期望为 E X 0 1 2 0.7.
480 480 480
16. 已知数列 an 的前 n项和 Sn n2 n.
(1)求 an 的通项公式;
1
(2)设b *n ,Tn 为数列 bn 的前 na a 项和,若对任意的 n N ,不等式 Tn n 5恒n n 1
成立,求实数 的取值范围.
【答案】(1) an 2n, n N
(2) , 42
【解析】
【分析】(1)利用 Sn与 an 的关系求出数列 an 的通项公式,
(2)由(1)的结论,用裂项相消法求得Tn ,再根据不等式的恒成立问题以及函数的单调
性与最值,求实数的取值范围.
【小问 1 详解】
当 n 1时, a1 S1 2,
2
当 n 2 时, an Sn Sn 1 n n n 1
2 n 1 2n,
当 n 1时, a1 2成立,
所以 an 2n, n N
【小问 2 详解】
b 1 1 1 1 1由(1)得 n
a a ,n n 1 2n 2n 2 4 n n 1
T 1 1 1 1 1 1 1 1 n所以 n
,
4 2
2 3 n n 1 4 n 1
第 19页/共 24页
T n 5 1 n
n 5 n 1
则 n n 5 4
4 n 5 6 ,
4 n 1 n n
5
由函数 y x 6在 0, 5 上单调递减,在 5, 上单调递增,x
当 x 1时, y 12
21
;当 x 2时, y ;
2
5 32
当 x 3时, y 3 6 ,
3 3
5
所以当 x 2时, 4 n 6 取最小值为 42,所以 42 ,
n
所以实数 的取值范围为 , 42 .
f x 117. 已知 x3 bx2 cx bc 4, 在 x 1处取得极值 ,
3 3
(1)求b,c的值.
(2) f x 在区间 4,4 上的最值.
【答案】(1)b 1,c 3
4 85
(2)最大值为 ,最小值为
3 3
【解析】
4
【分析】(1)求导,利用在 x 1处的导数值为 0,并且 f (1) ,解之检验即可求解;
3
(2)结合(1)的结果,列出在 x [ 4,4]时,随 x的变化, f (x), f (x)的变化情况,进而
即可求解.
【小问 1 详解】
1 3 2
因为函数 f x x bx cx bc,所以 f (x) x 2 2bx c,
3
4
又函数 f (x) 在 x 1处取得极值 .
3
f 1 1 2b c 0 1 2b c
b 1
则有 ,即 1 4 1
,解得:
f 1 b c bc b 1 2b b 1 2b
4
c 3
3 3 3 3
b 1
或
c 1
第 20页/共 24页
经检验,b 1,c 1时, f x x2 2x 1 x 1 2 0, f x 单调递减,无极值不
符合题意,
经检验,b 1,c 3时,符合题意,故b 1,c 3 .
【小问 2 详解】
1
由(1 3 2 2)知:函数 f x x x 3x 3,则 f x x 2x 3,
3
令 f (x) 0,解得: x1 3, x2 1,
在 x [ 4,4]时,随 x的变化, f (x), f (x)的变化情况如下表所示:
x 4 ( 4, 3) 3 ( 1,1) 1 (1, 4) 4
f (x) 0 0
单调递 单调递 单调递
f (x) 29 4 85 12
3 减 增 3 减 3
由表可知:当 x 1时,函数 f (x) 有极大值 f (1)
4
;
3
当 x 3时,函数 f (x) 有极小值 f ( 3) 12;
因为 f ( 4) 29 , f (4) 85 ,
3 3
故函数 f (x) 在[ 4,4] 85上的最小值为 f (4) ,最大值为 f (1) 4 .
3 3
18. 已知等比数列 an 的前 n项和为 Sn,且 an 1 3 Sn 1 .
(1)求数列 an 的通项公式;
(2)令bn nan,求 bn 的前 n项和Tn ;
1 1 1 8
(3)令 cn an 1,证明: c1 c2 c
.
n 9
n- 1
【答案】(1) an = 3 4
第 21页/共 24页
T n 1 n 1(2) n 4
3 3
(3)证明见解析
【解析】
【分析】(1)根据 an 和 Sn关系求得 an 1 4an n 2 ,即可求出公比 q 4,再利用条件
求出 a1 3,即可求解通项公式.
(2)利用错位相减法求和即可.
1 1 2
(3)通过变形得 n 1 dc 3 4 1 3 4n 1 n,结合等比数列求和公式及数列的有界性证n
明即可.
【小问 1 详解】
由 an 1 3 Sn 1 ,得 an 3 Sn 1 1 n 2 ,
两式相减,得 an 1 an 3an n 2 ,
即 an 1 4an n 2 ,又 an 是等比数列,故公比q 4,
由 a n- 12 3 a1 1 4a1,知 a1 3,则 an = 3 4 .
【小问 2 详解】
n 1
由题bn nan 3n 4 ,
则Tn 3 4
0 6 41 3n 4n 1,
4Tn 3 4
1 6 42 3n 4n,
两式相减,得
3 1 4n
3Tn 3 1 41 42 4n 1 3n 4n 3n 4n 1 3n 4n 1,1 4
T 1 n 1即 n n 4 .
3 3
【小问 3 详解】
第 22页/共 24页
2 1 3 4n 1 1 1cn an 1 3 4n 1 1,由 3 4n 1 0,3 4n 1 1 3 4n 1 3 4n 1 1
1 1 2
得: n 1 dcn 3 4 1 3 4
n 1 n
2 n 1
1
1 1 1 3 4
则 d1 d2 d
8 1 1 8 .
c c c n n 1 2 n 1 1 9 4 9
4
19. 设函数 f x ln x ax, x R.
(1)若 a 1,求 f x 在 e, e 1 处的切线方程;
(2)讨论函数 f x 的单调性;
(3)若 f x x 1恒成立,求实数 a的取值范围.
1
【答案】(1) y 1e
x
,1 1 (2)答案见解析 (3)
e2
【解析】
'
【分析】(1)先求 f x ,进而求切线斜率,再用点斜式求方程即可;
2 a 0 a 0 f '( )分 和 两种情况,分别研究 x 的正负性即可;
x 1 ln x
(3)利用参变分离,构造函数 g x ,求其最小值即可.
x
【小问 1 详解】
由题意 f x ln x x f ',得 x 1 1 1,所以切线的斜率为 k 1,
x e
y 1 1e, e 1 所以曲线在 处的切线方程为 1 x e e 1,即 y 1 x,
e e
则 f x 1在 e, e 1 处的切线方程为 y 1 x .
e
【小问 2 详解】
第 23页/共 24页
由 f x ln x ax ' 1,则 f x a, x 0 ,
x
a 0 f '当 时, x 0恒成立,则 f x 在 0, 上单调递增;
a 0 '
1 ' 1
当 时, f x 0得0 x ; f x 0得 x ,
a a
则 f x 在 0,
1 1 上单调递增,在 ,
上单调递减.
a a
综上,当 a 0时, f x 在 0, 上单调递增;
1 1
当 a 0 时, f x 在 0, 上单调递增,在 , 上单调递减.
a a
【小问 3 详解】
由题意 ln x ax x 1恒成立,
a x 1 ln x a
x 1 ln x
因为 x 0 ,即得 恒成立,即 x
, x 0 ,
x min
g x x 1 ln x
1 1 x 0 x x 1 ln x 记 , ,则 g ' x x ln x 2 ,x 2 x x2
令 g ' x 0 '得 0 x e2 ; g x 0 可得 x e2 ,
则 g x 在 0,e2 2上单调递减,在 e , 上单调递增,
2 1 1
所以 g x gmin e 1 2 ,所以a 1 e e2 ,
1
则实数 a的取值范围为 ,1 2 . e
第 24页/共 24页
同课章节目录
