2024-2025学年五年级下册数学期末高频易错押题培优卷(北京版)(含答案解析)
文档属性
| 名称 | 2024-2025学年五年级下册数学期末高频易错押题培优卷(北京版)(含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 356.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-25 12:05:30 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024-2025学年五年级下册数学期末高频易错押题培优卷(北京版)
一、填空题
1.在计算+时,先找到分母的最小公倍数是 ,再通分成同分母分数进行计算,最后将结果约分成最简分数是 。
2.在1—20中,既不是合数,也不是质数的是 ;既是奇数,又是合数的是 ;既是偶数,又是质数的是 。
3.在所有是20的倍数的正整数中,不超过2023并且是14的倍数的数之和是 。
4.一个正方体的每个面上都写有一个汉字,其平面展开图如图所示,那么在该正方体中,和“超”相对的字是 。
5.淘气在算一个分数加上时,错算成了减去,结果得,正确结果应该是 。
6.,,(n为质数),A、B两个数的最大公因数是 ,最小公倍数是 。
7.一个长方体底面积是80平方厘米,高是7分米,它的体积是 立方厘米。
8.把、18.3%,,1.83按从小到大的顺序排列。
< < < 。
9. ÷8== = = = (填小数)
10.在两位数中,同时能被3和5整除的最大奇数是 。
11.把化为假分数是 ;把化为小数是 ;把化为带分数是 。
12.有一塔形几何体由若干个正方体构成,构成方式如下图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点。已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是 。
13.一根3米长的方钢,把它横截成3段时,表面积增加60平方厘米,原来方钢的体积是 立方厘米。
二、判断题
14.两个长方体的表面积相等,它们的体积一定相等。( )
15.如果一个自然数既是3的倍数,又是5的倍数,那么它一定是一个奇数。( )
16.一个合数至少有3个因数。( )
17.自然数可以分为奇数和偶数;也可以分为质数和合数。( )
18.两个质数的积一定是合数.( )
19.乘数的末尾有2个0,积的末尾一定有2个0。( )
20.1 的分数单位是 ,再添3个这样的分数单位是最小的质数。( )
21.自然数a能整除自然数b,a又能被自然数c整除,则a、b、c的最小公倍数是b.(自然数a、b、c不等于0)。( )
22.用4个同样大小的小正方体能拼成一个大正方体。( )
三、单选题
23.用三个棱长都是a厘米的正方体拼成一个长方体,拼成的长方体的表面积是( )平方厘米。
A.18a2 B.16a2 C.14a2 D.12a2
24.制作一个长方体的鱼缸,要用多少玻璃是求鱼缸的( )
A.棱长总和 B.表面积 C.体积 D.容积
25. (偶数)如果用a表示自然数,那么偶数可以表示为( )。
A.a+2 B.2a C.2a-1 D.a-2
26.如图图形是正方体平面展开图的共有( )个。
A.2 B.3 C.4
27.盒子里有6个黄球,4个红球,每次摸一个,至少摸( )次一定会摸到红球。
A.7 B.6 C.5
28.偶数+奇数=( )
A.偶数 B.奇数 C.可能是偶数,也可能是奇数
29.在所有的质数中,偶数有( )个。
A.0 B.1 C.2
30.一个长4dm宽3dm,高5dm的长方体鱼缸,倒入水后量得水深3.5dm,倒入的水是( )L。
A.60 B.52.5 C.42
31.著名的哥德巴赫猜想说的是:“一个较大的偶合数一定可以写成两个奇质数的和”。你能举例验证吗?下面的( )组算式可以验证这个猜想。
A.14=3+11 16=7+9 B.48=11+37 32=13+19 C.48=23+25 36=17+19
32.一条绳子,对折三次,其中一段是这条绳子的( )
A. B. C.
四、计算题
33.直接写得数。
72÷3= 12×20= 125×8×0= 408÷2=
100-17=
34.计算下面各题,能简算的要简算。
35.解方程
(1)x+ = (2)x- = (3)1-x=
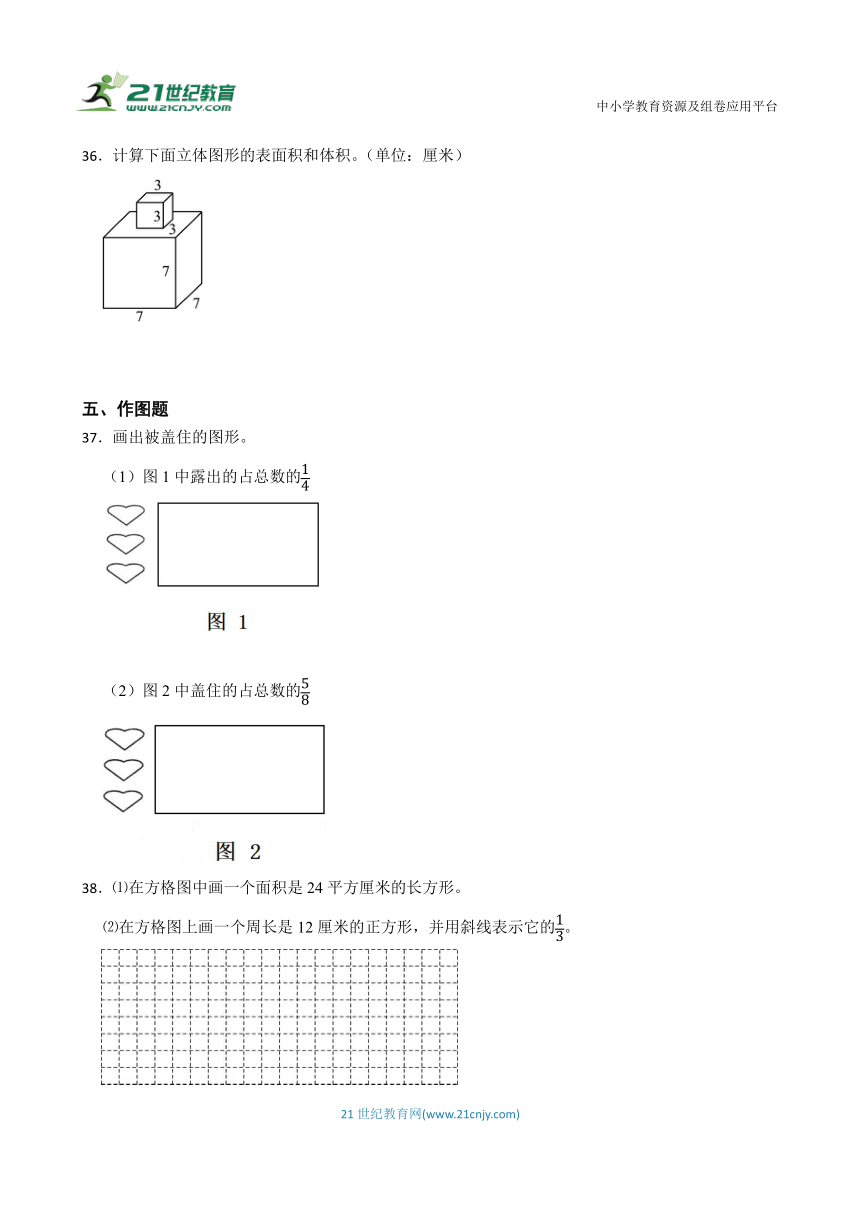
36.计算下面立体图形的表面积和体积。(单位:厘米)
五、作图题
37.画出被盖住的图形。
(1)图1中露出的占总数的
(2)图2中盖住的占总数的
38.⑴在方格图中画一个面积是24平方厘米的长方形。
⑵在方格图上画一个周长是12厘米的正方形,并用斜线表示它的。
六、解决问题
39.五(1)班有48名同学分成若干个学习小组,要求每组人数相同且至少有2人,有几种不同的分法?
40.有一批文章共15篇,各篇文章的页数是1页、2页、3页、、14页和15页的稿纸,如果将这些文章按某种次序装订成册,并统一编上页码,那么每篇文章的第一页是奇数页码的文章最多有多少篇?
41.某实验小学五(1)班的学生人数在40~50之间。如果每排站4人,正好站完;如果每排站6人,也正好站完。你能求出这个班有多少名学生吗?
42.“星星”花店将24朵玫瑰和36朵康乃馨扎成花束。要求每束花中两种花都有,并且每束花中每种花的朵数相同(所有花全部用完),最多可以扎多少束花?此时每束花中玫瑰和康乃馨各多少朵?
43.一块长12cm、宽8cm、高5cm的长方体铝锭,与另一块棱长为3cm的正方体铝锭,正好熔铸成一个底面边长为13cm2的正方形的长方体铝块。熔铸成的铝块高是多少厘米?
44.一盒铅笔平均分给一些同学,可以分给8个人,也可以分给10个人,都能刚好分完。这盒铅笔至少有几支?
45.在学校举办的读书日活动中,五(2)班有的同学借了《爱克斯探长》,的同学借了《荒岛历险》,的同学借了《奇妙的数学王国》,的同学借了《数学魔法师》,还有的同学借了《童趣逻辑》。请问,借阅哪些书籍的同学一样多
46.一根桥墩全长12m,垂直打入水中。打入河底淤泥的部分长 m,比露出水面的部分少水深多少米?
47.一个长方体水箱里装有15cm高的水,聪聪把一个直径6cm的铁球放入水中,水面上升了0.6cm,弟弟把一块石块放进了水箱,石块没入水中后水面又上升了1.5cm,问这块石块的体积是多少?
48.超白玻璃鱼缸备受水族爱好者们的青睐。
(1)下图这个无盖超白玻璃鱼缸的长是60厘米,高和宽都是40厘米,做这个鱼缸至少需要多少平方厘米的超白玻璃?
(2)若在这个鱼缸里放一座假山,会看到假山完全沉入水中,并且水面上升了3厘米,则这座假山的体积是多少立方厘米?
参考答案及试题解析
1.【答案】70;
【解析】解:
14和35的最小公倍数是:
7×2×5
=14×5
=70
+
=+
=。
故答案为:70;。
【分析】异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算;其中,通分时分母的最小公倍数用短除法求出。
2.【答案】1;9、15;2
3.【答案】14700
【解析】解:20和14的最小公倍数是140,在所有是20的倍数的正整数中,不超过2023并且是14的倍数最小是140,140×2=280,140×3=420,……,140×14=1960,140×15=2100,因为2100>2023,所以2100不符合要求,因此最大是1960,共14个;140+280+420+……+1960
=
=14700
故答案为:14700。
【分析】最小公倍数找法:
第一种方法是枚举法,将两个数的倍数分别列举出来,再从中找到最小的公倍数;
第二种方法是短除法,先用这两个数公有的质因数同时去除这两个数,直到所得的商互质(即没有公因数)为止,再将所有的除数与商相乘(即短除号左边和最下边的数),乘积即为这两个数的最小公倍数;
第三种方法利用分解质因数的方法,先将两个数分别写成质因数相乘的算式,再把相同的质因与不同质因数相乘,积即为最小公倍数;
分析题意可知需要找20和14的公倍数中不超过2023的公倍数,并且求和。所以需要先找到20和14的最小公倍数,然后用最小公倍数去乘2,去乘3……找到最小公倍数小于2023的所有倍数,然后将这些倍数及最小公倍数相加即可解答。
4.【答案】自
【解析】“信”和“着”相对, “沉” 和 “越” 相对, “超” 和 “自”相对。
故答案为:自。
【分析】本题是对正方体展开图的空间能力考查,因为图为展开图,可以对展开图进行逐层还原,先封顶,即“自”作为正方体的顶先盖上,然后再围边,即正对着我们的是“信”,向右一次是“沉”、“着”,这时会发现该折“超”了,而“超”在着的下面,因此可以断定,“超”是封底。底面和顶面是对应的,而顶面是“自”,因此得出答案。
5.【答案】
【解析】解:+=
+=
故答案为:。
【分析】根据题意,用加得到原来的另一个加数,再与相加,计算出正确的结果即可。
6.【答案】2n;30n
【解析】解:最大公因数为2n
最小公倍数为2×3×5×n=30n
故答案为:2n;30n。
【分析】最大公因数是两个数的公有质因数的乘积,最小公倍数是两个数的公有质因数和各自独有质因数的乘积,所以用最小公倍数除以最大公因数就得到了两个数的独有质因数的乘积,进而组合成要求的数即可。
7.【答案】5600
【解析】解:7分米=70厘米
80×70=5600(立方厘米)。
故答案为:5600。
【分析】长方体的体积=底面积×高。
8.【答案】18.3%;1.83;;
【解析】解:=1.833……;18.3%=0.183;=1.838383……;1.83;从小到大排列是:18.3%<1.83<<。
故答案为:18.3%;1.83;;。
【分析】用分子除以分母把分数化成小数;把百分数的百分号去掉,小数点向左移动两位,把百分数化成小数;把循环小数用普通表示法表示出来;然后根据小数大小的比较方法从小到大排列即可。
9.【答案】6;12;15;36;0.75
【解析】解:8÷4=2,3×2=6;9÷3=3,4×3=12;27÷3=9,4×9=36;
所以:6÷8=====0.75。
故答案为:6;12;15;36;0.75。
【分析】分数的分子相当于被除数,分母相当于除数。根据分数与除法的关系结合分数的基本性质确定被除数、分子或分母。用分子除以分母把分数化成小数。
10.【答案】75
【解析】解:在两位数中,同时能被3和5整除的最大奇数是75。
故答案为:75。
【分析】两位数中,要同时能被3和5整除,而且是奇数,那么这个两位数的个位是5,然后根据3的倍数的特征作答即可。
11.【答案】;3.25;
【解析】解:==;
=13÷4=3.25;
17÷6=2......5,=。
故答案为:;3.25;。
【分析】带分数化假分数:带分数的整数部分乘分母加分子得到的数作为假分数的分子,分母不变;
分数化小数:用分子除以分母,商写成小数的形式;
假分数化带分数:分子÷分母=商......余数;商就是带分数的整数部分,余数就是带分数的分子,分母不变。
12.【答案】6个
【解析】解:此几何体不论有多少层,其上、下表面积是固定不变的,为 ,
它的每个侧面的面积应该超过 。
最底层的正方体的单个侧面面积为 ,往上依次为2,1, , ,……
前五层正方体的单个侧面面积和为 ,
所以要想超过 ,至少应该是6个。
故答案为:6个
【分析】观察图形可知,此几何体不论有多少层,其上、下表面积是固定不变的,这个图形的表面积等于最下面的正方体的6个面的面积加上上面的几个小正方体的4个面的面积,根据题干分析,可得相邻两个正方体中,上边一个正方体的一个面积为下边一个正方体的一个面积的一半,最下面的正方体一个面的面积是2×2=4,由此即可得出倒数第二个正方体一个面的面积是2,倒数第三个正方体的一个面的面积是1,由此类推依次为: , ,……
13.【答案】4500
【解析】解:3米=30厘米
60÷4×300
=15×300
=4500(立方厘米)
故答案为:4500。
【分析】把它横截成3段,表面积就会增加4个横截面的面积,所以用横截面面积乘方钢的长度即可求出体积。注意统一单位。
14.【答案】错误
【解析】解:假设一个长方体的长、宽、高分别为6厘米、4厘米、2厘米;
另一个长方体的长、宽、高分别为10厘米、2厘米、2厘米;
表面积:(6×4+6×2+4×2)×2
=44×2
=88(平方厘米);
体积:6×4×2=48(立方厘米);
表面积:(10×2+10×2+2×2)×2
=44×2
=88(平方厘米);
体积:10×2×2=40(立方厘米);
所以两个长方体的表面积相等时,它们的体积不一定相等,原题说法错误。
故答案为:错误。
【分析】 长方体的表面积=(长×宽+长×高+宽×高)×2;长方体体积=长×宽×高,长方体的表面积相等,但它们的体积不一定相等,可举例判断。
15.【答案】错误
【解析】奇数的倍数不一定是奇数。如果一个自然数既是3的倍数,又是5的倍数,那么它的末位数是0或5,且各位数的和是3的倍数;当这个数的个位是0,且各位数相加的和是3的倍数时,它也是2的倍数,那么这个数是偶数,所以满足条件的数不一定是奇数.
故答案为:错误.
【分析】根据2、3、5的倍数特征进行解答.
16.【答案】正确
【解析】解:根据合数的定义可知,一个合数至少有3个因数,原题说法正确.
故答案为:正确
【分析】合数是除了1和本身外还有其它因数的数,因此一个合数的因数大于2,例如4的因数是1、2、4,所以合数至少有3个因数.
17.【答案】错误
【解析】自然数可以分为奇数和偶数;也可以分为质数、合数和1。原题说法错误。
故答案为:错误。
【分析】1既不是质数,又不是合数。所以按质数合数分,自然数分为三类,质数、合数和1。
18.【答案】正确
【解析】解:两个质数相乘得到的积,除了1和它本身外,还有这两个质数是它的因数.它有4个因数,所以一定是合数.
故答案为:正确.
【分析】一个数除了1和它本身还有其它因数,这样的数就是合数.
19.【答案】错误
【解析】解:200×5=1000,所以乘数末尾有2个0,积的末尾不一定有2个0,所以原题说法错误。
故答案为:错误。
【分析】偶数乘以5,积的末尾会出现0,所以本题采用举例法,即200×5的乘积去判断即可。
20.【答案】正确
【解析】解:1的分数单位是,再添上3个这样的分数单位是最小的质数,说法正确。
故答案为:正确。
【分析】把单位“1”平均分成若干份取其中的一份的数,叫做分数单位。即分子是1,分母是正整数的分数,又叫单位分数,记为。带分数的分数单位是与分数部分的分数单位相同。
最小的质数是2,所以用2-1得出的分数中的分子是几,就再添上几个这样的分数单位。
21.【答案】正确
【解析】b是a的倍数,a是c的倍数,那么b既是a的倍数又是c的倍数,则a、b、c的最小公倍数是b;原题说法正确.
故答案为:正确
【分析】自然数a能整除自然数b,b是a的倍数;a又能被自然数c整除,则a是c的倍数,那么b也是c的倍数;一个数是另外两个数的倍数,这个数就是这三个数的最小公倍数.
22.【答案】错误
【解析】2×2×2=8,小正方体拼大正方体,最少需要8个,本题错。
故答案为:错误。
【分析】大正方体最小时,一边有两个正方体,一共需要8个正方体。
23.【答案】C
【解析】长方体的表面积为:6a2×3-4a2=14a2(平方厘米); 故选:C.
【分析】棱长是a厘米的正方体的一个面的面积是a2;三个正方体拼组成一个长方体后,表面积减少了4个正方体的面,由此即可计算出这个长方体的表面积解答问题.
24.【答案】B
【解析】解:制作一个长方体的鱼缸,要用多少玻璃是求鱼缸的表面积。
故答案为:B。
【分析】求长方体或正方体6个面积的总面积,就是求它的表面积,本题中求鱼缸用的玻璃就是求5个面的总面积,即表面积。
25.【答案】B
【解析】解: 肯定是 2 的倍数,即 是偶数。
故答案为:B
【分析】本题主要考查偶数的定义和表示方式。偶数是能够被2整除的整数,即2的倍数。因此,要表示一个偶数,可以使用2乘以一个自然数的方式来表示。
26.【答案】B
【解析】从左往右,图1、2、4是正方体的展开图。
故答案为:B。
【分析】正方体的展开图有如下类型:第一类,141型,中间四连方,两侧各一个,共六种;第二类,132型,中间三连方,两侧各有一、二个,共三种;第三类,222型,中间二连方,两侧各有二个,只有一种;第四类,33型,两排各三个,只有一种,据此判断。
27.【答案】A
【解析】解:6+1=7(次)
故答案为:A。
【分析】考虑最不利的原则,前6次都是摸到的黄球,黄球没有了,再摸一次,一定能摸到红球。
28.【答案】B
【解析】 偶数+奇数=奇数。
故答案为:B。
【分析】奇数:不能被2整除的整数。
偶数:能够被2整除的整数。
29.【答案】B
【解析】解:在所有的质数中,只有2是偶数,所以偶数的个数有一个.
故答案为:B。
【分析】在所有的质数中,只有2既是质数又是偶数。
30.【答案】C
【解析】解:4×3×3.5=42dm3=42L,所以倒入的水是42L。
故答案为:C。
【分析】倒入水的体积=长×宽×倒入水的深度,据此代入数据作答即可。
31.【答案】B
【解析】A、9不是质数,故A错误;
B、48和32均为偶合数,11、37和13、19均为奇质数,故正确;
C、25不是质数,故错误;
故答案为:B
【分析】偶数都是2的倍数,不是2的倍数的数是奇数;合数是指这个数除了1和它本身以外还有其他的因数,质数只有1和它本身两个因数。根据以上定义判断三个选项是否符合要求。
32.【答案】C
【解析】解:一条绳子,对折三次,这条绳子被平均分成8份,其中一段是这条绳子的 。
故答案为:C。
【分析】一条绳子对折1次,平均分成两段,再对折一次平均分成4段,对折三次就平均分成8段。根据分数的意义确定其中一段是这条绳子的几分之几。
33.【答案】72÷3=24 12×20=240 125×8×0=0 408÷2=204
+=1 1-= -= 100-17=83
【解析】同分母分数相加减,分母不变,分子相加减;三位数除以一位数,先用被除数最高位上的数去除,如果它比除数小,就用前两位上的数去除,用哪一位上的数去除,商就和那一位对齐,每次除后余下的数必须比除数小;因数末尾有0的乘法,可以先把0前面的数相乘,再在积的末尾添上0。
34.【答案】(1) (2) (3)
=12- = =
=10 =
【解析】 题目需要计算三个分数运算表达式,其中可能涉及简算方法的应用。首先观察每个表达式的特点,判断能否通过运算顺序调整、通分或结合律等方法简化计算过程。
35.【答案】(1)解:
x=
(2)解:
x=
(3)解:1-x=
x=1-
x=
【解析】解方程要掌握等式的性质,即等式两边同时加上或减去一个相同的数,同时乘或除以一个相同的数(0除外),等式仍然成立。
36.【答案】表面积330平方厘米;体积370立方厘米
37.【答案】(1)解:
(2)解:
【解析】(1)图1中露出的占总数的,说明共有4份,每份是3个心形,再画3份;
(2)图2中盖住的占总数的,说明共有8个心形,露出了3个,盖住了5个,再画5个心形。
38.【答案】解:(1)长方形长画6格,宽画4格,长方形面积是6×4=24(平方厘米)
(2)正方形边长12÷4=3(厘米),正方形面积是3×3=9(平方厘米),它的是3格;
【解析】(1)长方形面积=长×宽;
(2)正方形的周长÷4=正方形的边长,正方形的边长×正方形的边长=正方形的面积,把正方形的面积平均分成3份,其中的1份用斜线表示。
39.【答案】解:48的因数有:1、2、3、4、6、8、12、16、24、48,要求每组人数相同且至少有2人,每个小组的人数有2人,3人,4人,6人,8人,12人,16人,24人,一共有8种不同的分法。(48人是一个班,不是一个组)
【解析】因为要把同学的分成若干个学习小组,而且每组的人数相同,所以本题就是求48的因数,据此作答即可。
40.【答案】解:7+4=11(篇)
答:每篇文章的第一页是奇数页码的文章最多有11篇。
【解析】先将偶数页的文章(2页、4页、···、14页)编排,这样共有7篇文章的第一页都是奇数页码。然后将奇数页的文章(1页、3页、5页、7页、9页、11页、13页和15页)依次编排,这样编排的1页、5页、9页和13页的4篇文章的第一页都是奇数页码。因此每篇文章的第一页是奇数页码的文章最多是 11篇。
41.【答案】解:
4和6的最小公倍数是2×2×3
=4×3
=12
12×4=48(名)
答:这个班有48名学生。
【解析】这个班有学生的人数=4和6的最小公倍数×4。
42.【答案】解:
所以36和24的最大公因数是:2×2×3
=4×3
=12
36÷12=3(朵)
24÷12=2(朵)
答:最多能扎12束,此时每束花中玫瑰有2朵,康乃馨有3朵。
【解析】最多可以扎的束数=24和36的最大公因数,用短除法求出;此时每束花中玫瑰的朵数=玫瑰花的总朵数÷24和36的最大公因数,每束花中康乃馨的朵数=康乃馨的总朵数÷24和36的最大公因数。
43.【答案】解:12×8×5+3×3×3
=480+27
=507(cm3)
507÷(13×13)=3(cm)
答:熔铸成的铝块高是3 cm。
【解析】长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,熔铸成的铝块的体积原长方体铅锭和正方体铅锭之和,先求出熔铸成的铝块的体积,利用体积除以底面积得到熔铸成的铝块高度。
44.【答案】解:[8,10]=40
答:这盒铅笔至少有40 支。
【解析】铅笔的总数一定是8和10的公倍数,由此求出8和10的最小公倍数就是这盒铅笔至少的只数。
45.【答案】解:
==
==
答:借阅 《奇妙的数学王国》 和 《童趣逻辑》 的同学人数一样多;
借阅 《爱克斯探长》 、 《荒岛历险》 、 《数学魔法师》 的同学人数一样多。
【解析】分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变。据此计算后再比较大小。
46.【答案】解:
=
=12-4.3
=7.7(m);
答:水深7.7m。
【解析】露出水面的部分就是+m,用全长减去河底淤泥的部分和露出水面的部分的和即可。
47.【答案】解:根据球的体积公式计算铁球体积:V球= πr3,
= ×3.14× ,
= ×3.14×27,
=3.14×36,
=113.04(立方厘米);
水箱的底面积:113.04÷0.6=188.4(平方厘米);
石块的体积:188.4×1.5=282.6(立方厘米);
答:这块石块的体积是282.6立方厘米
【解析】先依据放入铁球后升高的水的体积就等于铁球的体积,即可求出水箱的底面积,铁球的直径已知,从而可以求其体积,也就能求出水箱的底面积;投入石块后水面上升的高度已知,用水箱底面积成升高的水面高度,就是石块的体积.解答此题的关键是:先求出水箱的底面积,主要依据是浸入水中的物体体积,就等于升高部分的水的体积.
48.【答案】(1)解:60×40×3
=2400×3
=7200(平方厘米)
40×40×2
=1600×2
=3200(平方厘米)
7200+3200=10400(平方厘米)
答:做这个鱼缸至少需要10400平方厘米的超白玻璃。
(2)解:60×40×3
=2400×3
=7200(立方厘米)
答:这座假山的体积是7200立方厘米。
【解析】(1)此题主要考查了无盖长方体表面积的应用,高和宽相等,则前面、后面和底面的面积相等,左右侧面的面积相等,由此计算出5个面的面积之和即可;
(2)将假山放入鱼缸中,假山完全沉入水中,水面上升部分的体积就是假山的体积,鱼缸的长×宽×上升的水面高度=假山的体积。
21世纪教育网(www.21cnjy.com)
2024-2025学年五年级下册数学期末高频易错押题培优卷(北京版)
一、填空题
1.在计算+时,先找到分母的最小公倍数是 ,再通分成同分母分数进行计算,最后将结果约分成最简分数是 。
2.在1—20中,既不是合数,也不是质数的是 ;既是奇数,又是合数的是 ;既是偶数,又是质数的是 。
3.在所有是20的倍数的正整数中,不超过2023并且是14的倍数的数之和是 。
4.一个正方体的每个面上都写有一个汉字,其平面展开图如图所示,那么在该正方体中,和“超”相对的字是 。
5.淘气在算一个分数加上时,错算成了减去,结果得,正确结果应该是 。
6.,,(n为质数),A、B两个数的最大公因数是 ,最小公倍数是 。
7.一个长方体底面积是80平方厘米,高是7分米,它的体积是 立方厘米。
8.把、18.3%,,1.83按从小到大的顺序排列。
< < < 。
9. ÷8== = = = (填小数)
10.在两位数中,同时能被3和5整除的最大奇数是 。
11.把化为假分数是 ;把化为小数是 ;把化为带分数是 。
12.有一塔形几何体由若干个正方体构成,构成方式如下图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点。已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是 。
13.一根3米长的方钢,把它横截成3段时,表面积增加60平方厘米,原来方钢的体积是 立方厘米。
二、判断题
14.两个长方体的表面积相等,它们的体积一定相等。( )
15.如果一个自然数既是3的倍数,又是5的倍数,那么它一定是一个奇数。( )
16.一个合数至少有3个因数。( )
17.自然数可以分为奇数和偶数;也可以分为质数和合数。( )
18.两个质数的积一定是合数.( )
19.乘数的末尾有2个0,积的末尾一定有2个0。( )
20.1 的分数单位是 ,再添3个这样的分数单位是最小的质数。( )
21.自然数a能整除自然数b,a又能被自然数c整除,则a、b、c的最小公倍数是b.(自然数a、b、c不等于0)。( )
22.用4个同样大小的小正方体能拼成一个大正方体。( )
三、单选题
23.用三个棱长都是a厘米的正方体拼成一个长方体,拼成的长方体的表面积是( )平方厘米。
A.18a2 B.16a2 C.14a2 D.12a2
24.制作一个长方体的鱼缸,要用多少玻璃是求鱼缸的( )
A.棱长总和 B.表面积 C.体积 D.容积
25. (偶数)如果用a表示自然数,那么偶数可以表示为( )。
A.a+2 B.2a C.2a-1 D.a-2
26.如图图形是正方体平面展开图的共有( )个。
A.2 B.3 C.4
27.盒子里有6个黄球,4个红球,每次摸一个,至少摸( )次一定会摸到红球。
A.7 B.6 C.5
28.偶数+奇数=( )
A.偶数 B.奇数 C.可能是偶数,也可能是奇数
29.在所有的质数中,偶数有( )个。
A.0 B.1 C.2
30.一个长4dm宽3dm,高5dm的长方体鱼缸,倒入水后量得水深3.5dm,倒入的水是( )L。
A.60 B.52.5 C.42
31.著名的哥德巴赫猜想说的是:“一个较大的偶合数一定可以写成两个奇质数的和”。你能举例验证吗?下面的( )组算式可以验证这个猜想。
A.14=3+11 16=7+9 B.48=11+37 32=13+19 C.48=23+25 36=17+19
32.一条绳子,对折三次,其中一段是这条绳子的( )
A. B. C.
四、计算题
33.直接写得数。
72÷3= 12×20= 125×8×0= 408÷2=
100-17=
34.计算下面各题,能简算的要简算。
35.解方程
(1)x+ = (2)x- = (3)1-x=
36.计算下面立体图形的表面积和体积。(单位:厘米)
五、作图题
37.画出被盖住的图形。
(1)图1中露出的占总数的
(2)图2中盖住的占总数的
38.⑴在方格图中画一个面积是24平方厘米的长方形。
⑵在方格图上画一个周长是12厘米的正方形,并用斜线表示它的。
六、解决问题
39.五(1)班有48名同学分成若干个学习小组,要求每组人数相同且至少有2人,有几种不同的分法?
40.有一批文章共15篇,各篇文章的页数是1页、2页、3页、、14页和15页的稿纸,如果将这些文章按某种次序装订成册,并统一编上页码,那么每篇文章的第一页是奇数页码的文章最多有多少篇?
41.某实验小学五(1)班的学生人数在40~50之间。如果每排站4人,正好站完;如果每排站6人,也正好站完。你能求出这个班有多少名学生吗?
42.“星星”花店将24朵玫瑰和36朵康乃馨扎成花束。要求每束花中两种花都有,并且每束花中每种花的朵数相同(所有花全部用完),最多可以扎多少束花?此时每束花中玫瑰和康乃馨各多少朵?
43.一块长12cm、宽8cm、高5cm的长方体铝锭,与另一块棱长为3cm的正方体铝锭,正好熔铸成一个底面边长为13cm2的正方形的长方体铝块。熔铸成的铝块高是多少厘米?
44.一盒铅笔平均分给一些同学,可以分给8个人,也可以分给10个人,都能刚好分完。这盒铅笔至少有几支?
45.在学校举办的读书日活动中,五(2)班有的同学借了《爱克斯探长》,的同学借了《荒岛历险》,的同学借了《奇妙的数学王国》,的同学借了《数学魔法师》,还有的同学借了《童趣逻辑》。请问,借阅哪些书籍的同学一样多
46.一根桥墩全长12m,垂直打入水中。打入河底淤泥的部分长 m,比露出水面的部分少水深多少米?
47.一个长方体水箱里装有15cm高的水,聪聪把一个直径6cm的铁球放入水中,水面上升了0.6cm,弟弟把一块石块放进了水箱,石块没入水中后水面又上升了1.5cm,问这块石块的体积是多少?
48.超白玻璃鱼缸备受水族爱好者们的青睐。
(1)下图这个无盖超白玻璃鱼缸的长是60厘米,高和宽都是40厘米,做这个鱼缸至少需要多少平方厘米的超白玻璃?
(2)若在这个鱼缸里放一座假山,会看到假山完全沉入水中,并且水面上升了3厘米,则这座假山的体积是多少立方厘米?
参考答案及试题解析
1.【答案】70;
【解析】解:
14和35的最小公倍数是:
7×2×5
=14×5
=70
+
=+
=。
故答案为:70;。
【分析】异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算;其中,通分时分母的最小公倍数用短除法求出。
2.【答案】1;9、15;2
3.【答案】14700
【解析】解:20和14的最小公倍数是140,在所有是20的倍数的正整数中,不超过2023并且是14的倍数最小是140,140×2=280,140×3=420,……,140×14=1960,140×15=2100,因为2100>2023,所以2100不符合要求,因此最大是1960,共14个;140+280+420+……+1960
=
=14700
故答案为:14700。
【分析】最小公倍数找法:
第一种方法是枚举法,将两个数的倍数分别列举出来,再从中找到最小的公倍数;
第二种方法是短除法,先用这两个数公有的质因数同时去除这两个数,直到所得的商互质(即没有公因数)为止,再将所有的除数与商相乘(即短除号左边和最下边的数),乘积即为这两个数的最小公倍数;
第三种方法利用分解质因数的方法,先将两个数分别写成质因数相乘的算式,再把相同的质因与不同质因数相乘,积即为最小公倍数;
分析题意可知需要找20和14的公倍数中不超过2023的公倍数,并且求和。所以需要先找到20和14的最小公倍数,然后用最小公倍数去乘2,去乘3……找到最小公倍数小于2023的所有倍数,然后将这些倍数及最小公倍数相加即可解答。
4.【答案】自
【解析】“信”和“着”相对, “沉” 和 “越” 相对, “超” 和 “自”相对。
故答案为:自。
【分析】本题是对正方体展开图的空间能力考查,因为图为展开图,可以对展开图进行逐层还原,先封顶,即“自”作为正方体的顶先盖上,然后再围边,即正对着我们的是“信”,向右一次是“沉”、“着”,这时会发现该折“超”了,而“超”在着的下面,因此可以断定,“超”是封底。底面和顶面是对应的,而顶面是“自”,因此得出答案。
5.【答案】
【解析】解:+=
+=
故答案为:。
【分析】根据题意,用加得到原来的另一个加数,再与相加,计算出正确的结果即可。
6.【答案】2n;30n
【解析】解:最大公因数为2n
最小公倍数为2×3×5×n=30n
故答案为:2n;30n。
【分析】最大公因数是两个数的公有质因数的乘积,最小公倍数是两个数的公有质因数和各自独有质因数的乘积,所以用最小公倍数除以最大公因数就得到了两个数的独有质因数的乘积,进而组合成要求的数即可。
7.【答案】5600
【解析】解:7分米=70厘米
80×70=5600(立方厘米)。
故答案为:5600。
【分析】长方体的体积=底面积×高。
8.【答案】18.3%;1.83;;
【解析】解:=1.833……;18.3%=0.183;=1.838383……;1.83;从小到大排列是:18.3%<1.83<<。
故答案为:18.3%;1.83;;。
【分析】用分子除以分母把分数化成小数;把百分数的百分号去掉,小数点向左移动两位,把百分数化成小数;把循环小数用普通表示法表示出来;然后根据小数大小的比较方法从小到大排列即可。
9.【答案】6;12;15;36;0.75
【解析】解:8÷4=2,3×2=6;9÷3=3,4×3=12;27÷3=9,4×9=36;
所以:6÷8=====0.75。
故答案为:6;12;15;36;0.75。
【分析】分数的分子相当于被除数,分母相当于除数。根据分数与除法的关系结合分数的基本性质确定被除数、分子或分母。用分子除以分母把分数化成小数。
10.【答案】75
【解析】解:在两位数中,同时能被3和5整除的最大奇数是75。
故答案为:75。
【分析】两位数中,要同时能被3和5整除,而且是奇数,那么这个两位数的个位是5,然后根据3的倍数的特征作答即可。
11.【答案】;3.25;
【解析】解:==;
=13÷4=3.25;
17÷6=2......5,=。
故答案为:;3.25;。
【分析】带分数化假分数:带分数的整数部分乘分母加分子得到的数作为假分数的分子,分母不变;
分数化小数:用分子除以分母,商写成小数的形式;
假分数化带分数:分子÷分母=商......余数;商就是带分数的整数部分,余数就是带分数的分子,分母不变。
12.【答案】6个
【解析】解:此几何体不论有多少层,其上、下表面积是固定不变的,为 ,
它的每个侧面的面积应该超过 。
最底层的正方体的单个侧面面积为 ,往上依次为2,1, , ,……
前五层正方体的单个侧面面积和为 ,
所以要想超过 ,至少应该是6个。
故答案为:6个
【分析】观察图形可知,此几何体不论有多少层,其上、下表面积是固定不变的,这个图形的表面积等于最下面的正方体的6个面的面积加上上面的几个小正方体的4个面的面积,根据题干分析,可得相邻两个正方体中,上边一个正方体的一个面积为下边一个正方体的一个面积的一半,最下面的正方体一个面的面积是2×2=4,由此即可得出倒数第二个正方体一个面的面积是2,倒数第三个正方体的一个面的面积是1,由此类推依次为: , ,……
13.【答案】4500
【解析】解:3米=30厘米
60÷4×300
=15×300
=4500(立方厘米)
故答案为:4500。
【分析】把它横截成3段,表面积就会增加4个横截面的面积,所以用横截面面积乘方钢的长度即可求出体积。注意统一单位。
14.【答案】错误
【解析】解:假设一个长方体的长、宽、高分别为6厘米、4厘米、2厘米;
另一个长方体的长、宽、高分别为10厘米、2厘米、2厘米;
表面积:(6×4+6×2+4×2)×2
=44×2
=88(平方厘米);
体积:6×4×2=48(立方厘米);
表面积:(10×2+10×2+2×2)×2
=44×2
=88(平方厘米);
体积:10×2×2=40(立方厘米);
所以两个长方体的表面积相等时,它们的体积不一定相等,原题说法错误。
故答案为:错误。
【分析】 长方体的表面积=(长×宽+长×高+宽×高)×2;长方体体积=长×宽×高,长方体的表面积相等,但它们的体积不一定相等,可举例判断。
15.【答案】错误
【解析】奇数的倍数不一定是奇数。如果一个自然数既是3的倍数,又是5的倍数,那么它的末位数是0或5,且各位数的和是3的倍数;当这个数的个位是0,且各位数相加的和是3的倍数时,它也是2的倍数,那么这个数是偶数,所以满足条件的数不一定是奇数.
故答案为:错误.
【分析】根据2、3、5的倍数特征进行解答.
16.【答案】正确
【解析】解:根据合数的定义可知,一个合数至少有3个因数,原题说法正确.
故答案为:正确
【分析】合数是除了1和本身外还有其它因数的数,因此一个合数的因数大于2,例如4的因数是1、2、4,所以合数至少有3个因数.
17.【答案】错误
【解析】自然数可以分为奇数和偶数;也可以分为质数、合数和1。原题说法错误。
故答案为:错误。
【分析】1既不是质数,又不是合数。所以按质数合数分,自然数分为三类,质数、合数和1。
18.【答案】正确
【解析】解:两个质数相乘得到的积,除了1和它本身外,还有这两个质数是它的因数.它有4个因数,所以一定是合数.
故答案为:正确.
【分析】一个数除了1和它本身还有其它因数,这样的数就是合数.
19.【答案】错误
【解析】解:200×5=1000,所以乘数末尾有2个0,积的末尾不一定有2个0,所以原题说法错误。
故答案为:错误。
【分析】偶数乘以5,积的末尾会出现0,所以本题采用举例法,即200×5的乘积去判断即可。
20.【答案】正确
【解析】解:1的分数单位是,再添上3个这样的分数单位是最小的质数,说法正确。
故答案为:正确。
【分析】把单位“1”平均分成若干份取其中的一份的数,叫做分数单位。即分子是1,分母是正整数的分数,又叫单位分数,记为。带分数的分数单位是与分数部分的分数单位相同。
最小的质数是2,所以用2-1得出的分数中的分子是几,就再添上几个这样的分数单位。
21.【答案】正确
【解析】b是a的倍数,a是c的倍数,那么b既是a的倍数又是c的倍数,则a、b、c的最小公倍数是b;原题说法正确.
故答案为:正确
【分析】自然数a能整除自然数b,b是a的倍数;a又能被自然数c整除,则a是c的倍数,那么b也是c的倍数;一个数是另外两个数的倍数,这个数就是这三个数的最小公倍数.
22.【答案】错误
【解析】2×2×2=8,小正方体拼大正方体,最少需要8个,本题错。
故答案为:错误。
【分析】大正方体最小时,一边有两个正方体,一共需要8个正方体。
23.【答案】C
【解析】长方体的表面积为:6a2×3-4a2=14a2(平方厘米); 故选:C.
【分析】棱长是a厘米的正方体的一个面的面积是a2;三个正方体拼组成一个长方体后,表面积减少了4个正方体的面,由此即可计算出这个长方体的表面积解答问题.
24.【答案】B
【解析】解:制作一个长方体的鱼缸,要用多少玻璃是求鱼缸的表面积。
故答案为:B。
【分析】求长方体或正方体6个面积的总面积,就是求它的表面积,本题中求鱼缸用的玻璃就是求5个面的总面积,即表面积。
25.【答案】B
【解析】解: 肯定是 2 的倍数,即 是偶数。
故答案为:B
【分析】本题主要考查偶数的定义和表示方式。偶数是能够被2整除的整数,即2的倍数。因此,要表示一个偶数,可以使用2乘以一个自然数的方式来表示。
26.【答案】B
【解析】从左往右,图1、2、4是正方体的展开图。
故答案为:B。
【分析】正方体的展开图有如下类型:第一类,141型,中间四连方,两侧各一个,共六种;第二类,132型,中间三连方,两侧各有一、二个,共三种;第三类,222型,中间二连方,两侧各有二个,只有一种;第四类,33型,两排各三个,只有一种,据此判断。
27.【答案】A
【解析】解:6+1=7(次)
故答案为:A。
【分析】考虑最不利的原则,前6次都是摸到的黄球,黄球没有了,再摸一次,一定能摸到红球。
28.【答案】B
【解析】 偶数+奇数=奇数。
故答案为:B。
【分析】奇数:不能被2整除的整数。
偶数:能够被2整除的整数。
29.【答案】B
【解析】解:在所有的质数中,只有2是偶数,所以偶数的个数有一个.
故答案为:B。
【分析】在所有的质数中,只有2既是质数又是偶数。
30.【答案】C
【解析】解:4×3×3.5=42dm3=42L,所以倒入的水是42L。
故答案为:C。
【分析】倒入水的体积=长×宽×倒入水的深度,据此代入数据作答即可。
31.【答案】B
【解析】A、9不是质数,故A错误;
B、48和32均为偶合数,11、37和13、19均为奇质数,故正确;
C、25不是质数,故错误;
故答案为:B
【分析】偶数都是2的倍数,不是2的倍数的数是奇数;合数是指这个数除了1和它本身以外还有其他的因数,质数只有1和它本身两个因数。根据以上定义判断三个选项是否符合要求。
32.【答案】C
【解析】解:一条绳子,对折三次,这条绳子被平均分成8份,其中一段是这条绳子的 。
故答案为:C。
【分析】一条绳子对折1次,平均分成两段,再对折一次平均分成4段,对折三次就平均分成8段。根据分数的意义确定其中一段是这条绳子的几分之几。
33.【答案】72÷3=24 12×20=240 125×8×0=0 408÷2=204
+=1 1-= -= 100-17=83
【解析】同分母分数相加减,分母不变,分子相加减;三位数除以一位数,先用被除数最高位上的数去除,如果它比除数小,就用前两位上的数去除,用哪一位上的数去除,商就和那一位对齐,每次除后余下的数必须比除数小;因数末尾有0的乘法,可以先把0前面的数相乘,再在积的末尾添上0。
34.【答案】(1) (2) (3)
=12- = =
=10 =
【解析】 题目需要计算三个分数运算表达式,其中可能涉及简算方法的应用。首先观察每个表达式的特点,判断能否通过运算顺序调整、通分或结合律等方法简化计算过程。
35.【答案】(1)解:
x=
(2)解:
x=
(3)解:1-x=
x=1-
x=
【解析】解方程要掌握等式的性质,即等式两边同时加上或减去一个相同的数,同时乘或除以一个相同的数(0除外),等式仍然成立。
36.【答案】表面积330平方厘米;体积370立方厘米
37.【答案】(1)解:
(2)解:
【解析】(1)图1中露出的占总数的,说明共有4份,每份是3个心形,再画3份;
(2)图2中盖住的占总数的,说明共有8个心形,露出了3个,盖住了5个,再画5个心形。
38.【答案】解:(1)长方形长画6格,宽画4格,长方形面积是6×4=24(平方厘米)
(2)正方形边长12÷4=3(厘米),正方形面积是3×3=9(平方厘米),它的是3格;
【解析】(1)长方形面积=长×宽;
(2)正方形的周长÷4=正方形的边长,正方形的边长×正方形的边长=正方形的面积,把正方形的面积平均分成3份,其中的1份用斜线表示。
39.【答案】解:48的因数有:1、2、3、4、6、8、12、16、24、48,要求每组人数相同且至少有2人,每个小组的人数有2人,3人,4人,6人,8人,12人,16人,24人,一共有8种不同的分法。(48人是一个班,不是一个组)
【解析】因为要把同学的分成若干个学习小组,而且每组的人数相同,所以本题就是求48的因数,据此作答即可。
40.【答案】解:7+4=11(篇)
答:每篇文章的第一页是奇数页码的文章最多有11篇。
【解析】先将偶数页的文章(2页、4页、···、14页)编排,这样共有7篇文章的第一页都是奇数页码。然后将奇数页的文章(1页、3页、5页、7页、9页、11页、13页和15页)依次编排,这样编排的1页、5页、9页和13页的4篇文章的第一页都是奇数页码。因此每篇文章的第一页是奇数页码的文章最多是 11篇。
41.【答案】解:
4和6的最小公倍数是2×2×3
=4×3
=12
12×4=48(名)
答:这个班有48名学生。
【解析】这个班有学生的人数=4和6的最小公倍数×4。
42.【答案】解:
所以36和24的最大公因数是:2×2×3
=4×3
=12
36÷12=3(朵)
24÷12=2(朵)
答:最多能扎12束,此时每束花中玫瑰有2朵,康乃馨有3朵。
【解析】最多可以扎的束数=24和36的最大公因数,用短除法求出;此时每束花中玫瑰的朵数=玫瑰花的总朵数÷24和36的最大公因数,每束花中康乃馨的朵数=康乃馨的总朵数÷24和36的最大公因数。
43.【答案】解:12×8×5+3×3×3
=480+27
=507(cm3)
507÷(13×13)=3(cm)
答:熔铸成的铝块高是3 cm。
【解析】长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,熔铸成的铝块的体积原长方体铅锭和正方体铅锭之和,先求出熔铸成的铝块的体积,利用体积除以底面积得到熔铸成的铝块高度。
44.【答案】解:[8,10]=40
答:这盒铅笔至少有40 支。
【解析】铅笔的总数一定是8和10的公倍数,由此求出8和10的最小公倍数就是这盒铅笔至少的只数。
45.【答案】解:
==
==
答:借阅 《奇妙的数学王国》 和 《童趣逻辑》 的同学人数一样多;
借阅 《爱克斯探长》 、 《荒岛历险》 、 《数学魔法师》 的同学人数一样多。
【解析】分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变。据此计算后再比较大小。
46.【答案】解:
=
=12-4.3
=7.7(m);
答:水深7.7m。
【解析】露出水面的部分就是+m,用全长减去河底淤泥的部分和露出水面的部分的和即可。
47.【答案】解:根据球的体积公式计算铁球体积:V球= πr3,
= ×3.14× ,
= ×3.14×27,
=3.14×36,
=113.04(立方厘米);
水箱的底面积:113.04÷0.6=188.4(平方厘米);
石块的体积:188.4×1.5=282.6(立方厘米);
答:这块石块的体积是282.6立方厘米
【解析】先依据放入铁球后升高的水的体积就等于铁球的体积,即可求出水箱的底面积,铁球的直径已知,从而可以求其体积,也就能求出水箱的底面积;投入石块后水面上升的高度已知,用水箱底面积成升高的水面高度,就是石块的体积.解答此题的关键是:先求出水箱的底面积,主要依据是浸入水中的物体体积,就等于升高部分的水的体积.
48.【答案】(1)解:60×40×3
=2400×3
=7200(平方厘米)
40×40×2
=1600×2
=3200(平方厘米)
7200+3200=10400(平方厘米)
答:做这个鱼缸至少需要10400平方厘米的超白玻璃。
(2)解:60×40×3
=2400×3
=7200(立方厘米)
答:这座假山的体积是7200立方厘米。
【解析】(1)此题主要考查了无盖长方体表面积的应用,高和宽相等,则前面、后面和底面的面积相等,左右侧面的面积相等,由此计算出5个面的面积之和即可;
(2)将假山放入鱼缸中,假山完全沉入水中,水面上升部分的体积就是假山的体积,鱼缸的长×宽×上升的水面高度=假山的体积。
21世纪教育网(www.21cnjy.com)
同课章节目录
