上海卢湾区2009-2010学年九年级上数学期末考试及答案
文档属性
| 名称 | 上海卢湾区2009-2010学年九年级上数学期末考试及答案 |  | |
| 格式 | rar | ||
| 文件大小 | 154.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-30 13:17:00 | ||
图片预览


文档简介
卢湾区2009学年第一学期九年级期末考试
数学试卷
(时间100分钟,满分150分) 2010.1
(本试卷所有答案请书写在答题纸规定位置上)
一、选择题(本大题共6题,每题4分,满分24分)
1.东海大桥全长32.5千米,如果东海大桥在某张地图上的长为6.5厘米,那么该地图上距离与实际距离的比为…………………………………( ).
A.1:5000000; B.1:500000; C.1:50000; D.1:5000.
2.如果两个相似三角形对应高之比是9∶16,那么它们的对应周长之比是 ………………………………………………………………………( ).
A.3∶4; B.4∶3; C.9∶16; D.16∶9.
3.Rt△ABC中,∠C=90 ,若AC=a,∠A=,则AB的长为…………( ).
A.; B.; C.; D..
4.在平面直角坐标系中,将二次函数的图像向下平移2个单位,所得图像的解析式为………………………………………………………( ).
A.; B.; C.; D..
5.若点A(2,y1)、B(3,y2)是二次函数图像上的两点,则y1与y2的大小关系是…………………………………………………( ).
A.; B.; C.; D.不能确定.
6.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x,那么x的值………………………………( ).
A.有且仅有1个; B.有且仅有2个;
C.有3个及以上但个数有限; D.有无数个.
二、填空题(本大题共12题,每题4分,满分48分)
7.若,则__________.
8.若是单位向量,与的方向相反,且长度为3,则用表示是_______.
9.计算:__________.
10.抛物线的顶点坐标是__________.
11.若某二次函数图像的顶点在原点,且经过点(2,1),则此二次函数的解析式是__________.
12.抛物线与轴的交点坐标是 .
13.如图,在□ABCD中,点在边上,若,则的值为__________.
14.在△ABC中,如果,,那么BC的长为_________.
15.某山路的路面坡度为,若沿此山路向上前进90米,则升高了____米.
16.如图,在△ABC中,D是AC边上一点,且,设,,如果用向量,表示向量,那么_________.
17.如果将抛物线向右平移个单位后,恰好过点(3,6),那么的值为_________.
18.如图,有一所正方形的学校,北门(点A)和西门(点B)各开在北、西面围墙的正中间。在北门的正北方30米处(点C)有一颗大榕树。如果一个学生从西门出来,朝正西方走750米(点D),恰好见到学校北面的大榕树,那么这所学校占地__________平方米.
三、简答题(本大题共4题,每题10分,满分40分)
19.指出抛物线的开口方向、对称轴和顶点坐标,并在答题纸上的直角坐标系中画出的图像.
20.如图,已知△ABC中,点分别是边上的点, EF∥BC, AF=2,BF=4,BC=5,联结BE,CF相交于点.
(1) 求线段EF的长;
(2) 求的值.
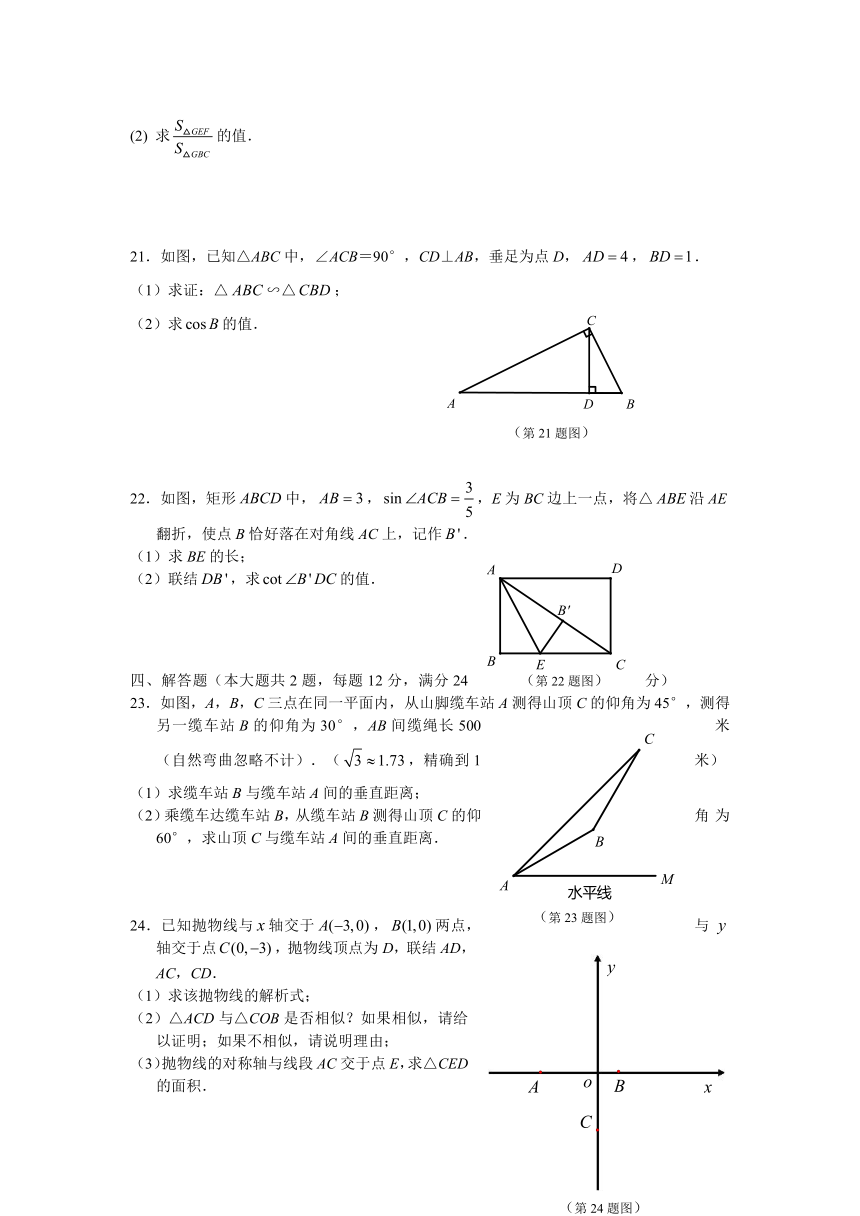
21.如图,已知△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,,.
(1)求证:△∽△;
(2)求的值.
22.如图,矩形中,,,E为BC边上一点,将△沿AE翻折,使点B恰好落在对角线AC上,记作.
(1)求BE的长;
(2)联结,求的值.
四、解答题(本大题共2题,每题12分,满分24分)
23.如图,A,B,C三点在同一平面内,从山脚缆车站A测得山顶C的仰角为45°,测得另一缆车站B的仰角为30°,AB间缆绳长500米(自然弯曲忽略不计).(,精确到1米)
(1)求缆车站B与缆车站A间的垂直距离;
(2)乘缆车达缆车站B,从缆车站B测得山顶C的仰角为60°,求山顶C与缆车站A间的垂直距离.
24.已知抛物线与轴交于,两点,与轴交于点,抛物线顶点为D,联结AD,AC,CD.
(1)求该抛物线的解析式;
(2)△ACD与△COB是否相似?如果相似,请给以证明;如果不相似,请说明理由;
(3)抛物线的对称轴与线段AC交于点E,求△CED的面积.
五、(本题满分14分)
25.已知正方形ABCD中,5,E是直线BC上的一点,联结AE,过点E作EF⊥AE,交直线CD于点F.
(1)当E点在BC边上运动时,设线段的长为,线段CF的长为y,
①求关于的函数解析式及其定义域;
②根据①中所得关于的函数图像,求当的长为何值时,线段CF最长,并求此时CF的长;
(2)当CF的长为时,求的值.
卢湾区2009学年第一学期九年级数学期末考试
参考答案及评分说明
一、选择题(本大题共6题,每题4分,满分24分)
1.B; 2.C; 3.D; 4.A; 5.A; 6.B .
二、填空题(本大题共12题,每题4分,满分48分)
7.; 8.; 9.; 10. (1,5); 11.;
12. (0,1); 13.; 14.12; 15.10;
16.; 17.2或4; 18.90000.
三、简答题(本大题共4题,每题10分,满分40分)
19. 解:开口向下,对称轴为直线,顶点坐标为(2,1)……各2分
画图正确…………………………………………………………………4分
20. 解:(1)∵EF∥BC,∴.…………………………………2分
∵AF=2,BF=4,BC=5,∴.∴.……………………3分
(2) EF∥BC,∴△∽△.…………………………………………2分
∴.………………………………………………………3分
21. 解(1)∵CD⊥AB,∴∠BDC=90°,∴∠A+∠ACD=90°.……1分
∵∠ACB=90°,∴∠DCB+∠ACD=90°,∴∠A=∠DCB.……………2分
又∵∠ACB=∠BDC=90°,∴△∽△.………………………2分
(2)∵△∽△,∴.…………………………………2分
∵,,∴.…………………………………………1分
∵∠BDC=90°,∴.……………………………2分
22. 解:(1)矩形中,∠B=90°,
∴.∴.………………………2分
由翻折得, ∠=90°.
在Rt△中, .
设,则,∴,…………………………………1分
解得.∴BE的长为.………………………………………………2分
(2)过点作,垂足为F.……………………………………1分
∵矩形中,∠D=90°,
∴∠=∠D=90°,∴∥.…………………………………1分
∴,∴,.……………………………2分
在Rt△中,.…………………1分
四、解答题(本大题共2题,每题12分,满分24分)
23. (1)过作⊥于点.
在Rt△中, ,………………2分
∵,,
∴.…………………………3分
即缆车站B与缆车站A间的垂直距离为250米.
(2)过作垂直于坡底的水平线,垂足为点,
过作∥,交CF与点E.…………………………………………1分
设山顶C与缆车站B间的垂直距离.
在Rt△中, ,
∴.……………………………………………………1分
在Rt△中,.……………………………1分
在Rt△中,, ∴.
又.
∴.…………………………………………………1分
解得.………………………………………………………………2分
.即山顶与缆车站A间的垂直距离约为米.1分
24. 解:(1)设抛物线解析式为………………1分
根据题意,得,解得. …………………2分
∴抛物线的解析式为. ……………………………………1分
(2)相似.……………………………………………………………………1分
由配方得,∴.………………1分
由两点间距离公式得 , ,.…………2分
又∵,, ,
∴.
∴△ACD∽△COB.……………………………………………………………2分
(3) 由(2)可知∠ACD=90°,∴,………………1分
∵,又,
∴.……………………………………………………1分
五、(本题满分14分)
25. 解:(1)∵四边形ABCD是正方形,∴∠B=90°.
∵EF⊥AE,∴∠AEF=90°.
又∵∠CEA=∠CEF +∠AEF,∠CEA=∠BAE +∠B,
∴∠CEF=∠BAE. …………………………………………………………1分
又∵∠B=∠C =90°∴△CEF∽△BAE.…………………………………1分
∴,∴.
∴.()………………………………………………2分
②.…………………………………………1分
根据函数图像可知,抛物线,开口向下,抛物线的顶点坐标是它的最高点.且在函数的定义域内.
所以当的长为时,CF的长最大为.………………………………2分
(2) 1 当点B在线段BC上时(如图25-1),,解得 .
当BE=2时,;当BE=3,时.……………2分
2 当点B在BC延长线上时(如图25-2),可得.
解得(舍)∴.………………………………2分
3 当点B在BC反向延长线上时(如图25-3),可得.
解得 (舍)∴.……………………………2分
综上所述可取的值分别为,,,.…………………1分
(第13题图)
(第18题图)
北
(第16题图)
(第20题图)
(第21题图)
(第22题图)
(第23题图)
(第24题图)
(第25题图)
(图25-3)
(图25-2)
(图25-1)
数学试卷
(时间100分钟,满分150分) 2010.1
(本试卷所有答案请书写在答题纸规定位置上)
一、选择题(本大题共6题,每题4分,满分24分)
1.东海大桥全长32.5千米,如果东海大桥在某张地图上的长为6.5厘米,那么该地图上距离与实际距离的比为…………………………………( ).
A.1:5000000; B.1:500000; C.1:50000; D.1:5000.
2.如果两个相似三角形对应高之比是9∶16,那么它们的对应周长之比是 ………………………………………………………………………( ).
A.3∶4; B.4∶3; C.9∶16; D.16∶9.
3.Rt△ABC中,∠C=90 ,若AC=a,∠A=,则AB的长为…………( ).
A.; B.; C.; D..
4.在平面直角坐标系中,将二次函数的图像向下平移2个单位,所得图像的解析式为………………………………………………………( ).
A.; B.; C.; D..
5.若点A(2,y1)、B(3,y2)是二次函数图像上的两点,则y1与y2的大小关系是…………………………………………………( ).
A.; B.; C.; D.不能确定.
6.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x,那么x的值………………………………( ).
A.有且仅有1个; B.有且仅有2个;
C.有3个及以上但个数有限; D.有无数个.
二、填空题(本大题共12题,每题4分,满分48分)
7.若,则__________.
8.若是单位向量,与的方向相反,且长度为3,则用表示是_______.
9.计算:__________.
10.抛物线的顶点坐标是__________.
11.若某二次函数图像的顶点在原点,且经过点(2,1),则此二次函数的解析式是__________.
12.抛物线与轴的交点坐标是 .
13.如图,在□ABCD中,点在边上,若,则的值为__________.
14.在△ABC中,如果,,那么BC的长为_________.
15.某山路的路面坡度为,若沿此山路向上前进90米,则升高了____米.
16.如图,在△ABC中,D是AC边上一点,且,设,,如果用向量,表示向量,那么_________.
17.如果将抛物线向右平移个单位后,恰好过点(3,6),那么的值为_________.
18.如图,有一所正方形的学校,北门(点A)和西门(点B)各开在北、西面围墙的正中间。在北门的正北方30米处(点C)有一颗大榕树。如果一个学生从西门出来,朝正西方走750米(点D),恰好见到学校北面的大榕树,那么这所学校占地__________平方米.
三、简答题(本大题共4题,每题10分,满分40分)
19.指出抛物线的开口方向、对称轴和顶点坐标,并在答题纸上的直角坐标系中画出的图像.
20.如图,已知△ABC中,点分别是边上的点, EF∥BC, AF=2,BF=4,BC=5,联结BE,CF相交于点.
(1) 求线段EF的长;
(2) 求的值.
21.如图,已知△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,,.
(1)求证:△∽△;
(2)求的值.
22.如图,矩形中,,,E为BC边上一点,将△沿AE翻折,使点B恰好落在对角线AC上,记作.
(1)求BE的长;
(2)联结,求的值.
四、解答题(本大题共2题,每题12分,满分24分)
23.如图,A,B,C三点在同一平面内,从山脚缆车站A测得山顶C的仰角为45°,测得另一缆车站B的仰角为30°,AB间缆绳长500米(自然弯曲忽略不计).(,精确到1米)
(1)求缆车站B与缆车站A间的垂直距离;
(2)乘缆车达缆车站B,从缆车站B测得山顶C的仰角为60°,求山顶C与缆车站A间的垂直距离.
24.已知抛物线与轴交于,两点,与轴交于点,抛物线顶点为D,联结AD,AC,CD.
(1)求该抛物线的解析式;
(2)△ACD与△COB是否相似?如果相似,请给以证明;如果不相似,请说明理由;
(3)抛物线的对称轴与线段AC交于点E,求△CED的面积.
五、(本题满分14分)
25.已知正方形ABCD中,5,E是直线BC上的一点,联结AE,过点E作EF⊥AE,交直线CD于点F.
(1)当E点在BC边上运动时,设线段的长为,线段CF的长为y,
①求关于的函数解析式及其定义域;
②根据①中所得关于的函数图像,求当的长为何值时,线段CF最长,并求此时CF的长;
(2)当CF的长为时,求的值.
卢湾区2009学年第一学期九年级数学期末考试
参考答案及评分说明
一、选择题(本大题共6题,每题4分,满分24分)
1.B; 2.C; 3.D; 4.A; 5.A; 6.B .
二、填空题(本大题共12题,每题4分,满分48分)
7.; 8.; 9.; 10. (1,5); 11.;
12. (0,1); 13.; 14.12; 15.10;
16.; 17.2或4; 18.90000.
三、简答题(本大题共4题,每题10分,满分40分)
19. 解:开口向下,对称轴为直线,顶点坐标为(2,1)……各2分
画图正确…………………………………………………………………4分
20. 解:(1)∵EF∥BC,∴.…………………………………2分
∵AF=2,BF=4,BC=5,∴.∴.……………………3分
(2) EF∥BC,∴△∽△.…………………………………………2分
∴.………………………………………………………3分
21. 解(1)∵CD⊥AB,∴∠BDC=90°,∴∠A+∠ACD=90°.……1分
∵∠ACB=90°,∴∠DCB+∠ACD=90°,∴∠A=∠DCB.……………2分
又∵∠ACB=∠BDC=90°,∴△∽△.………………………2分
(2)∵△∽△,∴.…………………………………2分
∵,,∴.…………………………………………1分
∵∠BDC=90°,∴.……………………………2分
22. 解:(1)矩形中,∠B=90°,
∴.∴.………………………2分
由翻折得, ∠=90°.
在Rt△中, .
设,则,∴,…………………………………1分
解得.∴BE的长为.………………………………………………2分
(2)过点作,垂足为F.……………………………………1分
∵矩形中,∠D=90°,
∴∠=∠D=90°,∴∥.…………………………………1分
∴,∴,.……………………………2分
在Rt△中,.…………………1分
四、解答题(本大题共2题,每题12分,满分24分)
23. (1)过作⊥于点.
在Rt△中, ,………………2分
∵,,
∴.…………………………3分
即缆车站B与缆车站A间的垂直距离为250米.
(2)过作垂直于坡底的水平线,垂足为点,
过作∥,交CF与点E.…………………………………………1分
设山顶C与缆车站B间的垂直距离.
在Rt△中, ,
∴.……………………………………………………1分
在Rt△中,.……………………………1分
在Rt△中,, ∴.
又.
∴.…………………………………………………1分
解得.………………………………………………………………2分
.即山顶与缆车站A间的垂直距离约为米.1分
24. 解:(1)设抛物线解析式为………………1分
根据题意,得,解得. …………………2分
∴抛物线的解析式为. ……………………………………1分
(2)相似.……………………………………………………………………1分
由配方得,∴.………………1分
由两点间距离公式得 , ,.…………2分
又∵,, ,
∴.
∴△ACD∽△COB.……………………………………………………………2分
(3) 由(2)可知∠ACD=90°,∴,………………1分
∵,又,
∴.……………………………………………………1分
五、(本题满分14分)
25. 解:(1)∵四边形ABCD是正方形,∴∠B=90°.
∵EF⊥AE,∴∠AEF=90°.
又∵∠CEA=∠CEF +∠AEF,∠CEA=∠BAE +∠B,
∴∠CEF=∠BAE. …………………………………………………………1分
又∵∠B=∠C =90°∴△CEF∽△BAE.…………………………………1分
∴,∴.
∴.()………………………………………………2分
②.…………………………………………1分
根据函数图像可知,抛物线,开口向下,抛物线的顶点坐标是它的最高点.且在函数的定义域内.
所以当的长为时,CF的长最大为.………………………………2分
(2) 1 当点B在线段BC上时(如图25-1),,解得 .
当BE=2时,;当BE=3,时.……………2分
2 当点B在BC延长线上时(如图25-2),可得.
解得(舍)∴.………………………………2分
3 当点B在BC反向延长线上时(如图25-3),可得.
解得 (舍)∴.……………………………2分
综上所述可取的值分别为,,,.…………………1分
(第13题图)
(第18题图)
北
(第16题图)
(第20题图)
(第21题图)
(第22题图)
(第23题图)
(第24题图)
(第25题图)
(图25-3)
(图25-2)
(图25-1)
同课章节目录
