上海浦东新区2009-2010学年九年级上数学期末考试及答案
文档属性
| 名称 | 上海浦东新区2009-2010学年九年级上数学期末考试及答案 |

|
|
| 格式 | rar | ||
| 文件大小 | 47.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-30 00:00:00 | ||
图片预览


文档简介
浦东新区2009学年度第一学期期末初三数学抽测试卷
(测试时间:100分钟,满分:150分)
考生注意:
1.本试卷含三个大题,共25题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.
2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.
3.本次测试可使用科学计算器.
一、选择题:(本大题共6题,每题4分,满分24分)
1.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,下列等式中,正确的是
(A); (B); (C); (D).
2.如图,已知AB∥CD,AD与BC相交于点O,AO∶DO=1∶2,那么下列式子错误的是
(A)BO∶CO=1∶2; (B)AB∶CD=1∶2;
(C)AD∶DO=3∶2; (D)CO∶BC=1∶2.
3.对于抛物线y=(x+2)2,下列说法正确的是
(A)最低点坐标是(,0); (B)最高点坐标是(,0);
(C)最低点坐标是(0,); (D)最高点坐标是(0,).
4.已知二次函数的图像如图所示,那么a、b的符号为
(A)a>0,b>0; (B)a<0,b>0;
(C)a>0,b<0; (D)a<0,b<0.
5.已知非零向量、和,下列条件中,不能判定∥的是
(A)∥,∥; (B)=,=;
(C)=; (D).
6.已知D是△ABC的边BC上的一点,∠BAD=∠C,那么下列结论中正确的是
(A); (B);
(C); (D).
二、填空题:(本大题共12题,每题4分,满分48分)
7.已知线段b是线段a、c的比例中项,且a=9,c=4,那么b= .
8.已知甲、乙两地之间的距离为10千米,画在一张地图上的距离为5厘米,那么在这张地图上量得距离为2厘米的A、B两地的实际距离为 千米.
9.已知是二次函数,那么的取值范围是 .
10.在平面直角坐标系中,如果把抛物线y=x2向左平移5个单位,那么所得抛物线的表达式为 .
11.已知抛物线,如果点P(,5)与点Q关于该抛物线的对称轴对称,那么点Q的坐标是 .
12.请写出一个以直线为对称轴,且在对称轴左侧部分是上升的抛物线的表达式,这条抛物线的表达式可以是 .
13.如果E、F是△ABC的边AB和AC的中点,=,=,那么= .
14.在Rt△ABC中,∠A=90°,BC=a,∠B=,那么AB= (用含a和的式子表示).
15.如果两个相似三角形的面积比为1∶2,那么它们的对应角平分线的比为 .
16.已知点G是△ABC的重心,AD是中线,AG=6,那么DG= .
17.小李在楼上点A处看到楼下点B处的小明的俯角是35度,那么点B处的小明看点A处的小李的仰角是 度.
18.如果在△ABC中,AB=AC= 3,BC=2,那么顶角的正弦值为 .
三、解答题:(本大题共7题,满分78分)
19.(本题满分10分)
如图,已知两个不平行的向量、.
先化简,再求作:.
(不要求写作法,但要指出图中表示结论的向量)
20.(本题满分10分)
已知二次函数的图像经过点(2,-1)和(1,0),求这个二次函数的解析式,并求出它的图像的顶点坐标和对称轴.
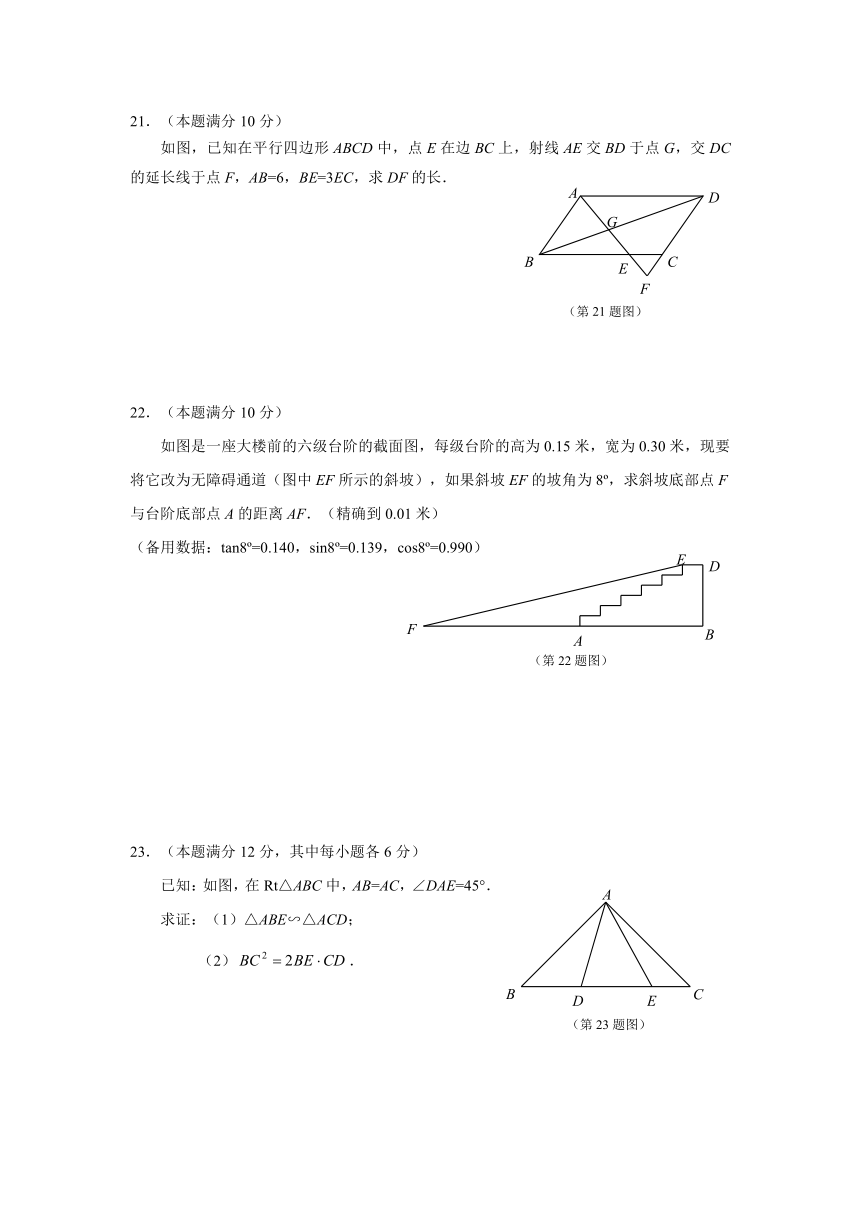
21.(本题满分10分)
如图,已知在平行四边形ABCD中,点E在边BC上,射线AE交BD于点G,交DC的延长线于点F,AB=6,BE=3EC,求DF的长.
22.(本题满分10分)
如图是一座大楼前的六级台阶的截面图,每级台阶的高为0.15米,宽为0.30米,现要将它改为无障碍通道(图中EF所示的斜坡),如果斜坡EF的坡角为8 ,求斜坡底部点F与台阶底部点A的距离AF.(精确到0.01米)
(备用数据:tan8 =0.140,sin8 =0.139,cos8 =0.990)
23.(本题满分12分,其中每小题各6分)
已知:如图,在Rt△ABC中,AB=AC,∠DAE=45°.
求证:(1)△ABE∽△ACD;
(2).
24.(本题满分12分,其中第(1)小题3分,第(2)小题3分,第(3)小题6分)
如图,一次函数的图像与轴、轴分别相交于点A和点B,二次函数的图像经过A、B两点.
(1)求这个一次函数的解析式;
(2)求二次函数的解析式;
(3)如果点C在这个二次函数的图像上,且点C的横坐标为5,求tan∠CAB的值.
25.(本题满分14分,其中第(1)小题4分,第(2)小题5分,第(3)小题5分)
已知:如图,在△ABC中,AB=AC=4,BC=AB,P是边AC上的一个点,AP=PD,∠APD=∠ABC,联结DC并延长交边AB的延长线于点E.
(1)求证:AD∥BC;
(2)设AP=x,BE=y,求y关于x的函数解析式,并写出它的定义域;
(3)联结BP,当△CDP与△CBE相似时,试判断BP与DE的位置关系,并说明理由.
浦东新区2009学年度第一学期期末质量抽测试卷
初三数学参考答案及评分说明
一、选择题:
1.C; 2.D; 3.A; 4.B; 5.D; 6.B.
二、填空题:
7.6; 8.4; 9.; 10.; 11.(4,5); 12.等; 13.; 14.; 15.1∶; 16.3; 17.35; 18.(或0.6285).
三、解答题:
19.解:原式=…………………………………………………………(2分)
=.……………………………………………………………………(2分)
图(略).…………………………………………………………………………(5分)
结论.………………………………………………………………………………(1分)
20.解:由题意,得……………………………………………………(2分)
解得……………………………………………………………(2分)
∴这个二次函数的解析式是.…………………………(2分)
顶点坐标是(2,-1),……………………………………………………(2分)
对称轴是直线x=2.………………………………………………………(2分)
21.解:在平行四边形ABCD中,
∵AB∥CD,∴.……………………………………………………(4分)
又∵BE=3EC,AB=6,∴CF=2.………………………………………………(3分)
∵CD=AB=6,∴DF=8.…………………………………………………………(3分)
22.解:作EH⊥AB,垂足为点H.………………………………………………………(1分)
由题意,得EH=0.9,AH=1.5.…………………………………………………(2分)
在Rt△EFH中,,∴.………………………………(3分)
∴FH≈6.429.……………………………………………………………………(2分)
∴AF=FH-AH=6.429-1.5=4.929≈4.93(米).…………………………………(2分)
注:如果使用计算器产生的误差,也可被认可,如FH≈6.404,AF≈4.90等.
23.证明:(1)在Rt△ABC中,∵AB=AC,∴∠B=∠C=45°.………………………(1分)
又∵∠BAE=∠BAD+∠DAE,∠DAE=45°,∴∠BAE=∠BAD+45°.…(1分)
而∠ADC=∠BAD+∠B=∠BAD+45°,………………………………………(1分)
∴∠BAE=∠ADC.……………………………………………………………(1分)
∴△ABE∽△ACD.……………………………………………………………(2分)
(2)由△ABE∽△ACD,得.……………………………………(2分)
∴.………………………………………………………(1分)
而AB=AC,,∴.………………………(2分)
∴.…………………………………………………………(1分)
24.解:(1)由题意,得点B的坐标为(0,6).………………………………………(1分)
∴m=6.………………………………………………………………………(1分)
∴一次函数的解析式为.……………………………………(1分)
(2)由题意,得点A的坐标为(8,0).………………………………………(1分)
∴.
∴.……………………………………………………………………(1分)
∴二次函数的解析式为.……………………………(1分)
(3)∵点C在这个二次函数的图像上,且点C的横坐标为5,
∴.
∴点C的坐标为(5,6).…………………………………………………(1分)
作CH⊥AB,垂足为点H.…………………………………………………(1分)
∵点B与点C的纵坐标相等,∴BC∥x轴.
∴∠CBH=∠BAO.…………………………………………………………(1分)
又∵∠CHB=∠BOA=90°,∴△CHB∽△BOA.
∴.
∵OB=6,OA=8,∴AB=10.
∴.………………………………………………………………(1分)
∴CH=3,BH=4,AH=6.…………………………………………………(1分)
∴.………………………………………………………(1分)
25.(1)证明:∵,,∴.…………………………(1分)
又∵∠APD=∠ABC,∴△APD∽△ABC.………………………………(1分)
∴∠DAP=∠ACB.…………………………………………………………(1分)
∴AD∥BC.…………………………………………………………………(1分)
(2)解:∵AB=AC,∴∠ABC=∠ACB.
∴∠DAP=∠DPA.
∴AD=PD.…………………………………………………………………(1分)
∵AP=x,∴AD=2x.…………………………………………………………(1分)
∵,AB=4,∴BC=2.
∵AD∥BC,∴,即.……………………………(1分)
整理,得y关于x的函数解析式为.……………………………(1分)
定义域为.…………………………………………………………(1分)
(3)解:平行.…………………………………………………………………………(1分)
证明:∵∠CPD=∠CBE,∠PCD>∠E,
∴当△CDP与△CBE相似时,∠PCD=∠BCE.…………………………(1分)
∴,即.………………………………………………(1分)
把代入,整理得.
∴x=2,x=-2(舍去).………………………………………………………(1分)
∴y=4.
∴AP=CP,AB=BE.…………………………………………………………(1分)
∴BP∥CE,即BP∥DE.
A
B
C
D
O
(第2题图)
O
x
y
(第4题图)
(第19题图)
A
B
C
D
F
E
(第21题图)
G
B
A
D
E
F
(第22题图)
A
B
D
E
C
(第23题图)
(第24题图)
y
x
O
A
B
C
A
B
C
E
D
P
(第25题图)
(测试时间:100分钟,满分:150分)
考生注意:
1.本试卷含三个大题,共25题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.
2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.
3.本次测试可使用科学计算器.
一、选择题:(本大题共6题,每题4分,满分24分)
1.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,下列等式中,正确的是
(A); (B); (C); (D).
2.如图,已知AB∥CD,AD与BC相交于点O,AO∶DO=1∶2,那么下列式子错误的是
(A)BO∶CO=1∶2; (B)AB∶CD=1∶2;
(C)AD∶DO=3∶2; (D)CO∶BC=1∶2.
3.对于抛物线y=(x+2)2,下列说法正确的是
(A)最低点坐标是(,0); (B)最高点坐标是(,0);
(C)最低点坐标是(0,); (D)最高点坐标是(0,).
4.已知二次函数的图像如图所示,那么a、b的符号为
(A)a>0,b>0; (B)a<0,b>0;
(C)a>0,b<0; (D)a<0,b<0.
5.已知非零向量、和,下列条件中,不能判定∥的是
(A)∥,∥; (B)=,=;
(C)=; (D).
6.已知D是△ABC的边BC上的一点,∠BAD=∠C,那么下列结论中正确的是
(A); (B);
(C); (D).
二、填空题:(本大题共12题,每题4分,满分48分)
7.已知线段b是线段a、c的比例中项,且a=9,c=4,那么b= .
8.已知甲、乙两地之间的距离为10千米,画在一张地图上的距离为5厘米,那么在这张地图上量得距离为2厘米的A、B两地的实际距离为 千米.
9.已知是二次函数,那么的取值范围是 .
10.在平面直角坐标系中,如果把抛物线y=x2向左平移5个单位,那么所得抛物线的表达式为 .
11.已知抛物线,如果点P(,5)与点Q关于该抛物线的对称轴对称,那么点Q的坐标是 .
12.请写出一个以直线为对称轴,且在对称轴左侧部分是上升的抛物线的表达式,这条抛物线的表达式可以是 .
13.如果E、F是△ABC的边AB和AC的中点,=,=,那么= .
14.在Rt△ABC中,∠A=90°,BC=a,∠B=,那么AB= (用含a和的式子表示).
15.如果两个相似三角形的面积比为1∶2,那么它们的对应角平分线的比为 .
16.已知点G是△ABC的重心,AD是中线,AG=6,那么DG= .
17.小李在楼上点A处看到楼下点B处的小明的俯角是35度,那么点B处的小明看点A处的小李的仰角是 度.
18.如果在△ABC中,AB=AC= 3,BC=2,那么顶角的正弦值为 .
三、解答题:(本大题共7题,满分78分)
19.(本题满分10分)
如图,已知两个不平行的向量、.
先化简,再求作:.
(不要求写作法,但要指出图中表示结论的向量)
20.(本题满分10分)
已知二次函数的图像经过点(2,-1)和(1,0),求这个二次函数的解析式,并求出它的图像的顶点坐标和对称轴.
21.(本题满分10分)
如图,已知在平行四边形ABCD中,点E在边BC上,射线AE交BD于点G,交DC的延长线于点F,AB=6,BE=3EC,求DF的长.
22.(本题满分10分)
如图是一座大楼前的六级台阶的截面图,每级台阶的高为0.15米,宽为0.30米,现要将它改为无障碍通道(图中EF所示的斜坡),如果斜坡EF的坡角为8 ,求斜坡底部点F与台阶底部点A的距离AF.(精确到0.01米)
(备用数据:tan8 =0.140,sin8 =0.139,cos8 =0.990)
23.(本题满分12分,其中每小题各6分)
已知:如图,在Rt△ABC中,AB=AC,∠DAE=45°.
求证:(1)△ABE∽△ACD;
(2).
24.(本题满分12分,其中第(1)小题3分,第(2)小题3分,第(3)小题6分)
如图,一次函数的图像与轴、轴分别相交于点A和点B,二次函数的图像经过A、B两点.
(1)求这个一次函数的解析式;
(2)求二次函数的解析式;
(3)如果点C在这个二次函数的图像上,且点C的横坐标为5,求tan∠CAB的值.
25.(本题满分14分,其中第(1)小题4分,第(2)小题5分,第(3)小题5分)
已知:如图,在△ABC中,AB=AC=4,BC=AB,P是边AC上的一个点,AP=PD,∠APD=∠ABC,联结DC并延长交边AB的延长线于点E.
(1)求证:AD∥BC;
(2)设AP=x,BE=y,求y关于x的函数解析式,并写出它的定义域;
(3)联结BP,当△CDP与△CBE相似时,试判断BP与DE的位置关系,并说明理由.
浦东新区2009学年度第一学期期末质量抽测试卷
初三数学参考答案及评分说明
一、选择题:
1.C; 2.D; 3.A; 4.B; 5.D; 6.B.
二、填空题:
7.6; 8.4; 9.; 10.; 11.(4,5); 12.等; 13.; 14.; 15.1∶; 16.3; 17.35; 18.(或0.6285).
三、解答题:
19.解:原式=…………………………………………………………(2分)
=.……………………………………………………………………(2分)
图(略).…………………………………………………………………………(5分)
结论.………………………………………………………………………………(1分)
20.解:由题意,得……………………………………………………(2分)
解得……………………………………………………………(2分)
∴这个二次函数的解析式是.…………………………(2分)
顶点坐标是(2,-1),……………………………………………………(2分)
对称轴是直线x=2.………………………………………………………(2分)
21.解:在平行四边形ABCD中,
∵AB∥CD,∴.……………………………………………………(4分)
又∵BE=3EC,AB=6,∴CF=2.………………………………………………(3分)
∵CD=AB=6,∴DF=8.…………………………………………………………(3分)
22.解:作EH⊥AB,垂足为点H.………………………………………………………(1分)
由题意,得EH=0.9,AH=1.5.…………………………………………………(2分)
在Rt△EFH中,,∴.………………………………(3分)
∴FH≈6.429.……………………………………………………………………(2分)
∴AF=FH-AH=6.429-1.5=4.929≈4.93(米).…………………………………(2分)
注:如果使用计算器产生的误差,也可被认可,如FH≈6.404,AF≈4.90等.
23.证明:(1)在Rt△ABC中,∵AB=AC,∴∠B=∠C=45°.………………………(1分)
又∵∠BAE=∠BAD+∠DAE,∠DAE=45°,∴∠BAE=∠BAD+45°.…(1分)
而∠ADC=∠BAD+∠B=∠BAD+45°,………………………………………(1分)
∴∠BAE=∠ADC.……………………………………………………………(1分)
∴△ABE∽△ACD.……………………………………………………………(2分)
(2)由△ABE∽△ACD,得.……………………………………(2分)
∴.………………………………………………………(1分)
而AB=AC,,∴.………………………(2分)
∴.…………………………………………………………(1分)
24.解:(1)由题意,得点B的坐标为(0,6).………………………………………(1分)
∴m=6.………………………………………………………………………(1分)
∴一次函数的解析式为.……………………………………(1分)
(2)由题意,得点A的坐标为(8,0).………………………………………(1分)
∴.
∴.……………………………………………………………………(1分)
∴二次函数的解析式为.……………………………(1分)
(3)∵点C在这个二次函数的图像上,且点C的横坐标为5,
∴.
∴点C的坐标为(5,6).…………………………………………………(1分)
作CH⊥AB,垂足为点H.…………………………………………………(1分)
∵点B与点C的纵坐标相等,∴BC∥x轴.
∴∠CBH=∠BAO.…………………………………………………………(1分)
又∵∠CHB=∠BOA=90°,∴△CHB∽△BOA.
∴.
∵OB=6,OA=8,∴AB=10.
∴.………………………………………………………………(1分)
∴CH=3,BH=4,AH=6.…………………………………………………(1分)
∴.………………………………………………………(1分)
25.(1)证明:∵,,∴.…………………………(1分)
又∵∠APD=∠ABC,∴△APD∽△ABC.………………………………(1分)
∴∠DAP=∠ACB.…………………………………………………………(1分)
∴AD∥BC.…………………………………………………………………(1分)
(2)解:∵AB=AC,∴∠ABC=∠ACB.
∴∠DAP=∠DPA.
∴AD=PD.…………………………………………………………………(1分)
∵AP=x,∴AD=2x.…………………………………………………………(1分)
∵,AB=4,∴BC=2.
∵AD∥BC,∴,即.……………………………(1分)
整理,得y关于x的函数解析式为.……………………………(1分)
定义域为.…………………………………………………………(1分)
(3)解:平行.…………………………………………………………………………(1分)
证明:∵∠CPD=∠CBE,∠PCD>∠E,
∴当△CDP与△CBE相似时,∠PCD=∠BCE.…………………………(1分)
∴,即.………………………………………………(1分)
把代入,整理得.
∴x=2,x=-2(舍去).………………………………………………………(1分)
∴y=4.
∴AP=CP,AB=BE.…………………………………………………………(1分)
∴BP∥CE,即BP∥DE.
A
B
C
D
O
(第2题图)
O
x
y
(第4题图)
(第19题图)
A
B
C
D
F
E
(第21题图)
G
B
A
D
E
F
(第22题图)
A
B
D
E
C
(第23题图)
(第24题图)
y
x
O
A
B
C
A
B
C
E
D
P
(第25题图)
同课章节目录
