湖北省2025届初中学业水平考试数学试卷(白)(含答案)
文档属性
| 名称 | 湖北省2025届初中学业水平考试数学试卷(白)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-25 17:09:30 | ||
图片预览




文档简介
2025年湖北省初中学业水平考试数学试卷(白)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.﹣3的相反数是( )
A. B. C. D.
2.下列常见的几何体中,左视图是三角形的是( )
A. B. C. D.
3.某不等式组的解集在数轴上表示为如图所示,则该不等式组的解集是( )
A. B. C.或 D.或
4.下列各式中,计算结果等于的是( )
A. B. C. D.
5.汽车大灯通常由灯泡、反光镜和配光镜三部分组成.如图,光源位于焦点处,光线经反射后平行于地面射出,已知,,则的度数为( )
A. B. C. D.
6.端午节是我国四大传统节日之一,吃粽子是端午节的传统习俗,端午节这天小颖的妈妈买了只红豆粽和只红枣粽,这些粽子除了内部馅料不同外其他均相同.小颖从中随意选一个,她选到红豆粽的概率是( )
A. B. C. D.
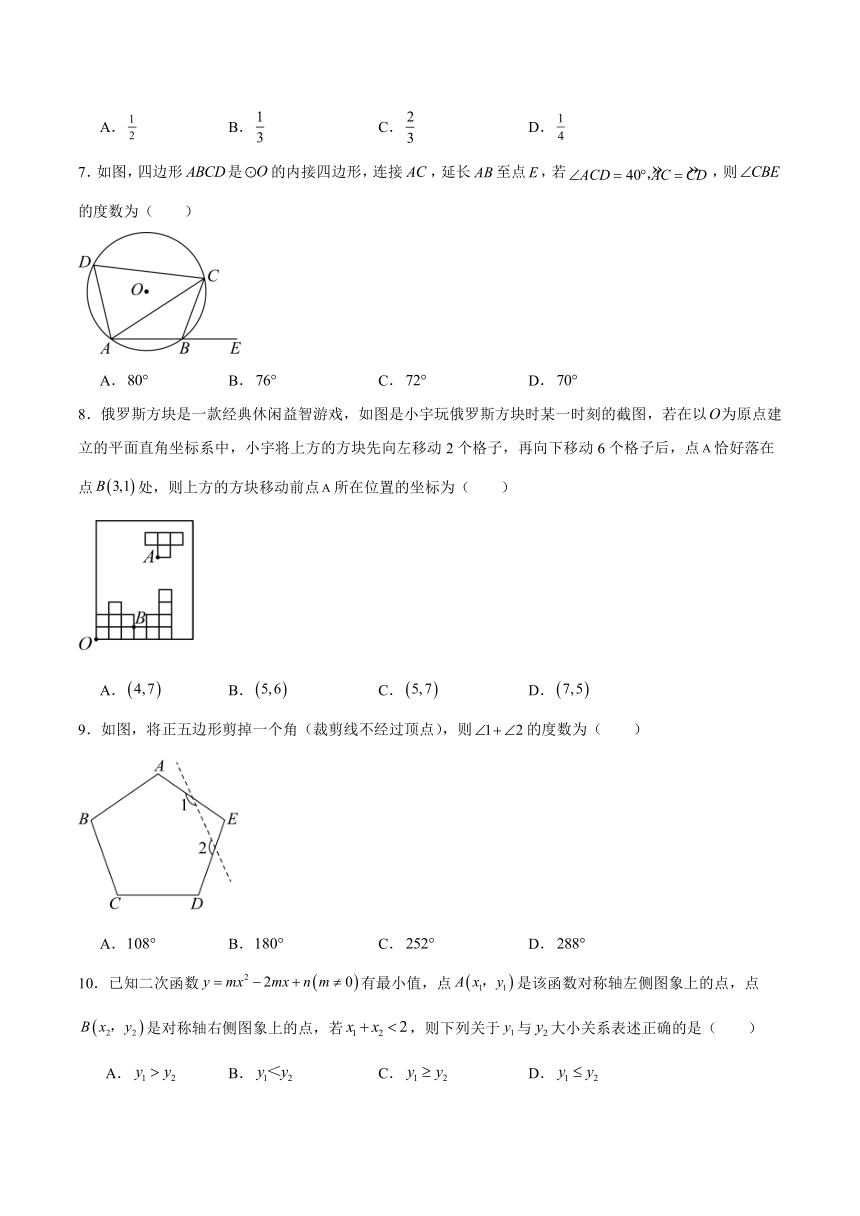
7.如图,四边形是的内接四边形,连接,延长至点,若,则的度数为( )
A. B. C. D.
8.俄罗斯方块是一款经典休闲益智游戏,如图是小宇玩俄罗斯方块时某一时刻的截图,若在以为原点建立的平面直角坐标系中,小宇将上方的方块先向左移动2个格子,再向下移动6个格子后,点恰好落在点处,则上方的方块移动前点所在位置的坐标为( )
A. B. C. D.
9.如图,将正五边形剪掉一个角(裁剪线不经过顶点),则的度数为( )
A. B. C. D.
10.已知二次函数有最小值,点是该函数对称轴左侧图象上的点,点是对称轴右侧图象上的点,若,则下列关于与大小关系表述正确的是( )
A. B. C. D.
二、填空题
11.计算:= .
12.已知一次函数,则当增加1时,的值增加 .
13.食物中一般有蛋白质、脂肪、膳食纤维等营养成分,这些营养成分都是人体所需的,在平时需要做到营养均衡,科学饮食.如图是小米中蛋白质、脂肪、膳食纤维的含量统计图,则小米中蛋白质共有 .
14.《九章算术》是中国古代重要的数学著作,书中有一道题,其大意为:现有走路慢的人先走10里,令走路快的人去追,追到100里时,已经领先走路慢的人20里.问走路快的人走到多少里时就已经追上走路慢的人?设走路快的人走到里时就已经追上走路慢的人,则可列方程 .
15.如图,在正方形纸片中,是的中点,连接,将沿折叠,点的对应点为点,连接并延长交于点,则线段与位置关系为 , .
三、解答题
16.化简:.
17.定滑轮的目的是改变力的方向,使得施力方向转变为容易出力的方向.某班“综合与实践”小组的同学在课余时间测量“定滑轮距地面的高度”.如图,点均在同一竖直平面内,在点处测得定滑轮的仰角为,小组成员站在处,拉动绳子,使得物体移动至点处,在点处测得定滑轮的仰角为,物体从点移动到点处绳子收回的长度为,已知物体的高度.求定滑轮距地面的高度.(结果精确到,参考数据:,
18.电动平衡车采用电能驱动,不仅有助于环境保护,而且轻便易携,受到广大群众的喜爱.甲、乙两个品牌的电动平衡车都宣传他们的产品在正常情况下最大续航里程不低于,相关部门分别对两个品牌电动平衡车的最大续航里程做了抽样调查,统计结果(单位:)如下:
甲品牌:;
乙品牌:;
甲、乙两个品牌电动平衡车调查数据统计表
(质检部门规定该产品最大续航里程不低于为合格产品)
平均数 中位数 众数 合格率
甲品牌 14.7 14.6 70%
乙品牌 14.7 14.9
根据以上信息,解答下列问题:
(1)填空:____,______,_____;
(2)若你是顾客,宜选择哪个品牌的电动平衡车?结合上表平均数、中位数、众数、合格率等数据说明理由.
19.如图,点在反比例函数的图象上,过点作轴,垂足为,连接.已知的面积为6.
(1)求反比例函数的解析式及点的坐标;
(2)是轴负半轴上一点,平分,现有条件:
①过点作轴的垂线,交于点;
②点在上(不与点重合),点在轴负半轴上,.
请从①②中任选一个作为已知条件,求出点的横坐标.
20.如图,在矩形中,为对角线.
(1)请用无刻度的直尺和圆规作对角线的垂直平分线,分别交,的延长线于点,(不写作法,保留作图痕迹);
(2)在(1)的基础上连接,求证:是等腰三角形.
21.如图,内接于为的直径,过点作的平行线交于点,交于点,点在的延长线上,连接,且.
(1)求证:是的切线;
(2)若,求的长.
22.某校学生为了参加学校组织的“投篮大赛”,利用课后时间积极地进行备赛训练.如图是小明训练投篮时的示意图,身高1.75米的小明将篮球从头顶上方0.25米处出手,已知篮筐中心到地面的距离为3.05米,当距出手处的水平距离为2.5米时,篮球达到最大高度为3.25米,篮球的轨迹示意图可近似看作抛物线的一部分,以小明起跳点为原点,建立如图所示的平面直角坐标系.
(1)求抛物线的解析式;
(2)小明投出球后,小刚在小明与篮筐之间跳起防守,已知小刚最高能摸到2.45米,则在球上升的过程中,小刚与小明的距离在什么范围内小刚才能在空中截住篮球?
(3)已知小明在距篮筐水平距离3.8米的位置,在只改变起跳高度的情况下,通过计算说明小明要竖直起跳多少米才能直接投中?
23.【问题背景】如图1,在中,,点在上(不与点重合),交于点为的中点,连接并延长至点,使,连接,将绕点逆时针旋转,如图2,连接,探究在绕点旋转的过程中,线段与的数量关系与位置关系.
【特例探究】
(1)①若,则______,与所在直线夹角(锐角)的度数为______;
②若,则_______,与所在直线夹角(锐角)的度数为______;
【得出结论】
(2)如图2,若,则线段与之间有怎样的数量关系(用含的式子表示),与所在直线夹角(锐角)的度数为多少?证明你的结论;
【深入探究】
(3)如图3,若的旋转角为,当点到直线的距离为2时,求的值.
24.如图,在平面直角坐标系中,已知抛物线与轴交于两点(点在点左侧),与轴正半轴交于点,点的坐标为,且.
(1)求抛物线的解析式;
(2)点为直线上方抛物线上一动点,过点作于点,设点的横坐标为.
①用含的代数式表示线段的长;
②连接,求四边形面积的最大值,并直接写出此时的长;
(3)设点的坐标为,点的坐标为,连接,当抛物线和线段只有一个公共点时,求的取值范围.
参考答案
1.D
根据相反数的定义可得:-3的相反数是3,
故选D.
2.A
解:A圆锥的左视图是三角形,故此选项符合题意;;
B三棱柱的左视图为长方形,故此选项不符合题意;
C正方体的左视图是正方形,故此选项不符合题意;
D圆柱的左视图是长方形,故此选项不符合题意;
故选:A
3.A
解:由数轴可得,该不等式组的解集为,
故选:A.
4.B
解:A. ,不符合题意;
B. ,符合题意;
C. ,不符合题意;
D. ,不符合题意.
故选B.
5.C
解:由题意可得,如图,
∴,
∵,
∴,
故选:C.
6.B
解:只红豆粽和只红枣粽,这些粽子除了内部馅料不同外其他均相同.小颖从中随意选一个,她选到红豆粽的概率是
故选:B.
7.D
解:,
∴,
∴,
四边形是的内接四边形,
∴
,
故选:D.
8.C
点先向左移动2个格子,再向下移动6个格子后的位置为点,
将点先向上移动6个格于,再向右移动2个格子后得到点
∴上方的方块移动前点所在位置的坐标为,
故选:C.
9.D
解:∵五边形是正五边形,,
∴,
∵六边形的内角和为:,
,
故选:D.
10.A
解:二次函数有最小值,,
∴抛物线开口向上,对称轴为直线,即,
∵点是该函数对称轴左侧图象上的点,点是对称轴右侧图象上的点,
∴,即
∵,
∴,
,
∴.
故选:A.
11.
解:原式,
故答案为:.
12.2
当增加1时,
.
当增加1时,的值增加2.
故答案为:2
13.
.
故答案为:
14.
解:设走路快的人走x步就能追上走路慢的人,
根据题意,得.
故答案为:.
15.
解:如图,连接,由折叠的性质可得,
是的中点,
,
四边形是平行四边形,
,.
设,则
,
即
.
故答案为:;;
16.
解:原式
.
17.定滑轮距地面的高度约为.
解:如解图,过点作,交的延长线于点,连接并延长交于点.
根据题意,得,
在中,
,
,
在中,
,
,
绳子收回的长度为,
,
解得,
,
答:定滑轮距地面的高度约为.
18.(1),15,;
(2)选择乙品牌的电动平衡车,理由见解析.
(1)将从甲品牌得到的10个数据按照从小到大的顺序排列,位于最中间的两个数为,
中位数;
从乙品牌得到的10个数据中,15出现的次数最多,出现了3次,
众数为15
大于等于13的数据为8个,
.
故答案为:,15,80%;
(2)选择乙品牌的电动平衡车,理由如下:
乙品牌的中位数、众数和合格率都高于甲品牌,
选择乙品牌的电动平衡车.(答案不唯一,合理即可)
19.(1)反比例函数的解析式为,;
(2)①选条件①,点的横坐标为;②选条件②,点的横坐标为.
(1)解:的面积为轴,
,
反比例函数的图象在第一象限,
,
反比例函数的解析式为,
点在反比例函数的图象上,
,
解得,
;
(2)选条件①:
如解图①,设与轴的交点为,
,
,
轴,
轴,,
,
平分,
,
,
,
,
点的横坐标为.
或选条件②:
如解图②,连接交轴于点,
,
,
,
,
平分,
,
,
,
四边形是平行四边形,
轴,,
,
,
点的横坐标为.
20.(1)见解析;
(2)见解析.
(1)解:作图如图①;
(2)证明:如图②,设与交于点,
是的垂直平分线,
,
四边形是矩形,
,
在和中,
,
∵
,
是等腰三角形.
21.(1)见解析;
(2).
(1)证明:内接于为的直径,
,
,
,即,
,
,
,即,
是的半径,
是的切线;
(2)解:是的中点,,
是的中点,
,
,
,
在中,,
,
,
.
22.(1)抛物线的解析式为;
(2)在球上升的过程中,小刚与小明的距离在0.5米以内才能在空中截住篮球;
(3)小明要竖直起跳0.138米才能直接投中.
(1)解:由题意可得抛物线顶点坐标为,
(米),
当时,,
设抛物线的解析式为,
把点代入,
解得,
抛物线的解析式为;
(2)令,则,
解得.
要在球上升的过程中截住篮球,
,
在球上升的过程中,小刚与小明的距离在0.5米以内才能在空中截住篮球;
(3)改变起跳高度只是对抛物线进行上下平移,而篮球飞行的抛物线形状不变,
设改变起跳高度后的抛物线解析式为
小明距篮筐水平距离为3.8米,篮筐中心到地面的距离为3.05米,
将点代入,
得,
解得,
小明要竖直起跳0.138米才能直接投中.
23.(1)①;②;(2)与所在直线夹角(锐角)的度数为,证明见解析;(3)的值为或.
解:(1)①连接并延长交直线于点,延长到点,设交于点K,
∵,
∴,
,
∴,
∴,,
∵,
∴,
∵,,,
∴,
∴,,
∴,
∴,
即与所在直线夹角(锐角)的度数为;
②当时,同理可证与所在直线夹角(锐角)的度数为.
(2)与所在直线夹角(锐角)的度数为.
证明如下: 如图
,
,
,
,
,
,
,
,
,
,
,
即与所在直线夹角(锐角)的度数为;
(3)①当时,过点作于点,
都是等腰直角三角形,,,
,
,
点到的距离为2,
与重合,
,
,
;
②当时,过点作交的延长线于点,
,
,
点在的延长线上,
到的距离为2,
,
,
.
综上所述,的值为或.
24.(1)抛物线的解析式为;
(2)①;②当时,四边形的面积最大,最大值为9,此时的长为;
(3)的取值范围为或
(1)点的坐标为,
,
,
,
,
设抛物线的解析式为,
将点代入,得,
抛物线的解析式为
(2)如图①,过点作轴交于点,
设直线的解析式为,
∵
∴直线的解析式为,
由题可知,
则,
①轴,
,
,
,
在中,,由勾股定理可得
,
;
②,且,,,,=
,
当时,四边形的面积最大,最大值为9,此时的长为;
(3)点的坐标为,点的坐标为,
点在直线上,点在直线上,轴,
如图②,设直线,直线与抛物线分别交于四点,
令,
解得,,
令,
解得,,
,
当点与点重合时,与抛物线只有一个交点,
,
当点与点重合时,与抛物线只有一个交点,
结合图②可知:当抛物线与线段只有一个公共点时,
或
或,
综上所述,的取值范围为或
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.﹣3的相反数是( )
A. B. C. D.
2.下列常见的几何体中,左视图是三角形的是( )
A. B. C. D.
3.某不等式组的解集在数轴上表示为如图所示,则该不等式组的解集是( )
A. B. C.或 D.或
4.下列各式中,计算结果等于的是( )
A. B. C. D.
5.汽车大灯通常由灯泡、反光镜和配光镜三部分组成.如图,光源位于焦点处,光线经反射后平行于地面射出,已知,,则的度数为( )
A. B. C. D.
6.端午节是我国四大传统节日之一,吃粽子是端午节的传统习俗,端午节这天小颖的妈妈买了只红豆粽和只红枣粽,这些粽子除了内部馅料不同外其他均相同.小颖从中随意选一个,她选到红豆粽的概率是( )
A. B. C. D.
7.如图,四边形是的内接四边形,连接,延长至点,若,则的度数为( )
A. B. C. D.
8.俄罗斯方块是一款经典休闲益智游戏,如图是小宇玩俄罗斯方块时某一时刻的截图,若在以为原点建立的平面直角坐标系中,小宇将上方的方块先向左移动2个格子,再向下移动6个格子后,点恰好落在点处,则上方的方块移动前点所在位置的坐标为( )
A. B. C. D.
9.如图,将正五边形剪掉一个角(裁剪线不经过顶点),则的度数为( )
A. B. C. D.
10.已知二次函数有最小值,点是该函数对称轴左侧图象上的点,点是对称轴右侧图象上的点,若,则下列关于与大小关系表述正确的是( )
A. B. C. D.
二、填空题
11.计算:= .
12.已知一次函数,则当增加1时,的值增加 .
13.食物中一般有蛋白质、脂肪、膳食纤维等营养成分,这些营养成分都是人体所需的,在平时需要做到营养均衡,科学饮食.如图是小米中蛋白质、脂肪、膳食纤维的含量统计图,则小米中蛋白质共有 .
14.《九章算术》是中国古代重要的数学著作,书中有一道题,其大意为:现有走路慢的人先走10里,令走路快的人去追,追到100里时,已经领先走路慢的人20里.问走路快的人走到多少里时就已经追上走路慢的人?设走路快的人走到里时就已经追上走路慢的人,则可列方程 .
15.如图,在正方形纸片中,是的中点,连接,将沿折叠,点的对应点为点,连接并延长交于点,则线段与位置关系为 , .
三、解答题
16.化简:.
17.定滑轮的目的是改变力的方向,使得施力方向转变为容易出力的方向.某班“综合与实践”小组的同学在课余时间测量“定滑轮距地面的高度”.如图,点均在同一竖直平面内,在点处测得定滑轮的仰角为,小组成员站在处,拉动绳子,使得物体移动至点处,在点处测得定滑轮的仰角为,物体从点移动到点处绳子收回的长度为,已知物体的高度.求定滑轮距地面的高度.(结果精确到,参考数据:,
18.电动平衡车采用电能驱动,不仅有助于环境保护,而且轻便易携,受到广大群众的喜爱.甲、乙两个品牌的电动平衡车都宣传他们的产品在正常情况下最大续航里程不低于,相关部门分别对两个品牌电动平衡车的最大续航里程做了抽样调查,统计结果(单位:)如下:
甲品牌:;
乙品牌:;
甲、乙两个品牌电动平衡车调查数据统计表
(质检部门规定该产品最大续航里程不低于为合格产品)
平均数 中位数 众数 合格率
甲品牌 14.7 14.6 70%
乙品牌 14.7 14.9
根据以上信息,解答下列问题:
(1)填空:____,______,_____;
(2)若你是顾客,宜选择哪个品牌的电动平衡车?结合上表平均数、中位数、众数、合格率等数据说明理由.
19.如图,点在反比例函数的图象上,过点作轴,垂足为,连接.已知的面积为6.
(1)求反比例函数的解析式及点的坐标;
(2)是轴负半轴上一点,平分,现有条件:
①过点作轴的垂线,交于点;
②点在上(不与点重合),点在轴负半轴上,.
请从①②中任选一个作为已知条件,求出点的横坐标.
20.如图,在矩形中,为对角线.
(1)请用无刻度的直尺和圆规作对角线的垂直平分线,分别交,的延长线于点,(不写作法,保留作图痕迹);
(2)在(1)的基础上连接,求证:是等腰三角形.
21.如图,内接于为的直径,过点作的平行线交于点,交于点,点在的延长线上,连接,且.
(1)求证:是的切线;
(2)若,求的长.
22.某校学生为了参加学校组织的“投篮大赛”,利用课后时间积极地进行备赛训练.如图是小明训练投篮时的示意图,身高1.75米的小明将篮球从头顶上方0.25米处出手,已知篮筐中心到地面的距离为3.05米,当距出手处的水平距离为2.5米时,篮球达到最大高度为3.25米,篮球的轨迹示意图可近似看作抛物线的一部分,以小明起跳点为原点,建立如图所示的平面直角坐标系.
(1)求抛物线的解析式;
(2)小明投出球后,小刚在小明与篮筐之间跳起防守,已知小刚最高能摸到2.45米,则在球上升的过程中,小刚与小明的距离在什么范围内小刚才能在空中截住篮球?
(3)已知小明在距篮筐水平距离3.8米的位置,在只改变起跳高度的情况下,通过计算说明小明要竖直起跳多少米才能直接投中?
23.【问题背景】如图1,在中,,点在上(不与点重合),交于点为的中点,连接并延长至点,使,连接,将绕点逆时针旋转,如图2,连接,探究在绕点旋转的过程中,线段与的数量关系与位置关系.
【特例探究】
(1)①若,则______,与所在直线夹角(锐角)的度数为______;
②若,则_______,与所在直线夹角(锐角)的度数为______;
【得出结论】
(2)如图2,若,则线段与之间有怎样的数量关系(用含的式子表示),与所在直线夹角(锐角)的度数为多少?证明你的结论;
【深入探究】
(3)如图3,若的旋转角为,当点到直线的距离为2时,求的值.
24.如图,在平面直角坐标系中,已知抛物线与轴交于两点(点在点左侧),与轴正半轴交于点,点的坐标为,且.
(1)求抛物线的解析式;
(2)点为直线上方抛物线上一动点,过点作于点,设点的横坐标为.
①用含的代数式表示线段的长;
②连接,求四边形面积的最大值,并直接写出此时的长;
(3)设点的坐标为,点的坐标为,连接,当抛物线和线段只有一个公共点时,求的取值范围.
参考答案
1.D
根据相反数的定义可得:-3的相反数是3,
故选D.
2.A
解:A圆锥的左视图是三角形,故此选项符合题意;;
B三棱柱的左视图为长方形,故此选项不符合题意;
C正方体的左视图是正方形,故此选项不符合题意;
D圆柱的左视图是长方形,故此选项不符合题意;
故选:A
3.A
解:由数轴可得,该不等式组的解集为,
故选:A.
4.B
解:A. ,不符合题意;
B. ,符合题意;
C. ,不符合题意;
D. ,不符合题意.
故选B.
5.C
解:由题意可得,如图,
∴,
∵,
∴,
故选:C.
6.B
解:只红豆粽和只红枣粽,这些粽子除了内部馅料不同外其他均相同.小颖从中随意选一个,她选到红豆粽的概率是
故选:B.
7.D
解:,
∴,
∴,
四边形是的内接四边形,
∴
,
故选:D.
8.C
点先向左移动2个格子,再向下移动6个格子后的位置为点,
将点先向上移动6个格于,再向右移动2个格子后得到点
∴上方的方块移动前点所在位置的坐标为,
故选:C.
9.D
解:∵五边形是正五边形,,
∴,
∵六边形的内角和为:,
,
故选:D.
10.A
解:二次函数有最小值,,
∴抛物线开口向上,对称轴为直线,即,
∵点是该函数对称轴左侧图象上的点,点是对称轴右侧图象上的点,
∴,即
∵,
∴,
,
∴.
故选:A.
11.
解:原式,
故答案为:.
12.2
当增加1时,
.
当增加1时,的值增加2.
故答案为:2
13.
.
故答案为:
14.
解:设走路快的人走x步就能追上走路慢的人,
根据题意,得.
故答案为:.
15.
解:如图,连接,由折叠的性质可得,
是的中点,
,
四边形是平行四边形,
,.
设,则
,
即
.
故答案为:;;
16.
解:原式
.
17.定滑轮距地面的高度约为.
解:如解图,过点作,交的延长线于点,连接并延长交于点.
根据题意,得,
在中,
,
,
在中,
,
,
绳子收回的长度为,
,
解得,
,
答:定滑轮距地面的高度约为.
18.(1),15,;
(2)选择乙品牌的电动平衡车,理由见解析.
(1)将从甲品牌得到的10个数据按照从小到大的顺序排列,位于最中间的两个数为,
中位数;
从乙品牌得到的10个数据中,15出现的次数最多,出现了3次,
众数为15
大于等于13的数据为8个,
.
故答案为:,15,80%;
(2)选择乙品牌的电动平衡车,理由如下:
乙品牌的中位数、众数和合格率都高于甲品牌,
选择乙品牌的电动平衡车.(答案不唯一,合理即可)
19.(1)反比例函数的解析式为,;
(2)①选条件①,点的横坐标为;②选条件②,点的横坐标为.
(1)解:的面积为轴,
,
反比例函数的图象在第一象限,
,
反比例函数的解析式为,
点在反比例函数的图象上,
,
解得,
;
(2)选条件①:
如解图①,设与轴的交点为,
,
,
轴,
轴,,
,
平分,
,
,
,
,
点的横坐标为.
或选条件②:
如解图②,连接交轴于点,
,
,
,
,
平分,
,
,
,
四边形是平行四边形,
轴,,
,
,
点的横坐标为.
20.(1)见解析;
(2)见解析.
(1)解:作图如图①;
(2)证明:如图②,设与交于点,
是的垂直平分线,
,
四边形是矩形,
,
在和中,
,
∵
,
是等腰三角形.
21.(1)见解析;
(2).
(1)证明:内接于为的直径,
,
,
,即,
,
,
,即,
是的半径,
是的切线;
(2)解:是的中点,,
是的中点,
,
,
,
在中,,
,
,
.
22.(1)抛物线的解析式为;
(2)在球上升的过程中,小刚与小明的距离在0.5米以内才能在空中截住篮球;
(3)小明要竖直起跳0.138米才能直接投中.
(1)解:由题意可得抛物线顶点坐标为,
(米),
当时,,
设抛物线的解析式为,
把点代入,
解得,
抛物线的解析式为;
(2)令,则,
解得.
要在球上升的过程中截住篮球,
,
在球上升的过程中,小刚与小明的距离在0.5米以内才能在空中截住篮球;
(3)改变起跳高度只是对抛物线进行上下平移,而篮球飞行的抛物线形状不变,
设改变起跳高度后的抛物线解析式为
小明距篮筐水平距离为3.8米,篮筐中心到地面的距离为3.05米,
将点代入,
得,
解得,
小明要竖直起跳0.138米才能直接投中.
23.(1)①;②;(2)与所在直线夹角(锐角)的度数为,证明见解析;(3)的值为或.
解:(1)①连接并延长交直线于点,延长到点,设交于点K,
∵,
∴,
,
∴,
∴,,
∵,
∴,
∵,,,
∴,
∴,,
∴,
∴,
即与所在直线夹角(锐角)的度数为;
②当时,同理可证与所在直线夹角(锐角)的度数为.
(2)与所在直线夹角(锐角)的度数为.
证明如下: 如图
,
,
,
,
,
,
,
,
,
,
,
即与所在直线夹角(锐角)的度数为;
(3)①当时,过点作于点,
都是等腰直角三角形,,,
,
,
点到的距离为2,
与重合,
,
,
;
②当时,过点作交的延长线于点,
,
,
点在的延长线上,
到的距离为2,
,
,
.
综上所述,的值为或.
24.(1)抛物线的解析式为;
(2)①;②当时,四边形的面积最大,最大值为9,此时的长为;
(3)的取值范围为或
(1)点的坐标为,
,
,
,
,
设抛物线的解析式为,
将点代入,得,
抛物线的解析式为
(2)如图①,过点作轴交于点,
设直线的解析式为,
∵
∴直线的解析式为,
由题可知,
则,
①轴,
,
,
,
在中,,由勾股定理可得
,
;
②,且,,,,=
,
当时,四边形的面积最大,最大值为9,此时的长为;
(3)点的坐标为,点的坐标为,
点在直线上,点在直线上,轴,
如图②,设直线,直线与抛物线分别交于四点,
令,
解得,,
令,
解得,,
,
当点与点重合时,与抛物线只有一个交点,
,
当点与点重合时,与抛物线只有一个交点,
结合图②可知:当抛物线与线段只有一个公共点时,
或
或,
综上所述,的取值范围为或
同课章节目录
