6.3数据的表示暑假预习练(含解析)
图片预览
文档简介
中小学教育资源及组卷应用平台
6.3数据的表示
学校:___________姓名:___________班级:___________考号:___________
一、单选题
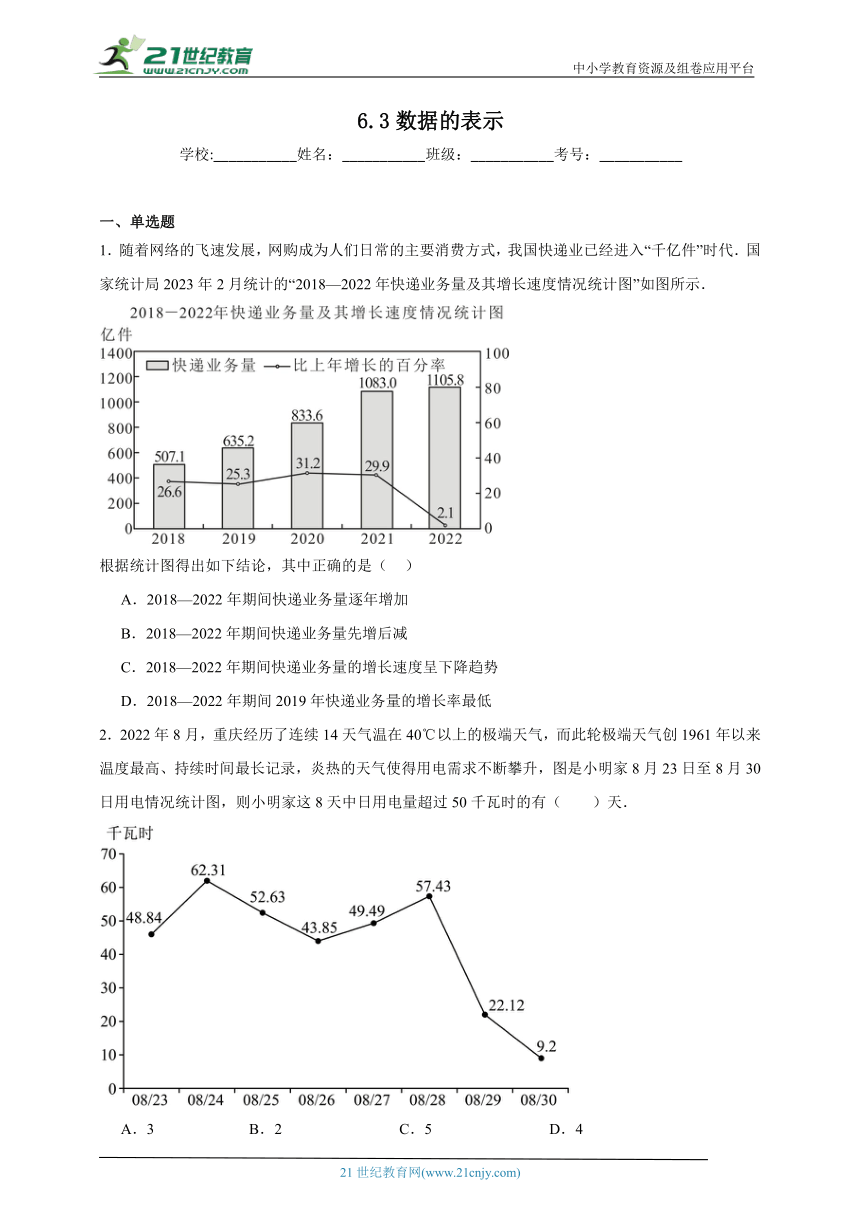
1.随着网络的飞速发展,网购成为人们日常的主要消费方式,我国快递业已经进入“千亿件”时代.国家统计局2023年2月统计的“2018—2022年快递业务量及其增长速度情况统计图”如图所示.
根据统计图得出如下结论,其中正确的是( )
A.2018—2022年期间快递业务量逐年增加
B.2018—2022年期间快递业务量先增后减
C.2018—2022年期间快递业务量的增长速度呈下降趋势
D.2018—2022年期间2019年快递业务量的增长率最低
2.2022年8月,重庆经历了连续14天气温在40℃以上的极端天气,而此轮极端天气创1961年以来温度最高、持续时间最长记录,炎热的天气使得用电需求不断攀升,图是小明家8月23日至8月30日用电情况统计图,则小明家这8天中日用电量超过50千瓦时的有( )天.
A.3 B.2 C.5 D.4
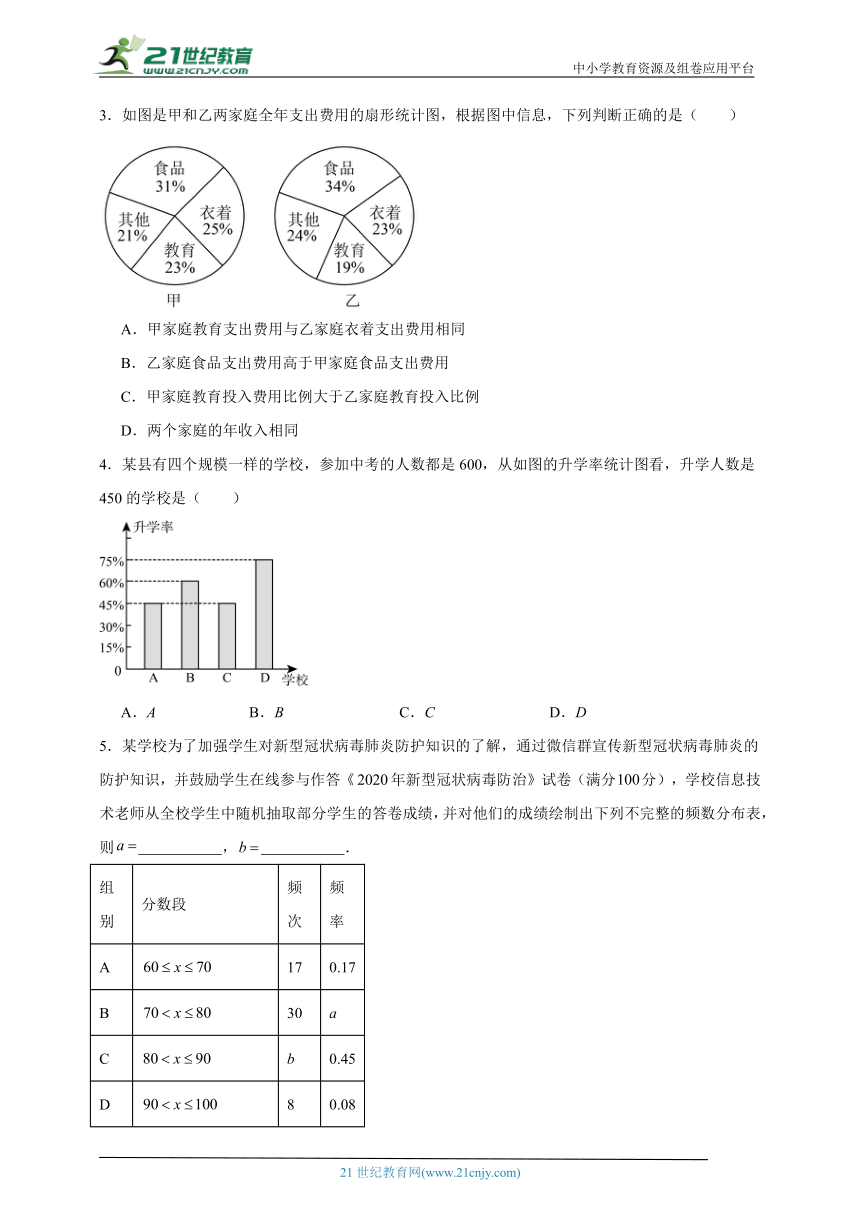
3.如图是甲和乙两家庭全年支出费用的扇形统计图,根据图中信息,下列判断正确的是( )
A.甲家庭教育支出费用与乙家庭衣着支出费用相同
B.乙家庭食品支出费用高于甲家庭食品支出费用
C.甲家庭教育投入费用比例大于乙家庭教育投入比例
D.两个家庭的年收入相同
4.某县有四个规模一样的学校,参加中考的人数都是600,从如图的升学率统计图看,升学人数是450的学校是( )
A.A B.B C.C D.D
5.某学校为了加强学生对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励学生在线参与作答《年新型冠状病毒防治》试卷(满分分),学校信息技术老师从全校学生中随机抽取部分学生的答卷成绩,并对他们的成绩绘制出下列不完整的频数分布表,则 , .
组别 分数段 频次 频率
A 17 0.17
B 30 a
C b 0.45
D 8 0.08
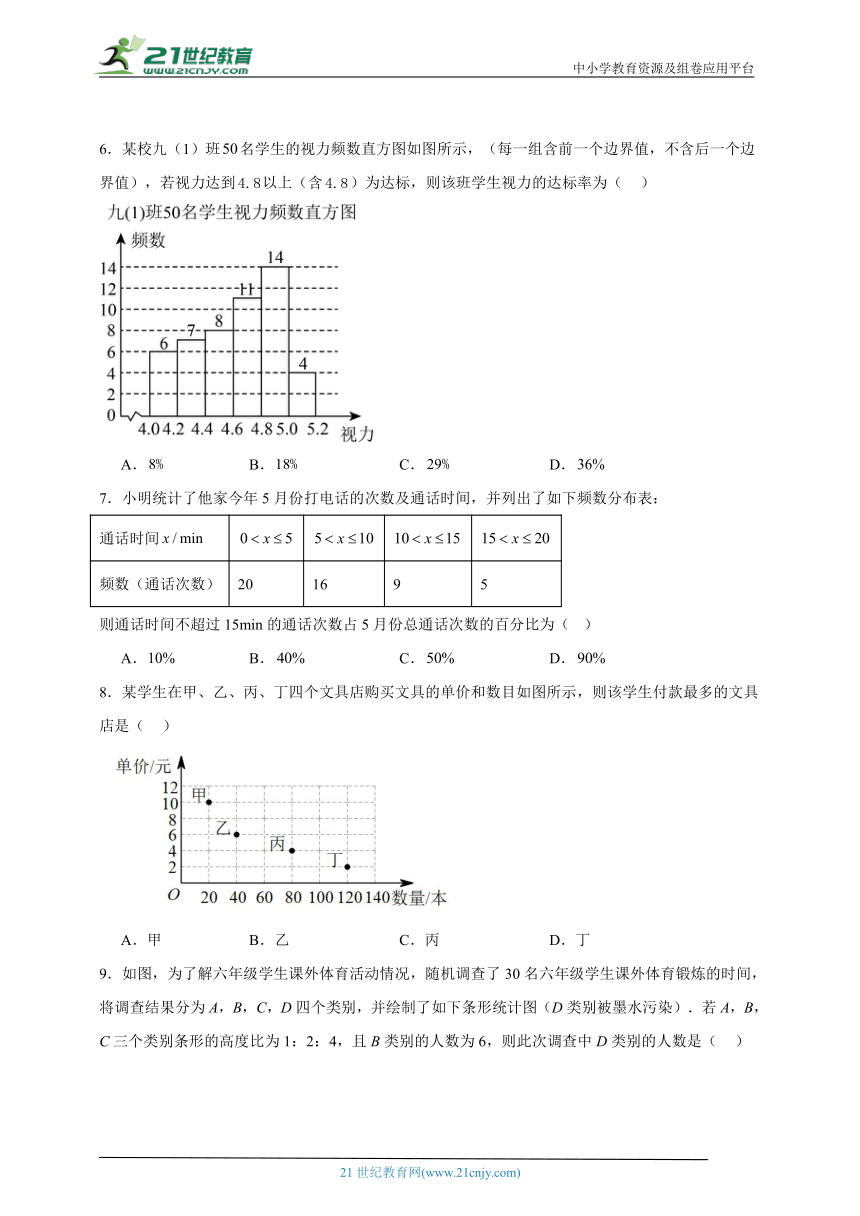
6.某校九(1)班名学生的视力频数直方图如图所示,(每一组含前一个边界值,不含后一个边界值),若视力达到以上(含)为达标,则该班学生视力的达标率为( )
A. B. C. D.
7.小明统计了他家今年5月份打电话的次数及通话时间,并列出了如下频数分布表:
通话时间
频数(通话次数) 20 16 9 5
则通话时间不超过15min的通话次数占5月份总通话次数的百分比为( )
A. B. C. D.
8.某学生在甲、乙、丙、丁四个文具店购买文具的单价和数目如图所示,则该学生付款最多的文具店是( )
A.甲 B.乙 C.丙 D.丁
9.如图,为了解六年级学生课外体育活动情况,随机调查了30名六年级学生课外体育锻炼的时间,将调查结果分为A,B,C,D四个类别,并绘制了如下条形统计图(D类别被墨水污染).若A,B,C三个类别条形的高度比为1:2:4,且B类别的人数为6,则此次调查中D类别的人数是( )
A.9 B.8 C.7 D.6
10.为了让使用者清楚、直观地看出计算机硬盘的“已用空间”占“整个磁盘空间”的百分比,宜采用( ).
A.条形图 B.折线图 C.扇形图 D.统计表
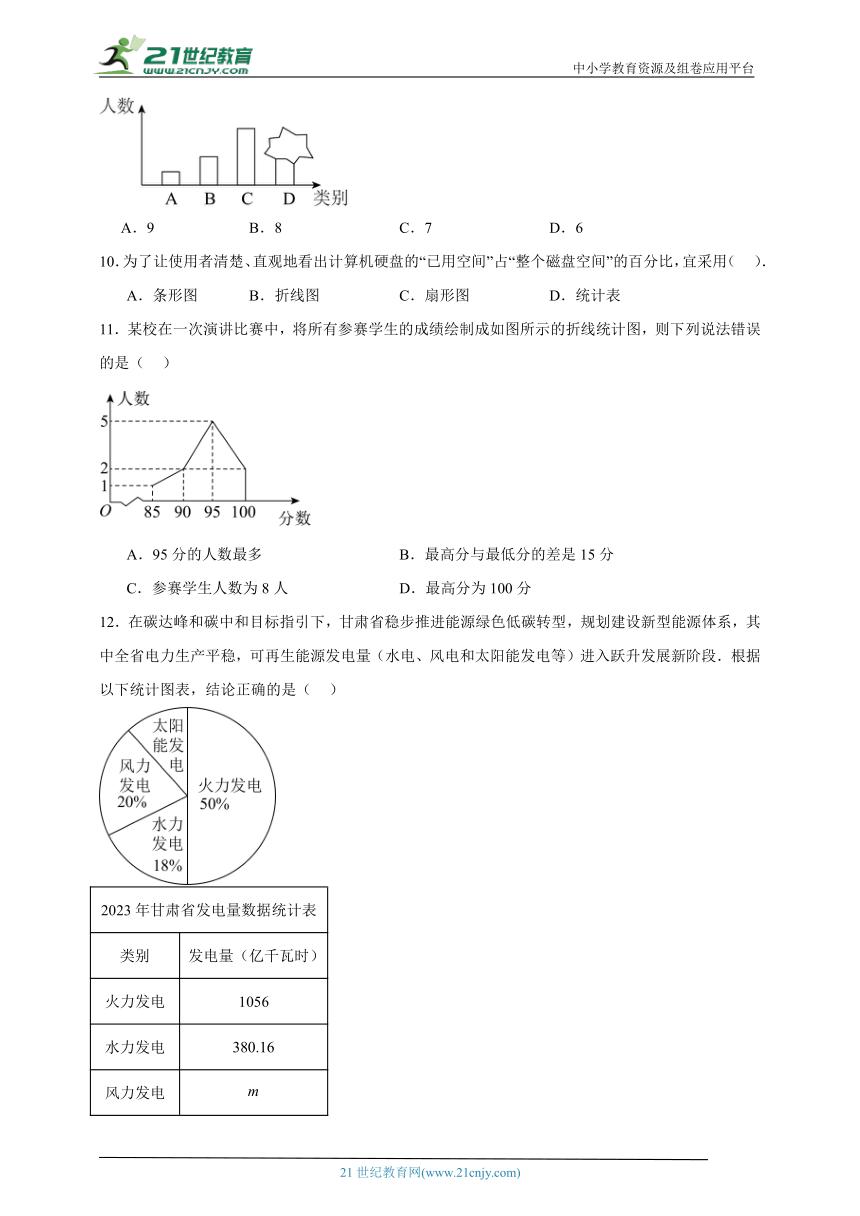
11.某校在一次演讲比赛中,将所有参赛学生的成绩绘制成如图所示的折线统计图,则下列说法错误的是( )
A.95分的人数最多 B.最高分与最低分的差是15分
C.参赛学生人数为8人 D.最高分为100分
12.在碳达峰和碳中和目标指引下,甘肃省稳步推进能源绿色低碳转型,规划建设新型能源体系,其中全省电力生产平稳,可再生能源发电量(水电、风电和太阳能发电等)进入跃升发展新阶段.根据以下统计图表,结论正确的是( )
2023年甘肃省发电量数据统计表
类别 发电量(亿千瓦时)
火力发电 1056
水力发电
风力发电
太阳能发电
总发电量 —
A.2023年甘肃省太阳能发电量占总发电量的
B.2023年甘肃省风力发电是最主要的发电方式
C.2023年甘肃省总发电量为2110亿千瓦时
D.的值为422.40
二、填空题
13.一个扇形统计图中,某部分占总体的三分之一,该部分所对应的扇形圆心角为 .
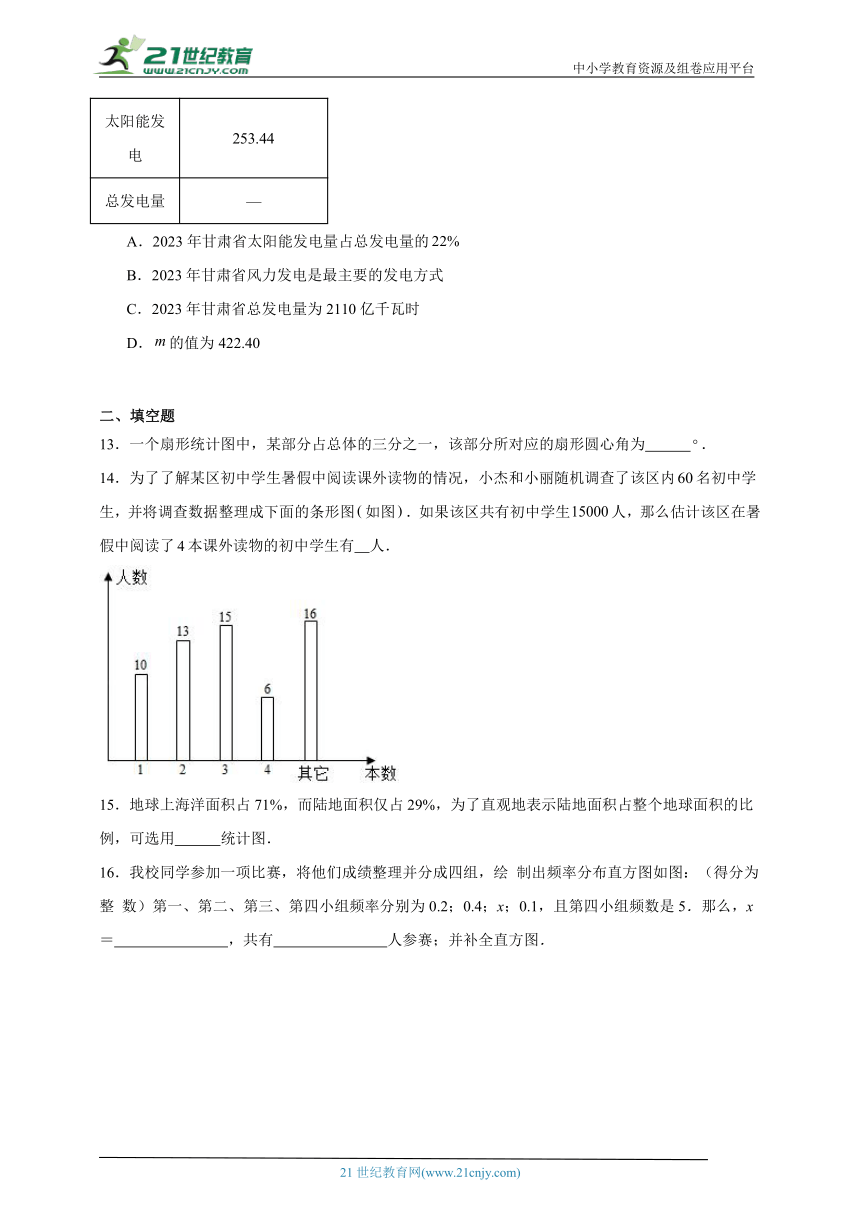
14.为了了解某区初中学生暑假中阅读课外读物的情况,小杰和小丽随机调查了该区内名初中学生,并将调查数据整理成下面的条形图如图.如果该区共有初中学生人,那么估计该区在暑假中阅读了本课外读物的初中学生有 人.
15.地球上海洋面积占71%,而陆地面积仅占29%,为了直观地表示陆地面积占整个地球面积的比例,可选用 统计图.
16.我校同学参加一项比赛,将他们成绩整理并分成四组,绘 制出频率分布直方图如图:(得分为整 数)第一、第二、第三、第四小组频率分别为0.2;0.4;x;0.1,且第四小组频数是5.那么,x= ,共有 人参赛;并补全直方图.
17.甲、乙两公司近年的销售收入情况如图所示, 公司近年的销售收入增长速度较快.
三、解答题
18.图1表示的是某书店今年1~5月的各月营业总额的情况,图2表示的是该书店“党史”类书籍的各月营业额占书店当月营业总额的百分比情况.若该书店1~5月的营业总额一共是182万元,观察图1、图2,解答下列问题:
(1)求该书店4月份的营业总额,并补全条形统计图;
(2)求5月份“党史”类书籍的营业额;
(3)这5个月中 月份“党史”类书籍的营业额最低
19.某中学为了提高学生对航天知识的了解,在全校开展了主题为“弘扬航天精神”的知识竞赛.为了解学生的竞赛情况,学校从中随机抽取了部分参赛学生的成绩(单位:分),整理后分为六组(A.,B.,C.,D.,E.,F.),并绘制出如下两幅不完整的统计图.请根据图中信息,解答下列问题:
(1)本次调查随机抽取了________名参赛学生的成绩.在扇形图中,F组所在扇形圆心角的度数是________;
(2)补全频数分布直方图;
(3)估计全校1200名学生中,知识竞赛成绩达到优秀的学生有多少人?
20.根据某校八年级部分学生的引体向上成绩绘制了如图所示的频数分布直方图,第三小组的频率是0.25.根据提供的信息回答下列问题:
(1)组距为_______;
(2)参加本次测试的学生总数是_______;
(3)如果做13次以上为优秀(包括13次),那么此次测试优秀的人数是_______.
21.为了解学生的艺术爱好,某校随机抽取了若干名学生进行问卷调查,问卷设有舞蹈、西洋乐器、民族乐器、声乐四个选项(每人只能选一项),根据调查结果绘制了如下扇形统计图和条形统计图.
根据以上信息回答下列问题:
(1)调查的学生人数为_______个,请补全条形统计图.
(2)若该校共有3000名学生,请根据调查结果估计喜欢民族乐器的学生人数.
22.某地方政府就“我最关心的城市建设问题”进行问卷调查,调查中要求每位被调查人员只写一个自己最关心的城市建设问题.经统计整理数据,画出条形统计图(如图),发现提出环境保护问题的市民最多,共700人.请回答下列问题:
(1)共收到调查表多少张?
(2)提道路交通问题的有多少人?
(3)请把这个条形统计图改成扇形统计图.
23.随着人们生活水平的提高,我国私家车拥有量在持续快速的增长.某市交通部门公布了《2018-2021年私人汽车拥有量调查报告》,根据报告信息绘制了私人汽车拥有量年增长率折线统计图和私人汽车拥有量不完整条形统计图.
(1)私人汽车拥有量年增长率最大的是哪一年?
(2)请你估算2017年该市拥有私人汽车约为多少万辆?并补全条形统计图.
(3)小明看了折线统计图后说:“私家车拥有量从2018年~2021年是先上升后下降的趋势,所以2020年私家车拥有量最高”.你认为小明的说法正确吗?若不正确,请说明理由.
24.目前,全球淡水资源分布不均、总量不足是人类面临的共同问题,某市在实施居民用水定额管理前,通过简单随机抽样对居民生活用水情况进行了调查,获得了若干个家庭去年的月均用水量数据(单位:t),整理出了频数分布表,频数分布直方图和扇形统计图,部分信息如下:
月均用水量(t) 2≤x<3.5 3.5≤x<5 5≤x<6.5 6.5≤x<8 8≤x<9.5
频数 7 6
对应的扇形区域 A B C D E
根据以上信息,解答下列问题:
(1)补全频数分布直方图,并求出扇形图中扇形E对应的圆心角的度数;
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使该市60%的家庭水费支出不受影响,你觉得家庭月均用水量应该定为多少?并说明理由.
《6.3数据的表示》参考答案
1.A
【分析】本题考查折线统计图于条形统计图综合,从统计图中获取有用的信息,逐一进行判断,是解题的关键.
【详解】解:A、2018—2022年期间快递业务量逐年增加,选项正确;
B、2018—2022年期间快递业务量一直在增加,选项错误;
C、2018—2022年期间快递业务量的增长速度先上升后下降,选项错误;
D、2018—2022年期间2022年快递业务量的增长率最低,选项错误;
故选A.
2.A
【分析】根据折线统计图找出电量超过50千瓦时的日期即可.
【详解】解:由折线统计图可知,电量超过50千瓦时的日期有8月24日、8月25日、8月28日,共三天,
故选:A.
【点睛】本题考查折线统计图,能看懂折线统计图是解题的关键.
3.C
【分析】本题考查根据扇形统计图分析数据信息.根据题意逐一对选项进行分析即可得到本题答案.
【详解】解:两个扇形统计图分别反映两家各类支出费用占各自的总支出费用的百分比,
∵不知道各家庭支出的总费用和收入,
∴无法比较两个家庭各类支出费用和年收入的多少,即A、B、D错误.
故选:C.
4.D
【分析】本题是一道统计试题,考查了百分比的运用,总人数升学率升学人数的数量关系的运用,解答时根据总人数升学率升学人数计算出各校的升学人数是关键.
【详解】解:由题意,得
A校的升学人数为:人,
B校的升学人数为:人,
C校的升学人数为:人,
D校的升学人数为:人,
∴D校的升学人数为450人.
故选:D.
5.
【分析】本题主要考查频数与频率的算法,关键是熟记计算方法.根据频率与频数的求法直接进行求解即可.
【详解】解:由题及表格可得:
,.
故答案为:;.
6.D
【分析】先算出视力达标的人数,即可算出该班视力的达标率.
【详解】解:视力达到以上(含)的人数:(人),
则该班学生视力的达标率为:,
故选:D.
【点睛】本题考查了频数分布直方图,解题的关键是理解题意,掌握频数分布直方图.
7.D
【分析】本题考查频数分布表,用不超过15min的通话次数除以总的通话次数进行计算即可.
【详解】解:;
故选D.
8.C
【分析】根据图象分别得出购买文具的单价和数目,然后计算求解即可.
【详解】解:由图可得,甲文具店单价元,数量是本,付款元;
乙文具店单价6元,数量是本,付款元;
丙文具店单价4元,数量是本,付款元;
丁文具店单价2元,数量是本,付款元;
∵,
∴付款最多的文具店是丙,
故选:C.
【点睛】题目主要考查从图象获取信息及有理数的乘法的应用,理解题意得出相关信息是解题关键.
9.A
【分析】设A类别的人数为,根据比例关系得到,即可求出,计算出A、B、C三个类别人数,即可求出D类别人数.
【详解】设A类别的人数为,则B类别的人数为,C类别的人数为,
∵B类别的人数为6,
∴,解得:
∴A、B、C三个类别的人数=,
∴D类别的人数=30-21=9,
故选:A.
【点睛】本题考查了条形统计图,掌握条形统计图的基本知识是解题关键.
10.C
【分析】本题主要考查了统计图的选择,理解扇形统计图的特点是解题的关键.
即扇形统计图的特点反映部分在总体中所占的百分比,根据统计图的特点解答即可.
【详解】解:根据题意,让使用者清楚、直观地看出计算机硬盘的“已用空间”占“整个磁盘空间”的百分比,需选用扇形统计图,
故选:C.
11.C
【分析】本题考查折线统计图数据分析.根据折线统计图对选项中得信息一一判断即可.
【详解】解: A、从统计图可以得出95分的人数最多,为5人,故本选项不符合题意;
B、从统计图可以得出最高分为100分,最低分为85分,最高分与最低分差是15分,故本选项不符合题意
C、从统计图可以得出参赛学生人数共有人,故本选项符合题意;
D、从统计图可以得出最高分为分,本选项不符合题意.
故选C.
12.D
【分析】本题主要考查扇形统计图、统计表等知识点,明确题意、利用数形结合是解答本题的关键.用“1”分别减去其它部分所占百分比即可判断选项A;由扇形统计图即可判断选项B;用火力发电的发电量可判断选项C;用总发电量乘可得判断选项D.
【详解】解:A.,即2023年甘肃省太阳能发电量占总发电量的,故选项A说法错误,不符合题意;
B.由扇形统计图可得2023年甘肃省火力发电是最主要的发电方式,故选项B说法错误,不符合题意;
C.2023年甘肃省总发电量为:(亿千瓦时),故选项C说法错误,不符合题意;
D.m的值为,故选项D说法正确,符合题意.
故选:D.
13.120
【分析】本题考查扇形统计图,对应的扇形的圆心角为,进一步计算即可.解题的关键是理解圆心角占比,属于中考常考题型.
【详解】解:对应的扇形圆心角的度数为.
故答案为:120.
14.1500
【分析】用样本的“读4本”课外读物的百分比估计总体的百分比,然后进行计算即可.
【详解】(人,
故答案为:.
【点睛】本题考查了条形统计图,样本估计总体,从统计图获取信息是解题的关键.
15.扇形
【分析】本题考查了扇形统计图,扇形统计图可以清楚的看到各部分所占的比例.
根据扇形统计图的特点即可得到答案.
【详解】解:扇形统计图可以清楚的看到各部分所占的比例,
可选用扇形统计图,
故答案为:扇形.
16. 0.3 50
【分析】利用总频率为“1”求第三小组的频率,运用第四小组的频数和频率求总人数.
【详解】解:第三小组的频率为:,
总共有:人,
故两个空的答案分别为0.3,50.
【点睛】本题主要考查频数直方图的应用,熟知频率总和为1,且知道如何运用频数和频率求总数是解题关键.
17.甲
【分析】结合折线统计图,分别求出甲、乙两公司近年销售收入各自的增长量即可求出答案.
【详解】从折线统计图中可以看出:
甲公司2017年的销售收入为100万元,2019年约为120万元,2021年约为160万元,则从2017~2021年甲公司增长了160-100=60万元;
乙公司2017年的销售收入为100万元,2019年约为110万元,2021年约为130万元,则从2017~2021年乙公司增长了130-100=30万元;
则销售收入增长速度较快的是甲.
故答案为:甲.
【点睛】本题考查了折线统计图,折线图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化情况.读懂统计图,从统计图中得到必要的信息是解决问题的关键.
18.(1)45;补全统计图见解析
(2)10.5
(3)3
【分析】(1)根据各组频率之和等于样本容量可求出“4月份”的营业总额,即可补全统计图;
(2)根据“5月份”的营业总额以及“党史”所占的百分比进行计算即可;
(3)求出各个月份“党史”类书籍的营业额即可.
【详解】(1)解:“4月份”的营业总额为:182-30-40-25-42=45(万元),补全统计图如下:
(2)42×25%=10.5(万元),
答:5月份“党史”类书籍的营业额为10.5万元;
(3)1月份“党史”类书籍的营业额为:30×15%=4.5(万元),
2月份“党史”类书籍的营业额为:40×10%=4(万元),
3月份“党史”类书籍的营业额为:25×12%=3(万元),
4月份“党史”类书籍的营业额为:45×20%=9(万元),
5月份“党史”类书籍的营业额为:42×25%=10.5(万元),
所以3月份“党史”类书籍的营业额最少,
故答案为:3.
【点睛】本题考查条形统计图、扇形统计图,理解统计图中数量之间的关系是正确解答的前提.
19.(1)50,
(2)见解析
(3)480人
【分析】本题考查直方图和扇形图,从统计图中有效的获取信息,是解题的关键.
(1)组学生人数除以所占的比例求出调查人数,组所占的比例乘以360度求出圆心角度数即可;
(2)求出组人数,补全条形图即可;
(3)利用样本估计总体的思想,进行求解即可.
【详解】(1)解:(名);
;
故答案为:50,;
(2)解:组人数为:(人),
补全直方图如图:
;
(3)解:(名);
答:知识竞赛成绩达到优秀的学生有480人.
20.(1)4
(2)100
(3)55
【分析】本题考查读频数分布直方图的能力和利用统计图获取信息的能力.
(1)根据组距的定义结合频数分布直方图可求得组距;
(2)用第三组的频数除以第三小组的频率,即可得参加本次测试的学生总数;
(3)用总人数减去13次以下的频数,即可得此次测试优秀的人数.
【详解】(1)解:组距为:,
故答案为:4;
(2)解:参加本次测试的学生总数是:(人),
故答案为:100;
(3)解:如果做13次以上为优秀(包括13次),那么此次测试优秀的人数是:
(人),
故答案为:55.
21.(1)500,见解析
(2)1050人
【分析】本题考查了扇形与条形统计图,运用样本估计总体,画条形统计图,正确掌握相关性质内容是解题的关键.
(1)运用西洋乐器的人数除以其占比,进行计算得出总人数,然后求出舞蹈人数,再补全条形统计图,即可作答.
(2)因为该校共有3000名学生,借助样本估计总体列式计算,即可作答.
【详解】(1)解:依题意,调查的学生人数为(人)
舞蹈人数:(人)
补全条形统计图如下:
(2)解:依题意, (人)
答:估计喜欢民族乐器的学生有1050人.
22.(1)2000张
(2)400人
(3)见解析
【分析】本题考查了条形统计图的运用,扇形统计图的运用,解答时根据条形统计图的数据求出调查的总人数是解答本题的关键.
(1)根据环境保护问题的数据就可以求出结论;
(2)用总人数提道路交通问题的百分数就可以得出结论;
(3)先由条形统计图的数据计算出个各个圆心角的度数就可以得出结论.
【详解】(1)解:由题意,得:
共收到调查表(张),
答:共收到调查表2000张;
(2)由题意,得
提道路交通问题的有(人),
答:提道路交通问题的有400人;
(3)由题意,得
其他:,
房屋建设:,
环境保护:,
绿化:,
道路交通:.
∴扇形统计图为:
23.(1)2020年
(2)85(84~85之间均可给分);见解析
(3)小明的说法不正确,从2018年~2021年汽车拥有量一直在增加,只是增长率呈先升后降,增长率反映的是增长速度
【分析】(1)根据私人汽车拥有量年增长率折线统计图即可得知增长率最大的一年;
(2)根据2018年的私家汽车拥有量为100万辆和增长率为,即可计算2017年的私人汽车数量;计算出2019年的私家汽车数量,补全条形统计图即可;
(3)增长率呈先升后降,增长率反映的是增长速度,但汽车拥有量一直在增加.
【详解】(1)根据私人汽车拥有量年增长率折线统计图得知增长率最大的一年为:2020年;
(2),
2017年该市拥有私人汽车约为85万辆;
2019年该市拥有私人汽车约为(辆),
条形统计图如图:
(3)小明的说法不正确,从2018年~2021年汽车拥有量一直在增加,只是增长率呈先升后降,增长率反映的是增长速度.
【点睛】本题考查折线统计图和条形统计图的应用,熟练掌握折线统计图和条形统计图的特点和区别是解题的关键.
24.(1)频数分布直方图见解析,E对应的圆心角的度数为:14.4°
(2)要使60%的家庭收费不受影响,家庭月均用水量应该定为5吨,理由见解析
【分析】(1)根据题A的频数和百分比得到抽取的总数,进而求得B、C的频数即可补全频数分布直方图,求出E的频数,360°乘以E所占的比例即可求解;
(2)由于50×60%=30,所以为了鼓励节约用水,要使60%的家庭收费不受影响,即要使30户的家庭收费不受影响,而7+23=30,故家庭月均用水量应该定为5吨.
【详解】(1)抽取的总数为:7÷14%=50,B的频数为:50×46%=23,C的频数为:50×24%=12,频数分布直方图如下:
扇形图中扇形E对应的圆心角的度数为:
360°=14.4°;
(2)要使60%的家庭收费不受影响,家庭月均用水量应该定为5吨,理由如下:
因为月平均用水量不超过5吨的有7+23=30(户),30÷50=60%.
【点睛】本题考查了读频数分布直方图和频数分布表的能力及利用统计图表获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.3数据的表示
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.随着网络的飞速发展,网购成为人们日常的主要消费方式,我国快递业已经进入“千亿件”时代.国家统计局2023年2月统计的“2018—2022年快递业务量及其增长速度情况统计图”如图所示.
根据统计图得出如下结论,其中正确的是( )
A.2018—2022年期间快递业务量逐年增加
B.2018—2022年期间快递业务量先增后减
C.2018—2022年期间快递业务量的增长速度呈下降趋势
D.2018—2022年期间2019年快递业务量的增长率最低
2.2022年8月,重庆经历了连续14天气温在40℃以上的极端天气,而此轮极端天气创1961年以来温度最高、持续时间最长记录,炎热的天气使得用电需求不断攀升,图是小明家8月23日至8月30日用电情况统计图,则小明家这8天中日用电量超过50千瓦时的有( )天.
A.3 B.2 C.5 D.4
3.如图是甲和乙两家庭全年支出费用的扇形统计图,根据图中信息,下列判断正确的是( )
A.甲家庭教育支出费用与乙家庭衣着支出费用相同
B.乙家庭食品支出费用高于甲家庭食品支出费用
C.甲家庭教育投入费用比例大于乙家庭教育投入比例
D.两个家庭的年收入相同
4.某县有四个规模一样的学校,参加中考的人数都是600,从如图的升学率统计图看,升学人数是450的学校是( )
A.A B.B C.C D.D
5.某学校为了加强学生对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励学生在线参与作答《年新型冠状病毒防治》试卷(满分分),学校信息技术老师从全校学生中随机抽取部分学生的答卷成绩,并对他们的成绩绘制出下列不完整的频数分布表,则 , .
组别 分数段 频次 频率
A 17 0.17
B 30 a
C b 0.45
D 8 0.08
6.某校九(1)班名学生的视力频数直方图如图所示,(每一组含前一个边界值,不含后一个边界值),若视力达到以上(含)为达标,则该班学生视力的达标率为( )
A. B. C. D.
7.小明统计了他家今年5月份打电话的次数及通话时间,并列出了如下频数分布表:
通话时间
频数(通话次数) 20 16 9 5
则通话时间不超过15min的通话次数占5月份总通话次数的百分比为( )
A. B. C. D.
8.某学生在甲、乙、丙、丁四个文具店购买文具的单价和数目如图所示,则该学生付款最多的文具店是( )
A.甲 B.乙 C.丙 D.丁
9.如图,为了解六年级学生课外体育活动情况,随机调查了30名六年级学生课外体育锻炼的时间,将调查结果分为A,B,C,D四个类别,并绘制了如下条形统计图(D类别被墨水污染).若A,B,C三个类别条形的高度比为1:2:4,且B类别的人数为6,则此次调查中D类别的人数是( )
A.9 B.8 C.7 D.6
10.为了让使用者清楚、直观地看出计算机硬盘的“已用空间”占“整个磁盘空间”的百分比,宜采用( ).
A.条形图 B.折线图 C.扇形图 D.统计表
11.某校在一次演讲比赛中,将所有参赛学生的成绩绘制成如图所示的折线统计图,则下列说法错误的是( )
A.95分的人数最多 B.最高分与最低分的差是15分
C.参赛学生人数为8人 D.最高分为100分
12.在碳达峰和碳中和目标指引下,甘肃省稳步推进能源绿色低碳转型,规划建设新型能源体系,其中全省电力生产平稳,可再生能源发电量(水电、风电和太阳能发电等)进入跃升发展新阶段.根据以下统计图表,结论正确的是( )
2023年甘肃省发电量数据统计表
类别 发电量(亿千瓦时)
火力发电 1056
水力发电
风力发电
太阳能发电
总发电量 —
A.2023年甘肃省太阳能发电量占总发电量的
B.2023年甘肃省风力发电是最主要的发电方式
C.2023年甘肃省总发电量为2110亿千瓦时
D.的值为422.40
二、填空题
13.一个扇形统计图中,某部分占总体的三分之一,该部分所对应的扇形圆心角为 .
14.为了了解某区初中学生暑假中阅读课外读物的情况,小杰和小丽随机调查了该区内名初中学生,并将调查数据整理成下面的条形图如图.如果该区共有初中学生人,那么估计该区在暑假中阅读了本课外读物的初中学生有 人.
15.地球上海洋面积占71%,而陆地面积仅占29%,为了直观地表示陆地面积占整个地球面积的比例,可选用 统计图.
16.我校同学参加一项比赛,将他们成绩整理并分成四组,绘 制出频率分布直方图如图:(得分为整 数)第一、第二、第三、第四小组频率分别为0.2;0.4;x;0.1,且第四小组频数是5.那么,x= ,共有 人参赛;并补全直方图.
17.甲、乙两公司近年的销售收入情况如图所示, 公司近年的销售收入增长速度较快.
三、解答题
18.图1表示的是某书店今年1~5月的各月营业总额的情况,图2表示的是该书店“党史”类书籍的各月营业额占书店当月营业总额的百分比情况.若该书店1~5月的营业总额一共是182万元,观察图1、图2,解答下列问题:
(1)求该书店4月份的营业总额,并补全条形统计图;
(2)求5月份“党史”类书籍的营业额;
(3)这5个月中 月份“党史”类书籍的营业额最低
19.某中学为了提高学生对航天知识的了解,在全校开展了主题为“弘扬航天精神”的知识竞赛.为了解学生的竞赛情况,学校从中随机抽取了部分参赛学生的成绩(单位:分),整理后分为六组(A.,B.,C.,D.,E.,F.),并绘制出如下两幅不完整的统计图.请根据图中信息,解答下列问题:
(1)本次调查随机抽取了________名参赛学生的成绩.在扇形图中,F组所在扇形圆心角的度数是________;
(2)补全频数分布直方图;
(3)估计全校1200名学生中,知识竞赛成绩达到优秀的学生有多少人?
20.根据某校八年级部分学生的引体向上成绩绘制了如图所示的频数分布直方图,第三小组的频率是0.25.根据提供的信息回答下列问题:
(1)组距为_______;
(2)参加本次测试的学生总数是_______;
(3)如果做13次以上为优秀(包括13次),那么此次测试优秀的人数是_______.
21.为了解学生的艺术爱好,某校随机抽取了若干名学生进行问卷调查,问卷设有舞蹈、西洋乐器、民族乐器、声乐四个选项(每人只能选一项),根据调查结果绘制了如下扇形统计图和条形统计图.
根据以上信息回答下列问题:
(1)调查的学生人数为_______个,请补全条形统计图.
(2)若该校共有3000名学生,请根据调查结果估计喜欢民族乐器的学生人数.
22.某地方政府就“我最关心的城市建设问题”进行问卷调查,调查中要求每位被调查人员只写一个自己最关心的城市建设问题.经统计整理数据,画出条形统计图(如图),发现提出环境保护问题的市民最多,共700人.请回答下列问题:
(1)共收到调查表多少张?
(2)提道路交通问题的有多少人?
(3)请把这个条形统计图改成扇形统计图.
23.随着人们生活水平的提高,我国私家车拥有量在持续快速的增长.某市交通部门公布了《2018-2021年私人汽车拥有量调查报告》,根据报告信息绘制了私人汽车拥有量年增长率折线统计图和私人汽车拥有量不完整条形统计图.
(1)私人汽车拥有量年增长率最大的是哪一年?
(2)请你估算2017年该市拥有私人汽车约为多少万辆?并补全条形统计图.
(3)小明看了折线统计图后说:“私家车拥有量从2018年~2021年是先上升后下降的趋势,所以2020年私家车拥有量最高”.你认为小明的说法正确吗?若不正确,请说明理由.
24.目前,全球淡水资源分布不均、总量不足是人类面临的共同问题,某市在实施居民用水定额管理前,通过简单随机抽样对居民生活用水情况进行了调查,获得了若干个家庭去年的月均用水量数据(单位:t),整理出了频数分布表,频数分布直方图和扇形统计图,部分信息如下:
月均用水量(t) 2≤x<3.5 3.5≤x<5 5≤x<6.5 6.5≤x<8 8≤x<9.5
频数 7 6
对应的扇形区域 A B C D E
根据以上信息,解答下列问题:
(1)补全频数分布直方图,并求出扇形图中扇形E对应的圆心角的度数;
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使该市60%的家庭水费支出不受影响,你觉得家庭月均用水量应该定为多少?并说明理由.
《6.3数据的表示》参考答案
1.A
【分析】本题考查折线统计图于条形统计图综合,从统计图中获取有用的信息,逐一进行判断,是解题的关键.
【详解】解:A、2018—2022年期间快递业务量逐年增加,选项正确;
B、2018—2022年期间快递业务量一直在增加,选项错误;
C、2018—2022年期间快递业务量的增长速度先上升后下降,选项错误;
D、2018—2022年期间2022年快递业务量的增长率最低,选项错误;
故选A.
2.A
【分析】根据折线统计图找出电量超过50千瓦时的日期即可.
【详解】解:由折线统计图可知,电量超过50千瓦时的日期有8月24日、8月25日、8月28日,共三天,
故选:A.
【点睛】本题考查折线统计图,能看懂折线统计图是解题的关键.
3.C
【分析】本题考查根据扇形统计图分析数据信息.根据题意逐一对选项进行分析即可得到本题答案.
【详解】解:两个扇形统计图分别反映两家各类支出费用占各自的总支出费用的百分比,
∵不知道各家庭支出的总费用和收入,
∴无法比较两个家庭各类支出费用和年收入的多少,即A、B、D错误.
故选:C.
4.D
【分析】本题是一道统计试题,考查了百分比的运用,总人数升学率升学人数的数量关系的运用,解答时根据总人数升学率升学人数计算出各校的升学人数是关键.
【详解】解:由题意,得
A校的升学人数为:人,
B校的升学人数为:人,
C校的升学人数为:人,
D校的升学人数为:人,
∴D校的升学人数为450人.
故选:D.
5.
【分析】本题主要考查频数与频率的算法,关键是熟记计算方法.根据频率与频数的求法直接进行求解即可.
【详解】解:由题及表格可得:
,.
故答案为:;.
6.D
【分析】先算出视力达标的人数,即可算出该班视力的达标率.
【详解】解:视力达到以上(含)的人数:(人),
则该班学生视力的达标率为:,
故选:D.
【点睛】本题考查了频数分布直方图,解题的关键是理解题意,掌握频数分布直方图.
7.D
【分析】本题考查频数分布表,用不超过15min的通话次数除以总的通话次数进行计算即可.
【详解】解:;
故选D.
8.C
【分析】根据图象分别得出购买文具的单价和数目,然后计算求解即可.
【详解】解:由图可得,甲文具店单价元,数量是本,付款元;
乙文具店单价6元,数量是本,付款元;
丙文具店单价4元,数量是本,付款元;
丁文具店单价2元,数量是本,付款元;
∵,
∴付款最多的文具店是丙,
故选:C.
【点睛】题目主要考查从图象获取信息及有理数的乘法的应用,理解题意得出相关信息是解题关键.
9.A
【分析】设A类别的人数为,根据比例关系得到,即可求出,计算出A、B、C三个类别人数,即可求出D类别人数.
【详解】设A类别的人数为,则B类别的人数为,C类别的人数为,
∵B类别的人数为6,
∴,解得:
∴A、B、C三个类别的人数=,
∴D类别的人数=30-21=9,
故选:A.
【点睛】本题考查了条形统计图,掌握条形统计图的基本知识是解题关键.
10.C
【分析】本题主要考查了统计图的选择,理解扇形统计图的特点是解题的关键.
即扇形统计图的特点反映部分在总体中所占的百分比,根据统计图的特点解答即可.
【详解】解:根据题意,让使用者清楚、直观地看出计算机硬盘的“已用空间”占“整个磁盘空间”的百分比,需选用扇形统计图,
故选:C.
11.C
【分析】本题考查折线统计图数据分析.根据折线统计图对选项中得信息一一判断即可.
【详解】解: A、从统计图可以得出95分的人数最多,为5人,故本选项不符合题意;
B、从统计图可以得出最高分为100分,最低分为85分,最高分与最低分差是15分,故本选项不符合题意
C、从统计图可以得出参赛学生人数共有人,故本选项符合题意;
D、从统计图可以得出最高分为分,本选项不符合题意.
故选C.
12.D
【分析】本题主要考查扇形统计图、统计表等知识点,明确题意、利用数形结合是解答本题的关键.用“1”分别减去其它部分所占百分比即可判断选项A;由扇形统计图即可判断选项B;用火力发电的发电量可判断选项C;用总发电量乘可得判断选项D.
【详解】解:A.,即2023年甘肃省太阳能发电量占总发电量的,故选项A说法错误,不符合题意;
B.由扇形统计图可得2023年甘肃省火力发电是最主要的发电方式,故选项B说法错误,不符合题意;
C.2023年甘肃省总发电量为:(亿千瓦时),故选项C说法错误,不符合题意;
D.m的值为,故选项D说法正确,符合题意.
故选:D.
13.120
【分析】本题考查扇形统计图,对应的扇形的圆心角为,进一步计算即可.解题的关键是理解圆心角占比,属于中考常考题型.
【详解】解:对应的扇形圆心角的度数为.
故答案为:120.
14.1500
【分析】用样本的“读4本”课外读物的百分比估计总体的百分比,然后进行计算即可.
【详解】(人,
故答案为:.
【点睛】本题考查了条形统计图,样本估计总体,从统计图获取信息是解题的关键.
15.扇形
【分析】本题考查了扇形统计图,扇形统计图可以清楚的看到各部分所占的比例.
根据扇形统计图的特点即可得到答案.
【详解】解:扇形统计图可以清楚的看到各部分所占的比例,
可选用扇形统计图,
故答案为:扇形.
16. 0.3 50
【分析】利用总频率为“1”求第三小组的频率,运用第四小组的频数和频率求总人数.
【详解】解:第三小组的频率为:,
总共有:人,
故两个空的答案分别为0.3,50.
【点睛】本题主要考查频数直方图的应用,熟知频率总和为1,且知道如何运用频数和频率求总数是解题关键.
17.甲
【分析】结合折线统计图,分别求出甲、乙两公司近年销售收入各自的增长量即可求出答案.
【详解】从折线统计图中可以看出:
甲公司2017年的销售收入为100万元,2019年约为120万元,2021年约为160万元,则从2017~2021年甲公司增长了160-100=60万元;
乙公司2017年的销售收入为100万元,2019年约为110万元,2021年约为130万元,则从2017~2021年乙公司增长了130-100=30万元;
则销售收入增长速度较快的是甲.
故答案为:甲.
【点睛】本题考查了折线统计图,折线图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化情况.读懂统计图,从统计图中得到必要的信息是解决问题的关键.
18.(1)45;补全统计图见解析
(2)10.5
(3)3
【分析】(1)根据各组频率之和等于样本容量可求出“4月份”的营业总额,即可补全统计图;
(2)根据“5月份”的营业总额以及“党史”所占的百分比进行计算即可;
(3)求出各个月份“党史”类书籍的营业额即可.
【详解】(1)解:“4月份”的营业总额为:182-30-40-25-42=45(万元),补全统计图如下:
(2)42×25%=10.5(万元),
答:5月份“党史”类书籍的营业额为10.5万元;
(3)1月份“党史”类书籍的营业额为:30×15%=4.5(万元),
2月份“党史”类书籍的营业额为:40×10%=4(万元),
3月份“党史”类书籍的营业额为:25×12%=3(万元),
4月份“党史”类书籍的营业额为:45×20%=9(万元),
5月份“党史”类书籍的营业额为:42×25%=10.5(万元),
所以3月份“党史”类书籍的营业额最少,
故答案为:3.
【点睛】本题考查条形统计图、扇形统计图,理解统计图中数量之间的关系是正确解答的前提.
19.(1)50,
(2)见解析
(3)480人
【分析】本题考查直方图和扇形图,从统计图中有效的获取信息,是解题的关键.
(1)组学生人数除以所占的比例求出调查人数,组所占的比例乘以360度求出圆心角度数即可;
(2)求出组人数,补全条形图即可;
(3)利用样本估计总体的思想,进行求解即可.
【详解】(1)解:(名);
;
故答案为:50,;
(2)解:组人数为:(人),
补全直方图如图:
;
(3)解:(名);
答:知识竞赛成绩达到优秀的学生有480人.
20.(1)4
(2)100
(3)55
【分析】本题考查读频数分布直方图的能力和利用统计图获取信息的能力.
(1)根据组距的定义结合频数分布直方图可求得组距;
(2)用第三组的频数除以第三小组的频率,即可得参加本次测试的学生总数;
(3)用总人数减去13次以下的频数,即可得此次测试优秀的人数.
【详解】(1)解:组距为:,
故答案为:4;
(2)解:参加本次测试的学生总数是:(人),
故答案为:100;
(3)解:如果做13次以上为优秀(包括13次),那么此次测试优秀的人数是:
(人),
故答案为:55.
21.(1)500,见解析
(2)1050人
【分析】本题考查了扇形与条形统计图,运用样本估计总体,画条形统计图,正确掌握相关性质内容是解题的关键.
(1)运用西洋乐器的人数除以其占比,进行计算得出总人数,然后求出舞蹈人数,再补全条形统计图,即可作答.
(2)因为该校共有3000名学生,借助样本估计总体列式计算,即可作答.
【详解】(1)解:依题意,调查的学生人数为(人)
舞蹈人数:(人)
补全条形统计图如下:
(2)解:依题意, (人)
答:估计喜欢民族乐器的学生有1050人.
22.(1)2000张
(2)400人
(3)见解析
【分析】本题考查了条形统计图的运用,扇形统计图的运用,解答时根据条形统计图的数据求出调查的总人数是解答本题的关键.
(1)根据环境保护问题的数据就可以求出结论;
(2)用总人数提道路交通问题的百分数就可以得出结论;
(3)先由条形统计图的数据计算出个各个圆心角的度数就可以得出结论.
【详解】(1)解:由题意,得:
共收到调查表(张),
答:共收到调查表2000张;
(2)由题意,得
提道路交通问题的有(人),
答:提道路交通问题的有400人;
(3)由题意,得
其他:,
房屋建设:,
环境保护:,
绿化:,
道路交通:.
∴扇形统计图为:
23.(1)2020年
(2)85(84~85之间均可给分);见解析
(3)小明的说法不正确,从2018年~2021年汽车拥有量一直在增加,只是增长率呈先升后降,增长率反映的是增长速度
【分析】(1)根据私人汽车拥有量年增长率折线统计图即可得知增长率最大的一年;
(2)根据2018年的私家汽车拥有量为100万辆和增长率为,即可计算2017年的私人汽车数量;计算出2019年的私家汽车数量,补全条形统计图即可;
(3)增长率呈先升后降,增长率反映的是增长速度,但汽车拥有量一直在增加.
【详解】(1)根据私人汽车拥有量年增长率折线统计图得知增长率最大的一年为:2020年;
(2),
2017年该市拥有私人汽车约为85万辆;
2019年该市拥有私人汽车约为(辆),
条形统计图如图:
(3)小明的说法不正确,从2018年~2021年汽车拥有量一直在增加,只是增长率呈先升后降,增长率反映的是增长速度.
【点睛】本题考查折线统计图和条形统计图的应用,熟练掌握折线统计图和条形统计图的特点和区别是解题的关键.
24.(1)频数分布直方图见解析,E对应的圆心角的度数为:14.4°
(2)要使60%的家庭收费不受影响,家庭月均用水量应该定为5吨,理由见解析
【分析】(1)根据题A的频数和百分比得到抽取的总数,进而求得B、C的频数即可补全频数分布直方图,求出E的频数,360°乘以E所占的比例即可求解;
(2)由于50×60%=30,所以为了鼓励节约用水,要使60%的家庭收费不受影响,即要使30户的家庭收费不受影响,而7+23=30,故家庭月均用水量应该定为5吨.
【详解】(1)抽取的总数为:7÷14%=50,B的频数为:50×46%=23,C的频数为:50×24%=12,频数分布直方图如下:
扇形图中扇形E对应的圆心角的度数为:
360°=14.4°;
(2)要使60%的家庭收费不受影响,家庭月均用水量应该定为5吨,理由如下:
因为月平均用水量不超过5吨的有7+23=30(户),30÷50=60%.
【点睛】本题考查了读频数分布直方图和频数分布表的能力及利用统计图表获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
