第四章基本平面图形暑假预习练(含解析)
文档属性
| 名称 | 第四章基本平面图形暑假预习练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 755.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-26 10:49:21 | ||
图片预览

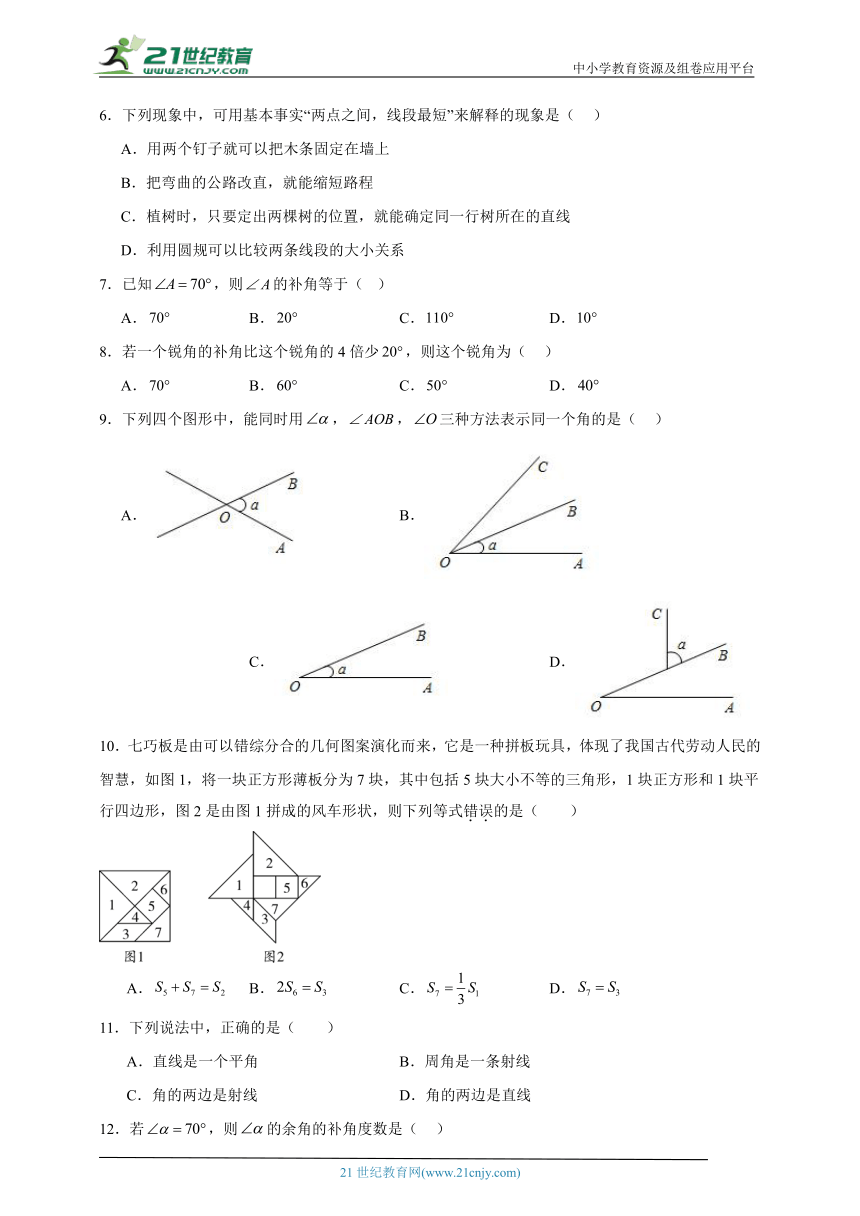


文档简介
中小学教育资源及组卷应用平台
第四章基本平面图形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知,那么的余角的度数是( )
A. B. C. D.
2.比较与的大小,把它们的顶点A和边重合,把它们的另一边和放在的同一侧,若,则( )
A.落在的内部 B.落在的外部
C.和重合 D.不能确定的位置
3.如图,有一种电子游戏,电子屏幕上有一条直线,在直线上有A,B,C,D四点.点P沿直线l从右向左移动,当出现点P与A,B,C,D四点中的至少两个点距离相等时,就会发出警报,则直线l上会发出警报的点P最多有( )个.
A.3 B.4 C.5 D.6
4.如图所示,能用,,三种方法表示同一个角的图形是( )
A. B.
C. D.
5.下列说法正确的是( )
A.钟表的时间是10点30分,此时时针与分针所成的夹角是105°
B.若经过某个多边形一个顶点的所有对角线,将这个多边形分成八个三角形,则这个多边形是九边形
C.若,则点是线段的中点
D.
6.下列现象中,可用基本事实“两点之间,线段最短”来解释的现象是( )
A.用两个钉子就可以把木条固定在墙上
B.把弯曲的公路改直,就能缩短路程
C.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
D.利用圆规可以比较两条线段的大小关系
7.已知,则的补角等于( )
A. B. C. D.
8.若一个锐角的补角比这个锐角的4倍少,则这个锐角为( )
A. B. C. D.
9.下列四个图形中,能同时用,,三种方法表示同一个角的是( )
A. B. C. D.
10.七巧板是由可以错综分合的几何图案演化而来,它是一种拼板玩具,体现了我国古代劳动人民的智慧,如图1,将一块正方形薄板分为7块,其中包括5块大小不等的三角形,1块正方形和1块平行四边形,图2是由图1拼成的风车形状,则下列等式错误的是( )
A. B. C. D.
11.下列说法中,正确的是( )
A.直线是一个平角 B.周角是一条射线
C.角的两边是射线 D.角的两边是直线
12.若,则的余角的补角度数是( )
A. B. C. D.
二、填空题
13.在一条直线上顺次取,,,四点,使,如果,,则 cm.
14.方向角是指以坐标轴方向为标准方向确定的方位角.方向角与目标方向正北或正南的夹角小于 .
15.如图,直线与相交于点O,∴,,∴,在此推理过程中,与相等的理由是 .
16.已知:线段AC和BC在同一直线上,如果AC=10cm,BC=6cm,D为AC的中点,E为BC的中点,则DE= .
17.把原来弯曲的河道改直,河道长度变短,其原理能用基本事实“ ”解释.
三、解答题
18.(1)数一数,找规律:下图中,角内部射线的条数依次增加,请数一数各图中有几个角.
(2)如果一个角内部有8条射线,那么该图中有 个角;
(3)如果一个角内部有n条射线,那么该图中有多少个角?
19.往返于A,B两地的客车,中途停靠三个车站.假设站点与站点之间的路程及站点与A,B两地之间的路程都不相等,请问:
(1)一共有多少种不同的票价?
(2)一共要准备多少种不同的车票?
20.某装饰材料加工厂有一批从生产线上下来的正六边形原材料(如图①),现从一个正六边形中剪去一个与其边长相等的等边三角形,将其移到如图②所示的位置.为了不浪费材料,你能利用它们铺满地面吗?若不能,请说明理由;若能,请你给出自己的一种设计.
21.我们知道,两条直线相交最多有一个交点,三条直线相交最多有三个交点,四条直线相交最多有6个交点,…,如图所示.
(1)五条直线相交最多有______个交点,六条直线相交最多有______个交点;
(2)若有条直线相交,求最多交点的个数.(用含的代数式表示)
22.计算下列各题:
(1)
(2)
(3)
(4)
23.已知,满足,数轴上点对应的数为,点对应的数为,线段在数轴上移动,点在点右侧,.
(1)填空:_____,_____;
(2)如图1,当点移动到的中点时,点对应的数是_____;
(3)如图2,若线段在点左侧,为中点,为中点,猜想与的数量关系并说明理由.
24.如图,A,B,C是同一直线上的三个点.图中有几条射线?在不增加字母的情况下,能表示出的射线共几条?是哪几条?
《第四章基本平面图形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D B D B C D C C
题号 11 12
答案 C B
1.B
【分析】本题考查了余角的定义,熟练掌握余角的定义是解题的关键.根据余角的定义:若两锐角的和为90度,则称这两个角互为余角解答即可.
【详解】解:
的余角为
故选:B.
2.A
【分析】此题考查利用重合的方法比较两个角的大小.如果两个角的顶点重合,且有一边重合,两角的另一边均落在重合边的同旁:如果这两边也重合,说明两角相等;如果两边不重合,另一条边在里面的小,在外面的大;由此方法直接填空即可.
【详解】解:比较与时,把它们的顶点A和边重合,把和放在AB的同一侧,若,则AD落在的内部.
故选:A.
3.D
【分析】本题考查的是直线与线段的相关内容,正确理解题意、利用转化的思想去思考线段的总条数是解决问题的关键,可以减少不必要的分类.点P与A,B,C,D四点中的至少两个点距离相等时,也就是点P恰好是其中一条线段中点.而图中共有线段6条,所以出现报警次数最多6次.
【详解】解:由题意知,当P点经过任意一条线段中点的时候会发出警报,
∵图中共有线段、、、、、,
∴发出警报的点P最多有6个.
故选:D.
4.B
【分析】本题考查了角的概念.解题的关键是掌握角的表示方法的运用.根据角的表示方法和图形逐个判断即可.
【详解】解:A、以为顶点的角不止一个,不能用表示一个角,故A选项错误;
B、能用,,三种方法表示同一个角,故B选项正确;
C、以为顶点的角不止一个,不能用表示一个角,故C选项错误;
D、,表示的是不同的角,故D选项错误;
故选:B.
5.D
【分析】根据钟面角、多边形的对角线与边数、线段中点的定义、角度单位换算逐项判断即可得.
【详解】解:A、钟表的时间是10点30分,此时时针与分针所成的夹角是,则此项错误,不符合题意;
B、若经过某个多边形一个顶点的所有对角线,将这个多边形分成八个三角形,则这个多边形是十边形,则此项错误,不符合题意;
C、若,但点不一定在同一条直线上,所以点不一定是线段的中点,则此项错误,不符合题意;
D、,则此项正确,符合题意;
故选:D.
【点睛】本题考查了钟面角、多边形的对角线与边数、线段中点的定义、角度单位换算,熟练掌握各概念和运算是解题关键.
6.B
【分析】根据线段的性质:两点之间线段最短进行解答即可.
【详解】A.用两根钉子将细木条固定在墙上,是两点确定一条直线,故此选项错误;
B.把弯曲的公路改直,就能缩短路程,可用基本事实“两点之间,线段最短”来解释,正确;
C.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线,是两点确定一条直线,故此选项错误;
D.利用圆规可以比较两条线段的大小关系,是线段长度比较,故此选项错误.
故选:B.
【点睛】本题考查了线段的性质,正确把握直线、射线的性质是解题的关键.
7.C
【分析】本题考查了求一个角的补角,根据相加等于180度的两个角互补,即可解答.
【详解】解:∵,
∴的补角,
故选:C.
8.D
【分析】先设出这个角,再表示出这个角的补角,根据题干中的等量关系进行计算即可求解.
【详解】解:设这个锐角为x,则这个锐角的补角为,
由题意可知:
解得:,
故选:D.
【点睛】本题考查补角,解题的关键是根据假设表示出补角列出方程.
9.C
【分析】根据角的表示方法,结合图形进行判断即可.
【详解】解:A、图中的不能用表示,故本选项错误,不合题意;
B、图中的不能用表示,故本选项错误,不合题意;
C、图中、、表示同一个角,故本选项正确,符合题意;
D、图中的不能用表示,故本选项错误,不合题意;
故选:C.
【点睛】本题考查了角的表示方法的应用,角可以用一个大写字母表示,也可以用三个大写字母表示.其中顶点字母要写在中间,唯有在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角,否则分不清这个字母究竟表示哪个角.
10.C
【分析】根据7块薄板的边长间的关系,结合面积公式逐项分析即可.
【详解】解:由题图可知,2与7都是等腰直角三角形,且7的斜边等于2的直角边,
∴,
∵5的边长等于2的直角边的一半,
∴,,A正确;
∵3相邻的两边分别与4的直角边和斜边相等,且3中的锐角为
∴3与4同底等高,,
∵4与6是两个全等的三角形,∴,
∴,B正确;
∵1与7都是等腰直角三角形,且7的斜边等于1的直角边,
∴,C错误;
∵6也是等腰直角三角形,且6的斜边等于7的直角边,
∴,
∵,
∴,D正确.
故选C.
【点睛】本题考查了应用与设计作图,认准分成的各块塑料板的形状与大小是解题的关键,另外本题渗透利用了七巧板的思想,熟练掌握七巧板也很关键.
11.C
【分析】此题主要考查了角的概念.直接利用角的概念,有公共端点是两条射线组成的图形叫做角,其中这个公共端点是角的顶点,这两条射线是角的两条边.进而分析得出即可.
【详解】解:角是有公共端点的两条射线组成的图形,直线上没有顶点,则直线是一个平角、周角是一条射线以及角的两边是直线的说法都是错误的,故选项ABD不符合题意;
角的两边是射线,故选项C符合题意.
故选:C.
12.B
【分析】本题考查了余角和补角的定义,先求出的余角,再求出的补角度数,即可作答.
【详解】解:∵,
∴的余角,
∴的补角度数是,
则的余角的补角度数是.
故选:B.
13.5
【分析】根据题意画出图,由已知条件得到,设,则,得到,求出的值即可.
【详解】解:根据题意画出图如图,
,,,
,
,
设,则,
,
解得:,
,
故答案为:5.
【点睛】本题主要考查了两点间的距离,线段的和差,熟练掌握两点间的距离计算方法进行求解是解决本题的关键.
14.
【解析】略
15.同角的补角相等
【分析】本题考查了补角的性质,根据同角的补角相等解答即可.
【详解】∵直线与相交于点O,
∴,,
∴,
在此推理过程中,与相等的理由是同角的补角相等.
故答案为:同角的补角相等.
16.2cm或8cm/8cm或2cm
【分析】根据题意分情况讨论A,B,C三点的位置关系,考查学生对图形的理解与运用,要考虑点B在线段AC上时和点B在线段AC的延长线上时.
【详解】∵D为AC的中点,E为BC的中点,
∴
①如图,当点B在线段AC上时,依题意得,
cm,
②如图,当点B在线段AC的延长线上时,依题意得,
cm,
故答案为:2cm或8cm
【点睛】本题考查了线段的和差计算,线段中点的性质,数形结合分类讨论是解题的关键.
17.两点之间,线段最短
【分析】本题主要考查了线段的性质,解题的关键是熟练掌握两点之间线段最短.
根据两点之间,线段最短求解即可.
【详解】解:把原来弯曲的河道改直,则河道的长度变短了,这里用到的数学知识是两点之间线段最短.
故答案为:两点之间,线段最短.
18.(1)1,3,6,10;(2)45;(3)
【分析】本题考查的是图形的变化直接观察图形可得图中角的数目,注意数角的个数时,能按一定的顺序计算,解题的关键是找到题目中的角的变化规律.
(1)根据角的定义确定即可;
(2)根据角的个数规律解答即可;
(3)根据角的个数规律解答即可
【详解】解:(1)观察图形可知:第一个图形中有1个角;
第二个图形中有3个角;
第三个图形中有6个角;
第四个图形中有10个角;
故答案为:1,3,6,10;
(2)根据题意可得:如果一个角内部有8条射线,那么该图中有个角.
故答案为:45;
(3)观察图形可知:当角内部有0条射线时,该图中有个角;
当角的内部有1条射线时,该图中有:个角;
当角的内部有2条射线时,该图中有:个角;
当角的内部有3条射线时,该图中有个角,
,
故当角的内部有n条射线时,该图中有个角.
19.(1)10种
(2)20种
【分析】本题主要考查运用线段知识解决生活中的问题,需要掌握正确数线段的方法.
(1)先画出示意图,求出线段的条数,再计算票价即可;
(2)根据往返的车票都不相同,计算车票的种数即可.
【详解】(1)解:如图,记中途三个车站分别为,则共有:
,
∴10种不同的票价,
(2)解:因为车票需要考虑方向性,如“”与“”票价相同,但车票不同,
所以共有种车票.
20.能,见解析
【分析】本题考查了作图—应用与设计;
根据正六边形可以进行平面镶嵌,类似的将等边三角形填充到剪去的位置即可.
【详解】解:能.设计方案图所示.
21.(1)10;15
(2)有条直线相交,最多交点的个数为.
【分析】此题考查图形规律的探究.
(1)根据图形相邻两个图形的交点个数的差为从2开始的连续整数,然后列式计算即可得解;
(2)根据(1)得到的规律,即可得解.
【详解】(1)解:三条直线交点最多为个,
四条直线交点最多为个,
五条直线交点最多为个,
六条直线交点最多为个;
故答案为:10;15;
(2)解:n条直线交点最多为.
答:有条直线相交,最多交点的个数为.
22.(1)
(2)
(3)
(4)
【分析】根据度分秒的运算法则计算即可.
【详解】(1)解:.
(2)解:.
(3)解:.
(4)解:.
【点睛】本题主要考查了度分秒的计算,掌握度分秒的运算法则是解答本题的关键.
23.(1),9
(2)2
(3),理由见解析
【分析】本题考查绝对值的非负性,线段中点的有关计算,数轴上的动点问题:
(1)根据绝对值和平方的非负性求解;
(2)根据中点的定义求出点D对应的数,再根据点在点右侧,,可求出点对应的数;
(3)根据中点的定义及线段的和差关系计算出的长度,即可得出.
【详解】(1)解:,,,
,,
,,
故答案为:,9;
(2)解:点移动到的中点时,点D对应的数为:,
点在点右侧,,
点对应的数为:,
故答案为:2;
(3)解:,理由如下:
,,
,
为中点,为中点,
,
,
.
24.图中有6条射线,在不增加字母的情况下,能表示出的射线共4条,分别是:射线,射线,射线,射线
【分析】本题考查了射线,根据射线的定义即可求解,熟练掌握射线的定义及表示方法是解题的关键.
【详解】解:图中有6条射线,在不增加字母的情况下,能表示出的射线共4条,
分别是:射线、射线、射线、射线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四章基本平面图形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知,那么的余角的度数是( )
A. B. C. D.
2.比较与的大小,把它们的顶点A和边重合,把它们的另一边和放在的同一侧,若,则( )
A.落在的内部 B.落在的外部
C.和重合 D.不能确定的位置
3.如图,有一种电子游戏,电子屏幕上有一条直线,在直线上有A,B,C,D四点.点P沿直线l从右向左移动,当出现点P与A,B,C,D四点中的至少两个点距离相等时,就会发出警报,则直线l上会发出警报的点P最多有( )个.
A.3 B.4 C.5 D.6
4.如图所示,能用,,三种方法表示同一个角的图形是( )
A. B.
C. D.
5.下列说法正确的是( )
A.钟表的时间是10点30分,此时时针与分针所成的夹角是105°
B.若经过某个多边形一个顶点的所有对角线,将这个多边形分成八个三角形,则这个多边形是九边形
C.若,则点是线段的中点
D.
6.下列现象中,可用基本事实“两点之间,线段最短”来解释的现象是( )
A.用两个钉子就可以把木条固定在墙上
B.把弯曲的公路改直,就能缩短路程
C.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
D.利用圆规可以比较两条线段的大小关系
7.已知,则的补角等于( )
A. B. C. D.
8.若一个锐角的补角比这个锐角的4倍少,则这个锐角为( )
A. B. C. D.
9.下列四个图形中,能同时用,,三种方法表示同一个角的是( )
A. B. C. D.
10.七巧板是由可以错综分合的几何图案演化而来,它是一种拼板玩具,体现了我国古代劳动人民的智慧,如图1,将一块正方形薄板分为7块,其中包括5块大小不等的三角形,1块正方形和1块平行四边形,图2是由图1拼成的风车形状,则下列等式错误的是( )
A. B. C. D.
11.下列说法中,正确的是( )
A.直线是一个平角 B.周角是一条射线
C.角的两边是射线 D.角的两边是直线
12.若,则的余角的补角度数是( )
A. B. C. D.
二、填空题
13.在一条直线上顺次取,,,四点,使,如果,,则 cm.
14.方向角是指以坐标轴方向为标准方向确定的方位角.方向角与目标方向正北或正南的夹角小于 .
15.如图,直线与相交于点O,∴,,∴,在此推理过程中,与相等的理由是 .
16.已知:线段AC和BC在同一直线上,如果AC=10cm,BC=6cm,D为AC的中点,E为BC的中点,则DE= .
17.把原来弯曲的河道改直,河道长度变短,其原理能用基本事实“ ”解释.
三、解答题
18.(1)数一数,找规律:下图中,角内部射线的条数依次增加,请数一数各图中有几个角.
(2)如果一个角内部有8条射线,那么该图中有 个角;
(3)如果一个角内部有n条射线,那么该图中有多少个角?
19.往返于A,B两地的客车,中途停靠三个车站.假设站点与站点之间的路程及站点与A,B两地之间的路程都不相等,请问:
(1)一共有多少种不同的票价?
(2)一共要准备多少种不同的车票?
20.某装饰材料加工厂有一批从生产线上下来的正六边形原材料(如图①),现从一个正六边形中剪去一个与其边长相等的等边三角形,将其移到如图②所示的位置.为了不浪费材料,你能利用它们铺满地面吗?若不能,请说明理由;若能,请你给出自己的一种设计.
21.我们知道,两条直线相交最多有一个交点,三条直线相交最多有三个交点,四条直线相交最多有6个交点,…,如图所示.
(1)五条直线相交最多有______个交点,六条直线相交最多有______个交点;
(2)若有条直线相交,求最多交点的个数.(用含的代数式表示)
22.计算下列各题:
(1)
(2)
(3)
(4)
23.已知,满足,数轴上点对应的数为,点对应的数为,线段在数轴上移动,点在点右侧,.
(1)填空:_____,_____;
(2)如图1,当点移动到的中点时,点对应的数是_____;
(3)如图2,若线段在点左侧,为中点,为中点,猜想与的数量关系并说明理由.
24.如图,A,B,C是同一直线上的三个点.图中有几条射线?在不增加字母的情况下,能表示出的射线共几条?是哪几条?
《第四章基本平面图形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D B D B C D C C
题号 11 12
答案 C B
1.B
【分析】本题考查了余角的定义,熟练掌握余角的定义是解题的关键.根据余角的定义:若两锐角的和为90度,则称这两个角互为余角解答即可.
【详解】解:
的余角为
故选:B.
2.A
【分析】此题考查利用重合的方法比较两个角的大小.如果两个角的顶点重合,且有一边重合,两角的另一边均落在重合边的同旁:如果这两边也重合,说明两角相等;如果两边不重合,另一条边在里面的小,在外面的大;由此方法直接填空即可.
【详解】解:比较与时,把它们的顶点A和边重合,把和放在AB的同一侧,若,则AD落在的内部.
故选:A.
3.D
【分析】本题考查的是直线与线段的相关内容,正确理解题意、利用转化的思想去思考线段的总条数是解决问题的关键,可以减少不必要的分类.点P与A,B,C,D四点中的至少两个点距离相等时,也就是点P恰好是其中一条线段中点.而图中共有线段6条,所以出现报警次数最多6次.
【详解】解:由题意知,当P点经过任意一条线段中点的时候会发出警报,
∵图中共有线段、、、、、,
∴发出警报的点P最多有6个.
故选:D.
4.B
【分析】本题考查了角的概念.解题的关键是掌握角的表示方法的运用.根据角的表示方法和图形逐个判断即可.
【详解】解:A、以为顶点的角不止一个,不能用表示一个角,故A选项错误;
B、能用,,三种方法表示同一个角,故B选项正确;
C、以为顶点的角不止一个,不能用表示一个角,故C选项错误;
D、,表示的是不同的角,故D选项错误;
故选:B.
5.D
【分析】根据钟面角、多边形的对角线与边数、线段中点的定义、角度单位换算逐项判断即可得.
【详解】解:A、钟表的时间是10点30分,此时时针与分针所成的夹角是,则此项错误,不符合题意;
B、若经过某个多边形一个顶点的所有对角线,将这个多边形分成八个三角形,则这个多边形是十边形,则此项错误,不符合题意;
C、若,但点不一定在同一条直线上,所以点不一定是线段的中点,则此项错误,不符合题意;
D、,则此项正确,符合题意;
故选:D.
【点睛】本题考查了钟面角、多边形的对角线与边数、线段中点的定义、角度单位换算,熟练掌握各概念和运算是解题关键.
6.B
【分析】根据线段的性质:两点之间线段最短进行解答即可.
【详解】A.用两根钉子将细木条固定在墙上,是两点确定一条直线,故此选项错误;
B.把弯曲的公路改直,就能缩短路程,可用基本事实“两点之间,线段最短”来解释,正确;
C.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线,是两点确定一条直线,故此选项错误;
D.利用圆规可以比较两条线段的大小关系,是线段长度比较,故此选项错误.
故选:B.
【点睛】本题考查了线段的性质,正确把握直线、射线的性质是解题的关键.
7.C
【分析】本题考查了求一个角的补角,根据相加等于180度的两个角互补,即可解答.
【详解】解:∵,
∴的补角,
故选:C.
8.D
【分析】先设出这个角,再表示出这个角的补角,根据题干中的等量关系进行计算即可求解.
【详解】解:设这个锐角为x,则这个锐角的补角为,
由题意可知:
解得:,
故选:D.
【点睛】本题考查补角,解题的关键是根据假设表示出补角列出方程.
9.C
【分析】根据角的表示方法,结合图形进行判断即可.
【详解】解:A、图中的不能用表示,故本选项错误,不合题意;
B、图中的不能用表示,故本选项错误,不合题意;
C、图中、、表示同一个角,故本选项正确,符合题意;
D、图中的不能用表示,故本选项错误,不合题意;
故选:C.
【点睛】本题考查了角的表示方法的应用,角可以用一个大写字母表示,也可以用三个大写字母表示.其中顶点字母要写在中间,唯有在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角,否则分不清这个字母究竟表示哪个角.
10.C
【分析】根据7块薄板的边长间的关系,结合面积公式逐项分析即可.
【详解】解:由题图可知,2与7都是等腰直角三角形,且7的斜边等于2的直角边,
∴,
∵5的边长等于2的直角边的一半,
∴,,A正确;
∵3相邻的两边分别与4的直角边和斜边相等,且3中的锐角为
∴3与4同底等高,,
∵4与6是两个全等的三角形,∴,
∴,B正确;
∵1与7都是等腰直角三角形,且7的斜边等于1的直角边,
∴,C错误;
∵6也是等腰直角三角形,且6的斜边等于7的直角边,
∴,
∵,
∴,D正确.
故选C.
【点睛】本题考查了应用与设计作图,认准分成的各块塑料板的形状与大小是解题的关键,另外本题渗透利用了七巧板的思想,熟练掌握七巧板也很关键.
11.C
【分析】此题主要考查了角的概念.直接利用角的概念,有公共端点是两条射线组成的图形叫做角,其中这个公共端点是角的顶点,这两条射线是角的两条边.进而分析得出即可.
【详解】解:角是有公共端点的两条射线组成的图形,直线上没有顶点,则直线是一个平角、周角是一条射线以及角的两边是直线的说法都是错误的,故选项ABD不符合题意;
角的两边是射线,故选项C符合题意.
故选:C.
12.B
【分析】本题考查了余角和补角的定义,先求出的余角,再求出的补角度数,即可作答.
【详解】解:∵,
∴的余角,
∴的补角度数是,
则的余角的补角度数是.
故选:B.
13.5
【分析】根据题意画出图,由已知条件得到,设,则,得到,求出的值即可.
【详解】解:根据题意画出图如图,
,,,
,
,
设,则,
,
解得:,
,
故答案为:5.
【点睛】本题主要考查了两点间的距离,线段的和差,熟练掌握两点间的距离计算方法进行求解是解决本题的关键.
14.
【解析】略
15.同角的补角相等
【分析】本题考查了补角的性质,根据同角的补角相等解答即可.
【详解】∵直线与相交于点O,
∴,,
∴,
在此推理过程中,与相等的理由是同角的补角相等.
故答案为:同角的补角相等.
16.2cm或8cm/8cm或2cm
【分析】根据题意分情况讨论A,B,C三点的位置关系,考查学生对图形的理解与运用,要考虑点B在线段AC上时和点B在线段AC的延长线上时.
【详解】∵D为AC的中点,E为BC的中点,
∴
①如图,当点B在线段AC上时,依题意得,
cm,
②如图,当点B在线段AC的延长线上时,依题意得,
cm,
故答案为:2cm或8cm
【点睛】本题考查了线段的和差计算,线段中点的性质,数形结合分类讨论是解题的关键.
17.两点之间,线段最短
【分析】本题主要考查了线段的性质,解题的关键是熟练掌握两点之间线段最短.
根据两点之间,线段最短求解即可.
【详解】解:把原来弯曲的河道改直,则河道的长度变短了,这里用到的数学知识是两点之间线段最短.
故答案为:两点之间,线段最短.
18.(1)1,3,6,10;(2)45;(3)
【分析】本题考查的是图形的变化直接观察图形可得图中角的数目,注意数角的个数时,能按一定的顺序计算,解题的关键是找到题目中的角的变化规律.
(1)根据角的定义确定即可;
(2)根据角的个数规律解答即可;
(3)根据角的个数规律解答即可
【详解】解:(1)观察图形可知:第一个图形中有1个角;
第二个图形中有3个角;
第三个图形中有6个角;
第四个图形中有10个角;
故答案为:1,3,6,10;
(2)根据题意可得:如果一个角内部有8条射线,那么该图中有个角.
故答案为:45;
(3)观察图形可知:当角内部有0条射线时,该图中有个角;
当角的内部有1条射线时,该图中有:个角;
当角的内部有2条射线时,该图中有:个角;
当角的内部有3条射线时,该图中有个角,
,
故当角的内部有n条射线时,该图中有个角.
19.(1)10种
(2)20种
【分析】本题主要考查运用线段知识解决生活中的问题,需要掌握正确数线段的方法.
(1)先画出示意图,求出线段的条数,再计算票价即可;
(2)根据往返的车票都不相同,计算车票的种数即可.
【详解】(1)解:如图,记中途三个车站分别为,则共有:
,
∴10种不同的票价,
(2)解:因为车票需要考虑方向性,如“”与“”票价相同,但车票不同,
所以共有种车票.
20.能,见解析
【分析】本题考查了作图—应用与设计;
根据正六边形可以进行平面镶嵌,类似的将等边三角形填充到剪去的位置即可.
【详解】解:能.设计方案图所示.
21.(1)10;15
(2)有条直线相交,最多交点的个数为.
【分析】此题考查图形规律的探究.
(1)根据图形相邻两个图形的交点个数的差为从2开始的连续整数,然后列式计算即可得解;
(2)根据(1)得到的规律,即可得解.
【详解】(1)解:三条直线交点最多为个,
四条直线交点最多为个,
五条直线交点最多为个,
六条直线交点最多为个;
故答案为:10;15;
(2)解:n条直线交点最多为.
答:有条直线相交,最多交点的个数为.
22.(1)
(2)
(3)
(4)
【分析】根据度分秒的运算法则计算即可.
【详解】(1)解:.
(2)解:.
(3)解:.
(4)解:.
【点睛】本题主要考查了度分秒的计算,掌握度分秒的运算法则是解答本题的关键.
23.(1),9
(2)2
(3),理由见解析
【分析】本题考查绝对值的非负性,线段中点的有关计算,数轴上的动点问题:
(1)根据绝对值和平方的非负性求解;
(2)根据中点的定义求出点D对应的数,再根据点在点右侧,,可求出点对应的数;
(3)根据中点的定义及线段的和差关系计算出的长度,即可得出.
【详解】(1)解:,,,
,,
,,
故答案为:,9;
(2)解:点移动到的中点时,点D对应的数为:,
点在点右侧,,
点对应的数为:,
故答案为:2;
(3)解:,理由如下:
,,
,
为中点,为中点,
,
,
.
24.图中有6条射线,在不增加字母的情况下,能表示出的射线共4条,分别是:射线,射线,射线,射线
【分析】本题考查了射线,根据射线的定义即可求解,熟练掌握射线的定义及表示方法是解题的关键.
【详解】解:图中有6条射线,在不增加字母的情况下,能表示出的射线共4条,
分别是:射线、射线、射线、射线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
