2024-2025学年五年级下册数学期末高频易错押题培优卷(人教版)(含解析)
文档属性
| 名称 | 2024-2025学年五年级下册数学期末高频易错押题培优卷(人教版)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 789.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-25 21:34:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年五年级下册数学期末高频易错押题培优卷(人教版)
一、填空题
1.要使是假分数,是真分数,a可能是( )(写出所有情况)。
2.把一根长2m,宽和高都是2dm的长方体木料平均锯成5段,每段是这根木料的,每段长m;这根木料的体积是( )dm3。
3.如果a÷b=26(a和b都是非零自然数),a和b的最大公因数是( ),最小公倍数是( )。
4.有10个羽毛球(外观完全相同),其中9个质量相同,另有1个次品略轻一些,至少称( )次就一定能找出这个次品羽毛球。
5.的分数单位是( ),再加上( )个这样的分数单位就是最小的质数,最小的质数是( )。
6.原定于周六的志愿者活动因故取消,老师要通知25名同学,以打电话的方式通知,每分钟通知1位同学,至少要( )分钟才能全部通知到位。
7.把两个表面积都是18平方分米的正方体拼成一个长方体,拼成的长方体的表面积是( )平方分米。
8.有9个乒乓球,其中一个是次品,比其它的轻一些。如果用天平称,至少称( )次保证可以找出次品。称第一次时,可以将9个乒乓球分为( )组。
9.一个几何体,从正面看到的是,从左面看到的是,摆成这样的几何体至少需要( )个小正方体。
10.中国结是一种我国特有的手工编织工艺品,深受人们的喜爱。用一根8米长的红绳正好可以编织5个相同的中国结,每个中国结用了这根红绳的( ),每个中国结用了( )米红绳。
11.把一个棱长是8厘米的正方体切成棱长为4厘米的小正方体,可以得到( )个小正方体,它们的表面积之和比原来大正方体表面积增加了( )平方厘米。
12.把一长方体铁块熔铸成正方体铁块,( )没变;如果将这个长方体铁块分割成两个小长方体铁块,它的( )不变,( )增加了。
13.端午节到了,奶奶做了40多个粽子,4个4个地数或6个6个地数都能正好数完没有剩余,奶奶一共做了( )个粽子。
14.一个长方体的底面是正方形,高是16厘米,侧面展开正好是一个正方形,这个长方体的体积是( )立方厘米。
15.“孝心如春水,爱意满人间。”端午节前夕,同同和爸爸妈妈为长辈们包粽子,一共包了24个豆沙粽和16个火腿粽,为方便保存,需分类包装,每个包装盒里只放一种口味的粽子,要使每盒的数量相等,每盒最多放( )个。
二、判断题
16.明明在计数器上用6颗珠子拨出了一个四位数,这个四位数一定是3的倍数。( )
17.同样长的路程,甲用了小时走完,乙用了0.2小时走完,甲的速度快。( )
18.在算式5÷2.5=2中,5是2.5的倍数,也是2的倍数。( )
19.大于而小于的真分数有无数个。( )
20.有6个羽毛球(外观完全相同),其中5个质量相等,另外1个次品略重一些,至少称2次就一定能找出这个次品羽毛球。( )
21.一个正方体的棱长扩大到原来的4倍,那它的表面积会扩大到原来的24倍。( )
22.(为整数,>1)的所有因数都小于。( )
23.一个数的倍数一定大于这个数的因数。( )
三、选择题
24.用阴影分别表示出“6张饼的”。下面图意不正确的是( )。
A.① B.② C.③ D.都不正确
25.妙妙和父母今年岁数的和是奇数,6年后,他们的岁数之和是( )。
A.奇数 B.偶数
C.可能是奇数也可能是偶数 D.无法确定
26.把10克糖加入100克水中,糖占糖水的( )。
A. B. C.
27.小男孩所看到的物体可能是下面的( )。
A. B. C. D.
28.根长方体木料,长4米,宽0.4米,厚3分米,把它锯成4段,表面积最少增加( )平方分米。
A.12 B.48 C.64 D.72
29.的分数单位是( ),它再加上( )个这样的分数单位就变成最小的质数。
A.;11 B.;11 C.;4
30.甲、乙两根绳子同样长,剪去甲绳的,从乙绳中剪去米,两根绳子剩下长度相比较,( )。
A.甲绳长 B.乙绳长 C.无法确定 D.一样长
31.有一张长方形纸片,长24厘米,宽18厘米。要剪成若干个同样大小的正方形而没有剩余,剪出的正方形的边长最大是( )厘米。
A.2 B.3 C.4 D.6
32.15瓶饮料,其中一瓶变质了(略重一些),用无砝码的天平称,至少称( )次一定能找出变质的那瓶饮料。
A.3 B.4 C.5 D.6
33.印章是一种雕刻和书法融合的传统艺术。为了测量一枚印章的体积,将其放入棱长为的正方体容器中,放入前水面高度为,放入后水面正好与容器齐平(完全浸没,水未溢出),那么印章的体积是( )。
A. B. C. D.
四、计算题
34.口算。
35.计算下面各题,能简算的要简算。
36.解方程。
2×(x+)=6
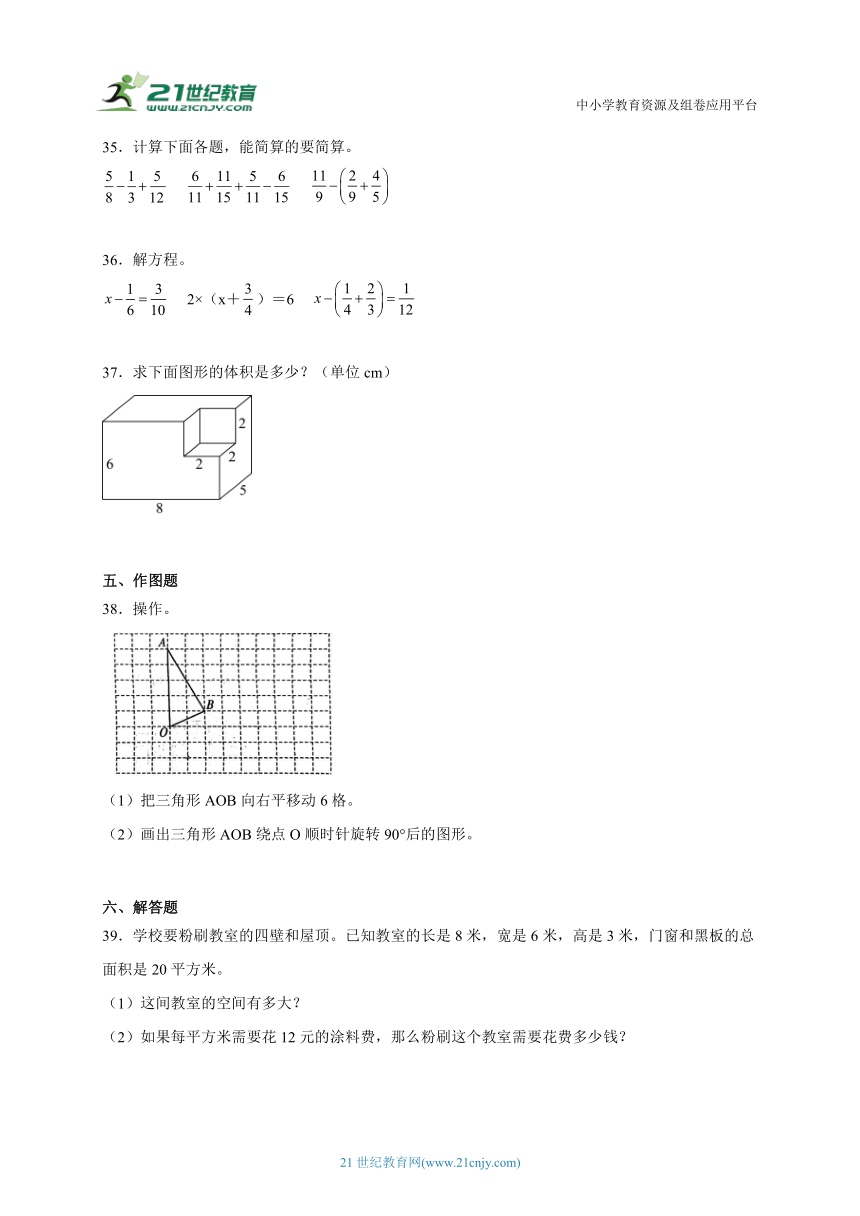
37.求下面图形的体积是多少?(单位cm)
五、作图题
38.操作。
(1)把三角形AOB向右平移动6格。
(2)画出三角形AOB绕点O顺时针旋转90°后的图形。
六、解答题
39.学校要粉刷教室的四壁和屋顶。已知教室的长是8米,宽是6米,高是3米,门窗和黑板的总面积是20平方米。
(1)这间教室的空间有多大?
(2)如果每平方米需要花12元的涂料费,那么粉刷这个教室需要花费多少钱?
40.五年级学生去参观学习,共用去10小时。其中路上用去的时间占,吃午饭与休息的时间共占,剩下的是参观学习时间。参观学习时间占几分之几?
41.甲鱼缸内有一条鳜鱼,量得鱼缸的长是40厘米,宽是40厘米,水面高度是25厘米。将鱼捞出放入乙鱼缸后,甲鱼缸水面高度下降到22厘米。你能求出乙鱼缸放入鱼后水面上升了多少厘米吗?
42.义蓬小区新建了一个游泳池,长50米,是宽的2倍,深2米。现在要在游泳池的四周和底面贴上瓷砖,一共需要多少平方米的瓷砖?如果用边长是50厘米的正方形瓷砖铺贴,至少需要准备多少块这样的瓷砖?
43.为了活动有更好的场地,学校重新粉刷了多功能报告厅。报告厅长30米,宽15米,高4.5米,门窗、大屏幕的面积共75平方米,如果每平方米需要5.5元涂料费,粉刷这间报告厅需要花费多少元?
44.在“青山绿水,就是金山银山”乡村振兴主题绘面比赛中(每人限投一幅作品),某校五(1)班同学热情参与踊跃投稿,把他们的绘画作品平均分成8组或者10组都多出3幅作品。按照一个班人数不能大于50人规定,该校五(1)班有多少人参与投稿?
45.火树银花元夕夜,彩灯万盏增霞流。为弘扬传统文化,元宵节前夕小军和同学们用一根铁丝扎成一个9分米,宽6分米,高3分米的长方体花灯框架。如果用同样长的铁丝扎成一个正方体花灯框架,这个正方体的棱长是多少分米?(接头处忽略不计)
46.一只乌鸦想喝水,可长方体容器里的水只有6厘米高(从里面量容器的长、宽、高分别为50厘米、40厘米、10厘米),乌鸦把小石子衔来放到了容器里,水面上升到容器口处(没有溢出),乌鸦喝到了水。这些小石子的体积是多少立方厘米?
47.学过体积之后,爸爸想考考小明的学习情况,请小明算一算家中土豆的体积,经过认真思考,小明决定用下面的方法来测量(如图),你能根据图求出土豆的体积吗?
48.一个封闭的长方体玻璃容器(如图所示,玻璃厚度忽略不计),长25厘米,宽10厘米,高8厘米,里面的水深4厘米,如果把这个容器向右竖起来,容器里面的水深应该是多少厘米?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.6,7,8
【分析】分子大于或等于分母的分数叫做假分数;分子小于分母的分数叫做真分数,据此解答。
【解析】是假分数,则a+1≥7;
a+1≥7,则a≥7-1,即a≥6;
是真分数,则a-1<8;
a-1<8,则a<8+1,即a<9;
a的值是6,7,8。
要是是假分数,是真分数,a可能是6,7,8。
2.;;80
【分析】把木料的长度看作单位“1”,平均锯成5段,即平均分成5份,求每段是这个木料的分率,用1÷5解答,求每段长,用木料的长度÷5,即用2÷5解答;根据长方体体积=长×宽×高,代入数据,即可求出木料的体积,注意单位名数的换算。
【解析】1÷5=
2÷5=(m)
2m=20dm
20×2×2
=40×2
=80(dm3)
把一根长2m,宽和高都是2dm的长方体木料平均锯成5段,每段是这根木料的,每段长m,这根木料的体积是80dm3。
3.b a
【分析】倍数关系的两个数的最大公因数是较小数,最小公倍数是较大数;因为a和b都是非零自然数,a÷b=26可知a和b是倍数关系,且b是较小数,a是较大数,据此解答。
【解析】如果a÷b=26(a和b都是非零自然数),a和b的最大公因数是b,最小公倍数是a。
4.3
【分析】找次品时把物品数量分成尽可能平均的三组,先称其中的两组,分天平平衡和不平衡两种情况,依次称重找出次品所在的组,称到只剩下2个物品时即可找出次品,根据称重过程准确数出称重次数,据此解答。
【解析】把10个羽毛球分成(3,3,4)三组,第一次先称(3,3)这两组。
①如果天平平衡,则次品在剩余的一组中;再把剩余的4个羽毛球分成(1,1,2)三组,第二次称(1,1)两组,如果天平不平衡,则次品在天平翘起的一端;如果天平平衡,则次品在剩余的2个羽毛球中,最后把2个羽毛球分成(1,1)两组,第三次称(1,1)两组,天平翘起的一端为次品。
②如果天平不平衡,则次品在天平翘起的一端中;再把翘起的这一端的3个羽毛球分成(1,1,1)三组,第二次随意选择(1,1)两组称,如果天平平衡,则次品在没有称的一组;如果天平不平衡,则次品在天平翘起的一端。
因此有10个羽毛球(外观完全相同),其中9个质量相同,另有1个次品略轻一些,至少称3次就一定能找出这个次品羽毛球。
5.
11
2
【分析】就是将单位“1”平均分成8份,其中的1份就是分数单位,即分数单位是;
质数的因数只有1和它本身两个数,则最小的质数是2,用2减去,得到需要添加的分数单位个数。
【解析】
则的分数单位是,再加上11个这样的分数单位就是最小的质数,最小的质数是2。
6.5
【分析】老师首先用1分钟通知第1个同学,第2分钟由老师和第1个同学分别通知1个同学,现在通知了1+2=3个同学,以此类推,第3分钟可以通知1+2+4=7个同学,第4分钟可以通知1+2+4+8=15个同学,第5分钟可以通知1+2+4+8+16=31个同学,据此解答。
【解析】第1分钟通知1名
第2分钟:1+2=3(名)
第3分钟:1+2+4=7(名)
第4分钟:1+2+4+8=15(名)
第5分钟:1+2+4+8+16=31(名)
31>25
所以至少要5分钟才能全部通知到位。
7.30
【分析】根据正方体的表面积公式的逆运算,用18除以6可得正方体每个面的面积,由题意可知,拼成的长方体的表面积比两个正方体的表面积之和少2个面,据此计算即可。
【解析】
(平方分米)
把两个表面积都是18平方分米的正方体拼成一个长方体,拼成的长方体的表面积是30平方分米。
8.2/两 3/三
【分析】把称重物品分成尽可能平均的三组,先称其中数量相同的两组,如果天平平衡,那么次品在剩下一组里面,如果天平不平衡,那么次品在天平上翘的一组里面,依次找出次品所在的组,直到最后找出次品,最后根据称重过程准确数出称重次数,据此解答。
【解析】分析可知:
综上所述,如果用天平称,至少称2次保证可以找出次品,称第一次时,可以将9个乒乓球分为3组。
9.4
【分析】根据从正面看到的形状,可以确定一共摆了2层,根据从左面看到的形状,可以确定底层摆了2行,底层可以错位摆放,不影响观察到的形状,据此画出示意图,确定至少需要的小正方体。
【解析】
一个几何体,从正面看到的是,从左面看到的是,从上面看这个几何体得到的图形以及数量应为,即摆成这样的几何体至少需要4个小正方体。
10.
【分析】把这根红绳的总长度看作单位“1”,平均分成5份,每份占总长度的;要求每个中国结用了多少米红绳,用红绳的总长度除以5,据此解答。
【解析】
(米)
因此每个中国结用了这根红绳的,每个中国结用了米红绳。
11.8 384
【分析】根据题意,把棱长8厘米的正方体切成棱长为4厘米的小正方体,每条棱长可以切出8÷4=2个小正方体,根据正方体的体积公式V=a3,求出一共可以切出小正方体的个数。
把棱长8厘米的正方体切成棱长为4厘米的小正方体,需切3次,每切一次增加2个面,共增加2×3=6个面;正方体的每个面都是相同的正方形,根据正方形的面积S=a2,求出一个面的面积,再乘6,即是增加的表面积。
【解析】8÷4=2(个)
2×2×2=8(个)
8×8×6
=64×6
=384(平方厘米)
把一个棱长是8厘米的正方体切成棱长为4厘米的小正方体,可以得到(8)个小正方体,它们的表面积之和比原来大正方体表面积增加了(384)平方厘米。
12.体积 体积 表面积
【分析】物体所占空间的大小叫做物体的体积。物体各个面的面积之和叫做物体的表面积。
把一个长方体铁块熔铸成正方体铁块,铁块的形状变了,则表面积发生了变化;但铁块的大小不变,即体积没变。
如果将这个长方体铁块分割成两个小长方体铁块,那么两个小长方体铁块的表面积比原来增加了两个截面的面积之和,体积不变。
【解析】把一长方体铁块熔铸成正方体铁块,(体积)没变;如果将这个长方体铁块分割成两个小长方体铁块,它的(体积)不变,(表面积)增加了。
13.48
【分析】根据题意,4个4个地数或6个6个地数都能正好数完没有剩余,那么粽子的总个数是4和6的公倍数;先求出4和6的最小公倍数,再求最小公倍数在40~50以内的倍数,就是粽子的总个数。
【解析】4=2×2
6=2×3
4和6的最小公倍数是:2×2×3=12
12×4=48(个)
40<48<50
奶奶一共做了48个粽子。
14.256
【分析】根据题意,长方体的底面是正方形,即长方体的长、宽相等;侧面展开正好是一个正方形,则长方体的底面周长等于高16厘米;
根据正方形的周长=边长×4可知,正方形的边长=周长÷4,求出长方体的长、宽;
再根据长方体的体积=长×宽×高,代入数据计算,求出这个长方体的体积。
【解析】长方体的长、宽是:
16÷4=4(厘米)
长方体的体积:
4×4×16
=16×16
=256(立方厘米)
这个长方体的体积是256立方厘米。
15.8
【分析】要将24个豆沙粽和16个火腿粽分类包装,且每盒只放一种口味、每盒数量相等,那么每盒最多放的个数就是24和16的最大公因数,因为最大公因数是两个数的公有质因数的乘积,它能保证是满足“每盒数量相等且最多”这一条件的数;通过分解质因数的方法求出24和16的最大公因数,即每盒最多放的个数。
【解析】24=2×2×2×3
16=2×2×2×2
24和16公有的质因数是2、2、2,将这些公有质因数相乘,即2×2×2=8,所以24和16的最大公因数是8。
所以要使每盒的数量相等,每盒最多放8个。
16.√
【分析】3的倍数的特征:一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。据此判断。
【解析】用6颗珠子拔出一个四位数,这个四位数的各个数位上的数字之和一定是6,6能被3整除,6是3的倍数,所以这个四位数一定是3的倍数。题干说法正确。
故答案为:√
17.×
【分析】根据速度=路程÷时间,比较两人速度的快慢,当路程相同时,时间越短,速度越快。甲用了小时,即0.5小时,乙用了0.2小时;0.2小时比0.5小时短,因此乙的速度更快,据此判断。
【解析】,即小时=0.5小时
当路程相同时,时间越短,速度越快。
因为0.2小时<0.5小时,所以乙的速度>甲的速度。
因此同样长的路程,甲用了小时走完,乙用了0.2小时走完,乙的速度快,原题干的说法是错误的。
故答案为:×
18.×
【分析】根据因数和倍数的定义,倍数和因数的研究范围仅限于整数,且必须满足被除数、除数、商均为整数,题目中除数为小数,不符合条件。
【解析】在算式5÷2.5=2中,虽然商是整数,但除数2.5是小数。由于2.5不是整数,因此5不是2.5的倍数,也不是2的倍数,原题干的说法是错误的。
故答案为:×
19.√
【分析】分子比分母小的分数叫做真分数。
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
根据分数的基本性质,把两个分数的分子、分母同时乘2、3、4……可以得到无数个大于而小于的真分数。据此解答。
【解析】分母为9且大于而小于的真分数有、、、;
==,==,分母为18且大于而小于的真分数有、、……;
==,==,分母为27且大于而小于的真分数有、、……;
……
所以,大于而小于的真分数有无数个。
原题说法正确。
故答案为:√
20.√
【分析】找次品的最优策略:(1)把待分物品分成3份;(2)每份数量尽量平均,如果不能平均分的,也应该使多的一份与少的一份只相差1。
【解析】将6个羽毛球分成(2,2,2),取其中两组各2个称量。无论平衡不平衡,都可确定次品在其中2个;将2个分成(1、1),再称一次即可确定次品,共2次,所以原题说法正确。
故答案为:√
21.×
【分析】正方体表面积=棱长×棱长×6,一个正方体的棱长扩大到原来的几倍,表面积扩大到原来的倍数×倍数,据此分析。
【解析】4×4=16
一个正方体的棱长扩大到原来的4倍,那它的表面积会扩大到原来的16倍,原题说法错误。
故答案为:×
22.×
【分析】根据因数的定义,一个数的因数包括1和它本身,其中最大的因数是这个数本身,举例说明即可。
【解析】对于任意整数a(a>1),其因数包括1和a本身。例如,当a=6时,因数有1、2、3、6,其中最大的因数6等于a,所以原题说法错误。
故答案为:×
23.×
【分析】一个数的倍数的个数是无限的,最小的是它本身,没有最大的倍数。一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身。可举例说明。
【解析】一个数的最小倍数等于这个数的最大因数,如7既是7的倍数也是7的因数,所以原题说法错误。
故答案为:×
24.C
【分析】把单位“1”平均分成若干份,这样的一份或几份都可以用分数来表示,根据分数的意义用分数表示出各图形取出的部分,即可求得。
【解析】①把6个圆看作单位“1”,把单位“1”平均分成3份,每份2个圆,取出其中的2份,用分数表示为,图中阴影部分表示6个圆的,可以表示6张饼的;
②把每个大长方形看作单位“1”,把单位“1”平均分成3份,取出其中的2份,用分数表示为,6个阴影部分可以表示6张饼的;
③把整个图形看作单位“1”,把单位“1”平均分成6份,取出其中的2份,用分数表示为,阴影部分不能表示6张饼的;
由上可知,③图不能用阴影表示出“6张饼的”。
故答案为:C
25.A
【分析】奇数:像1,3,5,7…不是2的倍数的数叫做奇数。6年后,妙妙和父母分别都增加了6岁,即他们的岁数和增加了(岁),偶数+奇数=奇数,据此解答。
【解析】据分析可知,妙妙和父母今年岁数的和是奇数,6年后,他们的岁数之和是奇数。
故答案为:A
26.C
【分析】糖占糖水质量的分率=糖的质量÷糖水的质量,据此解答。
【解析】10÷(10+100)
=10÷110
=
糖占糖水的。
故答案为:C
27.C
【分析】
先数出各选项物体所用小正方体的个数,排除个数不是7个的物体;再观察由7个小正方体组成的物体,上面看到的形状是否是,据此解答即可。
【解析】A.有8个小正方体,不符合题意。
B.有8个小正方体,不符合题意。
C.有7个小正方体,且从上面看到的是,符合题意。
D.有7个小正方体,但从上面看到的是,不符合题意。
故答案为:C
28.D
【分析】 切割次数与截面增加:将长方体锯成4段需锯3次,每次锯切增加2个新截面,共增加6个截面。 最小表面积增加原则:为使表面积增加最少,应选择原长方体中最小的面(宽×厚)作为新增截面。 单位统一与计算:将长度单位统一为分米(4米=40分米,0.4米=4分米,厚3分米),计算单个截面面积后乘新增截面数。
【解析】长:4米=40分米
宽:0.4米=4分米
厚:3分米
最小截面面积:
4×3=12(平方分米)
新增表面积:
12×6=72(平方分米)
故答案为:D
29.A
【分析】把单位“1”平均分成若干份,这样的一份或几份都可以用分数来表示,表示其中一份的数叫作分数单位,分数的分母是几,分数单位就是几分之一;再根据最小的质数2求出需要添加分数单位的个数,据此解答。
【解析】分析可知,的分数单位是,最小的质数为2,2=,3+11=14,所以再加上11个这样的分数单位就变成最小的质数。
故答案为:A
30.C
【分析】两根同样长的绳子,因为绳子的总长度不知道,所以全长的无法确定,无法与第二根的长度比较,据此选择。
【解析】由分析可知,第一根剪去全长的,第二根剪去米,两根剩下的长度无法比较。
故答案为:C
31.D
【分析】要将长方形纸片剪成若干同样大小的正方形且无剩余,剪出的正方形边长需是长方形长和宽的公因数,而边长最大时即为长和宽的最大公因数。
【解析】24=2×2×2×3
18=2×3×3
24和18的最大公因数为:2×3=6
所以剪出的正方形的边长最大是6厘米。
故答案为:D
32.A
【分析】把称重物品平均分成三组(5,5,5),先称其中的两组,如果天平平衡,那么变质的饮料在剩下一组里面,如果天平不平衡,那么变质的饮料在天平下沉的一组里面,依次找出变质的饮料所在的组,直到最后找出变质的饮料,根据称重过程准确数出称重次数,据此解答。
【解析】分析可知:
综上所述,至少称3次一定能找出变质的那瓶饮料。
故答案为:A
33.B
【分析】根据1dm=10cm,统一单位。水面上升的体积就是印章的体积,根据长方体体积公式,容器底面积×水面上升的高度=印章的体积,据此列式计算。
【解析】1dm=10cm
10×10×(10-8)
=100×2
=200(cm3)
印章的体积是200cm3。
故答案为:B
34.1;;;
;;;0
【解析】略
35.;;
【分析】-+,按照运算顺序,进行计算。
++-,根据带符号搬家,原式化为:++-,再根据加法结合律,原式化为:(+)+(-),再进行计算。
-(+),根据减法性质,原式化为:--,再按照运算顺序,进行计算。
【解析】-+
=-+
=+
=
++-
=++-
=(+)+(-)
=1+
=
-(+)
=--
=1-
=
36.x=;x=;x=1
【分析】x-=,根据等式的性质1,方程两边同时加上即可。
2×(x+)=6,根据等式的性质2,方程两边同时除以2,再根据等式的性质1,方程两边同时减去即可。
x-(+)=,先计算出+的和,再根据等式的性质2,方程两边同时加上+的和即可。
【解析】x-=
解:x-+=+
x=+
x=
2×(x+)=6
解:2×(x+)÷2=6÷2
x+=3
x+-=3-
x=
x-(+)=
解:x-(+ )=
x-=
x-+=+
x=1
37.232cm3
【分析】求图形的体积,用长8cm,宽5cm,高6cm的长方体体积减去棱长为2cm的正方体体积;根据长方体和体积=长×宽×高,正方体的体积=棱长×棱长×棱长,代入数值计算分别计算出长方体的体积和正方体的体积,再相减即可解答。
【解析】8×5×6-2×2×2
=40×6-4×2
=240-8
=232(cm3)
图形的体积是232cm3。
38.见详解
【分析】(1)找到三角形AOB的三个顶点 A、O、B,将点A沿着水平方向右数6格,确定平移后的位置;同样地,把点O向右平移6格,得到平移后的点;把点B向右平移6格,得到平移后的点;对照原图连接各点,就得到向右平移6格后的三角形。
(2)以点O为旋转中心,将OA绕点O顺时针旋转90°,同样把OB绕点O顺时针旋转90°,对比原图形连接AB,就得到三角形AOB绕点O顺时针旋转90°后的三角形。
【解析】(1)、(2)作图如下:
39.(1)144立方米;(2)1344元
【分析】(1)求这间教室的空间,就是求这间教室的体积,根据长方体体积=长×宽×高,代入数据,即可解答。
(2)粉刷这个教室,就是求这个教师5个面的面积和,再减去门窗和黑板的面积,根据长方体表面积=长×宽+(长×高+宽×高)×2,代入数据,求出粉刷的面积,再乘12,即可解答。
【解析】(1)8×6×3
=48×3
=144(立方米)
答:这间教室的空间有144立方米。
(2)8×6+(8×3+6×3)×2-20
=8×6+(24+18)×2-20
=8×6+42×2-20
=48+84-20
=132-20
=112(立方米)
112×12=1344(元)
答:粉刷这个教室需要花费1344元。
40.
【分析】已知路上用去的时间占,吃午饭与休息的时间共占,剩下的是参观学习时间,这里是把去革命老区参观学习的总时间看作单位“1”,用1减去路上用去的时间、吃午饭和休息的时间分别占总时间的分率,即可求出参观学习的时间占几分之几。
【解析】1--
=1--
=-
=
=
答:参观学习时间占。
41.
8厘米
【分析】根据不规则物体的体积计算方法可知,甲鱼缸下降的水的体积就是鳜鱼的体积,由题意可知,捞出鳜鱼后甲鱼缸水面下降了(厘米),根据,可求出鳜鱼的体积,再用鳜鱼的体积除以乙水缸的长与宽的积(或用用鳜鱼的体积除以乙水缸的长再除以宽)即可得解。
【解析】40×40×(25-22)÷(50×12)
=40×40×3÷600
=8(厘米)
或40×40×(25-22)÷50÷12
=40×40×3÷50÷12
=8(厘米)
答:乙鱼缸放入鱼后水面上升了8厘米。
42.1550平方米;6200块
【分析】已知长50米,长是宽的2倍,那么宽为50÷2=25米;游泳池贴瓷砖只需算底面和四周,所以面积为底面面积(长×宽)加四周面积(两个长×高的面和两个宽×高的面);
已知瓷砖边长是50厘米,50厘米=0.5米;根据“正方形面积=边长×边长”,计算出每块瓷砖面积为0.5×0.5=0.25平方米,最后用贴瓷砖的总面积除以每块瓷砖的面积可得瓷砖数量。
【解析】宽:50÷2=25(米)
50×25+50×2×2+25×2×2
=1250+200+100
=1550(平方米)
答:一共需要1550平方米的瓷砖。
50厘米=0.5米
1550÷(0.5×0.5)
=1550÷0.25
=6200(块)
答:至少需要准备6200块这样的瓷砖。
43.
4290元
【分析】由题意可知,要刷多功能报告厅,除了地板其它5个面要刷,即用长×宽+长×高×2+宽×高×2,再减去门窗、大屏幕的面积,最后再乘5.5即可得解。
【解析】(30×15+30×4.5×2+15×4.5×2)-75
=(450+270+135)-75
=855-75
=780(平方米)
780×5.5=4290(元)
答:粉刷这间报告厅需要花费4290元。
44.43人
【分析】他们的绘画作品平均分成8组或10组都多3幅,由此可知,他们的作品的总数量减去3就是8和10的公倍数;由于每人限投一幅作品,且一个班人数不能大于50人,则五(1)班参与投稿的人数与3的差是8和10的公倍数,且这个公倍数不能大于50;最后用求出的这个公倍数再加上3,据此解答。
【解析】8=2×2×2
10=2×5
8和10的最小公倍数是2×2×2×5=40,8和10的公倍数有:40,80,120,…。
因为一个班人数不能大于50,所以40+3=43(人)。
答:该校五(1)班有43人参与投稿。
45.6分米
【分析】根据长方体的棱长总和=(长+宽+高)×4,代入数值计算出这个长方体花灯框架的棱长总和,也就是这根铁丝的总长度,铁丝的总长度不变,把它扎成一个正方体花灯框架,根据正方体的棱长总和=棱长×12,用棱长总和÷12,所得结果即为这个正方体的棱长是多少分米。
【解析】(9+6+3)×4÷12
=18×4÷12
=72÷12
=6(分米)
答:这个正方体的棱长是6分米。
46.8000立方厘米
【分析】根据长方体体积=长×宽×高,代入数据,求出长方体容器的容积,再求出6厘米水的体积,再用长方体容器的容积-水的体积,就是小石子的体积,据此解答。
【解析】(50×40×10)-(50×40×6)
=(2000×10)-(2000×6)
=20000-12000
=8000(立方厘米)
答:这些小石子的体积是8000立方厘米。
47.0.2立方分米
【分析】根据题意,土豆的体积=上升的水的体积,而上升的水的形状是长1分米,宽1分米,高(8-6)厘米的长方体,根据长方体的体积=长×宽×高,统一单位后代入数据计算即可解答。
【解析】8-6=2(厘米)=0.2分米
1×1×0.2=0.2(立方分米)
答:土豆的体积是0.2立方分米。
48.12.5厘米
【分析】先求出长是25厘米,宽是10厘米,高是4厘米长方体的体积,也就是4厘米高水的体积;根据长方体体积=长×宽×高,代入数据,求出长方体容器内水的体积;由于体积不变,把这个容器向右竖起来,长方体的长为10厘米,宽8厘米,求高,根据体积=长×宽×高,高=体积÷(长×宽),代入数据,即可解答。
【解析】(25×10×4)÷(10×8)
=(250×4)÷80
=1000÷80
=12.5(厘米)
答:容器里面水深12.5厘米。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年五年级下册数学期末高频易错押题培优卷(人教版)
一、填空题
1.要使是假分数,是真分数,a可能是( )(写出所有情况)。
2.把一根长2m,宽和高都是2dm的长方体木料平均锯成5段,每段是这根木料的,每段长m;这根木料的体积是( )dm3。
3.如果a÷b=26(a和b都是非零自然数),a和b的最大公因数是( ),最小公倍数是( )。
4.有10个羽毛球(外观完全相同),其中9个质量相同,另有1个次品略轻一些,至少称( )次就一定能找出这个次品羽毛球。
5.的分数单位是( ),再加上( )个这样的分数单位就是最小的质数,最小的质数是( )。
6.原定于周六的志愿者活动因故取消,老师要通知25名同学,以打电话的方式通知,每分钟通知1位同学,至少要( )分钟才能全部通知到位。
7.把两个表面积都是18平方分米的正方体拼成一个长方体,拼成的长方体的表面积是( )平方分米。
8.有9个乒乓球,其中一个是次品,比其它的轻一些。如果用天平称,至少称( )次保证可以找出次品。称第一次时,可以将9个乒乓球分为( )组。
9.一个几何体,从正面看到的是,从左面看到的是,摆成这样的几何体至少需要( )个小正方体。
10.中国结是一种我国特有的手工编织工艺品,深受人们的喜爱。用一根8米长的红绳正好可以编织5个相同的中国结,每个中国结用了这根红绳的( ),每个中国结用了( )米红绳。
11.把一个棱长是8厘米的正方体切成棱长为4厘米的小正方体,可以得到( )个小正方体,它们的表面积之和比原来大正方体表面积增加了( )平方厘米。
12.把一长方体铁块熔铸成正方体铁块,( )没变;如果将这个长方体铁块分割成两个小长方体铁块,它的( )不变,( )增加了。
13.端午节到了,奶奶做了40多个粽子,4个4个地数或6个6个地数都能正好数完没有剩余,奶奶一共做了( )个粽子。
14.一个长方体的底面是正方形,高是16厘米,侧面展开正好是一个正方形,这个长方体的体积是( )立方厘米。
15.“孝心如春水,爱意满人间。”端午节前夕,同同和爸爸妈妈为长辈们包粽子,一共包了24个豆沙粽和16个火腿粽,为方便保存,需分类包装,每个包装盒里只放一种口味的粽子,要使每盒的数量相等,每盒最多放( )个。
二、判断题
16.明明在计数器上用6颗珠子拨出了一个四位数,这个四位数一定是3的倍数。( )
17.同样长的路程,甲用了小时走完,乙用了0.2小时走完,甲的速度快。( )
18.在算式5÷2.5=2中,5是2.5的倍数,也是2的倍数。( )
19.大于而小于的真分数有无数个。( )
20.有6个羽毛球(外观完全相同),其中5个质量相等,另外1个次品略重一些,至少称2次就一定能找出这个次品羽毛球。( )
21.一个正方体的棱长扩大到原来的4倍,那它的表面积会扩大到原来的24倍。( )
22.(为整数,>1)的所有因数都小于。( )
23.一个数的倍数一定大于这个数的因数。( )
三、选择题
24.用阴影分别表示出“6张饼的”。下面图意不正确的是( )。
A.① B.② C.③ D.都不正确
25.妙妙和父母今年岁数的和是奇数,6年后,他们的岁数之和是( )。
A.奇数 B.偶数
C.可能是奇数也可能是偶数 D.无法确定
26.把10克糖加入100克水中,糖占糖水的( )。
A. B. C.
27.小男孩所看到的物体可能是下面的( )。
A. B. C. D.
28.根长方体木料,长4米,宽0.4米,厚3分米,把它锯成4段,表面积最少增加( )平方分米。
A.12 B.48 C.64 D.72
29.的分数单位是( ),它再加上( )个这样的分数单位就变成最小的质数。
A.;11 B.;11 C.;4
30.甲、乙两根绳子同样长,剪去甲绳的,从乙绳中剪去米,两根绳子剩下长度相比较,( )。
A.甲绳长 B.乙绳长 C.无法确定 D.一样长
31.有一张长方形纸片,长24厘米,宽18厘米。要剪成若干个同样大小的正方形而没有剩余,剪出的正方形的边长最大是( )厘米。
A.2 B.3 C.4 D.6
32.15瓶饮料,其中一瓶变质了(略重一些),用无砝码的天平称,至少称( )次一定能找出变质的那瓶饮料。
A.3 B.4 C.5 D.6
33.印章是一种雕刻和书法融合的传统艺术。为了测量一枚印章的体积,将其放入棱长为的正方体容器中,放入前水面高度为,放入后水面正好与容器齐平(完全浸没,水未溢出),那么印章的体积是( )。
A. B. C. D.
四、计算题
34.口算。
35.计算下面各题,能简算的要简算。
36.解方程。
2×(x+)=6
37.求下面图形的体积是多少?(单位cm)
五、作图题
38.操作。
(1)把三角形AOB向右平移动6格。
(2)画出三角形AOB绕点O顺时针旋转90°后的图形。
六、解答题
39.学校要粉刷教室的四壁和屋顶。已知教室的长是8米,宽是6米,高是3米,门窗和黑板的总面积是20平方米。
(1)这间教室的空间有多大?
(2)如果每平方米需要花12元的涂料费,那么粉刷这个教室需要花费多少钱?
40.五年级学生去参观学习,共用去10小时。其中路上用去的时间占,吃午饭与休息的时间共占,剩下的是参观学习时间。参观学习时间占几分之几?
41.甲鱼缸内有一条鳜鱼,量得鱼缸的长是40厘米,宽是40厘米,水面高度是25厘米。将鱼捞出放入乙鱼缸后,甲鱼缸水面高度下降到22厘米。你能求出乙鱼缸放入鱼后水面上升了多少厘米吗?
42.义蓬小区新建了一个游泳池,长50米,是宽的2倍,深2米。现在要在游泳池的四周和底面贴上瓷砖,一共需要多少平方米的瓷砖?如果用边长是50厘米的正方形瓷砖铺贴,至少需要准备多少块这样的瓷砖?
43.为了活动有更好的场地,学校重新粉刷了多功能报告厅。报告厅长30米,宽15米,高4.5米,门窗、大屏幕的面积共75平方米,如果每平方米需要5.5元涂料费,粉刷这间报告厅需要花费多少元?
44.在“青山绿水,就是金山银山”乡村振兴主题绘面比赛中(每人限投一幅作品),某校五(1)班同学热情参与踊跃投稿,把他们的绘画作品平均分成8组或者10组都多出3幅作品。按照一个班人数不能大于50人规定,该校五(1)班有多少人参与投稿?
45.火树银花元夕夜,彩灯万盏增霞流。为弘扬传统文化,元宵节前夕小军和同学们用一根铁丝扎成一个9分米,宽6分米,高3分米的长方体花灯框架。如果用同样长的铁丝扎成一个正方体花灯框架,这个正方体的棱长是多少分米?(接头处忽略不计)
46.一只乌鸦想喝水,可长方体容器里的水只有6厘米高(从里面量容器的长、宽、高分别为50厘米、40厘米、10厘米),乌鸦把小石子衔来放到了容器里,水面上升到容器口处(没有溢出),乌鸦喝到了水。这些小石子的体积是多少立方厘米?
47.学过体积之后,爸爸想考考小明的学习情况,请小明算一算家中土豆的体积,经过认真思考,小明决定用下面的方法来测量(如图),你能根据图求出土豆的体积吗?
48.一个封闭的长方体玻璃容器(如图所示,玻璃厚度忽略不计),长25厘米,宽10厘米,高8厘米,里面的水深4厘米,如果把这个容器向右竖起来,容器里面的水深应该是多少厘米?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.6,7,8
【分析】分子大于或等于分母的分数叫做假分数;分子小于分母的分数叫做真分数,据此解答。
【解析】是假分数,则a+1≥7;
a+1≥7,则a≥7-1,即a≥6;
是真分数,则a-1<8;
a-1<8,则a<8+1,即a<9;
a的值是6,7,8。
要是是假分数,是真分数,a可能是6,7,8。
2.;;80
【分析】把木料的长度看作单位“1”,平均锯成5段,即平均分成5份,求每段是这个木料的分率,用1÷5解答,求每段长,用木料的长度÷5,即用2÷5解答;根据长方体体积=长×宽×高,代入数据,即可求出木料的体积,注意单位名数的换算。
【解析】1÷5=
2÷5=(m)
2m=20dm
20×2×2
=40×2
=80(dm3)
把一根长2m,宽和高都是2dm的长方体木料平均锯成5段,每段是这根木料的,每段长m,这根木料的体积是80dm3。
3.b a
【分析】倍数关系的两个数的最大公因数是较小数,最小公倍数是较大数;因为a和b都是非零自然数,a÷b=26可知a和b是倍数关系,且b是较小数,a是较大数,据此解答。
【解析】如果a÷b=26(a和b都是非零自然数),a和b的最大公因数是b,最小公倍数是a。
4.3
【分析】找次品时把物品数量分成尽可能平均的三组,先称其中的两组,分天平平衡和不平衡两种情况,依次称重找出次品所在的组,称到只剩下2个物品时即可找出次品,根据称重过程准确数出称重次数,据此解答。
【解析】把10个羽毛球分成(3,3,4)三组,第一次先称(3,3)这两组。
①如果天平平衡,则次品在剩余的一组中;再把剩余的4个羽毛球分成(1,1,2)三组,第二次称(1,1)两组,如果天平不平衡,则次品在天平翘起的一端;如果天平平衡,则次品在剩余的2个羽毛球中,最后把2个羽毛球分成(1,1)两组,第三次称(1,1)两组,天平翘起的一端为次品。
②如果天平不平衡,则次品在天平翘起的一端中;再把翘起的这一端的3个羽毛球分成(1,1,1)三组,第二次随意选择(1,1)两组称,如果天平平衡,则次品在没有称的一组;如果天平不平衡,则次品在天平翘起的一端。
因此有10个羽毛球(外观完全相同),其中9个质量相同,另有1个次品略轻一些,至少称3次就一定能找出这个次品羽毛球。
5.
11
2
【分析】就是将单位“1”平均分成8份,其中的1份就是分数单位,即分数单位是;
质数的因数只有1和它本身两个数,则最小的质数是2,用2减去,得到需要添加的分数单位个数。
【解析】
则的分数单位是,再加上11个这样的分数单位就是最小的质数,最小的质数是2。
6.5
【分析】老师首先用1分钟通知第1个同学,第2分钟由老师和第1个同学分别通知1个同学,现在通知了1+2=3个同学,以此类推,第3分钟可以通知1+2+4=7个同学,第4分钟可以通知1+2+4+8=15个同学,第5分钟可以通知1+2+4+8+16=31个同学,据此解答。
【解析】第1分钟通知1名
第2分钟:1+2=3(名)
第3分钟:1+2+4=7(名)
第4分钟:1+2+4+8=15(名)
第5分钟:1+2+4+8+16=31(名)
31>25
所以至少要5分钟才能全部通知到位。
7.30
【分析】根据正方体的表面积公式的逆运算,用18除以6可得正方体每个面的面积,由题意可知,拼成的长方体的表面积比两个正方体的表面积之和少2个面,据此计算即可。
【解析】
(平方分米)
把两个表面积都是18平方分米的正方体拼成一个长方体,拼成的长方体的表面积是30平方分米。
8.2/两 3/三
【分析】把称重物品分成尽可能平均的三组,先称其中数量相同的两组,如果天平平衡,那么次品在剩下一组里面,如果天平不平衡,那么次品在天平上翘的一组里面,依次找出次品所在的组,直到最后找出次品,最后根据称重过程准确数出称重次数,据此解答。
【解析】分析可知:
综上所述,如果用天平称,至少称2次保证可以找出次品,称第一次时,可以将9个乒乓球分为3组。
9.4
【分析】根据从正面看到的形状,可以确定一共摆了2层,根据从左面看到的形状,可以确定底层摆了2行,底层可以错位摆放,不影响观察到的形状,据此画出示意图,确定至少需要的小正方体。
【解析】
一个几何体,从正面看到的是,从左面看到的是,从上面看这个几何体得到的图形以及数量应为,即摆成这样的几何体至少需要4个小正方体。
10.
【分析】把这根红绳的总长度看作单位“1”,平均分成5份,每份占总长度的;要求每个中国结用了多少米红绳,用红绳的总长度除以5,据此解答。
【解析】
(米)
因此每个中国结用了这根红绳的,每个中国结用了米红绳。
11.8 384
【分析】根据题意,把棱长8厘米的正方体切成棱长为4厘米的小正方体,每条棱长可以切出8÷4=2个小正方体,根据正方体的体积公式V=a3,求出一共可以切出小正方体的个数。
把棱长8厘米的正方体切成棱长为4厘米的小正方体,需切3次,每切一次增加2个面,共增加2×3=6个面;正方体的每个面都是相同的正方形,根据正方形的面积S=a2,求出一个面的面积,再乘6,即是增加的表面积。
【解析】8÷4=2(个)
2×2×2=8(个)
8×8×6
=64×6
=384(平方厘米)
把一个棱长是8厘米的正方体切成棱长为4厘米的小正方体,可以得到(8)个小正方体,它们的表面积之和比原来大正方体表面积增加了(384)平方厘米。
12.体积 体积 表面积
【分析】物体所占空间的大小叫做物体的体积。物体各个面的面积之和叫做物体的表面积。
把一个长方体铁块熔铸成正方体铁块,铁块的形状变了,则表面积发生了变化;但铁块的大小不变,即体积没变。
如果将这个长方体铁块分割成两个小长方体铁块,那么两个小长方体铁块的表面积比原来增加了两个截面的面积之和,体积不变。
【解析】把一长方体铁块熔铸成正方体铁块,(体积)没变;如果将这个长方体铁块分割成两个小长方体铁块,它的(体积)不变,(表面积)增加了。
13.48
【分析】根据题意,4个4个地数或6个6个地数都能正好数完没有剩余,那么粽子的总个数是4和6的公倍数;先求出4和6的最小公倍数,再求最小公倍数在40~50以内的倍数,就是粽子的总个数。
【解析】4=2×2
6=2×3
4和6的最小公倍数是:2×2×3=12
12×4=48(个)
40<48<50
奶奶一共做了48个粽子。
14.256
【分析】根据题意,长方体的底面是正方形,即长方体的长、宽相等;侧面展开正好是一个正方形,则长方体的底面周长等于高16厘米;
根据正方形的周长=边长×4可知,正方形的边长=周长÷4,求出长方体的长、宽;
再根据长方体的体积=长×宽×高,代入数据计算,求出这个长方体的体积。
【解析】长方体的长、宽是:
16÷4=4(厘米)
长方体的体积:
4×4×16
=16×16
=256(立方厘米)
这个长方体的体积是256立方厘米。
15.8
【分析】要将24个豆沙粽和16个火腿粽分类包装,且每盒只放一种口味、每盒数量相等,那么每盒最多放的个数就是24和16的最大公因数,因为最大公因数是两个数的公有质因数的乘积,它能保证是满足“每盒数量相等且最多”这一条件的数;通过分解质因数的方法求出24和16的最大公因数,即每盒最多放的个数。
【解析】24=2×2×2×3
16=2×2×2×2
24和16公有的质因数是2、2、2,将这些公有质因数相乘,即2×2×2=8,所以24和16的最大公因数是8。
所以要使每盒的数量相等,每盒最多放8个。
16.√
【分析】3的倍数的特征:一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。据此判断。
【解析】用6颗珠子拔出一个四位数,这个四位数的各个数位上的数字之和一定是6,6能被3整除,6是3的倍数,所以这个四位数一定是3的倍数。题干说法正确。
故答案为:√
17.×
【分析】根据速度=路程÷时间,比较两人速度的快慢,当路程相同时,时间越短,速度越快。甲用了小时,即0.5小时,乙用了0.2小时;0.2小时比0.5小时短,因此乙的速度更快,据此判断。
【解析】,即小时=0.5小时
当路程相同时,时间越短,速度越快。
因为0.2小时<0.5小时,所以乙的速度>甲的速度。
因此同样长的路程,甲用了小时走完,乙用了0.2小时走完,乙的速度快,原题干的说法是错误的。
故答案为:×
18.×
【分析】根据因数和倍数的定义,倍数和因数的研究范围仅限于整数,且必须满足被除数、除数、商均为整数,题目中除数为小数,不符合条件。
【解析】在算式5÷2.5=2中,虽然商是整数,但除数2.5是小数。由于2.5不是整数,因此5不是2.5的倍数,也不是2的倍数,原题干的说法是错误的。
故答案为:×
19.√
【分析】分子比分母小的分数叫做真分数。
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
根据分数的基本性质,把两个分数的分子、分母同时乘2、3、4……可以得到无数个大于而小于的真分数。据此解答。
【解析】分母为9且大于而小于的真分数有、、、;
==,==,分母为18且大于而小于的真分数有、、……;
==,==,分母为27且大于而小于的真分数有、、……;
……
所以,大于而小于的真分数有无数个。
原题说法正确。
故答案为:√
20.√
【分析】找次品的最优策略:(1)把待分物品分成3份;(2)每份数量尽量平均,如果不能平均分的,也应该使多的一份与少的一份只相差1。
【解析】将6个羽毛球分成(2,2,2),取其中两组各2个称量。无论平衡不平衡,都可确定次品在其中2个;将2个分成(1、1),再称一次即可确定次品,共2次,所以原题说法正确。
故答案为:√
21.×
【分析】正方体表面积=棱长×棱长×6,一个正方体的棱长扩大到原来的几倍,表面积扩大到原来的倍数×倍数,据此分析。
【解析】4×4=16
一个正方体的棱长扩大到原来的4倍,那它的表面积会扩大到原来的16倍,原题说法错误。
故答案为:×
22.×
【分析】根据因数的定义,一个数的因数包括1和它本身,其中最大的因数是这个数本身,举例说明即可。
【解析】对于任意整数a(a>1),其因数包括1和a本身。例如,当a=6时,因数有1、2、3、6,其中最大的因数6等于a,所以原题说法错误。
故答案为:×
23.×
【分析】一个数的倍数的个数是无限的,最小的是它本身,没有最大的倍数。一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身。可举例说明。
【解析】一个数的最小倍数等于这个数的最大因数,如7既是7的倍数也是7的因数,所以原题说法错误。
故答案为:×
24.C
【分析】把单位“1”平均分成若干份,这样的一份或几份都可以用分数来表示,根据分数的意义用分数表示出各图形取出的部分,即可求得。
【解析】①把6个圆看作单位“1”,把单位“1”平均分成3份,每份2个圆,取出其中的2份,用分数表示为,图中阴影部分表示6个圆的,可以表示6张饼的;
②把每个大长方形看作单位“1”,把单位“1”平均分成3份,取出其中的2份,用分数表示为,6个阴影部分可以表示6张饼的;
③把整个图形看作单位“1”,把单位“1”平均分成6份,取出其中的2份,用分数表示为,阴影部分不能表示6张饼的;
由上可知,③图不能用阴影表示出“6张饼的”。
故答案为:C
25.A
【分析】奇数:像1,3,5,7…不是2的倍数的数叫做奇数。6年后,妙妙和父母分别都增加了6岁,即他们的岁数和增加了(岁),偶数+奇数=奇数,据此解答。
【解析】据分析可知,妙妙和父母今年岁数的和是奇数,6年后,他们的岁数之和是奇数。
故答案为:A
26.C
【分析】糖占糖水质量的分率=糖的质量÷糖水的质量,据此解答。
【解析】10÷(10+100)
=10÷110
=
糖占糖水的。
故答案为:C
27.C
【分析】
先数出各选项物体所用小正方体的个数,排除个数不是7个的物体;再观察由7个小正方体组成的物体,上面看到的形状是否是,据此解答即可。
【解析】A.有8个小正方体,不符合题意。
B.有8个小正方体,不符合题意。
C.有7个小正方体,且从上面看到的是,符合题意。
D.有7个小正方体,但从上面看到的是,不符合题意。
故答案为:C
28.D
【分析】 切割次数与截面增加:将长方体锯成4段需锯3次,每次锯切增加2个新截面,共增加6个截面。 最小表面积增加原则:为使表面积增加最少,应选择原长方体中最小的面(宽×厚)作为新增截面。 单位统一与计算:将长度单位统一为分米(4米=40分米,0.4米=4分米,厚3分米),计算单个截面面积后乘新增截面数。
【解析】长:4米=40分米
宽:0.4米=4分米
厚:3分米
最小截面面积:
4×3=12(平方分米)
新增表面积:
12×6=72(平方分米)
故答案为:D
29.A
【分析】把单位“1”平均分成若干份,这样的一份或几份都可以用分数来表示,表示其中一份的数叫作分数单位,分数的分母是几,分数单位就是几分之一;再根据最小的质数2求出需要添加分数单位的个数,据此解答。
【解析】分析可知,的分数单位是,最小的质数为2,2=,3+11=14,所以再加上11个这样的分数单位就变成最小的质数。
故答案为:A
30.C
【分析】两根同样长的绳子,因为绳子的总长度不知道,所以全长的无法确定,无法与第二根的长度比较,据此选择。
【解析】由分析可知,第一根剪去全长的,第二根剪去米,两根剩下的长度无法比较。
故答案为:C
31.D
【分析】要将长方形纸片剪成若干同样大小的正方形且无剩余,剪出的正方形边长需是长方形长和宽的公因数,而边长最大时即为长和宽的最大公因数。
【解析】24=2×2×2×3
18=2×3×3
24和18的最大公因数为:2×3=6
所以剪出的正方形的边长最大是6厘米。
故答案为:D
32.A
【分析】把称重物品平均分成三组(5,5,5),先称其中的两组,如果天平平衡,那么变质的饮料在剩下一组里面,如果天平不平衡,那么变质的饮料在天平下沉的一组里面,依次找出变质的饮料所在的组,直到最后找出变质的饮料,根据称重过程准确数出称重次数,据此解答。
【解析】分析可知:
综上所述,至少称3次一定能找出变质的那瓶饮料。
故答案为:A
33.B
【分析】根据1dm=10cm,统一单位。水面上升的体积就是印章的体积,根据长方体体积公式,容器底面积×水面上升的高度=印章的体积,据此列式计算。
【解析】1dm=10cm
10×10×(10-8)
=100×2
=200(cm3)
印章的体积是200cm3。
故答案为:B
34.1;;;
;;;0
【解析】略
35.;;
【分析】-+,按照运算顺序,进行计算。
++-,根据带符号搬家,原式化为:++-,再根据加法结合律,原式化为:(+)+(-),再进行计算。
-(+),根据减法性质,原式化为:--,再按照运算顺序,进行计算。
【解析】-+
=-+
=+
=
++-
=++-
=(+)+(-)
=1+
=
-(+)
=--
=1-
=
36.x=;x=;x=1
【分析】x-=,根据等式的性质1,方程两边同时加上即可。
2×(x+)=6,根据等式的性质2,方程两边同时除以2,再根据等式的性质1,方程两边同时减去即可。
x-(+)=,先计算出+的和,再根据等式的性质2,方程两边同时加上+的和即可。
【解析】x-=
解:x-+=+
x=+
x=
2×(x+)=6
解:2×(x+)÷2=6÷2
x+=3
x+-=3-
x=
x-(+)=
解:x-(+ )=
x-=
x-+=+
x=1
37.232cm3
【分析】求图形的体积,用长8cm,宽5cm,高6cm的长方体体积减去棱长为2cm的正方体体积;根据长方体和体积=长×宽×高,正方体的体积=棱长×棱长×棱长,代入数值计算分别计算出长方体的体积和正方体的体积,再相减即可解答。
【解析】8×5×6-2×2×2
=40×6-4×2
=240-8
=232(cm3)
图形的体积是232cm3。
38.见详解
【分析】(1)找到三角形AOB的三个顶点 A、O、B,将点A沿着水平方向右数6格,确定平移后的位置;同样地,把点O向右平移6格,得到平移后的点;把点B向右平移6格,得到平移后的点;对照原图连接各点,就得到向右平移6格后的三角形。
(2)以点O为旋转中心,将OA绕点O顺时针旋转90°,同样把OB绕点O顺时针旋转90°,对比原图形连接AB,就得到三角形AOB绕点O顺时针旋转90°后的三角形。
【解析】(1)、(2)作图如下:
39.(1)144立方米;(2)1344元
【分析】(1)求这间教室的空间,就是求这间教室的体积,根据长方体体积=长×宽×高,代入数据,即可解答。
(2)粉刷这个教室,就是求这个教师5个面的面积和,再减去门窗和黑板的面积,根据长方体表面积=长×宽+(长×高+宽×高)×2,代入数据,求出粉刷的面积,再乘12,即可解答。
【解析】(1)8×6×3
=48×3
=144(立方米)
答:这间教室的空间有144立方米。
(2)8×6+(8×3+6×3)×2-20
=8×6+(24+18)×2-20
=8×6+42×2-20
=48+84-20
=132-20
=112(立方米)
112×12=1344(元)
答:粉刷这个教室需要花费1344元。
40.
【分析】已知路上用去的时间占,吃午饭与休息的时间共占,剩下的是参观学习时间,这里是把去革命老区参观学习的总时间看作单位“1”,用1减去路上用去的时间、吃午饭和休息的时间分别占总时间的分率,即可求出参观学习的时间占几分之几。
【解析】1--
=1--
=-
=
=
答:参观学习时间占。
41.
8厘米
【分析】根据不规则物体的体积计算方法可知,甲鱼缸下降的水的体积就是鳜鱼的体积,由题意可知,捞出鳜鱼后甲鱼缸水面下降了(厘米),根据,可求出鳜鱼的体积,再用鳜鱼的体积除以乙水缸的长与宽的积(或用用鳜鱼的体积除以乙水缸的长再除以宽)即可得解。
【解析】40×40×(25-22)÷(50×12)
=40×40×3÷600
=8(厘米)
或40×40×(25-22)÷50÷12
=40×40×3÷50÷12
=8(厘米)
答:乙鱼缸放入鱼后水面上升了8厘米。
42.1550平方米;6200块
【分析】已知长50米,长是宽的2倍,那么宽为50÷2=25米;游泳池贴瓷砖只需算底面和四周,所以面积为底面面积(长×宽)加四周面积(两个长×高的面和两个宽×高的面);
已知瓷砖边长是50厘米,50厘米=0.5米;根据“正方形面积=边长×边长”,计算出每块瓷砖面积为0.5×0.5=0.25平方米,最后用贴瓷砖的总面积除以每块瓷砖的面积可得瓷砖数量。
【解析】宽:50÷2=25(米)
50×25+50×2×2+25×2×2
=1250+200+100
=1550(平方米)
答:一共需要1550平方米的瓷砖。
50厘米=0.5米
1550÷(0.5×0.5)
=1550÷0.25
=6200(块)
答:至少需要准备6200块这样的瓷砖。
43.
4290元
【分析】由题意可知,要刷多功能报告厅,除了地板其它5个面要刷,即用长×宽+长×高×2+宽×高×2,再减去门窗、大屏幕的面积,最后再乘5.5即可得解。
【解析】(30×15+30×4.5×2+15×4.5×2)-75
=(450+270+135)-75
=855-75
=780(平方米)
780×5.5=4290(元)
答:粉刷这间报告厅需要花费4290元。
44.43人
【分析】他们的绘画作品平均分成8组或10组都多3幅,由此可知,他们的作品的总数量减去3就是8和10的公倍数;由于每人限投一幅作品,且一个班人数不能大于50人,则五(1)班参与投稿的人数与3的差是8和10的公倍数,且这个公倍数不能大于50;最后用求出的这个公倍数再加上3,据此解答。
【解析】8=2×2×2
10=2×5
8和10的最小公倍数是2×2×2×5=40,8和10的公倍数有:40,80,120,…。
因为一个班人数不能大于50,所以40+3=43(人)。
答:该校五(1)班有43人参与投稿。
45.6分米
【分析】根据长方体的棱长总和=(长+宽+高)×4,代入数值计算出这个长方体花灯框架的棱长总和,也就是这根铁丝的总长度,铁丝的总长度不变,把它扎成一个正方体花灯框架,根据正方体的棱长总和=棱长×12,用棱长总和÷12,所得结果即为这个正方体的棱长是多少分米。
【解析】(9+6+3)×4÷12
=18×4÷12
=72÷12
=6(分米)
答:这个正方体的棱长是6分米。
46.8000立方厘米
【分析】根据长方体体积=长×宽×高,代入数据,求出长方体容器的容积,再求出6厘米水的体积,再用长方体容器的容积-水的体积,就是小石子的体积,据此解答。
【解析】(50×40×10)-(50×40×6)
=(2000×10)-(2000×6)
=20000-12000
=8000(立方厘米)
答:这些小石子的体积是8000立方厘米。
47.0.2立方分米
【分析】根据题意,土豆的体积=上升的水的体积,而上升的水的形状是长1分米,宽1分米,高(8-6)厘米的长方体,根据长方体的体积=长×宽×高,统一单位后代入数据计算即可解答。
【解析】8-6=2(厘米)=0.2分米
1×1×0.2=0.2(立方分米)
答:土豆的体积是0.2立方分米。
48.12.5厘米
【分析】先求出长是25厘米,宽是10厘米,高是4厘米长方体的体积,也就是4厘米高水的体积;根据长方体体积=长×宽×高,代入数据,求出长方体容器内水的体积;由于体积不变,把这个容器向右竖起来,长方体的长为10厘米,宽8厘米,求高,根据体积=长×宽×高,高=体积÷(长×宽),代入数据,即可解答。
【解析】(25×10×4)÷(10×8)
=(250×4)÷80
=1000÷80
=12.5(厘米)
答:容器里面水深12.5厘米。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
