2024-2025学年五年级下册数学期末高频易错押题冲刺卷(人教版)(含解析)
文档属性
| 名称 | 2024-2025学年五年级下册数学期末高频易错押题冲刺卷(人教版)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 625.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-25 22:00:58 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年五年级下册数学期末高频易错押题冲刺卷(人教版)
一、填空题
1.3÷( )( )(填小数)。
2.28个乒乓球,其中有27个质量合格,一个是次品,比质量合格的乒乓球略轻,假如用天平称,至少称( )次能保证找出这个次品。
3.若a-b=1(a、b是非零自然数),那么a和b的最大公因数是( ),最小公倍数是( )。
4.将长30cm,宽18cm,高12cm的长方体切割成若干个同样大的小正方体,且没有剩余(损耗忽略不计),每个小正方体的表面积最大是( )cm2。
5.一个两位数,个位上的数字与十位上的数字的积是24,且这个两位数是一个奇数,则这个两位数是( )。
6.一个正方体棱长总和是60厘米,这个正方体的体积是( )立方厘米。
7.从甲地到乙地原来每隔45米安装一根电线杆,加上两端的两根共21根,现在改成每隔60米安装一根,除起始端的电线杆不需要移动外,中间还有( )根不必移动。
8.一个正方体棱长是5分米,它的棱长总和是( )分米,它的表面积是( )平方分米。
9.把3千克糖块平均装在6个盘子中,每个盘子中的糖块是糖块总量的,每盘糖块重( )千克。
10.的分数单位是( ),再加上( )个这样的分数单位就是最小的质数。
11.一个正方体的棱长总和是96cm ,这个正方体的表面积是( )cm2,体积是( )cm3。
12.能同时被2,3,5整除的最小三位数是 ;m和n都是非零自然数,如果m=3n,那么m和n的最大公因数是 。
13.一个长方体的长是8cm,宽是5cm,高是2cm,这个长方体的表面积是( )cm2,体积是( )cm3。
14.一项工程要求20天完成,平均每天完成这项工程的( ),7天完成这项工程的( ),19天完成这项工程的( )。
15.一个立体图形,从上面看到的图形是,从前面看到的图形是,摆这个立体图形至少需要( )个正方体小块。
二、判断题
16.三个连续偶数的和一定是6的倍数。( )
17.一根3米长的铁丝,切下米后,还剩下2米。( )
18.自然数中除了奇数就是偶数,除了质数就是合数。( )
19.因为2.1÷0.3=7,所以2.1是0.3的倍数,0.3是2.1的因数。( )
20.如果a÷b=,那么a一定等于1,b一定等于5。( )
21.一个分数的分子和分母同时加上10,分数的大小不变。( )
22.如果m-n=1(m、n为非零自然数),那么m、n的最大公因数是1。( )
23.折线统计图用高低不同的点来表示数据多少,通过点与点的连线能看出数据的变化趋势。( )
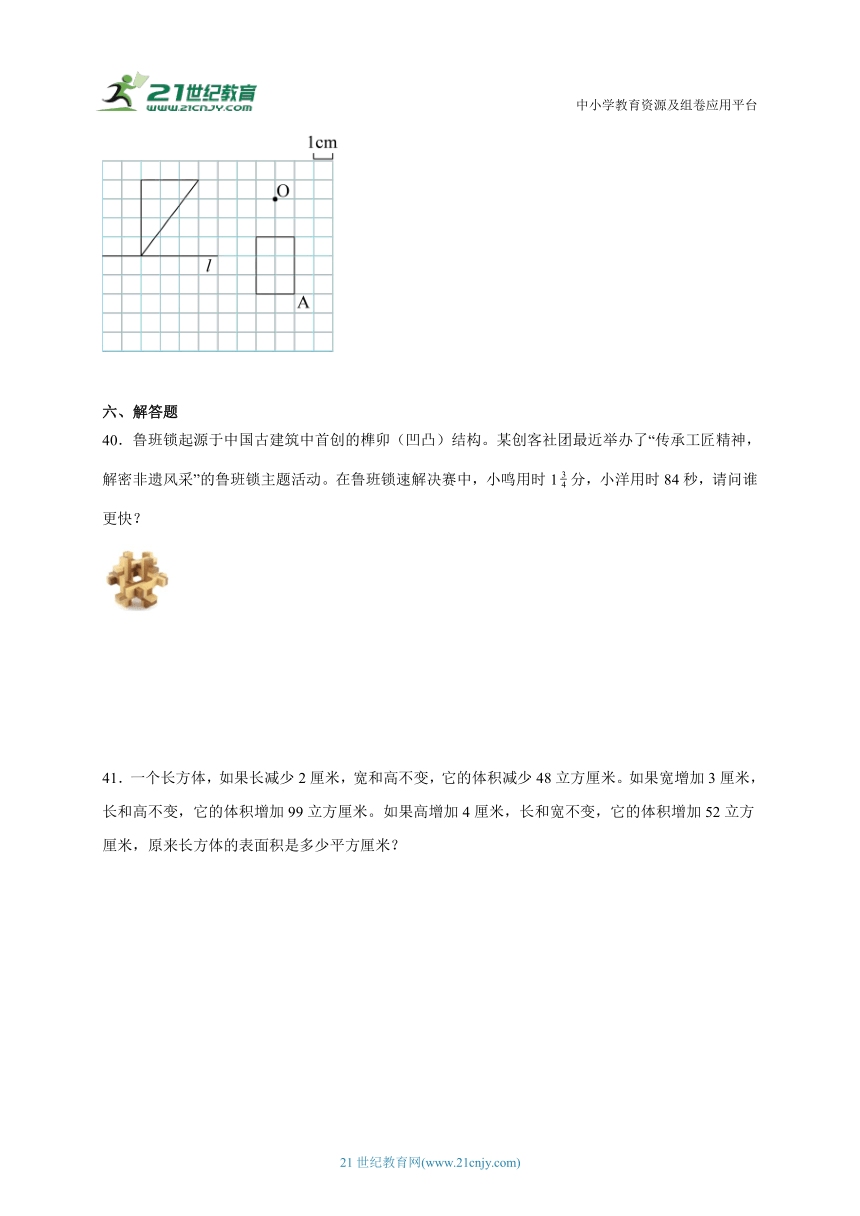
24.正方体的棱长扩大到原来的3倍,那么它的表面积扩大到原来的6倍,体积扩大到原来的9倍。( )
三、选择题
25.用同样大小的正方体摆成的物体,从前面看到,从上面看到,从左面看到的是( )。
A. B. C. D.
26.如图,把3个相同的小长方体拼成1个15cm高的大长方体,表面积减少了48cm2,那么原来1个小长方体的体积是( )cm3。
A.180 B.120 C.60
27.如下图,直线上箭头( )所指位置,与算式“”的结果最接近。
A.A B.B C.C D.D
28.如图,在边长为2的正方形中剪去一个边长为1的小正方形,动点从点出发,沿的路线绕多边形的边匀速运动到点时停止(不含点和点),则的面积随着时间变化的图像大致是( )。
A. B. C. D.
29.下面四个六位数,如果数字是不等于0的且比10小的自然数,数字为0,则下面一定是3和5的公倍数的六位数是( )。
A. B. C. D.
30.甲、乙两车同时从A,B两地相对开出,2小时后甲车行了全程的,乙车行了全程的,( )车离中点近一些。
A.甲 B.乙 C.一样 D.不确定
31.有16个零件,其中15个质量相同,有一个是轻一点的次品。如果用天平称,至少要称( )次才能保证找到次品。
A.3 B.4 C.5 D.6
32.如图,实线部分是一个正方体展开图的其中5个面,再在( )的位置添一个面,就可补全这个正方体的展开图。
A.① B.② C.③ D.④
33.三瓶同样的饮料,小星喝了一瓶的,小月喝了一瓶的,小林喝了一瓶的。他们三个人( )剩下的饮料最多。
A.小星 B.小月 C.小林 D.无法判断
34.如图的长方形是用5个同样的正方形拼成的,阴影部分的面积之和占整个长方形的( )。
A. B. C. D.
四、计算题
35.直接写得数。
0.75+= -= 10-= +-+=
-= 2-= 0.4-= +(+)=
36.脱式计算,能简算的要简算。
++0.6 3-- -(-)
++- +(-) +5.26++4.74
37.解方程。
38.计算下列图形的表面积和体积。(单位:dm)
五、作图题
39.国务院决定从2017年开始把每年的5月30日设立为“全国科技工作者日”。今年的5月30日,小科学爱好者明明用数学知识设计了一枚图标,请你在如图方格纸上完成这枚图标。
①画出直角三角形关于直线L的轴对称图形。
②以点O为圆心、1cm为半径画圆。
③将长方形绕点A逆时针旋转90°。
六、解答题
40.鲁班锁起源于中国古建筑中首创的榫卯(凹凸)结构。某创客社团最近举办了“传承工匠精神,解密非遗风采”的鲁班锁主题活动。在鲁班锁速解决赛中,小鸣用时1分,小洋用时84秒,请问谁更快?
41.一个长方体,如果长减少2厘米,宽和高不变,它的体积减少48立方厘米。如果宽增加3厘米,长和高不变,它的体积增加99立方厘米。如果高增加4厘米,长和宽不变,它的体积增加52立方厘米,原来长方体的表面积是多少平方厘米?
42.一个长方体玻璃容器,向容器里倒入6升水,这时水面高度是15厘米,再把一个苹果放入水中,量得这时水面的高度是16.5厘米,请你计算苹果的体积。
43.在长50米、宽35米的长方形操场四周插上彩旗,要求每两面彩旗之间的距离相等,而且在长方形的四个角上都要各有一面彩旗。那么每两面彩旗之间的距离最大可以是多少米?
44.工人加工三批零件,每加工一批零件,除了王师傅比其他工人多加工若干个外,其他工人加工的个数都相等。已知他们第一批共加工2100个,其中王师傅比其他工人多加工7个,第二批加工1800个,其中王师傅比每个工人多加工6个;第三批加工1600个,其中王师傅比每个工人多加工13个。这批工人最多有多少个?
45.一条公路由王村经张镇到李庄,已知王村和张镇相距1200米,张镇和李庄相距4320米,现在准备在路边栽树,要求相邻两棵树之间的距离相等,并且在王村和张镇的中点、张镇和李庄的中点都要栽上树。那么相邻两树之间的距离最多是多少米?
46.一条道路由甲村经乙村到丙村。甲、乙两村相距,乙、丙两村相距。现在准备在路边栽树,要求相邻两棵树之间的距离相等,并且在甲、乙两村的中点和乙、丙两村的中点都要栽上树。那么相邻两棵树之间的距离最多是多少米?
47.宾馆的游泳池要做几个跳水台,如图,上面是用树脂材料做成的面板,下面是不锈钢支架。上面的面板是一个直柱体形状,长60厘米,宽50厘米,最厚处20厘米,最薄处10厘米。(直柱体的体积可以用“底面积×高”进行计算)
(1)一个面板的体积是多少立方厘米?
(2)在面板的四周(不含上、下两面)涂上颜色,涂色部分的面积是多少平方厘米?
48.一个封闭的长方体容器(如下图),长20厘米、宽15厘米、高10厘米,里面的水深6厘米,如果把这个容器向右转,竖起来,里面的水深是多少厘米?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.4;15;0.75
【分析】(1)商不变的性质:被除数和除数同时乘或除以一个相同的数(0除外),商不变 ,据此判断被除数除以几,则除数也要除以几;
(2)除法和分数的关系:被除数相当于分子,除号相当于分数线,除数相当于分母,据此把18÷24写成分数,再根据分数的基本性质化成最简分数,最后根据分数的基本性质判断分母乘几,则分子也要乘几;
(3)根据被除数÷除数=商,把结果写成小数即可。
【解析】18÷24=(18÷6)÷(24÷6)=3÷4
18÷24====
18÷24=0.75
即3÷4==18÷24=0.75。
2.4
【分析】找次品时尽量把总数平均分成3份,如果不能平均分,也要使多或少的那份比其它的少1或多1;这样称1次就能把次品所在的范围缩小到最少。找出次品称的次数也会最少。我们可以根据规律:当所测的物品的个数符合“3n-1+1≤物品的数量≤3n(n≥1)”时,所称次数至少为n次;据此即可解答。
【解析】33<28<34,所以至少称4次能保证找出这个次品。
3.1 ab
【分析】如果b-1=a(a、b是非零自然数),那么a和b相差1,即a和b是相邻的自然数。两个相邻的自然数是互质数,它们的最大公因数是1,最小公倍数是它们相乘的积。
【解析】据分析可知,若a-b=1(a、b是非零自然数),那么a和b的最大公因数是1,最小公倍数是ab。
4.216
【分析】要把长方体切割成同样大小的小正方体,且没有剩余,就是求长方体长、宽、高的公因数。要求切割成的小正方体的表面积最大是多少,就要先求小正方体的棱长最长是多少厘米,就是求长方体的长、宽、高的最大公因数。再根据正方体的表面积:表面积=棱长×棱长×6,代入数值,计算即可解答。
【解析】30=2×3×5
18=2×3×3
12=2×2×3
30、18和12的最大公因数是2×3=6
所以小正方形的棱长最长为6厘米
6×6×6
=36×6
=216(cm2)
所以每个小正方体的表面积最大是216cm2。
5.83
【分析】先求出积为24的两个数,再组成两位数,再根据奇数的意义:不能被2整除的数叫做奇数,据此解答。
【解析】24=3×8=4×6
3和8组成的数是38和83;38是偶数,83是奇数。
4和6组成的数是46和64;46和64都是偶数。
一个两位数,个位上的数字与十位上的数字的积是24,且这个两位数是一个奇数,则这个两位数是83。
6.125
【分析】正方体有12条棱,每条棱长度相等,据此用60除以12可以求出正方体的棱长,再根据正方体的体积=棱长×棱长×棱长,代入数据计算即可求出它的体积。
【解析】60÷12=5(厘米)
5×5×5=125(立方厘米)
则这个正方体的体积是125立方厘米。
7.4
【分析】原来安装间隔是每隔45米,共21根电线杆,间隔数为(21-1),用每根间隔的距离×间隔数,计算出甲地到乙地的总路程;现在的间隔是60米,需要找出与原来间隔45米的公倍数,先计算出45和60的最小公倍数,判断新旧电线杆有哪些位置是重合的,排除起始端的两根电线杆不移动外,中间其余重合的位置也不必移动,据此解答。
【解析】甲地和乙地的总路程:
45×(21-1)
=45×20
=900(米)
45=3×3×5
60=2×2×3×5
45和60的最小公倍数为3×5×3×2×2=180,即在0,180,360,540,720,900米处,新旧电线杆位置重合。
因此改成每隔60米安装一根,除起始端的电线杆不需要移动外,中间还有4根不必移动。
8.60 150
【分析】根据正方体的总棱长公式:L=12a,正方体的表面积公式:S=6a2,据此代入数值进行计算即可。
【解析】5×12=60(分米)
5×5×6
=25×6
=150(平方分米)
则它的棱长总和是60分米,它的表面积是150平方分米。
9.;
【分析】把盘子中的糖块的重量看作单位“1”,平均分成6份,则每个盘子中的糖块是糖块总量的;用每盘糖块的重量除以盘子的个数即可求出每盘糖块重多少千克。
【解析】1÷6=
3÷6=(千克)
把3千克糖块平均装在6个盘子中,每个盘子中的糖块是糖块总量的,每盘糖块重千克。
10. 10
【分析】判定一个分数的单位看分母,分母是几,分数单位就是几分之一;最小的质数是2,用2减去原分数求出差,再看有几个这样的分数单位即可。
【解析】的分数单位是,最小的质数是2。
,里有10个。
因此的分数单位是,再加上10个这样的分数单位就是最小的质数。
11.384 512
【分析】根据正方体棱长总和公式:棱长总和=棱长×12,棱长=棱长总和÷12,代入数据,求出正方体的棱长;再根据正方体表面积公式:表面积=棱长×棱长×6,代入数据,求出正方体的表面积;根据正方体体积公式:体积=棱长×棱长×棱长,代入数据,求出正方体体积,据此解答。
【解析】96÷12=8(cm)
8×8×6
=64×6
=384(cm2)
8×8×8
=64×8
=512(cm3)
一个正方体的棱长总和是96cm ,这个正方体的表面积是384cm2,体积是512cm3。
12.120; n
【分析】(1)2的倍数:个位是2,4,6,8,0的数,3的倍数:各个数位数字之和能被3整除的数,5的倍数:个位是0或5的数,据此可知要满足既是2的倍数又是5的倍数,个位必须是0,这个数要最小,则这个数百位的数是1,结合3的倍数特征确定十位数字最小是几即可;
(2)根据m=3n可知m是n的3倍,存在倍数关系的两个数,它们的最大公因数是两个数中的较小数,据此解答。
【解析】据分析可知,这个三位数个位是0,百位是1,1+0=1,十位最小是3-1=2,这个最小的三位数是120;
m=3n,m是n的3倍,m和n的最大公因数是较小数n。
能同时被2,3,5整除的最小三位数是120;m和n都是非零自然数,如果m=3n,那么m和n的最大公因数是n。
13.132 80
【分析】已知长方体的长、宽、高,根据长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,代入数据计算求出它的表面积和体积。
【解析】(8×5+8×2+5×2)×2
=(40+16+10)×2
=66×2
=132(cm2)
8×5×2=80(cm3)
这个长方体的表面积是132cm2,体积是80cm3。
14.
【分析】把这项工程的工作总量看作单位“1”,要求20天完成,用1÷20求出平均每天完成这项工程的几分之几;
求7天完成这项工程的几分之几,就是求7占20的几分之几,用除法计算;
求19天完成这项工程的几分之几,就是求19占20的几分之几,用除法计算。
【解析】1÷20=
7÷20=
19÷20=
一项工程要求20天完成,平均每天完成这项工程的(),7天完成这项工程的(),19天完成这项工程的()。
15.11
【分析】根据从上面看到的图形可知,这个立体图形底下一层有9个正方体小块。再根据从前面看到的图形可知,上面一层至少有2个正方体小块。据此解题。
【解析】9+2=11(个)
所以,摆这个立体图形至少需要11个正方体小块。
16.√
【分析】可以用字母表示中间数为2a,根据偶数的特征分别表示出3个偶数,比它小的偶数是2a-2,比它大的偶数是2a+2,再相加计算即可。
【解析】2a-2+2a+2a+2=6a
6a是6的倍数,所以原题说法正确。
故答案为:√
17.×
【分析】切下米,分数后面加单位表示具体的长度,用总长度减去切下去的长度即可求出还剩下的长度。
【解析】3-=(米)
还剩下米,原题说法错误。
故答案为:×
18.×
【分析】能被2整除的数是偶数,不能被2整除的数叫做奇数;只有本身和1两个因数的数叫做质数,除了1和它本身之外还有其他因数的数是合数,1既不是质数也不是合数。据此判断。
【解析】由分析可知,在自然数中,除了奇数就是偶数,说法正确。1既不是质数也不是合数,所以除了质数、合数外还有1,后半句说法错误。
故答案为:×
19.×
【分析】在整数除法中如果被除数除以除数,商是整数而没有余数,我们就说被除数是除数的倍数,除数是被除数的因数。据此回答。
【解析】根据因数和倍数的意义可知,我们研究的因数和倍数是在整数除法范围之内的,不包括小数除法。所以题目中的说法是错误的。
故答案为:×
20.×
【分析】由a÷b=,可以把a看作1份,b看作5份;当a、b同时乘2、3、4……时,a÷b的商仍是,据此判断。
【解析】当a=1,b=5时,a÷b=;
当a=2,b=10时,a÷b==;
当a=3,b=15时,a÷b==;
……
所以,如果a÷b=,a不一定等于1, b不一定等于5。
原题说法错误。
故答案为:×
21.×
【分析】分数的分子和分母,同时乘或除以相同的数(0除外),分数的大小不变,据此分析。
【解析】根据分数的基本性质,一个分数的分子和分母同时乘10,分数的大小不变,原题说法错误。
故答案为:×
22.√
【分析】m-n=1(m、n均为非零自然数),说明m、n是两个相邻的非0的自然数,相邻的两个非0自然数是互质数,所以m、n的最大公因数是1。
【解析】由分析可知,如果m-n=1(m、n为非零自然数),那么m、n的最大公因数是1。例如:4-3=1,4和3互质,所以4和3的最大公因数是1。
所以原题说法正确。
故答案为:√
23.√
【分析】折线统计图是用点来表示数量的,通过用数据点的连线来表示数据的变化趋势,是以折线的上升或下降来表示统计数量的增减变化的统计图。
【解析】折线统计图是用点来表示数量的,以折线的上升或下降来表示统计数量的增减变化。
所以折线统计图用高低不同的点来表示数据多少,通过点与点的连线能看出数据的变化趋势。
故答案为:√
24.×
【分析】正方体表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长,正方体棱长扩大到原来的几倍,表面积扩大到原来的倍数×倍数,体积扩大到原来的倍数×倍数×倍数,据此分析。
【解析】3×3=9
3×3×3=27
正方体的棱长扩大到原来的3倍,那么它的表面积扩大到原来的9倍,体积扩大到原来的27倍,所以原题说法错误。
故答案为:×
25.A
【分析】分析题目,根据从前面看到与从上面看到的图形可知该几何体一共由4个小正方体组成,其中前排有3个,后排中间有1个,据此可知从左面看到的是左右并列的两个小正方形,据此解答。
【解析】
用同样大小的正方体摆成的物体,从前面看到,从上面看到,从左面看到的是。
故答案为:A
26.C
【分析】把3个相同的小长方体拼成了1个15cm高的大长方体,表面积减少了 48cm2 ,减少的面积是小长方体的4个底面面积,用48÷4,求出一个长方体的底面积,再用15÷3,求出一个长方体的高,再根据长方体体积=底面积×高,即可求出一个长方体的体积。
【解析】(48÷4)×(15÷3)
=12×5
=60(cm3)
那么原来1个小长方体的体积是60cm3。
故答案为:C
27.C
【分析】根据异分母分数加法法则:异分母分数相加,先通分,然后再计算,据此计算出算式“”的结果,再将计算结果再与箭头的位置对比即可。
【解析】
因为
所以的位置在1和2的正中间偏向左侧一点,即最接近的点为C。
故答案为:C
28.B
【分析】三角形的面积=底×高÷2,△ABP的面积=AB×高÷2。
当点P在AD边上运动时,底为AB、高是AP,△ABP的面积=AB×AP÷2(0<AP≤2),此时AP越来越大,所以△ABP的面积也越来越大;
当点P在DE边上运动时,底为AB、高不变,此时△ABP的面积也保持不变;
当点P在EF边上运动时,底为AB、高越来越小,此时△ABP的面积也越来越小;
当点P在FG边上运动时,底为AB、高不变,此时△ABP的面积也保持不变;
当点P在GB边上运动时,底为AB、高越来越小,此时△ABP的面积也越来越小。
综上所述,△ABP的面积的变化情况为:先是由小变大,再保持不变,然后逐渐变小,再保持不变,最后又逐渐变小。
据此逐选项进行分析即可解答。
【解析】A.表示先保持不变,再变小,然后保持不变再变小,不符合题意;
B.表示先是由小变大,再保持不变,然后逐渐变小,再保持不变,最后又逐渐变小,符合题意;
C.表示逐渐变大,再逐渐变小,然后保持不变,最后又逐渐变小,不符合题意;
D.表示先由小变大,再保持不变,然后逐渐变小,不符合题意。
所以的面积随着时间变化的图像大致是。
故答案为:B
29.A
【分析】5的倍数的特征,一个数的个位是0或5,这个数就是5的倍数;3的倍数的特征,各个数位的数字之和是3的倍数。据此可知,这个六位数各数位相加的和是3的倍数,又因数字是不等于0的且比10小的自然数,即不一定是5,则可知,这个六位数的个位上应是0,即。据此解答。
【解析】A.个位是 ,因此一定是 5 的倍数。各数位上的和是,一定是3的倍数,所以该数一定是3和5的公倍数。
B.个位是 不是, 不一定是5,因为这个数不一定是5的倍数,所以不符合题意。
C.个位是 ,因此一定是 5 的倍数。各数位上的和是,当时,不是3的倍数,所以不符合题意。
D.个位是 不是,不一定是5,因为这个数不一定是5的倍数,所以不符合题意。
故答案为:A
30.B
【分析】根据题意,把全程长度看作单位“1”,中点是全程的,离中点近,也就是与的差最小,所以用甲车行驶的路程与作差,用乙车行驶的路程与作差,然后比较它们的差,差小的近。
【解析】-=-=
-=-=
<
所以乙车离中点更近一些。
故答案为:B
31.A
【分析】将16个零件分成三组(5,5,6),先把两组5个放在天平两侧,若平衡,次品在剩余6个零件中;若不平衡,次品在较轻的5个中。
若次品在剩余6个零件中,将6个零件分成三组(2,2,2),先把两组2个放在天平两侧,若平衡,则次品在剩余2个中,若不平衡,次品在较轻的一组中;再把次品的一组放在天平两次,较轻的一边为次品;
若次品在第一次称的5个零件中,把5个零件分成(2,2,1)三组,把两组2个放在天平两侧,若平衡,剩下的为次品,若不平衡,次品在较轻的一侧;再把较轻的一侧的2个零件放在天平两侧,即可测出次品零件;至少需要3次才能保证找出次品。
【解析】根据分析可知,有16个零件,其中15个质量相同,有一个是轻一点的次品。如果用天平称,至少要称3次才能保证找到次品。
故答案为:A
32.C
【分析】正方体展开图有四大类型,分别是1-4-1型、1-3-2型、2-2-2型、3-3型。据此解题。
【解析】观察目前的正方体展开图,发现再在③的位置添一个面,就可成为正方体展开图的1-4-1型,就可补全这个正方体的展开图。
故答案为:C
33.A
【分析】分数的大小比较:分母相同的分数,分子大的分数大;分子相同的分数,分母小的分数大;分母不同的分数,先通分再比较。根据题意,三瓶同样的饮料,先比较谁喝的最少,那么他剩下的饮料最多。
【解析】
小星喝的最少,所以他剩下的饮料最多。
故答案为:A
34.C
【分析】设小正方形边长为1,求出长方形面积;阴影部分面积为两个三角形面积;根据三角形面积公式:面积=底×高÷2,据此求出阴影部分面积,再用阴影部分面积÷长方形面积,即可解答。
【解析】假设小正方形边长为1。
长方形面积:
1×1×5
=1×5
=5
阴影部分面积:
1×1÷2+1×1÷2
=1÷2+1÷2
=0.5+0.5
=1
1÷5=
长方形是用5个同样的正方形拼成的,阴影部分的面积之和占整个长方形的。
故答案为:C
35.;;;;
;;;
【解析】略
36.1;2;1
1;;11
【分析】(1)先把0.6转化为,再根据加法交换律进行简便运算。
(2)根据减法的运算性质,把算式转化为3-(+),先算括号里的加法,再算括号外的减法。
(3)根据减法的运算性质,把算式转化为-+,再根据加法交换律进行简便运算。
(4)根据加法交换律和加法结合律,把算式转化为(+)+(-),先分别计算括号里的加法和减法,再计算括号外的加法。
(5)通分后,先计算括号里的减法,再计算括号外的加法。
(6)根据加法交换律和加法结合律,把算式转化为(+)+(5.26+4.74),先分别计算括号里的加法,再计算括号外的加法。
【解析】++0.6
=++
=++
=1
3--
=3-(+)
=3-1
=2
-(-)
=-+
=+-
=2-
=1
++-
=(+)+(-)
=1+
=1
+(-)
=+(-)
=+
=
=
+5.26++4.74
=(+)+(5.26+4.74)
=1+10
=11
37.;;
【分析】根据等式的性质,方程两边同时加上,通分计算求解出x;
根据等式的性质,方程两边同时减去,通分计算求解出x;
根据等式的性质,方程两边同时加上x,方程两边交换位置,再同时减去,通分计算求解出x;
【解析】
解:
解:
解:
38.2532dm2,6688dm3;150dm2,113dm3
【分析】第一个组合体,通过平移,表面积=完整的大长方体表面积+小长方体前后左右4个面的面积和,长方体表面积=(长×宽+长×高+宽×高)×2,小长方体4个面的面积和=(长×高+宽×高)×2;体积=大长方体体积+小长方体体积,长方体体积=长×宽×高;
第二个组合体,挖去一个长方体,减少了3个面,又出现了同样的3个面,因此表面积=完整的正方体表面积,正方体表面积=棱长×棱长×6;体积=正方体体积-长方体体积,正方体体积=棱长×棱长×棱长,长方体体积=长×宽×高,据此列式计算。
【解析】第一个组合体:
表面积:(37×16+37×10+16×10)×2+(16×6+8×6)×2
=(592+370+160)×2+(96+48)×2
=1122×2+144×2
=2244+288
=2532(dm2)
体积:37×16×10=5920(dm3)
16×8×6=768(dm3)
5920+768=6688(dm3)
第二个组合体:
表面积:5×5×6=150(dm2)
体积:5×5×5-2×2×3
=125-12
=113(dm3)
第一个组合体的表面积是2532dm2,体积是5920dm3;第二个组合体的表面积是150dm2,体积是113dm3。
39.(1)(2)(3)见详解
【分析】(1)根据轴对称图形的意义:对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出三角形的关键对称点,依次连接即可。
(2)以点O圆心,画出半径是1cm的圆即可。
(3)根据旋转的特征,长方形绕点A逆时针旋转90°后,点A的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,得到旋转后的图形。
【解析】(1)如下图:
(2)如下图:
(3)如下图:
40.小洋
【分析】根据1时=60秒,把分转化为以秒为单位,再比较两人的用时,用时短的就更快。
【解析】(秒)
84<105
答:小洋更快。
41.140平方厘米
【分析】一个长方体,如果长减少2厘米,宽和高不变,它的体积减少48立方厘米,根据长方体的体积,得出左右面的面积是24平方厘米;同理得出上下面和前后面的面积,再根据长方体的表面积=(左面面积+前面面积+上面面积)×2。
【解析】48÷2=24(平方厘米)
99÷3=33(平方厘米)
52÷4=13(平方厘米)
(24+33+13)×2
=70×2
=140(平方厘米)
答:答:原长方体的表面积是140平方厘米。
42.600立方厘米
【分析】根据长方体的体积=底面积×高,得出底面积是400平方厘米。然后乘水面升高部分的高度(16.5-15)厘米就是苹果的体积。注意根据1升=1000毫升,1毫升=1立方厘米换算单位。
【解析】6升=6000毫升=6000立方厘米
6000÷15=400(平方厘米)
400×(16.5-15)
=400×1.5
=600(立方厘米)
答:苹果的体积是600立方厘米。
43.5米
【分析】在长方形操场长的方向上,相邻两面彩旗之间的距离×段数=50米,即间距是50的因数,同样的道理,间距也是35的因数,因此间距是50和35的公因数,又题目要求间距要最大,即找最大公因数即可。
【解析】50=2×5×5
35=5×7
所以50和35的最大公因数是5
即每两面彩旗之间的距离最大可以是5米。
答:每两面彩旗之间的距离最大可以是5米。
44.23人
【分析】第一批共2100个,王师傅比其他工人多加工7个,扣除这7个,则王师傅和其他工人加工的个数相同,即每人加工的个数×人数=2100-7=2093,即总人数是2093的因数,同样的道理,根据第二批和第三批,分别可知,总人数是1794和1587的因数,也就是这三个数的公因数,现要求人数最多,即找最大公因数,即可得出答案。
【解析】2100-7=2093
1800-6=1794
1600-13=1587
2093=7×13×23
1794=2×3×13×23
1587=3×23×23
所以2093,1794,1587的最大公因数是23
因此总人数为23个。
答:这批工人最多有23个。
45.120米
【分析】因为相邻两棵树之间的距离相等,并且在王村和张镇的中点、张镇和李庄的中点都要栽上树,所以相邻两树之间的距离能够整除王村和张镇以及张镇和李庄的一半距离,找出最大公因数即可。
【解析】1200÷2=600(米)
4320÷2=2160(米)
600=2×2×2×3×5×5
2160=2×2×2×2×3×3×3×5
所以600和2160的最大公因数是:2×2×2×3×5=120
即相邻两棵树之间的距离最多是120米。
答:相邻两棵树之间的距离最多是120米。
46.45米
【分析】甲乙两村一半的路程是225米,因为中点要栽树,因此间距×段数=225,则间距必须是225的因数,同样的道理,乙丙中点也要中,即间距也必须是630÷2=315的因数,也就是找225和315的公因数,又要求相邻两棵树之间的距离最多,即间距最大,也就是找最大公因数。
【解析】450÷2=225(米)
630÷2=315(米)
225=3×3×5×5
315=3×3×5×7
225和315的最大公因数是:3×3×5=45
所以相邻两棵树之间的间距最大是45米。
答:相邻两棵树之间的距离最多是45米。
47.(1)45000立方厘米
(2)3300平方厘米
【分析】(1)面板的底面是一个上底是10厘米、下底是20厘米、高是60厘米的梯形,根据梯形的面积=(上底+下底)×高÷2,求出直柱体的底面积,再根据直柱体的体积=底面积×高,求出面板的体积。
(2)面板涂色部分是前后面完全一样的梯形和左右面两个不同的长方形。根据梯形的面积=(上底+下底)×高÷2,长方形的面积=长×宽,代入数据计算,把这四个面的面积相加,求出需要涂色的面积即可。
【解析】(1)(10+20)×60÷2
=30×60÷2
=900(平方厘米)
900×50=45000(立方厘米)
答:一个面板的体积是45000立方厘米。
(2)(10+20)×60÷2×2+50×10+50×20
=30×60÷2×2+50×10+50×20
=1800+500+1000
=3300(平方厘米)
答:涂色部分的面积是3300平方厘米。
48.12厘米
【分析】已知一个封闭长方体容器的长为20厘米、宽为15厘米、水深6厘米,根据长方体的体积公式V=abh,求出水的体积;
如果把这个容器向右转,水的体积不变,但容器的底面变成(15×10),根据长方体的高h=V÷S,求出此时水的深度。
【解析】水的体积:
20×15×6
=300×6
=1800(立方厘米)
水深:
1800÷(15×10)
=1800÷150
=12(厘米)
答:里面的水深是12厘米。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年五年级下册数学期末高频易错押题冲刺卷(人教版)
一、填空题
1.3÷( )( )(填小数)。
2.28个乒乓球,其中有27个质量合格,一个是次品,比质量合格的乒乓球略轻,假如用天平称,至少称( )次能保证找出这个次品。
3.若a-b=1(a、b是非零自然数),那么a和b的最大公因数是( ),最小公倍数是( )。
4.将长30cm,宽18cm,高12cm的长方体切割成若干个同样大的小正方体,且没有剩余(损耗忽略不计),每个小正方体的表面积最大是( )cm2。
5.一个两位数,个位上的数字与十位上的数字的积是24,且这个两位数是一个奇数,则这个两位数是( )。
6.一个正方体棱长总和是60厘米,这个正方体的体积是( )立方厘米。
7.从甲地到乙地原来每隔45米安装一根电线杆,加上两端的两根共21根,现在改成每隔60米安装一根,除起始端的电线杆不需要移动外,中间还有( )根不必移动。
8.一个正方体棱长是5分米,它的棱长总和是( )分米,它的表面积是( )平方分米。
9.把3千克糖块平均装在6个盘子中,每个盘子中的糖块是糖块总量的,每盘糖块重( )千克。
10.的分数单位是( ),再加上( )个这样的分数单位就是最小的质数。
11.一个正方体的棱长总和是96cm ,这个正方体的表面积是( )cm2,体积是( )cm3。
12.能同时被2,3,5整除的最小三位数是 ;m和n都是非零自然数,如果m=3n,那么m和n的最大公因数是 。
13.一个长方体的长是8cm,宽是5cm,高是2cm,这个长方体的表面积是( )cm2,体积是( )cm3。
14.一项工程要求20天完成,平均每天完成这项工程的( ),7天完成这项工程的( ),19天完成这项工程的( )。
15.一个立体图形,从上面看到的图形是,从前面看到的图形是,摆这个立体图形至少需要( )个正方体小块。
二、判断题
16.三个连续偶数的和一定是6的倍数。( )
17.一根3米长的铁丝,切下米后,还剩下2米。( )
18.自然数中除了奇数就是偶数,除了质数就是合数。( )
19.因为2.1÷0.3=7,所以2.1是0.3的倍数,0.3是2.1的因数。( )
20.如果a÷b=,那么a一定等于1,b一定等于5。( )
21.一个分数的分子和分母同时加上10,分数的大小不变。( )
22.如果m-n=1(m、n为非零自然数),那么m、n的最大公因数是1。( )
23.折线统计图用高低不同的点来表示数据多少,通过点与点的连线能看出数据的变化趋势。( )
24.正方体的棱长扩大到原来的3倍,那么它的表面积扩大到原来的6倍,体积扩大到原来的9倍。( )
三、选择题
25.用同样大小的正方体摆成的物体,从前面看到,从上面看到,从左面看到的是( )。
A. B. C. D.
26.如图,把3个相同的小长方体拼成1个15cm高的大长方体,表面积减少了48cm2,那么原来1个小长方体的体积是( )cm3。
A.180 B.120 C.60
27.如下图,直线上箭头( )所指位置,与算式“”的结果最接近。
A.A B.B C.C D.D
28.如图,在边长为2的正方形中剪去一个边长为1的小正方形,动点从点出发,沿的路线绕多边形的边匀速运动到点时停止(不含点和点),则的面积随着时间变化的图像大致是( )。
A. B. C. D.
29.下面四个六位数,如果数字是不等于0的且比10小的自然数,数字为0,则下面一定是3和5的公倍数的六位数是( )。
A. B. C. D.
30.甲、乙两车同时从A,B两地相对开出,2小时后甲车行了全程的,乙车行了全程的,( )车离中点近一些。
A.甲 B.乙 C.一样 D.不确定
31.有16个零件,其中15个质量相同,有一个是轻一点的次品。如果用天平称,至少要称( )次才能保证找到次品。
A.3 B.4 C.5 D.6
32.如图,实线部分是一个正方体展开图的其中5个面,再在( )的位置添一个面,就可补全这个正方体的展开图。
A.① B.② C.③ D.④
33.三瓶同样的饮料,小星喝了一瓶的,小月喝了一瓶的,小林喝了一瓶的。他们三个人( )剩下的饮料最多。
A.小星 B.小月 C.小林 D.无法判断
34.如图的长方形是用5个同样的正方形拼成的,阴影部分的面积之和占整个长方形的( )。
A. B. C. D.
四、计算题
35.直接写得数。
0.75+= -= 10-= +-+=
-= 2-= 0.4-= +(+)=
36.脱式计算,能简算的要简算。
++0.6 3-- -(-)
++- +(-) +5.26++4.74
37.解方程。
38.计算下列图形的表面积和体积。(单位:dm)
五、作图题
39.国务院决定从2017年开始把每年的5月30日设立为“全国科技工作者日”。今年的5月30日,小科学爱好者明明用数学知识设计了一枚图标,请你在如图方格纸上完成这枚图标。
①画出直角三角形关于直线L的轴对称图形。
②以点O为圆心、1cm为半径画圆。
③将长方形绕点A逆时针旋转90°。
六、解答题
40.鲁班锁起源于中国古建筑中首创的榫卯(凹凸)结构。某创客社团最近举办了“传承工匠精神,解密非遗风采”的鲁班锁主题活动。在鲁班锁速解决赛中,小鸣用时1分,小洋用时84秒,请问谁更快?
41.一个长方体,如果长减少2厘米,宽和高不变,它的体积减少48立方厘米。如果宽增加3厘米,长和高不变,它的体积增加99立方厘米。如果高增加4厘米,长和宽不变,它的体积增加52立方厘米,原来长方体的表面积是多少平方厘米?
42.一个长方体玻璃容器,向容器里倒入6升水,这时水面高度是15厘米,再把一个苹果放入水中,量得这时水面的高度是16.5厘米,请你计算苹果的体积。
43.在长50米、宽35米的长方形操场四周插上彩旗,要求每两面彩旗之间的距离相等,而且在长方形的四个角上都要各有一面彩旗。那么每两面彩旗之间的距离最大可以是多少米?
44.工人加工三批零件,每加工一批零件,除了王师傅比其他工人多加工若干个外,其他工人加工的个数都相等。已知他们第一批共加工2100个,其中王师傅比其他工人多加工7个,第二批加工1800个,其中王师傅比每个工人多加工6个;第三批加工1600个,其中王师傅比每个工人多加工13个。这批工人最多有多少个?
45.一条公路由王村经张镇到李庄,已知王村和张镇相距1200米,张镇和李庄相距4320米,现在准备在路边栽树,要求相邻两棵树之间的距离相等,并且在王村和张镇的中点、张镇和李庄的中点都要栽上树。那么相邻两树之间的距离最多是多少米?
46.一条道路由甲村经乙村到丙村。甲、乙两村相距,乙、丙两村相距。现在准备在路边栽树,要求相邻两棵树之间的距离相等,并且在甲、乙两村的中点和乙、丙两村的中点都要栽上树。那么相邻两棵树之间的距离最多是多少米?
47.宾馆的游泳池要做几个跳水台,如图,上面是用树脂材料做成的面板,下面是不锈钢支架。上面的面板是一个直柱体形状,长60厘米,宽50厘米,最厚处20厘米,最薄处10厘米。(直柱体的体积可以用“底面积×高”进行计算)
(1)一个面板的体积是多少立方厘米?
(2)在面板的四周(不含上、下两面)涂上颜色,涂色部分的面积是多少平方厘米?
48.一个封闭的长方体容器(如下图),长20厘米、宽15厘米、高10厘米,里面的水深6厘米,如果把这个容器向右转,竖起来,里面的水深是多少厘米?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.4;15;0.75
【分析】(1)商不变的性质:被除数和除数同时乘或除以一个相同的数(0除外),商不变 ,据此判断被除数除以几,则除数也要除以几;
(2)除法和分数的关系:被除数相当于分子,除号相当于分数线,除数相当于分母,据此把18÷24写成分数,再根据分数的基本性质化成最简分数,最后根据分数的基本性质判断分母乘几,则分子也要乘几;
(3)根据被除数÷除数=商,把结果写成小数即可。
【解析】18÷24=(18÷6)÷(24÷6)=3÷4
18÷24====
18÷24=0.75
即3÷4==18÷24=0.75。
2.4
【分析】找次品时尽量把总数平均分成3份,如果不能平均分,也要使多或少的那份比其它的少1或多1;这样称1次就能把次品所在的范围缩小到最少。找出次品称的次数也会最少。我们可以根据规律:当所测的物品的个数符合“3n-1+1≤物品的数量≤3n(n≥1)”时,所称次数至少为n次;据此即可解答。
【解析】33<28<34,所以至少称4次能保证找出这个次品。
3.1 ab
【分析】如果b-1=a(a、b是非零自然数),那么a和b相差1,即a和b是相邻的自然数。两个相邻的自然数是互质数,它们的最大公因数是1,最小公倍数是它们相乘的积。
【解析】据分析可知,若a-b=1(a、b是非零自然数),那么a和b的最大公因数是1,最小公倍数是ab。
4.216
【分析】要把长方体切割成同样大小的小正方体,且没有剩余,就是求长方体长、宽、高的公因数。要求切割成的小正方体的表面积最大是多少,就要先求小正方体的棱长最长是多少厘米,就是求长方体的长、宽、高的最大公因数。再根据正方体的表面积:表面积=棱长×棱长×6,代入数值,计算即可解答。
【解析】30=2×3×5
18=2×3×3
12=2×2×3
30、18和12的最大公因数是2×3=6
所以小正方形的棱长最长为6厘米
6×6×6
=36×6
=216(cm2)
所以每个小正方体的表面积最大是216cm2。
5.83
【分析】先求出积为24的两个数,再组成两位数,再根据奇数的意义:不能被2整除的数叫做奇数,据此解答。
【解析】24=3×8=4×6
3和8组成的数是38和83;38是偶数,83是奇数。
4和6组成的数是46和64;46和64都是偶数。
一个两位数,个位上的数字与十位上的数字的积是24,且这个两位数是一个奇数,则这个两位数是83。
6.125
【分析】正方体有12条棱,每条棱长度相等,据此用60除以12可以求出正方体的棱长,再根据正方体的体积=棱长×棱长×棱长,代入数据计算即可求出它的体积。
【解析】60÷12=5(厘米)
5×5×5=125(立方厘米)
则这个正方体的体积是125立方厘米。
7.4
【分析】原来安装间隔是每隔45米,共21根电线杆,间隔数为(21-1),用每根间隔的距离×间隔数,计算出甲地到乙地的总路程;现在的间隔是60米,需要找出与原来间隔45米的公倍数,先计算出45和60的最小公倍数,判断新旧电线杆有哪些位置是重合的,排除起始端的两根电线杆不移动外,中间其余重合的位置也不必移动,据此解答。
【解析】甲地和乙地的总路程:
45×(21-1)
=45×20
=900(米)
45=3×3×5
60=2×2×3×5
45和60的最小公倍数为3×5×3×2×2=180,即在0,180,360,540,720,900米处,新旧电线杆位置重合。
因此改成每隔60米安装一根,除起始端的电线杆不需要移动外,中间还有4根不必移动。
8.60 150
【分析】根据正方体的总棱长公式:L=12a,正方体的表面积公式:S=6a2,据此代入数值进行计算即可。
【解析】5×12=60(分米)
5×5×6
=25×6
=150(平方分米)
则它的棱长总和是60分米,它的表面积是150平方分米。
9.;
【分析】把盘子中的糖块的重量看作单位“1”,平均分成6份,则每个盘子中的糖块是糖块总量的;用每盘糖块的重量除以盘子的个数即可求出每盘糖块重多少千克。
【解析】1÷6=
3÷6=(千克)
把3千克糖块平均装在6个盘子中,每个盘子中的糖块是糖块总量的,每盘糖块重千克。
10. 10
【分析】判定一个分数的单位看分母,分母是几,分数单位就是几分之一;最小的质数是2,用2减去原分数求出差,再看有几个这样的分数单位即可。
【解析】的分数单位是,最小的质数是2。
,里有10个。
因此的分数单位是,再加上10个这样的分数单位就是最小的质数。
11.384 512
【分析】根据正方体棱长总和公式:棱长总和=棱长×12,棱长=棱长总和÷12,代入数据,求出正方体的棱长;再根据正方体表面积公式:表面积=棱长×棱长×6,代入数据,求出正方体的表面积;根据正方体体积公式:体积=棱长×棱长×棱长,代入数据,求出正方体体积,据此解答。
【解析】96÷12=8(cm)
8×8×6
=64×6
=384(cm2)
8×8×8
=64×8
=512(cm3)
一个正方体的棱长总和是96cm ,这个正方体的表面积是384cm2,体积是512cm3。
12.120; n
【分析】(1)2的倍数:个位是2,4,6,8,0的数,3的倍数:各个数位数字之和能被3整除的数,5的倍数:个位是0或5的数,据此可知要满足既是2的倍数又是5的倍数,个位必须是0,这个数要最小,则这个数百位的数是1,结合3的倍数特征确定十位数字最小是几即可;
(2)根据m=3n可知m是n的3倍,存在倍数关系的两个数,它们的最大公因数是两个数中的较小数,据此解答。
【解析】据分析可知,这个三位数个位是0,百位是1,1+0=1,十位最小是3-1=2,这个最小的三位数是120;
m=3n,m是n的3倍,m和n的最大公因数是较小数n。
能同时被2,3,5整除的最小三位数是120;m和n都是非零自然数,如果m=3n,那么m和n的最大公因数是n。
13.132 80
【分析】已知长方体的长、宽、高,根据长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,代入数据计算求出它的表面积和体积。
【解析】(8×5+8×2+5×2)×2
=(40+16+10)×2
=66×2
=132(cm2)
8×5×2=80(cm3)
这个长方体的表面积是132cm2,体积是80cm3。
14.
【分析】把这项工程的工作总量看作单位“1”,要求20天完成,用1÷20求出平均每天完成这项工程的几分之几;
求7天完成这项工程的几分之几,就是求7占20的几分之几,用除法计算;
求19天完成这项工程的几分之几,就是求19占20的几分之几,用除法计算。
【解析】1÷20=
7÷20=
19÷20=
一项工程要求20天完成,平均每天完成这项工程的(),7天完成这项工程的(),19天完成这项工程的()。
15.11
【分析】根据从上面看到的图形可知,这个立体图形底下一层有9个正方体小块。再根据从前面看到的图形可知,上面一层至少有2个正方体小块。据此解题。
【解析】9+2=11(个)
所以,摆这个立体图形至少需要11个正方体小块。
16.√
【分析】可以用字母表示中间数为2a,根据偶数的特征分别表示出3个偶数,比它小的偶数是2a-2,比它大的偶数是2a+2,再相加计算即可。
【解析】2a-2+2a+2a+2=6a
6a是6的倍数,所以原题说法正确。
故答案为:√
17.×
【分析】切下米,分数后面加单位表示具体的长度,用总长度减去切下去的长度即可求出还剩下的长度。
【解析】3-=(米)
还剩下米,原题说法错误。
故答案为:×
18.×
【分析】能被2整除的数是偶数,不能被2整除的数叫做奇数;只有本身和1两个因数的数叫做质数,除了1和它本身之外还有其他因数的数是合数,1既不是质数也不是合数。据此判断。
【解析】由分析可知,在自然数中,除了奇数就是偶数,说法正确。1既不是质数也不是合数,所以除了质数、合数外还有1,后半句说法错误。
故答案为:×
19.×
【分析】在整数除法中如果被除数除以除数,商是整数而没有余数,我们就说被除数是除数的倍数,除数是被除数的因数。据此回答。
【解析】根据因数和倍数的意义可知,我们研究的因数和倍数是在整数除法范围之内的,不包括小数除法。所以题目中的说法是错误的。
故答案为:×
20.×
【分析】由a÷b=,可以把a看作1份,b看作5份;当a、b同时乘2、3、4……时,a÷b的商仍是,据此判断。
【解析】当a=1,b=5时,a÷b=;
当a=2,b=10时,a÷b==;
当a=3,b=15时,a÷b==;
……
所以,如果a÷b=,a不一定等于1, b不一定等于5。
原题说法错误。
故答案为:×
21.×
【分析】分数的分子和分母,同时乘或除以相同的数(0除外),分数的大小不变,据此分析。
【解析】根据分数的基本性质,一个分数的分子和分母同时乘10,分数的大小不变,原题说法错误。
故答案为:×
22.√
【分析】m-n=1(m、n均为非零自然数),说明m、n是两个相邻的非0的自然数,相邻的两个非0自然数是互质数,所以m、n的最大公因数是1。
【解析】由分析可知,如果m-n=1(m、n为非零自然数),那么m、n的最大公因数是1。例如:4-3=1,4和3互质,所以4和3的最大公因数是1。
所以原题说法正确。
故答案为:√
23.√
【分析】折线统计图是用点来表示数量的,通过用数据点的连线来表示数据的变化趋势,是以折线的上升或下降来表示统计数量的增减变化的统计图。
【解析】折线统计图是用点来表示数量的,以折线的上升或下降来表示统计数量的增减变化。
所以折线统计图用高低不同的点来表示数据多少,通过点与点的连线能看出数据的变化趋势。
故答案为:√
24.×
【分析】正方体表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长,正方体棱长扩大到原来的几倍,表面积扩大到原来的倍数×倍数,体积扩大到原来的倍数×倍数×倍数,据此分析。
【解析】3×3=9
3×3×3=27
正方体的棱长扩大到原来的3倍,那么它的表面积扩大到原来的9倍,体积扩大到原来的27倍,所以原题说法错误。
故答案为:×
25.A
【分析】分析题目,根据从前面看到与从上面看到的图形可知该几何体一共由4个小正方体组成,其中前排有3个,后排中间有1个,据此可知从左面看到的是左右并列的两个小正方形,据此解答。
【解析】
用同样大小的正方体摆成的物体,从前面看到,从上面看到,从左面看到的是。
故答案为:A
26.C
【分析】把3个相同的小长方体拼成了1个15cm高的大长方体,表面积减少了 48cm2 ,减少的面积是小长方体的4个底面面积,用48÷4,求出一个长方体的底面积,再用15÷3,求出一个长方体的高,再根据长方体体积=底面积×高,即可求出一个长方体的体积。
【解析】(48÷4)×(15÷3)
=12×5
=60(cm3)
那么原来1个小长方体的体积是60cm3。
故答案为:C
27.C
【分析】根据异分母分数加法法则:异分母分数相加,先通分,然后再计算,据此计算出算式“”的结果,再将计算结果再与箭头的位置对比即可。
【解析】
因为
所以的位置在1和2的正中间偏向左侧一点,即最接近的点为C。
故答案为:C
28.B
【分析】三角形的面积=底×高÷2,△ABP的面积=AB×高÷2。
当点P在AD边上运动时,底为AB、高是AP,△ABP的面积=AB×AP÷2(0<AP≤2),此时AP越来越大,所以△ABP的面积也越来越大;
当点P在DE边上运动时,底为AB、高不变,此时△ABP的面积也保持不变;
当点P在EF边上运动时,底为AB、高越来越小,此时△ABP的面积也越来越小;
当点P在FG边上运动时,底为AB、高不变,此时△ABP的面积也保持不变;
当点P在GB边上运动时,底为AB、高越来越小,此时△ABP的面积也越来越小。
综上所述,△ABP的面积的变化情况为:先是由小变大,再保持不变,然后逐渐变小,再保持不变,最后又逐渐变小。
据此逐选项进行分析即可解答。
【解析】A.表示先保持不变,再变小,然后保持不变再变小,不符合题意;
B.表示先是由小变大,再保持不变,然后逐渐变小,再保持不变,最后又逐渐变小,符合题意;
C.表示逐渐变大,再逐渐变小,然后保持不变,最后又逐渐变小,不符合题意;
D.表示先由小变大,再保持不变,然后逐渐变小,不符合题意。
所以的面积随着时间变化的图像大致是。
故答案为:B
29.A
【分析】5的倍数的特征,一个数的个位是0或5,这个数就是5的倍数;3的倍数的特征,各个数位的数字之和是3的倍数。据此可知,这个六位数各数位相加的和是3的倍数,又因数字是不等于0的且比10小的自然数,即不一定是5,则可知,这个六位数的个位上应是0,即。据此解答。
【解析】A.个位是 ,因此一定是 5 的倍数。各数位上的和是,一定是3的倍数,所以该数一定是3和5的公倍数。
B.个位是 不是, 不一定是5,因为这个数不一定是5的倍数,所以不符合题意。
C.个位是 ,因此一定是 5 的倍数。各数位上的和是,当时,不是3的倍数,所以不符合题意。
D.个位是 不是,不一定是5,因为这个数不一定是5的倍数,所以不符合题意。
故答案为:A
30.B
【分析】根据题意,把全程长度看作单位“1”,中点是全程的,离中点近,也就是与的差最小,所以用甲车行驶的路程与作差,用乙车行驶的路程与作差,然后比较它们的差,差小的近。
【解析】-=-=
-=-=
<
所以乙车离中点更近一些。
故答案为:B
31.A
【分析】将16个零件分成三组(5,5,6),先把两组5个放在天平两侧,若平衡,次品在剩余6个零件中;若不平衡,次品在较轻的5个中。
若次品在剩余6个零件中,将6个零件分成三组(2,2,2),先把两组2个放在天平两侧,若平衡,则次品在剩余2个中,若不平衡,次品在较轻的一组中;再把次品的一组放在天平两次,较轻的一边为次品;
若次品在第一次称的5个零件中,把5个零件分成(2,2,1)三组,把两组2个放在天平两侧,若平衡,剩下的为次品,若不平衡,次品在较轻的一侧;再把较轻的一侧的2个零件放在天平两侧,即可测出次品零件;至少需要3次才能保证找出次品。
【解析】根据分析可知,有16个零件,其中15个质量相同,有一个是轻一点的次品。如果用天平称,至少要称3次才能保证找到次品。
故答案为:A
32.C
【分析】正方体展开图有四大类型,分别是1-4-1型、1-3-2型、2-2-2型、3-3型。据此解题。
【解析】观察目前的正方体展开图,发现再在③的位置添一个面,就可成为正方体展开图的1-4-1型,就可补全这个正方体的展开图。
故答案为:C
33.A
【分析】分数的大小比较:分母相同的分数,分子大的分数大;分子相同的分数,分母小的分数大;分母不同的分数,先通分再比较。根据题意,三瓶同样的饮料,先比较谁喝的最少,那么他剩下的饮料最多。
【解析】
小星喝的最少,所以他剩下的饮料最多。
故答案为:A
34.C
【分析】设小正方形边长为1,求出长方形面积;阴影部分面积为两个三角形面积;根据三角形面积公式:面积=底×高÷2,据此求出阴影部分面积,再用阴影部分面积÷长方形面积,即可解答。
【解析】假设小正方形边长为1。
长方形面积:
1×1×5
=1×5
=5
阴影部分面积:
1×1÷2+1×1÷2
=1÷2+1÷2
=0.5+0.5
=1
1÷5=
长方形是用5个同样的正方形拼成的,阴影部分的面积之和占整个长方形的。
故答案为:C
35.;;;;
;;;
【解析】略
36.1;2;1
1;;11
【分析】(1)先把0.6转化为,再根据加法交换律进行简便运算。
(2)根据减法的运算性质,把算式转化为3-(+),先算括号里的加法,再算括号外的减法。
(3)根据减法的运算性质,把算式转化为-+,再根据加法交换律进行简便运算。
(4)根据加法交换律和加法结合律,把算式转化为(+)+(-),先分别计算括号里的加法和减法,再计算括号外的加法。
(5)通分后,先计算括号里的减法,再计算括号外的加法。
(6)根据加法交换律和加法结合律,把算式转化为(+)+(5.26+4.74),先分别计算括号里的加法,再计算括号外的加法。
【解析】++0.6
=++
=++
=1
3--
=3-(+)
=3-1
=2
-(-)
=-+
=+-
=2-
=1
++-
=(+)+(-)
=1+
=1
+(-)
=+(-)
=+
=
=
+5.26++4.74
=(+)+(5.26+4.74)
=1+10
=11
37.;;
【分析】根据等式的性质,方程两边同时加上,通分计算求解出x;
根据等式的性质,方程两边同时减去,通分计算求解出x;
根据等式的性质,方程两边同时加上x,方程两边交换位置,再同时减去,通分计算求解出x;
【解析】
解:
解:
解:
38.2532dm2,6688dm3;150dm2,113dm3
【分析】第一个组合体,通过平移,表面积=完整的大长方体表面积+小长方体前后左右4个面的面积和,长方体表面积=(长×宽+长×高+宽×高)×2,小长方体4个面的面积和=(长×高+宽×高)×2;体积=大长方体体积+小长方体体积,长方体体积=长×宽×高;
第二个组合体,挖去一个长方体,减少了3个面,又出现了同样的3个面,因此表面积=完整的正方体表面积,正方体表面积=棱长×棱长×6;体积=正方体体积-长方体体积,正方体体积=棱长×棱长×棱长,长方体体积=长×宽×高,据此列式计算。
【解析】第一个组合体:
表面积:(37×16+37×10+16×10)×2+(16×6+8×6)×2
=(592+370+160)×2+(96+48)×2
=1122×2+144×2
=2244+288
=2532(dm2)
体积:37×16×10=5920(dm3)
16×8×6=768(dm3)
5920+768=6688(dm3)
第二个组合体:
表面积:5×5×6=150(dm2)
体积:5×5×5-2×2×3
=125-12
=113(dm3)
第一个组合体的表面积是2532dm2,体积是5920dm3;第二个组合体的表面积是150dm2,体积是113dm3。
39.(1)(2)(3)见详解
【分析】(1)根据轴对称图形的意义:对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出三角形的关键对称点,依次连接即可。
(2)以点O圆心,画出半径是1cm的圆即可。
(3)根据旋转的特征,长方形绕点A逆时针旋转90°后,点A的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,得到旋转后的图形。
【解析】(1)如下图:
(2)如下图:
(3)如下图:
40.小洋
【分析】根据1时=60秒,把分转化为以秒为单位,再比较两人的用时,用时短的就更快。
【解析】(秒)
84<105
答:小洋更快。
41.140平方厘米
【分析】一个长方体,如果长减少2厘米,宽和高不变,它的体积减少48立方厘米,根据长方体的体积,得出左右面的面积是24平方厘米;同理得出上下面和前后面的面积,再根据长方体的表面积=(左面面积+前面面积+上面面积)×2。
【解析】48÷2=24(平方厘米)
99÷3=33(平方厘米)
52÷4=13(平方厘米)
(24+33+13)×2
=70×2
=140(平方厘米)
答:答:原长方体的表面积是140平方厘米。
42.600立方厘米
【分析】根据长方体的体积=底面积×高,得出底面积是400平方厘米。然后乘水面升高部分的高度(16.5-15)厘米就是苹果的体积。注意根据1升=1000毫升,1毫升=1立方厘米换算单位。
【解析】6升=6000毫升=6000立方厘米
6000÷15=400(平方厘米)
400×(16.5-15)
=400×1.5
=600(立方厘米)
答:苹果的体积是600立方厘米。
43.5米
【分析】在长方形操场长的方向上,相邻两面彩旗之间的距离×段数=50米,即间距是50的因数,同样的道理,间距也是35的因数,因此间距是50和35的公因数,又题目要求间距要最大,即找最大公因数即可。
【解析】50=2×5×5
35=5×7
所以50和35的最大公因数是5
即每两面彩旗之间的距离最大可以是5米。
答:每两面彩旗之间的距离最大可以是5米。
44.23人
【分析】第一批共2100个,王师傅比其他工人多加工7个,扣除这7个,则王师傅和其他工人加工的个数相同,即每人加工的个数×人数=2100-7=2093,即总人数是2093的因数,同样的道理,根据第二批和第三批,分别可知,总人数是1794和1587的因数,也就是这三个数的公因数,现要求人数最多,即找最大公因数,即可得出答案。
【解析】2100-7=2093
1800-6=1794
1600-13=1587
2093=7×13×23
1794=2×3×13×23
1587=3×23×23
所以2093,1794,1587的最大公因数是23
因此总人数为23个。
答:这批工人最多有23个。
45.120米
【分析】因为相邻两棵树之间的距离相等,并且在王村和张镇的中点、张镇和李庄的中点都要栽上树,所以相邻两树之间的距离能够整除王村和张镇以及张镇和李庄的一半距离,找出最大公因数即可。
【解析】1200÷2=600(米)
4320÷2=2160(米)
600=2×2×2×3×5×5
2160=2×2×2×2×3×3×3×5
所以600和2160的最大公因数是:2×2×2×3×5=120
即相邻两棵树之间的距离最多是120米。
答:相邻两棵树之间的距离最多是120米。
46.45米
【分析】甲乙两村一半的路程是225米,因为中点要栽树,因此间距×段数=225,则间距必须是225的因数,同样的道理,乙丙中点也要中,即间距也必须是630÷2=315的因数,也就是找225和315的公因数,又要求相邻两棵树之间的距离最多,即间距最大,也就是找最大公因数。
【解析】450÷2=225(米)
630÷2=315(米)
225=3×3×5×5
315=3×3×5×7
225和315的最大公因数是:3×3×5=45
所以相邻两棵树之间的间距最大是45米。
答:相邻两棵树之间的距离最多是45米。
47.(1)45000立方厘米
(2)3300平方厘米
【分析】(1)面板的底面是一个上底是10厘米、下底是20厘米、高是60厘米的梯形,根据梯形的面积=(上底+下底)×高÷2,求出直柱体的底面积,再根据直柱体的体积=底面积×高,求出面板的体积。
(2)面板涂色部分是前后面完全一样的梯形和左右面两个不同的长方形。根据梯形的面积=(上底+下底)×高÷2,长方形的面积=长×宽,代入数据计算,把这四个面的面积相加,求出需要涂色的面积即可。
【解析】(1)(10+20)×60÷2
=30×60÷2
=900(平方厘米)
900×50=45000(立方厘米)
答:一个面板的体积是45000立方厘米。
(2)(10+20)×60÷2×2+50×10+50×20
=30×60÷2×2+50×10+50×20
=1800+500+1000
=3300(平方厘米)
答:涂色部分的面积是3300平方厘米。
48.12厘米
【分析】已知一个封闭长方体容器的长为20厘米、宽为15厘米、水深6厘米,根据长方体的体积公式V=abh,求出水的体积;
如果把这个容器向右转,水的体积不变,但容器的底面变成(15×10),根据长方体的高h=V÷S,求出此时水的深度。
【解析】水的体积:
20×15×6
=300×6
=1800(立方厘米)
水深:
1800÷(15×10)
=1800÷150
=12(厘米)
答:里面的水深是12厘米。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
