2024-2025学年五年级下册数学期末高频易错押题提升卷(人教版)(含解析)
文档属性
| 名称 | 2024-2025学年五年级下册数学期末高频易错押题提升卷(人教版)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 566.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-25 22:03:05 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年五年级下册数学期末高频易错押题提升卷(人教版)
一、填空题
1.一个长方体的长是6.8厘米,宽是5厘米,高是4厘米,它的表面积是( )平方厘米,体积是( )立方厘米。
2.在2,5,0,8四个数字中任选三个组成的有因数3的最大数是( );同时是2,5的倍数的最小的数是( );2,3的公倍数有( )。
3.一项工作,甲用了0.35小时完成,乙用了小时完成,( )做得快些。
4.如图:指针从“12”绕点O顺时针旋转( )到“5”。指针从“2”绕点O顺时针旋转180°到( )。指针从“10”绕点O顺时针旋转90°到( )。
5.要将长分别为15cm、21cm、33cm的小棒截成同样长的小棒且不剩余,每根小棒最长( )cm。
6.观察左图,从( )面看到的图形是,从( )面看到的图形是,从( )面看到的图形是。
7.把一根长3m的铁丝平均分成5段,小明拿了其中的2段,每段长( ),小明拿的铁丝是这根铁丝的( )(填上合适的分数)。
8.实验小学开展“我是小小宣传员”公益活动,参加人员每16人分成一组,或者每12人分成一组,都正好分完,该校参加“我是小小宣传员”公益活动的学生至少有( )人。
9.去年重阳节那天,李宇涵用自己的压岁钱买了50kg桃,跟爸爸一起送到了敬老院,把这些桃平均分给10位老人,每位老人得到这些桃的,每位老人分到( )kg桃。
10.王伯伯的车牌号是鲁,其中△即是偶数又是质数;◎是最小的合数;◇是10以内最大的质数;☆是9的最大因数。王伯伯的车牌号是鲁( )。
11.如图所示,一段长方体木料的长是a厘米,宽是b厘米,高是h厘米。如果锯去m厘米高,则它的表面积减少( )平方厘米,体积减少( )立方厘米。
12.如图,由棱长是3和5的两个正方体搭成的图形,它的表面积是( ),体积是( )。
13.10件物品,其中一件是次品(略重些),用天平称至少要称( )次才能保证找出次品。
14.要在平地上挖一个长20米、宽8米、深50厘米的长方体土坑,一共要挖出( )方的土,土坑占地面积是( )平方厘米。
15.下图是一个长方体一个顶点处的3条棱(单位:cm)。用铁丝焊接这样一个框架,至少需要铁丝( )cm;给框架焊上铁皮,至少需要铁皮( );用做成的铁皮箱子装水,最多能装( )L。
二、判断题
16.两个数的乘积一定是这两个数的公倍数。( )
17.真分数都比1小,假分数都比1大。( )
18.把的分子加上20,要使分数大小不变,分母应乘5。( )
19.过山车是一种平移现象。( )
20.如果n是自然数,那么2n+1一定是奇数。( )
21.5个连续偶数的和是m,这些偶数中最大的数是m÷5+4。( )
22.在4.06m3、406000cm3、4060dm3、4060000cm3这4个数据中,4.06m3与其它3个数据不相等。( )
23.白兔有24只,是灰兔的,是把灰兔的只数看作单位“1”。( )
三、选择题
24.下面4个数都是四位数,T是比10小的自然数,M是0,下面4个数一定既是3的倍数又是5的倍数的数是( )。
A. B. C. D.
25.想要知道某市2024年5月份的气温变化情况,要搜集的数据是( )。
A.2024年各个季度平均气温 B.2024年各月平均气温
C.2024年5月每天的平均气温 D.2024年5月1日各时刻的气温
26.把一张长72cm,宽60cm的长方形纸,裁成同样大小、面积尽可能大的正方形纸,且纸无剩余,至少能裁( )张。
A.2 B.4 C.30 D.6
27.从3时15分到3时45分这段时间里,分针旋转了( )。
A.180° B.90° C.60° D.30°
28.在下面的分数中,( )不是最简真分数。
A. B. C. D.
29.把一个长8厘米,宽和高都是5厘米的长方体截成一个最大的正方体后,表面积( )。
A.减少110平方厘米 B.减少85平方厘米 C.减少60平方厘米
30.下面说法中,正确的一项是( )。
A.一个非零自然数,不是质数就是合数
B.把分数的分子和分母同时加上4,分数的大小不变
C.图形旋转时,它的位置、方向发生变化,大小不变
31.12个羽毛球特征相同,其中只有一个质量异常。现在要用一架没有砝码的天平去称,至少要称( )次才能找出那个质量异常的羽毛球。
A.4 B.3 C.2 D.1
32.下图是一个立体图形从正面、右面看到的形状。要搭成这样的立体图形,最多可以用( )个小方体。
A.6 B.7 C.8 D.9
33.把写有1、2、3、4、5、6、7、8、9、10数字卡片装入盒子中,任意摸出1张,摸到下面选项中( )可能性最小。
A.偶数 B.奇数 C.质数 D.合数
四、计算题
34.直接写出结果。
35.计算下面各题,能简算的要简算。
+- +++ 7.25-(1.25+)
-(+) 1.75-+1.25- -0.6-
36.解方程。
+﹦ -﹦1-
37.计算下面立体图形的表面积和体积。(单位:厘米)
五、作图题
38.请按要求在如图方格上画图并涂上阴影。
(1)以直线L为对称轴,画出下面图形的另一半。
(2)再将整个图形向右平移5格。
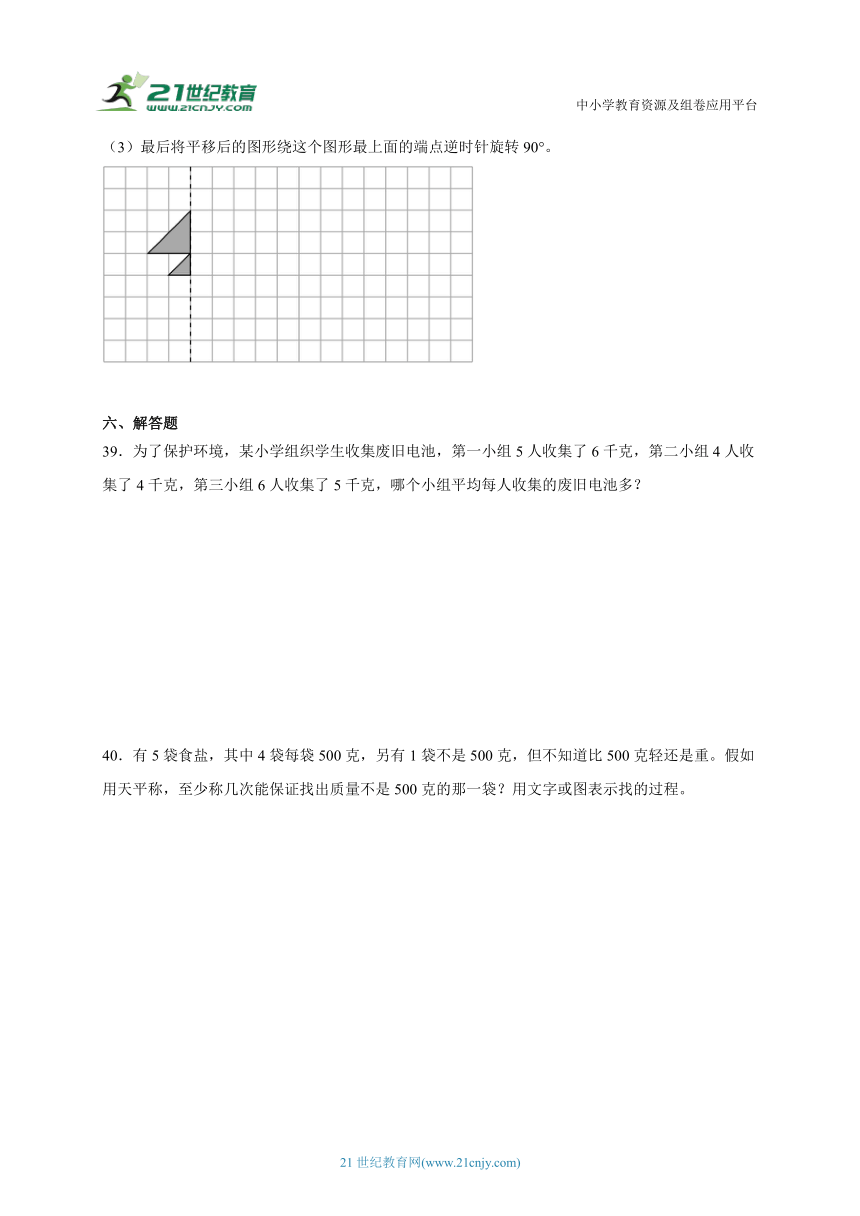
(3)最后将平移后的图形绕这个图形最上面的端点逆时针旋转90°。
六、解答题
39.为了保护环境,某小学组织学生收集废旧电池,第一小组5人收集了6千克,第二小组4人收集了4千克,第三小组6人收集了5千克,哪个小组平均每人收集的废旧电池多?
40.有5袋食盐,其中4袋每袋500克,另有1袋不是500克,但不知道比500克轻还是重。假如用天平称,至少称几次能保证找出质量不是500克的那一袋?用文字或图表示找的过程。
41.厦门市某购物中心要将一批垃圾桶(不到100个)平均分配到各个垃圾投放点,每个垃圾投放点放2个或3个或5个垃圾桶,都能正好分完。这批垃圾桶最多有多少个?
42.小兵在文具店买了3本笔记本、1支钢笔、2支自动铅笔和4块橡皮。笔记本每本2元,钢笔每支5元,自动铅笔和橡皮的价格小兵记不清了售货员要小兵付18元,小兵马上说售货员把账算错了,你知道为什么吗?
43.实践课上,老师布置了一个任务:已知一个长和宽均为8分米的长方体透明鱼缸(厚度忽略不计),鱼缸内水深5分米。聪聪将一个长6分米、宽4分米的长方体石块竖直立入鱼缸中(接触面之间无缝隙),并记录水位变化。石块放入后,水面迅速上升,聪聪惊呼:“现在水的高度是多少呢?”结合以前你所学知识,帮助聪聪解决这个问题。
44.为响应国家“体重管理年”的号召,小胖一家坚持进行体育锻炼。爸爸绕湖走一圈要用12分钟,爷爷绕湖走一圈要用24分钟,小胖绕湖走一圈要用18分钟。如果三人同时从同一起点沿同一方向出发,至少多少分钟后小胖和爷爷在起点处再次相遇?此时爸爸走了几圈?
45.“度量衡”是我国古代计量长度、容积、质量的标准或器具的统称。“度”用以计量长短;“量”用以测量容积大小;“衡”用以测量物体轻重。“商鞅变法”的重要物证——商鞅方升(如下图),就是“度量衡”中的“量”。它全长18.7厘米,内口长约12.5厘米、宽约7厘米、深约2.3厘米。它的容积便是商鞅规定的“一升”。算一算,商鞅规定的“一升”大约相当于现在的多少升?(得数保留一位小数)
46.学了体积后,妈妈拿出一块不规则的土豆问小华,你能算出它的体积吗?小华想了想,找来一个从里面量长12厘米,宽10厘米,高15厘米的长方体容器,里面水深8厘米,放入土豆后,土豆全部浸没在水中,水面上升到9.5厘米,你能帮小华算出土豆的体积是多少立方厘米?
47.在一块长方形铁皮的两个角上各剪掉一个边长为10厘米的小正方形,并把剪下的两个小正方形焊接到长方形的另一边的中间(如图),然后制成一个无盖的长方体盒子。这个盒子的体积是多少立方分米?(软皮的损耗不计)
48.一个长方体容器装有45升的水,将一个铁球浸没在水中时,容器内的水深达到5.7分米。如果再放入一个体积为3.2立方分米的铁球,这个长方体容器里的水会溢出来吗?(请通过计算说明)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.162.4 136
【分析】根据长方体的表面积=(长×宽+长×高+宽×高)×2、长方体的体积=长×宽×高,代入数据即可解答。
【解析】(6.8×5+6.8×4+5×4)×2
=(34+27.2+20)×2
=81.2×2
=162.4(平方厘米)
6.8×5×4=136(立方厘米)
长方体的表面积是162.4平方厘米,体积是136立方厘米。
2.852 250 852,582,528,258
【分析】3的倍数的特征:一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。既是2的倍数又是5的倍数的特征:个位上的数字是0的数,既是2的倍数,又是5的倍数。既是2的倍数又是3的倍数的特征:个位上的数字是0、2、4、6、8,各个数位上的数字的和是3的倍数的数。
从题意可知:在2,5,0,8四个数字中选取3个数字,且数字和是3的倍数的只有2,5,8。即2+5+8=18,将2,5,8三个数字从大到小排列,即可组成的有因数3的最大数。将2,5,8三个数字组成的3的倍数中,个位上是2或8,这个就是2,3的公倍数。
同时是2,5的倍数的个位上的数字一定是0,与较小的2和5组成最小的数即可。
【解析】在2,5,0,8四个数字中任选三个组成的有因数3的最大数是852;同时是2,5的倍数的最小的数是250;2,3的公倍数有852,582,528,258。
3.甲
【分析】比较两人用的时间,同样一项工作,用时越少速度越快。小数和分数比大小,将分数化成小数再比较,分数化小数,直接用分子÷分母即可。
【解析】=11÷25=0.44、0.35小时<小时,甲做得快些。
4.150°/150度 8 1
【分析】决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度。钟面指针的转动方向是顺时针方向,钟面1个大格是30°,据此通过转动的大格数确定旋转度数,旋转度数÷30°=转动的大格数,据此分析。
【解析】30°×5=150°,指针从“12”绕点O顺时针旋转150°到“5”。
180°÷30°=6(格),2+6=8(格),指针从“2”绕点O顺时针旋转180°到8。
90°÷30°=3(格),从10开始顺时针方向数3大格子,即指针从“10”绕点O顺时针旋转90°到1。
5.3
【分析】将不同长度的3根小棒截成同样长的小棒且不剩余,每根小棒最长应该是3根小棒长度的最大公因数,全部共有的质因数(公有质因数)相乘的积就是这几个数的最大公因数。
【解析】15=3×5
21=3×7
33=3×11
15、21和33的最大公因数是3。
每根小棒最长3cm。
6.上 左 正/前
【分析】从上面看有2行,前边1行4个小正方形,后边1行靠右1个小正方形;从左面看有2列,左边1列3个小正方形,右边1列1个小正方形;从正面看有3行,下边1行4个小正方形,中间1行左边1个小正方形右边2个小正方形,最上边1行右数第二个位置有1个小正方形,据此分析。
【解析】
从上面看到的图形是,从左面看到的图形是,从正面看到的图形是。
7./0.6
【分析】分析题目,把这根铁丝看作单位“1”,用铁丝的总长度除以分成的段数即可得到每段长多少米;再用分成的总段数除以小明拿的段数即可得到小明拿的铁丝是这根铁丝的几分之几。
【解析】3÷5=(m)
2÷5=
把一根长3m的铁丝平均分成5段,小明拿了其中的2段,每段长,小明拿的铁丝是这根铁丝的(填上合适的分数)。
8.48
【分析】根据题意,每16人分成一组,或者每12人分成一组,都正好分完,说明参加公益活动的最少学生人数是16和12的最小公倍数。
先把16和12分解质因数,再把它们的公有质因数和各自独有质因数的连乘积就是它们的最小公倍数。
【解析】16=2×2×2×2
12=2×2×3
16和12的最小公倍数是:2×2×2×2×3=48
该校参加“我是小小宣传员”公益活动的学生至少有48人。
9.;5
【分析】把桃的总质量看作单位“1”,把这些桃平均分给10位老人,相当于平均分成10份,用1除以10,即是每位老人得到这些桃的几分之几;
把50kg的桃平均分给10位老人,用桃的总质量除以10,即是每位老人分到桃的质量。
【解析】1÷10=
50÷10=5(kg)
每位老人得到这些桃的(),每位老人分到(5)kg桃。
10.2479
【分析】一个数,如果只有1和它本身两个因数,那么这样的数叫做质数。
一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。
整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身。
【解析】王伯伯的车牌号是鲁,
其中△即是偶数又是质数,即2;
◎是最小的合数,即4;
◇是10以内最大的质数,即7;
☆是9的最大因数,即9;
所以,王伯伯的车牌号是鲁(2479)。
11.2am+2bm abm
【分析】根据题意,一段长方体木料锯去m厘米高,则减少的表面积是4个侧面的面积,即2个长为a厘米、宽为m厘米的长方形的面积与2个长为b厘米、宽为m厘米的长方形的面积之和;根据“长方形的面积=长×宽”求出减少的表面积;
减少的体积是长为a厘米、宽为b厘米、高为m厘米的长方体的体积;根据“长方体的体积=长×宽×高”求出减少的体积。
【解析】a×m×2+b×m×2=(2am+2bm)(平方厘米)
a×b×m=abm(立方厘米)
填空如下:
则它的表面积减少(2am+2bm)平方厘米,体积减少(abm)立方厘米。
12.186 152
【分析】通过平移,将小正方体上面的面平移到下面,它的表面积=大正方体的表面积+小正方体1个面的面积×4,正方体表面积=棱长×棱长×6;它的体积=大正方体的体积+小正方体的体积,正方体体积=棱长×棱长×棱长,据此列式计算。
【解析】5×5×6+3×3×4
=150+36
=186()
5×5×5+3×3×3
=125+27
=152()
它的表面积是186,体积是152。
13.3
【分析】找次品的最优策略:一是把待测物品分成2份或3份;二是要尽量平均分,不能平均分的,应该使多的一份与少的一份只相差1,这样不但能保证找出次品,而且称的次数一定最少,据此解答。
【解析】有10件物品,其中有一件是次品,比其它略重。
第一次称重:先分成两份,天平两边各放5件,次品在较重的5件中;
第二次称重:把5件分成2件,2件和1件,天平两边各放2件,①若天平平衡,则次品就是剩下的1件;②若天平不平衡,次品就在较重的那2件中;
第三次称重:把较重的2件分成两份,天平两边各放1件,次品就是较重的1件。
10件物品,其中一件是次品(略重些),用天平称至少要称3次才能保证找出次品。
14.80 1600000
【分析】第一问就是要求长方体的体积,根据1方=1立方米,先把50厘米转化为0.5米,再根据,代入数据计算后把单位转化为方即可。
第二问就是要求长方体的底面积,土坑占地面积是一个长是20米,宽是8米的长方形,根据长方形的面积=长×宽,代入数据计算,再根据1平方米=10000平方厘米,把单位转化为平方厘米即可。
【解析】50厘米=0.5米
(立方米)=80(方)
(平方米)=1600000(平方厘米)
要在平地上挖一个长20米、宽8米、深50厘米的长方体土坑,一共要挖出80方的土,土坑占地面积是1600000平方厘米。
15.40 66 0.036
【分析】分析题目,一个顶点处的三条棱就是长方体的一组长宽高,据此根据长方体的棱长总和=(长+宽+高)×4,长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,代入数据计算即可,注意体积单位要根据1L=1000mL=1000cm3换算成L。
【解析】(4+3+3)×4
=10×4
=40(cm)
(4×3+4×3+3×3)×2
=(12+12+9)×2
=33×2
=66(cm2)
4×3×3
=12×3
=36(cm3)
36cm3=36mL=0.036L
用铁丝焊接这样一个框架,至少需要铁丝40cm;给框架焊上铁皮,至少需要铁皮66cm2;用做成的铁皮箱子装水,最多能装0.036L。
16.√
【分析】只在自然数(零除外)范围内研究倍数和因数。研究两个数的公倍数,说明这两个数都是非零自然数。两个或多个整数公有的倍数叫做它们的公倍数,据此举例说明即可。
【解析】两个数的乘积一定是这两个数的公倍数说法正确。如3×2=6,6是3和2的公倍数;4÷6=24,24是4和6的公倍数;8×2=16,16是8和2的公倍数……
故答案为:√
17.×
【分析】分子比分母小的分数叫作真分数,真分数小于1;分子比分母大或分子和分母相等的分数叫作假分数,假分数大于或者等于1,据此解答。
【解析】分析可知,真分数都比1小,如<1;假分数可能比1大,如>1,假分数也可能等于1,如=1,所以题目说法不正确。
故答案为:×
18.×
【分析】的分子加上20后,变为24,分子相当于乘6,根据分数的基本性质,分子、分母同时乘或除以同一个不为0的数,分数的大小不变;要使分数的大小不变,分母也应乘6。据此解答。
【解析】4+20=24
24÷4=6 ,相当于分子乘6,要使分数大小不变,其分母也要乘6。原说法错误。
故答案为:×
19.×
【分析】过山车的运动的过程中,要转几个圈,转圈的过程是绕一点作圆周运动,属于旋转,也有一段作的是直线运动,属于平移,据此解答。
【解析】过山车是一种平移现象,这句话说法不对。
故答案为:×
20.√
【分析】整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数,可以举例,据此判断即可。
【解析】n为奇数:2×1+1=2+1=3,3是奇数;
n为偶数:2×2+1=4+1=5,5是奇数。
如果n是自然数,那么2n+1一定是奇数,原题说法正确。
故答案为:√
21.√
【分析】由于5个连续的偶数和是m,由于相邻的两个偶数的和相差2,可知5个连续偶数的和其实相当于5个中间数的和,即用和除以5即可求出中间的数,由于最大的数比中间的数大4,用据此即可列式。
【解析】由分析可知:
5个连续偶数的和是m,这些偶数中最大的数是m÷5+4。原题说法正确。
故答案为:√
22.×
【分析】根据1 m3=1000 dm3,1 dm3=1000 cm3,高级单位换算成低级单位,乘进率,低级单位换算成高级单位,除以进率。先将所有数据都换算成以dm3为单位,再比较即可判断。
【解析】因为:4.06m3=4060 dm3
406000cm3=406 dm3
4060000cm3=4060 dm3
所以:4.06m3=4060 dm3=4060000cm3
4.06m3≠406000 dm3
在4.06m3、406000cm3、4060dm3、4060000cm3这4个数据中,4.06m3与4060dm3、4060000cm3相等,4.06m3与406000cm3不相等。因此原题说法不正确。
故答案为:×
23.√
【分析】一般把“的”字之间的物体看作单位“1”,或者平均分得是谁谁就是单位“1”;据此判断即可。
【解析】由分析可知:
白兔有24只,是灰兔的,是把灰兔的只数看作单位“1”。说法正确。
故答案为:√
24.D
【分析】要判断这四个选项中的数哪个一定既是3的倍数又是5 的倍数,需要分别根据3和5的倍数特征来对每个选项进行分析。5的倍数特征是个位是0或5,3的倍数特征是一个数的各位数之和是3的倍数,这个数就是3的倍数。
【解析】A.当T=5时,它是5的倍数。此时这个数各位数之和为5+5+5+5=20。根据3的倍数特征,因为20÷3=6……2,20 不能被3整除,所以 20 不是3的倍数,那么这个数不是的倍数,所以该选项不符合题意。
B.个位上是M,已知M=0,根据5的倍数特征,个位是 0,所以它是5的倍数。再看它是否为3的倍数,这个数各位数之和为T+0+T+0=2T。只有当T是3、6、9时,2T分别为2×3=6、2×6=12、2×9=18,6、12、18 是3的倍数此时这个数才是3的倍数。当T取其他值时,比如T=1,2×1=2,2不是3的倍数,所以它不一定是3的倍数,该选项不符合题意。
C.要成为5的倍数,个位T需为 5,此时这个数各位数之和为5+5+0+5=15。因为15÷3=5,15 能被3整除,所以当T=5时它是3的倍数。但当T取其他值时,比如T=1,个位不是 5,不是 5的倍数,所以它不一定既是3的倍数又是 5的倍数,C该选项不符合题意。
D.由于M=0,根据5的倍数特征,个位是 0,所以它是5的倍数。这个数各位数之和为T+T+T+0=3T,因为T是1、2、3、4、5、6、7、8、9中任意一个数,3T÷3=T,3T一定能被3整除,所以它一定是3的倍数。因此它一定既是3的倍数又是5的倍数。该选项符合题意。
故答案为:D
25.C
【分析】根据题意,要知道的是某市2024年5月份的气温变化情况,那么搜集的数据应该能够反映出这个月内气温的每日变化,而不是某个时间点或更长时间段的数据。
【解析】A.2024年各个季度平均气温,一年有4个季度,各个季度的数据范围太大了,无法具体看出5月份的气温变化情况,不符合题意;
B.2024年各月平均气温,一年有12个月,可以看出不同月份的平均气温,但不是5月份的气温变化情况,不符合题意;
C.2024年5月每天的平均气温,每天的数据能详细展示一个月内气温的变化情况,符合题意;
D.2024年5月1日各时刻的气温,只能看出这一天的气温变化,无法反映整个月的情况,不符合题意。
故答案为:C
26.C
【分析】把一块长方形纸裁成同样大小、面积尽可能大的正方形,且没有剩余,说明正方形的边长是长、宽的最大公因数,把72、60分解质因数后,把公有的相同质因数乘起来就是最大公因数,即是正方形的最大边长。再看长、宽里面分别有几个这样的最大公因数,最后相乘,即可求出至少能裁的张数。
【解析】72=2×2×2×3×3
60=2×2×3×5
72和60的最大公因数是:2×2×3=12
即正方形的边长最大是12cm。
72÷12=6(张)
60÷12=5(张)
一共:6×5=30(张)
至少能裁30张。
故答案为:C
27.A
【分析】一个钟面平均分成60小格,分针走1小格表示1分钟,分针走一圈是60分钟,一圈是360°,分针走1小格是(360÷60)°;从3时15分到3时45分,分针共走了(45-15)分钟,再乘每小格的度数即可。
【解析】3时45分-3时15分=30(分钟)
360°÷60=6°
6°×30=180°
分针旋转了180°。
故答案为:A
28.C
【分析】分子比分母小的分数叫做真分数;真分数<1。分子比分母大或分子和分母相等的分数叫做假分数;假分数≥1。
最简分数是指分子和分母只有公因数1的分数。
【解析】A.<1,且24和25是互质数,所以是最简真分数;
B.<1,且7和8是互质数,所以是最简真分数;
C.>1,==,所以不是最简真分数;
D.<1,且4和21是互质数,所以是最简真分数。
故答案为:C
29.C
【分析】根据正方体的特征可知,把这个长方体截成一个最大的正方体,这个正方体的棱长为5厘米,减少的面积相当于长为5厘米、宽为(8-5)厘米的4个小长方形的面积,根据长方形面积公式解答。
【解析】5×(8-5)×4
=5×3×4
=60(平方厘米)
把一个长8厘米,宽和高都是5厘米的长方体截成一个最大的正方体后,表面积减少60平方厘米。
故答案为:C
30.C
【分析】1既不是质数也不是合数;分数的分子和分母同时乘或除以相同的数(0除外)大小不变;图形旋转时形状大小不变,但是位置方向会变化,据此解答。
【解析】A.非零自然数中的1,既不是质数也不是合数,所以该项错误;
B.分数的分子和分母同时加上4,分数的大小会发生变化,如分数不等于变化后的分数,所以该项错误;
C.图形旋转时,它的位置、方向发生变化,大小不变,所以该项正确。
故答案为:C
31.A
【分析】根据题意,12个羽毛球特征相同,其中只有一个质量异常,但不知轻重,分组称重时,考虑天平平衡或不平衡时的各种情况,逐一讨论,得出至少称的次数。
【解析】第1次称量,将12个羽毛球平均分为三份①②③(每份4个),先把①和②放在天平的两边,如果天平平衡,则③里面有异常球;如果天平不平衡,则①和②中有异常羽毛球,③都是正常羽毛球;第2次称量,把①和②中的任意一份取下来,把③放上去,即可判断异常羽毛球在哪一份里,并且知道异常羽毛球的轻重;第3次称量,把有异常羽毛球的4个球平均分成两份(每份2个),把它们放在天平的两边,天平不平衡,根据轻重,判断出异常羽毛球在哪一份里;第4次称量,再把有异常羽毛球的2个球分成两份(每份1个),把它们放在天平的两边,天平不平衡,根据轻重,判断出异常羽毛球是哪一个。
所以至少要称4次才能找出那个质量异常的羽毛球。
故答案为:A
32.D
【分析】根据从正面和右面看到的形状可知,这个立体图形有2层2排,上层只有1个小正方体,且在前一排;下层最多有8个小正方体,每排4个;据此得出搭这个立体图形最多可用(1+8)个小正方体。
【解析】如图:
最多可以用9个小方体。
故答案为:D
33.C
【分析】1~10的数中:2、4、6、8、10是偶数;1、3、5、7、9是奇数;2、3、5、7是质数;4、6、8、9、10是合数;数字出现的次数越少,即被摸出的可能性最小,据此作答。
【解析】由分析可知:
1~10的数中,其中偶数有5个,奇数有5个,质数有4个,合数有5个,因此抽到质数的可能性最小。
故答案为:C
34.;2;;;1
;;;;
【解析】略
35.;;;
;2;
【分析】(1)按照从左往右的顺序,先计算+,再计算这个算式的结果与的差;
(2)先利用加法交换律把算式转化为+++,再利用加法结合律计算同分母分数加法;
(3)先利用减法性质a-(b+c)=a-b-c计算小数减法,再计算整数与分数的差;
(4)先利用减法性质a-(b+c)=a-b-c去掉括号,再利用减法性质a-b-c=a-c-b计算同分母分数减法,最后计算异分母分数减法-;
(5)先利用加法交换律把算式转化为1.75+1.25--,再计算小数加法的和并利用减法性质a-b-c=a-(b+c)计算同分母分数加法;
(6)先把0.6转化为,再利用减法性质a-b-c=a-(b+c)计算同分母分数加法,最后计算分数与整数的差。
【解析】(1)+-
=-
=
(2)+++
=+++
=(+)+(+)
=1+
=
(3)7.25-(1.25+)
=7.25-1.25-
=6-
=
(4)-(+)
=--
=--
=-
=
(5)1.75-+1.25-
=1.75+1.25--
=3--
=3-(+)
=3-1
=2
(6)-0.6-
=--
=-(+)
=-1
=
36.x=;x=;x=1
【分析】+﹦,根据等式的性质1,方程两边同时减去即可。
-﹦1-,先计算出方程右边1-的差,再根据等式的性质1,方程两边同时加上即可。
2x-=,根据等式的性质1,方程两边同时加上,再根据等式的性质2,方程两边同时除以2即可。
【解析】+﹦
解:+-﹦-
x=-
x=
-﹦1-
解:-﹦
-+﹦+
x=
2x-=
解:2x-+=+
2x=2
2x÷2=2÷2
x=1
37.表面积330平方厘米;体积370立方厘米
【分析】观察可知,立体图形的表面积等于大正方体的表面积加上小正方体的侧面积(即4个小正方形的面积),根据,计算即可;立体图形的体积等于大正方体的体积加小正方体的体积,根据,计算即可。
【解析】表面积:
(平方厘米)
体积:
(立方厘米)
立体图形的表面积是330平方厘米;体积是370立方厘米。
38.(1)(2)(3)见详解
【分析】(1)根据轴对称图形的画法,以直线L为对称轴,找出轴对称图形的任意一组对称点,连接对称点;画出对称点所连线段的中心,沿着中心作这条线段的垂线,就可以得到该图形的对称轴;
(2)根据图形平移的方法,将图形的顶点向右平移5格,然后再连线成图即可;
(3)根据旋转的方法,最上面的端点不动,将平移后的图形每条边绕这个图形最上面的端点逆时针旋转90°即可。
【解析】(1)(2)(3)作图如下:
39.第一小组
【分析】先用各小组收集废旧电池的质量除以小组人数,求出各小组每人收集废旧电池的质量;再根据分数大小比较的方法进行比较,得出哪个小组平均每人收集的废旧电池多。
真分数<1,假分数≥1,则假分数>真分数。
【解析】6÷5=(千克)
4÷4=1(千克)
5÷6=(千克)
>1>
答:第一小组平均每人收集的废旧电池多。
40.3次;过程见解答
【分析】根据天平的平衡原理对托盘两边的物品进行比较,把待测物品分成三份,要分得尽量平均,能够均分的就平均分成3份,不能平均分的,也应该使多的一份与少的一份只相差1。因为不知道次品偏轻还是偏重,所以要先用天平称一次,确定哪个物品不是次品,用这个物品和可能是次品的物品进行比较,进而找出次品。
【解析】把5袋食盐依次标号为①、②、③、④、⑤。用天平称,第一次称,左边放①、②,右边放③、④,天平外是⑤。如果平衡,那么⑤就是次品;如果不平衡,那么次品在①—④中,⑤不是次品。
第二次称,在①—④中任取2袋,例如取①和③,分别放在天平两边称。如果不平衡,那么次品在这2袋中,然后天平一边仍然放①,另一边换成⑤,由于⑤不是次品,所以这时如果天平平衡,那么①不是次品,③是次品;如果天平不平衡,那么①就是次品。
如果天平上①与③平衡,那么次品是②或④,第三次称,此时称一下②和⑤,如果天平平衡,那么④是次品;如果天平不平衡,那么②是次品。
至少称3次能保证找出质量不是500克的那一袋。
41.90个
【分析】由“每个垃圾投放点放2个或3个或5个垃圾桶,都能正好分完”可知,这批垃圾桶的数量是2、3、5的公倍数,这个公倍数接近100且小于100,所以可先找2、3、5的最小公倍数,再找出这个公倍数的倍数中接近100且小于100的数即可得解。
【解析】2、3、5的最小公倍数是:
30的倍数有:30、60、90、120……
90接近100且小于100
答:这批垃圾桶最多有90个。
42.见详解
【分析】从题意可以知道,四种商品的数量已知,根据,笔记本和钢笔的价格能够算出来一共是11元,但是因为自动笔和橡皮的数量是双数,所以,不管买多少,它们的总价格也应该是双数,因为偶数乘偶数,偶数乘奇数积都是偶数,而11是奇数,根据奇数加偶数等于奇数,因此,要付款的钱数应是奇数,但是根据售货员算的价格是偶,所以判断是错误的。
【解析】
(元)
答:因为2支自动铅笔和4块橡皮的价格是偶数,而3本笔记本、1支钢笔的价格是奇数,根据奇数加偶数等于奇数可知,总价应该是奇数,而售货员算的是18元(偶数),所以账算错了。
43.8分米
【分析】已知长方体鱼缸长和宽均为8分米,水深5分米,根据长方体的体积=长×宽×高,求出水的体积;
将一个长6分米、宽4分米的长方体石块竖直立入鱼缸中,石块占据部分底面积,导致水的底面积变成(8×8-6×4)平方分米,水的体积不变,根据长方体的高=体积÷底面积,求出此时水的高度。
【解析】8×8×5
=64×5
=320(立方分米)
8×8-6×4
=64-24
=40(平方分米)
320÷40=8(分米)
答:现在水的高度是8分米。
44.72分钟;6圈
【分析】当两人在起点再次相遇时,所用时间一定是他们各自走一圈所用时间的公倍数,要求至少多少分钟后再次相遇,就是求他们走一圈所用时间的最小公倍数;已知爸爸绕湖走一圈要用12分钟,用24和18的最小公倍数除以12就是此时爸爸走的圈数。
【解析】24=2×2×2×3
18=2×3×3
所以24和18的最小公倍数是72。
72÷12=6(圈)
答:至少72分钟后小胖和爷爷在起点处再次相遇,此时爸爸走了6圈。
45.0.2升
【分析】本题求商鞅规定的“一升”相当于现在的多少升,关键是先算其容积再换算单位。已知内口长约12.5厘米、宽约7厘米、深约2.3厘米,根据“长方体体积(容积)=长×宽×高”计算出长方体容积;然后将立方厘米换算为立方分米,再换算为升;最后根据题目要求按“四舍五入”原则保留一位小数。
【解析】12.5×7×2.3
=87.5×2.3
=201.25(立方厘米)
201.25立方厘米=0.20125立方分米=0.20125升
0.20125升≈0.2升
答:商鞅规定的“一升”大约相当于现在的0.2升。
46.180立方厘米
【分析】分析题目,土豆的体积等于一个长是12厘米,宽是10厘米,高是(9.5-8)厘米的长方体的体积,根据长方体的体积=长×宽×高代入数据列式计算即可。
【解析】12×10×(9.5-8)
=12×10×1.5
=120×1.5
=180(立方厘米)
答:土豆的体积是180立方厘米。
47.10立方分米
【分析】看图可知,制成的长方体盒子的长=(60-10)厘米,宽=(40-10×2)厘米,高=10厘米,根据长方体体积=长×宽×高,列式解答即可。根据1立方分米=1000立方厘米,统一单位。
【解析】60-10=50(厘米)
40-10×2
=40-20
=20(厘米)
50×20×10=10000(立方厘米)=10(立方分米)
答:这个盒子的体积是10立方分米。
48.会
【分析】由题意可知,容器内无水部分可以看作一个长方体,长方体的长和宽都是3分米,高为(6-5.7)分米,根据“长方体的体积=长×宽×高”求出无水部分的体积,最后和铁球的体积比较大小,即可求得。
【解析】3×3×(6-5.7)
=3×3×0.3
=9×0.3
=2.7(立方分米)
因为3.2立方分米>2.7立方分米,所以水会溢出来。
答:这个长方体容器里的水会溢出来。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年五年级下册数学期末高频易错押题提升卷(人教版)
一、填空题
1.一个长方体的长是6.8厘米,宽是5厘米,高是4厘米,它的表面积是( )平方厘米,体积是( )立方厘米。
2.在2,5,0,8四个数字中任选三个组成的有因数3的最大数是( );同时是2,5的倍数的最小的数是( );2,3的公倍数有( )。
3.一项工作,甲用了0.35小时完成,乙用了小时完成,( )做得快些。
4.如图:指针从“12”绕点O顺时针旋转( )到“5”。指针从“2”绕点O顺时针旋转180°到( )。指针从“10”绕点O顺时针旋转90°到( )。
5.要将长分别为15cm、21cm、33cm的小棒截成同样长的小棒且不剩余,每根小棒最长( )cm。
6.观察左图,从( )面看到的图形是,从( )面看到的图形是,从( )面看到的图形是。
7.把一根长3m的铁丝平均分成5段,小明拿了其中的2段,每段长( ),小明拿的铁丝是这根铁丝的( )(填上合适的分数)。
8.实验小学开展“我是小小宣传员”公益活动,参加人员每16人分成一组,或者每12人分成一组,都正好分完,该校参加“我是小小宣传员”公益活动的学生至少有( )人。
9.去年重阳节那天,李宇涵用自己的压岁钱买了50kg桃,跟爸爸一起送到了敬老院,把这些桃平均分给10位老人,每位老人得到这些桃的,每位老人分到( )kg桃。
10.王伯伯的车牌号是鲁,其中△即是偶数又是质数;◎是最小的合数;◇是10以内最大的质数;☆是9的最大因数。王伯伯的车牌号是鲁( )。
11.如图所示,一段长方体木料的长是a厘米,宽是b厘米,高是h厘米。如果锯去m厘米高,则它的表面积减少( )平方厘米,体积减少( )立方厘米。
12.如图,由棱长是3和5的两个正方体搭成的图形,它的表面积是( ),体积是( )。
13.10件物品,其中一件是次品(略重些),用天平称至少要称( )次才能保证找出次品。
14.要在平地上挖一个长20米、宽8米、深50厘米的长方体土坑,一共要挖出( )方的土,土坑占地面积是( )平方厘米。
15.下图是一个长方体一个顶点处的3条棱(单位:cm)。用铁丝焊接这样一个框架,至少需要铁丝( )cm;给框架焊上铁皮,至少需要铁皮( );用做成的铁皮箱子装水,最多能装( )L。
二、判断题
16.两个数的乘积一定是这两个数的公倍数。( )
17.真分数都比1小,假分数都比1大。( )
18.把的分子加上20,要使分数大小不变,分母应乘5。( )
19.过山车是一种平移现象。( )
20.如果n是自然数,那么2n+1一定是奇数。( )
21.5个连续偶数的和是m,这些偶数中最大的数是m÷5+4。( )
22.在4.06m3、406000cm3、4060dm3、4060000cm3这4个数据中,4.06m3与其它3个数据不相等。( )
23.白兔有24只,是灰兔的,是把灰兔的只数看作单位“1”。( )
三、选择题
24.下面4个数都是四位数,T是比10小的自然数,M是0,下面4个数一定既是3的倍数又是5的倍数的数是( )。
A. B. C. D.
25.想要知道某市2024年5月份的气温变化情况,要搜集的数据是( )。
A.2024年各个季度平均气温 B.2024年各月平均气温
C.2024年5月每天的平均气温 D.2024年5月1日各时刻的气温
26.把一张长72cm,宽60cm的长方形纸,裁成同样大小、面积尽可能大的正方形纸,且纸无剩余,至少能裁( )张。
A.2 B.4 C.30 D.6
27.从3时15分到3时45分这段时间里,分针旋转了( )。
A.180° B.90° C.60° D.30°
28.在下面的分数中,( )不是最简真分数。
A. B. C. D.
29.把一个长8厘米,宽和高都是5厘米的长方体截成一个最大的正方体后,表面积( )。
A.减少110平方厘米 B.减少85平方厘米 C.减少60平方厘米
30.下面说法中,正确的一项是( )。
A.一个非零自然数,不是质数就是合数
B.把分数的分子和分母同时加上4,分数的大小不变
C.图形旋转时,它的位置、方向发生变化,大小不变
31.12个羽毛球特征相同,其中只有一个质量异常。现在要用一架没有砝码的天平去称,至少要称( )次才能找出那个质量异常的羽毛球。
A.4 B.3 C.2 D.1
32.下图是一个立体图形从正面、右面看到的形状。要搭成这样的立体图形,最多可以用( )个小方体。
A.6 B.7 C.8 D.9
33.把写有1、2、3、4、5、6、7、8、9、10数字卡片装入盒子中,任意摸出1张,摸到下面选项中( )可能性最小。
A.偶数 B.奇数 C.质数 D.合数
四、计算题
34.直接写出结果。
35.计算下面各题,能简算的要简算。
+- +++ 7.25-(1.25+)
-(+) 1.75-+1.25- -0.6-
36.解方程。
+﹦ -﹦1-
37.计算下面立体图形的表面积和体积。(单位:厘米)
五、作图题
38.请按要求在如图方格上画图并涂上阴影。
(1)以直线L为对称轴,画出下面图形的另一半。
(2)再将整个图形向右平移5格。
(3)最后将平移后的图形绕这个图形最上面的端点逆时针旋转90°。
六、解答题
39.为了保护环境,某小学组织学生收集废旧电池,第一小组5人收集了6千克,第二小组4人收集了4千克,第三小组6人收集了5千克,哪个小组平均每人收集的废旧电池多?
40.有5袋食盐,其中4袋每袋500克,另有1袋不是500克,但不知道比500克轻还是重。假如用天平称,至少称几次能保证找出质量不是500克的那一袋?用文字或图表示找的过程。
41.厦门市某购物中心要将一批垃圾桶(不到100个)平均分配到各个垃圾投放点,每个垃圾投放点放2个或3个或5个垃圾桶,都能正好分完。这批垃圾桶最多有多少个?
42.小兵在文具店买了3本笔记本、1支钢笔、2支自动铅笔和4块橡皮。笔记本每本2元,钢笔每支5元,自动铅笔和橡皮的价格小兵记不清了售货员要小兵付18元,小兵马上说售货员把账算错了,你知道为什么吗?
43.实践课上,老师布置了一个任务:已知一个长和宽均为8分米的长方体透明鱼缸(厚度忽略不计),鱼缸内水深5分米。聪聪将一个长6分米、宽4分米的长方体石块竖直立入鱼缸中(接触面之间无缝隙),并记录水位变化。石块放入后,水面迅速上升,聪聪惊呼:“现在水的高度是多少呢?”结合以前你所学知识,帮助聪聪解决这个问题。
44.为响应国家“体重管理年”的号召,小胖一家坚持进行体育锻炼。爸爸绕湖走一圈要用12分钟,爷爷绕湖走一圈要用24分钟,小胖绕湖走一圈要用18分钟。如果三人同时从同一起点沿同一方向出发,至少多少分钟后小胖和爷爷在起点处再次相遇?此时爸爸走了几圈?
45.“度量衡”是我国古代计量长度、容积、质量的标准或器具的统称。“度”用以计量长短;“量”用以测量容积大小;“衡”用以测量物体轻重。“商鞅变法”的重要物证——商鞅方升(如下图),就是“度量衡”中的“量”。它全长18.7厘米,内口长约12.5厘米、宽约7厘米、深约2.3厘米。它的容积便是商鞅规定的“一升”。算一算,商鞅规定的“一升”大约相当于现在的多少升?(得数保留一位小数)
46.学了体积后,妈妈拿出一块不规则的土豆问小华,你能算出它的体积吗?小华想了想,找来一个从里面量长12厘米,宽10厘米,高15厘米的长方体容器,里面水深8厘米,放入土豆后,土豆全部浸没在水中,水面上升到9.5厘米,你能帮小华算出土豆的体积是多少立方厘米?
47.在一块长方形铁皮的两个角上各剪掉一个边长为10厘米的小正方形,并把剪下的两个小正方形焊接到长方形的另一边的中间(如图),然后制成一个无盖的长方体盒子。这个盒子的体积是多少立方分米?(软皮的损耗不计)
48.一个长方体容器装有45升的水,将一个铁球浸没在水中时,容器内的水深达到5.7分米。如果再放入一个体积为3.2立方分米的铁球,这个长方体容器里的水会溢出来吗?(请通过计算说明)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.162.4 136
【分析】根据长方体的表面积=(长×宽+长×高+宽×高)×2、长方体的体积=长×宽×高,代入数据即可解答。
【解析】(6.8×5+6.8×4+5×4)×2
=(34+27.2+20)×2
=81.2×2
=162.4(平方厘米)
6.8×5×4=136(立方厘米)
长方体的表面积是162.4平方厘米,体积是136立方厘米。
2.852 250 852,582,528,258
【分析】3的倍数的特征:一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。既是2的倍数又是5的倍数的特征:个位上的数字是0的数,既是2的倍数,又是5的倍数。既是2的倍数又是3的倍数的特征:个位上的数字是0、2、4、6、8,各个数位上的数字的和是3的倍数的数。
从题意可知:在2,5,0,8四个数字中选取3个数字,且数字和是3的倍数的只有2,5,8。即2+5+8=18,将2,5,8三个数字从大到小排列,即可组成的有因数3的最大数。将2,5,8三个数字组成的3的倍数中,个位上是2或8,这个就是2,3的公倍数。
同时是2,5的倍数的个位上的数字一定是0,与较小的2和5组成最小的数即可。
【解析】在2,5,0,8四个数字中任选三个组成的有因数3的最大数是852;同时是2,5的倍数的最小的数是250;2,3的公倍数有852,582,528,258。
3.甲
【分析】比较两人用的时间,同样一项工作,用时越少速度越快。小数和分数比大小,将分数化成小数再比较,分数化小数,直接用分子÷分母即可。
【解析】=11÷25=0.44、0.35小时<小时,甲做得快些。
4.150°/150度 8 1
【分析】决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度。钟面指针的转动方向是顺时针方向,钟面1个大格是30°,据此通过转动的大格数确定旋转度数,旋转度数÷30°=转动的大格数,据此分析。
【解析】30°×5=150°,指针从“12”绕点O顺时针旋转150°到“5”。
180°÷30°=6(格),2+6=8(格),指针从“2”绕点O顺时针旋转180°到8。
90°÷30°=3(格),从10开始顺时针方向数3大格子,即指针从“10”绕点O顺时针旋转90°到1。
5.3
【分析】将不同长度的3根小棒截成同样长的小棒且不剩余,每根小棒最长应该是3根小棒长度的最大公因数,全部共有的质因数(公有质因数)相乘的积就是这几个数的最大公因数。
【解析】15=3×5
21=3×7
33=3×11
15、21和33的最大公因数是3。
每根小棒最长3cm。
6.上 左 正/前
【分析】从上面看有2行,前边1行4个小正方形,后边1行靠右1个小正方形;从左面看有2列,左边1列3个小正方形,右边1列1个小正方形;从正面看有3行,下边1行4个小正方形,中间1行左边1个小正方形右边2个小正方形,最上边1行右数第二个位置有1个小正方形,据此分析。
【解析】
从上面看到的图形是,从左面看到的图形是,从正面看到的图形是。
7./0.6
【分析】分析题目,把这根铁丝看作单位“1”,用铁丝的总长度除以分成的段数即可得到每段长多少米;再用分成的总段数除以小明拿的段数即可得到小明拿的铁丝是这根铁丝的几分之几。
【解析】3÷5=(m)
2÷5=
把一根长3m的铁丝平均分成5段,小明拿了其中的2段,每段长,小明拿的铁丝是这根铁丝的(填上合适的分数)。
8.48
【分析】根据题意,每16人分成一组,或者每12人分成一组,都正好分完,说明参加公益活动的最少学生人数是16和12的最小公倍数。
先把16和12分解质因数,再把它们的公有质因数和各自独有质因数的连乘积就是它们的最小公倍数。
【解析】16=2×2×2×2
12=2×2×3
16和12的最小公倍数是:2×2×2×2×3=48
该校参加“我是小小宣传员”公益活动的学生至少有48人。
9.;5
【分析】把桃的总质量看作单位“1”,把这些桃平均分给10位老人,相当于平均分成10份,用1除以10,即是每位老人得到这些桃的几分之几;
把50kg的桃平均分给10位老人,用桃的总质量除以10,即是每位老人分到桃的质量。
【解析】1÷10=
50÷10=5(kg)
每位老人得到这些桃的(),每位老人分到(5)kg桃。
10.2479
【分析】一个数,如果只有1和它本身两个因数,那么这样的数叫做质数。
一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。
整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身。
【解析】王伯伯的车牌号是鲁,
其中△即是偶数又是质数,即2;
◎是最小的合数,即4;
◇是10以内最大的质数,即7;
☆是9的最大因数,即9;
所以,王伯伯的车牌号是鲁(2479)。
11.2am+2bm abm
【分析】根据题意,一段长方体木料锯去m厘米高,则减少的表面积是4个侧面的面积,即2个长为a厘米、宽为m厘米的长方形的面积与2个长为b厘米、宽为m厘米的长方形的面积之和;根据“长方形的面积=长×宽”求出减少的表面积;
减少的体积是长为a厘米、宽为b厘米、高为m厘米的长方体的体积;根据“长方体的体积=长×宽×高”求出减少的体积。
【解析】a×m×2+b×m×2=(2am+2bm)(平方厘米)
a×b×m=abm(立方厘米)
填空如下:
则它的表面积减少(2am+2bm)平方厘米,体积减少(abm)立方厘米。
12.186 152
【分析】通过平移,将小正方体上面的面平移到下面,它的表面积=大正方体的表面积+小正方体1个面的面积×4,正方体表面积=棱长×棱长×6;它的体积=大正方体的体积+小正方体的体积,正方体体积=棱长×棱长×棱长,据此列式计算。
【解析】5×5×6+3×3×4
=150+36
=186()
5×5×5+3×3×3
=125+27
=152()
它的表面积是186,体积是152。
13.3
【分析】找次品的最优策略:一是把待测物品分成2份或3份;二是要尽量平均分,不能平均分的,应该使多的一份与少的一份只相差1,这样不但能保证找出次品,而且称的次数一定最少,据此解答。
【解析】有10件物品,其中有一件是次品,比其它略重。
第一次称重:先分成两份,天平两边各放5件,次品在较重的5件中;
第二次称重:把5件分成2件,2件和1件,天平两边各放2件,①若天平平衡,则次品就是剩下的1件;②若天平不平衡,次品就在较重的那2件中;
第三次称重:把较重的2件分成两份,天平两边各放1件,次品就是较重的1件。
10件物品,其中一件是次品(略重些),用天平称至少要称3次才能保证找出次品。
14.80 1600000
【分析】第一问就是要求长方体的体积,根据1方=1立方米,先把50厘米转化为0.5米,再根据,代入数据计算后把单位转化为方即可。
第二问就是要求长方体的底面积,土坑占地面积是一个长是20米,宽是8米的长方形,根据长方形的面积=长×宽,代入数据计算,再根据1平方米=10000平方厘米,把单位转化为平方厘米即可。
【解析】50厘米=0.5米
(立方米)=80(方)
(平方米)=1600000(平方厘米)
要在平地上挖一个长20米、宽8米、深50厘米的长方体土坑,一共要挖出80方的土,土坑占地面积是1600000平方厘米。
15.40 66 0.036
【分析】分析题目,一个顶点处的三条棱就是长方体的一组长宽高,据此根据长方体的棱长总和=(长+宽+高)×4,长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,代入数据计算即可,注意体积单位要根据1L=1000mL=1000cm3换算成L。
【解析】(4+3+3)×4
=10×4
=40(cm)
(4×3+4×3+3×3)×2
=(12+12+9)×2
=33×2
=66(cm2)
4×3×3
=12×3
=36(cm3)
36cm3=36mL=0.036L
用铁丝焊接这样一个框架,至少需要铁丝40cm;给框架焊上铁皮,至少需要铁皮66cm2;用做成的铁皮箱子装水,最多能装0.036L。
16.√
【分析】只在自然数(零除外)范围内研究倍数和因数。研究两个数的公倍数,说明这两个数都是非零自然数。两个或多个整数公有的倍数叫做它们的公倍数,据此举例说明即可。
【解析】两个数的乘积一定是这两个数的公倍数说法正确。如3×2=6,6是3和2的公倍数;4÷6=24,24是4和6的公倍数;8×2=16,16是8和2的公倍数……
故答案为:√
17.×
【分析】分子比分母小的分数叫作真分数,真分数小于1;分子比分母大或分子和分母相等的分数叫作假分数,假分数大于或者等于1,据此解答。
【解析】分析可知,真分数都比1小,如<1;假分数可能比1大,如>1,假分数也可能等于1,如=1,所以题目说法不正确。
故答案为:×
18.×
【分析】的分子加上20后,变为24,分子相当于乘6,根据分数的基本性质,分子、分母同时乘或除以同一个不为0的数,分数的大小不变;要使分数的大小不变,分母也应乘6。据此解答。
【解析】4+20=24
24÷4=6 ,相当于分子乘6,要使分数大小不变,其分母也要乘6。原说法错误。
故答案为:×
19.×
【分析】过山车的运动的过程中,要转几个圈,转圈的过程是绕一点作圆周运动,属于旋转,也有一段作的是直线运动,属于平移,据此解答。
【解析】过山车是一种平移现象,这句话说法不对。
故答案为:×
20.√
【分析】整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数,可以举例,据此判断即可。
【解析】n为奇数:2×1+1=2+1=3,3是奇数;
n为偶数:2×2+1=4+1=5,5是奇数。
如果n是自然数,那么2n+1一定是奇数,原题说法正确。
故答案为:√
21.√
【分析】由于5个连续的偶数和是m,由于相邻的两个偶数的和相差2,可知5个连续偶数的和其实相当于5个中间数的和,即用和除以5即可求出中间的数,由于最大的数比中间的数大4,用据此即可列式。
【解析】由分析可知:
5个连续偶数的和是m,这些偶数中最大的数是m÷5+4。原题说法正确。
故答案为:√
22.×
【分析】根据1 m3=1000 dm3,1 dm3=1000 cm3,高级单位换算成低级单位,乘进率,低级单位换算成高级单位,除以进率。先将所有数据都换算成以dm3为单位,再比较即可判断。
【解析】因为:4.06m3=4060 dm3
406000cm3=406 dm3
4060000cm3=4060 dm3
所以:4.06m3=4060 dm3=4060000cm3
4.06m3≠406000 dm3
在4.06m3、406000cm3、4060dm3、4060000cm3这4个数据中,4.06m3与4060dm3、4060000cm3相等,4.06m3与406000cm3不相等。因此原题说法不正确。
故答案为:×
23.√
【分析】一般把“的”字之间的物体看作单位“1”,或者平均分得是谁谁就是单位“1”;据此判断即可。
【解析】由分析可知:
白兔有24只,是灰兔的,是把灰兔的只数看作单位“1”。说法正确。
故答案为:√
24.D
【分析】要判断这四个选项中的数哪个一定既是3的倍数又是5 的倍数,需要分别根据3和5的倍数特征来对每个选项进行分析。5的倍数特征是个位是0或5,3的倍数特征是一个数的各位数之和是3的倍数,这个数就是3的倍数。
【解析】A.当T=5时,它是5的倍数。此时这个数各位数之和为5+5+5+5=20。根据3的倍数特征,因为20÷3=6……2,20 不能被3整除,所以 20 不是3的倍数,那么这个数不是的倍数,所以该选项不符合题意。
B.个位上是M,已知M=0,根据5的倍数特征,个位是 0,所以它是5的倍数。再看它是否为3的倍数,这个数各位数之和为T+0+T+0=2T。只有当T是3、6、9时,2T分别为2×3=6、2×6=12、2×9=18,6、12、18 是3的倍数此时这个数才是3的倍数。当T取其他值时,比如T=1,2×1=2,2不是3的倍数,所以它不一定是3的倍数,该选项不符合题意。
C.要成为5的倍数,个位T需为 5,此时这个数各位数之和为5+5+0+5=15。因为15÷3=5,15 能被3整除,所以当T=5时它是3的倍数。但当T取其他值时,比如T=1,个位不是 5,不是 5的倍数,所以它不一定既是3的倍数又是 5的倍数,C该选项不符合题意。
D.由于M=0,根据5的倍数特征,个位是 0,所以它是5的倍数。这个数各位数之和为T+T+T+0=3T,因为T是1、2、3、4、5、6、7、8、9中任意一个数,3T÷3=T,3T一定能被3整除,所以它一定是3的倍数。因此它一定既是3的倍数又是5的倍数。该选项符合题意。
故答案为:D
25.C
【分析】根据题意,要知道的是某市2024年5月份的气温变化情况,那么搜集的数据应该能够反映出这个月内气温的每日变化,而不是某个时间点或更长时间段的数据。
【解析】A.2024年各个季度平均气温,一年有4个季度,各个季度的数据范围太大了,无法具体看出5月份的气温变化情况,不符合题意;
B.2024年各月平均气温,一年有12个月,可以看出不同月份的平均气温,但不是5月份的气温变化情况,不符合题意;
C.2024年5月每天的平均气温,每天的数据能详细展示一个月内气温的变化情况,符合题意;
D.2024年5月1日各时刻的气温,只能看出这一天的气温变化,无法反映整个月的情况,不符合题意。
故答案为:C
26.C
【分析】把一块长方形纸裁成同样大小、面积尽可能大的正方形,且没有剩余,说明正方形的边长是长、宽的最大公因数,把72、60分解质因数后,把公有的相同质因数乘起来就是最大公因数,即是正方形的最大边长。再看长、宽里面分别有几个这样的最大公因数,最后相乘,即可求出至少能裁的张数。
【解析】72=2×2×2×3×3
60=2×2×3×5
72和60的最大公因数是:2×2×3=12
即正方形的边长最大是12cm。
72÷12=6(张)
60÷12=5(张)
一共:6×5=30(张)
至少能裁30张。
故答案为:C
27.A
【分析】一个钟面平均分成60小格,分针走1小格表示1分钟,分针走一圈是60分钟,一圈是360°,分针走1小格是(360÷60)°;从3时15分到3时45分,分针共走了(45-15)分钟,再乘每小格的度数即可。
【解析】3时45分-3时15分=30(分钟)
360°÷60=6°
6°×30=180°
分针旋转了180°。
故答案为:A
28.C
【分析】分子比分母小的分数叫做真分数;真分数<1。分子比分母大或分子和分母相等的分数叫做假分数;假分数≥1。
最简分数是指分子和分母只有公因数1的分数。
【解析】A.<1,且24和25是互质数,所以是最简真分数;
B.<1,且7和8是互质数,所以是最简真分数;
C.>1,==,所以不是最简真分数;
D.<1,且4和21是互质数,所以是最简真分数。
故答案为:C
29.C
【分析】根据正方体的特征可知,把这个长方体截成一个最大的正方体,这个正方体的棱长为5厘米,减少的面积相当于长为5厘米、宽为(8-5)厘米的4个小长方形的面积,根据长方形面积公式解答。
【解析】5×(8-5)×4
=5×3×4
=60(平方厘米)
把一个长8厘米,宽和高都是5厘米的长方体截成一个最大的正方体后,表面积减少60平方厘米。
故答案为:C
30.C
【分析】1既不是质数也不是合数;分数的分子和分母同时乘或除以相同的数(0除外)大小不变;图形旋转时形状大小不变,但是位置方向会变化,据此解答。
【解析】A.非零自然数中的1,既不是质数也不是合数,所以该项错误;
B.分数的分子和分母同时加上4,分数的大小会发生变化,如分数不等于变化后的分数,所以该项错误;
C.图形旋转时,它的位置、方向发生变化,大小不变,所以该项正确。
故答案为:C
31.A
【分析】根据题意,12个羽毛球特征相同,其中只有一个质量异常,但不知轻重,分组称重时,考虑天平平衡或不平衡时的各种情况,逐一讨论,得出至少称的次数。
【解析】第1次称量,将12个羽毛球平均分为三份①②③(每份4个),先把①和②放在天平的两边,如果天平平衡,则③里面有异常球;如果天平不平衡,则①和②中有异常羽毛球,③都是正常羽毛球;第2次称量,把①和②中的任意一份取下来,把③放上去,即可判断异常羽毛球在哪一份里,并且知道异常羽毛球的轻重;第3次称量,把有异常羽毛球的4个球平均分成两份(每份2个),把它们放在天平的两边,天平不平衡,根据轻重,判断出异常羽毛球在哪一份里;第4次称量,再把有异常羽毛球的2个球分成两份(每份1个),把它们放在天平的两边,天平不平衡,根据轻重,判断出异常羽毛球是哪一个。
所以至少要称4次才能找出那个质量异常的羽毛球。
故答案为:A
32.D
【分析】根据从正面和右面看到的形状可知,这个立体图形有2层2排,上层只有1个小正方体,且在前一排;下层最多有8个小正方体,每排4个;据此得出搭这个立体图形最多可用(1+8)个小正方体。
【解析】如图:
最多可以用9个小方体。
故答案为:D
33.C
【分析】1~10的数中:2、4、6、8、10是偶数;1、3、5、7、9是奇数;2、3、5、7是质数;4、6、8、9、10是合数;数字出现的次数越少,即被摸出的可能性最小,据此作答。
【解析】由分析可知:
1~10的数中,其中偶数有5个,奇数有5个,质数有4个,合数有5个,因此抽到质数的可能性最小。
故答案为:C
34.;2;;;1
;;;;
【解析】略
35.;;;
;2;
【分析】(1)按照从左往右的顺序,先计算+,再计算这个算式的结果与的差;
(2)先利用加法交换律把算式转化为+++,再利用加法结合律计算同分母分数加法;
(3)先利用减法性质a-(b+c)=a-b-c计算小数减法,再计算整数与分数的差;
(4)先利用减法性质a-(b+c)=a-b-c去掉括号,再利用减法性质a-b-c=a-c-b计算同分母分数减法,最后计算异分母分数减法-;
(5)先利用加法交换律把算式转化为1.75+1.25--,再计算小数加法的和并利用减法性质a-b-c=a-(b+c)计算同分母分数加法;
(6)先把0.6转化为,再利用减法性质a-b-c=a-(b+c)计算同分母分数加法,最后计算分数与整数的差。
【解析】(1)+-
=-
=
(2)+++
=+++
=(+)+(+)
=1+
=
(3)7.25-(1.25+)
=7.25-1.25-
=6-
=
(4)-(+)
=--
=--
=-
=
(5)1.75-+1.25-
=1.75+1.25--
=3--
=3-(+)
=3-1
=2
(6)-0.6-
=--
=-(+)
=-1
=
36.x=;x=;x=1
【分析】+﹦,根据等式的性质1,方程两边同时减去即可。
-﹦1-,先计算出方程右边1-的差,再根据等式的性质1,方程两边同时加上即可。
2x-=,根据等式的性质1,方程两边同时加上,再根据等式的性质2,方程两边同时除以2即可。
【解析】+﹦
解:+-﹦-
x=-
x=
-﹦1-
解:-﹦
-+﹦+
x=
2x-=
解:2x-+=+
2x=2
2x÷2=2÷2
x=1
37.表面积330平方厘米;体积370立方厘米
【分析】观察可知,立体图形的表面积等于大正方体的表面积加上小正方体的侧面积(即4个小正方形的面积),根据,计算即可;立体图形的体积等于大正方体的体积加小正方体的体积,根据,计算即可。
【解析】表面积:
(平方厘米)
体积:
(立方厘米)
立体图形的表面积是330平方厘米;体积是370立方厘米。
38.(1)(2)(3)见详解
【分析】(1)根据轴对称图形的画法,以直线L为对称轴,找出轴对称图形的任意一组对称点,连接对称点;画出对称点所连线段的中心,沿着中心作这条线段的垂线,就可以得到该图形的对称轴;
(2)根据图形平移的方法,将图形的顶点向右平移5格,然后再连线成图即可;
(3)根据旋转的方法,最上面的端点不动,将平移后的图形每条边绕这个图形最上面的端点逆时针旋转90°即可。
【解析】(1)(2)(3)作图如下:
39.第一小组
【分析】先用各小组收集废旧电池的质量除以小组人数,求出各小组每人收集废旧电池的质量;再根据分数大小比较的方法进行比较,得出哪个小组平均每人收集的废旧电池多。
真分数<1,假分数≥1,则假分数>真分数。
【解析】6÷5=(千克)
4÷4=1(千克)
5÷6=(千克)
>1>
答:第一小组平均每人收集的废旧电池多。
40.3次;过程见解答
【分析】根据天平的平衡原理对托盘两边的物品进行比较,把待测物品分成三份,要分得尽量平均,能够均分的就平均分成3份,不能平均分的,也应该使多的一份与少的一份只相差1。因为不知道次品偏轻还是偏重,所以要先用天平称一次,确定哪个物品不是次品,用这个物品和可能是次品的物品进行比较,进而找出次品。
【解析】把5袋食盐依次标号为①、②、③、④、⑤。用天平称,第一次称,左边放①、②,右边放③、④,天平外是⑤。如果平衡,那么⑤就是次品;如果不平衡,那么次品在①—④中,⑤不是次品。
第二次称,在①—④中任取2袋,例如取①和③,分别放在天平两边称。如果不平衡,那么次品在这2袋中,然后天平一边仍然放①,另一边换成⑤,由于⑤不是次品,所以这时如果天平平衡,那么①不是次品,③是次品;如果天平不平衡,那么①就是次品。
如果天平上①与③平衡,那么次品是②或④,第三次称,此时称一下②和⑤,如果天平平衡,那么④是次品;如果天平不平衡,那么②是次品。
至少称3次能保证找出质量不是500克的那一袋。
41.90个
【分析】由“每个垃圾投放点放2个或3个或5个垃圾桶,都能正好分完”可知,这批垃圾桶的数量是2、3、5的公倍数,这个公倍数接近100且小于100,所以可先找2、3、5的最小公倍数,再找出这个公倍数的倍数中接近100且小于100的数即可得解。
【解析】2、3、5的最小公倍数是:
30的倍数有:30、60、90、120……
90接近100且小于100
答:这批垃圾桶最多有90个。
42.见详解
【分析】从题意可以知道,四种商品的数量已知,根据,笔记本和钢笔的价格能够算出来一共是11元,但是因为自动笔和橡皮的数量是双数,所以,不管买多少,它们的总价格也应该是双数,因为偶数乘偶数,偶数乘奇数积都是偶数,而11是奇数,根据奇数加偶数等于奇数,因此,要付款的钱数应是奇数,但是根据售货员算的价格是偶,所以判断是错误的。
【解析】
(元)
答:因为2支自动铅笔和4块橡皮的价格是偶数,而3本笔记本、1支钢笔的价格是奇数,根据奇数加偶数等于奇数可知,总价应该是奇数,而售货员算的是18元(偶数),所以账算错了。
43.8分米
【分析】已知长方体鱼缸长和宽均为8分米,水深5分米,根据长方体的体积=长×宽×高,求出水的体积;
将一个长6分米、宽4分米的长方体石块竖直立入鱼缸中,石块占据部分底面积,导致水的底面积变成(8×8-6×4)平方分米,水的体积不变,根据长方体的高=体积÷底面积,求出此时水的高度。
【解析】8×8×5
=64×5
=320(立方分米)
8×8-6×4
=64-24
=40(平方分米)
320÷40=8(分米)
答:现在水的高度是8分米。
44.72分钟;6圈
【分析】当两人在起点再次相遇时,所用时间一定是他们各自走一圈所用时间的公倍数,要求至少多少分钟后再次相遇,就是求他们走一圈所用时间的最小公倍数;已知爸爸绕湖走一圈要用12分钟,用24和18的最小公倍数除以12就是此时爸爸走的圈数。
【解析】24=2×2×2×3
18=2×3×3
所以24和18的最小公倍数是72。
72÷12=6(圈)
答:至少72分钟后小胖和爷爷在起点处再次相遇,此时爸爸走了6圈。
45.0.2升
【分析】本题求商鞅规定的“一升”相当于现在的多少升,关键是先算其容积再换算单位。已知内口长约12.5厘米、宽约7厘米、深约2.3厘米,根据“长方体体积(容积)=长×宽×高”计算出长方体容积;然后将立方厘米换算为立方分米,再换算为升;最后根据题目要求按“四舍五入”原则保留一位小数。
【解析】12.5×7×2.3
=87.5×2.3
=201.25(立方厘米)
201.25立方厘米=0.20125立方分米=0.20125升
0.20125升≈0.2升
答:商鞅规定的“一升”大约相当于现在的0.2升。
46.180立方厘米
【分析】分析题目,土豆的体积等于一个长是12厘米,宽是10厘米,高是(9.5-8)厘米的长方体的体积,根据长方体的体积=长×宽×高代入数据列式计算即可。
【解析】12×10×(9.5-8)
=12×10×1.5
=120×1.5
=180(立方厘米)
答:土豆的体积是180立方厘米。
47.10立方分米
【分析】看图可知,制成的长方体盒子的长=(60-10)厘米,宽=(40-10×2)厘米,高=10厘米,根据长方体体积=长×宽×高,列式解答即可。根据1立方分米=1000立方厘米,统一单位。
【解析】60-10=50(厘米)
40-10×2
=40-20
=20(厘米)
50×20×10=10000(立方厘米)=10(立方分米)
答:这个盒子的体积是10立方分米。
48.会
【分析】由题意可知,容器内无水部分可以看作一个长方体,长方体的长和宽都是3分米,高为(6-5.7)分米,根据“长方体的体积=长×宽×高”求出无水部分的体积,最后和铁球的体积比较大小,即可求得。
【解析】3×3×(6-5.7)
=3×3×0.3
=9×0.3
=2.7(立方分米)
因为3.2立方分米>2.7立方分米,所以水会溢出来。
答:这个长方体容器里的水会溢出来。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
