2024-2025学年五年级下册数学期末高频易错押题提升卷(苏教版)(含解析)
文档属性
| 名称 | 2024-2025学年五年级下册数学期末高频易错押题提升卷(苏教版)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 589.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-25 22:03:44 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年五年级下册数学期末高频易错押题提升卷(苏教版)
一、填空题
1.一个三位数37□,当它既是2的倍数又是5的倍数时,□里填( )。当它是3的倍数时,□里可以填的数是( )。
2.小静打开数学书时,发现两页页码之积是420,这两页分别是( )页和( )页。
3.一个四位数,千位上既不是质数也不是合数,百位上是最小的合数,十位上是最大的一位数,个位上是10以内最大的质数,这个数是( )。
4.一根铁丝长1m,用它来围直径为10cm的圆(接头处不计),最多可以围( )个这样的圆。
5.一辆自行车的车轮半径是40厘米,车轮每分钟转100圈,要通过2512米的大桥,需要( )分钟。
6.一个圆柱形旋转展台,台面周长为18.84米,台面的面积是( )平方米。
7.的分数单位是( ),它化成带分数是( );它再加( )这样的分数单位就是最小的合数。
8.三个连续自然数,如果中间的数是N,那么这三个数的和是( );如果这三个数的和是120,那么最大数是( )。
9.五(1)班的学生人数在40~50人,王老师想把全体学生平均分成若干个学习小组,无论按4人一组还是6人一组,都正好多出1人。这个班有( )人。
10.如图a和b的最大公因数是( ),a和b的最小公倍数是( )。
11.将一个圆平均分成48等份后拼成一个近似的长方形。如果测得这个长方形的长为6.28dm,那么原来的圆的面积是( )dm2,长方形的周长是( )dm。
12.小东住在小南和小北两家的中间,三家门牌号是相邻的奇数,而且三家门牌号之和是69,小东家的门牌号是( )。
13.五(1)班购买来3箱苹果共有120个,共重20千克,把这些苹果平均分给班上的30名学生,每名学生分得( )个苹果,每名学生分得箱苹果,每名学生分得千克苹果。
14.某小学篮球社团有x人,“小百灵”社团的人数是篮球社团的2倍,这两个社团一共有( )人。当x=5时,这两个社团一共有( )人。
15.五年级学生分组举行“畅想未来”科技比赛,五(1)班学生每组8人或每组12人都正好分完。五(1)班学生人数在40~50人之间,五(1)班学生有( )人。
二、判断题
16.走同一段路,小刚要用20分,小明要用16分,小刚的速度比小明的速度快。( )
17.圆和圆环都是轴对称图形,都有无数条对称轴。( )
18.世界上第一个把圆周率的值精确到小数点后7位的科学家是刘徽。( )
19.如果n是一个奇数,那么n+3一定是奇数。( )
20.圆的半径扩大到原来的3倍,它的周长扩大到原来的3倍,面积扩大到原来的6倍。( )
21.大圆的圆周率大于小圆的圆周率。( )
22.分子和分母都是合数的分数,一定不是最简分数。( )
23.既是2的倍数又是5的倍数的数,个位上必定是1。( )
24.既是2和5的倍数,又有因数3的最大两位数是90。( )
三、选择题
25.下面运用了“转化”思想的是( )。
①求多边形内角和 ②异分母分数加法 ③求平行四边形面积
A.①② B.②③ C.①②③
26.一杯金银花露,爸爸先喝杯,用水加满,又喝杯,再用水加满后喝完。爸喝的金银花露和水相比,( )。
A.金银花露多 B.水多 C.一样多
27.高速列车的速度是300千米/时,如果速度减少80千米/时,就相当于一辆轿车速度的2倍。要知道轿车的速度,可以用下面的方程( )求解。
A.2x+80=300 B.x+80=300+2
C.2x-80=300 D.2x+80=300+2
28.一个圆形射击靶的周长是2.826米,射中靶心代表是10环,一个运动员射击时得了4环,他射中的位置距离靶心可能是( )厘米。
A.900 B.90 C.50 D.30
29.生产同一个零件,甲需要小时,乙需要小时,甲和乙相比,( )。
A.甲生产得快 B.乙生产得快 C.生产得一样快
30.如图,正方形的面积是64平方厘米,圆的面积是( )平方厘米。
A. B. C. D.
31.在住院病房中,护士每天要多次测量患者的体温,为了观察一个患者的体温变化情况,应绘制( )比较合适。
A.折线统计图 B.条形统计图 C.统计表 D.以上答案都不正确
32.如图所示的各图都表示“1”,阴影部分表示的大小或问号对应的长度,可以用“++”计算的有( )。
A.1个 B.2个 C.3个 D.4个
33.如图是一个钟面,分针长8厘米,时针长4厘米,分针走一圈比时针走一圈扫过的面积多( )平方厘米。
A.25.12 B.150.72 C.20.24
34.三张边长都是16厘米的正方形纸板,分别按右边三种不同剪法剪下不同规格的圆片。从浪费材料的角度考虑,( )。
A.第一种浪费多 B.第二种浪费多 C.第三种浪费多 D.三种浪费同样多
四、计算题
35.直接写出得数。
= = = =
= = = =
36.计算下面各题,能简算的要简算。
37.解方程。
38.求下面长方形中涂色部分的面积。
五、作图题
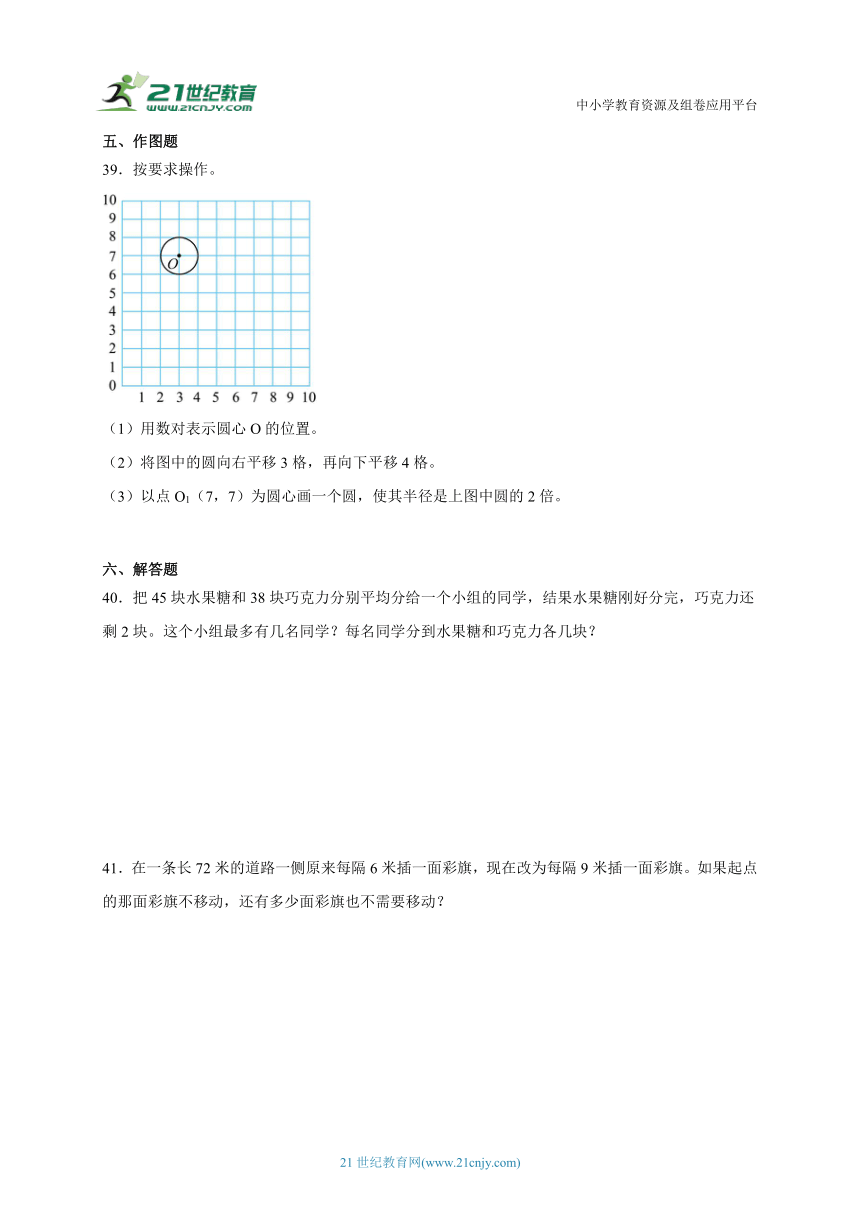
39.按要求操作。
(1)用数对表示圆心O的位置。
(2)将图中的圆向右平移3格,再向下平移4格。
(3)以点O1(7,7)为圆心画一个圆,使其半径是上图中圆的2倍。
六、解答题
40.把45块水果糖和38块巧克力分别平均分给一个小组的同学,结果水果糖刚好分完,巧克力还剩2块。这个小组最多有几名同学?每名同学分到水果糖和巧克力各几块?
41.在一条长72米的道路一侧原来每隔6米插一面彩旗,现在改为每隔9米插一面彩旗。如果起点的那面彩旗不移动,还有多少面彩旗也不需要移动?
42.快、慢两车同时从甲地到乙地,快车每小时行70千米,慢车每小时行55千米。途中快车因故停留3小时,结果两车同时到达乙地。甲、乙两地间的距离是多少千米?
43.同学们做了48朵黄花和60朵红花。把这些花分成若干束(所有花都分完),要求每束里的黄花朵数同样多,红花朵数也同样多。最多可以分成几束?每束里共有几朵花?
44.欢欢用同样大小的长方形拼正方形。长方形的长是8厘米,宽是6厘米,至少用多少个长方形才能拼成一个正方形?拼成的正方形面积是多少平方厘米?
45.爸爸和小明在400米的环形操场跑步,从同一起点同向而行,爸爸的速度是每秒5.5米,小明的速度是每秒3.5米,多少秒后,爸爸第二次追上小明?(列方程解题)
46.有一面长方形墙(示意图如图),如果用一种边长是整分米数的正方形瓷砖把这面墙贴满(瓷砖为整块),那么可以选择边长是多少分米的瓷砖?瓷砖边长最长是多少分米?
(1)瓷砖边长的分米数必须是40和24的( )数。
(2)试着写下你的解决方案。
(3)在图中,请你试着将你的解决方案在图里画一画,沿着长方形的长能贴( )块,宽能贴( )块,一共可以贴( )块。
47.迷你马拉松正在海城举行,如图是赛道的一部分,赛道在B点拐弯,根据比赛要求需要在路的一边排志愿者,志愿者之间的距离必须相等,而且A、B、C处必须安排志愿者。那么这段赛道至少要安排多少名志愿者?
48.国家标准《住宅设计规范》中规定:普通住宅层高宜为2.80米(除一层外)。幸福小区一幢20层的楼高57米,除一层高度是3.8米外,其余每层的高度都相等,其余每层的高度符合国家标准吗?(列方程解答)
49.为弘扬中华传统文化,西渚实验小学在端午节期间举行了1000米龙舟比赛。
(1)五年级参加龙舟比赛的学生有40~50人,分组时4人一组或6人一组,都剩余1人,五年级参加龙舟比赛的学生有多少人?
(2)甲、乙两支龙舟队在比赛中路程与时间的关系如图。
①开赛2分钟后,处于领先位置的是( )龙舟队。
②乙龙舟队平均每分钟行多少米?开赛4分钟后,乙龙舟队离终点还有多少米?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.0 2、5或8
【分析】2的倍数特征:个位上是0、2、4、6、8的数。
5的倍数特征:个位上是0或5的数。
2、5的倍数特征:个位上是0的数。
3的倍数特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数。
【解析】个位数字是0,这样的数既是2的倍数又是5的倍数,370既是2的倍数又是5的倍数;
3+7+2=12,12是3的倍数,372是3的倍数;
3+7+5=15,15是3的倍数,375是3的倍数;
3+7+8=18,18是3的倍数,378是3的倍数。
一个三位数37□,当它既是2的倍数又是5的倍数时,□里填0。当它是3的倍数时,□里可以填的数是2、5或8。
2.20 21
【分析】根据题意,两页页码之积是420,先把420分解质因数,再把这些质因数重新组合,变成连续两个自然数相乘的形式,即可得解。
【解析】420=2×2×3×5×7=(2×2×5)×(3×7)=20×21
这两页分别是20页和21页。
3.1497
【分析】一个数,如果只有1和它本身两个因数,那么这样的数叫做质数。
一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。
【解析】一个四位数,千位上既不是质数也不是合数,即1;
百位上是最小的合数,即4;
十位上是最大的一位数,即9;
个位上是10以内最大的质数,即7;
这个数是1497。
4.3
【分析】根据题意,用一根铁丝围成直径为10cm的圆,那么铁丝长度等于圆的周长;根据公式C=πd求出圆的周长,也就是围成一个圆所需的铁丝长度;
求长1m的铁丝最多可以围几个这样的圆,就是看1m里面有几个圆的周长,用除法计算,计算结果用“去尾法”保留整数。
【解析】1m=100cm
3.14×10=31.4(cm)
100÷31.4≈3(个)
最多可以围3个这样的圆。
5.10
【分析】根据圆的周长公式:周长=π×半径×2,代入数据,求出自行车的车轮的周长,再用自行车车轮的周长×100,求出车轮每分钟行驶的距离,再用大桥的长度÷车轮每分钟行驶的距离,即可解答,注意单位名数的统一。
【解析】3.14×40×2×100
=125.6×2×100
=251.2×100
=25120(厘米)
25120厘米=251.2米
2512÷251.2=10(分钟)
一辆自行车的车轮半径是40厘米,车轮每分钟转100圈,要通过2512米的大桥,需要10分钟。
6.28.26
【分析】台面是一个圆形,根据圆的周长=,得出圆形的半径,再根据圆的面积=,得出圆的面积。
【解析】18.84÷3.14÷2=3(米)
3.14×32
=3.14×9
=28.26(平方米)
则台面的面积是28.26平方米。
7.
【分析】把单位“1”平均分成若干份,表示其中一份的数叫分数单位。对于真分数、假分数来说,分子是几,就有几个这样的分数单位。把假分数化成带分数的方法:用分子除以分母,得到的商和余数;商是带分数的整数部分,余数是带分数的分子,分母不变。最小的合数是4,先把4化成分母为5而大小不变的假分数,再看分子与的分子相差几,就需要再增加几个这样的分数单位就是最小的合数。
【解析】
的分数单位是,里有14个。
里有20个。
(个)
的分数单位是,它化成带分数是;它再加6个这样的分数单位就是最小的合数。
8.3N 41
【分析】连续两个数相差1,中间的数是N,则最小的数是N-1,最大的数是N+1,据此用含N的式子表示这三个数的和;把这三个数的和是120,代入式子中,利用等式的性质求出N的值,再求出最大数即可。
【解析】三个数的和:N+N-1+N+1=3N
当3个数的和是120,则3N=120
3N÷3=120÷3
N=40
最大数是:40+1=41
所以这三个数的和是3N;如果这三个数的和是120,那么最大数是41。
9.49
【分析】由题意可知,五(1)班的学生人数减少1后是4和6的公倍数,五(1)班的学生人数在40~50人,所以先求出在40~50之间4和6的公倍数,再用所求的公倍数再加1,即可求出五(1)班的学生人数,据此解答。
【解析】在40~50之间4的倍数有:40、44、48。
在40~50之间6的倍数有:42、48。
因此在40~50之间4和6的公倍数有:48。
48+1=49(人)
即这个班有49人。
10.12 72
【分析】最大公因数指几个整数共有因数中最大的一个;
一个数的最大因数是它本身;
最小公倍数指几个整数公有的倍数中最小的一个。把a和b分解质因数后,把公有的相同质因数与独有质因数乘起来就是它们的最小公倍数,据此解答。
【解析】由题可知,a和b的公因数有:1、2、3、4、6、12,最大的是12,所以a和b的最大公因数是12;
a的最大因数是24,所以a是24,b的最大因数是36,所以b是36。
24=2×2×2×3
36=2×2×3×3
所以24和36的最小公倍数是:2×2×2×3×3=72。
即a和b的最大公因数是12,a和b的最小公倍数是72。
11.12.56 16.56
【分析】将圆平均分成48等份后拼成一个近似的长方形,长方形的长是这个圆的半个圆弧的长度,则乘2求出圆的周长。再根据圆的周长C=,得出。圆的面积S=,将圆的半径带入公式计算即可。长方形的宽就是圆的半径,则长方形的周长=(长+宽)×2。
【解析】6.28×2÷3.14÷2
=12.56÷3.14÷2
=4÷2
=2(dm)
3.14×22
=3.14×4
=12.56(dm2)
(6.28+2)×2
=8.28×2
=16.56(dm)
原来的圆的面积是12.56dm2,长方形的周长是16.56dm。
12.23
【分析】相邻的奇数之间相差2,三个奇数的和÷3=中间奇数,据此列式计算。
【解析】69÷3=23
小东家的门牌号是23。
13.4;;
【分析】用苹果的总个数除以学生人数,可得到每名学生分得的苹果个数;用总箱数除以学生人数,可得到每名学生分得的箱数占比;用总质量除以学生人数,可得到每名学生分得的质量占比,据此解答。
【解析】120÷30=4(个)
3÷30=(箱)
20÷30=(千克)
即每名学生分得4个苹果,每名学生分得箱苹果,每名学生分得千克苹果。
14.3x 15
【分析】由题可得:篮球社团人数+“小百灵”社团的人数=这两个社团的总人数,篮球社团有x人,“小百灵”社团的人数是篮球社团的2倍,则“小百灵”社团的人数是2x,因此这两个社团一共有(x+2x)人,把x=5时,代入计算,即可求出这两个社团一共有的人数,据此解答。
【解析】2x+x=3x(人)
当x=5时,3×5=15(人)
即这两个社团一共有3x人,当x=5时,这两个社团一共有15人。
15.48
【分析】根据题意可知,五(1)班学生人数既是8的倍数,也是12的倍数,先求出8和12的最小公倍数,再找出40~50之间的8和12的公倍数,即可解答。
【解析】8=2×2×2
12=2×2×3
8和12的最小公倍数是2×2×2×3=24;
24×2=48,五(1)班学生有48人。
五年级学生分组举行“畅想未来”科技比赛,五(1)班学生每组8个或每组12人都正好分完。五(1)班学生人数在40~50人之间,五(1)班学生有48人。
16.×
【分析】在比赛中,走同一段路,谁用的时间少,说明了谁的速度就快,据此解答。
【解析】由分析可得:走同一段路,谁用的时间少,说明了谁的速度就快,小明要用16分钟,小刚要用20分钟,
16<20
所以小明用时比小刚少,所以小明的速度快,原题说法错误。
故答案为:×
17.√
【分析】如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫对称轴;判断一个图形是否是轴对称图形,关键是找它的对称轴,要想象沿着这条线翻折能不能重叠,据此判断。
【解析】
如图,圆和圆环都是轴对称图形,都有无数条对称轴,此题说法正确。
故答案为:√
18.×
【分析】我国魏晋时期数学家刘徽求得圆周率的近似值是3.14。我国南北朝科学家祖冲之算出圆周率大约在3.1415926和3.1415927之间,成为世界上第一个把圆周率的值精确到小数点后7位的人。
【解析】世界上第一个把圆周率的值精确到小数点后7位的科学家是祖冲之。即原题说法错误。
故答案为:×
19.×
【分析】整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数;根据题意,n是奇数,3是奇数;奇数+奇数=偶数;奇数+偶数=奇数;偶数+偶数=偶数;据此解答。
【解析】假设n=1,1+3=4,4是偶数,所以原题说法错误;
故答案为:×
20.×
【分析】假设原来的半径是1厘米,半径扩大到原来的3倍,则直径变为3厘米。根据圆的周长公式:C=2πr,圆面积公式:S=πr2,代入数据求出变化前后的周长和面积,进而求出周长扩大到原来的几倍以及面积扩大到原来的几倍。据此解答。
【解析】假设原来的半径是1厘米,
1×3=3(厘米)
(2×π×3)÷(2×π×1)
=6π÷2π
=3
(π×32)÷(π×12)
=(π×9)÷(π×1)
=9π÷π
=9
圆的半径扩大到原来的3倍,它的周长就扩大到原来的3倍,面积就扩大到原来的9倍。原题干说法错误。
故答案为:×
21.×
【分析】根据圆周率的含义:圆的周长和它直径的比值,叫做圆周率;圆周率用“π”表示,π是一个无限不循环小数;进而判断即可。
【解析】根据分析可知,圆周率是一个定值,不存在大圆的圆周率大于小圆的圆周率。
原题干说法错误。
故答案为:×
22.×
【分析】只要分子分母互质,这个分数就是最简分数;例如4和9都是合数,但是4和9互质,就是最简分数,据此判断即可。
【解析】分子和分母都是合数的分数,可能是最简分数,如是最简分数,原题说法错误。
故答案为:×
23.×
【分析】2的倍数特征:个位是0、2、4、6、8的数是2的倍数,5的倍数特征:个位是0、5的数是5的倍数,据此即可知道既是2的倍数,又是5的倍数,它的个位是0,据此即可判断。
【解析】由分析可知:
既是2的倍数又是5的倍数的数,个位上必定是0,原说法错误。
故答案为:×
24.√
【分析】2的倍数特征:末尾数字是0、2、4、6、8的数是2的倍数;3的倍数特征:各个数位上的数字之和是3的倍数,这个数字就是3的倍数;5的倍数特征:末尾数字是0或5的数是5的倍数,既是2和5的倍数,又有因数3,这个数的个位必须是0,据此解答。
【解析】根据分析可知,既是2和5的倍数,又有因数3的最大两位数是90。
原题干说法正确。
故答案为:√
25.C
【分析】①根据三角形内角和可知多边形的内角和;②根据异分母分数的加法运算法则可知同分母分数的加法运算;③根据长方形的面积可知平行四边形的面积。综上可知①②③都用了转化思想。
【解析】因为三角形的内角和为,
所以多边形的内角和为,
所以①用了转化思想;
因为,
所以,
所以②用了转化思想;
因为图中长方形的面积等于平行四边形的面积,
所以③用了转化思想;
综上,运用转化思想的是①②③,
故答案为:C
26.A
【分析】先确定爸爸喝的金银花露的量,一杯金银花露最后全部喝完,所以爸爸喝的金银花露是1杯;再分析爸爸喝的水的量,爸爸先喝杯,此时加了杯水,又喝了杯后再用水加满,又加了杯水,所以列式为+,算出结果即可。
【解析】爸爸喝的金银花露的量:一杯金银花露最后全部喝完,所以爸爸喝的金银花露是1杯,爸爸喝的水的量:+=+=,因为1>,所以爸爸喝的金银花露多。
故答案为:A
27.A
【分析】根据题意,此题的等量关系是:轿车的速度×2+80千米/小时=300千米/时,据此列方程。
【解析】根据上面的分析,假设轿车的速度为x,可以用方程2x+80=300求解。
故答案为:A
28.D
【分析】根据圆的周长公式:C=2πr,计算其半径,再把半径平均分成10份,4环与靶心的距离应该在(10-4)份到(10-3)份之间。
【解析】2.826米=282.6厘米
282.6÷3.14÷2=45(厘米)
45÷10×(10-4)
=45÷10×6
=27(厘米)
45÷10×(10-3)
=45÷10×7
=31.5(厘米)
A.900>31.5,不符合题意;
B.90>31.5,不符合题意;
C.50>31.5,不符合题意;
D.27<30<31.5,符合题意;
他射中的位置距离靶心可能是30厘米。
故答案为:D
29.A
【分析】生产同一个零件,谁用的时间少,谁就生产得快;根据分数比较大小的方法比较甲、乙用的时间,即可得解。
分数大小的比较:分母相同时,分子越大,分数值就越大;分子相同时,分母越大,分数值反而越小;分子、分母都不相同时,化成同分母或同分子的分数进行比较。
【解析】
,即;
甲需要的时间比乙少,所以甲生产得快。
故答案为:A
30.B
【分析】观察图形可知,正方形的对角线等于圆的直径;直径=半径×2;正方形的面积可以看成两个三角形的面积和,其中一个三角形的底是直径,高是半径,由此即可知道正方形的面积=(半径×2)×半径;即正方形的面积=2×半径2;由此可知,半径2=正方形面积÷2,再根据圆的面积公式:面积=π×半径2,据此求出圆的面积。
【解析】π×(64÷2)=32π(平方厘米)
正方形的面积是64平方厘米,圆的面积是32π平方厘米。
故答案为:B
31.A
【分析】统计表以表格呈现数据,条形统计图以直条呈现数据,都能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;由此根据情况选择即可。
【解析】观察患者的体温变化情况,选择折线统计图比较合适。
故答案为:A
32.C
【分析】图一:把圆先平均分成了2份,每份占,再把圆看作单位“1”,平均分成了4份,每份占,最后又把圆平均分成了8份,每份占,阴影部分表示为:++。
图二:把整个图形平均分成了2份,每份占,再把整个图形看作单位“1”,平均分成了4份,每份占,又把整个图形平均分成了8份,每份占,最后把整个图形平均分成了16份,每份占,阴影部分表示为:+++。
图三:把整个图形平均分成了2份,每份占,再把整个图形看作单位“1”,平均分成了4份,每份占,又把整个图形平均分成了8份,每份占,阴影部分表示为:++。
图四:把整个图形平均分成了2份,每份占,再把整个图形看作单位“1”,平均分成了4份,每份占,又把整个图形平均分成了8份,每份占,阴影部分表示为:++。
【解析】由分析可知:
如图所示的各图都表示“1”,阴影部分表示的大小或问号对应的长度,可以用“++”计算的有3个。
故答案为:C
33.B
【分析】分针走一圈比时针走一圈多扫过的面是个圆环,分针和时针的长分别是大圆和小圆的半径,根据圆环面积=圆周率×(大圆半径的平方-小圆半径的平方),列式计算即可。
【解析】3.14×(82-42)
=3.14×(64-16)
=3.14×48
=150.72(平方厘米)
分针走一圈比时针走一圈扫过的面积多150.72平方厘米。
故答案为:B
34.D
【分析】根据正方形周长公式:周长=边长×4,边长=周长÷4,求出正方形的边长;根据圆的面积公式:面积=π×半径2,代入数据,分别求出三种不同图形中的圆的面积,哪种圆的面积大,哪种剪法浪费的少,反之,哪种圆的面积小,哪种剪法浪费的所,如果三种面积相同,浪费的一样多,据此解答。
【解析】16÷4=4(厘米)
第一种剪法:圆的直径等于4厘米
面积:3.14×(4÷2)2
=3.14×22
=3.14×4
=12.56(平方厘米)
第二种剪法:一个圆的直径:4÷2=2(厘米)
3.14×(2÷2)2×4
=3.14×12×4
=3.14×1×4
=3.14×4
=12.56(平方厘米)
第三种剪法:一个圆的直径:4÷4=1(厘米)
3.14×(1÷2)2×16
=3.14×0.52×16
=3.14×0.25×16
=0.785×16
=12.56(平方厘米)
12.56=12.56=12.56,三种剪法浪费同样多。
三张边长都是16厘米的正方形纸板,分别按右边三种不同剪法剪下不同规格的圆片。从浪费材料的角度考虑,三种浪费同样多。
故答案为:D
35.;;;
;1;;
【解析】略
36.;;;
0;;
【分析】按照从左到右的顺序计算;
根据加法交换律和结合律,把原式化为+(-)进行计算;
根据加法交换律和结合律把原式化为:()+()进行简算;
根据加法交换律和减法的性质把原式化为:(+)-()进行简算;
先去括号,把原式化为-+,再根据加法交换律把原式化为:+-进行简算;
先去括号,再根据加法交换律和结合律把原式化为:-+(+)进行简算。
【解析】
=-+
=+
=+
=
=+(-)
=+
=+
=
=()+()
=1+
=
=(+)-()
=1-1
=0
=-+
=+-
=1-
=
=+-+
=-+(+)
=-+(+)
=+1
=
37.;;;
;;
【分析】根据等式的性质2,方程两边同时除以3.8;
根据等式的性质2,方程两边同时乘0.72;
方程两边同时减去0.36,两边再同时除以2;
方程两边同时乘7,两边再同时除以4.2;
先把方程左边 1.2x,两边再同时除以1.2;
先计算出4×9=36,两边再同时加上36,最后两边再同时除以3。
【解析】3.8x=15.2
解:3.8x÷3.8=15.2÷3.8
x=4
x÷0.72=2
解:x÷0.72×0.72=2×0.72
x=1.44
解:0.36+2x-0.36=0.64-0.36
2x=0.28
2x÷2=0.28÷2
x=0.14
4.2x÷7=12.6
解:4.2x÷7×7=12.6×7
4.2x=88.2
4.2x÷4.2=88.2÷4.2
x=21
2.2x-x=0.3
解:1.2x=0.3
1.2x÷1.2=0.3÷1.2
x=0.25
3x-4×9=66
解:3x-36=66
3x-36+36=66+36
3x=102
3x÷3=102÷3
x=34
38.10.75cm2;34.83cm2
【分析】图一和图二涂色部分的面积=长方形的面积-半圆的面积,根据长方形的面积=ab,半圆的面积=πr2÷2,代入数据解答即可;
【解析】
图一涂色部分的面积是10.75cm2,图二涂色部分的面积是34.83cm2。
39.(1)(3,7)
(2)见详解
(3)见详解
【分析】(1)用数对表示位置的方法:第一个数表示列,第二个数表示行,据此表示出圆心的位置即可;
(2)根据图形平移的方法,先把这个图形的圆心向右平移3格,再把圆心向下平移4格,得到平移后的图形的圆心,再以1格为半径画圆即可得出平移后的图形;
(3)根据数对表示位置的方法,找出(7,7)在图中的点,以该点为圆心,以(1×2)个格的长度为半径作圆即可。
【解析】(1)圆心O的位置用数对表示是:(3,7)。
(2)平移后圆心O的位置用数对表示是:(6,3),平移后的圆如下图所示。
(3)1×2=2(格)
作图如下:
40.9名;5块;4块
【分析】把45块水果糖和38块巧克力分别平均分给一个小组的同学,结果水果糖刚好分完,巧克力剩2块;则45、38减去2后就都能平均分给这个小组的学生,要求这个组最多有几位同学,只要求出这45和36的最大公因数即可;然后根据水果糖和巧克力的块数和学生数即可求出每个同学分到水果糖和巧克力的块数,据此解答。
【解析】38-2=36(块)
45=3×3×5
36=2×2×3×3
所以45和36的最大公因数是3×3=9。
即这个小组最多有9名同学。
45÷9=5(块)
36÷9=4(块)
答:这个小组最多有9名同学,每名同学分到水果糖5块,巧克力4块。
41.4面
【分析】根据题意,原来每隔6米插一面彩旗,现在改为每隔9米插一面彩旗,那么不需要移动的彩旗位置是6米和9米公倍数;先求出6和9的最小公倍数,再看全长72米里面有几个这样的最小公倍数,即可求出除起点的那面彩旗以外不需要移动的彩旗数量。
【解析】6=2×3
9=3×3
6和9的最小公倍数是2×3×3=18
即每隔18米的彩旗不需要移动。
72÷18=4(面)
答:还有4面彩旗也不需要移动。
42.770千米
【分析】由题意可知,从甲地到乙地快车比慢车少行驶3小时,把慢车的行驶时间设为未知数,快车的行驶时间=慢车的行驶时间-3小时,等量关系式:快车的速度×快车的时间=慢车的速度×慢车的时间,据此列方程并求出慢车的行驶时间,最后根据“路程=速度×时间”求出甲、乙两地间的距离,据此解答。
【解析】解:设从甲地到乙地慢车行驶x小时,则快车行驶(x-3)小时。
70×(x-3)=55x
70x-70×3=55x
70x-210=55x
70x-210-55x=55x-55x
70x-55x-210=0
15x-210=0
15x-210+210=0+210
15x=210
15x÷15=210÷15
x=14
14×55=770(千米)
答:甲、乙两地间的距离是770千米。
43.12束;9朵
【分析】把48朵黄花和60朵红花分成若干束(所有花都分完),要求每束里的黄花朵数同样多,红花朵数也同样多,那么最多能分成的束数是48和60的最大公因数;
先将48和60分解质因数,把公有的相同质因数乘起来就是它们的最大公因数。再看48和60里面分别有几个这个最大公因数,最后相加,即是每束里共有花的朵数。
【解析】48=2×2×2×2×3
60=2×2×3×5
48和60的最大公因数是:2×2×3=12
即最多可以分成12束。
48÷12=4(朵)
60÷12=5(朵)
4+5=9(朵)
答:最多可以分成12束,每束里共有9朵花。
44.12个;576平方厘米
【分析】首先要拼成正方形,正方形的边长应是长方形长和宽的最小公倍数,分解质因数求出8和6的最小公倍数;然后计算正方形边长分别是长方形长和宽的倍数,正方形边长是长方形长的24÷8=3倍,是长方形宽的24÷6=4倍,所以拼成这个正方形需要长方形的个数为3×4 = 12个;由前面可知正方形的边长,根据“正方形面积=边长×边长”计算出正方形面积。
【解析】8=2×2×2
6=2×3
所以8和6的最小公倍数是2×2×2×3=24
24÷8=3
24÷6=4
3×4=12(个)
答:至少用12个长方形才能拼成一个正方形;
24×24=576(平方厘米)
答:拼成的正方形面积是576平方厘米。
45.400秒
【分析】分析题目,爸爸第二次追上小明时,爸爸比小明多跑了2个全程,设x秒后,爸爸第二次追上小明,根据等量关系:爸爸的速度×时间-小明的速度×时间=400×2列出方程5.5x-3.5x=400×2,进一步解出方程即可。
【解析】解:设x秒后,爸爸第二次追上小明。
5.5x-3.5x=400×2
2x=800
2x÷2=800÷2
x=400
答:400秒后,爸爸第二次追上小明。
46.(1)公因;
(2)见详解;
(3)画图见详解;5;3;15
【分析】由题意可知,如果瓷砖为整块,那么瓷砖的边长同时是长方形墙长和宽的因数,求瓷砖的最长边长就是求长和宽的最大公因数,先按顺序列举出40的因数和24的因数,再找出它们的公因数和最大公因数,长方形的长需要瓷砖的块数=长方形的长÷瓷砖的边长,长方形的宽需要瓷砖的块数=长方形的宽÷瓷砖的边长,最后把块数相乘求出需要瓷砖的总块数,据此解答。
【解析】(1)分析可知,瓷砖边长的分米数必须是40和24的公因数。
(2)40的因数有:1,2,4,5,8,10,20,40。
24的因数有:1,2,3,4,6,8,12,24。
40和24的公因数有:1,2,4,8,其中最大公因数是8。
答:可以选择边长是1分米、2分米、4分米、8分米的瓷砖,瓷砖边长最长是8分米。
(3)
40÷8=5(块)
24÷8=3(块)
5×3=15(块)
所以,沿着长方形的长能贴5块,宽能贴3块,一共可以贴15块。
47.8名
【分析】由题意可知,找出80和60的最大公因数即最大的间距,再用80与60的和去除以最大的间距,起点A处还需1人,所以再加1,即可得至少要安排的志愿者人数。
【解析】80=2×2×2×2×5
60=2×2×3×5
最大公约数是2×2×5=20
(80+60)÷20
=140÷20
=7(名)
7+1=8(名)
答:这段赛道至少安排8名志愿者。
48.符合国家标准
【分析】根据题意,可知数量关系:(楼层数-1)×除一层外的每层高度+一楼的高度=一幢的高度;设其余每层的高度都是x米,然后根据数量关系列方程,运用等式的性质解方程即可。
【解析】解:设其余每层的高度都是x米。
(20-1)x+3.8=57
19x+3.8=57
19x=57-3.8
19x=53.2
x=53.2÷19
x=2.8
2.8米=2.80米
答:其余每层的高度符合国家标准。
49.(1)49人
(2)①乙
②200米;200米
【分析】(1)分组时4人一组或6人一组都余1人,将这1人减去剩下的人数正好同时被4和6整除,找出4和6的最小公倍数是12,用找倍数的方式找出40到50之间12的倍数,再加上1即可。
(2)根据折线统计图,找出2分钟的位置,乙的路程在甲的上面则领先的是乙龙舟队;
乙龙舟队5分钟行驶了1000米,根据平均速度=路程÷时间,根据路程=时间×速度,得出4分钟乙龙舟行驶了800米,再用全程减去800米就是乙龙舟的距离。
【解析】(1)4=2×2
6=2×3
[4,6]=2×2×3=12
50以内12的倍数:12、24、36、48
48+1=49(人)
答:五年级参加龙舟比赛的学生有49人。
(2)①开赛2分钟后,处于领先位置的是乙龙舟队。
②1000÷5=200(米/分)
1000-200×4
=1000-800
=200(米)
答:乙龙舟队平均每分钟行200米,开赛4分钟后,乙龙舟队离终点还有200米。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年五年级下册数学期末高频易错押题提升卷(苏教版)
一、填空题
1.一个三位数37□,当它既是2的倍数又是5的倍数时,□里填( )。当它是3的倍数时,□里可以填的数是( )。
2.小静打开数学书时,发现两页页码之积是420,这两页分别是( )页和( )页。
3.一个四位数,千位上既不是质数也不是合数,百位上是最小的合数,十位上是最大的一位数,个位上是10以内最大的质数,这个数是( )。
4.一根铁丝长1m,用它来围直径为10cm的圆(接头处不计),最多可以围( )个这样的圆。
5.一辆自行车的车轮半径是40厘米,车轮每分钟转100圈,要通过2512米的大桥,需要( )分钟。
6.一个圆柱形旋转展台,台面周长为18.84米,台面的面积是( )平方米。
7.的分数单位是( ),它化成带分数是( );它再加( )这样的分数单位就是最小的合数。
8.三个连续自然数,如果中间的数是N,那么这三个数的和是( );如果这三个数的和是120,那么最大数是( )。
9.五(1)班的学生人数在40~50人,王老师想把全体学生平均分成若干个学习小组,无论按4人一组还是6人一组,都正好多出1人。这个班有( )人。
10.如图a和b的最大公因数是( ),a和b的最小公倍数是( )。
11.将一个圆平均分成48等份后拼成一个近似的长方形。如果测得这个长方形的长为6.28dm,那么原来的圆的面积是( )dm2,长方形的周长是( )dm。
12.小东住在小南和小北两家的中间,三家门牌号是相邻的奇数,而且三家门牌号之和是69,小东家的门牌号是( )。
13.五(1)班购买来3箱苹果共有120个,共重20千克,把这些苹果平均分给班上的30名学生,每名学生分得( )个苹果,每名学生分得箱苹果,每名学生分得千克苹果。
14.某小学篮球社团有x人,“小百灵”社团的人数是篮球社团的2倍,这两个社团一共有( )人。当x=5时,这两个社团一共有( )人。
15.五年级学生分组举行“畅想未来”科技比赛,五(1)班学生每组8人或每组12人都正好分完。五(1)班学生人数在40~50人之间,五(1)班学生有( )人。
二、判断题
16.走同一段路,小刚要用20分,小明要用16分,小刚的速度比小明的速度快。( )
17.圆和圆环都是轴对称图形,都有无数条对称轴。( )
18.世界上第一个把圆周率的值精确到小数点后7位的科学家是刘徽。( )
19.如果n是一个奇数,那么n+3一定是奇数。( )
20.圆的半径扩大到原来的3倍,它的周长扩大到原来的3倍,面积扩大到原来的6倍。( )
21.大圆的圆周率大于小圆的圆周率。( )
22.分子和分母都是合数的分数,一定不是最简分数。( )
23.既是2的倍数又是5的倍数的数,个位上必定是1。( )
24.既是2和5的倍数,又有因数3的最大两位数是90。( )
三、选择题
25.下面运用了“转化”思想的是( )。
①求多边形内角和 ②异分母分数加法 ③求平行四边形面积
A.①② B.②③ C.①②③
26.一杯金银花露,爸爸先喝杯,用水加满,又喝杯,再用水加满后喝完。爸喝的金银花露和水相比,( )。
A.金银花露多 B.水多 C.一样多
27.高速列车的速度是300千米/时,如果速度减少80千米/时,就相当于一辆轿车速度的2倍。要知道轿车的速度,可以用下面的方程( )求解。
A.2x+80=300 B.x+80=300+2
C.2x-80=300 D.2x+80=300+2
28.一个圆形射击靶的周长是2.826米,射中靶心代表是10环,一个运动员射击时得了4环,他射中的位置距离靶心可能是( )厘米。
A.900 B.90 C.50 D.30
29.生产同一个零件,甲需要小时,乙需要小时,甲和乙相比,( )。
A.甲生产得快 B.乙生产得快 C.生产得一样快
30.如图,正方形的面积是64平方厘米,圆的面积是( )平方厘米。
A. B. C. D.
31.在住院病房中,护士每天要多次测量患者的体温,为了观察一个患者的体温变化情况,应绘制( )比较合适。
A.折线统计图 B.条形统计图 C.统计表 D.以上答案都不正确
32.如图所示的各图都表示“1”,阴影部分表示的大小或问号对应的长度,可以用“++”计算的有( )。
A.1个 B.2个 C.3个 D.4个
33.如图是一个钟面,分针长8厘米,时针长4厘米,分针走一圈比时针走一圈扫过的面积多( )平方厘米。
A.25.12 B.150.72 C.20.24
34.三张边长都是16厘米的正方形纸板,分别按右边三种不同剪法剪下不同规格的圆片。从浪费材料的角度考虑,( )。
A.第一种浪费多 B.第二种浪费多 C.第三种浪费多 D.三种浪费同样多
四、计算题
35.直接写出得数。
= = = =
= = = =
36.计算下面各题,能简算的要简算。
37.解方程。
38.求下面长方形中涂色部分的面积。
五、作图题
39.按要求操作。
(1)用数对表示圆心O的位置。
(2)将图中的圆向右平移3格,再向下平移4格。
(3)以点O1(7,7)为圆心画一个圆,使其半径是上图中圆的2倍。
六、解答题
40.把45块水果糖和38块巧克力分别平均分给一个小组的同学,结果水果糖刚好分完,巧克力还剩2块。这个小组最多有几名同学?每名同学分到水果糖和巧克力各几块?
41.在一条长72米的道路一侧原来每隔6米插一面彩旗,现在改为每隔9米插一面彩旗。如果起点的那面彩旗不移动,还有多少面彩旗也不需要移动?
42.快、慢两车同时从甲地到乙地,快车每小时行70千米,慢车每小时行55千米。途中快车因故停留3小时,结果两车同时到达乙地。甲、乙两地间的距离是多少千米?
43.同学们做了48朵黄花和60朵红花。把这些花分成若干束(所有花都分完),要求每束里的黄花朵数同样多,红花朵数也同样多。最多可以分成几束?每束里共有几朵花?
44.欢欢用同样大小的长方形拼正方形。长方形的长是8厘米,宽是6厘米,至少用多少个长方形才能拼成一个正方形?拼成的正方形面积是多少平方厘米?
45.爸爸和小明在400米的环形操场跑步,从同一起点同向而行,爸爸的速度是每秒5.5米,小明的速度是每秒3.5米,多少秒后,爸爸第二次追上小明?(列方程解题)
46.有一面长方形墙(示意图如图),如果用一种边长是整分米数的正方形瓷砖把这面墙贴满(瓷砖为整块),那么可以选择边长是多少分米的瓷砖?瓷砖边长最长是多少分米?
(1)瓷砖边长的分米数必须是40和24的( )数。
(2)试着写下你的解决方案。
(3)在图中,请你试着将你的解决方案在图里画一画,沿着长方形的长能贴( )块,宽能贴( )块,一共可以贴( )块。
47.迷你马拉松正在海城举行,如图是赛道的一部分,赛道在B点拐弯,根据比赛要求需要在路的一边排志愿者,志愿者之间的距离必须相等,而且A、B、C处必须安排志愿者。那么这段赛道至少要安排多少名志愿者?
48.国家标准《住宅设计规范》中规定:普通住宅层高宜为2.80米(除一层外)。幸福小区一幢20层的楼高57米,除一层高度是3.8米外,其余每层的高度都相等,其余每层的高度符合国家标准吗?(列方程解答)
49.为弘扬中华传统文化,西渚实验小学在端午节期间举行了1000米龙舟比赛。
(1)五年级参加龙舟比赛的学生有40~50人,分组时4人一组或6人一组,都剩余1人,五年级参加龙舟比赛的学生有多少人?
(2)甲、乙两支龙舟队在比赛中路程与时间的关系如图。
①开赛2分钟后,处于领先位置的是( )龙舟队。
②乙龙舟队平均每分钟行多少米?开赛4分钟后,乙龙舟队离终点还有多少米?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.0 2、5或8
【分析】2的倍数特征:个位上是0、2、4、6、8的数。
5的倍数特征:个位上是0或5的数。
2、5的倍数特征:个位上是0的数。
3的倍数特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数。
【解析】个位数字是0,这样的数既是2的倍数又是5的倍数,370既是2的倍数又是5的倍数;
3+7+2=12,12是3的倍数,372是3的倍数;
3+7+5=15,15是3的倍数,375是3的倍数;
3+7+8=18,18是3的倍数,378是3的倍数。
一个三位数37□,当它既是2的倍数又是5的倍数时,□里填0。当它是3的倍数时,□里可以填的数是2、5或8。
2.20 21
【分析】根据题意,两页页码之积是420,先把420分解质因数,再把这些质因数重新组合,变成连续两个自然数相乘的形式,即可得解。
【解析】420=2×2×3×5×7=(2×2×5)×(3×7)=20×21
这两页分别是20页和21页。
3.1497
【分析】一个数,如果只有1和它本身两个因数,那么这样的数叫做质数。
一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。
【解析】一个四位数,千位上既不是质数也不是合数,即1;
百位上是最小的合数,即4;
十位上是最大的一位数,即9;
个位上是10以内最大的质数,即7;
这个数是1497。
4.3
【分析】根据题意,用一根铁丝围成直径为10cm的圆,那么铁丝长度等于圆的周长;根据公式C=πd求出圆的周长,也就是围成一个圆所需的铁丝长度;
求长1m的铁丝最多可以围几个这样的圆,就是看1m里面有几个圆的周长,用除法计算,计算结果用“去尾法”保留整数。
【解析】1m=100cm
3.14×10=31.4(cm)
100÷31.4≈3(个)
最多可以围3个这样的圆。
5.10
【分析】根据圆的周长公式:周长=π×半径×2,代入数据,求出自行车的车轮的周长,再用自行车车轮的周长×100,求出车轮每分钟行驶的距离,再用大桥的长度÷车轮每分钟行驶的距离,即可解答,注意单位名数的统一。
【解析】3.14×40×2×100
=125.6×2×100
=251.2×100
=25120(厘米)
25120厘米=251.2米
2512÷251.2=10(分钟)
一辆自行车的车轮半径是40厘米,车轮每分钟转100圈,要通过2512米的大桥,需要10分钟。
6.28.26
【分析】台面是一个圆形,根据圆的周长=,得出圆形的半径,再根据圆的面积=,得出圆的面积。
【解析】18.84÷3.14÷2=3(米)
3.14×32
=3.14×9
=28.26(平方米)
则台面的面积是28.26平方米。
7.
【分析】把单位“1”平均分成若干份,表示其中一份的数叫分数单位。对于真分数、假分数来说,分子是几,就有几个这样的分数单位。把假分数化成带分数的方法:用分子除以分母,得到的商和余数;商是带分数的整数部分,余数是带分数的分子,分母不变。最小的合数是4,先把4化成分母为5而大小不变的假分数,再看分子与的分子相差几,就需要再增加几个这样的分数单位就是最小的合数。
【解析】
的分数单位是,里有14个。
里有20个。
(个)
的分数单位是,它化成带分数是;它再加6个这样的分数单位就是最小的合数。
8.3N 41
【分析】连续两个数相差1,中间的数是N,则最小的数是N-1,最大的数是N+1,据此用含N的式子表示这三个数的和;把这三个数的和是120,代入式子中,利用等式的性质求出N的值,再求出最大数即可。
【解析】三个数的和:N+N-1+N+1=3N
当3个数的和是120,则3N=120
3N÷3=120÷3
N=40
最大数是:40+1=41
所以这三个数的和是3N;如果这三个数的和是120,那么最大数是41。
9.49
【分析】由题意可知,五(1)班的学生人数减少1后是4和6的公倍数,五(1)班的学生人数在40~50人,所以先求出在40~50之间4和6的公倍数,再用所求的公倍数再加1,即可求出五(1)班的学生人数,据此解答。
【解析】在40~50之间4的倍数有:40、44、48。
在40~50之间6的倍数有:42、48。
因此在40~50之间4和6的公倍数有:48。
48+1=49(人)
即这个班有49人。
10.12 72
【分析】最大公因数指几个整数共有因数中最大的一个;
一个数的最大因数是它本身;
最小公倍数指几个整数公有的倍数中最小的一个。把a和b分解质因数后,把公有的相同质因数与独有质因数乘起来就是它们的最小公倍数,据此解答。
【解析】由题可知,a和b的公因数有:1、2、3、4、6、12,最大的是12,所以a和b的最大公因数是12;
a的最大因数是24,所以a是24,b的最大因数是36,所以b是36。
24=2×2×2×3
36=2×2×3×3
所以24和36的最小公倍数是:2×2×2×3×3=72。
即a和b的最大公因数是12,a和b的最小公倍数是72。
11.12.56 16.56
【分析】将圆平均分成48等份后拼成一个近似的长方形,长方形的长是这个圆的半个圆弧的长度,则乘2求出圆的周长。再根据圆的周长C=,得出。圆的面积S=,将圆的半径带入公式计算即可。长方形的宽就是圆的半径,则长方形的周长=(长+宽)×2。
【解析】6.28×2÷3.14÷2
=12.56÷3.14÷2
=4÷2
=2(dm)
3.14×22
=3.14×4
=12.56(dm2)
(6.28+2)×2
=8.28×2
=16.56(dm)
原来的圆的面积是12.56dm2,长方形的周长是16.56dm。
12.23
【分析】相邻的奇数之间相差2,三个奇数的和÷3=中间奇数,据此列式计算。
【解析】69÷3=23
小东家的门牌号是23。
13.4;;
【分析】用苹果的总个数除以学生人数,可得到每名学生分得的苹果个数;用总箱数除以学生人数,可得到每名学生分得的箱数占比;用总质量除以学生人数,可得到每名学生分得的质量占比,据此解答。
【解析】120÷30=4(个)
3÷30=(箱)
20÷30=(千克)
即每名学生分得4个苹果,每名学生分得箱苹果,每名学生分得千克苹果。
14.3x 15
【分析】由题可得:篮球社团人数+“小百灵”社团的人数=这两个社团的总人数,篮球社团有x人,“小百灵”社团的人数是篮球社团的2倍,则“小百灵”社团的人数是2x,因此这两个社团一共有(x+2x)人,把x=5时,代入计算,即可求出这两个社团一共有的人数,据此解答。
【解析】2x+x=3x(人)
当x=5时,3×5=15(人)
即这两个社团一共有3x人,当x=5时,这两个社团一共有15人。
15.48
【分析】根据题意可知,五(1)班学生人数既是8的倍数,也是12的倍数,先求出8和12的最小公倍数,再找出40~50之间的8和12的公倍数,即可解答。
【解析】8=2×2×2
12=2×2×3
8和12的最小公倍数是2×2×2×3=24;
24×2=48,五(1)班学生有48人。
五年级学生分组举行“畅想未来”科技比赛,五(1)班学生每组8个或每组12人都正好分完。五(1)班学生人数在40~50人之间,五(1)班学生有48人。
16.×
【分析】在比赛中,走同一段路,谁用的时间少,说明了谁的速度就快,据此解答。
【解析】由分析可得:走同一段路,谁用的时间少,说明了谁的速度就快,小明要用16分钟,小刚要用20分钟,
16<20
所以小明用时比小刚少,所以小明的速度快,原题说法错误。
故答案为:×
17.√
【分析】如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫对称轴;判断一个图形是否是轴对称图形,关键是找它的对称轴,要想象沿着这条线翻折能不能重叠,据此判断。
【解析】
如图,圆和圆环都是轴对称图形,都有无数条对称轴,此题说法正确。
故答案为:√
18.×
【分析】我国魏晋时期数学家刘徽求得圆周率的近似值是3.14。我国南北朝科学家祖冲之算出圆周率大约在3.1415926和3.1415927之间,成为世界上第一个把圆周率的值精确到小数点后7位的人。
【解析】世界上第一个把圆周率的值精确到小数点后7位的科学家是祖冲之。即原题说法错误。
故答案为:×
19.×
【分析】整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数;根据题意,n是奇数,3是奇数;奇数+奇数=偶数;奇数+偶数=奇数;偶数+偶数=偶数;据此解答。
【解析】假设n=1,1+3=4,4是偶数,所以原题说法错误;
故答案为:×
20.×
【分析】假设原来的半径是1厘米,半径扩大到原来的3倍,则直径变为3厘米。根据圆的周长公式:C=2πr,圆面积公式:S=πr2,代入数据求出变化前后的周长和面积,进而求出周长扩大到原来的几倍以及面积扩大到原来的几倍。据此解答。
【解析】假设原来的半径是1厘米,
1×3=3(厘米)
(2×π×3)÷(2×π×1)
=6π÷2π
=3
(π×32)÷(π×12)
=(π×9)÷(π×1)
=9π÷π
=9
圆的半径扩大到原来的3倍,它的周长就扩大到原来的3倍,面积就扩大到原来的9倍。原题干说法错误。
故答案为:×
21.×
【分析】根据圆周率的含义:圆的周长和它直径的比值,叫做圆周率;圆周率用“π”表示,π是一个无限不循环小数;进而判断即可。
【解析】根据分析可知,圆周率是一个定值,不存在大圆的圆周率大于小圆的圆周率。
原题干说法错误。
故答案为:×
22.×
【分析】只要分子分母互质,这个分数就是最简分数;例如4和9都是合数,但是4和9互质,就是最简分数,据此判断即可。
【解析】分子和分母都是合数的分数,可能是最简分数,如是最简分数,原题说法错误。
故答案为:×
23.×
【分析】2的倍数特征:个位是0、2、4、6、8的数是2的倍数,5的倍数特征:个位是0、5的数是5的倍数,据此即可知道既是2的倍数,又是5的倍数,它的个位是0,据此即可判断。
【解析】由分析可知:
既是2的倍数又是5的倍数的数,个位上必定是0,原说法错误。
故答案为:×
24.√
【分析】2的倍数特征:末尾数字是0、2、4、6、8的数是2的倍数;3的倍数特征:各个数位上的数字之和是3的倍数,这个数字就是3的倍数;5的倍数特征:末尾数字是0或5的数是5的倍数,既是2和5的倍数,又有因数3,这个数的个位必须是0,据此解答。
【解析】根据分析可知,既是2和5的倍数,又有因数3的最大两位数是90。
原题干说法正确。
故答案为:√
25.C
【分析】①根据三角形内角和可知多边形的内角和;②根据异分母分数的加法运算法则可知同分母分数的加法运算;③根据长方形的面积可知平行四边形的面积。综上可知①②③都用了转化思想。
【解析】因为三角形的内角和为,
所以多边形的内角和为,
所以①用了转化思想;
因为,
所以,
所以②用了转化思想;
因为图中长方形的面积等于平行四边形的面积,
所以③用了转化思想;
综上,运用转化思想的是①②③,
故答案为:C
26.A
【分析】先确定爸爸喝的金银花露的量,一杯金银花露最后全部喝完,所以爸爸喝的金银花露是1杯;再分析爸爸喝的水的量,爸爸先喝杯,此时加了杯水,又喝了杯后再用水加满,又加了杯水,所以列式为+,算出结果即可。
【解析】爸爸喝的金银花露的量:一杯金银花露最后全部喝完,所以爸爸喝的金银花露是1杯,爸爸喝的水的量:+=+=,因为1>,所以爸爸喝的金银花露多。
故答案为:A
27.A
【分析】根据题意,此题的等量关系是:轿车的速度×2+80千米/小时=300千米/时,据此列方程。
【解析】根据上面的分析,假设轿车的速度为x,可以用方程2x+80=300求解。
故答案为:A
28.D
【分析】根据圆的周长公式:C=2πr,计算其半径,再把半径平均分成10份,4环与靶心的距离应该在(10-4)份到(10-3)份之间。
【解析】2.826米=282.6厘米
282.6÷3.14÷2=45(厘米)
45÷10×(10-4)
=45÷10×6
=27(厘米)
45÷10×(10-3)
=45÷10×7
=31.5(厘米)
A.900>31.5,不符合题意;
B.90>31.5,不符合题意;
C.50>31.5,不符合题意;
D.27<30<31.5,符合题意;
他射中的位置距离靶心可能是30厘米。
故答案为:D
29.A
【分析】生产同一个零件,谁用的时间少,谁就生产得快;根据分数比较大小的方法比较甲、乙用的时间,即可得解。
分数大小的比较:分母相同时,分子越大,分数值就越大;分子相同时,分母越大,分数值反而越小;分子、分母都不相同时,化成同分母或同分子的分数进行比较。
【解析】
,即;
甲需要的时间比乙少,所以甲生产得快。
故答案为:A
30.B
【分析】观察图形可知,正方形的对角线等于圆的直径;直径=半径×2;正方形的面积可以看成两个三角形的面积和,其中一个三角形的底是直径,高是半径,由此即可知道正方形的面积=(半径×2)×半径;即正方形的面积=2×半径2;由此可知,半径2=正方形面积÷2,再根据圆的面积公式:面积=π×半径2,据此求出圆的面积。
【解析】π×(64÷2)=32π(平方厘米)
正方形的面积是64平方厘米,圆的面积是32π平方厘米。
故答案为:B
31.A
【分析】统计表以表格呈现数据,条形统计图以直条呈现数据,都能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;由此根据情况选择即可。
【解析】观察患者的体温变化情况,选择折线统计图比较合适。
故答案为:A
32.C
【分析】图一:把圆先平均分成了2份,每份占,再把圆看作单位“1”,平均分成了4份,每份占,最后又把圆平均分成了8份,每份占,阴影部分表示为:++。
图二:把整个图形平均分成了2份,每份占,再把整个图形看作单位“1”,平均分成了4份,每份占,又把整个图形平均分成了8份,每份占,最后把整个图形平均分成了16份,每份占,阴影部分表示为:+++。
图三:把整个图形平均分成了2份,每份占,再把整个图形看作单位“1”,平均分成了4份,每份占,又把整个图形平均分成了8份,每份占,阴影部分表示为:++。
图四:把整个图形平均分成了2份,每份占,再把整个图形看作单位“1”,平均分成了4份,每份占,又把整个图形平均分成了8份,每份占,阴影部分表示为:++。
【解析】由分析可知:
如图所示的各图都表示“1”,阴影部分表示的大小或问号对应的长度,可以用“++”计算的有3个。
故答案为:C
33.B
【分析】分针走一圈比时针走一圈多扫过的面是个圆环,分针和时针的长分别是大圆和小圆的半径,根据圆环面积=圆周率×(大圆半径的平方-小圆半径的平方),列式计算即可。
【解析】3.14×(82-42)
=3.14×(64-16)
=3.14×48
=150.72(平方厘米)
分针走一圈比时针走一圈扫过的面积多150.72平方厘米。
故答案为:B
34.D
【分析】根据正方形周长公式:周长=边长×4,边长=周长÷4,求出正方形的边长;根据圆的面积公式:面积=π×半径2,代入数据,分别求出三种不同图形中的圆的面积,哪种圆的面积大,哪种剪法浪费的少,反之,哪种圆的面积小,哪种剪法浪费的所,如果三种面积相同,浪费的一样多,据此解答。
【解析】16÷4=4(厘米)
第一种剪法:圆的直径等于4厘米
面积:3.14×(4÷2)2
=3.14×22
=3.14×4
=12.56(平方厘米)
第二种剪法:一个圆的直径:4÷2=2(厘米)
3.14×(2÷2)2×4
=3.14×12×4
=3.14×1×4
=3.14×4
=12.56(平方厘米)
第三种剪法:一个圆的直径:4÷4=1(厘米)
3.14×(1÷2)2×16
=3.14×0.52×16
=3.14×0.25×16
=0.785×16
=12.56(平方厘米)
12.56=12.56=12.56,三种剪法浪费同样多。
三张边长都是16厘米的正方形纸板,分别按右边三种不同剪法剪下不同规格的圆片。从浪费材料的角度考虑,三种浪费同样多。
故答案为:D
35.;;;
;1;;
【解析】略
36.;;;
0;;
【分析】按照从左到右的顺序计算;
根据加法交换律和结合律,把原式化为+(-)进行计算;
根据加法交换律和结合律把原式化为:()+()进行简算;
根据加法交换律和减法的性质把原式化为:(+)-()进行简算;
先去括号,把原式化为-+,再根据加法交换律把原式化为:+-进行简算;
先去括号,再根据加法交换律和结合律把原式化为:-+(+)进行简算。
【解析】
=-+
=+
=+
=
=+(-)
=+
=+
=
=()+()
=1+
=
=(+)-()
=1-1
=0
=-+
=+-
=1-
=
=+-+
=-+(+)
=-+(+)
=+1
=
37.;;;
;;
【分析】根据等式的性质2,方程两边同时除以3.8;
根据等式的性质2,方程两边同时乘0.72;
方程两边同时减去0.36,两边再同时除以2;
方程两边同时乘7,两边再同时除以4.2;
先把方程左边 1.2x,两边再同时除以1.2;
先计算出4×9=36,两边再同时加上36,最后两边再同时除以3。
【解析】3.8x=15.2
解:3.8x÷3.8=15.2÷3.8
x=4
x÷0.72=2
解:x÷0.72×0.72=2×0.72
x=1.44
解:0.36+2x-0.36=0.64-0.36
2x=0.28
2x÷2=0.28÷2
x=0.14
4.2x÷7=12.6
解:4.2x÷7×7=12.6×7
4.2x=88.2
4.2x÷4.2=88.2÷4.2
x=21
2.2x-x=0.3
解:1.2x=0.3
1.2x÷1.2=0.3÷1.2
x=0.25
3x-4×9=66
解:3x-36=66
3x-36+36=66+36
3x=102
3x÷3=102÷3
x=34
38.10.75cm2;34.83cm2
【分析】图一和图二涂色部分的面积=长方形的面积-半圆的面积,根据长方形的面积=ab,半圆的面积=πr2÷2,代入数据解答即可;
【解析】
图一涂色部分的面积是10.75cm2,图二涂色部分的面积是34.83cm2。
39.(1)(3,7)
(2)见详解
(3)见详解
【分析】(1)用数对表示位置的方法:第一个数表示列,第二个数表示行,据此表示出圆心的位置即可;
(2)根据图形平移的方法,先把这个图形的圆心向右平移3格,再把圆心向下平移4格,得到平移后的图形的圆心,再以1格为半径画圆即可得出平移后的图形;
(3)根据数对表示位置的方法,找出(7,7)在图中的点,以该点为圆心,以(1×2)个格的长度为半径作圆即可。
【解析】(1)圆心O的位置用数对表示是:(3,7)。
(2)平移后圆心O的位置用数对表示是:(6,3),平移后的圆如下图所示。
(3)1×2=2(格)
作图如下:
40.9名;5块;4块
【分析】把45块水果糖和38块巧克力分别平均分给一个小组的同学,结果水果糖刚好分完,巧克力剩2块;则45、38减去2后就都能平均分给这个小组的学生,要求这个组最多有几位同学,只要求出这45和36的最大公因数即可;然后根据水果糖和巧克力的块数和学生数即可求出每个同学分到水果糖和巧克力的块数,据此解答。
【解析】38-2=36(块)
45=3×3×5
36=2×2×3×3
所以45和36的最大公因数是3×3=9。
即这个小组最多有9名同学。
45÷9=5(块)
36÷9=4(块)
答:这个小组最多有9名同学,每名同学分到水果糖5块,巧克力4块。
41.4面
【分析】根据题意,原来每隔6米插一面彩旗,现在改为每隔9米插一面彩旗,那么不需要移动的彩旗位置是6米和9米公倍数;先求出6和9的最小公倍数,再看全长72米里面有几个这样的最小公倍数,即可求出除起点的那面彩旗以外不需要移动的彩旗数量。
【解析】6=2×3
9=3×3
6和9的最小公倍数是2×3×3=18
即每隔18米的彩旗不需要移动。
72÷18=4(面)
答:还有4面彩旗也不需要移动。
42.770千米
【分析】由题意可知,从甲地到乙地快车比慢车少行驶3小时,把慢车的行驶时间设为未知数,快车的行驶时间=慢车的行驶时间-3小时,等量关系式:快车的速度×快车的时间=慢车的速度×慢车的时间,据此列方程并求出慢车的行驶时间,最后根据“路程=速度×时间”求出甲、乙两地间的距离,据此解答。
【解析】解:设从甲地到乙地慢车行驶x小时,则快车行驶(x-3)小时。
70×(x-3)=55x
70x-70×3=55x
70x-210=55x
70x-210-55x=55x-55x
70x-55x-210=0
15x-210=0
15x-210+210=0+210
15x=210
15x÷15=210÷15
x=14
14×55=770(千米)
答:甲、乙两地间的距离是770千米。
43.12束;9朵
【分析】把48朵黄花和60朵红花分成若干束(所有花都分完),要求每束里的黄花朵数同样多,红花朵数也同样多,那么最多能分成的束数是48和60的最大公因数;
先将48和60分解质因数,把公有的相同质因数乘起来就是它们的最大公因数。再看48和60里面分别有几个这个最大公因数,最后相加,即是每束里共有花的朵数。
【解析】48=2×2×2×2×3
60=2×2×3×5
48和60的最大公因数是:2×2×3=12
即最多可以分成12束。
48÷12=4(朵)
60÷12=5(朵)
4+5=9(朵)
答:最多可以分成12束,每束里共有9朵花。
44.12个;576平方厘米
【分析】首先要拼成正方形,正方形的边长应是长方形长和宽的最小公倍数,分解质因数求出8和6的最小公倍数;然后计算正方形边长分别是长方形长和宽的倍数,正方形边长是长方形长的24÷8=3倍,是长方形宽的24÷6=4倍,所以拼成这个正方形需要长方形的个数为3×4 = 12个;由前面可知正方形的边长,根据“正方形面积=边长×边长”计算出正方形面积。
【解析】8=2×2×2
6=2×3
所以8和6的最小公倍数是2×2×2×3=24
24÷8=3
24÷6=4
3×4=12(个)
答:至少用12个长方形才能拼成一个正方形;
24×24=576(平方厘米)
答:拼成的正方形面积是576平方厘米。
45.400秒
【分析】分析题目,爸爸第二次追上小明时,爸爸比小明多跑了2个全程,设x秒后,爸爸第二次追上小明,根据等量关系:爸爸的速度×时间-小明的速度×时间=400×2列出方程5.5x-3.5x=400×2,进一步解出方程即可。
【解析】解:设x秒后,爸爸第二次追上小明。
5.5x-3.5x=400×2
2x=800
2x÷2=800÷2
x=400
答:400秒后,爸爸第二次追上小明。
46.(1)公因;
(2)见详解;
(3)画图见详解;5;3;15
【分析】由题意可知,如果瓷砖为整块,那么瓷砖的边长同时是长方形墙长和宽的因数,求瓷砖的最长边长就是求长和宽的最大公因数,先按顺序列举出40的因数和24的因数,再找出它们的公因数和最大公因数,长方形的长需要瓷砖的块数=长方形的长÷瓷砖的边长,长方形的宽需要瓷砖的块数=长方形的宽÷瓷砖的边长,最后把块数相乘求出需要瓷砖的总块数,据此解答。
【解析】(1)分析可知,瓷砖边长的分米数必须是40和24的公因数。
(2)40的因数有:1,2,4,5,8,10,20,40。
24的因数有:1,2,3,4,6,8,12,24。
40和24的公因数有:1,2,4,8,其中最大公因数是8。
答:可以选择边长是1分米、2分米、4分米、8分米的瓷砖,瓷砖边长最长是8分米。
(3)
40÷8=5(块)
24÷8=3(块)
5×3=15(块)
所以,沿着长方形的长能贴5块,宽能贴3块,一共可以贴15块。
47.8名
【分析】由题意可知,找出80和60的最大公因数即最大的间距,再用80与60的和去除以最大的间距,起点A处还需1人,所以再加1,即可得至少要安排的志愿者人数。
【解析】80=2×2×2×2×5
60=2×2×3×5
最大公约数是2×2×5=20
(80+60)÷20
=140÷20
=7(名)
7+1=8(名)
答:这段赛道至少安排8名志愿者。
48.符合国家标准
【分析】根据题意,可知数量关系:(楼层数-1)×除一层外的每层高度+一楼的高度=一幢的高度;设其余每层的高度都是x米,然后根据数量关系列方程,运用等式的性质解方程即可。
【解析】解:设其余每层的高度都是x米。
(20-1)x+3.8=57
19x+3.8=57
19x=57-3.8
19x=53.2
x=53.2÷19
x=2.8
2.8米=2.80米
答:其余每层的高度符合国家标准。
49.(1)49人
(2)①乙
②200米;200米
【分析】(1)分组时4人一组或6人一组都余1人,将这1人减去剩下的人数正好同时被4和6整除,找出4和6的最小公倍数是12,用找倍数的方式找出40到50之间12的倍数,再加上1即可。
(2)根据折线统计图,找出2分钟的位置,乙的路程在甲的上面则领先的是乙龙舟队;
乙龙舟队5分钟行驶了1000米,根据平均速度=路程÷时间,根据路程=时间×速度,得出4分钟乙龙舟行驶了800米,再用全程减去800米就是乙龙舟的距离。
【解析】(1)4=2×2
6=2×3
[4,6]=2×2×3=12
50以内12的倍数:12、24、36、48
48+1=49(人)
答:五年级参加龙舟比赛的学生有49人。
(2)①开赛2分钟后,处于领先位置的是乙龙舟队。
②1000÷5=200(米/分)
1000-200×4
=1000-800
=200(米)
答:乙龙舟队平均每分钟行200米,开赛4分钟后,乙龙舟队离终点还有200米。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
