青岛版2024—2025学年七年级下册数学期末复习提分强化训练(含答案)
文档属性
| 名称 | 青岛版2024—2025学年七年级下册数学期末复习提分强化训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 797.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-26 08:32:06 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
青岛版2024—2025学年七年级下册数学期末复习提分强化训练
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列调查中,适合用抽样调查的是( )
A.对登机的旅客进行安全检查 B.考察一批灯泡的使用寿命
C.发射运载火箭前的检查 D.订购校服时了解某班学生衣服的尺寸
2.如图所示,下列说法错误的是( )
A.由,可得到
B.由,可得到
C.由,可得到
D.由,可得到
3.若是二元一次方程组的解,则的值为( )
A. B. C. D.
4.已知,,,则a,b,c之间满足的等式是( )
A. B.
C. D.
5.若是完全平方式,则的值是( )
A.或 B.或 C.或 D.或
6.若多项式因式分解的结果为,则的值为( )
A. B. C.19 D.21
7.下列长度的三条线段能组成三角形的是( )
A.3,4,9 B.3,4,8 C.3,4,7 D.3,4,6
8.如图,等于( )
B. C. D.
9.已知关于的二元一次方程组的解为,若满足二元一次方程组,则( )
A.1 B.2 C. D.
10.如图,将两张长为a,宽为b的长方形纸片按图1,图2两种方式放置,图1和图2中两张长方形纸片重叠的部分分别记为①和②,正方形中未被这两张长方形纸片覆盖的部分用阴影表示,①和②的面积分别记为和.若知道下列条件,可以求值的是( )
A.长方形纸片的面积 B.长方形纸片的周长
C.长方形纸片和①的面积差 D.图1与图2阴影部分的面积差
二、填空题(6小题,每题3分,共18分)
11.分解因式: .
12.计算: .
13.已知关于x,y的方程组的解满足.则m的值是 .
14.某口袋中有红色、黄色、黑色的小球共个,这些小球除颜色外都相同,通过多次试验后发现摸到红色球的频率稳定在,则袋中红色球是 个.
15.如图,,,平分,则的度数 .
16.如图,,,分别是的边,,的中点,连接,,交于点,的面积为6,设的面积为,的面积为,则 .
青岛版2024—2025学年七年级下册数学期末复习提分强化训练
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解方程组
(1); (2).
18.(1)化简:;
(2)先化简再求值:,其中,.
19.因式分解.
(1).
(2)
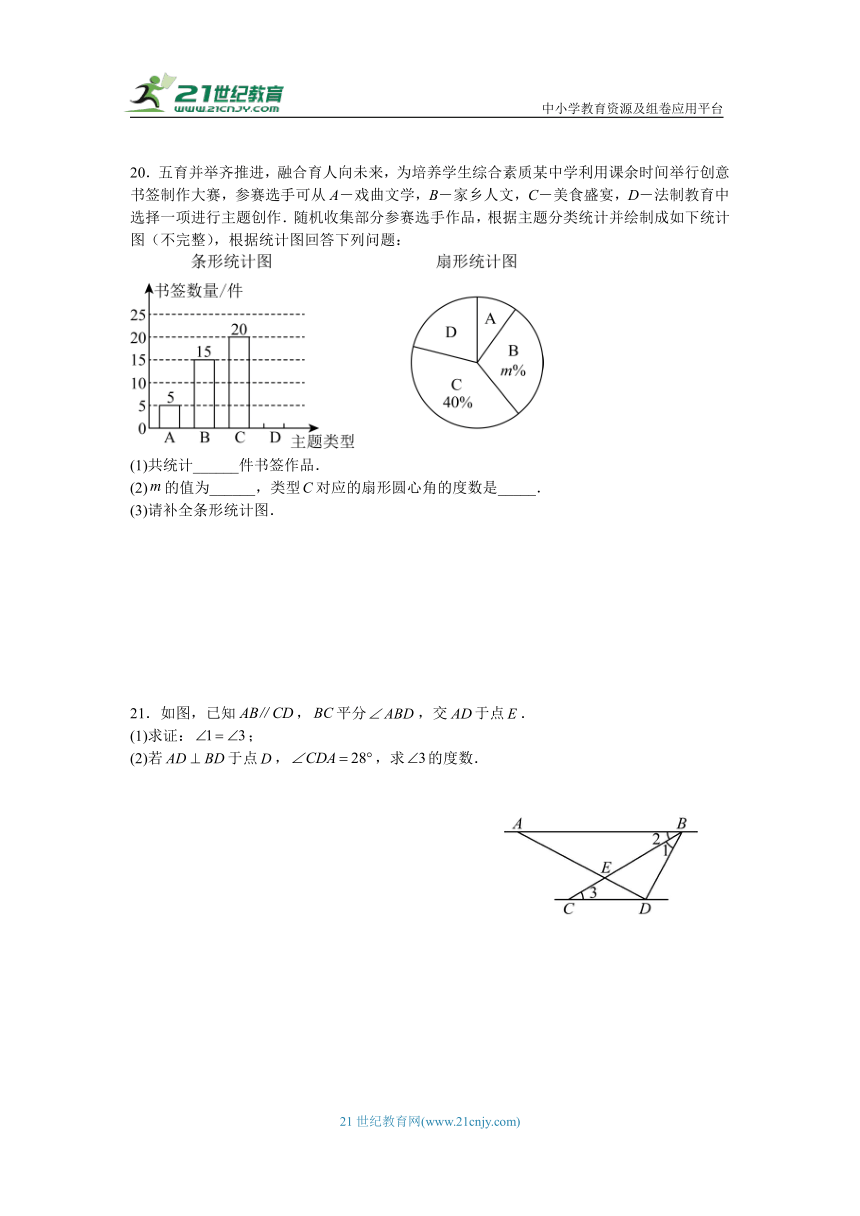
20.五育并举齐推进,融合育人向未来,为培养学生综合素质某中学利用课余时间举行创意书签制作大赛,参赛选手可从A-戏曲文学,B-家乡人文,C-美食盛宴,D-法制教育中选择一项进行主题创作.随机收集部分参赛选手作品,根据主题分类统计并绘制成如下统计图(不完整),根据统计图回答下列问题:
(1)共统计______件书签作品.
(2)的值为______,类型对应的扇形圆心角的度数是_____.
(3)请补全条形统计图.
21.如图,已知,平分,交于点.
(1)求证:;
(2)若于点,,求的度数.
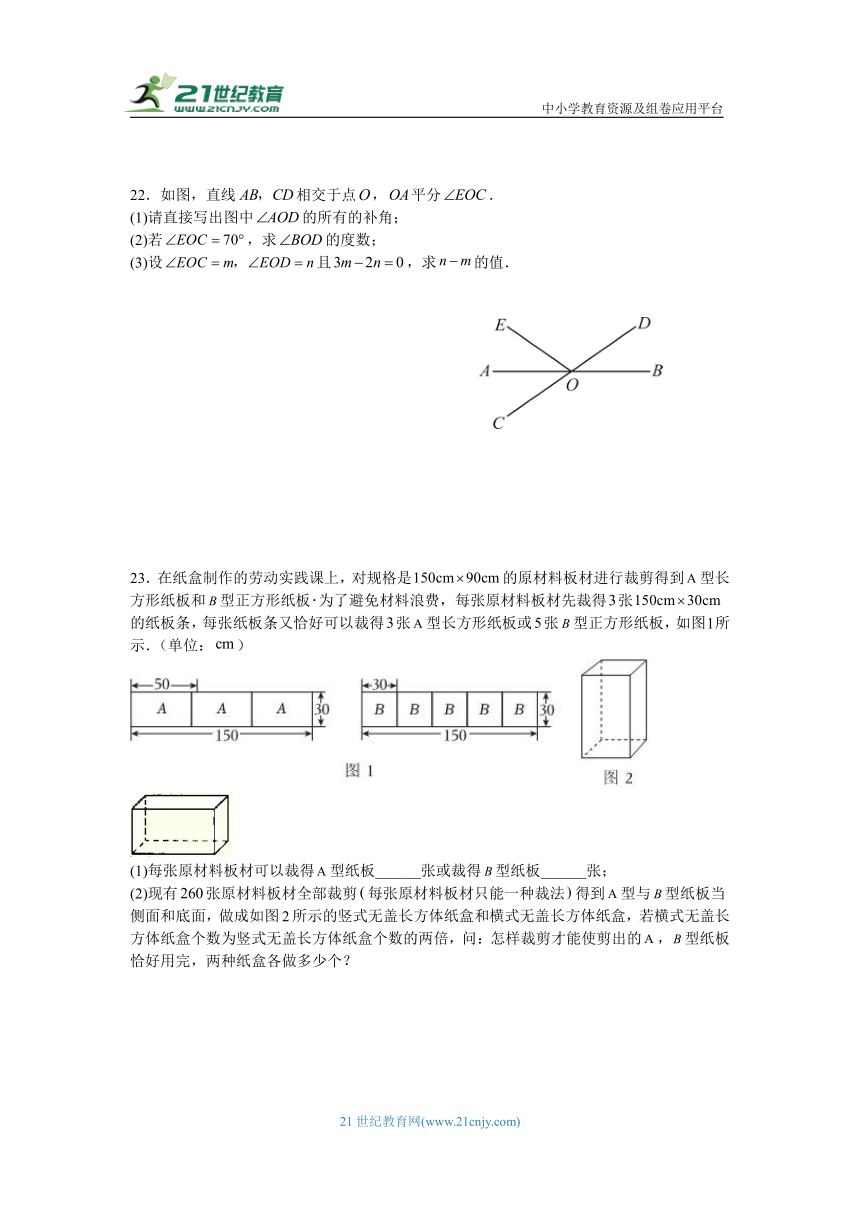
22.如图,直线相交于点,平分.
(1)请直接写出图中的所有的补角;
(2)若,求的度数;
(3)设且,求的值.
23.在纸盒制作的劳动实践课上,对规格是的原材料板材进行裁剪得到型长方形纸板和型正方形纸板为了避免材料浪费,每张原材料板材先裁得张的纸板条,每张纸板条又恰好可以裁得张型长方形纸板或张型正方形纸板,如图所示.(单位:)
(1)每张原材料板材可以裁得型纸板______张或裁得型纸板______张;
(2)现有张原材料板材全部裁剪每张原材料板材只能一种裁法得到型与型纸板当侧面和底面,做成如图所示的竖式无盖长方体纸盒和横式无盖长方体纸盒,若横式无盖长方体纸盒个数为竖式无盖长方体纸盒个数的两倍,问:怎样裁剪才能使剪出的,型纸板恰好用完,两种纸盒各做多少个?
24.在综合与实践课上,同学们以“一个含角的直角三角板和两条平行线为背景开展数学活动.在三角板中,,,,,直线.
(1)如图1,当三角板的顶点C在直线上,点A落在直线上时,若,求的度数;
(2)如图2,当三角板的顶点C在直线上,点A在直线和之间时,求的度数;
(3)如图3,当三角板的顶点C在直线上,点A在直线的上方时,若的延长线与的角平分线相交于点M,,求的度数.
25.【材料阅读】
利用两数和(差)的完全平方公式可以解决很多数学问题.
例:若满足,求的值.
解:设,则,
.
请仿照上面的方法求解下面问题:
【初步应用】(1)已知,,则___________;
【问题解决】(2),求;
【拓展延伸】(3)已知正方形的边长为x,E、F分别是、上的点,且,,长方形的面积是15,分别以,为边长作正方形,求阴影部分的面积.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B D D A A B D C B D
二、填空题
11.【解】解:;
故答案为:.
12.【解】解:
,
故答案为:2.
13.【解】解:,
,得:,
∵,
∴,
∴;
故答案为:3.
14.【解】解:∵通过多次试验后发现摸到红色球的频率稳定在,
∴袋中红色球是个,
故答案为:.
15.【解】解:∵,
∴,
∴,
∵平分,
∴,
故答案为:.
16.【解】∵,分别是的边,的中点,的面积为6,
∴,.
∵是中点,是中点,的面积为,的面积为,
∴,
∴
.
∴,即,
解得.
故答案为:2.
三、解答题
17.【解】(1)解:,
由②①得:,
解得,
将代入①得:,
解得,
所以方程组的解为.
(2)解:,
由①②得:,
解得,
将代入①得:,
解得,
所以方程组的解为.
18.【解】解:(1)原式
;
(2)
,
当,时,原式.
19.【解】(1)解:
;
(2)解:
.
20.【解】(1)解:,
共统计50件书签作品;
故答案为:50.
(2),
∴,
∴类型对应的扇形圆心角的度数是,
故答案为:30,;
(3)类型D的书签作品有,
补全条形统计图如下:
21.【解】(1)证明:平分,
,
,
,
;
(2)解:,
,
,
,
,
,
,
平分,
,
,
.
22.【解】(1)解:∵,,
∴和都是的补角,
∵平分,
∴,
∴,
∴是的补角,
综上,的所有的补角为.
(2)解:∵平分,,
∴,
由对顶角相等得:.
(3)解:∵,,
∴,
∵,
解得,
∴.
23.【解】(1)解:根据题意,每张原材料板材可裁得张的纸板条,每张纸板条又恰好可以裁得张型长方形纸板或张型正方形纸板,
∴每张原材料板材可以裁得型纸板张,每张原材料板材可以裁得型纸板张,
故答案为:,;
(2)解:设用张原材料板材裁剪型纸板,则用张原材料板材裁剪型纸板,设竖式无盖长方体纸盒个,横式无盖长方体纸盒个,
根据题意得, ,
解得,
,,
答:用张原材料板材裁剪型纸板,用张原材料板材裁剪型纸板,能做竖式无盖长方体纸盒个,横式无盖长方体纸盒个.
24.【解】(1)∵
∴
∴;
(2)如图,延长交于点D
∵
∴
∴;
(3)∵平分,
∴
∴.
25.【解】解:(1)∵,
∴,
∵,
∴,
∴;
(2)设,,
则,
,
∵,
∴,
∴;
(3)由题意得,长方形的长,宽,
则有,
由题意得,
即,
∴,
∴或(舍去).
∴阴影部分的面积为:,
答:阴影部分的面积为16.
21世纪教育网(www.21cnjy.com)
青岛版2024—2025学年七年级下册数学期末复习提分强化训练
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列调查中,适合用抽样调查的是( )
A.对登机的旅客进行安全检查 B.考察一批灯泡的使用寿命
C.发射运载火箭前的检查 D.订购校服时了解某班学生衣服的尺寸
2.如图所示,下列说法错误的是( )
A.由,可得到
B.由,可得到
C.由,可得到
D.由,可得到
3.若是二元一次方程组的解,则的值为( )
A. B. C. D.
4.已知,,,则a,b,c之间满足的等式是( )
A. B.
C. D.
5.若是完全平方式,则的值是( )
A.或 B.或 C.或 D.或
6.若多项式因式分解的结果为,则的值为( )
A. B. C.19 D.21
7.下列长度的三条线段能组成三角形的是( )
A.3,4,9 B.3,4,8 C.3,4,7 D.3,4,6
8.如图,等于( )
B. C. D.
9.已知关于的二元一次方程组的解为,若满足二元一次方程组,则( )
A.1 B.2 C. D.
10.如图,将两张长为a,宽为b的长方形纸片按图1,图2两种方式放置,图1和图2中两张长方形纸片重叠的部分分别记为①和②,正方形中未被这两张长方形纸片覆盖的部分用阴影表示,①和②的面积分别记为和.若知道下列条件,可以求值的是( )
A.长方形纸片的面积 B.长方形纸片的周长
C.长方形纸片和①的面积差 D.图1与图2阴影部分的面积差
二、填空题(6小题,每题3分,共18分)
11.分解因式: .
12.计算: .
13.已知关于x,y的方程组的解满足.则m的值是 .
14.某口袋中有红色、黄色、黑色的小球共个,这些小球除颜色外都相同,通过多次试验后发现摸到红色球的频率稳定在,则袋中红色球是 个.
15.如图,,,平分,则的度数 .
16.如图,,,分别是的边,,的中点,连接,,交于点,的面积为6,设的面积为,的面积为,则 .
青岛版2024—2025学年七年级下册数学期末复习提分强化训练
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解方程组
(1); (2).
18.(1)化简:;
(2)先化简再求值:,其中,.
19.因式分解.
(1).
(2)
20.五育并举齐推进,融合育人向未来,为培养学生综合素质某中学利用课余时间举行创意书签制作大赛,参赛选手可从A-戏曲文学,B-家乡人文,C-美食盛宴,D-法制教育中选择一项进行主题创作.随机收集部分参赛选手作品,根据主题分类统计并绘制成如下统计图(不完整),根据统计图回答下列问题:
(1)共统计______件书签作品.
(2)的值为______,类型对应的扇形圆心角的度数是_____.
(3)请补全条形统计图.
21.如图,已知,平分,交于点.
(1)求证:;
(2)若于点,,求的度数.
22.如图,直线相交于点,平分.
(1)请直接写出图中的所有的补角;
(2)若,求的度数;
(3)设且,求的值.
23.在纸盒制作的劳动实践课上,对规格是的原材料板材进行裁剪得到型长方形纸板和型正方形纸板为了避免材料浪费,每张原材料板材先裁得张的纸板条,每张纸板条又恰好可以裁得张型长方形纸板或张型正方形纸板,如图所示.(单位:)
(1)每张原材料板材可以裁得型纸板______张或裁得型纸板______张;
(2)现有张原材料板材全部裁剪每张原材料板材只能一种裁法得到型与型纸板当侧面和底面,做成如图所示的竖式无盖长方体纸盒和横式无盖长方体纸盒,若横式无盖长方体纸盒个数为竖式无盖长方体纸盒个数的两倍,问:怎样裁剪才能使剪出的,型纸板恰好用完,两种纸盒各做多少个?
24.在综合与实践课上,同学们以“一个含角的直角三角板和两条平行线为背景开展数学活动.在三角板中,,,,,直线.
(1)如图1,当三角板的顶点C在直线上,点A落在直线上时,若,求的度数;
(2)如图2,当三角板的顶点C在直线上,点A在直线和之间时,求的度数;
(3)如图3,当三角板的顶点C在直线上,点A在直线的上方时,若的延长线与的角平分线相交于点M,,求的度数.
25.【材料阅读】
利用两数和(差)的完全平方公式可以解决很多数学问题.
例:若满足,求的值.
解:设,则,
.
请仿照上面的方法求解下面问题:
【初步应用】(1)已知,,则___________;
【问题解决】(2),求;
【拓展延伸】(3)已知正方形的边长为x,E、F分别是、上的点,且,,长方形的面积是15,分别以,为边长作正方形,求阴影部分的面积.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B D D A A B D C B D
二、填空题
11.【解】解:;
故答案为:.
12.【解】解:
,
故答案为:2.
13.【解】解:,
,得:,
∵,
∴,
∴;
故答案为:3.
14.【解】解:∵通过多次试验后发现摸到红色球的频率稳定在,
∴袋中红色球是个,
故答案为:.
15.【解】解:∵,
∴,
∴,
∵平分,
∴,
故答案为:.
16.【解】∵,分别是的边,的中点,的面积为6,
∴,.
∵是中点,是中点,的面积为,的面积为,
∴,
∴
.
∴,即,
解得.
故答案为:2.
三、解答题
17.【解】(1)解:,
由②①得:,
解得,
将代入①得:,
解得,
所以方程组的解为.
(2)解:,
由①②得:,
解得,
将代入①得:,
解得,
所以方程组的解为.
18.【解】解:(1)原式
;
(2)
,
当,时,原式.
19.【解】(1)解:
;
(2)解:
.
20.【解】(1)解:,
共统计50件书签作品;
故答案为:50.
(2),
∴,
∴类型对应的扇形圆心角的度数是,
故答案为:30,;
(3)类型D的书签作品有,
补全条形统计图如下:
21.【解】(1)证明:平分,
,
,
,
;
(2)解:,
,
,
,
,
,
,
平分,
,
,
.
22.【解】(1)解:∵,,
∴和都是的补角,
∵平分,
∴,
∴,
∴是的补角,
综上,的所有的补角为.
(2)解:∵平分,,
∴,
由对顶角相等得:.
(3)解:∵,,
∴,
∵,
解得,
∴.
23.【解】(1)解:根据题意,每张原材料板材可裁得张的纸板条,每张纸板条又恰好可以裁得张型长方形纸板或张型正方形纸板,
∴每张原材料板材可以裁得型纸板张,每张原材料板材可以裁得型纸板张,
故答案为:,;
(2)解:设用张原材料板材裁剪型纸板,则用张原材料板材裁剪型纸板,设竖式无盖长方体纸盒个,横式无盖长方体纸盒个,
根据题意得, ,
解得,
,,
答:用张原材料板材裁剪型纸板,用张原材料板材裁剪型纸板,能做竖式无盖长方体纸盒个,横式无盖长方体纸盒个.
24.【解】(1)∵
∴
∴;
(2)如图,延长交于点D
∵
∴
∴;
(3)∵平分,
∴
∴.
25.【解】解:(1)∵,
∴,
∵,
∴,
∴;
(2)设,,
则,
,
∵,
∴,
∴;
(3)由题意得,长方形的长,宽,
则有,
由题意得,
即,
∴,
∴或(舍去).
∴阴影部分的面积为:,
答:阴影部分的面积为16.
21世纪教育网(www.21cnjy.com)
同课章节目录
