青岛版2024—2025学年七年级下册数学期末考试押题卷(含答案)
文档属性
| 名称 | 青岛版2024—2025学年七年级下册数学期末考试押题卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 880.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-26 08:42:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
青岛版2024—2025学年七年级下册数学期末考试押题卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.为提高我国居民身体素质,减少肥胖,2025年年初国家卫健委提出“体重管理年”的决策,某中学为了解该校900名学生的体重情况,抽查了其中70名学生的体重进行统计,下列叙述正确的是( )
A.以上调查属于全面调查 B.900名学生是总体
C.900是样本容量 D.每名学生的体重是个体
2.下列调查适合做普查的是( )
A.调查游客对花果山景点的满意程度 B.调查江苏省中小学生的身高情况
C.调查某校九年级(3)班全体学生的体重 D.调查连云港市中小学生保护淡水资源的意识
3.一个三角形的两边长分别为2和3,则第三边的长可以是( )
A.1 B.2 C.6 D.9
4.下列能用平方差公式因式分解的是( )
A. B. C. D.
5.下列运算中正确的是( )
A. B.
C. D.
6.若,,则的值为( )
A.4 B. C. D.2
7.我国古代数学著作《九章算术》中记载着这样一道题:今有牛五、羊二,直金十两;牛二、羊五,直金八两.问牛、羊各直金几何?意思是:假设5头牛、2只羊,共值金10两;2头牛、5只羊,共值金8两.那么每头牛、每只羊分别值金多少两?若设每头牛、每只羊分别值金两和两,根据题意列方程组得( )
A.B.C.D.
8.已知方程组中未知数,则m的值是( )
A.0 B.1 C.2 D.3
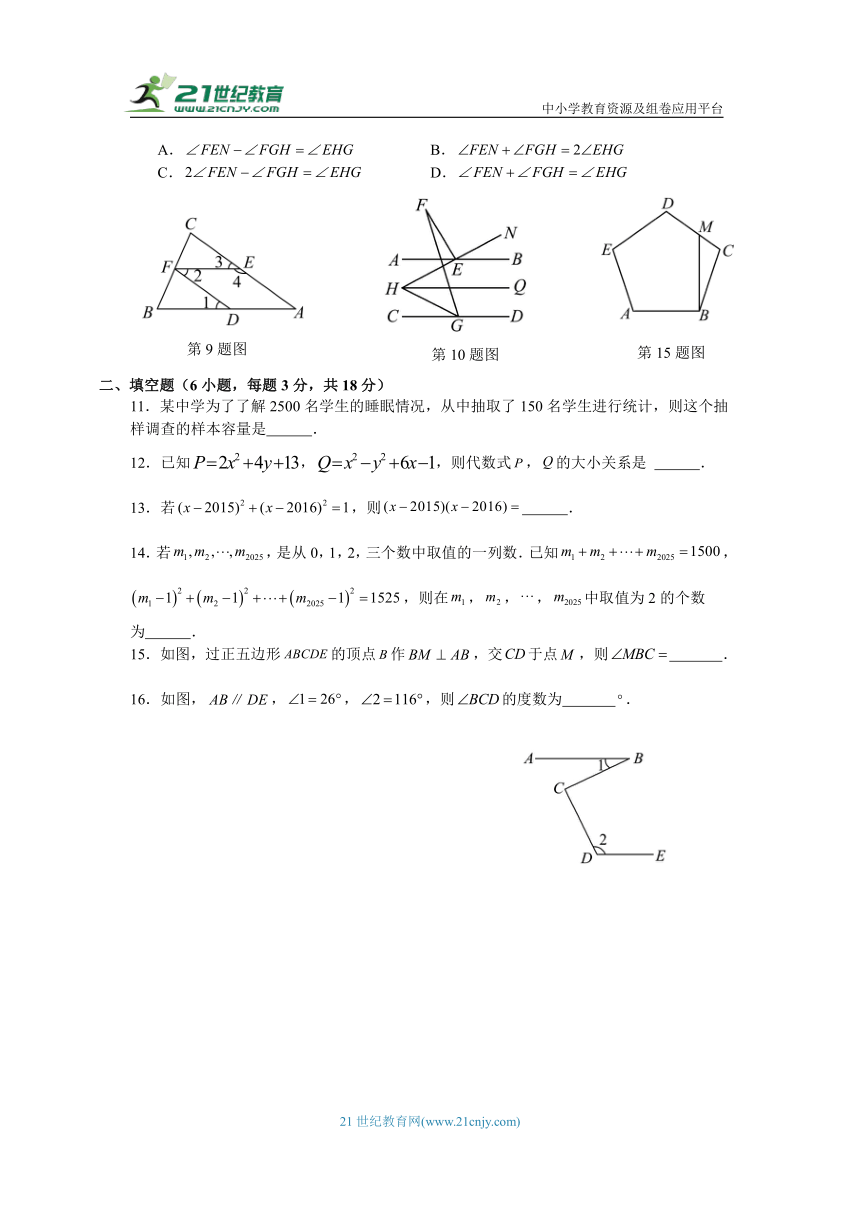
9.如图所示,下列给出的条件中,不能直接判定的是( )
A. B. C. D.
10.如图,直线,点是直线与直线中间一点,点、分别在直线、上,连接并延长至点,连接,过点作,点是直线上方一点,连接,.已知,,则、与之间的数量关系为( )
A. B.
C. D.
二、填空题(6小题,每题3分,共18分)
11.某中学为了了解2500名学生的睡眠情况,从中抽取了150名学生进行统计,则这个抽样调查的样本容量是 .
12.已知,,则代数式,的大小关系是 .
13.若,则 .
14.若,是从0,1,2,三个数中取值的一列数.已知,,则在,,,中取值为2的个数为 .
15.如图,过正五边形的顶点作,交于点,则 .
16.如图,,,,则的度数为 .
青岛版2024—2025学年七年级下册数学期末考试押题卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
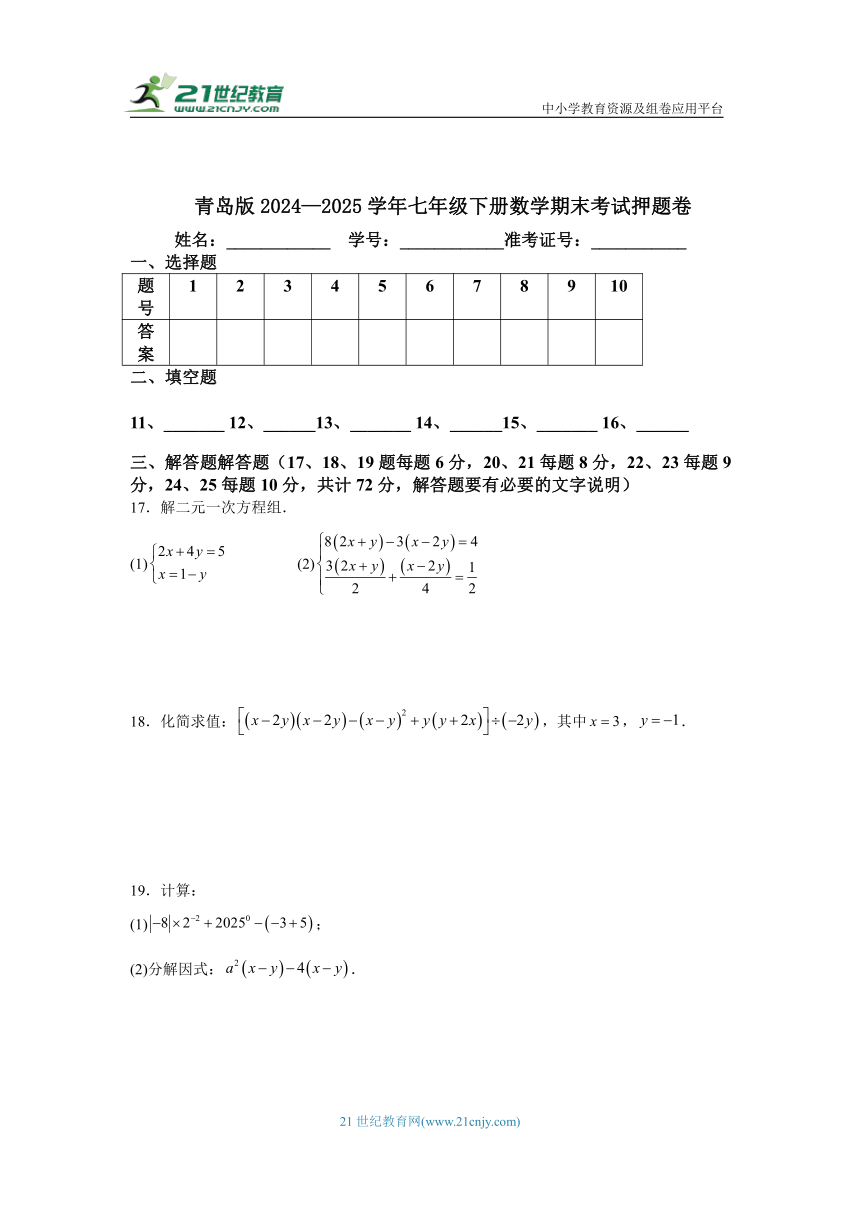
17.解二元一次方程组.
(1) (2)
18.化简求值:,其中,.
19.计算:
(1);
(2)分解因式:.
20.某市教育部门为进一步开展“初中生睡眠管理”工作,对本市部分学生的睡眠情况进行了抽样调查.将数据整理后,设每名学生平均每天的睡眠时间为x小时,其中的分组情况是:A 组 :;B组:;C组:;D组:;E 组 :.根据调查结果绘制成两幅不完整的统计图:
请根据图中信息解答下列问题:
(1)本次共调查了______名学生,在扇形统计图中,C 组所对扇形圆心角的度数为______° ;
(2)该市现有260000名初中生,请估计平均每天的睡眠时间为9小时及以上的学生共有 多少人
(3)根据上述调查数据,简要谈谈你关于“初中生睡眠管理”的看法,并结合自己的实际, 提一条合理化的建议.(字数不超过30个字)
21.如图,点C,D在直线上,,.
(1)求证:;
(2)已知的角平分线交于点G,过点F作交的延长线于点M.若,求出的度数.
22.宜宾五粮液配送公司与一家小型货车租赁公司有过两次业务往来.第一次租用2辆A型车和1辆B型车装满五粮液一次运货;第二次租用1辆A型车和2辆B型车装满五粮液一次运货.现在公司有五粮液需要送给某商家,计划同时租用A型车和B型车一次运完,且每辆车都恰好装满五粮液.
(1)每辆A型车和每辆B型车都装满时各装多少吨?
(2)五粮液配送公司有哪几种租车方案?
(3)若A型车每辆租金200元,B型车每辆租金300元,哪种租车方案最省钱,最省钱的方案租金为多少元?
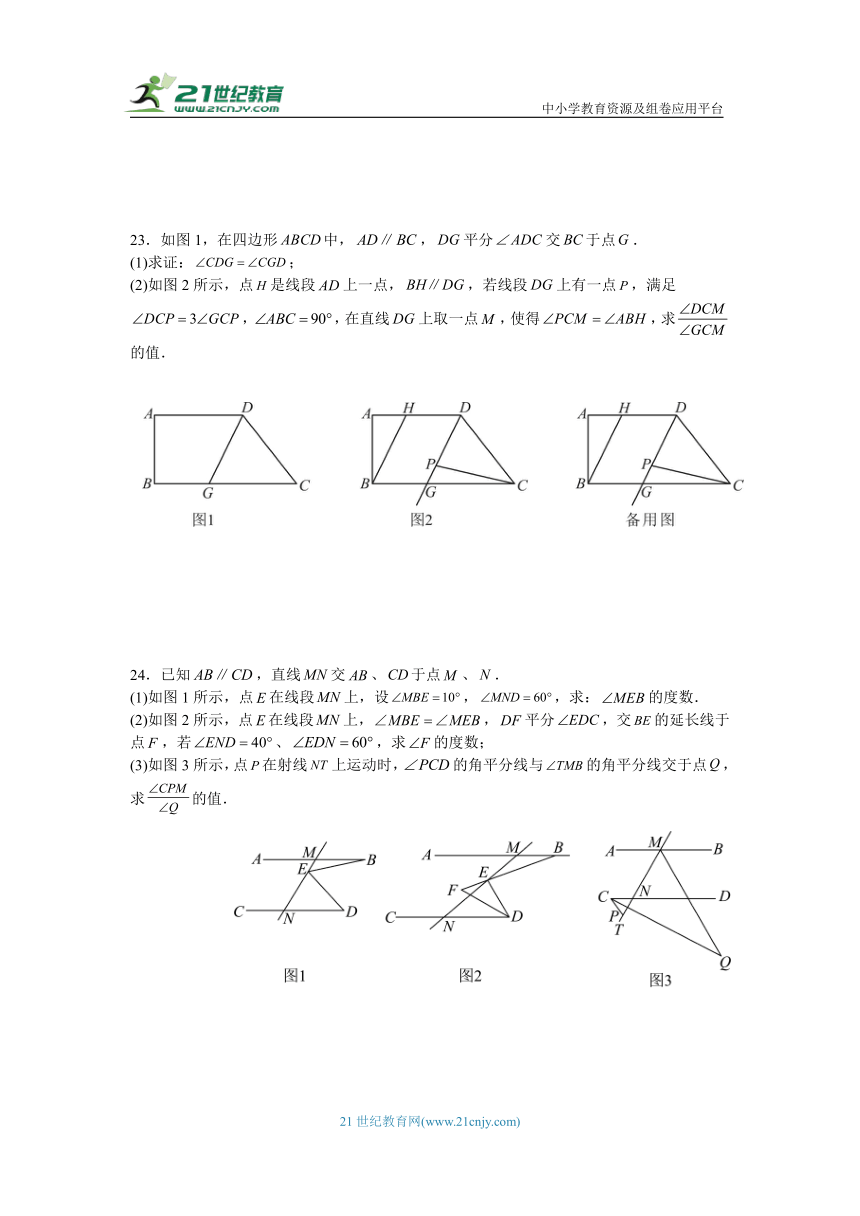
23.如图1,在四边形中,,平分交于点.
(1)求证:;
(2)如图2所示,点是线段上一点,,若线段上有一点,满足,,在直线上取一点,使得,求的值.
24.已知,直线交、于点、.
(1)如图1所示,点在线段上,设,,求:的度数.
(2)如图2所示,点在线段上,,平分,交的延长线于点,若、,求的度数;
(3)如图3所示,点在射线上运动时,的角平分线与的角平分线交于点,求的值.
25.对于任意四个有理数,,,,可以组成两个有理数对与.我们规定:
.例如:.
(1)若是一个完全平方式,求常数的值;
(2)若,且,求的值;
(3)在(2)的条件下,将长方形及长方形按照如图方式放置,其中点、分别在边、上,连接、、、.若,,,,求图中阴影部分的面积.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B D B C A B B B
二、填空题
11.【解】解:根据题意得,这个抽样调查的样本容量是150.
故答案为:150.
12.【解】解:,,
,
,
,
,
故答案为:.
13.【解】解:设,
则,;
∵,
∴,
∴,
即,
故答案为:0.
14.【解】解:,,,是从0,1,2,三个数中取的一列数,且,
∵,,,
,,,中为1的个数是,
,
的个数是,
故答案为:500.
15.【解】解:正五边形每个内角为,
即,
,
.
16.【解】解:如图,过点作的平行线,
,,
,
,.
,
.
,
,
.
故答案为:90.
三、解答题
17.【解】(1)解:,
将②代入①得:,
解得,
将代入②得:,
所以方程组的解为.
(2)解:整理为,
由①②得:,
解得,
将代入②得:,
解得,
所以方程组的解为.
18.【解】解:
;
当时,原式.
19.【解】(1)解:
;
(2)解:
.
20.【解】(1)解:本次共调查了学生(名),
C组所对应的扇形圆心角的度数为;
(2)解:(人),
故平均每天的睡眠时间为9小时及以上的学生共有人;
(3)解:根据调查情况,平均每天的睡眠时间为9小时及以上的学生人数占比较小,建议增加学生睡眠时间(答案不唯一).
21.【解】(1)证明:∵,
∴,
∴;
(2)解:∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵平分,
∴,
∵,
∴,
∴.
22.【解】(1)解:设1辆A型车装满物资一次可运x吨,1辆B型车装满物资一次可运y吨,
依题意:得,
解得:,
答:1辆A型车装满物资一次可运3吨,1辆B型车装满物资一次可运4吨.
(2)解:设租用a辆A型车,b辆A型车,
依题意:得,
,
又∵a,b均为正整数,
或或,
∴该公司共有3种租车方案,
方案1:租用9辆A型车,1辆B型车;
方案2:租用5辆A型车,4辆B型车;
方案3:租用1辆A型车,7辆B型车.
(3)解:方案1所需租金为(元);
方案2所需租金为(元);
方案3所需租金为(元).
,
∴最省钱的租车方案为租用1辆A型车,7辆B型车,最少租车费为2100元.
23.【解】(1)证明:∵,
∴,
∵平分,
∴,
∴.
(2)解:设,
,
由(1)得:,
,
,
,
,
由题意,分以下两种情况:①如图,当点在的下方时,
,
,
;
②如图,当点M在的上方时,
,
,
,
综上,的值是5或.
24.【详解】(1)解:如图所示,过点E作,
∵,
∴,
∴,,
∴.
故答案为:;
(2)解:如图,过点E作,
∵,
∴,
∵,
∴,
∵,,
∴,
∴,,
∴,
∴,
∵平分,
∴,
∵,
∴.
(3)解:如图所示,设交于I,,交于K,过点K作交于H,
∵,
∴,
∵,
∴;
∵平分,
∴,
∵,,
∴,;
∵平分,
∴,
同理可得:,
∴
∴.
25.【解】(1)解:,
,
,
是完全平方式,
,
;
(2)
,
去括号得:,
合并同类项得:,
,
,
,
,
解得:;
(3),,
,
,
,
,
,
阴影部分的面积为:,
,,
阴影部分的面积为:.
21世纪教育网(www.21cnjy.com)
青岛版2024—2025学年七年级下册数学期末考试押题卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.为提高我国居民身体素质,减少肥胖,2025年年初国家卫健委提出“体重管理年”的决策,某中学为了解该校900名学生的体重情况,抽查了其中70名学生的体重进行统计,下列叙述正确的是( )
A.以上调查属于全面调查 B.900名学生是总体
C.900是样本容量 D.每名学生的体重是个体
2.下列调查适合做普查的是( )
A.调查游客对花果山景点的满意程度 B.调查江苏省中小学生的身高情况
C.调查某校九年级(3)班全体学生的体重 D.调查连云港市中小学生保护淡水资源的意识
3.一个三角形的两边长分别为2和3,则第三边的长可以是( )
A.1 B.2 C.6 D.9
4.下列能用平方差公式因式分解的是( )
A. B. C. D.
5.下列运算中正确的是( )
A. B.
C. D.
6.若,,则的值为( )
A.4 B. C. D.2
7.我国古代数学著作《九章算术》中记载着这样一道题:今有牛五、羊二,直金十两;牛二、羊五,直金八两.问牛、羊各直金几何?意思是:假设5头牛、2只羊,共值金10两;2头牛、5只羊,共值金8两.那么每头牛、每只羊分别值金多少两?若设每头牛、每只羊分别值金两和两,根据题意列方程组得( )
A.B.C.D.
8.已知方程组中未知数,则m的值是( )
A.0 B.1 C.2 D.3
9.如图所示,下列给出的条件中,不能直接判定的是( )
A. B. C. D.
10.如图,直线,点是直线与直线中间一点,点、分别在直线、上,连接并延长至点,连接,过点作,点是直线上方一点,连接,.已知,,则、与之间的数量关系为( )
A. B.
C. D.
二、填空题(6小题,每题3分,共18分)
11.某中学为了了解2500名学生的睡眠情况,从中抽取了150名学生进行统计,则这个抽样调查的样本容量是 .
12.已知,,则代数式,的大小关系是 .
13.若,则 .
14.若,是从0,1,2,三个数中取值的一列数.已知,,则在,,,中取值为2的个数为 .
15.如图,过正五边形的顶点作,交于点,则 .
16.如图,,,,则的度数为 .
青岛版2024—2025学年七年级下册数学期末考试押题卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解二元一次方程组.
(1) (2)
18.化简求值:,其中,.
19.计算:
(1);
(2)分解因式:.
20.某市教育部门为进一步开展“初中生睡眠管理”工作,对本市部分学生的睡眠情况进行了抽样调查.将数据整理后,设每名学生平均每天的睡眠时间为x小时,其中的分组情况是:A 组 :;B组:;C组:;D组:;E 组 :.根据调查结果绘制成两幅不完整的统计图:
请根据图中信息解答下列问题:
(1)本次共调查了______名学生,在扇形统计图中,C 组所对扇形圆心角的度数为______° ;
(2)该市现有260000名初中生,请估计平均每天的睡眠时间为9小时及以上的学生共有 多少人
(3)根据上述调查数据,简要谈谈你关于“初中生睡眠管理”的看法,并结合自己的实际, 提一条合理化的建议.(字数不超过30个字)
21.如图,点C,D在直线上,,.
(1)求证:;
(2)已知的角平分线交于点G,过点F作交的延长线于点M.若,求出的度数.
22.宜宾五粮液配送公司与一家小型货车租赁公司有过两次业务往来.第一次租用2辆A型车和1辆B型车装满五粮液一次运货;第二次租用1辆A型车和2辆B型车装满五粮液一次运货.现在公司有五粮液需要送给某商家,计划同时租用A型车和B型车一次运完,且每辆车都恰好装满五粮液.
(1)每辆A型车和每辆B型车都装满时各装多少吨?
(2)五粮液配送公司有哪几种租车方案?
(3)若A型车每辆租金200元,B型车每辆租金300元,哪种租车方案最省钱,最省钱的方案租金为多少元?
23.如图1,在四边形中,,平分交于点.
(1)求证:;
(2)如图2所示,点是线段上一点,,若线段上有一点,满足,,在直线上取一点,使得,求的值.
24.已知,直线交、于点、.
(1)如图1所示,点在线段上,设,,求:的度数.
(2)如图2所示,点在线段上,,平分,交的延长线于点,若、,求的度数;
(3)如图3所示,点在射线上运动时,的角平分线与的角平分线交于点,求的值.
25.对于任意四个有理数,,,,可以组成两个有理数对与.我们规定:
.例如:.
(1)若是一个完全平方式,求常数的值;
(2)若,且,求的值;
(3)在(2)的条件下,将长方形及长方形按照如图方式放置,其中点、分别在边、上,连接、、、.若,,,,求图中阴影部分的面积.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B D B C A B B B
二、填空题
11.【解】解:根据题意得,这个抽样调查的样本容量是150.
故答案为:150.
12.【解】解:,,
,
,
,
,
故答案为:.
13.【解】解:设,
则,;
∵,
∴,
∴,
即,
故答案为:0.
14.【解】解:,,,是从0,1,2,三个数中取的一列数,且,
∵,,,
,,,中为1的个数是,
,
的个数是,
故答案为:500.
15.【解】解:正五边形每个内角为,
即,
,
.
16.【解】解:如图,过点作的平行线,
,,
,
,.
,
.
,
,
.
故答案为:90.
三、解答题
17.【解】(1)解:,
将②代入①得:,
解得,
将代入②得:,
所以方程组的解为.
(2)解:整理为,
由①②得:,
解得,
将代入②得:,
解得,
所以方程组的解为.
18.【解】解:
;
当时,原式.
19.【解】(1)解:
;
(2)解:
.
20.【解】(1)解:本次共调查了学生(名),
C组所对应的扇形圆心角的度数为;
(2)解:(人),
故平均每天的睡眠时间为9小时及以上的学生共有人;
(3)解:根据调查情况,平均每天的睡眠时间为9小时及以上的学生人数占比较小,建议增加学生睡眠时间(答案不唯一).
21.【解】(1)证明:∵,
∴,
∴;
(2)解:∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵平分,
∴,
∵,
∴,
∴.
22.【解】(1)解:设1辆A型车装满物资一次可运x吨,1辆B型车装满物资一次可运y吨,
依题意:得,
解得:,
答:1辆A型车装满物资一次可运3吨,1辆B型车装满物资一次可运4吨.
(2)解:设租用a辆A型车,b辆A型车,
依题意:得,
,
又∵a,b均为正整数,
或或,
∴该公司共有3种租车方案,
方案1:租用9辆A型车,1辆B型车;
方案2:租用5辆A型车,4辆B型车;
方案3:租用1辆A型车,7辆B型车.
(3)解:方案1所需租金为(元);
方案2所需租金为(元);
方案3所需租金为(元).
,
∴最省钱的租车方案为租用1辆A型车,7辆B型车,最少租车费为2100元.
23.【解】(1)证明:∵,
∴,
∵平分,
∴,
∴.
(2)解:设,
,
由(1)得:,
,
,
,
,
由题意,分以下两种情况:①如图,当点在的下方时,
,
,
;
②如图,当点M在的上方时,
,
,
,
综上,的值是5或.
24.【详解】(1)解:如图所示,过点E作,
∵,
∴,
∴,,
∴.
故答案为:;
(2)解:如图,过点E作,
∵,
∴,
∵,
∴,
∵,,
∴,
∴,,
∴,
∴,
∵平分,
∴,
∵,
∴.
(3)解:如图所示,设交于I,,交于K,过点K作交于H,
∵,
∴,
∵,
∴;
∵平分,
∴,
∵,,
∴,;
∵平分,
∴,
同理可得:,
∴
∴.
25.【解】(1)解:,
,
,
是完全平方式,
,
;
(2)
,
去括号得:,
合并同类项得:,
,
,
,
,
解得:;
(3),,
,
,
,
,
,
阴影部分的面积为:,
,,
阴影部分的面积为:.
21世纪教育网(www.21cnjy.com)
同课章节目录
