【期末押题卷】期末模拟高频易错培优卷(含解析)-2024-2025学年人教版数学六年级下册
文档属性
| 名称 | 【期末押题卷】期末模拟高频易错培优卷(含解析)-2024-2025学年人教版数学六年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 390.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-25 22:35:54 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末模拟高频易错培优卷-2024-2025学年人教版数学六年级下册
一、选择题
1.为了计算方便,一般把比例尺写成( )是1的形式。
A.前项 B.后项 C.前项或后项
2.从武汉到北京,甲车用了8小时,乙车用了10小时。甲、乙两车速度的最简整数比是( )。
A.8∶10 B.5∶4 C. D.4∶5
3.圆柱的侧面沿直线剪开,在下列的图形中,不可能出现( )。
A.长方形 B.三角形 C.平行四边形 D.正方形
4.一杯盐水,盐占盐水的,则盐和水的比是( )。
A.30∶20 B.3∶17 C.3∶23
5.一袋土豆,吃了它的,正好是30千克,这袋土豆原有( )千克。
A.20 B.50 C.25 D.36
6.小军的身高是150cm,小雪的身高是1m。小军和小雪身高的比是( )。
A.150∶1 B.3∶2 C.2∶3
7.在8:11中,如果前项增加24,要使比值不变,后项应( ).
A.增加24 B.乘3 C.乘4
二、填空题
8.甲数除以乙数,商是,甲乙两数的比是( )。
9.在一个长12厘米、宽8厘米的长方形纸上画一个最大的圆,这个圆的面积是( )平方厘米;如果在这个长方形纸上画一个最大的半圆,这个半圆的周长是( )厘米。
10.小时=( )分钟 平方米=( )平方分米 千克=( )克
11.王老师把20000元存入银行,定期2年,年利率为1.7%,到期后可取回( )元。
12.一堆煤已烧掉了它的25%,已烧掉的是这堆煤的,已烧掉的与这堆煤总数的比是( )∶100。
13.一个圆的半径恰好是一个小圆的直径,这个小圆的面积是大圆面积的 .
14.=15÷ = ÷30=20: =0.25.
15.A、B、C、D、E五支足球队进行循环赛(每两队之间要比赛1场)。到现在为止,A队已经比了4场,B队已经比了3场,C队已经比了2场,E队已经比了1场,则D队已经比了( )场。
三、判断题
16.3个米和1米的一样长。( )
17.(b≠0)是倒数。( )
18.0.8m∶4cm化成最简的整数比是1∶5。( )
19.不管圆的大小,圆的周长与直径的比值都是一样的。( )
20.苹果的质量比桃子的质量重,桃子的质量比苹果的质量轻。( )
四、计算题
21.口算。
3.6÷1.2=
22.递等式计算(怎么简便就怎样计算)
1.25×3.2×0.25
23.解下列方程。
① ②
24.求如图圆环和阴影部分的面积。(单位:厘米)
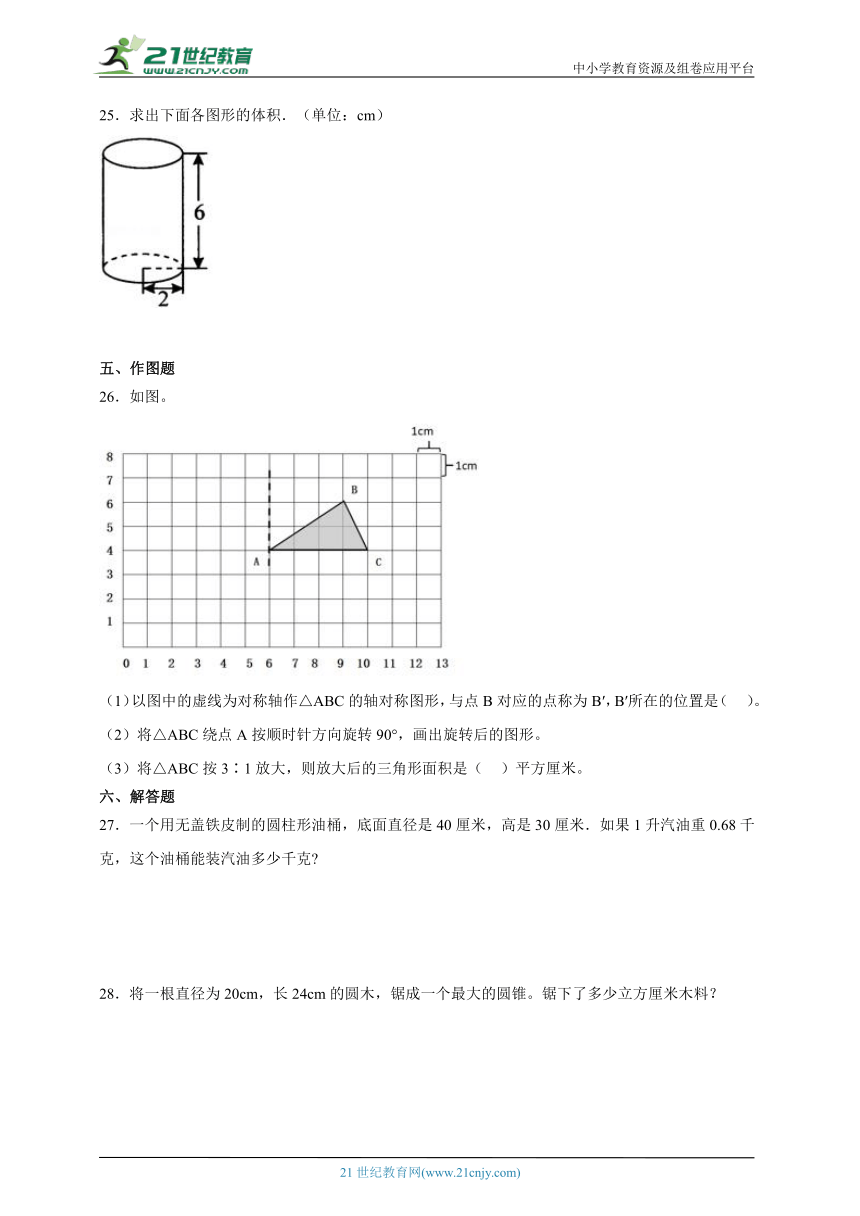
25.求出下面各图形的体积.(单位:cm)
五、作图题
26.如图。
(1)以图中的虚线为对称轴作△ABC的轴对称图形,与点B对应的点称为B′,B′所在的位置是( )。
(2)将△ABC绕点A按顺时针方向旋转90°,画出旋转后的图形。
(3)将△ABC按3∶1放大,则放大后的三角形面积是( )平方厘米。
六、解答题
27.一个用无盖铁皮制的圆柱形油桶,底面直径是40厘米,高是30厘米.如果1升汽油重0.68千克,这个油桶能装汽油多少千克
28.将一根直径为20cm,长24cm的圆木,锯成一个最大的圆锥。锯下了多少立方厘米木料?
29.星期天,乐乐帮妈妈包韭菜猪肉馅饺子,韭菜与猪肉的质量比是。现在要准备450克这样的馅料,需要韭菜、猪肉各多少克?
30.大厅内挂着一只大钟,它的分针长4dm,时针长3dm,从5点到7点分针的尖端走过的路程是多少分米?时针扫过的面积是多少平方分米?
31.甲、乙、丙三人同时从A向B跑.当甲跑到B时,乙离B还有15米,丙离B还有32米;当乙跑到B时,丙离B还有20米;当丙跑到B时,一共用了25秒,乙每秒跑多少米?
32.在一个长是10厘米、宽4厘米的长方形塑料板中裁剪出一个最大的半圆,并在半圆的周围包上金属条,至少需要多少厘米的金属条?(接头处忽略不计)
33.华为“麒麟980”是世界上第一个采用台积电7纳米工艺制造的商用手机SoC芯片组。在一次产品发布会上,按40∶1的比例尺展示了“麒麟980”的外形图片,该图片的尺寸为“70厘米×70厘米”。
答案与解析
1.C
【解题思路】比例尺按比例尺的意义有缩小比例尺和放大比例尺两种,一般,地图是缩小比例尺,前项为1;精密零件图是放大比例尺,后项为1;据此解答。
【精讲精析】由分析可知:为了计算方便,一般把比例尺写成前项或后项是1的形式。
故答案为:C
【要点提示】本题主要考查比例尺的实际应用,理解有缩小比例尺和放大比例尺两种是解题的关键。
2.B
【解题思路】根据题意可知,从武汉到北京的总路程为单位“1”,则甲车的速度为1÷8=,乙车的速度为1÷10=,再写出甲、乙两车速度的最简整数比即可。
【精讲精析】1÷8=;
1÷10=;
甲、乙两车速度的比为=5∶4;
故答案为:B。
【要点提示】明确题目中的单位“1”,分别求出甲车和乙车的速度,再进一步解答即可。
3.B
【解题思路】圆柱的侧面是一个曲面,圆柱的侧面沿着高剪开会得到一个长方形或正方形,不沿高而沿着斜线剪开会得到平行四边形,据此解答。
【精讲精析】圆柱的侧面沿高展开,会得到长方形或正方形,沿着斜线展开会得到平行四边形,但不论怎么剪开都不可能得到三角形。
故答案为:B
4.B
【解题思路】盐占盐水的,可知盐水相当于20份,盐是3份,水就相当于20-3=17份,由此解答即可。
【精讲精析】20-3=17
盐:水=3∶17
故选:B
【要点提示】此题考查的是比的应用,解答本题要找准单位“1”,确定它平均分成的份数和比较量的份数再比,进一步化简比。
5.D
【精讲精析】由题可知,30千克是这袋土豆的,利用除法求解这袋土豆的重量即可。
【精讲精析】30÷=36(千克)
所以,这袋土豆原有36千克。
故答案为:D
【要点提示】本题考查了分数除法的应用,已知一个数是另一个数的几分之几,求另一个数用除法。
6.B
【解题思路】先统一单位,把小军的身高150cm换成1.5m,再用小军的身高比上小雪的身高即可。
【精讲精析】150cm=1.5m
1.5∶1=3∶2
故答案为:B
【要点提示】此题考查了单位之间的换算以及比的应用。
7.C
【精讲精析】8+24=32,32÷8=4;后项要乘4.
故答案为C.
【要点提示】用原来的前项加上24求出现在的前项,然后求出前项扩大的倍数,根据比的基本性质把后项也扩大相同的倍数即可.
8.3∶7
【解题思路】根据题意,可得出:甲数÷乙数=,再根据分数与比的关系把分数改写成比即可。
【精讲精析】因为甲数÷乙数=;
所以甲数∶乙数=3∶7。
9. 50.24 30.84
【解题思路】由题意可知在长方形内画一个最大的圆,圆的直径是长方形的宽,S=π(d÷2)2;如果在长方形里画一个最大的半圆,半圆所在圆的直径就是长方形的长,那么此半圆的半径=d÷2,半圆的周长=πd÷2+d,半圆的面积=πr2÷2,据此解答即可。
【精讲精析】由分析可知在一个长为长12厘米、宽8厘米的长方形里画一个最大的圆,这个圆的直径是8厘米,则面积是:
3.14×(8÷2)2
=3.14×16
=50.24(平方厘米)
如果在这个长方形里画一个最大的半圆,半圆的半径是:
12÷2=6(厘米)
则周长是:3.14×6+12
=18.84+12
=30.84(厘米)
10. 45 900
【解题思路】1时=60分,1平方米=100平方分米,1千克=1000克;大单位变小单位乘进率,小单位变大单位除以进率,由此解答即可。
【精讲精析】小时=45分钟;
平方米=平方分米;
千克=900克
【要点提示】熟练掌握面积单位、时间单位和质量单位之间的进率是解答本题的关键。
11.20680
【解题思路】根据利息=本金×利率×时间,代入数据,求出到期的利息,再加上本金,即可解答。
【精讲精析】20000×1.7%×2+20000
=340×2+20000
=680+20000
=20680(元)
王老师把20000元存入银行,定期2年,年利率为1.7%,到期后可取回20680元。
12.25;25
【解题思路】把百分数写成分母是100的分数即,分子相当于比的前项,分母相当于比的后项。
【精讲精析】一堆煤已烧掉了它的25%,已烧掉的是这堆煤的,已烧掉的与这堆煤总数的比是25∶100。
【要点提示】熟练掌握分数、百分数、比的互化方法。
13.
【精讲精析】根据题意,假设大圆的半径是2,那么小圆的直径也是2,小圆的半径就是2÷2=1,由圆的面积公式可知:大圆的面积是:π×22=4π,小圆的面积是:π×12=π,则小圆面积是大圆面积的:.
14.18,60,7.5,80
【精讲精析】把0.25化成分数并化简是,根据分数的基本性质,分子、分母都乘18就是;根据分数与除法的关系,=1÷4,再根据商不变的性质,被除数、除数都乘7.5就是7.5÷30;都乘15就是15÷60;根据比与分数的关系,=1:4,再根据比的基本性质,比的前、后项都乘20就是20:80.
【要点提示】解答此题的关键是0.25,根据小数、分数、除法、比之间的关系及分数的基本性质、商不变的性质、比的基本性质即可进行转化.
15.2
【解题思路】由题意可知,A队已经赛了4场,A队分别与B队、C队、D队、E队进行了比赛;E队赛了1场,E队只与A队进行了比赛;B队赛了3场,B队分别与A队、C队、D队进行了比赛,最后求出D队比赛的场数,据此结合画图解答。
【精讲精析】如图:
由图可知:D队与A队进行了1场比赛,又与B队进行了1场比赛,所以D队已经比了2场比赛。
16.√
【解题思路】3个米是米,1米的是米,然后进行大小比较即可判断。
【精讲精析】(米)
(米)
所以3个米和1米的一样长,说法正确;
故答案为:√
17.×
【解题思路】如果两个数的乘积为1,我们就说这两个数互为倒数,或者说一个数是另一个数的倒数,倒数是相互依存的不能独立存在,据此解答。
【精讲精析】如果b×=1(b≠0),那么b和互为倒数,b是的倒数,是b的倒数,所以题目说法不正确。
故答案为:×
【要点提示】本题主要考查倒数的认识,掌握倒数的意义是解答题目的关键。
18.×
【解题思路】1m=100cm,先把0.8m换算成cm,然后把前项和后项同时除以4即可化成最简整数比。
【精讲精析】0.8m∶4cm=80cm∶4cm=20∶1,原题说法错误。
故答案为:×。
【要点提示】 在化简带单位的比时,单位不统一是没有意义的;只有单位统一了,所得到的比才能够准确描述两个量之间的倍比关系。
19.√
【解题思路】任意一个圆,其周长和直径的比值都是圆周率,圆周率不随圆的大小的改变而改变,据此解答。
【精讲精析】由分析可得:
不管圆的大小,圆的周长与直径的比值都是一样的,原题说法正确。
故答案为:√
20.×
【解题思路】以桃子的质量为单位“1”,苹果的质量是桃子的质量的1+=。根据分数与比的关系,=8∶5,即苹果的质量∶桃子的质量=8∶5。再以苹果的质量为单位“1”,根据求一个数比另一个数多(或少)几分之几,用除法计算,用苹果与桃子的质量差÷苹果的质量即可。
【精讲精析】1+=
=8∶5
(8-5)÷8=3÷8=
苹果的质量比桃子的质量重,桃子的质量比苹果的质量轻。原题说法错误。
故答案为:×
21.;;;3;
;1;;
【精讲精析】略
22.75;1
2;
【解题思路】47×75%+53×,把百分数和分数化成小数,75%=0.75;=0.75,原式化为:47×0.75+53×0.75,再根据乘法分配律,原式化为:(47+53)×0.75,再进行计算;
1.25×3.2×0.25,把3.2化为0.8×4,原式化为:1.25×0.8×4×0.25,再根据乘法结合律,原式化为:(1.25×0.8)×(4×0.25),再进行计算;
3-÷-,先把除法换算成乘法,原式化为:3-×-,计算出乘法的积,原式化为:3--,再根据减法性质,原式化为:3-(+),再进行计算;
÷[×(-)],先计算小括号里的减法,再计算中括号里的乘法,最后计算括号外的除法。
【精讲精析】47×75%+53×
=47×0.75+53×0.75
=(47+53)×0.75
=100×0.75
=75
1.25×3.2×0.25
=1.25×0.8×4×0.25
=(1.25×0.8)×(4×0.25)
=1×1
=1
3-÷-
=3-×-
=3--
=3-(+)
=3-1
=2
÷[×(-)]
=÷[×(-)]
=÷[×]
=÷
=×
=
23.①x=9;;②x=
【解题思路】①方程左右两边同时乘,将其转化为x=6,再左右两边同时除以即可;
②将方程化简为x=,再左右两边同时除以即可。
【精讲精析】①
解:
x=6
x÷=6÷
x=9;
②
解:x=
x÷=÷
x=
24.65.94平方厘米;114平方厘米
【解题思路】通过观察可知,第一个图形圆环的面积=外圆的面积-内圆的面积;根据圆环的面积公式:S=π(R2-r2),代入数据即可求出圆环的面积;
第二个图形阴影部分的面积=圆的面积-对角线是直径的正方形的面积,如图:
根据圆面积公式:S=πR2,代入数据即可求出圆的面积;根据三角形的面积=底×高÷2,求出正方形的面积。进而得出阴影部分的面积。
【精讲精析】2+3=5(厘米)
3.14×(52-22)
=3.14×(25-4)
=3.14×21
=65.94(平方厘米)
20÷2=10
3.14×102
=3.14×100
=314(平方厘米)
20×10÷2×2
=200÷2×2
=200(平方厘米)
314-200=114(平方厘米)
圆环的面积是65.94平方厘米,阴影的面积是114平方厘米。
25.75.36立方厘米
【精讲精析】试题分析:根据圆柱的体积公式:v=sh,把数据分别代入公式解答.
解: 3.14×22×6
=3.14×4×6
=75.36(立方厘米)
答:这个圆柱的体积是75.36立方厘米.
26.(1)图形见详解;(3,6);
(2)图形见详解;
(3)36
【解题思路】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的左边画出三角形顶点的对称点,最后依次连接各点,并用(列数,行数)表示出B′的位置;
(2)根据题目要求确定旋转中心(点A)、旋转方向(顺时针)、旋转角度(90°);分析所作图形,找出构成图形的关键边;按一定的方向和角度分别找出各关键边的对应边;最后依次连接组成封闭图形;
(3)由图可知,原来三角形的底为4厘米,高为2厘米,放大后三角形的底为4×3=12厘米,高为2×3=6厘米,利用“三角形的面积=底×高÷2”求出放大后三角形的面积,据此解答。
【精讲精析】(1)B′的位置用数对表示为(3,6)。
(2)
(3)(4×3)×(2×3)÷2
=12×6÷2
=72÷2
=36(平方厘米)
所以,则放大后的三角形面积是36平方厘米。
【要点提示】掌握轴对称图形和旋转图形的作图方法是解答题目的关键。
27.26千克
【精讲精析】油桶的容积:3.14×(40÷2)2×30
=3.14×12000
=37680(立方厘米)=37.68(升)
油桶装油的重量:37.68×0.68=25.6224≈26(千克)
答:这个油桶可装油26千克.
28.5024立方厘米
【解题思路】把圆柱削成一个最大的圆锥体,则这个圆柱与圆锥是等底等高的,根据等底等高的圆锥的体积是圆柱体积的,所以应削去圆柱体积的(1﹣),根据一个数乘分数的意义解答即可。
【精讲精析】3.14×(20÷2)2×24×(1﹣)
=3.14×100×24×
=314×16
=5024(立方厘米)
答:锯下了5024立方厘米木料。
【要点提示】抓住圆柱内最大圆锥的特点,明确等底等高的圆锥的体积是圆柱的体积的,是解答本题的关键。
29.韭菜300克,猪肉150克
【解题思路】根据韭菜与猪肉的质量比是,可把韭菜看作2份,猪肉看作1份,总份数为2+1=3份。先用总重量除以总份数求出一份是多少克,即为猪肉的重量,再用一份的重量×2即为韭菜的重量。
【精讲精析】450÷(2+1)
=450÷3
=150(克)
150×2=300(克)
答:需要韭菜300克,猪肉150克。
30.50.24分米;4.71平方分米
【解题思路】(1)从5点到7点经过2个小时,分针尖端刚好绕大钟的中心旋转2周,分针尖端走过的路程是以分针长度为半径圆的周长的2倍;
(2)时针走一大格是30°从5点到7点时针走了两大格,计算出两大格占360°的分率,时针扫过的面积=以时针长度为半径圆的面积×分率;据此解答。
【精讲精析】(1)3.14×4×2×2
=12.56×2×2
=25.12×2
=50.24(分米)
答:从5点到7点分针的尖端走过的路程是50.24分米。
(2)5点到7点时针走了两大格,一大格是30°
3.14×32×
=3.14×32×
=28.26×
=4.71(平方分米)
答:时针扫过的面积是4.71平方分米。
【要点提示】掌握圆的周长和面积计算公式是解答题目的关键。
31.乙每秒跑5米
【精讲精析】试题分析:根据题意,乙行15米,丙行32﹣20=12米,由此可以求出,乙和丙的速度比是15:12(即5:4),也就是乙行5份,丙行4份,这样就可以求出全程是多少米,又知丙一共用了25秒,即可求出丙的速度,由乙和丙的速度比是5:4,即可求出乙的速度.
解:乙行15米,丙行32﹣20=12米.所以乙和丙的速度比是:15:12=5:4;
因为当乙行到B时,行了5份,丙行了4份,所以全程是:20÷(5﹣4)×5=100(米);
由此丙的速度是每秒:100÷25=4(米);
乙的速度是每秒4÷4×5=5(米);
答:乙每秒跑5米.
点评:此题解答的关键是先求出乙和丙的速度比,进而求出全程有多少米,根据丙用25秒,就可以求出丙的速度,由乙和丙的速度比,问题就得到解决.
32.20.56厘米
【解题思路】在长方形上裁剪最大的半圆与在长方形上裁剪最大的圆考虑方向截然不同:裁剪最大的圆只能以宽为直径,圆才不会超出长方形;而裁剪最大的半圆,先考虑长能不能作直径,如果不行,再考虑宽作半径,本题如果以长作直径,宽的长度不够,只能以宽作半径,即可裁剪最大的半圆,圆的周长的一半加上一条直径的长度,即是这个半圆的周长,根据圆的周长公式求出圆的周长,再除以2,求出圆的周长的一半,加上一条直径的长度,即可求出这个半圆的周长。
【精讲精析】2×3.14×4÷2+4×2
=6.28×4÷2+8
=12.56+8
=20.56(厘米)
答:至少需要20.56厘米的金属条。
【要点提示】此题的解题关键是掌握在长方形上裁剪最大的半圆的方法以及半圆的周长的计算方法。
33.17.5毫米
【解题思路】由题意可知,这个“麒麟980”的图片尺寸是“70厘米×70厘米”,即图上边长为70厘米,根据实际距离=图上距离÷比例尺可得出“麒麟980”的实际边长。
【精讲精析】70÷=70÷40=1.75(厘米)
1.75厘米=17.5毫米
答:“麒麟980”的实际边长为17.5毫米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末模拟高频易错培优卷-2024-2025学年人教版数学六年级下册
一、选择题
1.为了计算方便,一般把比例尺写成( )是1的形式。
A.前项 B.后项 C.前项或后项
2.从武汉到北京,甲车用了8小时,乙车用了10小时。甲、乙两车速度的最简整数比是( )。
A.8∶10 B.5∶4 C. D.4∶5
3.圆柱的侧面沿直线剪开,在下列的图形中,不可能出现( )。
A.长方形 B.三角形 C.平行四边形 D.正方形
4.一杯盐水,盐占盐水的,则盐和水的比是( )。
A.30∶20 B.3∶17 C.3∶23
5.一袋土豆,吃了它的,正好是30千克,这袋土豆原有( )千克。
A.20 B.50 C.25 D.36
6.小军的身高是150cm,小雪的身高是1m。小军和小雪身高的比是( )。
A.150∶1 B.3∶2 C.2∶3
7.在8:11中,如果前项增加24,要使比值不变,后项应( ).
A.增加24 B.乘3 C.乘4
二、填空题
8.甲数除以乙数,商是,甲乙两数的比是( )。
9.在一个长12厘米、宽8厘米的长方形纸上画一个最大的圆,这个圆的面积是( )平方厘米;如果在这个长方形纸上画一个最大的半圆,这个半圆的周长是( )厘米。
10.小时=( )分钟 平方米=( )平方分米 千克=( )克
11.王老师把20000元存入银行,定期2年,年利率为1.7%,到期后可取回( )元。
12.一堆煤已烧掉了它的25%,已烧掉的是这堆煤的,已烧掉的与这堆煤总数的比是( )∶100。
13.一个圆的半径恰好是一个小圆的直径,这个小圆的面积是大圆面积的 .
14.=15÷ = ÷30=20: =0.25.
15.A、B、C、D、E五支足球队进行循环赛(每两队之间要比赛1场)。到现在为止,A队已经比了4场,B队已经比了3场,C队已经比了2场,E队已经比了1场,则D队已经比了( )场。
三、判断题
16.3个米和1米的一样长。( )
17.(b≠0)是倒数。( )
18.0.8m∶4cm化成最简的整数比是1∶5。( )
19.不管圆的大小,圆的周长与直径的比值都是一样的。( )
20.苹果的质量比桃子的质量重,桃子的质量比苹果的质量轻。( )
四、计算题
21.口算。
3.6÷1.2=
22.递等式计算(怎么简便就怎样计算)
1.25×3.2×0.25
23.解下列方程。
① ②
24.求如图圆环和阴影部分的面积。(单位:厘米)
25.求出下面各图形的体积.(单位:cm)
五、作图题
26.如图。
(1)以图中的虚线为对称轴作△ABC的轴对称图形,与点B对应的点称为B′,B′所在的位置是( )。
(2)将△ABC绕点A按顺时针方向旋转90°,画出旋转后的图形。
(3)将△ABC按3∶1放大,则放大后的三角形面积是( )平方厘米。
六、解答题
27.一个用无盖铁皮制的圆柱形油桶,底面直径是40厘米,高是30厘米.如果1升汽油重0.68千克,这个油桶能装汽油多少千克
28.将一根直径为20cm,长24cm的圆木,锯成一个最大的圆锥。锯下了多少立方厘米木料?
29.星期天,乐乐帮妈妈包韭菜猪肉馅饺子,韭菜与猪肉的质量比是。现在要准备450克这样的馅料,需要韭菜、猪肉各多少克?
30.大厅内挂着一只大钟,它的分针长4dm,时针长3dm,从5点到7点分针的尖端走过的路程是多少分米?时针扫过的面积是多少平方分米?
31.甲、乙、丙三人同时从A向B跑.当甲跑到B时,乙离B还有15米,丙离B还有32米;当乙跑到B时,丙离B还有20米;当丙跑到B时,一共用了25秒,乙每秒跑多少米?
32.在一个长是10厘米、宽4厘米的长方形塑料板中裁剪出一个最大的半圆,并在半圆的周围包上金属条,至少需要多少厘米的金属条?(接头处忽略不计)
33.华为“麒麟980”是世界上第一个采用台积电7纳米工艺制造的商用手机SoC芯片组。在一次产品发布会上,按40∶1的比例尺展示了“麒麟980”的外形图片,该图片的尺寸为“70厘米×70厘米”。
答案与解析
1.C
【解题思路】比例尺按比例尺的意义有缩小比例尺和放大比例尺两种,一般,地图是缩小比例尺,前项为1;精密零件图是放大比例尺,后项为1;据此解答。
【精讲精析】由分析可知:为了计算方便,一般把比例尺写成前项或后项是1的形式。
故答案为:C
【要点提示】本题主要考查比例尺的实际应用,理解有缩小比例尺和放大比例尺两种是解题的关键。
2.B
【解题思路】根据题意可知,从武汉到北京的总路程为单位“1”,则甲车的速度为1÷8=,乙车的速度为1÷10=,再写出甲、乙两车速度的最简整数比即可。
【精讲精析】1÷8=;
1÷10=;
甲、乙两车速度的比为=5∶4;
故答案为:B。
【要点提示】明确题目中的单位“1”,分别求出甲车和乙车的速度,再进一步解答即可。
3.B
【解题思路】圆柱的侧面是一个曲面,圆柱的侧面沿着高剪开会得到一个长方形或正方形,不沿高而沿着斜线剪开会得到平行四边形,据此解答。
【精讲精析】圆柱的侧面沿高展开,会得到长方形或正方形,沿着斜线展开会得到平行四边形,但不论怎么剪开都不可能得到三角形。
故答案为:B
4.B
【解题思路】盐占盐水的,可知盐水相当于20份,盐是3份,水就相当于20-3=17份,由此解答即可。
【精讲精析】20-3=17
盐:水=3∶17
故选:B
【要点提示】此题考查的是比的应用,解答本题要找准单位“1”,确定它平均分成的份数和比较量的份数再比,进一步化简比。
5.D
【精讲精析】由题可知,30千克是这袋土豆的,利用除法求解这袋土豆的重量即可。
【精讲精析】30÷=36(千克)
所以,这袋土豆原有36千克。
故答案为:D
【要点提示】本题考查了分数除法的应用,已知一个数是另一个数的几分之几,求另一个数用除法。
6.B
【解题思路】先统一单位,把小军的身高150cm换成1.5m,再用小军的身高比上小雪的身高即可。
【精讲精析】150cm=1.5m
1.5∶1=3∶2
故答案为:B
【要点提示】此题考查了单位之间的换算以及比的应用。
7.C
【精讲精析】8+24=32,32÷8=4;后项要乘4.
故答案为C.
【要点提示】用原来的前项加上24求出现在的前项,然后求出前项扩大的倍数,根据比的基本性质把后项也扩大相同的倍数即可.
8.3∶7
【解题思路】根据题意,可得出:甲数÷乙数=,再根据分数与比的关系把分数改写成比即可。
【精讲精析】因为甲数÷乙数=;
所以甲数∶乙数=3∶7。
9. 50.24 30.84
【解题思路】由题意可知在长方形内画一个最大的圆,圆的直径是长方形的宽,S=π(d÷2)2;如果在长方形里画一个最大的半圆,半圆所在圆的直径就是长方形的长,那么此半圆的半径=d÷2,半圆的周长=πd÷2+d,半圆的面积=πr2÷2,据此解答即可。
【精讲精析】由分析可知在一个长为长12厘米、宽8厘米的长方形里画一个最大的圆,这个圆的直径是8厘米,则面积是:
3.14×(8÷2)2
=3.14×16
=50.24(平方厘米)
如果在这个长方形里画一个最大的半圆,半圆的半径是:
12÷2=6(厘米)
则周长是:3.14×6+12
=18.84+12
=30.84(厘米)
10. 45 900
【解题思路】1时=60分,1平方米=100平方分米,1千克=1000克;大单位变小单位乘进率,小单位变大单位除以进率,由此解答即可。
【精讲精析】小时=45分钟;
平方米=平方分米;
千克=900克
【要点提示】熟练掌握面积单位、时间单位和质量单位之间的进率是解答本题的关键。
11.20680
【解题思路】根据利息=本金×利率×时间,代入数据,求出到期的利息,再加上本金,即可解答。
【精讲精析】20000×1.7%×2+20000
=340×2+20000
=680+20000
=20680(元)
王老师把20000元存入银行,定期2年,年利率为1.7%,到期后可取回20680元。
12.25;25
【解题思路】把百分数写成分母是100的分数即,分子相当于比的前项,分母相当于比的后项。
【精讲精析】一堆煤已烧掉了它的25%,已烧掉的是这堆煤的,已烧掉的与这堆煤总数的比是25∶100。
【要点提示】熟练掌握分数、百分数、比的互化方法。
13.
【精讲精析】根据题意,假设大圆的半径是2,那么小圆的直径也是2,小圆的半径就是2÷2=1,由圆的面积公式可知:大圆的面积是:π×22=4π,小圆的面积是:π×12=π,则小圆面积是大圆面积的:.
14.18,60,7.5,80
【精讲精析】把0.25化成分数并化简是,根据分数的基本性质,分子、分母都乘18就是;根据分数与除法的关系,=1÷4,再根据商不变的性质,被除数、除数都乘7.5就是7.5÷30;都乘15就是15÷60;根据比与分数的关系,=1:4,再根据比的基本性质,比的前、后项都乘20就是20:80.
【要点提示】解答此题的关键是0.25,根据小数、分数、除法、比之间的关系及分数的基本性质、商不变的性质、比的基本性质即可进行转化.
15.2
【解题思路】由题意可知,A队已经赛了4场,A队分别与B队、C队、D队、E队进行了比赛;E队赛了1场,E队只与A队进行了比赛;B队赛了3场,B队分别与A队、C队、D队进行了比赛,最后求出D队比赛的场数,据此结合画图解答。
【精讲精析】如图:
由图可知:D队与A队进行了1场比赛,又与B队进行了1场比赛,所以D队已经比了2场比赛。
16.√
【解题思路】3个米是米,1米的是米,然后进行大小比较即可判断。
【精讲精析】(米)
(米)
所以3个米和1米的一样长,说法正确;
故答案为:√
17.×
【解题思路】如果两个数的乘积为1,我们就说这两个数互为倒数,或者说一个数是另一个数的倒数,倒数是相互依存的不能独立存在,据此解答。
【精讲精析】如果b×=1(b≠0),那么b和互为倒数,b是的倒数,是b的倒数,所以题目说法不正确。
故答案为:×
【要点提示】本题主要考查倒数的认识,掌握倒数的意义是解答题目的关键。
18.×
【解题思路】1m=100cm,先把0.8m换算成cm,然后把前项和后项同时除以4即可化成最简整数比。
【精讲精析】0.8m∶4cm=80cm∶4cm=20∶1,原题说法错误。
故答案为:×。
【要点提示】 在化简带单位的比时,单位不统一是没有意义的;只有单位统一了,所得到的比才能够准确描述两个量之间的倍比关系。
19.√
【解题思路】任意一个圆,其周长和直径的比值都是圆周率,圆周率不随圆的大小的改变而改变,据此解答。
【精讲精析】由分析可得:
不管圆的大小,圆的周长与直径的比值都是一样的,原题说法正确。
故答案为:√
20.×
【解题思路】以桃子的质量为单位“1”,苹果的质量是桃子的质量的1+=。根据分数与比的关系,=8∶5,即苹果的质量∶桃子的质量=8∶5。再以苹果的质量为单位“1”,根据求一个数比另一个数多(或少)几分之几,用除法计算,用苹果与桃子的质量差÷苹果的质量即可。
【精讲精析】1+=
=8∶5
(8-5)÷8=3÷8=
苹果的质量比桃子的质量重,桃子的质量比苹果的质量轻。原题说法错误。
故答案为:×
21.;;;3;
;1;;
【精讲精析】略
22.75;1
2;
【解题思路】47×75%+53×,把百分数和分数化成小数,75%=0.75;=0.75,原式化为:47×0.75+53×0.75,再根据乘法分配律,原式化为:(47+53)×0.75,再进行计算;
1.25×3.2×0.25,把3.2化为0.8×4,原式化为:1.25×0.8×4×0.25,再根据乘法结合律,原式化为:(1.25×0.8)×(4×0.25),再进行计算;
3-÷-,先把除法换算成乘法,原式化为:3-×-,计算出乘法的积,原式化为:3--,再根据减法性质,原式化为:3-(+),再进行计算;
÷[×(-)],先计算小括号里的减法,再计算中括号里的乘法,最后计算括号外的除法。
【精讲精析】47×75%+53×
=47×0.75+53×0.75
=(47+53)×0.75
=100×0.75
=75
1.25×3.2×0.25
=1.25×0.8×4×0.25
=(1.25×0.8)×(4×0.25)
=1×1
=1
3-÷-
=3-×-
=3--
=3-(+)
=3-1
=2
÷[×(-)]
=÷[×(-)]
=÷[×]
=÷
=×
=
23.①x=9;;②x=
【解题思路】①方程左右两边同时乘,将其转化为x=6,再左右两边同时除以即可;
②将方程化简为x=,再左右两边同时除以即可。
【精讲精析】①
解:
x=6
x÷=6÷
x=9;
②
解:x=
x÷=÷
x=
24.65.94平方厘米;114平方厘米
【解题思路】通过观察可知,第一个图形圆环的面积=外圆的面积-内圆的面积;根据圆环的面积公式:S=π(R2-r2),代入数据即可求出圆环的面积;
第二个图形阴影部分的面积=圆的面积-对角线是直径的正方形的面积,如图:
根据圆面积公式:S=πR2,代入数据即可求出圆的面积;根据三角形的面积=底×高÷2,求出正方形的面积。进而得出阴影部分的面积。
【精讲精析】2+3=5(厘米)
3.14×(52-22)
=3.14×(25-4)
=3.14×21
=65.94(平方厘米)
20÷2=10
3.14×102
=3.14×100
=314(平方厘米)
20×10÷2×2
=200÷2×2
=200(平方厘米)
314-200=114(平方厘米)
圆环的面积是65.94平方厘米,阴影的面积是114平方厘米。
25.75.36立方厘米
【精讲精析】试题分析:根据圆柱的体积公式:v=sh,把数据分别代入公式解答.
解: 3.14×22×6
=3.14×4×6
=75.36(立方厘米)
答:这个圆柱的体积是75.36立方厘米.
26.(1)图形见详解;(3,6);
(2)图形见详解;
(3)36
【解题思路】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的左边画出三角形顶点的对称点,最后依次连接各点,并用(列数,行数)表示出B′的位置;
(2)根据题目要求确定旋转中心(点A)、旋转方向(顺时针)、旋转角度(90°);分析所作图形,找出构成图形的关键边;按一定的方向和角度分别找出各关键边的对应边;最后依次连接组成封闭图形;
(3)由图可知,原来三角形的底为4厘米,高为2厘米,放大后三角形的底为4×3=12厘米,高为2×3=6厘米,利用“三角形的面积=底×高÷2”求出放大后三角形的面积,据此解答。
【精讲精析】(1)B′的位置用数对表示为(3,6)。
(2)
(3)(4×3)×(2×3)÷2
=12×6÷2
=72÷2
=36(平方厘米)
所以,则放大后的三角形面积是36平方厘米。
【要点提示】掌握轴对称图形和旋转图形的作图方法是解答题目的关键。
27.26千克
【精讲精析】油桶的容积:3.14×(40÷2)2×30
=3.14×12000
=37680(立方厘米)=37.68(升)
油桶装油的重量:37.68×0.68=25.6224≈26(千克)
答:这个油桶可装油26千克.
28.5024立方厘米
【解题思路】把圆柱削成一个最大的圆锥体,则这个圆柱与圆锥是等底等高的,根据等底等高的圆锥的体积是圆柱体积的,所以应削去圆柱体积的(1﹣),根据一个数乘分数的意义解答即可。
【精讲精析】3.14×(20÷2)2×24×(1﹣)
=3.14×100×24×
=314×16
=5024(立方厘米)
答:锯下了5024立方厘米木料。
【要点提示】抓住圆柱内最大圆锥的特点,明确等底等高的圆锥的体积是圆柱的体积的,是解答本题的关键。
29.韭菜300克,猪肉150克
【解题思路】根据韭菜与猪肉的质量比是,可把韭菜看作2份,猪肉看作1份,总份数为2+1=3份。先用总重量除以总份数求出一份是多少克,即为猪肉的重量,再用一份的重量×2即为韭菜的重量。
【精讲精析】450÷(2+1)
=450÷3
=150(克)
150×2=300(克)
答:需要韭菜300克,猪肉150克。
30.50.24分米;4.71平方分米
【解题思路】(1)从5点到7点经过2个小时,分针尖端刚好绕大钟的中心旋转2周,分针尖端走过的路程是以分针长度为半径圆的周长的2倍;
(2)时针走一大格是30°从5点到7点时针走了两大格,计算出两大格占360°的分率,时针扫过的面积=以时针长度为半径圆的面积×分率;据此解答。
【精讲精析】(1)3.14×4×2×2
=12.56×2×2
=25.12×2
=50.24(分米)
答:从5点到7点分针的尖端走过的路程是50.24分米。
(2)5点到7点时针走了两大格,一大格是30°
3.14×32×
=3.14×32×
=28.26×
=4.71(平方分米)
答:时针扫过的面积是4.71平方分米。
【要点提示】掌握圆的周长和面积计算公式是解答题目的关键。
31.乙每秒跑5米
【精讲精析】试题分析:根据题意,乙行15米,丙行32﹣20=12米,由此可以求出,乙和丙的速度比是15:12(即5:4),也就是乙行5份,丙行4份,这样就可以求出全程是多少米,又知丙一共用了25秒,即可求出丙的速度,由乙和丙的速度比是5:4,即可求出乙的速度.
解:乙行15米,丙行32﹣20=12米.所以乙和丙的速度比是:15:12=5:4;
因为当乙行到B时,行了5份,丙行了4份,所以全程是:20÷(5﹣4)×5=100(米);
由此丙的速度是每秒:100÷25=4(米);
乙的速度是每秒4÷4×5=5(米);
答:乙每秒跑5米.
点评:此题解答的关键是先求出乙和丙的速度比,进而求出全程有多少米,根据丙用25秒,就可以求出丙的速度,由乙和丙的速度比,问题就得到解决.
32.20.56厘米
【解题思路】在长方形上裁剪最大的半圆与在长方形上裁剪最大的圆考虑方向截然不同:裁剪最大的圆只能以宽为直径,圆才不会超出长方形;而裁剪最大的半圆,先考虑长能不能作直径,如果不行,再考虑宽作半径,本题如果以长作直径,宽的长度不够,只能以宽作半径,即可裁剪最大的半圆,圆的周长的一半加上一条直径的长度,即是这个半圆的周长,根据圆的周长公式求出圆的周长,再除以2,求出圆的周长的一半,加上一条直径的长度,即可求出这个半圆的周长。
【精讲精析】2×3.14×4÷2+4×2
=6.28×4÷2+8
=12.56+8
=20.56(厘米)
答:至少需要20.56厘米的金属条。
【要点提示】此题的解题关键是掌握在长方形上裁剪最大的半圆的方法以及半圆的周长的计算方法。
33.17.5毫米
【解题思路】由题意可知,这个“麒麟980”的图片尺寸是“70厘米×70厘米”,即图上边长为70厘米,根据实际距离=图上距离÷比例尺可得出“麒麟980”的实际边长。
【精讲精析】70÷=70÷40=1.75(厘米)
1.75厘米=17.5毫米
答:“麒麟980”的实际边长为17.5毫米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
