人教版五年级上册数学7 数学广角——植树问题(课件)(共43张PPT)
文档属性
| 名称 | 人教版五年级上册数学7 数学广角——植树问题(课件)(共43张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-26 07:38:49 | ||
图片预览





文档简介
(共43张PPT)
数学广角 -植树问题
教学目标
1.通过猜测、试验等数学活动,初步体会两端都栽的植树问题的规律。
2.经历和体验将复杂问题简单化的解题策略和方法。
3.感受数学知识在日常生活中的广泛应用,尝试用数学的方法来解决实际生活中的简单问题,培养应用意识和解决实际问题的能力。
教学重难点
1.理解间隔数与棵数之间的关系并应用到生活中去。(重点)
2.理解间隔数与棵数之间的规律(总长÷间距=间隔数,间隔数+1=植树棵数),并能运用规律解决问题。 (难点)
大象馆和猩猩馆相距60米。绿化队要在两馆间的小路两旁栽树,相邻两棵树之间的距离是3米。一共要栽几棵树?
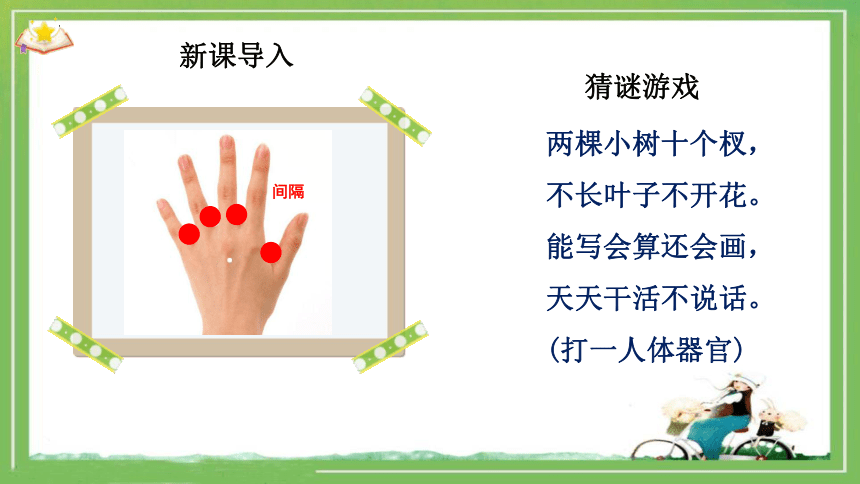
新课导入
猜谜游戏
两棵小树十个杈,不长叶子不开花。能写会算还会画,天天干活不说话。(打一人体器官)
间隔
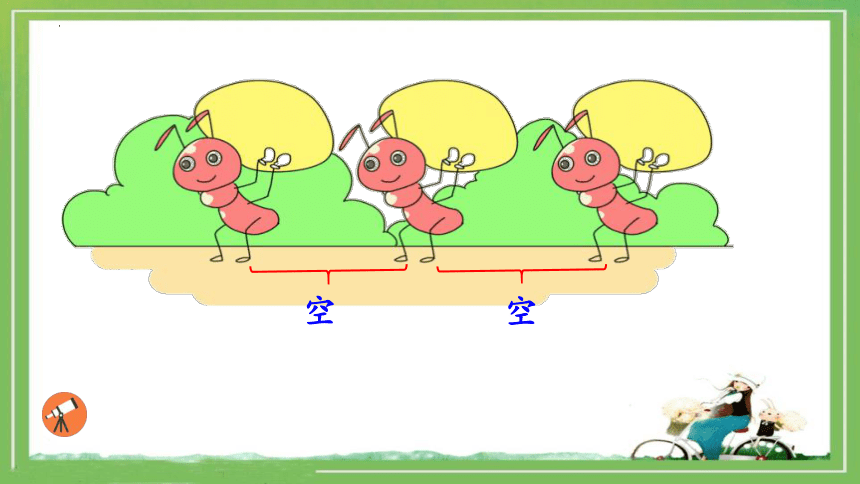
空
空
在数学上,我们把像这样的空叫作间隔。
想一想:这些“空”叫什么?
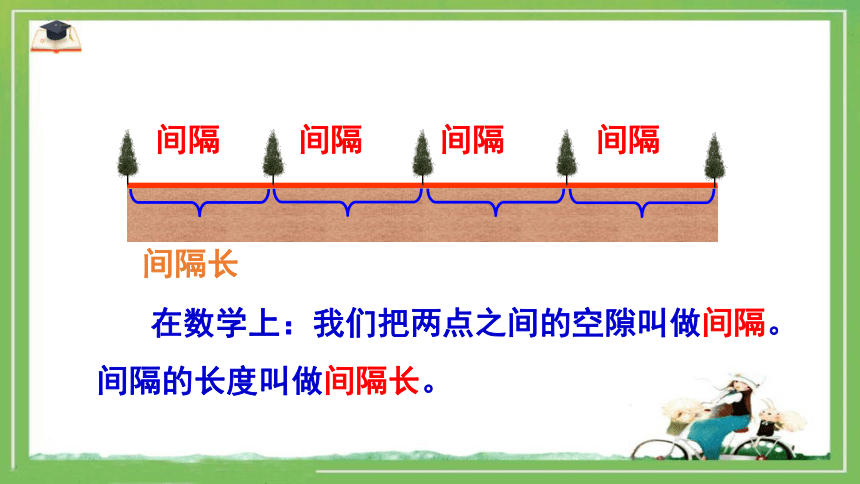
在数学上:我们把两点之间的空隙叫做间隔。间隔的长度叫做间隔长。
间隔长
间隔
间隔
间隔
间隔
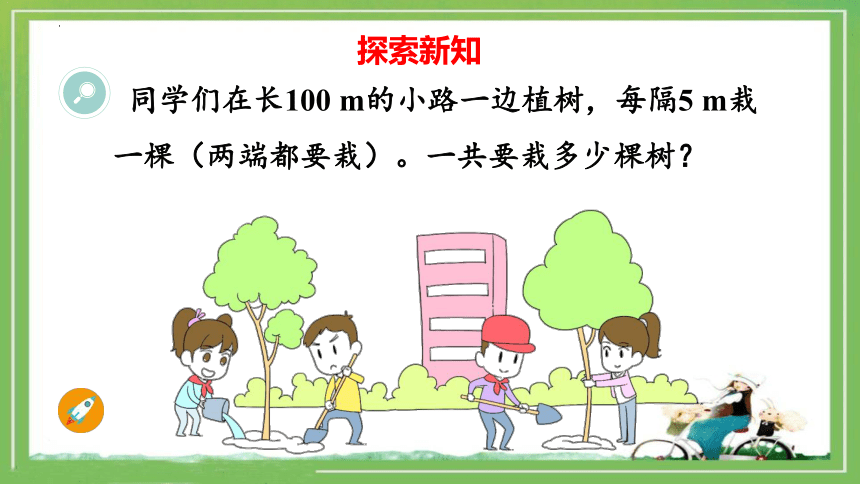
探索新知
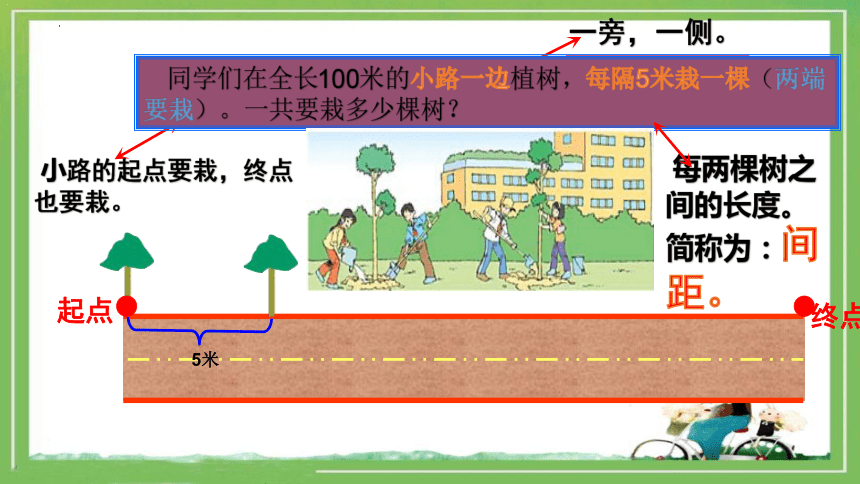
同学们在长100 m的小路一边植树,每隔5 m栽一棵(两端都要栽)。一共要栽多少棵树?
一边
一边
一旁,一侧。
每两棵树之间的长度。简称为:间距。
小路的起点要栽,终点也要栽。
5米
同学们在全长100米的小路一边植树,每隔5米栽一棵(两端要栽)。一共要栽多少棵树?
起点
终点
想一想,说一说:“一边”“两端都要栽” “每隔 5 m”各是什么意思?
只在小路的一边栽树,另一边不栽树
探索新知
小路的两端都要栽树
两棵树之间的间隔是5 m。
3.12 植树节
第一组
第二组
每隔5米:每个间隔长5米
两端要栽:起点和终点都要种树
活动一:分一分、画一画、比一比。
每隔5米栽一棵 (两端要栽) 间隔数 棵数
10米
15米
20米
2
3
3
4
4
5
当两端要栽时
棵数比间隔数多1
间隔数比棵数少1
我发现了:
活动二:根据规律填一填,算一算。
每隔5米栽一棵(两端要栽) 间隔数 棵数 列式求棵数
25米
30米
35米
……
你能概括植树问题(两端要栽)求棵数的解决方法吗?
总长度÷每个间隔的长度=间隔数,间隔数+1=棵数。
5
6
6
7
7
8
25÷5+1=6
30÷5+1=7
35÷5+1=8
探索新知
同学们在长100 m的小路一边植树,每隔5 m栽一棵(两端都要栽)。一共要栽多少棵树?
100÷5=20(棵)
小红这样算:
小红算得对吗?画图检验一下。
100÷5=20(棵)
小红这样算:
同学们在长100 m的小路一边植树,每隔5 m栽一棵(两端都要栽)。一共要栽多少棵树?
100 m太长了,我先用20 m来检验,20÷5=4(棵)。
20 m
5 m
5 m
5 m
5 m
有4个间隔,能栽5棵树。
应该栽5棵,直接用除法计算不对。
自己选一些长度试一试,看看有什么规律。
25 m
5 m
5 m
5 m
5 m
5 m
25÷5=5
能栽6棵
用25 m试试看,能栽多少棵树?
你发现了什么规律?不画图,试着填一填。
距离(米) 间隔数(个) 棵数(棵)
20
25
30
35
4
5
5
6
6
7
7
8
比较两种情况,有什么相同?有什么不同?
两头种
棵数=间隔数+1
棵数=间隔数-1
100米
60米
交流探究
两头不种
我发现栽树的棵数比间隔数多1。
100 m共有20个间隔,两端都要栽,所以一共要栽_____棵树。
间隔数:100 ÷ 5 = 20(个)
植树棵数:20 + 1 =21(棵)
答:一共要栽21棵树。
21
大象馆和猴山相距60m。绿化队要在两馆间的小路两旁栽树(两端不栽),相邻两棵树之间的距离是3m。一共要栽多少棵树?
两端都不栽,栽的棵树比间隔数……。
我们也先画一个简单的线段图看看。
解法探究
小路两旁都要栽树,所以还要……。
60÷3=20
( )=( )
( )×2=( )
答:一共要栽 棵树。
-
1
19
19
38
38
规范解答
60÷3=20 20-1=19 (棵) 19×2=38(棵)
答:一共要栽38棵。
小明家门前有一条35m的小路,绿化队要在路旁栽一排树。每隔5m栽一棵树(一端栽一端不栽)。一共要栽多少棵?
35÷5=7(棵)
答:一共要栽7棵树。
做完后,可以画线段图验证一下。
40
40
40
40
20
20
20
20
棵数=间隔数+1
棵数=间隔数-1
棵数=间隔数
两端都种
两端不种
只种一端
两头种
棵数=间隔数+1
100米
棵数=间隔数-1
60米
棵数=间隔数
35米
交流探究
植树问题有哪几种情况?每种情况中棵数与间隔数之间是什么关系?
植树问题是研究总距离、株距、段数、棵数之间的数量关系的实际问题,在不封闭的植树路线中有下面三种情况:(1)两端都不植树,则总距离÷株距=段数,棵数=段数-1;(2)两端都植树,则总距离÷株距=段数,棵数=段数+1;(3)只有一端植树,则棵数=段数=总距离÷株距。封闭的植树路线与只有一端植树的不封闭路线情况相同。
在全长15米的小路一边植树,哪一个是两端都不栽呢?选一选
CC
AA
BB
刘翔在跨栏比赛中,从第一个栏到最后一个栏的距离约90米,每10米放一个栏,一共放了多少个栏架?
列式计算
90÷10+1=10(个)
间隔数
全班45名同学
同学都排成一排,每两个同学之间8分米,第1个到最后一个同学之间的距离是多少?
4个同学
7个同学
(4-1)×8=24(分米)
(7-1)×8=48(分米)
(45-1)×8=352(分米)
人数-1=间隔数,间隔数×每个间隔的长度=总长度
排队
间隔数
从头到尾8个间隔,有( )个箭靶。
9
箭靶个数=间隔数+1
抢答
每两面旗之间的距离是2米,从第一面到最后一面的距离是90米,一共有( )面旗。
90÷2+1=46(面)
46
间隔数
抢答
随堂小练
1.在一条全长2 km的街道两旁安装路灯(两端都要安装),每隔50 m安装一盏。一共要安装多少盏路灯?
2000÷50+ 1 = 41(盏)
2 km = 2000 m
41×2 = 82(盏)
答:一共要安装82盏路灯。
提示:可以把一盏路灯看成一棵树,当成植树问题来回答。
做一做
注意街道两旁都要安装路灯,求出一边安装路灯的盏数再乘2即可。
2.马路一边栽了 25 棵梧桐树。如果每两棵梧桐中间栽一棵银杏树,一共要栽多少棵银杏树?
25 - 1 = 24(棵)
答:一共要栽 24 棵银杏树。
提示:把银杏树当成两棵树之间的间隔,这样就可根据“植数棵树-1=间隔数” 来解答。
随堂小练
随堂小练
3. 5路公共汽车行驶路线全长12 km,相邻两站之间的路程都是1 km。一共设有多少个车站?
12÷1 = 12(个)
12+1 = 13(个)
答:一共设有13个车站。
4.工人们正在架设电线杆,相邻两根间的距离是200 m。 在总长 3000 m 的笔直路上,一共要架设多少根电线杆(两端都架设)?
3000÷200 = 15(个)
15+1 = 16(根)
答:一共要架设16根电线杆。
提示:可以把一根电线杆看成一棵树,当成植树问题来回答。
随堂小练
1.园林工人沿一条笔直的公路一侧植树,每隔6 m种一棵,一共种了36棵。从第一棵到最后一棵的距离有多远?
当堂检测
36 - 1 = 35(个)
35 ×6 = 210(m)
答:从第一棵到最后一棵的距离有210 m。
2.某地300 m长的步行街的两边每隔30 m挂一个红灯笼(两端都挂),一共挂了多少个红灯笼?
当堂检测
(300÷30 +1 )×2= 22(个)
答:一共挂了22个红灯笼。
当堂检测
3.一条跑道长120m,要在跑道的一边每隔8 m插一面小旗(两端又要插),一面小旗0.5元钱,一共需要多少钱?
(120÷8 +1)×0.5 = 8(元)
答:一共需要8元钱。
你有什么收获?
植树问题
课堂小结
1.间隔数=总路长÷间距,植树棵数=间隔数+1。
不封闭路线上两端都栽的植树问题
2.公路安装路灯、架设电线杆、设置站点、排队、上楼梯等,都可以看成植树问题来解答。
数学广角 -植树问题
教学目标
1.通过猜测、试验等数学活动,初步体会两端都栽的植树问题的规律。
2.经历和体验将复杂问题简单化的解题策略和方法。
3.感受数学知识在日常生活中的广泛应用,尝试用数学的方法来解决实际生活中的简单问题,培养应用意识和解决实际问题的能力。
教学重难点
1.理解间隔数与棵数之间的关系并应用到生活中去。(重点)
2.理解间隔数与棵数之间的规律(总长÷间距=间隔数,间隔数+1=植树棵数),并能运用规律解决问题。 (难点)
大象馆和猩猩馆相距60米。绿化队要在两馆间的小路两旁栽树,相邻两棵树之间的距离是3米。一共要栽几棵树?
新课导入
猜谜游戏
两棵小树十个杈,不长叶子不开花。能写会算还会画,天天干活不说话。(打一人体器官)
间隔
空
空
在数学上,我们把像这样的空叫作间隔。
想一想:这些“空”叫什么?
在数学上:我们把两点之间的空隙叫做间隔。间隔的长度叫做间隔长。
间隔长
间隔
间隔
间隔
间隔
探索新知
同学们在长100 m的小路一边植树,每隔5 m栽一棵(两端都要栽)。一共要栽多少棵树?
一边
一边
一旁,一侧。
每两棵树之间的长度。简称为:间距。
小路的起点要栽,终点也要栽。
5米
同学们在全长100米的小路一边植树,每隔5米栽一棵(两端要栽)。一共要栽多少棵树?
起点
终点
想一想,说一说:“一边”“两端都要栽” “每隔 5 m”各是什么意思?
只在小路的一边栽树,另一边不栽树
探索新知
小路的两端都要栽树
两棵树之间的间隔是5 m。
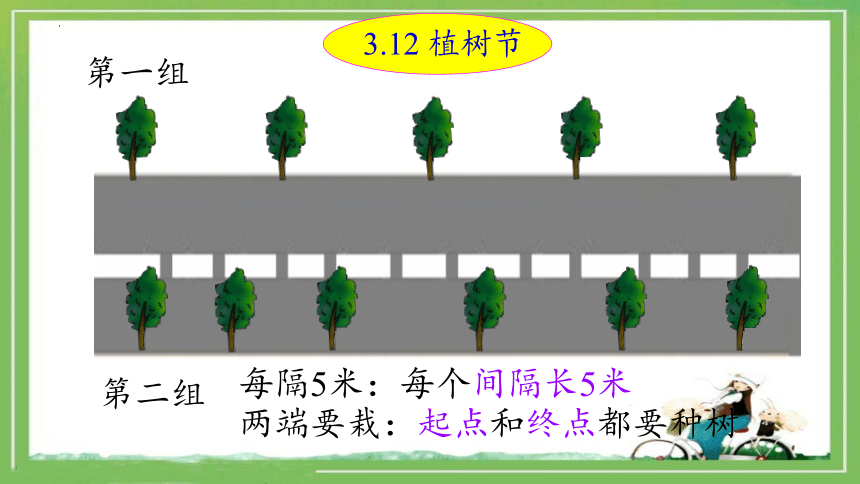
3.12 植树节
第一组
第二组
每隔5米:每个间隔长5米
两端要栽:起点和终点都要种树
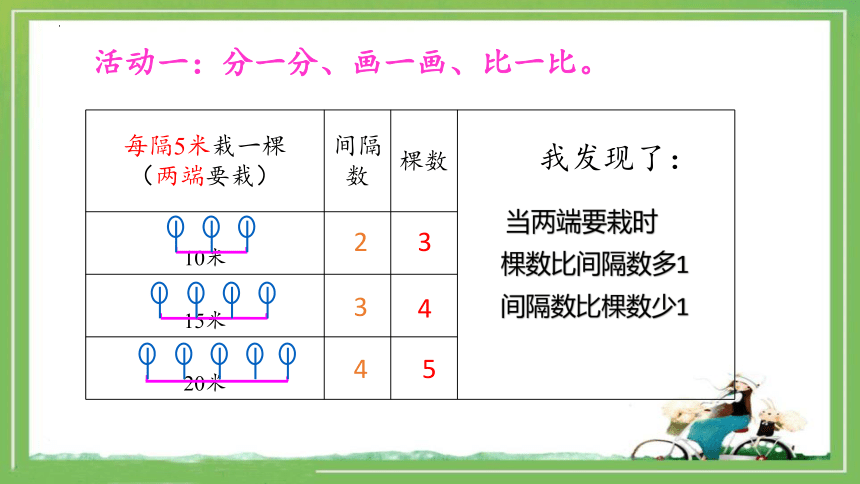
活动一:分一分、画一画、比一比。
每隔5米栽一棵 (两端要栽) 间隔数 棵数
10米
15米
20米
2
3
3
4
4
5
当两端要栽时
棵数比间隔数多1
间隔数比棵数少1
我发现了:
活动二:根据规律填一填,算一算。
每隔5米栽一棵(两端要栽) 间隔数 棵数 列式求棵数
25米
30米
35米
……
你能概括植树问题(两端要栽)求棵数的解决方法吗?
总长度÷每个间隔的长度=间隔数,间隔数+1=棵数。
5
6
6
7
7
8
25÷5+1=6
30÷5+1=7
35÷5+1=8
探索新知
同学们在长100 m的小路一边植树,每隔5 m栽一棵(两端都要栽)。一共要栽多少棵树?
100÷5=20(棵)
小红这样算:
小红算得对吗?画图检验一下。
100÷5=20(棵)
小红这样算:
同学们在长100 m的小路一边植树,每隔5 m栽一棵(两端都要栽)。一共要栽多少棵树?
100 m太长了,我先用20 m来检验,20÷5=4(棵)。
20 m
5 m
5 m
5 m
5 m
有4个间隔,能栽5棵树。
应该栽5棵,直接用除法计算不对。
自己选一些长度试一试,看看有什么规律。
25 m
5 m
5 m
5 m
5 m
5 m
25÷5=5
能栽6棵
用25 m试试看,能栽多少棵树?
你发现了什么规律?不画图,试着填一填。
距离(米) 间隔数(个) 棵数(棵)
20
25
30
35
4
5
5
6
6
7
7
8
比较两种情况,有什么相同?有什么不同?
两头种
棵数=间隔数+1
棵数=间隔数-1
100米
60米
交流探究
两头不种
我发现栽树的棵数比间隔数多1。
100 m共有20个间隔,两端都要栽,所以一共要栽_____棵树。
间隔数:100 ÷ 5 = 20(个)
植树棵数:20 + 1 =21(棵)
答:一共要栽21棵树。
21
大象馆和猴山相距60m。绿化队要在两馆间的小路两旁栽树(两端不栽),相邻两棵树之间的距离是3m。一共要栽多少棵树?
两端都不栽,栽的棵树比间隔数……。
我们也先画一个简单的线段图看看。
解法探究
小路两旁都要栽树,所以还要……。
60÷3=20
( )=( )
( )×2=( )
答:一共要栽 棵树。
-
1
19
19
38
38
规范解答
60÷3=20 20-1=19 (棵) 19×2=38(棵)
答:一共要栽38棵。
小明家门前有一条35m的小路,绿化队要在路旁栽一排树。每隔5m栽一棵树(一端栽一端不栽)。一共要栽多少棵?
35÷5=7(棵)
答:一共要栽7棵树。
做完后,可以画线段图验证一下。
40
40
40
40
20
20
20
20
棵数=间隔数+1
棵数=间隔数-1
棵数=间隔数
两端都种
两端不种
只种一端
两头种
棵数=间隔数+1
100米
棵数=间隔数-1
60米
棵数=间隔数
35米
交流探究
植树问题有哪几种情况?每种情况中棵数与间隔数之间是什么关系?
植树问题是研究总距离、株距、段数、棵数之间的数量关系的实际问题,在不封闭的植树路线中有下面三种情况:(1)两端都不植树,则总距离÷株距=段数,棵数=段数-1;(2)两端都植树,则总距离÷株距=段数,棵数=段数+1;(3)只有一端植树,则棵数=段数=总距离÷株距。封闭的植树路线与只有一端植树的不封闭路线情况相同。
在全长15米的小路一边植树,哪一个是两端都不栽呢?选一选
CC
AA
BB
刘翔在跨栏比赛中,从第一个栏到最后一个栏的距离约90米,每10米放一个栏,一共放了多少个栏架?
列式计算
90÷10+1=10(个)
间隔数
全班45名同学
同学都排成一排,每两个同学之间8分米,第1个到最后一个同学之间的距离是多少?
4个同学
7个同学
(4-1)×8=24(分米)
(7-1)×8=48(分米)
(45-1)×8=352(分米)
人数-1=间隔数,间隔数×每个间隔的长度=总长度
排队
间隔数
从头到尾8个间隔,有( )个箭靶。
9
箭靶个数=间隔数+1
抢答
每两面旗之间的距离是2米,从第一面到最后一面的距离是90米,一共有( )面旗。
90÷2+1=46(面)
46
间隔数
抢答
随堂小练
1.在一条全长2 km的街道两旁安装路灯(两端都要安装),每隔50 m安装一盏。一共要安装多少盏路灯?
2000÷50+ 1 = 41(盏)
2 km = 2000 m
41×2 = 82(盏)
答:一共要安装82盏路灯。
提示:可以把一盏路灯看成一棵树,当成植树问题来回答。
做一做
注意街道两旁都要安装路灯,求出一边安装路灯的盏数再乘2即可。
2.马路一边栽了 25 棵梧桐树。如果每两棵梧桐中间栽一棵银杏树,一共要栽多少棵银杏树?
25 - 1 = 24(棵)
答:一共要栽 24 棵银杏树。
提示:把银杏树当成两棵树之间的间隔,这样就可根据“植数棵树-1=间隔数” 来解答。
随堂小练
随堂小练
3. 5路公共汽车行驶路线全长12 km,相邻两站之间的路程都是1 km。一共设有多少个车站?
12÷1 = 12(个)
12+1 = 13(个)
答:一共设有13个车站。
4.工人们正在架设电线杆,相邻两根间的距离是200 m。 在总长 3000 m 的笔直路上,一共要架设多少根电线杆(两端都架设)?
3000÷200 = 15(个)
15+1 = 16(根)
答:一共要架设16根电线杆。
提示:可以把一根电线杆看成一棵树,当成植树问题来回答。
随堂小练
1.园林工人沿一条笔直的公路一侧植树,每隔6 m种一棵,一共种了36棵。从第一棵到最后一棵的距离有多远?
当堂检测
36 - 1 = 35(个)
35 ×6 = 210(m)
答:从第一棵到最后一棵的距离有210 m。
2.某地300 m长的步行街的两边每隔30 m挂一个红灯笼(两端都挂),一共挂了多少个红灯笼?
当堂检测
(300÷30 +1 )×2= 22(个)
答:一共挂了22个红灯笼。
当堂检测
3.一条跑道长120m,要在跑道的一边每隔8 m插一面小旗(两端又要插),一面小旗0.5元钱,一共需要多少钱?
(120÷8 +1)×0.5 = 8(元)
答:一共需要8元钱。
你有什么收获?
植树问题
课堂小结
1.间隔数=总路长÷间距,植树棵数=间隔数+1。
不封闭路线上两端都栽的植树问题
2.公路安装路灯、架设电线杆、设置站点、排队、上楼梯等,都可以看成植树问题来解答。
