【暑假专项培优】专题05 环形跑道问题(含解析)—小升初奥数思维之典型应用题精讲精练讲义(通用版)
文档属性
| 名称 | 【暑假专项培优】专题05 环形跑道问题(含解析)—小升初奥数思维之典型应用题精讲精练讲义(通用版) |  | |
| 格式 | docx | ||
| 文件大小 | 662.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-26 11:27:43 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
小升初奥数思维之典型应用题精讲精练讲义(通用版)
专题05 环形跑道问题
【第一部分:知识归纳】
一、基本概念
1、环形跑道问题是指运动物体在闭合环形路径上的相遇或追及问题。
2、这类问题的特点是:
(1)运动路线是闭合的环形,没有起点和终点的区别
(2)相遇和追及的计算与直线型不同,需要考虑"圈数"的概念
(3)解题时需要明确运动方向(同向或反向)
二、核心公式
1. 同向运动(追及问题)
追及时间 = 跑道周长 ÷ 速度差
第n次追及时,快者比慢者多跑n圈
2. 反向运动(相遇问题)
相遇时间 = 跑道周长 ÷ 速度和
第n次相遇时,两人共跑n圈
3. 平均速度
平均速度 = 总路程 ÷ 总时间
在环形跑道上,跑完一圈的平均速度 = 周长 ÷ 一圈所用时间
三、常见题型与解题方法
1. 基本追及问题
例题:甲、乙两人在400米的环形跑道上跑步,甲的速度是6m/s,乙的速度是4m/s。如果两人从同一点同时同向出发,甲第一次追上乙需要多长时间?
解答:速度差 = 6 - 4 = 2m/s
跑道周长 = 400m
追及时间 = 400 ÷ 2 = 200秒
2. 基本相遇问题
例题:在300米的圆形跑道上,A以5m/s、B以3m/s的速度同时从同一点反向出发。他们第3次相遇需要多少时间?
解答:速度和 = 5 + 3 = 8m/s
第3次相遇共跑3圈 = 3×300 = 900m
时间 = 900 ÷ 8 = 112.5秒
3. 变速运动问题
例题:在600米的跑道上,小明前一半时间以4m/s跑,后一半时间以6m/s跑。求他跑完一圈的平均速度。
解答:设总时间为T秒
前T/2秒跑的距离 = 4×(T/2) = 2T
后T/2秒跑的距离 = 6×(T/2) = 3T
总距离 = 2T + 3T = 5T = 600 → T = 120秒
平均速度 = 600 ÷ 120 = 5m/s
4. 多次相遇问题
例题:在250米的环形跑道上,甲、乙两人分别以3m/s和5m/s的速度同时从同一点反向出发。当他们第5次相遇时,甲跑了多少米?
解答:速度和 = 3 + 5 = 8m/s
第5次相遇共跑5圈 = 5×250 = 1250m
时间 = 1250 ÷ 8 = 156.25秒
甲跑的距离 = 3 × 156.25 = 468.75m
四、解题技巧
1、画图辅助:用圆形图标记起点和运动方向
2、确定运动方向:同向用速度差,反向用速度和
3、注意单位统一:确保所有速度、时间、距离的单位一致
4、特殊值法:当题目未给出具体数值时,可以假设一个方便的数值(如周长取速度的公倍数)
【第二部分:能力提升】
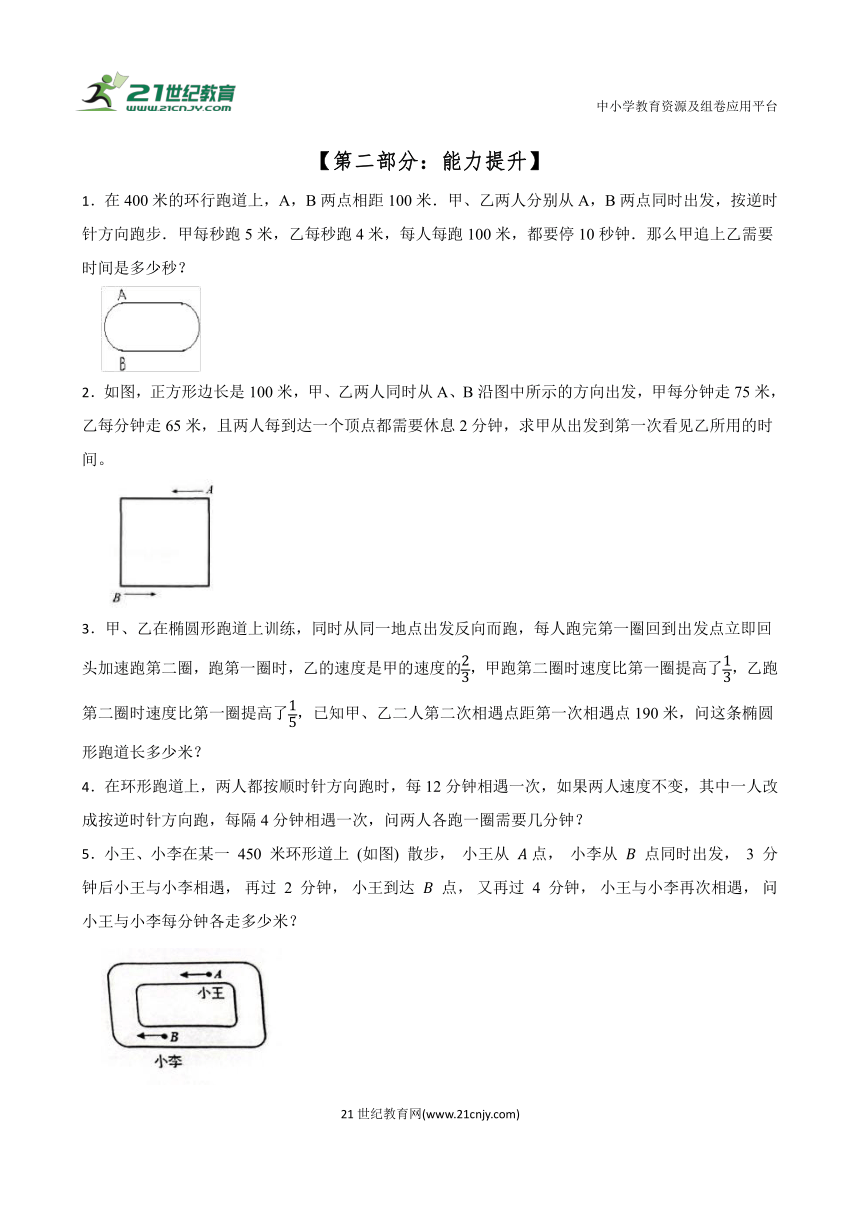
1.在400米的环行跑道上,A,B两点相距100米.甲、乙两人分别从A,B两点同时出发,按逆时针方向跑步.甲每秒跑5米,乙每秒跑4米,每人每跑100米,都要停10秒钟.那么甲追上乙需要时间是多少秒?
2.如图,正方形边长是100米,甲、乙两人同时从A、B沿图中所示的方向出发,甲每分钟走75米,乙每分钟走65米,且两人每到达一个顶点都需要休息2分钟,求甲从出发到第一次看见乙所用的时间。
3.甲、乙在椭圆形跑道上训练,同时从同一地点出发反向而跑,每人跑完第一圈回到出发点立即回头加速跑第二圈,跑第一圈时,乙的速度是甲的速度的,甲跑第二圈时速度比第一圈提高了,乙跑第二圈时速度比第一圈提高了,已知甲、乙二人第二次相遇点距第一次相遇点190米,问这条椭圆形跑道长多少米?
4.在环形跑道上,两人都按顺时针方向跑时,每12分钟相遇一次,如果两人速度不变,其中一人改成按逆时针方向跑,每隔4分钟相遇一次,问两人各跑一圈需要几分钟?
5.小王、小李在某一 450 米环形道上 (如图) 散步, 小王从 点, 小李从 点同时出发, 3 分钟后小王与小李相遇, 再过 2 分钟, 小王到达 点, 又再过 4 分钟, 小王与小李再次相遇, 问小王与小李每分钟各走多少米?
6.成才和许三多两人在钢七连军训场的同一条环形跑道上进行跑步训练。他们同时同地出发,沿相反方向开始跑步,开始时许三多的速度是成才的。每人跑完一圈后,都立即回头加速跑下一圈,成才的速度比前一圈提高,许三多的速度比前一圈提高。两人每相遇两次,就以其中第二次的相遇点作为新的出发点,跑步规则不变(第一圈仍回到原速,第二圈加速),如此持续跑下去。记他们最初的出发点为A,第一次相遇点为B,第二次相遇点为C。已知B和C在环形跑道上的最短距离为190米。
(1)求这条环形跑道的长度。
(2)他们能否同时回到最初的出发点?如果能,这时成才和许三多两人各跑了多少米?如果不能,说明理由。
7.如图,学校操场的400米跑道中套着300米小跑道,大跑道与小跑道有200米路程相重,甲以每秒6米的速度沿大跑道逆时针方向跑,乙以每秒4米的速度沿小跑道顺时针方向跑,两人同时从两条跑道的交点处出发,当他们第二次在跑道上相遇时,甲共跑了多少米?
8.如图是圆环岛示意图阴影部分为绿地AB=CD=200米。甲车在A处按A处箭头方向行驶,车速每小时60千米,乙车在D处按D处箭头方向行驶,车速为每小时54千米如果车辆在这环岛的所有路口只能右转或直行,那么甲车追上乙车至少要多少分钟?(圆周率取3)
9.如图所示,甲、乙两人从长为400米的圆形跑道的A点背向出发跑步.跑道右半部分 (AB为圆的直径) 道路比较泥泞,所以两人的速度都将减慢,在正常的跑道上甲、乙速度均为每秒8米,而在泥泞道路上两人的速度均为每秒4米.两人一直跑下去,问他们第79次迎面相遇的地方距A点还有多少米 请写出简要的解题步骤.
10.小新和正南在操场上比赛跑步,小新每分钟跑250米,正南每分钟跑210米,一圈跑道长800米,他们同时从起跑点出发,那么小新第三次超过正南需要多少分钟?
11.甲、乙两车绕周长为400千米的环形跑道行驶,它们从同一地点同时出发,背向而行,5小时相遇,如果两车每小时各加快10千米,那么相遇点距离前一次相遇地点3千米,已知乙车比甲车快,求原来每小时行多少千米?
12.有一个200米的环形跑道,甲、乙两人同时从同一地点同方向出发.甲以每秒0.8米的速度步行,乙以每秒2.4米的速度跑步,乙在第二次追上甲时用了多少秒
13.有一个200米的环形跑道,甲、乙两人同时从同一地点同方向出发.甲以每秒0.8米的速度步行;乙以每秒2.4米的速度跑步,乙在第2次追上甲时用了多少秒?
14.如图,在长为490米的环形跑道上,A,B两点之间的跑道长50米,甲、乙两人同时从4,B两点出发反向奔跑.两人相遇后,乙立刻转身与甲同向奔跑,同时甲把速度提高了25%,乙把速度提高了20%、结果当甲跑到点A时,乙恰好跑到了点B.如果以后甲、乙的速度和方向都不变,那么当甲追上乙时,从一开始算起,甲一共跑了多少米?
15. 3辆汽车在环形公路上试车,3辆汽车跑一圈分别需要30分钟,18分钟,10分钟,现在3辆汽车在同一起点,同时同向而行。问:最少多长时间,它们相遇在一起?
16.环形跑道400米,小百、小合背向而行,小百速度是6米/秒,小合速度是4米/秒,当小百碰上小合时立即转向跑,小合不改变方向,小百追上小合时也立即转向跑,小合仍不改变方向,问两人第11次相遇离起点多少米?(按较短距离算,追上和迎面都算相遇)
17.(环形跑道问题) 甲、乙两车绕周长为 400 千米的环形跑道行驶, 他们从同一地点同时出发, 背向而行, 5 小时相遇, 如果两车每小时各加快 10 千米, 那么相遇点距离前一次相遇地点 3 千米。已知乙车比甲车快, 求甲车原来每小时行多少千米。
18.可可和乐乐绕一条长400米的环形跑道跑步锻炼身体,他们同时从同一地点出发,向相反方向跑去,可可的速度是6米/秒,乐乐的速度是4米/秒。30秒后两人相遇了吗?如果没有相遇,两人还相距多少米
19.甲、乙两人, 在一圆形跑道上同时同地出发, 反向跑步.已知甲的速度是每分钟 , 乙的速度是每分钟 , 在 30 分钟内, 它们相遇了 24 次, 问跑道的长度最多是多少米?
20.有一个200米的环形跑道, 甲、乙两人同时从同一地点同方向出发, 甲以每秒 0.8 米的速度为步行, 乙以每秒2.4米的速度跑步, 当乙第2次追上甲时用了多少秒?
21.甲乙二人沿400米环形跑道同时从某点开始反方向跑步,已知甲的速度比乙的速度快,当两人第一次相遇时甲跑了多少米?
22.如图,大圈是400米跑道,由A到B的跑道长是200米,直线距离是50米。父子俩同时从A点出发逆时针方向沿跑道进行长跑炼,儿子跑大圈,父亲每跑到B点使沿各直线跑。父亲每100米用20秒,儿子每100米用19秒。如果他们按这样的速度比,儿子在跑第几圈时,第一次与父亲再相遇?
23.在某一运动场的450米的环形跑道上(如下图),小王从A点出发,逆时针行驶,同时小李从B点出发顺时针行驶,6分钟后小王与小李相遇,再过4分钟,小王到达B点,又过8分钟,小王与小李再次相遇,问:小王与小李每分钟各走多少米
24.甲、乙两人,在一圆形跑道上同时同地出发,反向跑步,已知甲的速度是每分钟 , 乙的速度是每分钟 。在 30 分钟内, 它们相迎了24 次, 问跑道的长度最多是多少米?
25.(追及问题)在周长为200米的圆形跑道一条直径的两端,甲、乙两人分别以6米/秒、5米/秒的速度骑车同时同向出发,沿跑道行驶,问:16分钟内,甲追上乙多少次
26.一个圆形操场跑道的周长是500米,两个学生同时同地背向而行.黄莺每分钟走66米,麻雀每分钟走59米.经过几分钟才能相遇
27.甲、乙两人在环形跑道上练习跑步,若同时同地点同方向出发,4分钟后甲从后面超过乙一圈;若同时同地点反方向出发,1分钟后两人相遇。问甲、乙跑完一圈各需多少分钟?
28.两名运动员在湖的周围环形道上练习长跑.甲每分钟跑250米,乙每分钟跑200米,两人同时同地同向出发,经过45分钟甲追上乙;如果两人同时同地反向出发,经过多少分钟两人相遇?
29.如图﹐在长为400公尺的环形跑道上﹐A﹑B两点之间的跑道长100公尺.甲从A点﹑乙从B点同时出发相背而跑.两人相遇后﹐乙即转身与甲同向而跑﹐当甲跑到A时乙恰好跑到B.继续跑若甲追上乙时﹐甲从出发开始算起共跑了多少公尺﹖
30.绕湖一周是20千米,甲乙二人从湖边某一地点同时出发反向而行,甲以每小时4千米的速度每走1小时后休息5分钟,乙以每小时6千米的速度每走50分钟后休息10分钟,则两人从出发到第一次相遇用了多少分钟?
31.如下图,一只甲虫从A点出发,在圆形路线上沿顺时针方向爬行;一只蚂蚁同时从B点出发,在半圆BmA上往返爬行。已知甲虫爬行速度是蚂蚁的2.4倍,他们第二次相遇点与第三次相遇点之间的路程是30厘米。那么,这条圆形路线的全场是多少?
32.小明和谷等一起去换场散步。如果两人同时同地出发,相背而行, 分钟相遇:如果两人同时同地出发,同方向而行,24分钟小明超出爷爷一整圈。问小明和爷爷走一圈,各自需要多少分钟?
33.在400米的环形跑道上,甲、乙两人同时同地起跑,如果同向而行3分20秒相遇,如果背向而行40秒相遇,已知甲比乙快,求甲、乙的速度各是多少?
34.甲、乙二人在同一条椭圆形跑道上作特殊训练:他们同时从同一地点出发,沿相反方向跑,每人跑完第一圈到达出发点后立即回头加速跑第二圈,跑第一圈时,乙的速度是甲速度的2/3.甲跑第二圈时速度比第一圈提高了1/3;乙跑第二圈时速度提高了1/5.已知沿跑道看从甲、乙两人第二次相遇点到第一次相遇点的最短路程是190米,那么这条椭圆形跑道长多少米
35.如图所示,A,B,C三地之间有三条公路相连,三条公路的路程之比是AB:BC:AC=2:4:5.甲乙两车同时从A地出发,甲车沿A→B→C方向行驶,乙车沿A→C→B方向行驶,2小时后在B地和C地之间的D地相遇.已知汽车沿A→B方向和C→B方向行驶的速度都是每小时60千米,沿B→C方向行驶的速度是每小时90千米,沿A→C方向行驶的速度是每小时75千米,求C、D两地之间的距离是多少千米?
36.在一个600米的环形跑道上,兄弟两人同时从同一个起点按顺时针方向跑步,两人每隔12分钟相遇一次,若两个人速度不变,还是在原来出发点同时出发,哥哥改为按逆时针方向跑,则两人每隔4 分钟相遇一次,两人跑一圈各要多少分钟?
37.甲乙两人以匀速绕圆形跑道相向跑步。出发点在圆直径的两端。如果他们同时出发,并在甲跑完60米时第一次相遇,乙跑一圈还差100米时俩人第二次相遇,求跑道的长是多少米?
38.甲、乙、丙三人环湖跑步锻炼,同时从湖边一固定点出发,乙、丙二人同向,甲与乙丙反向,在甲第一次遇上乙后1.25分钟第一次遇上丙,再经过3.75分钟第二次遇乙.已知甲速遇乙速的比是3:2,湖的周长是2000米.求甲、乙、丙三人的速度每分钟各是多少米?
39.甲、乙两名运动员在周长400 米的环形跑道上进行10000米长跑比赛,两人从同一起跑线同时起跑,甲每分钟跑400 米,乙每分钟视频讲解跑360米,当甲比乙领先整整一圈时,两人同时加速,乙的速度比原来快 甲每分钟比原来多跑18 米,并且都以这样的速度保持到终点。甲、乙两人谁先到达终点?
40. 如下图,A、B是周长为360m的圆形跑道上一条直径的两个端点,早晨小明和小华约好两人去跑步,小明从A点出发,同时小华从B点出发,沿着跑道相向而行,两人在C点第一次相遇。已知C点离A点有80m,求他俩第二次相遇点在圆周上距B点多远?
41.第三届中国大学生方程式汽车比赛赛前,甲、乙两辆参赛小汽车在一个封闭的环形跑道内进行耐久测试。两车从同一地点沿相同方向同时起步后,乙车速超过甲车速,在第15分钟时甲车提速,在第18分钟时甲车追上乙车并且开始超过乙,在第23分钟时,甲车再次追上乙车。已知在测试中甲、乙两车均是匀速行驶,那么如果甲车不提速,乙车首次超过甲车所用的时间是多少分钟?
42.绕湖的一周是24千米,小明和小青从湖边某一地点同时出发,反向而行,小明以每小时4千米的速度,每走一小时后休息5分钟,小青以每小时6千米的速度每走50分钟后休息10分钟,两人出发后多长时间第1次相遇?
43.如图,A、B是圆的直径的两端,小张在A点,小王在B点同时出发反向行走,他们在C点第一次相遇,C离A点80米;在D点第二次相遇,D点离B点6O米.求这个圆的周长.
44.甲、乙两人沿一个周长为400米的环形跑道匀速前进,甲行走一圈需4分钟,乙行走一圈需7分钟,他们同时同地同向出发,甲走完10圈后,改为反向行走.出发后,每一次甲追上乙或和乙迎面相遇时,二人都击掌示意.当二人第15次击掌时,乙走的路程是多少米?
45.甲、乙、丙三人环湖跑步锻炼,同时从湖边一固定点出发,乙、丙二人同向,甲与乙丙反向,在甲第一次遇上乙后1.25分钟第一次遇上丙,再经过3.75分钟第二次遇乙。已知甲速是乙速的1.5倍,湖的周长是2000米。求甲、乙、丙三人的速度每分钟各是多少米?
46.湛湛和粤粤周六相约去湖边跑步,湛湛每分跑150m,粤粤每分跑200m。环湖路一周的长度是7000m,两人同时同地反方向跑步。
(1)估计两人在何处相遇?在图中用△标出来。
(2)几分后两人相遇?相遇时两人各行了多少米?
47.两只小爬虫甲和乙,从A点同时出发,沿长方形ABCD的边按箭头方向爬行(如图)。在距C点32厘米的E点它们第一次相用,在距D点16厘米的F点第二次相遇,在距A点16厘米的G点第三次相遇,求长方形的边AB长多少厘米?
48.下图中有两个圆只有一个公共点A,大圆直径48厘米,小圆直径30厘米。两只甲虫同时从A点出发,按箭头所指的方向以相同速度分别沿两个圆爬行。问:当小圆上甲虫爬了几圈时,两只甲虫首次相距最远?
49.如图是一个跑道的示意图,沿 走一圈是 米,沿 走一圈是 米,其中 到 的直线距离是 米.甲、乙二人同时从 点出发练习长跑,甲沿 的小圈跑,每 米用 秒,乙沿 的大圈跑,每 米用 秒,问:
(1)乙跑第几圈时第一次与甲相遇?
(2)出发多长时间甲、乙再次在A相遇?
50.在 400 米的环行跑道上,A,B 两点相距 100 米。甲、乙两人分别从 A,B 两点同时出发,按逆时针方向跑步。甲每秒跑 5 米,乙每秒跑 4 米,每人每跑 100 米,都要停 10 秒钟。那么甲追上乙需要时间是多少秒?
参考答案及试题解析
1.【答案】解:如果两人不休息,那么甲追上乙需要:100÷(5﹣4)=100(秒),
100秒内甲实际跑了:100×5=500(米),
所以甲休息了4次,
100+4×10=140(秒);
答:甲追上乙需要时间是140秒.
【解析】甲实际跑100÷(5﹣4)=100秒时追上乙,则甲实际跑了100×5=500米,所以甲已经休息了4次,由此即可求得追上乙所用的时间.
2.【答案】解:根据图示可知:甲乙的距离是正方形的两个边长,甲走每个边长用时:100÷75=(分钟),加上休息需要分钟
乙走每个边长用时:100÷65=(分钟),加上休息需要分钟
甲走两周回到A点用时×8=(分钟)
乙走7个边长到A左边的顶点用时:
7×-2
=-2
=(分钟)
分钟离开
因为<,甲到A顶点时,乙还没有离开A左侧顶点,此时甲第一次看到乙
答:甲从出发到第一次看见乙所用的时间为分钟。
【解析】首先根据图示,可得甲乙距离是正方形的两个边长,分别求出甲乙走每个边长加上休息的时间;然后根据乙走7个边长到A左边的顶点用时7×=(分钟),分钟离开,因为<,甲到A顶点时,乙还没有离开A左侧顶点,此时甲第一次看到乙,据此解答即可。
3.【答案】解:设一开始时甲的速度是a,于是乙的速度便是,设跑道长是L,
则甲、乙第一次相遇点,按甲前进方向距出发点为.
甲跑完第一圈,乙跑了,乙再跑余下的,甲已折返,且以的速度跑,所以在乙跑完第一圈时,甲已折返跑了,
这时,乙折返并以的速度跑着.
从这时起,甲、乙速度之比是,即5:3.
所以在二人第二次相遇时,甲跑了余下的的,而乙跑了它的,即第二次相遇时距出发点为.
可见两次相遇点间的距离是(米),即(米).
解得L=400(米)
答:跑道长为400米.
【解析】设一开始时甲的速度是a,于是乙的速度便是,设跑道长是L,根据题干条件求出甲乙两人的速度之比,再求出每次相遇的时间,由此即可求出甲第二次相遇时,距离出发点的距离,从而解决问题.
4.【答案】解:把这个跑道的长度看做整体“1”,
则甲的速度为:(+)÷2=,
乙的速度是:﹣=;
所以跑完一圈甲需要时间:1÷=6(分钟),
乙跑完一圈需要时间:1÷=12(分钟),
答:各跑一圈时,较快的需要6分钟,较慢的需要12分钟.
【解析】把这个跑道的长度看做整体“1”:分别求得二人的速度,即可求出他们跑一圈各自用的时间;
(1)两人都按顺时针方向跑时,属于追及问题:假设甲比乙跑的快,12分钟相遇说明二人的速度差是:;
(2)其中一人改成按逆时针方向跑,属于相遇问题:每隔4分钟相遇一次说明二人的速度之和是;
有上述推理即可得出甲的速度为:(+)÷2=,从而得出乙的速度是:﹣=;由此即可解决问题.
5.【答案】解:根据题干分析可得:相遇后,小王与小李行驶相同的路程所用的时间之比是2:3,所以小王与小李的速度之比就是3:2,
设小王的速度是3x米每分,小李的速度是2x米每分,根据题意可得方程:
(3x+2x)×(4+2)=450,
30x=450,
x=15,
小王的速度是:15×3=45(米/分),
小李的速度是:15×2=30(米/分),
答:小王的速度是45米/分,小李的速度是30米/分.
【解析】 根据题干分析可得,3分钟相遇后,小王与小李又行驶了4+2分钟后正好行驶了环形跑道一周450米,又根据“3分钟后小王与小李相遇,再过2分钟,小王到达B点”可得:相遇后,小王2分钟行驶的路程与小李3分钟行驶的路程,所用的时间之比是2:3,所以小王与小李的速度之比就是3:2,据此设小王的速度是3x米每分,小李的速度是2x米每分,据此利用等量关系二人行驶6分钟的路程=跑道总长度,据此即可解答.
6.【答案】(1)解:设许三多的速度是2,成才的速度是3,全程为单位“1”。
=
=2.4
=3+1
=4
2.4:4=3:5
=
=
=400(米)
答:这条环形跑道的长度400米。
(2)解:根据题意,可得
400÷50=8(次)
8×2=16(次)
(400×2-50)×8
=(800-50)×8
=750×8
=6000(米)
(400+50)×8
=450×8
=3600(米)
答:他们在第16次时回到了出发点A,成才跑了6000米,许三多跑了3600米。
【解析】(1)许三多的速度是成才的,即在第一次相遇在B店的过程中,时间是相等的,则速度比就等式路程比,则许三多的路程是成才的,即成才跑了整个圆(A逆时针到B)的,许三多跑了整个圆(A顺时针到B)设许三多的速度是2,成才的速度是3,当成才到了A点时,速度比前一圈提高,以原来的速度为单位“1”,提高了原来的,也就是提高了1,就是4.开始回头,也就是成才跑了一圈了,许三多跑的路程是成才的,许三多还有才能到A点,也就是需要的时间,的时间里面成才用4速度已经跑了全程的,这时许三多的速度提高了,即以原来的速度为单位“1”,就是提高了0.4,加上原来的速度就是2.4.即许三多和成才开始以4和2.5的速度以相遇的形式跑全程的,路程比就是速度比为3∶5.即成才跑了的是,许三多跑了的即(A逆时针B)是。则B到C最短的距离占整个圆分率=逆时针B的分率-A顺时针C的分率=。即全程的是190米,已知一个数的几分之几是多少用除法。
(2)从(1)中可知,这个环形跑道的总长度是400米,AC之间的距离占整个环形跑道的,也就是离起始点A点50米。也就是两个人每两次相遇相遇点会在跑道逆时针前进50米。全程是400米,前进8次就是400米,8次里面每次有2次相遇,则是第16次相遇时两人同时在起点A。每两次相遇的时候成才相当于走了2圈少50米,即每两次走了750米,再×8即可,同理许三多每两个相遇走了一圈带50米,即每两次走了450米,再×8即可。
7.【答案】解: 第一次相遇的时间是400÷(6+4)=40(秒)
第一次相遇甲行驶的路程是:40×6=240(米)
第一次相遇乙行驶的路程是:40×4=160(米)
乙回到出发点A的时间:
(300-160)÷4
=140÷4
=35(秒)
甲行驶的路程是:
6×35=210(米)
甲处的位置:
210-(400-240)
=210-160
=50(米)
即甲在A点左50米处;
再相遇还需要的时间是:
(400-50)÷(6+4)
=350÷10
=35(秒)
甲一共跑的路程是:
6×(40+35+35)
=6×110
=660(米)
答:甲共跑了660米.
【解析】 根据题意,甲乙第一次相遇的时间是400÷(6+4)=40秒,第一次相遇甲跑的路程是40×6=240(米),第一次相遇乙跑的路程是40×4=160(米),然后再求出乙跑完(300-160)米的路程用的时间,即(300-160)÷4=35秒,即乙回到出发点A的时间,这时甲跑的路程是6×35=210米,这时甲所处的地点在A点左50米处,即与乙错开,再相遇还需要的时间是(400-50)÷(6+4)=35秒,所以从第一次相遇到第二次相遇时间是2个35秒,第一次相遇用40秒,所以在第二次相遇时,他们一共跑了40+70=110秒,再用甲的速度乘以跑的时间,即可求出甲共跑的路程是多少.
8.【答案】解:甲沿 追赶乙, 200 米 千米, 设乙行驶 千米时被甲追上, 需 分钟。
, 解之
答: 甲车追上乙车至少要 5.5 分钟
【解析】 根据题意,按照交通规则,可知先从A行驶到B,然后沿圆弧行驶到C,再从C行驶到D;由追及问题可知,甲比乙多行驶的距离就是A到D的距离,求出A到D的距离,再根据他们的速度差就可以求出甲车要追上乙车的时间.
9.【答案】由题意可知:奇数次相遇地点相同,偶数次相遇点为A点.
设奇数次相遇地点距A点还有x米,
依题意,得:,
解得:.
答: 第79次迎面相遇的地方距A点还有150米
【解析】由两人的速度相同(正常道速度相同,泥泞路速度也相同)可知:奇数次相遇地点相同(此时相遇点在泥泞路上),偶数次相遇点为A点,设奇数次相遇地点距A点还有x米,由时间=路程÷速度,即可得出关于x的一元一次方程,解之即可得出结论
10.【答案】解:800×3+(250-210)=60(分钟)
答:小新第三次超过正南需要60分钟。
【解析】小新第三次超过正南是比正南多跑了三圈,所以小新第三次超过正南需要需要的时间=跑道的周长×3÷速度差。
11.【答案】解:加速后两车的相遇时间为:400÷(400÷5+10×2)=400÷(80+20)=400÷100=4(小时)甲车原来的速度:(40﹣3)÷(5﹣4)=37÷1=37(千米/小时)答:原来甲车每小时行37千米
【解析】分析】甲、乙两车原来的速度和=400÷5=80(千米/小时) 现在两车的速度和=80+10+10=100(千米/小时); 现在的相遇用时=400÷100=4(小时),由于乙车比甲车快,甲车现在4小时比原来多走:10×4=40(千米),这40千米甲以原来的速度走(5﹣4=)1小时,还多出3千米. 所以甲车原来的速度:(40﹣3)÷(5﹣4)=37(千米/小时).
12.【答案】解:乙第二次追上甲时,乙比甲多跑了2圈,
即它们的距离差是200×2=400(米),
速度差是2.4-0.8=1.6(米/秒)
400÷1.6=250(秒)
答: 乙在第二次追上甲时用了250秒。
【解析】要求乙在第二次追上甲时用了多少秒,应先求出乙在第二次追上甲时他们的路程差和速度差,再利用 ‘路程÷速度=时间’,即可求得结果。
13.【答案】解:200×2=400(米)
400÷(2.4-0.8)
=400÷1.6
=250(秒)
答:乙在第2次追上甲时用了250秒。
【解析】乙两次追上甲则乙跑的路程是环形跑道两圈的长度,乙的速度-甲的速度=两人的速度差,乙跑的路程÷(乙的速度-甲的速度)=乙在第2次追上甲时用的时间。据此可以解答。
14.【答案】解:设甲原来每单位时间的速度为,乙原来每单位时间的速度为。
所以,他们所花时间的比为:
由此,可以得到以下方程:
解得:(米)
从A点到相遇点的路程为:(米)
因此,乙的速度为:(米)
两人速度变化后,甲的速度为:(米)
乙的速度为:(米)
从相遇点开始,甲追上乙时,甲比乙多行一圈,即490米。因此,甲追上乙所需的时间为:
(单位时间)
因此,甲追上乙时一共跑的路程为:(米)
答:甲一共跑了2690米。
【解析】首先,设定甲乙两人原来的速度,并根据题目描述建立速度比和时间比的关系。接着,根据这些比例关系,结合已知的跑道长度和甲乙两人的相遇位置,求解出甲乙两人原来的速度。然后,根据题目描述,计算出甲乙两人速度变化后的速度。最后,利用追及问题的原理,结合已知的速度差和跑道长度,求解出甲追上乙时甲一共跑了多少米。
15.【答案】解:30=2×3×5,18=2×3×3,10=2×5
所以30、18、10的最小公倍数为2×3×3×5=9×10=90
答:最少90分钟,它们相遇在一起。
【解析】因为是在环形公路上试车,三辆车跑一圈所用的时间都不同,所以可以计算出当它们跑了一定数量的圈数以后得到的时间一样,这个时间就是它们相遇的时间。所以算出30,18,10的最小公倍数,这样就是在最少时间内,它们会相遇。
16.【答案】解:小百和小合的相对速度是:6+4=10米/秒。
故他们每次相遇的时间是:400÷10=40秒。
小合的速度是4米/秒,所以他在40秒内行进的路程是40×4=160米。
故小合在11次相遇后行进的总路程是:160×11=1760米。
环形跑道的长度是400米,所以小合在11次相遇后离起点的距离是1760 ÷400=4圈余160米。
因此,小合在第11次相遇时离起点160米。
【解析】需要确定小百和小合每次相遇的时间。由于他们是背向而行,所以他们的相对速度是他们的速度之和。可以计算出小合在每次相遇时行进的距离,以及在11次相遇后行进的总路程。将小合行进的总路程除以环形跑道的长度,得到小合行进的圈数和余数,即他离起点的距离。
17.【答案】解:甲乙两车原速度和为400÷5=80(千米/时),两车速度增加后,相遇时间为:400÷(80+10×2)=4(小时),
甲车现在4小时比原来多走:10 4=40(千米)
所以甲车原来的速度为:(40-3)÷(5-4)=37÷1=37(千米/时)
答:甲车原来每小时行37千米
【解析】两车速度差不变,第一次两车5小时相遇速度增加后,两车4小时相遇,用现在多走的路程减去多出的3千米,除以时间差,就是甲原来的速度
18.【答案】解:(6+4)×30
=10×30
=300(米)
400>300
400-300=100(米)
答:两人没有相遇,还相距100米。
【解析】可可的速度 +乐乐的速度=两人的速度和,(可可的速度 +乐乐的速度)×跑步时间=两人的路程和。然后用两人的路程和与跑道长比较:如果路程和等于跑道长度说明两已经相遇;如果路程和小于跑道长度说明两人还没有相遇,跑道长度与路程和的差就是两人之间相距的距离;如果路程和大于跑道长度说明两人已经相遇并又向相反方向跑了一段距离了。
19.【答案】解:30×(180+240)
=30×420
=12600(米)
12600÷24=525(米)
答:跑道的长度最多是525米。
【解析】根据相遇问题的经验可知两人相遇一次即走了一个跑道的长度,所以相遇24次即走了24个跑道的长度,而跑道的长度要最大就不需要考虑这30分钟内走的总路程除了相遇外还有没有相遇的路程长度,因此用两人30分钟内走的总路程除以24即为一个跑道的最多长度;(甲的速度+乙的速度)×时间=两人30分钟内所走的总路程,两人30分钟内所走的总路程÷24=跑道最大的长度,据此可以解答。
20.【答案】解: 200×2=400(米)
400÷(2.4-0.8)
=400÷1.6
=250(秒)
答:乙第2次追上甲用了250秒。
【解析】根据题意可知:因为甲、乙两人是沿环形跑道同时同地同方向出发,所以当乙第2次追上甲时,乙比甲多跑了2圈,即他们的距离差=环形跑道长×圈数=200×2=400米;乙第2次追上甲用的时间=两人的距离差÷(乙的速度-甲的速度)=400÷(2.4-0.8)=250秒。
21.【答案】解:甲乙速度比=(1+):1=11:10,
当两人第一次相遇时甲跑了:
400÷(10+11)×11,
=400÷21×11,
=4400÷21,
=209(米),
答:当两人第一次相遇时甲跑了209米.
【解析】由甲的速度比乙的速度快,可得甲乙速度比=(1+):1=11:10,从而求出在相同时间甲乙所行的路程比11:10,根据甲乙二人沿400米环形跑道同时从某点开始反方向跑步,是相遇问题就用环形跑道长除以甲乙所行路程总份数,即可得出1份的,再乘以11就是甲跑的米.
22.【答案】解:儿子每次到达A点所用时间:
400÷100×19
=4×19
=76(秒)
父亲:
(200+50)÷100×20
=250÷100×20
=50(秒)
从A到B逆时针跑,儿子需要时间:76÷2=38(秒),父亲需要:
200÷100×20
=2×20
=40(秒)
40-38=2(秒),即只要在父亲到达A点后的2秒之内,儿子也到达A点,儿子就能从后面追上父亲;
父亲到达A点的时间有50,100,150,200,……
儿子到达A点的时间有76,152,228,……
相差2秒的有152和150,即父子第一次相遇时,儿子已经跑完第2圈,也就是正在跑第3圈。
答:儿子在跑第3圈时,第一次与父亲再相遇。
【解析】根据题意可知:父子俩的相遇是在从A到B的逆时针的这个路段上。先求出儿子和父亲在这一路段各自的用时是38秒、40秒,这说明只要父亲到达A点后的2秒内儿子到达A点即可追上父亲;再求出儿子、父亲每次到达A点所有时间的周期分别为76秒和50秒,进而列出父子俩到达A点的几个时间并进行比较找出相差2秒的时间便可解答。
23.【答案】解:根据题干分析可得:相遇后,小王与小李行驶相同的路程所用的时间之比是4:6=2:3,所以小王与小李的速度之比就是3:2,
设小王的速度是3x米每分,小李的速度是2x米每分,根据题意可得方程:
(3x+2x)×(4+8)=450
60x=450
x=7.5
小王的速度是:7.5×3=22.5(米/分),
小李的速度是:7.5×2=15(米/分),
答:小王的速度是22.5米/分,小李的速度是15米/分.
【解析】 根据题干分析可得,6分钟相遇后,小王与小李又行驶了4+8分钟后正好行驶了环形跑道一周450米,又根据“6分钟后小王与小李相遇,再过4分钟,小王到达B点”可得:相遇后,小王4分钟行驶的路程与小李6分钟行驶的路程,所用的时间之比是4:6=2:3,所以小王与小李的速度之比就是3:2,据此设小王的速度是3x米每分,小李的速度是2x米每分,据此利用等量关系二人行驶12分钟的路程=跑道总长度,据此即可解答.
24.【答案】解:(180+240)×30
=420×30
=12600(米)
12600÷24=525(米)
答:跑道的长度最多是525米。
【解析】因为是同时同地出发,反向跑步,所以第一次相遇两人路程之和等于跑道长,因此第一次相遇时两人跑的路程和是跑道1圈的长度。从第一次相遇开始,两人每相遇一次,两人的路程和是跑道长的1圈的长度。因此30分钟内相遇24次,即共跑了24圈,此时共跑了(跑道1圈的长度×24)米。 求出24圈的长度,再除以24即可求出跑道的长度。
25.【答案】解:第一次甲追上乙需:200÷2÷(6-5)=100(秒)
(圈)
超过1圈追上1次,
因此共追上 (次)。
答:16分钟内,甲追上乙5次。
【解析】 根据“追及时间=路程差÷速度差”,如图,第一次甲追上乙是在200÷2÷(6-5)=100秒后,16分=60×16=960秒,后来又行了16×60-100=860(秒),后来甲行了860×6÷200=25.8(圈),乙行了860×5÷200=21.(圈);超过1圈追上1次,所以后来又追上了25-21=4(次),因此共追上4+1=5次;
此题属于复杂的环形跑道追及问题,解答此题的关键是根据路程差、速度差和追及时间三者之间的关系,进行分析解答即可
26.【答案】解:500÷(66+59)=500÷125=4(分钟)
答:经过4分钟才能相遇。
【解析】相遇用的时间=跑道的周长÷两人的速度和,据此作答即可。
27.【答案】解:甲、乙两人的速度和是1÷1 =1,
两人的速度差是
甲速度
甲跑完全程所用的时间是 分钟)
乙的速度是
乙跑完全程所用的时间是 (分钟)
答:甲跑完一圈需要 分钟,乙跑完一圈需要 分钟。
【解析】把这个环形跑道的路程看作“1”,甲、乙两人的速度和是1÷1=1,速度差是 从而求出甲的速度,用环形跑道的路程除以甲的速度就是甲跑完全程所需要的时间;再求出乙的速度,近而求出乙跑完全程所需要的时间.
28.【答案】解:250-200=50(米/分)
50×45=2250(米)
2250÷(250+200)=5(分钟)
答:经过5分钟两人相遇。
【解析】两人同向而行,甲追上乙,甲比乙多跑一圈,所以两人的路程差=跑道一圈的长度=速度差×同向出发相遇用的时间,所以反向而行的相遇时间=跑道一圈的长度÷速度和。
29.【答案】解:400+[400﹣(400÷2﹣100)]×2
=400+[400﹣(200﹣100)]
=400+[400﹣100]×2
=400+600
=1000(米)
答:当甲追上乙时,甲共跑了1000米.
【解析】根据在相同的时间内,乙从B跑到C,甲可以从A跑到C(相向而行),乙如果按原路返回(从C跑到B),甲又可以同向从C经过B跑到A,可知 甲前后跑的两段路程是相等的,则AC=400÷2=200米.又因A、B两点间的距离是100米,所以乙每次跑的路程是200﹣100=100米,即甲的 速度是乙的速度的2倍.现在乙在前300米,甲在后追及,甲跑300×2=600米可以追上乙,原来乙跑了400米,所以甲从出发开始共跑的路程是 400+(400﹣100)×2=1000米.
30.【答案】解:假设甲乙不休息,二人相遇时间为:
20÷(4+6)=2(小时)
因二人中途休息,所以两人相遇所用时间超过2小时,且都休息了两次,
当二人同时出发130分钟时:
甲走了:4×2=8(千米)
乙走了:6×(130-20)÷60=11(千米)
(20-8-11)÷(4+6)=0.1(小时)
130+0.1×60=136(分钟)
答: 两人从出发到第一次相遇用了 136分钟。
【解析】由题意可知,当甲乙二人走的路程和为20千米时,二人相遇。实际上甲每走3千米花费时间为1小时又5分钟,即65分钟;乙每走6千米花费时间为1小时又10分钟,即70分钟;
假设甲乙不休息,求相遇需要时间是2小时,因中途休息,所以相遇时间超过2小时,先求2小时甲乙走的路程,再求出剩余路程甲乙走需要的时间,即可求得相遇用的时间。依据‘路程=速度×时间’
31.【答案】解:如图所示
甲虫与蚂蚁爬完半个圆图长所用时间之比是
甲虫: 蚂蚁 。依次绘制甲虫与蚂蚁朵行的折线图:
从图中可以看出,第二次相過点是 , 第三次相颫点是 , 且有:
所以
。由题意 (厘米), 所以 .
图周长是 (厘米)。
(注:上面的解答中,用 代表 的弧长,其他同)
【解析】理解甲虫和蚂蚁的运动规律。已知甲虫的速度是蚂蚁速度的2.4倍,这意味着在相同的时间内,甲虫能爬行的距离是蚂蚁的2.4倍。通过分析它们的相遇点,可以推断出圆形路线的全长。
32.【答案】解:设小明走一圈需x分钟,爷爷走一圈需y分钟。
()=1
=①
24()=1
=②
①-②解得y=8
=
=
=+
x=6
答:小明走一圈需要6分钟,爷爷走一圈需要8分钟。
【解析】本题为行程问题中的相遇与追及问题,涉及的是小明和爷爷同时同地出发在环形跑道上的运动。通过相背而行的相遇时间和同向而行的追及时间,可以分别建立方程来求解小明和爷爷走一圈所需的时间。关键在于理解相遇和追及的条件,并将其转化为速度的表达式,进而求解未知数。
33.【答案】解:甲乙的速度和为: (米/秒),甲乙的速度差为: (米/秒),甲的速度为: (米/秒),乙的速度为: (米/秒).
【解析】先将单位进行换算,即3分20秒=200秒,那么两人的速度和=跑道一圈的长度÷背向而行相遇用的时间,两人的速度差=跑道一圈的长度÷同向而行相遇用的时间,因为甲比乙快,所以甲的速度=(速度和+速度差)÷2;乙的速度=(速度和-速度差)÷2。
34.【答案】解:根据题意,可得
=
=
=4:2
=2:1
=
=
=
=
=5:3
=
=
=
=80×5
=400(米)
答:这条椭圆形跑道长400米
【解析】甲、乙从A点出发,沿相反方向跑,他们的速度比是。第一次相遇时,他们所行路程比是3:2。把全程平均分成5份,则他们第一次相遇点在B点,当甲到A点时,乙又行了。这时甲反向而行,速度提高了,甲、乙速度比为,当乙到达A点时,甲反向行了。这时乙反向而行,甲、乙的速度比变成了,这样,乙又行了,与甲在C点相遇。B、C的路程为190米,对应的份数为。则跑道长为:(米)
35.【答案】解:设AB为2a,BC为4a,CA为5a,CD为x千米,可得:
+=2
即6a+8a﹣2x=495
14a﹣2x=495①
+=2
即20a+5x=825
a=
将a代入①,可得:
14×﹣2x=825
解得:x=45
答:求C、D两地之间的距离是45千米.
【解析】由于是AB:BC:AC=2:4:5,设AB为2a,BC为4a,CA为5a,CD为x千米,则相遇时,甲车行了AB与BD,即2a与4a﹣x,由于甲在AB每小时行60千米,则在AB用了小时,沿B→C方向行驶的速度是每小时90千米,则在BD用了小时,又相遇时间是2小时,由此可得:+=2①,同理,乙车在AC段用了小时,在CD段用了小时,根据相遇时间可得:+=2②,分析①②式求出x即可.
36.【答案】解:速度差:600÷12=50(米),
速度和:600÷4=150(米),
哥哥的速度:(50+150)÷2=100(米),
弟弟的速度:150-100=50(米),
哥哥跑一圈用的时间:600÷100=6(分钟),
弟弟跑一圈用的时间:600÷50=12(分钟),
答:哥哥用6分钟,弟弟用12分钟。
【解析】题中要求两人跑一圈各用多少分钟?根据题意要求两人跑一圈各用多少分钟,那么我们就需要计算出两人的速度,题中告诉我们兄弟两人同时从同一地点出发,一前一后,每隔12分钟相遇一次,也就是路程差,即一圈路程;每隔4分钟相遇一次,也就是路程和,即一圈路程。所以两人合跑一圈用4分钟,根据路程=速度×时间,可以分别算出两个人的速度,再根据时间=路程÷速度,即可解答。
37.【答案】解:半跑道长为x米,则有
3(x-60)=2x-100
3x-180=2x-100
x=80
2x=2×80=160
答: 跑道的长是 160米。
【解析】根据第一次相遇甲、乙共跑了半圈,其中甲跑了60米。设半跑道长为x米,则乙在俩人第一次相遇时跑了(x-60)米。又因为从出发到甲、乙第二次相遇共跑了3个半圈长,由于他俩匀速跑步,在3个半圈长里乙应跑3(x-60)米,而这个距离恰好是乙跑一圈还差100米,即(2x-100)米,根据此数量关系列方程解答即可。
38.【答案】解:甲的速度为每分钟:
2000÷(1.25+3.75)×
=2000÷5×,
=240(米);
乙的速度为每分钟:
2000÷5﹣240
=4000﹣240,
=160(米).
丙的速度为每分钟:
2000÷6.25﹣240
=320﹣240,
=80(米).
答:甲每分钟跑240米,乙每分钟跑160米,丙每分钟跑80米.
【解析】在甲第一次遇上乙后1.25分钟第一次遇上丙,再经过3.75分钟第二次遇乙,则甲乙二人相时间为1.25+3.75=5分钟,两人相遇时 共行了一周即2000米,所以两人的速度和为每分钟2000÷5=400米.甲乙两人的速度比为3:2.由此可知甲的速度为每分钟400×=240米.由于甲与乙相遇时间为5分钟,甲第一次遇上乙后1.25分钟第一次遇上丙,则甲丙的相遇时间为5+1.25=6.25分钟,则丙的速度为每分钟2000÷6.25﹣240米.
39.【答案】解:甲比乙领先整整一圈所用时间:
400÷(400-360)
=400÷40
=10(分钟)
甲到达终点还需要时间:
(10000-400×10)÷(400+18)
=6000÷418
=
≈14.4(分钟)
乙到达终点还需要时间为:
=6400÷450
=
≈14.2(分钟)
14.4>14.2
答:乙先到达终点。
【解析】先求出甲比乙领先整整一圈时所用时间,求出剩余米数,再求出两人分别所用时间,再相加比较即可求解。
40.【答案】解:圆形跑道的周长为360米,因此半圆的长度为360 ÷ 2 = 180米。
已知C点离A点有80米,因此C点到B点的距离为180 - 80 = 100米。
小明从A点出发,小华从B点出发,沿着跑道相向而行。
两人在C点第一次相遇,说明小明跑过的路程与小华跑过的路程之比为80:100,即4:5。
两人第一次相遇后,他们将继续在跑道上跑步,直到第二次相遇。
在此期间,两人合起来跑过的总路程将是圆形跑道的周长,即360米。
由于时间相同,路程比等于速度比,因此在第二次相遇时,小明跑过的路程与小华跑过的路程之比仍为4:5。
因此,小明跑过的路程为米。
在第一次相遇后,小明从C点出发,继续跑了160米,到达第二次相遇点。
因此,第二次相遇点距离B点的距离为小明跑过的路程减去C点到B点的距离,即160 - 100 = 60米。
答: 他俩第二次相遇点在圆周上距B点 60m。
【解析】首先,根据题目给出的信息,需要确定C点到B点的距离。接着,需要分析小明和小华的速度比,以及他们第一次相遇到第二次相遇所走过的总路程。通过速度比和总路程,可以计算出小明在第二次相遇时跑过的路程。最后,根据小明跑过的路程和C点到B点的距离,可以确定第二次相遇点距离B点的距离。
41.【答案】解:设甲车提速前速度比乙车慢a/分钟,提速后速度比乙车快b/分钟。
那么有甲车在第15分钟时,离乙车的距离为15a。
这个距离在第18分钟追回来。
那么15a=(18-15)b,
即b=5a,
而且在第23分钟时,甲车比乙车多跑一圈.
那么一圈的路程为:(23-18)b=5b=25a,
所以甲车不提速时,乙车首次超过甲车(即多跑一圈)所需时间为:25a÷a=25分钟。
答: 如果甲车不提速,乙车首次超过甲车所用的时间是25分钟。
【解析】首先表示出甲车提速前速度比乙车慢a/分钟,提速后速度比乙车快b/分钟,进而利用甲车在第15分钟时,离乙车的距离为15a,这个距离在第18分钟追回来,即可得出等式方程求出a,b关系,再表示出一圈的路程即可得出答案 。
42.【答案】解:小王到第二轮休息结束时花了2小时10分,2小时10分=1小时+5分+1小时+5分,所以小王共走了4×2=8(千米),
2小时10分=50分+10分+50分+10分+10分,小张走的时间为50分+50分+10分=110分,所以小张走了=11(千米)。
这时两人还相距24-(8+11)=5(千米)
由于从此时到相遇已经不需要休息,因此,共同走完这5千米两人共需的时间是:5-(4+6) =0.5 (时) =30 (分)
所以,他们第一次相遇共需2小时10分+30分=2小时40分
答:两人出发后经过2小时40分第一次相遇。
【解析】先求出小王到第二轮休息结束时花的时间,然后计算出小王实际走的时间,再根据“速度×时间”求出小王这段时间内走的路程,同理可求出小张再这段时间内走的路程;然后求出此时两人之间的距离,两人不休息了,计算出还需走的时间,用已走的时间加上还需走的时间就是相遇时间。
43.【答案】解:1+=(圈)
80×3=240(米)
(240-60)÷(-1)=360(米)
答:此圆形场地的周长是360米。
【解析】从图中可以用看出,当甲、乙第一次相遇时,甲乙共走完圈的路程,当甲、乙第二次相遇时,甲乙共走完1+=圈的路程.所以从开始到第一、二次相遇所需的时间比为1:3,因而第二次相遇时乙行走的总路程为第一次相遇时行走的总路程的3倍,即80×3=240米.有甲、乙第二次相遇时,共行走(1圈的长度-60)+240,为圈,所以此圆形场地的周长为360米。
44.【答案】解:①甲乙同向;
10-10×4÷7
=10-5
=4(圈)
两人击掌4次;
②甲乙反向;
÷(+)
=÷
=(分钟)
15-4-1=10(次)
1÷(+)
=1÷
=(分钟)
×10=25(分钟)
40++25=66(分钟)
×66=(米)
答:乙走的路程是米。
【解析】为了计算简便,把一圈看成“1”,则甲的速度为, 乙的速度为,把整个过程分两个阶段考虑:
①甲走10圈时,共用了10×4=40(分钟),这段时间乙行走了40÷7=5(圈),每当甲比乙多走1圈时,甲便追上乙一次,所以甲走完10圈时,比乙多走了10-5=4(圈),两人共击掌4次,此时,甲、乙两人相距一圈;
②甲反向行走后,经过÷(+)=(分钟),两人第一次相遇,还应再相遇15-4-1=10(次),以后两人每相遇1次便合走一圈,即相遇事件发生的时间间隔为1÷(+)=(分钟),经过×10=25(分钟),两人最后一次相遇,因此,二人第15次击掌时,两人分别走了40++25=66(分钟),最后用乙的速度乘二人第15次击掌的时间即可求出乙走的路程。
45.【答案】解:甲乙速度和:
2000÷(1.25+3.75)
=2000÷5
=400(米/分)
乙的速度为:
400÷(1.5+1)=160(米/分)
甲的速度为:
400-160=240(米/分)
丙的速度为:
2000÷(1.25 +1.25+3.75)-240
=2000÷6.25-240
=320-240
=80(米/分)
答:甲每分钟跑240米,乙每分钟跑160米,丙每分钟跑80米。
【解析】由题意可知,从甲第一次遇到乙到第二次遇到乙,两人所走的路程和是湖的周长,所用时间是(1.25+3.75)小时,因此,用两人的路程和除以相遇时间即可求出甲乙的路程和;再根据和倍公式,较小数=和÷(倍数+1),可求出乙的速度,再用两人的速度和减去乙的速度求出甲的速度;甲丙的相遇时间比甲乙的相遇时间多1.25分钟,所以甲丙的相遇时间是(1.25+3.75+1.25)分钟,最后用路程和除以甲丙的相遇时间再减去甲的速度即可求出丙的速度。
46.【答案】(1)解:如图:
(2)解:7000÷(150+200)
=7000÷350
=20(分)
湛湛:150×20=3000(m)
粤粤:200×20=4000(m)
答:20分后两人相遇,相遇时湛湛行了3000米,粤粤行了4000米。
【解析】(1)粤粤速度快,湛湛速度慢,所以相遇点应靠近湛湛;
(2)相遇时间=总路程÷总速度,根据公式求出时间,再根据路程=速度×时间,据此求解。
47.【答案】解:设长方形长为a厘米,宽为b厘米,
第一次相遇,共同爬行第一个全程
甲爬行的路程是(a+b-32)厘米
乙爬行的路程是(a+b+32)厘米
乙比甲多爬行64厘米
第二次相遇,共同爬行第二个全程
甲爬行的路程是(32+a-16=a+16)厘米
乙爬行的路程是(b-32+a+b+16=2b+a-16)厘米
乙比甲多爬行(2b+a-16-a-16=2b-32)厘米
2b-32=64,求出b=48厘米
第三次相遇,共同爬行第三个全程
甲爬行的路程是(16+b+16=b+32)厘米
乙爬行的路程是(a-16+b+a-16=2a+b-32)厘米
乙比甲多爬行2a+b-32-b-32=2a-64厘米
2a-64=64 求出a=64厘米
答:长方形AB是64厘米。
【解析】每相遇一次甲乙共爬行一个全程,根据第一次相遇点求出乙比甲多次64厘米,也就是每相遇一次乙比甲都多行64厘米,设长方形的长边为a厘米,短边为b厘米,分别用a、b表示表示第二次,第三次甲乙爬行的路程,根据路程差等于64可以求出a和b的值。
48.【答案】解:我们知道,大小圆只有一个公共点(内切),而在圆上最远的两点为直径两端,所以当一只甲虫在A点,另一只在过A的直径另一直径端点B,
所以在小圆甲虫跑了n圈,在大圆甲虫跑了m+ 圈;于是小圆甲虫跑了30n,大圆甲虫跑了48(m+ )=48m+24。因为速度相同,所以相同时内路程相同,起点相同,所以30n=48m+24;即5n=8m+4,解出有n=4,m=2,所以小甲虫跑了4圈后,大小甲虫相距最远。
【解析】小圆的周长是:30π(厘米);
大圆周长的一半是:48π÷2=24π(厘米);
30π,24π的最小公倍数:120π;
小圆上甲虫爬的圈数:120π÷30π=4(圈);
答:当小圆上甲虫爬了4圈时,两只甲虫首次相距最远。
【分析】借助画图分析。圆内的任意两点,以直径两端点的距离最远。可知如果沿小圆爬行的甲虫爬到A点,沿大圆爬行的甲虫恰好爬到B点,二甲虫的距离便最远。小圆周长为30π,大圆周长为48π,一半便是24π。问题变为求30π和24π的“最小公倍数”问题了。二者最小公倍数是120π,此时,小圆上甲虫爬了4整圈到达A点,大圆上甲虫爬了整5个半圈到达B点,两只甲虫首次相距最远。
49.【答案】(1)解:甲跑半圈ACB用时48秒,乙跑半圈ACB用时42秒.也就是说如果某次乙经过A点的时间比甲晚不超过6秒,他就能在这半圈上追上甲.
甲跑一圈用的时间为 秒,乙跑一圈用的时间为 秒,下面看甲、乙经过 点的时间序列表(单位:秒)
甲 0 66 132 198 264 330
乙 0 84 168 252 336
可以看出336秒与330秒恰好差6秒,由此可知乙跑完第四圈、在跑第五圈时会第一次与甲相遇.
(2)解:要在A点相遇,两人跑的必须都是整数圈,甲跑一圈用 66秒,乙跑一圈用84秒,它们的最小公倍数为[66,84]=924.因此924秒即15分24秒后,甲、乙第一次同时回到A点.
【解析】(1)相遇只可能发生在他们共同经过的路线 ACB上;用ACB里包含几个100米,求出跑 甲、乙分别所需时间,求出时间差;用路程÷速度,分别求出甲跑一小圈,乙跑一大圈所用时间。用乙跑完第某圈到达点A所用时间-甲跑完第某圈到点A所用时间,若在6秒内,乙就能追上甲,第一次相遇;此题得解。
(2)要在A点相遇,两人跑的必须都是整数圈。甲跑一圈所用时间与乙跑一圈所用时间的最小公倍数即是甲、乙第一次同时回到A点。
50.【答案】解:甲实际跑 100÷(5-4)=100(秒)时追上乙,甲跑100÷5=20(秒),休息 10 秒; 乙跑 100÷4=25(秒),休息 10 秒,甲实际跑 100 秒时,已经休息 4 次,刚跑完第 5 次,共用 140 秒; 这时乙实际跑了 100 秒,第 4 次休息结束。正好追上。
【解析】因为A,B 两点相距100米,所以甲追上乙需要跑的时间=100÷速度差,然后分别求出用甲和乙各自跑100米需要的时间,所以根据甲追上乙需要跑的时间计算出休息的次数,然后根据乙跑的时间得出休息的时间,而此时,甲和乙都跑完了。
21世纪教育网(www.21cnjy.com)
小升初奥数思维之典型应用题精讲精练讲义(通用版)
专题05 环形跑道问题
【第一部分:知识归纳】
一、基本概念
1、环形跑道问题是指运动物体在闭合环形路径上的相遇或追及问题。
2、这类问题的特点是:
(1)运动路线是闭合的环形,没有起点和终点的区别
(2)相遇和追及的计算与直线型不同,需要考虑"圈数"的概念
(3)解题时需要明确运动方向(同向或反向)
二、核心公式
1. 同向运动(追及问题)
追及时间 = 跑道周长 ÷ 速度差
第n次追及时,快者比慢者多跑n圈
2. 反向运动(相遇问题)
相遇时间 = 跑道周长 ÷ 速度和
第n次相遇时,两人共跑n圈
3. 平均速度
平均速度 = 总路程 ÷ 总时间
在环形跑道上,跑完一圈的平均速度 = 周长 ÷ 一圈所用时间
三、常见题型与解题方法
1. 基本追及问题
例题:甲、乙两人在400米的环形跑道上跑步,甲的速度是6m/s,乙的速度是4m/s。如果两人从同一点同时同向出发,甲第一次追上乙需要多长时间?
解答:速度差 = 6 - 4 = 2m/s
跑道周长 = 400m
追及时间 = 400 ÷ 2 = 200秒
2. 基本相遇问题
例题:在300米的圆形跑道上,A以5m/s、B以3m/s的速度同时从同一点反向出发。他们第3次相遇需要多少时间?
解答:速度和 = 5 + 3 = 8m/s
第3次相遇共跑3圈 = 3×300 = 900m
时间 = 900 ÷ 8 = 112.5秒
3. 变速运动问题
例题:在600米的跑道上,小明前一半时间以4m/s跑,后一半时间以6m/s跑。求他跑完一圈的平均速度。
解答:设总时间为T秒
前T/2秒跑的距离 = 4×(T/2) = 2T
后T/2秒跑的距离 = 6×(T/2) = 3T
总距离 = 2T + 3T = 5T = 600 → T = 120秒
平均速度 = 600 ÷ 120 = 5m/s
4. 多次相遇问题
例题:在250米的环形跑道上,甲、乙两人分别以3m/s和5m/s的速度同时从同一点反向出发。当他们第5次相遇时,甲跑了多少米?
解答:速度和 = 3 + 5 = 8m/s
第5次相遇共跑5圈 = 5×250 = 1250m
时间 = 1250 ÷ 8 = 156.25秒
甲跑的距离 = 3 × 156.25 = 468.75m
四、解题技巧
1、画图辅助:用圆形图标记起点和运动方向
2、确定运动方向:同向用速度差,反向用速度和
3、注意单位统一:确保所有速度、时间、距离的单位一致
4、特殊值法:当题目未给出具体数值时,可以假设一个方便的数值(如周长取速度的公倍数)
【第二部分:能力提升】
1.在400米的环行跑道上,A,B两点相距100米.甲、乙两人分别从A,B两点同时出发,按逆时针方向跑步.甲每秒跑5米,乙每秒跑4米,每人每跑100米,都要停10秒钟.那么甲追上乙需要时间是多少秒?
2.如图,正方形边长是100米,甲、乙两人同时从A、B沿图中所示的方向出发,甲每分钟走75米,乙每分钟走65米,且两人每到达一个顶点都需要休息2分钟,求甲从出发到第一次看见乙所用的时间。
3.甲、乙在椭圆形跑道上训练,同时从同一地点出发反向而跑,每人跑完第一圈回到出发点立即回头加速跑第二圈,跑第一圈时,乙的速度是甲的速度的,甲跑第二圈时速度比第一圈提高了,乙跑第二圈时速度比第一圈提高了,已知甲、乙二人第二次相遇点距第一次相遇点190米,问这条椭圆形跑道长多少米?
4.在环形跑道上,两人都按顺时针方向跑时,每12分钟相遇一次,如果两人速度不变,其中一人改成按逆时针方向跑,每隔4分钟相遇一次,问两人各跑一圈需要几分钟?
5.小王、小李在某一 450 米环形道上 (如图) 散步, 小王从 点, 小李从 点同时出发, 3 分钟后小王与小李相遇, 再过 2 分钟, 小王到达 点, 又再过 4 分钟, 小王与小李再次相遇, 问小王与小李每分钟各走多少米?
6.成才和许三多两人在钢七连军训场的同一条环形跑道上进行跑步训练。他们同时同地出发,沿相反方向开始跑步,开始时许三多的速度是成才的。每人跑完一圈后,都立即回头加速跑下一圈,成才的速度比前一圈提高,许三多的速度比前一圈提高。两人每相遇两次,就以其中第二次的相遇点作为新的出发点,跑步规则不变(第一圈仍回到原速,第二圈加速),如此持续跑下去。记他们最初的出发点为A,第一次相遇点为B,第二次相遇点为C。已知B和C在环形跑道上的最短距离为190米。
(1)求这条环形跑道的长度。
(2)他们能否同时回到最初的出发点?如果能,这时成才和许三多两人各跑了多少米?如果不能,说明理由。
7.如图,学校操场的400米跑道中套着300米小跑道,大跑道与小跑道有200米路程相重,甲以每秒6米的速度沿大跑道逆时针方向跑,乙以每秒4米的速度沿小跑道顺时针方向跑,两人同时从两条跑道的交点处出发,当他们第二次在跑道上相遇时,甲共跑了多少米?
8.如图是圆环岛示意图阴影部分为绿地AB=CD=200米。甲车在A处按A处箭头方向行驶,车速每小时60千米,乙车在D处按D处箭头方向行驶,车速为每小时54千米如果车辆在这环岛的所有路口只能右转或直行,那么甲车追上乙车至少要多少分钟?(圆周率取3)
9.如图所示,甲、乙两人从长为400米的圆形跑道的A点背向出发跑步.跑道右半部分 (AB为圆的直径) 道路比较泥泞,所以两人的速度都将减慢,在正常的跑道上甲、乙速度均为每秒8米,而在泥泞道路上两人的速度均为每秒4米.两人一直跑下去,问他们第79次迎面相遇的地方距A点还有多少米 请写出简要的解题步骤.
10.小新和正南在操场上比赛跑步,小新每分钟跑250米,正南每分钟跑210米,一圈跑道长800米,他们同时从起跑点出发,那么小新第三次超过正南需要多少分钟?
11.甲、乙两车绕周长为400千米的环形跑道行驶,它们从同一地点同时出发,背向而行,5小时相遇,如果两车每小时各加快10千米,那么相遇点距离前一次相遇地点3千米,已知乙车比甲车快,求原来每小时行多少千米?
12.有一个200米的环形跑道,甲、乙两人同时从同一地点同方向出发.甲以每秒0.8米的速度步行,乙以每秒2.4米的速度跑步,乙在第二次追上甲时用了多少秒
13.有一个200米的环形跑道,甲、乙两人同时从同一地点同方向出发.甲以每秒0.8米的速度步行;乙以每秒2.4米的速度跑步,乙在第2次追上甲时用了多少秒?
14.如图,在长为490米的环形跑道上,A,B两点之间的跑道长50米,甲、乙两人同时从4,B两点出发反向奔跑.两人相遇后,乙立刻转身与甲同向奔跑,同时甲把速度提高了25%,乙把速度提高了20%、结果当甲跑到点A时,乙恰好跑到了点B.如果以后甲、乙的速度和方向都不变,那么当甲追上乙时,从一开始算起,甲一共跑了多少米?
15. 3辆汽车在环形公路上试车,3辆汽车跑一圈分别需要30分钟,18分钟,10分钟,现在3辆汽车在同一起点,同时同向而行。问:最少多长时间,它们相遇在一起?
16.环形跑道400米,小百、小合背向而行,小百速度是6米/秒,小合速度是4米/秒,当小百碰上小合时立即转向跑,小合不改变方向,小百追上小合时也立即转向跑,小合仍不改变方向,问两人第11次相遇离起点多少米?(按较短距离算,追上和迎面都算相遇)
17.(环形跑道问题) 甲、乙两车绕周长为 400 千米的环形跑道行驶, 他们从同一地点同时出发, 背向而行, 5 小时相遇, 如果两车每小时各加快 10 千米, 那么相遇点距离前一次相遇地点 3 千米。已知乙车比甲车快, 求甲车原来每小时行多少千米。
18.可可和乐乐绕一条长400米的环形跑道跑步锻炼身体,他们同时从同一地点出发,向相反方向跑去,可可的速度是6米/秒,乐乐的速度是4米/秒。30秒后两人相遇了吗?如果没有相遇,两人还相距多少米
19.甲、乙两人, 在一圆形跑道上同时同地出发, 反向跑步.已知甲的速度是每分钟 , 乙的速度是每分钟 , 在 30 分钟内, 它们相遇了 24 次, 问跑道的长度最多是多少米?
20.有一个200米的环形跑道, 甲、乙两人同时从同一地点同方向出发, 甲以每秒 0.8 米的速度为步行, 乙以每秒2.4米的速度跑步, 当乙第2次追上甲时用了多少秒?
21.甲乙二人沿400米环形跑道同时从某点开始反方向跑步,已知甲的速度比乙的速度快,当两人第一次相遇时甲跑了多少米?
22.如图,大圈是400米跑道,由A到B的跑道长是200米,直线距离是50米。父子俩同时从A点出发逆时针方向沿跑道进行长跑炼,儿子跑大圈,父亲每跑到B点使沿各直线跑。父亲每100米用20秒,儿子每100米用19秒。如果他们按这样的速度比,儿子在跑第几圈时,第一次与父亲再相遇?
23.在某一运动场的450米的环形跑道上(如下图),小王从A点出发,逆时针行驶,同时小李从B点出发顺时针行驶,6分钟后小王与小李相遇,再过4分钟,小王到达B点,又过8分钟,小王与小李再次相遇,问:小王与小李每分钟各走多少米
24.甲、乙两人,在一圆形跑道上同时同地出发,反向跑步,已知甲的速度是每分钟 , 乙的速度是每分钟 。在 30 分钟内, 它们相迎了24 次, 问跑道的长度最多是多少米?
25.(追及问题)在周长为200米的圆形跑道一条直径的两端,甲、乙两人分别以6米/秒、5米/秒的速度骑车同时同向出发,沿跑道行驶,问:16分钟内,甲追上乙多少次
26.一个圆形操场跑道的周长是500米,两个学生同时同地背向而行.黄莺每分钟走66米,麻雀每分钟走59米.经过几分钟才能相遇
27.甲、乙两人在环形跑道上练习跑步,若同时同地点同方向出发,4分钟后甲从后面超过乙一圈;若同时同地点反方向出发,1分钟后两人相遇。问甲、乙跑完一圈各需多少分钟?
28.两名运动员在湖的周围环形道上练习长跑.甲每分钟跑250米,乙每分钟跑200米,两人同时同地同向出发,经过45分钟甲追上乙;如果两人同时同地反向出发,经过多少分钟两人相遇?
29.如图﹐在长为400公尺的环形跑道上﹐A﹑B两点之间的跑道长100公尺.甲从A点﹑乙从B点同时出发相背而跑.两人相遇后﹐乙即转身与甲同向而跑﹐当甲跑到A时乙恰好跑到B.继续跑若甲追上乙时﹐甲从出发开始算起共跑了多少公尺﹖
30.绕湖一周是20千米,甲乙二人从湖边某一地点同时出发反向而行,甲以每小时4千米的速度每走1小时后休息5分钟,乙以每小时6千米的速度每走50分钟后休息10分钟,则两人从出发到第一次相遇用了多少分钟?
31.如下图,一只甲虫从A点出发,在圆形路线上沿顺时针方向爬行;一只蚂蚁同时从B点出发,在半圆BmA上往返爬行。已知甲虫爬行速度是蚂蚁的2.4倍,他们第二次相遇点与第三次相遇点之间的路程是30厘米。那么,这条圆形路线的全场是多少?
32.小明和谷等一起去换场散步。如果两人同时同地出发,相背而行, 分钟相遇:如果两人同时同地出发,同方向而行,24分钟小明超出爷爷一整圈。问小明和爷爷走一圈,各自需要多少分钟?
33.在400米的环形跑道上,甲、乙两人同时同地起跑,如果同向而行3分20秒相遇,如果背向而行40秒相遇,已知甲比乙快,求甲、乙的速度各是多少?
34.甲、乙二人在同一条椭圆形跑道上作特殊训练:他们同时从同一地点出发,沿相反方向跑,每人跑完第一圈到达出发点后立即回头加速跑第二圈,跑第一圈时,乙的速度是甲速度的2/3.甲跑第二圈时速度比第一圈提高了1/3;乙跑第二圈时速度提高了1/5.已知沿跑道看从甲、乙两人第二次相遇点到第一次相遇点的最短路程是190米,那么这条椭圆形跑道长多少米
35.如图所示,A,B,C三地之间有三条公路相连,三条公路的路程之比是AB:BC:AC=2:4:5.甲乙两车同时从A地出发,甲车沿A→B→C方向行驶,乙车沿A→C→B方向行驶,2小时后在B地和C地之间的D地相遇.已知汽车沿A→B方向和C→B方向行驶的速度都是每小时60千米,沿B→C方向行驶的速度是每小时90千米,沿A→C方向行驶的速度是每小时75千米,求C、D两地之间的距离是多少千米?
36.在一个600米的环形跑道上,兄弟两人同时从同一个起点按顺时针方向跑步,两人每隔12分钟相遇一次,若两个人速度不变,还是在原来出发点同时出发,哥哥改为按逆时针方向跑,则两人每隔4 分钟相遇一次,两人跑一圈各要多少分钟?
37.甲乙两人以匀速绕圆形跑道相向跑步。出发点在圆直径的两端。如果他们同时出发,并在甲跑完60米时第一次相遇,乙跑一圈还差100米时俩人第二次相遇,求跑道的长是多少米?
38.甲、乙、丙三人环湖跑步锻炼,同时从湖边一固定点出发,乙、丙二人同向,甲与乙丙反向,在甲第一次遇上乙后1.25分钟第一次遇上丙,再经过3.75分钟第二次遇乙.已知甲速遇乙速的比是3:2,湖的周长是2000米.求甲、乙、丙三人的速度每分钟各是多少米?
39.甲、乙两名运动员在周长400 米的环形跑道上进行10000米长跑比赛,两人从同一起跑线同时起跑,甲每分钟跑400 米,乙每分钟视频讲解跑360米,当甲比乙领先整整一圈时,两人同时加速,乙的速度比原来快 甲每分钟比原来多跑18 米,并且都以这样的速度保持到终点。甲、乙两人谁先到达终点?
40. 如下图,A、B是周长为360m的圆形跑道上一条直径的两个端点,早晨小明和小华约好两人去跑步,小明从A点出发,同时小华从B点出发,沿着跑道相向而行,两人在C点第一次相遇。已知C点离A点有80m,求他俩第二次相遇点在圆周上距B点多远?
41.第三届中国大学生方程式汽车比赛赛前,甲、乙两辆参赛小汽车在一个封闭的环形跑道内进行耐久测试。两车从同一地点沿相同方向同时起步后,乙车速超过甲车速,在第15分钟时甲车提速,在第18分钟时甲车追上乙车并且开始超过乙,在第23分钟时,甲车再次追上乙车。已知在测试中甲、乙两车均是匀速行驶,那么如果甲车不提速,乙车首次超过甲车所用的时间是多少分钟?
42.绕湖的一周是24千米,小明和小青从湖边某一地点同时出发,反向而行,小明以每小时4千米的速度,每走一小时后休息5分钟,小青以每小时6千米的速度每走50分钟后休息10分钟,两人出发后多长时间第1次相遇?
43.如图,A、B是圆的直径的两端,小张在A点,小王在B点同时出发反向行走,他们在C点第一次相遇,C离A点80米;在D点第二次相遇,D点离B点6O米.求这个圆的周长.
44.甲、乙两人沿一个周长为400米的环形跑道匀速前进,甲行走一圈需4分钟,乙行走一圈需7分钟,他们同时同地同向出发,甲走完10圈后,改为反向行走.出发后,每一次甲追上乙或和乙迎面相遇时,二人都击掌示意.当二人第15次击掌时,乙走的路程是多少米?
45.甲、乙、丙三人环湖跑步锻炼,同时从湖边一固定点出发,乙、丙二人同向,甲与乙丙反向,在甲第一次遇上乙后1.25分钟第一次遇上丙,再经过3.75分钟第二次遇乙。已知甲速是乙速的1.5倍,湖的周长是2000米。求甲、乙、丙三人的速度每分钟各是多少米?
46.湛湛和粤粤周六相约去湖边跑步,湛湛每分跑150m,粤粤每分跑200m。环湖路一周的长度是7000m,两人同时同地反方向跑步。
(1)估计两人在何处相遇?在图中用△标出来。
(2)几分后两人相遇?相遇时两人各行了多少米?
47.两只小爬虫甲和乙,从A点同时出发,沿长方形ABCD的边按箭头方向爬行(如图)。在距C点32厘米的E点它们第一次相用,在距D点16厘米的F点第二次相遇,在距A点16厘米的G点第三次相遇,求长方形的边AB长多少厘米?
48.下图中有两个圆只有一个公共点A,大圆直径48厘米,小圆直径30厘米。两只甲虫同时从A点出发,按箭头所指的方向以相同速度分别沿两个圆爬行。问:当小圆上甲虫爬了几圈时,两只甲虫首次相距最远?
49.如图是一个跑道的示意图,沿 走一圈是 米,沿 走一圈是 米,其中 到 的直线距离是 米.甲、乙二人同时从 点出发练习长跑,甲沿 的小圈跑,每 米用 秒,乙沿 的大圈跑,每 米用 秒,问:
(1)乙跑第几圈时第一次与甲相遇?
(2)出发多长时间甲、乙再次在A相遇?
50.在 400 米的环行跑道上,A,B 两点相距 100 米。甲、乙两人分别从 A,B 两点同时出发,按逆时针方向跑步。甲每秒跑 5 米,乙每秒跑 4 米,每人每跑 100 米,都要停 10 秒钟。那么甲追上乙需要时间是多少秒?
参考答案及试题解析
1.【答案】解:如果两人不休息,那么甲追上乙需要:100÷(5﹣4)=100(秒),
100秒内甲实际跑了:100×5=500(米),
所以甲休息了4次,
100+4×10=140(秒);
答:甲追上乙需要时间是140秒.
【解析】甲实际跑100÷(5﹣4)=100秒时追上乙,则甲实际跑了100×5=500米,所以甲已经休息了4次,由此即可求得追上乙所用的时间.
2.【答案】解:根据图示可知:甲乙的距离是正方形的两个边长,甲走每个边长用时:100÷75=(分钟),加上休息需要分钟
乙走每个边长用时:100÷65=(分钟),加上休息需要分钟
甲走两周回到A点用时×8=(分钟)
乙走7个边长到A左边的顶点用时:
7×-2
=-2
=(分钟)
分钟离开
因为<,甲到A顶点时,乙还没有离开A左侧顶点,此时甲第一次看到乙
答:甲从出发到第一次看见乙所用的时间为分钟。
【解析】首先根据图示,可得甲乙距离是正方形的两个边长,分别求出甲乙走每个边长加上休息的时间;然后根据乙走7个边长到A左边的顶点用时7×=(分钟),分钟离开,因为<,甲到A顶点时,乙还没有离开A左侧顶点,此时甲第一次看到乙,据此解答即可。
3.【答案】解:设一开始时甲的速度是a,于是乙的速度便是,设跑道长是L,
则甲、乙第一次相遇点,按甲前进方向距出发点为.
甲跑完第一圈,乙跑了,乙再跑余下的,甲已折返,且以的速度跑,所以在乙跑完第一圈时,甲已折返跑了,
这时,乙折返并以的速度跑着.
从这时起,甲、乙速度之比是,即5:3.
所以在二人第二次相遇时,甲跑了余下的的,而乙跑了它的,即第二次相遇时距出发点为.
可见两次相遇点间的距离是(米),即(米).
解得L=400(米)
答:跑道长为400米.
【解析】设一开始时甲的速度是a,于是乙的速度便是,设跑道长是L,根据题干条件求出甲乙两人的速度之比,再求出每次相遇的时间,由此即可求出甲第二次相遇时,距离出发点的距离,从而解决问题.
4.【答案】解:把这个跑道的长度看做整体“1”,
则甲的速度为:(+)÷2=,
乙的速度是:﹣=;
所以跑完一圈甲需要时间:1÷=6(分钟),
乙跑完一圈需要时间:1÷=12(分钟),
答:各跑一圈时,较快的需要6分钟,较慢的需要12分钟.
【解析】把这个跑道的长度看做整体“1”:分别求得二人的速度,即可求出他们跑一圈各自用的时间;
(1)两人都按顺时针方向跑时,属于追及问题:假设甲比乙跑的快,12分钟相遇说明二人的速度差是:;
(2)其中一人改成按逆时针方向跑,属于相遇问题:每隔4分钟相遇一次说明二人的速度之和是;
有上述推理即可得出甲的速度为:(+)÷2=,从而得出乙的速度是:﹣=;由此即可解决问题.
5.【答案】解:根据题干分析可得:相遇后,小王与小李行驶相同的路程所用的时间之比是2:3,所以小王与小李的速度之比就是3:2,
设小王的速度是3x米每分,小李的速度是2x米每分,根据题意可得方程:
(3x+2x)×(4+2)=450,
30x=450,
x=15,
小王的速度是:15×3=45(米/分),
小李的速度是:15×2=30(米/分),
答:小王的速度是45米/分,小李的速度是30米/分.
【解析】 根据题干分析可得,3分钟相遇后,小王与小李又行驶了4+2分钟后正好行驶了环形跑道一周450米,又根据“3分钟后小王与小李相遇,再过2分钟,小王到达B点”可得:相遇后,小王2分钟行驶的路程与小李3分钟行驶的路程,所用的时间之比是2:3,所以小王与小李的速度之比就是3:2,据此设小王的速度是3x米每分,小李的速度是2x米每分,据此利用等量关系二人行驶6分钟的路程=跑道总长度,据此即可解答.
6.【答案】(1)解:设许三多的速度是2,成才的速度是3,全程为单位“1”。
=
=2.4
=3+1
=4
2.4:4=3:5
=
=
=400(米)
答:这条环形跑道的长度400米。
(2)解:根据题意,可得
400÷50=8(次)
8×2=16(次)
(400×2-50)×8
=(800-50)×8
=750×8
=6000(米)
(400+50)×8
=450×8
=3600(米)
答:他们在第16次时回到了出发点A,成才跑了6000米,许三多跑了3600米。
【解析】(1)许三多的速度是成才的,即在第一次相遇在B店的过程中,时间是相等的,则速度比就等式路程比,则许三多的路程是成才的,即成才跑了整个圆(A逆时针到B)的,许三多跑了整个圆(A顺时针到B)设许三多的速度是2,成才的速度是3,当成才到了A点时,速度比前一圈提高,以原来的速度为单位“1”,提高了原来的,也就是提高了1,就是4.开始回头,也就是成才跑了一圈了,许三多跑的路程是成才的,许三多还有才能到A点,也就是需要的时间,的时间里面成才用4速度已经跑了全程的,这时许三多的速度提高了,即以原来的速度为单位“1”,就是提高了0.4,加上原来的速度就是2.4.即许三多和成才开始以4和2.5的速度以相遇的形式跑全程的,路程比就是速度比为3∶5.即成才跑了的是,许三多跑了的即(A逆时针B)是。则B到C最短的距离占整个圆分率=逆时针B的分率-A顺时针C的分率=。即全程的是190米,已知一个数的几分之几是多少用除法。
(2)从(1)中可知,这个环形跑道的总长度是400米,AC之间的距离占整个环形跑道的,也就是离起始点A点50米。也就是两个人每两次相遇相遇点会在跑道逆时针前进50米。全程是400米,前进8次就是400米,8次里面每次有2次相遇,则是第16次相遇时两人同时在起点A。每两次相遇的时候成才相当于走了2圈少50米,即每两次走了750米,再×8即可,同理许三多每两个相遇走了一圈带50米,即每两次走了450米,再×8即可。
7.【答案】解: 第一次相遇的时间是400÷(6+4)=40(秒)
第一次相遇甲行驶的路程是:40×6=240(米)
第一次相遇乙行驶的路程是:40×4=160(米)
乙回到出发点A的时间:
(300-160)÷4
=140÷4
=35(秒)
甲行驶的路程是:
6×35=210(米)
甲处的位置:
210-(400-240)
=210-160
=50(米)
即甲在A点左50米处;
再相遇还需要的时间是:
(400-50)÷(6+4)
=350÷10
=35(秒)
甲一共跑的路程是:
6×(40+35+35)
=6×110
=660(米)
答:甲共跑了660米.
【解析】 根据题意,甲乙第一次相遇的时间是400÷(6+4)=40秒,第一次相遇甲跑的路程是40×6=240(米),第一次相遇乙跑的路程是40×4=160(米),然后再求出乙跑完(300-160)米的路程用的时间,即(300-160)÷4=35秒,即乙回到出发点A的时间,这时甲跑的路程是6×35=210米,这时甲所处的地点在A点左50米处,即与乙错开,再相遇还需要的时间是(400-50)÷(6+4)=35秒,所以从第一次相遇到第二次相遇时间是2个35秒,第一次相遇用40秒,所以在第二次相遇时,他们一共跑了40+70=110秒,再用甲的速度乘以跑的时间,即可求出甲共跑的路程是多少.
8.【答案】解:甲沿 追赶乙, 200 米 千米, 设乙行驶 千米时被甲追上, 需 分钟。
, 解之
答: 甲车追上乙车至少要 5.5 分钟
【解析】 根据题意,按照交通规则,可知先从A行驶到B,然后沿圆弧行驶到C,再从C行驶到D;由追及问题可知,甲比乙多行驶的距离就是A到D的距离,求出A到D的距离,再根据他们的速度差就可以求出甲车要追上乙车的时间.
9.【答案】由题意可知:奇数次相遇地点相同,偶数次相遇点为A点.
设奇数次相遇地点距A点还有x米,
依题意,得:,
解得:.
答: 第79次迎面相遇的地方距A点还有150米
【解析】由两人的速度相同(正常道速度相同,泥泞路速度也相同)可知:奇数次相遇地点相同(此时相遇点在泥泞路上),偶数次相遇点为A点,设奇数次相遇地点距A点还有x米,由时间=路程÷速度,即可得出关于x的一元一次方程,解之即可得出结论
10.【答案】解:800×3+(250-210)=60(分钟)
答:小新第三次超过正南需要60分钟。
【解析】小新第三次超过正南是比正南多跑了三圈,所以小新第三次超过正南需要需要的时间=跑道的周长×3÷速度差。
11.【答案】解:加速后两车的相遇时间为:400÷(400÷5+10×2)=400÷(80+20)=400÷100=4(小时)甲车原来的速度:(40﹣3)÷(5﹣4)=37÷1=37(千米/小时)答:原来甲车每小时行37千米
【解析】分析】甲、乙两车原来的速度和=400÷5=80(千米/小时) 现在两车的速度和=80+10+10=100(千米/小时); 现在的相遇用时=400÷100=4(小时),由于乙车比甲车快,甲车现在4小时比原来多走:10×4=40(千米),这40千米甲以原来的速度走(5﹣4=)1小时,还多出3千米. 所以甲车原来的速度:(40﹣3)÷(5﹣4)=37(千米/小时).
12.【答案】解:乙第二次追上甲时,乙比甲多跑了2圈,
即它们的距离差是200×2=400(米),
速度差是2.4-0.8=1.6(米/秒)
400÷1.6=250(秒)
答: 乙在第二次追上甲时用了250秒。
【解析】要求乙在第二次追上甲时用了多少秒,应先求出乙在第二次追上甲时他们的路程差和速度差,再利用 ‘路程÷速度=时间’,即可求得结果。
13.【答案】解:200×2=400(米)
400÷(2.4-0.8)
=400÷1.6
=250(秒)
答:乙在第2次追上甲时用了250秒。
【解析】乙两次追上甲则乙跑的路程是环形跑道两圈的长度,乙的速度-甲的速度=两人的速度差,乙跑的路程÷(乙的速度-甲的速度)=乙在第2次追上甲时用的时间。据此可以解答。
14.【答案】解:设甲原来每单位时间的速度为,乙原来每单位时间的速度为。
所以,他们所花时间的比为:
由此,可以得到以下方程:
解得:(米)
从A点到相遇点的路程为:(米)
因此,乙的速度为:(米)
两人速度变化后,甲的速度为:(米)
乙的速度为:(米)
从相遇点开始,甲追上乙时,甲比乙多行一圈,即490米。因此,甲追上乙所需的时间为:
(单位时间)
因此,甲追上乙时一共跑的路程为:(米)
答:甲一共跑了2690米。
【解析】首先,设定甲乙两人原来的速度,并根据题目描述建立速度比和时间比的关系。接着,根据这些比例关系,结合已知的跑道长度和甲乙两人的相遇位置,求解出甲乙两人原来的速度。然后,根据题目描述,计算出甲乙两人速度变化后的速度。最后,利用追及问题的原理,结合已知的速度差和跑道长度,求解出甲追上乙时甲一共跑了多少米。
15.【答案】解:30=2×3×5,18=2×3×3,10=2×5
所以30、18、10的最小公倍数为2×3×3×5=9×10=90
答:最少90分钟,它们相遇在一起。
【解析】因为是在环形公路上试车,三辆车跑一圈所用的时间都不同,所以可以计算出当它们跑了一定数量的圈数以后得到的时间一样,这个时间就是它们相遇的时间。所以算出30,18,10的最小公倍数,这样就是在最少时间内,它们会相遇。
16.【答案】解:小百和小合的相对速度是:6+4=10米/秒。
故他们每次相遇的时间是:400÷10=40秒。
小合的速度是4米/秒,所以他在40秒内行进的路程是40×4=160米。
故小合在11次相遇后行进的总路程是:160×11=1760米。
环形跑道的长度是400米,所以小合在11次相遇后离起点的距离是1760 ÷400=4圈余160米。
因此,小合在第11次相遇时离起点160米。
【解析】需要确定小百和小合每次相遇的时间。由于他们是背向而行,所以他们的相对速度是他们的速度之和。可以计算出小合在每次相遇时行进的距离,以及在11次相遇后行进的总路程。将小合行进的总路程除以环形跑道的长度,得到小合行进的圈数和余数,即他离起点的距离。
17.【答案】解:甲乙两车原速度和为400÷5=80(千米/时),两车速度增加后,相遇时间为:400÷(80+10×2)=4(小时),
甲车现在4小时比原来多走:10 4=40(千米)
所以甲车原来的速度为:(40-3)÷(5-4)=37÷1=37(千米/时)
答:甲车原来每小时行37千米
【解析】两车速度差不变,第一次两车5小时相遇速度增加后,两车4小时相遇,用现在多走的路程减去多出的3千米,除以时间差,就是甲原来的速度
18.【答案】解:(6+4)×30
=10×30
=300(米)
400>300
400-300=100(米)
答:两人没有相遇,还相距100米。
【解析】可可的速度 +乐乐的速度=两人的速度和,(可可的速度 +乐乐的速度)×跑步时间=两人的路程和。然后用两人的路程和与跑道长比较:如果路程和等于跑道长度说明两已经相遇;如果路程和小于跑道长度说明两人还没有相遇,跑道长度与路程和的差就是两人之间相距的距离;如果路程和大于跑道长度说明两人已经相遇并又向相反方向跑了一段距离了。
19.【答案】解:30×(180+240)
=30×420
=12600(米)
12600÷24=525(米)
答:跑道的长度最多是525米。
【解析】根据相遇问题的经验可知两人相遇一次即走了一个跑道的长度,所以相遇24次即走了24个跑道的长度,而跑道的长度要最大就不需要考虑这30分钟内走的总路程除了相遇外还有没有相遇的路程长度,因此用两人30分钟内走的总路程除以24即为一个跑道的最多长度;(甲的速度+乙的速度)×时间=两人30分钟内所走的总路程,两人30分钟内所走的总路程÷24=跑道最大的长度,据此可以解答。
20.【答案】解: 200×2=400(米)
400÷(2.4-0.8)
=400÷1.6
=250(秒)
答:乙第2次追上甲用了250秒。
【解析】根据题意可知:因为甲、乙两人是沿环形跑道同时同地同方向出发,所以当乙第2次追上甲时,乙比甲多跑了2圈,即他们的距离差=环形跑道长×圈数=200×2=400米;乙第2次追上甲用的时间=两人的距离差÷(乙的速度-甲的速度)=400÷(2.4-0.8)=250秒。
21.【答案】解:甲乙速度比=(1+):1=11:10,
当两人第一次相遇时甲跑了:
400÷(10+11)×11,
=400÷21×11,
=4400÷21,
=209(米),
答:当两人第一次相遇时甲跑了209米.
【解析】由甲的速度比乙的速度快,可得甲乙速度比=(1+):1=11:10,从而求出在相同时间甲乙所行的路程比11:10,根据甲乙二人沿400米环形跑道同时从某点开始反方向跑步,是相遇问题就用环形跑道长除以甲乙所行路程总份数,即可得出1份的,再乘以11就是甲跑的米.
22.【答案】解:儿子每次到达A点所用时间:
400÷100×19
=4×19
=76(秒)
父亲:
(200+50)÷100×20
=250÷100×20
=50(秒)
从A到B逆时针跑,儿子需要时间:76÷2=38(秒),父亲需要:
200÷100×20
=2×20
=40(秒)
40-38=2(秒),即只要在父亲到达A点后的2秒之内,儿子也到达A点,儿子就能从后面追上父亲;
父亲到达A点的时间有50,100,150,200,……
儿子到达A点的时间有76,152,228,……
相差2秒的有152和150,即父子第一次相遇时,儿子已经跑完第2圈,也就是正在跑第3圈。
答:儿子在跑第3圈时,第一次与父亲再相遇。
【解析】根据题意可知:父子俩的相遇是在从A到B的逆时针的这个路段上。先求出儿子和父亲在这一路段各自的用时是38秒、40秒,这说明只要父亲到达A点后的2秒内儿子到达A点即可追上父亲;再求出儿子、父亲每次到达A点所有时间的周期分别为76秒和50秒,进而列出父子俩到达A点的几个时间并进行比较找出相差2秒的时间便可解答。
23.【答案】解:根据题干分析可得:相遇后,小王与小李行驶相同的路程所用的时间之比是4:6=2:3,所以小王与小李的速度之比就是3:2,
设小王的速度是3x米每分,小李的速度是2x米每分,根据题意可得方程:
(3x+2x)×(4+8)=450
60x=450
x=7.5
小王的速度是:7.5×3=22.5(米/分),
小李的速度是:7.5×2=15(米/分),
答:小王的速度是22.5米/分,小李的速度是15米/分.
【解析】 根据题干分析可得,6分钟相遇后,小王与小李又行驶了4+8分钟后正好行驶了环形跑道一周450米,又根据“6分钟后小王与小李相遇,再过4分钟,小王到达B点”可得:相遇后,小王4分钟行驶的路程与小李6分钟行驶的路程,所用的时间之比是4:6=2:3,所以小王与小李的速度之比就是3:2,据此设小王的速度是3x米每分,小李的速度是2x米每分,据此利用等量关系二人行驶12分钟的路程=跑道总长度,据此即可解答.
24.【答案】解:(180+240)×30
=420×30
=12600(米)
12600÷24=525(米)
答:跑道的长度最多是525米。
【解析】因为是同时同地出发,反向跑步,所以第一次相遇两人路程之和等于跑道长,因此第一次相遇时两人跑的路程和是跑道1圈的长度。从第一次相遇开始,两人每相遇一次,两人的路程和是跑道长的1圈的长度。因此30分钟内相遇24次,即共跑了24圈,此时共跑了(跑道1圈的长度×24)米。 求出24圈的长度,再除以24即可求出跑道的长度。
25.【答案】解:第一次甲追上乙需:200÷2÷(6-5)=100(秒)
(圈)
超过1圈追上1次,
因此共追上 (次)。
答:16分钟内,甲追上乙5次。
【解析】 根据“追及时间=路程差÷速度差”,如图,第一次甲追上乙是在200÷2÷(6-5)=100秒后,16分=60×16=960秒,后来又行了16×60-100=860(秒),后来甲行了860×6÷200=25.8(圈),乙行了860×5÷200=21.(圈);超过1圈追上1次,所以后来又追上了25-21=4(次),因此共追上4+1=5次;
此题属于复杂的环形跑道追及问题,解答此题的关键是根据路程差、速度差和追及时间三者之间的关系,进行分析解答即可
26.【答案】解:500÷(66+59)=500÷125=4(分钟)
答:经过4分钟才能相遇。
【解析】相遇用的时间=跑道的周长÷两人的速度和,据此作答即可。
27.【答案】解:甲、乙两人的速度和是1÷1 =1,
两人的速度差是
甲速度
甲跑完全程所用的时间是 分钟)
乙的速度是
乙跑完全程所用的时间是 (分钟)
答:甲跑完一圈需要 分钟,乙跑完一圈需要 分钟。
【解析】把这个环形跑道的路程看作“1”,甲、乙两人的速度和是1÷1=1,速度差是 从而求出甲的速度,用环形跑道的路程除以甲的速度就是甲跑完全程所需要的时间;再求出乙的速度,近而求出乙跑完全程所需要的时间.
28.【答案】解:250-200=50(米/分)
50×45=2250(米)
2250÷(250+200)=5(分钟)
答:经过5分钟两人相遇。
【解析】两人同向而行,甲追上乙,甲比乙多跑一圈,所以两人的路程差=跑道一圈的长度=速度差×同向出发相遇用的时间,所以反向而行的相遇时间=跑道一圈的长度÷速度和。
29.【答案】解:400+[400﹣(400÷2﹣100)]×2
=400+[400﹣(200﹣100)]
=400+[400﹣100]×2
=400+600
=1000(米)
答:当甲追上乙时,甲共跑了1000米.
【解析】根据在相同的时间内,乙从B跑到C,甲可以从A跑到C(相向而行),乙如果按原路返回(从C跑到B),甲又可以同向从C经过B跑到A,可知 甲前后跑的两段路程是相等的,则AC=400÷2=200米.又因A、B两点间的距离是100米,所以乙每次跑的路程是200﹣100=100米,即甲的 速度是乙的速度的2倍.现在乙在前300米,甲在后追及,甲跑300×2=600米可以追上乙,原来乙跑了400米,所以甲从出发开始共跑的路程是 400+(400﹣100)×2=1000米.
30.【答案】解:假设甲乙不休息,二人相遇时间为:
20÷(4+6)=2(小时)
因二人中途休息,所以两人相遇所用时间超过2小时,且都休息了两次,
当二人同时出发130分钟时:
甲走了:4×2=8(千米)
乙走了:6×(130-20)÷60=11(千米)
(20-8-11)÷(4+6)=0.1(小时)
130+0.1×60=136(分钟)
答: 两人从出发到第一次相遇用了 136分钟。
【解析】由题意可知,当甲乙二人走的路程和为20千米时,二人相遇。实际上甲每走3千米花费时间为1小时又5分钟,即65分钟;乙每走6千米花费时间为1小时又10分钟,即70分钟;
假设甲乙不休息,求相遇需要时间是2小时,因中途休息,所以相遇时间超过2小时,先求2小时甲乙走的路程,再求出剩余路程甲乙走需要的时间,即可求得相遇用的时间。依据‘路程=速度×时间’
31.【答案】解:如图所示
甲虫与蚂蚁爬完半个圆图长所用时间之比是
甲虫: 蚂蚁 。依次绘制甲虫与蚂蚁朵行的折线图:
从图中可以看出,第二次相過点是 , 第三次相颫点是 , 且有:
所以
。由题意 (厘米), 所以 .
图周长是 (厘米)。
(注:上面的解答中,用 代表 的弧长,其他同)
【解析】理解甲虫和蚂蚁的运动规律。已知甲虫的速度是蚂蚁速度的2.4倍,这意味着在相同的时间内,甲虫能爬行的距离是蚂蚁的2.4倍。通过分析它们的相遇点,可以推断出圆形路线的全长。
32.【答案】解:设小明走一圈需x分钟,爷爷走一圈需y分钟。
()=1
=①
24()=1
=②
①-②解得y=8
=
=
=+
x=6
答:小明走一圈需要6分钟,爷爷走一圈需要8分钟。
【解析】本题为行程问题中的相遇与追及问题,涉及的是小明和爷爷同时同地出发在环形跑道上的运动。通过相背而行的相遇时间和同向而行的追及时间,可以分别建立方程来求解小明和爷爷走一圈所需的时间。关键在于理解相遇和追及的条件,并将其转化为速度的表达式,进而求解未知数。
33.【答案】解:甲乙的速度和为: (米/秒),甲乙的速度差为: (米/秒),甲的速度为: (米/秒),乙的速度为: (米/秒).
【解析】先将单位进行换算,即3分20秒=200秒,那么两人的速度和=跑道一圈的长度÷背向而行相遇用的时间,两人的速度差=跑道一圈的长度÷同向而行相遇用的时间,因为甲比乙快,所以甲的速度=(速度和+速度差)÷2;乙的速度=(速度和-速度差)÷2。
34.【答案】解:根据题意,可得
=
=
=4:2
=2:1
=
=
=
=
=5:3
=
=
=
=80×5
=400(米)
答:这条椭圆形跑道长400米
【解析】甲、乙从A点出发,沿相反方向跑,他们的速度比是。第一次相遇时,他们所行路程比是3:2。把全程平均分成5份,则他们第一次相遇点在B点,当甲到A点时,乙又行了。这时甲反向而行,速度提高了,甲、乙速度比为,当乙到达A点时,甲反向行了。这时乙反向而行,甲、乙的速度比变成了,这样,乙又行了,与甲在C点相遇。B、C的路程为190米,对应的份数为。则跑道长为:(米)
35.【答案】解:设AB为2a,BC为4a,CA为5a,CD为x千米,可得:
+=2
即6a+8a﹣2x=495
14a﹣2x=495①
+=2
即20a+5x=825
a=
将a代入①,可得:
14×﹣2x=825
解得:x=45
答:求C、D两地之间的距离是45千米.
【解析】由于是AB:BC:AC=2:4:5,设AB为2a,BC为4a,CA为5a,CD为x千米,则相遇时,甲车行了AB与BD,即2a与4a﹣x,由于甲在AB每小时行60千米,则在AB用了小时,沿B→C方向行驶的速度是每小时90千米,则在BD用了小时,又相遇时间是2小时,由此可得:+=2①,同理,乙车在AC段用了小时,在CD段用了小时,根据相遇时间可得:+=2②,分析①②式求出x即可.
36.【答案】解:速度差:600÷12=50(米),
速度和:600÷4=150(米),
哥哥的速度:(50+150)÷2=100(米),
弟弟的速度:150-100=50(米),
哥哥跑一圈用的时间:600÷100=6(分钟),
弟弟跑一圈用的时间:600÷50=12(分钟),
答:哥哥用6分钟,弟弟用12分钟。
【解析】题中要求两人跑一圈各用多少分钟?根据题意要求两人跑一圈各用多少分钟,那么我们就需要计算出两人的速度,题中告诉我们兄弟两人同时从同一地点出发,一前一后,每隔12分钟相遇一次,也就是路程差,即一圈路程;每隔4分钟相遇一次,也就是路程和,即一圈路程。所以两人合跑一圈用4分钟,根据路程=速度×时间,可以分别算出两个人的速度,再根据时间=路程÷速度,即可解答。
37.【答案】解:半跑道长为x米,则有
3(x-60)=2x-100
3x-180=2x-100
x=80
2x=2×80=160
答: 跑道的长是 160米。
【解析】根据第一次相遇甲、乙共跑了半圈,其中甲跑了60米。设半跑道长为x米,则乙在俩人第一次相遇时跑了(x-60)米。又因为从出发到甲、乙第二次相遇共跑了3个半圈长,由于他俩匀速跑步,在3个半圈长里乙应跑3(x-60)米,而这个距离恰好是乙跑一圈还差100米,即(2x-100)米,根据此数量关系列方程解答即可。
38.【答案】解:甲的速度为每分钟:
2000÷(1.25+3.75)×
=2000÷5×,
=240(米);
乙的速度为每分钟:
2000÷5﹣240
=4000﹣240,
=160(米).
丙的速度为每分钟:
2000÷6.25﹣240
=320﹣240,
=80(米).
答:甲每分钟跑240米,乙每分钟跑160米,丙每分钟跑80米.
【解析】在甲第一次遇上乙后1.25分钟第一次遇上丙,再经过3.75分钟第二次遇乙,则甲乙二人相时间为1.25+3.75=5分钟,两人相遇时 共行了一周即2000米,所以两人的速度和为每分钟2000÷5=400米.甲乙两人的速度比为3:2.由此可知甲的速度为每分钟400×=240米.由于甲与乙相遇时间为5分钟,甲第一次遇上乙后1.25分钟第一次遇上丙,则甲丙的相遇时间为5+1.25=6.25分钟,则丙的速度为每分钟2000÷6.25﹣240米.
39.【答案】解:甲比乙领先整整一圈所用时间:
400÷(400-360)
=400÷40
=10(分钟)
甲到达终点还需要时间:
(10000-400×10)÷(400+18)
=6000÷418
=
≈14.4(分钟)
乙到达终点还需要时间为:
=6400÷450
=
≈14.2(分钟)
14.4>14.2
答:乙先到达终点。
【解析】先求出甲比乙领先整整一圈时所用时间,求出剩余米数,再求出两人分别所用时间,再相加比较即可求解。
40.【答案】解:圆形跑道的周长为360米,因此半圆的长度为360 ÷ 2 = 180米。
已知C点离A点有80米,因此C点到B点的距离为180 - 80 = 100米。
小明从A点出发,小华从B点出发,沿着跑道相向而行。
两人在C点第一次相遇,说明小明跑过的路程与小华跑过的路程之比为80:100,即4:5。
两人第一次相遇后,他们将继续在跑道上跑步,直到第二次相遇。
在此期间,两人合起来跑过的总路程将是圆形跑道的周长,即360米。
由于时间相同,路程比等于速度比,因此在第二次相遇时,小明跑过的路程与小华跑过的路程之比仍为4:5。
因此,小明跑过的路程为米。
在第一次相遇后,小明从C点出发,继续跑了160米,到达第二次相遇点。
因此,第二次相遇点距离B点的距离为小明跑过的路程减去C点到B点的距离,即160 - 100 = 60米。
答: 他俩第二次相遇点在圆周上距B点 60m。
【解析】首先,根据题目给出的信息,需要确定C点到B点的距离。接着,需要分析小明和小华的速度比,以及他们第一次相遇到第二次相遇所走过的总路程。通过速度比和总路程,可以计算出小明在第二次相遇时跑过的路程。最后,根据小明跑过的路程和C点到B点的距离,可以确定第二次相遇点距离B点的距离。
41.【答案】解:设甲车提速前速度比乙车慢a/分钟,提速后速度比乙车快b/分钟。
那么有甲车在第15分钟时,离乙车的距离为15a。
这个距离在第18分钟追回来。
那么15a=(18-15)b,
即b=5a,
而且在第23分钟时,甲车比乙车多跑一圈.
那么一圈的路程为:(23-18)b=5b=25a,
所以甲车不提速时,乙车首次超过甲车(即多跑一圈)所需时间为:25a÷a=25分钟。
答: 如果甲车不提速,乙车首次超过甲车所用的时间是25分钟。
【解析】首先表示出甲车提速前速度比乙车慢a/分钟,提速后速度比乙车快b/分钟,进而利用甲车在第15分钟时,离乙车的距离为15a,这个距离在第18分钟追回来,即可得出等式方程求出a,b关系,再表示出一圈的路程即可得出答案 。
42.【答案】解:小王到第二轮休息结束时花了2小时10分,2小时10分=1小时+5分+1小时+5分,所以小王共走了4×2=8(千米),
2小时10分=50分+10分+50分+10分+10分,小张走的时间为50分+50分+10分=110分,所以小张走了=11(千米)。
这时两人还相距24-(8+11)=5(千米)
由于从此时到相遇已经不需要休息,因此,共同走完这5千米两人共需的时间是:5-(4+6) =0.5 (时) =30 (分)
所以,他们第一次相遇共需2小时10分+30分=2小时40分
答:两人出发后经过2小时40分第一次相遇。
【解析】先求出小王到第二轮休息结束时花的时间,然后计算出小王实际走的时间,再根据“速度×时间”求出小王这段时间内走的路程,同理可求出小张再这段时间内走的路程;然后求出此时两人之间的距离,两人不休息了,计算出还需走的时间,用已走的时间加上还需走的时间就是相遇时间。
43.【答案】解:1+=(圈)
80×3=240(米)
(240-60)÷(-1)=360(米)
答:此圆形场地的周长是360米。
【解析】从图中可以用看出,当甲、乙第一次相遇时,甲乙共走完圈的路程,当甲、乙第二次相遇时,甲乙共走完1+=圈的路程.所以从开始到第一、二次相遇所需的时间比为1:3,因而第二次相遇时乙行走的总路程为第一次相遇时行走的总路程的3倍,即80×3=240米.有甲、乙第二次相遇时,共行走(1圈的长度-60)+240,为圈,所以此圆形场地的周长为360米。
44.【答案】解:①甲乙同向;
10-10×4÷7
=10-5
=4(圈)
两人击掌4次;
②甲乙反向;
÷(+)
=÷
=(分钟)
15-4-1=10(次)
1÷(+)
=1÷
=(分钟)
×10=25(分钟)
40++25=66(分钟)
×66=(米)
答:乙走的路程是米。
【解析】为了计算简便,把一圈看成“1”,则甲的速度为, 乙的速度为,把整个过程分两个阶段考虑:
①甲走10圈时,共用了10×4=40(分钟),这段时间乙行走了40÷7=5(圈),每当甲比乙多走1圈时,甲便追上乙一次,所以甲走完10圈时,比乙多走了10-5=4(圈),两人共击掌4次,此时,甲、乙两人相距一圈;
②甲反向行走后,经过÷(+)=(分钟),两人第一次相遇,还应再相遇15-4-1=10(次),以后两人每相遇1次便合走一圈,即相遇事件发生的时间间隔为1÷(+)=(分钟),经过×10=25(分钟),两人最后一次相遇,因此,二人第15次击掌时,两人分别走了40++25=66(分钟),最后用乙的速度乘二人第15次击掌的时间即可求出乙走的路程。
45.【答案】解:甲乙速度和:
2000÷(1.25+3.75)
=2000÷5
=400(米/分)
乙的速度为:
400÷(1.5+1)=160(米/分)
甲的速度为:
400-160=240(米/分)
丙的速度为:
2000÷(1.25 +1.25+3.75)-240
=2000÷6.25-240
=320-240
=80(米/分)
答:甲每分钟跑240米,乙每分钟跑160米,丙每分钟跑80米。
【解析】由题意可知,从甲第一次遇到乙到第二次遇到乙,两人所走的路程和是湖的周长,所用时间是(1.25+3.75)小时,因此,用两人的路程和除以相遇时间即可求出甲乙的路程和;再根据和倍公式,较小数=和÷(倍数+1),可求出乙的速度,再用两人的速度和减去乙的速度求出甲的速度;甲丙的相遇时间比甲乙的相遇时间多1.25分钟,所以甲丙的相遇时间是(1.25+3.75+1.25)分钟,最后用路程和除以甲丙的相遇时间再减去甲的速度即可求出丙的速度。
46.【答案】(1)解:如图:
(2)解:7000÷(150+200)
=7000÷350
=20(分)
湛湛:150×20=3000(m)
粤粤:200×20=4000(m)
答:20分后两人相遇,相遇时湛湛行了3000米,粤粤行了4000米。
【解析】(1)粤粤速度快,湛湛速度慢,所以相遇点应靠近湛湛;
(2)相遇时间=总路程÷总速度,根据公式求出时间,再根据路程=速度×时间,据此求解。
47.【答案】解:设长方形长为a厘米,宽为b厘米,
第一次相遇,共同爬行第一个全程
甲爬行的路程是(a+b-32)厘米
乙爬行的路程是(a+b+32)厘米
乙比甲多爬行64厘米
第二次相遇,共同爬行第二个全程
甲爬行的路程是(32+a-16=a+16)厘米
乙爬行的路程是(b-32+a+b+16=2b+a-16)厘米
乙比甲多爬行(2b+a-16-a-16=2b-32)厘米
2b-32=64,求出b=48厘米
第三次相遇,共同爬行第三个全程
甲爬行的路程是(16+b+16=b+32)厘米
乙爬行的路程是(a-16+b+a-16=2a+b-32)厘米
乙比甲多爬行2a+b-32-b-32=2a-64厘米
2a-64=64 求出a=64厘米
答:长方形AB是64厘米。
【解析】每相遇一次甲乙共爬行一个全程,根据第一次相遇点求出乙比甲多次64厘米,也就是每相遇一次乙比甲都多行64厘米,设长方形的长边为a厘米,短边为b厘米,分别用a、b表示表示第二次,第三次甲乙爬行的路程,根据路程差等于64可以求出a和b的值。
48.【答案】解:我们知道,大小圆只有一个公共点(内切),而在圆上最远的两点为直径两端,所以当一只甲虫在A点,另一只在过A的直径另一直径端点B,
所以在小圆甲虫跑了n圈,在大圆甲虫跑了m+ 圈;于是小圆甲虫跑了30n,大圆甲虫跑了48(m+ )=48m+24。因为速度相同,所以相同时内路程相同,起点相同,所以30n=48m+24;即5n=8m+4,解出有n=4,m=2,所以小甲虫跑了4圈后,大小甲虫相距最远。
【解析】小圆的周长是:30π(厘米);
大圆周长的一半是:48π÷2=24π(厘米);
30π,24π的最小公倍数:120π;
小圆上甲虫爬的圈数:120π÷30π=4(圈);
答:当小圆上甲虫爬了4圈时,两只甲虫首次相距最远。
【分析】借助画图分析。圆内的任意两点,以直径两端点的距离最远。可知如果沿小圆爬行的甲虫爬到A点,沿大圆爬行的甲虫恰好爬到B点,二甲虫的距离便最远。小圆周长为30π,大圆周长为48π,一半便是24π。问题变为求30π和24π的“最小公倍数”问题了。二者最小公倍数是120π,此时,小圆上甲虫爬了4整圈到达A点,大圆上甲虫爬了整5个半圈到达B点,两只甲虫首次相距最远。
49.【答案】(1)解:甲跑半圈ACB用时48秒,乙跑半圈ACB用时42秒.也就是说如果某次乙经过A点的时间比甲晚不超过6秒,他就能在这半圈上追上甲.
甲跑一圈用的时间为 秒,乙跑一圈用的时间为 秒,下面看甲、乙经过 点的时间序列表(单位:秒)
甲 0 66 132 198 264 330
乙 0 84 168 252 336
可以看出336秒与330秒恰好差6秒,由此可知乙跑完第四圈、在跑第五圈时会第一次与甲相遇.
(2)解:要在A点相遇,两人跑的必须都是整数圈,甲跑一圈用 66秒,乙跑一圈用84秒,它们的最小公倍数为[66,84]=924.因此924秒即15分24秒后,甲、乙第一次同时回到A点.
【解析】(1)相遇只可能发生在他们共同经过的路线 ACB上;用ACB里包含几个100米,求出跑 甲、乙分别所需时间,求出时间差;用路程÷速度,分别求出甲跑一小圈,乙跑一大圈所用时间。用乙跑完第某圈到达点A所用时间-甲跑完第某圈到点A所用时间,若在6秒内,乙就能追上甲,第一次相遇;此题得解。
(2)要在A点相遇,两人跑的必须都是整数圈。甲跑一圈所用时间与乙跑一圈所用时间的最小公倍数即是甲、乙第一次同时回到A点。
50.【答案】解:甲实际跑 100÷(5-4)=100(秒)时追上乙,甲跑100÷5=20(秒),休息 10 秒; 乙跑 100÷4=25(秒),休息 10 秒,甲实际跑 100 秒时,已经休息 4 次,刚跑完第 5 次,共用 140 秒; 这时乙实际跑了 100 秒,第 4 次休息结束。正好追上。
【解析】因为A,B 两点相距100米,所以甲追上乙需要跑的时间=100÷速度差,然后分别求出用甲和乙各自跑100米需要的时间,所以根据甲追上乙需要跑的时间计算出休息的次数,然后根据乙跑的时间得出休息的时间,而此时,甲和乙都跑完了。
21世纪教育网(www.21cnjy.com)
同课章节目录
