期末重难点检测卷(含解析)-2024-2025学年数学五年级下册人教版
文档属性
| 名称 | 期末重难点检测卷(含解析)-2024-2025学年数学五年级下册人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 529.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-26 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末重难点检测卷-2024-2025学年数学五年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.m3表示( )。
A.m×3 B.m+m+m C.m×m×m D.m+3
2.在100克的水中加入10克盐,这时盐占盐水的( )。
A. B. C. D.无法计算
3.如图中的N点表示的数是( )。
A. B. C. D.1.1
4.如图是一个正方体展开图,要把这个展开图重新折叠成正方体,折叠后与A点重合的是( )。
A.O点 B.M点 C.P点 D.N点
5.下面两者之间的关系不适合用如图表示的是( )。
A.真分数和分数 B.奇数和偶数
C.长方体和正方体 D.最大公因数和因数
6.M和N都是非零的自然数,且M÷N=3,M和N的最大公因数是( )。
A.M B.3 C.N D.M和N的乘积
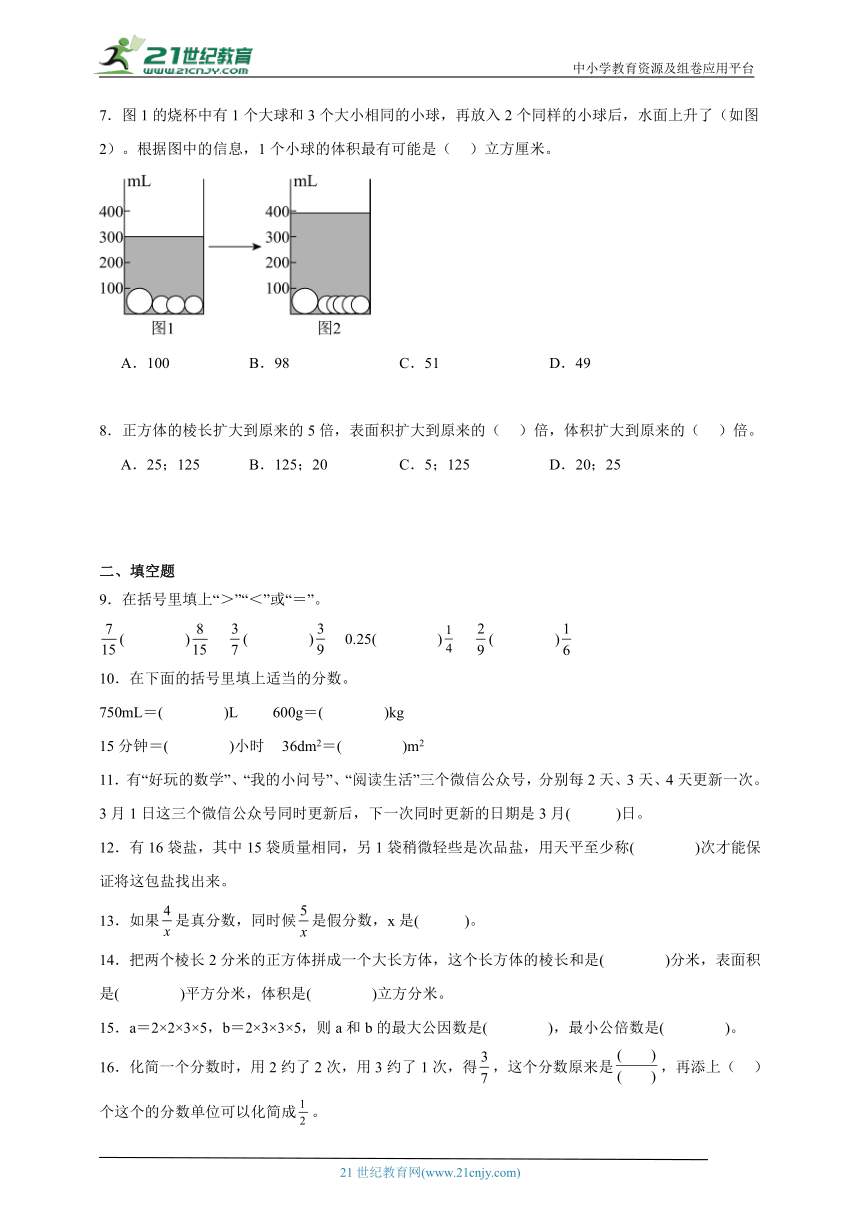
7.图1的烧杯中有1个大球和3个大小相同的小球,再放入2个同样的小球后,水面上升了(如图2)。根据图中的信息,1个小球的体积最有可能是( )立方厘米。
A.100 B.98 C.51 D.49
8.正方体的棱长扩大到原来的5倍,表面积扩大到原来的( )倍,体积扩大到原来的( )倍。
A.25;125 B.125;20 C.5;125 D.20;25
二、填空题
9.在括号里填上“>”“<”或“=”。
( ) ( ) 0.25( ) ( )
10.在下面的括号里填上适当的分数。
750mL=( )L 600g=( )kg
15分钟=( )小时 36dm2=( )m2
11.有“好玩的数学”、“我的小问号”、“阅读生活”三个微信公众号,分别每2天、3天、4天更新一次。3月1日这三个微信公众号同时更新后,下一次同时更新的日期是3月( )日。
12.有16袋盐,其中15袋质量相同,另1袋稍微轻些是次品盐,用天平至少称( )次才能保证将这包盐找出来。
13.如果是真分数,同时候是假分数,x是( )。
14.把两个棱长2分米的正方体拼成一个大长方体,这个长方体的棱长和是( )分米,表面积是( )平方分米,体积是( )立方分米。
15.a=2×2×3×5,b=2×3×3×5,则a和b的最大公因数是( ),最小公倍数是( )。
16.化简一个分数时,用2约了2次,用3约了1次,得,这个分数原来是,再添上( )个这个的分数单位可以化简成。
三、计算题
17.直接写得数。
18.计算下面各题,能简算的要简算。
19.解方程。
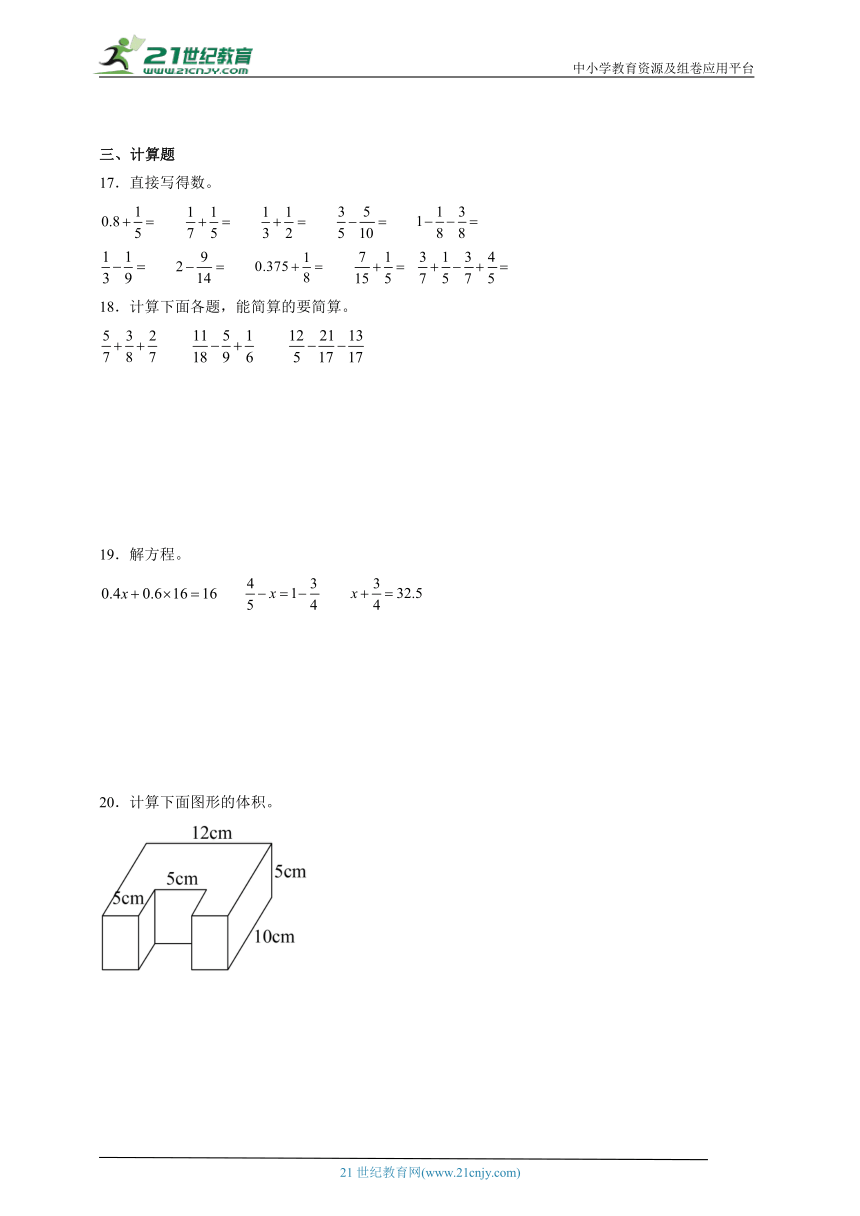
20.计算下面图形的体积。
四、解答题
21.用铁皮做一个长方体通风管,管道长为25米,通风口处是边长为5分米的正方形。做这个通风管至少需要多少平方米铁皮?(接缝处不计)
22.春天到了,农民伯伯给果树浇水。第一天上午浇了所有果树的,下午浇了,第二天上午浇了。你能提出什么数学问题并解答吗?
23.贝贝用三个完全一样的小正方体拼成一个长方体(如下图)。拼成之后,棱长之和减少了160厘米。原来每个小正方体的体积是多少立方厘米?
24.实验小学举行“爱我中华,践行文明”主题演讲比赛,设一、二、三等奖若干名。比赛结束后经统计,一、二等奖获奖人数共占获奖总人数的,二、三等奖获奖人数共占获奖总人数,一、二、三等奖获奖人数分别占获奖总人数的几分之几?
25.张伯伯挖了一个长9米、宽7米、深2米的蓄水池(如图)。
(1)这个蓄水池的占地面积是多少平方米?
(2)如果给这个蓄水浊的四周和底部抹上水泥,抹水泥部分的面积是多少平方米?
(3)这个水池最多能蓄水多少立方米?
26.“粽”享美食,由于粽子具有品种多样,方便快捷的特点,近年来,以下是2018~2023年我国粽子供需情况统计表。
2018~2023年我国粽子供需情况统计表
年份 2018 2019 2020 2021 2022 2023
产量/万吨 35 38 42 45 47 49
需求量/万吨 31.5 34.3 37.7 40.9 44.6 48.1
(1)根据上面统计表把复式折线统计图补充完整。
(2)观察统计图,根据已有信息,请你预测2024年我国粽子产量和需求量分别为多少万吨?
《期末重难点检测卷-2024-2025学年数学五年级下册人教版》参考答案
题号 1 2 3 4 5 6 7 8
答案 C A C B B C D A
1.C
【分析】m3表示3个m相乘,3m表示3个m相加,据此判断即可。
【详解】A.m×3=3m
B.m+m+m=3m
C.m×m×m=m3
D.m+3=m+3
m3表示m×m×m。
故答案为:C
2.A
【分析】先用水的质量加上盐的质量,求出盐水的质量,求一个数占另一个数的几分之几,用这个数除以另一个数解答;据此用盐的质量除以盐水的质量即可解答。
【详解】10÷(100+10)
=10÷110
=
所以这时盐占盐水的。
故答案为:A
3.C
【分析】分数的意义:把单位“1”平均分成若干份,表示其中一份或几份的数;通过观察可知,N在1到2之间,把每2个数字之间的线段平均分成4份,从1往右数,N在1右边的第1份,所以N是(1+),结果用假分数表示。
【详解】1+
=+
=
如图中的N点表示的数是。
故答案为:C
4.B
【分析】这是正方体的1-4-1型的展开图,通过折叠,发现1个3是对面,2和4是对面,5和6是对面,则和A点重合的是M点。
【详解】折叠后与A点重合的是M点。
故答案为:B
5.B
【分析】由图可知,该图表示包含关系的两个量。逐项分析选项中两个量的关系,即可解答。
【详解】A.分数包括真分数和假分数,真分数是分子小于分母的分数,是分数的一部分,因此可用包含关系的图表示;
B.奇数:不是2的倍数的数叫作奇数。偶数:是2的倍数的数叫作偶数。因此,它们不是包含关系的两个量,不能用包含关系的图表示;
C.正方体是特殊的长方体,因此,可用包含关系的图表示;
D.几个数的共有因数中最大的因数就是它们的最大公因数,因此,可用包含关系的图表示。
故答案为:B
6.C
【分析】根据题意,M÷N=3,即M是N的3倍,根据“当两个数是倍数关系时,最大公因数是较小数”进行解答。
【详解】M÷N=3,说明M和N是倍数关系,且M>N;那么M和N的最大公因数是N。
故答案为:C
7.D
【分析】观察图2和图1,图2水面上升的体积就是放入的2个小球的体积,图2刻度-图1刻度=2个小球的体积,2个小球的体积÷2=1个小球的体积,据此分析。
【详解】图2刻度不到400毫升。
(400-300)÷2
=100÷2
=50(毫升)
=50(立方厘米)
因为图2刻度不到400毫升,因此1个小球的体积一定小于50立方厘米,最有可能是49立方厘米。
故答案为:D
8.A
【分析】根据正方体的表面积公式S=6a2,正方体的体积公式V=a3,以及积的变化规律可知,正方体的棱长扩大到原来的5倍,则表面积扩大到原来的(5×5)倍,体积扩大到原来的(5×5×5)倍。
【详解】5×5=25
5×5×5=125
正方体的棱长扩大到原来的5倍,表面积扩大到原来的25倍,体积扩大到原来的125倍。
故答案为:A
9. < > = >
【分析】(1)分母相同时,分子越大,分数值就越大;
(2)分子相同时,分母越大,分数值反而越小;
(3)先把分数化成小数,用分子除以分母即可,再根据小数大小比较的方法进行比较;
(4)分子、分母都不相同时,化成同分母或同分子的分数进行比较。
【详解】(1)分母都是15,分子7<8,所以<;
(2)分子都是3,分母7<9,所以>;
(3)=1÷4=0.25,所以0.25=;
(4)==,==;>,所以>。
10.
【分析】高级单位化低级单位,乘单位之间的进率;低级单位化高级单位,除以单位之间的进率。1L=1000mL,1kg=1000g,1小时=60分,1m2=100dm2。根据分数与除法的关系:分子相当于被除数,分母相当于除数;用分数表示后,再约分,用最简分数表示结果。
【详解】750÷1000==,则750mL=L;
600÷1000==,则600g=kg;
15÷60==,则15分钟=小时;
36÷100==,则36dm2=m2。
11.13
【分析】根据题意,求下一次同时更新的日期,先求2、3、4的最小公倍数,就是再过的天数,完成做题即可。
【详解】
2、3、4的最小公倍数是
(日)
下一次同时更新的日期是3月13日。
12.3
【分析】要达到次数最少,需要将要识别的物品的数目尽可能均匀的分成三份,然后每次称重时,需要将数目相等的两份放到天平两遍称重,不断识别,一直到找到次品为止。据此答题即可。
【详解】经分析得:
将16袋分成3份:5,5,6;第一次称重,在天平两边各放5袋,手里留6袋;
(1)如果天平平衡,则次品在手里,将手里的6袋分为2,2,2,在天平两边各放2袋,手里留2袋,
①如果天平平衡,则次品在手里2袋中,接下来,将这2袋分别放在天平的两边就可以鉴别出次品;
②如果天平不平衡,则次品在升起的天平托盘的2袋中,接下来,将这2袋分别放在天平的两边就可以鉴别出次品。
(2)如果天平不平衡,则次品在升起的天平托盘的5袋中,将这5袋分成三份:2,2,1,在天平两边各放2袋,手里留1袋,
①如果天平不平衡,则找到次品在升起的天平托盘的2袋中,接下来,将这2袋分别放在天平的两边就可以鉴别出次品。
②如果天平平衡,则次品在手中的1袋中。
用天平至少称3次才能保证将这包盐找出来。
【点睛】本题考查找次品的问题,分3份操作找到最优方法。
13.5
【分析】真分数的分子小于分母,假分数的分母小于等于分子,据此分析的取值即可。
【详解】因为是真分数,所以,又因为是假分数,所以。大于4且小于等于5的整数只有5,因此是5。
14. 32 40 16
【分析】观察题意可知,拼成的长方体长是(2×2)分米,宽和高都是2分米,根据长方体的棱长和=(长+宽+高)×4,、长方体的表面积=(长×宽+长×高+宽×高)×2和长方体的体积=长×宽×高,代入数据解笞即可。
【详解】2×2=4(分米)
(4+2+2)×4
=(6+2)×4
=8×4
=32(分米)
(4×2+4×2+2×2)×2
=(8+8+4)×2
=20×2
=40(平方分米)
4×2×2
=8×2
=16(立方分米)
这个长方体的棱长是32分米,长方体的表面积是40平方分米,体积是16立方分米。
15. 30 180
【分析】把它们公有的质因数连乘起来,所得的积就是它们的最大公因数,把它们公有的质因数和独有的质因数连乘起来,所得的积就是它们的最小公倍数。
【详解】a=2×2×3×5,b=2×3×3×5,则a和b的最大公因数是2×3×5=30;
最小公倍数是2×2×3×5×3=180。
则a和b的最大公因数是30,最小公倍数是180。
16.;6
【分析】(1)求原分数:因为化简时用2约了2次,用3约了1次后得到。那么要还原原来的分数,就把的分子分母逆向计算,分子3×2×2×3=36,分母7×2×2×3=84,所以这个分数原来是。
(2)求再添几个分数单位可化简成原分数的分数单位是。=,42-36=6,所以再添上6个这样的分数单位可以化简成。
【详解】3×2×2×3=36,分母7×2×2×3=84,这个分数原来是。
=
(42-36)÷1
=6÷1
=6
这个分数原来是,再添上6个这个的分数单位可以化简成。
17.1;;;;
;;0.5;;1
【详解】略
18.;;
【分析】++,根据加法交换律,原式化为:++,再进行计算;
-+,按照运算顺序,从左向右进行计算;
--,根据减法性质,原式化为:-(+),再进行计算。
【详解】++
=++
=1+
=
-+
=-+
=+
=
--
=-(+)
=-2
=
19.;;
【分析】(1)先算乘法,再把方程左右两边同时减去9.6,再把方程左右两边同时除以0.4,求出方程的解;
(2)先计算减法,再把方程左右两边同时加上x,交换方程左右两边,再把方程左右两边同时减去,求出方程的解;
(3)把化成小数0.75,方程左右两边同时减去0.75,求出方程的解。
【详解】
解:
解:
解:
20.475cm3
【分析】如下图,把图形的缺口补上,缺口处是一个棱长为5cm的正方体,则图形的体积=长方体的体积-正方体的体积;
根据长方体的体积公式V=abh,正方体的体积公式V=a3,代入数据计算求解。
【详解】12×10×5-5×5×5
=600-125
=475(cm3)
图形的体积是475cm3。
21.50平方米
【分析】分析题目,根据米与分米之间的进率为10,将5分米化成以米作单位的数;接下来根据需要铁皮的面积=4个长为25分米、宽为0.5分米的长方形的面积,然后根据长方形的面积=长×宽,列式计算,即可解答。
【详解】5分米=0.5米
25×0.5×4
=12.5×4
=50(平方米)
答:做这个通风管至少需要50平方米铁皮。
22.第一天浇的果树占所有果树的几分之几?
【分析】已知第一天上午浇了所有果树的,下午浇了,由此可提出问题:第一天浇的果树占所有果树的几分之几?用第一天上午浇了的分率加上第一天下午浇了的分率,即可解答。
【详解】提出问题:第一天浇的果树占所有果树的几分之几?(答案不唯一)
+
=+
=
答:第一天浇的果树占所有果树的。
23.1000立方厘米
【分析】由题意可知,三个完全一样的小正方体拼成一个长方体,减少了4个面,即条棱长,已知拼成之后,棱长之和减少了160cm,即160cm是条棱长的和,用除法计算出每条棱长的长度,再根据,代入数据,即可得解。
【详解】
(厘米)
(立方厘米)
答:原来每个小正方体的体积是1000立方厘米。
24.;;
【分析】把获一、二、三等奖的总人数看作单位“1”,从“1”里面减去获一、二等奖的人数占获奖总人数的分率,即是获三等奖人数占获奖总人数的分率,再用获二、三等奖的人数占获奖总人数的分率减去获三等奖人数占获奖总人数的分率即是获二等奖的人数点获奖总人数的分率;最后用获一、二等奖的人数占获奖总人数的分率减去获二等奖人数占获奖总人数的分率即是获一等奖的人数点获奖总人数的分率。
【详解】三等奖:
二等奖:
一等奖:
答:一等奖获奖人数占获奖总人数的,二等奖获奖人数占获奖总人数的,三等奖获奖人数占获奖总人数的。
25.(1)63平方米
(2)127平方米
(3)126立方米
【分析】(1)求蓄水池的占地面积就是求长方体的底面积,利用“长方形的面积=长×宽”求出蓄水池的占地面积;
(2)求抹水泥部分的面积,就是求这个蓄水池四周和底面的五个面的面积和,根据长方体表面积公式:表面积=长×宽+(长×高+宽×高)×2,代入数据,即可解答;
(3)根据长方体体积公式:体积=长×宽×高,代入数据,即可解答。
【详解】(1)9×7=63(平方米)
答:这个蓄水池的占地面积是63平方米。
(2)9×7+(9×2+7×2)×2
=63+(18+14)×2
=63+32×2
=63+64
=127(平方米)
答:抹水泥部分的面积是127平方米。
(3)9×7×2
=63×2
=126(立方米)
答:这个水池最多能蓄水126立方米。
26.(1)见详解
(2)见详解
【分析】(1)根据统计表中提供的产量和需求量的数据,先描点,再连线即可完成折线统计图;
(2)折线往上表示上升趋势,观察折线统计图,产量和需求量都呈上升趋势,即每年的产量和需求量都在逐渐增加,据此预测合理的数据即可,(答案不唯一)。
【详解】(1)统计图如下:
(2)观察复式折线统计图,2024年我国粽子产量为52万吨、需求量为51.5万吨。(答案不唯一)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末重难点检测卷-2024-2025学年数学五年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.m3表示( )。
A.m×3 B.m+m+m C.m×m×m D.m+3
2.在100克的水中加入10克盐,这时盐占盐水的( )。
A. B. C. D.无法计算
3.如图中的N点表示的数是( )。
A. B. C. D.1.1
4.如图是一个正方体展开图,要把这个展开图重新折叠成正方体,折叠后与A点重合的是( )。
A.O点 B.M点 C.P点 D.N点
5.下面两者之间的关系不适合用如图表示的是( )。
A.真分数和分数 B.奇数和偶数
C.长方体和正方体 D.最大公因数和因数
6.M和N都是非零的自然数,且M÷N=3,M和N的最大公因数是( )。
A.M B.3 C.N D.M和N的乘积
7.图1的烧杯中有1个大球和3个大小相同的小球,再放入2个同样的小球后,水面上升了(如图2)。根据图中的信息,1个小球的体积最有可能是( )立方厘米。
A.100 B.98 C.51 D.49
8.正方体的棱长扩大到原来的5倍,表面积扩大到原来的( )倍,体积扩大到原来的( )倍。
A.25;125 B.125;20 C.5;125 D.20;25
二、填空题
9.在括号里填上“>”“<”或“=”。
( ) ( ) 0.25( ) ( )
10.在下面的括号里填上适当的分数。
750mL=( )L 600g=( )kg
15分钟=( )小时 36dm2=( )m2
11.有“好玩的数学”、“我的小问号”、“阅读生活”三个微信公众号,分别每2天、3天、4天更新一次。3月1日这三个微信公众号同时更新后,下一次同时更新的日期是3月( )日。
12.有16袋盐,其中15袋质量相同,另1袋稍微轻些是次品盐,用天平至少称( )次才能保证将这包盐找出来。
13.如果是真分数,同时候是假分数,x是( )。
14.把两个棱长2分米的正方体拼成一个大长方体,这个长方体的棱长和是( )分米,表面积是( )平方分米,体积是( )立方分米。
15.a=2×2×3×5,b=2×3×3×5,则a和b的最大公因数是( ),最小公倍数是( )。
16.化简一个分数时,用2约了2次,用3约了1次,得,这个分数原来是,再添上( )个这个的分数单位可以化简成。
三、计算题
17.直接写得数。
18.计算下面各题,能简算的要简算。
19.解方程。
20.计算下面图形的体积。
四、解答题
21.用铁皮做一个长方体通风管,管道长为25米,通风口处是边长为5分米的正方形。做这个通风管至少需要多少平方米铁皮?(接缝处不计)
22.春天到了,农民伯伯给果树浇水。第一天上午浇了所有果树的,下午浇了,第二天上午浇了。你能提出什么数学问题并解答吗?
23.贝贝用三个完全一样的小正方体拼成一个长方体(如下图)。拼成之后,棱长之和减少了160厘米。原来每个小正方体的体积是多少立方厘米?
24.实验小学举行“爱我中华,践行文明”主题演讲比赛,设一、二、三等奖若干名。比赛结束后经统计,一、二等奖获奖人数共占获奖总人数的,二、三等奖获奖人数共占获奖总人数,一、二、三等奖获奖人数分别占获奖总人数的几分之几?
25.张伯伯挖了一个长9米、宽7米、深2米的蓄水池(如图)。
(1)这个蓄水池的占地面积是多少平方米?
(2)如果给这个蓄水浊的四周和底部抹上水泥,抹水泥部分的面积是多少平方米?
(3)这个水池最多能蓄水多少立方米?
26.“粽”享美食,由于粽子具有品种多样,方便快捷的特点,近年来,以下是2018~2023年我国粽子供需情况统计表。
2018~2023年我国粽子供需情况统计表
年份 2018 2019 2020 2021 2022 2023
产量/万吨 35 38 42 45 47 49
需求量/万吨 31.5 34.3 37.7 40.9 44.6 48.1
(1)根据上面统计表把复式折线统计图补充完整。
(2)观察统计图,根据已有信息,请你预测2024年我国粽子产量和需求量分别为多少万吨?
《期末重难点检测卷-2024-2025学年数学五年级下册人教版》参考答案
题号 1 2 3 4 5 6 7 8
答案 C A C B B C D A
1.C
【分析】m3表示3个m相乘,3m表示3个m相加,据此判断即可。
【详解】A.m×3=3m
B.m+m+m=3m
C.m×m×m=m3
D.m+3=m+3
m3表示m×m×m。
故答案为:C
2.A
【分析】先用水的质量加上盐的质量,求出盐水的质量,求一个数占另一个数的几分之几,用这个数除以另一个数解答;据此用盐的质量除以盐水的质量即可解答。
【详解】10÷(100+10)
=10÷110
=
所以这时盐占盐水的。
故答案为:A
3.C
【分析】分数的意义:把单位“1”平均分成若干份,表示其中一份或几份的数;通过观察可知,N在1到2之间,把每2个数字之间的线段平均分成4份,从1往右数,N在1右边的第1份,所以N是(1+),结果用假分数表示。
【详解】1+
=+
=
如图中的N点表示的数是。
故答案为:C
4.B
【分析】这是正方体的1-4-1型的展开图,通过折叠,发现1个3是对面,2和4是对面,5和6是对面,则和A点重合的是M点。
【详解】折叠后与A点重合的是M点。
故答案为:B
5.B
【分析】由图可知,该图表示包含关系的两个量。逐项分析选项中两个量的关系,即可解答。
【详解】A.分数包括真分数和假分数,真分数是分子小于分母的分数,是分数的一部分,因此可用包含关系的图表示;
B.奇数:不是2的倍数的数叫作奇数。偶数:是2的倍数的数叫作偶数。因此,它们不是包含关系的两个量,不能用包含关系的图表示;
C.正方体是特殊的长方体,因此,可用包含关系的图表示;
D.几个数的共有因数中最大的因数就是它们的最大公因数,因此,可用包含关系的图表示。
故答案为:B
6.C
【分析】根据题意,M÷N=3,即M是N的3倍,根据“当两个数是倍数关系时,最大公因数是较小数”进行解答。
【详解】M÷N=3,说明M和N是倍数关系,且M>N;那么M和N的最大公因数是N。
故答案为:C
7.D
【分析】观察图2和图1,图2水面上升的体积就是放入的2个小球的体积,图2刻度-图1刻度=2个小球的体积,2个小球的体积÷2=1个小球的体积,据此分析。
【详解】图2刻度不到400毫升。
(400-300)÷2
=100÷2
=50(毫升)
=50(立方厘米)
因为图2刻度不到400毫升,因此1个小球的体积一定小于50立方厘米,最有可能是49立方厘米。
故答案为:D
8.A
【分析】根据正方体的表面积公式S=6a2,正方体的体积公式V=a3,以及积的变化规律可知,正方体的棱长扩大到原来的5倍,则表面积扩大到原来的(5×5)倍,体积扩大到原来的(5×5×5)倍。
【详解】5×5=25
5×5×5=125
正方体的棱长扩大到原来的5倍,表面积扩大到原来的25倍,体积扩大到原来的125倍。
故答案为:A
9. < > = >
【分析】(1)分母相同时,分子越大,分数值就越大;
(2)分子相同时,分母越大,分数值反而越小;
(3)先把分数化成小数,用分子除以分母即可,再根据小数大小比较的方法进行比较;
(4)分子、分母都不相同时,化成同分母或同分子的分数进行比较。
【详解】(1)分母都是15,分子7<8,所以<;
(2)分子都是3,分母7<9,所以>;
(3)=1÷4=0.25,所以0.25=;
(4)==,==;>,所以>。
10.
【分析】高级单位化低级单位,乘单位之间的进率;低级单位化高级单位,除以单位之间的进率。1L=1000mL,1kg=1000g,1小时=60分,1m2=100dm2。根据分数与除法的关系:分子相当于被除数,分母相当于除数;用分数表示后,再约分,用最简分数表示结果。
【详解】750÷1000==,则750mL=L;
600÷1000==,则600g=kg;
15÷60==,则15分钟=小时;
36÷100==,则36dm2=m2。
11.13
【分析】根据题意,求下一次同时更新的日期,先求2、3、4的最小公倍数,就是再过的天数,完成做题即可。
【详解】
2、3、4的最小公倍数是
(日)
下一次同时更新的日期是3月13日。
12.3
【分析】要达到次数最少,需要将要识别的物品的数目尽可能均匀的分成三份,然后每次称重时,需要将数目相等的两份放到天平两遍称重,不断识别,一直到找到次品为止。据此答题即可。
【详解】经分析得:
将16袋分成3份:5,5,6;第一次称重,在天平两边各放5袋,手里留6袋;
(1)如果天平平衡,则次品在手里,将手里的6袋分为2,2,2,在天平两边各放2袋,手里留2袋,
①如果天平平衡,则次品在手里2袋中,接下来,将这2袋分别放在天平的两边就可以鉴别出次品;
②如果天平不平衡,则次品在升起的天平托盘的2袋中,接下来,将这2袋分别放在天平的两边就可以鉴别出次品。
(2)如果天平不平衡,则次品在升起的天平托盘的5袋中,将这5袋分成三份:2,2,1,在天平两边各放2袋,手里留1袋,
①如果天平不平衡,则找到次品在升起的天平托盘的2袋中,接下来,将这2袋分别放在天平的两边就可以鉴别出次品。
②如果天平平衡,则次品在手中的1袋中。
用天平至少称3次才能保证将这包盐找出来。
【点睛】本题考查找次品的问题,分3份操作找到最优方法。
13.5
【分析】真分数的分子小于分母,假分数的分母小于等于分子,据此分析的取值即可。
【详解】因为是真分数,所以,又因为是假分数,所以。大于4且小于等于5的整数只有5,因此是5。
14. 32 40 16
【分析】观察题意可知,拼成的长方体长是(2×2)分米,宽和高都是2分米,根据长方体的棱长和=(长+宽+高)×4,、长方体的表面积=(长×宽+长×高+宽×高)×2和长方体的体积=长×宽×高,代入数据解笞即可。
【详解】2×2=4(分米)
(4+2+2)×4
=(6+2)×4
=8×4
=32(分米)
(4×2+4×2+2×2)×2
=(8+8+4)×2
=20×2
=40(平方分米)
4×2×2
=8×2
=16(立方分米)
这个长方体的棱长是32分米,长方体的表面积是40平方分米,体积是16立方分米。
15. 30 180
【分析】把它们公有的质因数连乘起来,所得的积就是它们的最大公因数,把它们公有的质因数和独有的质因数连乘起来,所得的积就是它们的最小公倍数。
【详解】a=2×2×3×5,b=2×3×3×5,则a和b的最大公因数是2×3×5=30;
最小公倍数是2×2×3×5×3=180。
则a和b的最大公因数是30,最小公倍数是180。
16.;6
【分析】(1)求原分数:因为化简时用2约了2次,用3约了1次后得到。那么要还原原来的分数,就把的分子分母逆向计算,分子3×2×2×3=36,分母7×2×2×3=84,所以这个分数原来是。
(2)求再添几个分数单位可化简成原分数的分数单位是。=,42-36=6,所以再添上6个这样的分数单位可以化简成。
【详解】3×2×2×3=36,分母7×2×2×3=84,这个分数原来是。
=
(42-36)÷1
=6÷1
=6
这个分数原来是,再添上6个这个的分数单位可以化简成。
17.1;;;;
;;0.5;;1
【详解】略
18.;;
【分析】++,根据加法交换律,原式化为:++,再进行计算;
-+,按照运算顺序,从左向右进行计算;
--,根据减法性质,原式化为:-(+),再进行计算。
【详解】++
=++
=1+
=
-+
=-+
=+
=
--
=-(+)
=-2
=
19.;;
【分析】(1)先算乘法,再把方程左右两边同时减去9.6,再把方程左右两边同时除以0.4,求出方程的解;
(2)先计算减法,再把方程左右两边同时加上x,交换方程左右两边,再把方程左右两边同时减去,求出方程的解;
(3)把化成小数0.75,方程左右两边同时减去0.75,求出方程的解。
【详解】
解:
解:
解:
20.475cm3
【分析】如下图,把图形的缺口补上,缺口处是一个棱长为5cm的正方体,则图形的体积=长方体的体积-正方体的体积;
根据长方体的体积公式V=abh,正方体的体积公式V=a3,代入数据计算求解。
【详解】12×10×5-5×5×5
=600-125
=475(cm3)
图形的体积是475cm3。
21.50平方米
【分析】分析题目,根据米与分米之间的进率为10,将5分米化成以米作单位的数;接下来根据需要铁皮的面积=4个长为25分米、宽为0.5分米的长方形的面积,然后根据长方形的面积=长×宽,列式计算,即可解答。
【详解】5分米=0.5米
25×0.5×4
=12.5×4
=50(平方米)
答:做这个通风管至少需要50平方米铁皮。
22.第一天浇的果树占所有果树的几分之几?
【分析】已知第一天上午浇了所有果树的,下午浇了,由此可提出问题:第一天浇的果树占所有果树的几分之几?用第一天上午浇了的分率加上第一天下午浇了的分率,即可解答。
【详解】提出问题:第一天浇的果树占所有果树的几分之几?(答案不唯一)
+
=+
=
答:第一天浇的果树占所有果树的。
23.1000立方厘米
【分析】由题意可知,三个完全一样的小正方体拼成一个长方体,减少了4个面,即条棱长,已知拼成之后,棱长之和减少了160cm,即160cm是条棱长的和,用除法计算出每条棱长的长度,再根据,代入数据,即可得解。
【详解】
(厘米)
(立方厘米)
答:原来每个小正方体的体积是1000立方厘米。
24.;;
【分析】把获一、二、三等奖的总人数看作单位“1”,从“1”里面减去获一、二等奖的人数占获奖总人数的分率,即是获三等奖人数占获奖总人数的分率,再用获二、三等奖的人数占获奖总人数的分率减去获三等奖人数占获奖总人数的分率即是获二等奖的人数点获奖总人数的分率;最后用获一、二等奖的人数占获奖总人数的分率减去获二等奖人数占获奖总人数的分率即是获一等奖的人数点获奖总人数的分率。
【详解】三等奖:
二等奖:
一等奖:
答:一等奖获奖人数占获奖总人数的,二等奖获奖人数占获奖总人数的,三等奖获奖人数占获奖总人数的。
25.(1)63平方米
(2)127平方米
(3)126立方米
【分析】(1)求蓄水池的占地面积就是求长方体的底面积,利用“长方形的面积=长×宽”求出蓄水池的占地面积;
(2)求抹水泥部分的面积,就是求这个蓄水池四周和底面的五个面的面积和,根据长方体表面积公式:表面积=长×宽+(长×高+宽×高)×2,代入数据,即可解答;
(3)根据长方体体积公式:体积=长×宽×高,代入数据,即可解答。
【详解】(1)9×7=63(平方米)
答:这个蓄水池的占地面积是63平方米。
(2)9×7+(9×2+7×2)×2
=63+(18+14)×2
=63+32×2
=63+64
=127(平方米)
答:抹水泥部分的面积是127平方米。
(3)9×7×2
=63×2
=126(立方米)
答:这个水池最多能蓄水126立方米。
26.(1)见详解
(2)见详解
【分析】(1)根据统计表中提供的产量和需求量的数据,先描点,再连线即可完成折线统计图;
(2)折线往上表示上升趋势,观察折线统计图,产量和需求量都呈上升趋势,即每年的产量和需求量都在逐渐增加,据此预测合理的数据即可,(答案不唯一)。
【详解】(1)统计图如下:
(2)观察复式折线统计图,2024年我国粽子产量为52万吨、需求量为51.5万吨。(答案不唯一)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
