浙江省宁波市江北区八年级下册数学期末试题卷(PDF版,含答案)
文档属性
| 名称 | 浙江省宁波市江北区八年级下册数学期末试题卷(PDF版,含答案) |  | |
| 格式 | |||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-27 08:28:43 | ||
图片预览



文档简介
2024 学年第二学期八年级学业质量检测(数学试题)
考生须知:
1.全卷分试题卷Ⅰ、试题卷Ⅱ和答题卷.试题卷共 6 页,有三个大题,24 个小题.满分
为 120 分,考试时长为 120 分钟.
2.请将姓名、准考证号等信息分别填写在试题卷和答题卷的规定位置上.
3.答题时,请将试题卷 I 的答案在答题卷 I 上对应的选项位置用 2B 铅笔涂黑、涂满.将
试题卷Ⅱ的答案用黑色字迹的钢笔或签字笔书写,答案必须按照题号顺序在答题卷Ⅱ各题目
规定区域内作答,做在试题卷上或超出答题卷区域书写的答案无效.
4.不允许使用计算器,没有近似计算要求的试题,结果都不能用近似数表示.
试 题 卷 Ⅰ
一、选择题(本大题有 10小题,每小题 3分,共 30分,在每小题给出的四个选项中,只有一项
符合题目要求)
1. 二次根式 x 2中字母 x的取值范围是 ( ▲ )
A.x≥2 B.x≤2 C.x>2 D.x<2
2. 在中国的传统文化中,图案纹饰承载着人们对美好生活的期盼和祝福,下列图案纹饰中是
中心对称图形的是 ( ▲ )
A.团花纹 B.山茶纹 C.鱼纹 D.祥云边三兔纹
3.下列计算正确的是 ( ▲ )
A. 2 5 7 B.5 2 2 2 3 C 2 5 10 D 2 2. . 2
4. 用配方法解方程 x2 4x 10 0时,下列配方结果正确的是 ( ▲ )
A. x 2 2 12 B. x 2 2 12 C. x 2 2 14 D. x 2 2 14
5. 牛顿高度评价反证法在数学证明中的关键作用,认为“反证法是数学家最精当的武器之一”.
用反证法证明“在△ABC中,若∠A>∠B>∠C,则∠C<60°”时,应先假设( ▲ )
A.∠C=60° B.∠C>60° C.∠C≠60° D.∠C≥60°
2024 学年第二学期八年级学业质量检测(数学试卷) 第 1 页 共 6 页
6. 已知一组数据:3,3,4,6,若再添加一个数据 4得到一组新数据,则这组新数据的统计
量不会发生变化的是 ( ▲ )
A.平均数 B.众数 C.中位数 D.方差
7. 2已知反比例函数 y ,下列结论正.确.的是 ( ▲ )x
A.图象必经过点(2,1) B.图象在第二、四象限内
C.y随 x的增大而减小 D.若 x>1,则 y>2
8. 如图,在一个对边平行的纸条上有两点 A,B及线段 AB的中点 O,以下操作和判断不.正.
确.的是 ( ▲ )
A.过点 O作任意直线(除直线 AB)交纸条两边于点 C,D,得到平行四边形 ACBD
B.过点 O作 AB的垂线 l交纸条两边于点 C,D,得到菱形 ACBD
C.分别过点 A,B作对边的垂线,交对边于点 C,D,得到矩形 ACBD
D.在点 A,B所在边的对边分别取 C,D两点,使得 AC=BD,得到平行四边形 ACBD
(第 8题图) (第 9题图) (第 10题图)
9. 如图,在菱形 ABCD中,AD 2 3, BAD 60 ,BD与 AC相交于点O,点 P是线段 AB
上的任意点,以 PB为对角线作平行四边形 POBQ,连结DQ,则DQ的最小值是 ( ▲ )
A. 2 3 B.4 C 9. D. 4 3
2
10. 如图,正方形 EFGH的顶点 E在正方形 ABCD上,四边形 FGKD也是正方形,且点 B,
H,K在同一直线上,则正方形 EFGH与正方形 ABCD的面积比为 ( ▲ )
A. 2 B. 2 1 C. 2 2 D. 3 2
2 2 2 2
2024 学年第二学期八年级学业质量检测(数学试卷) 第 2 页 共 6 页
试 题 卷 Ⅱ
二、填空题(本大题有 6小题,每小题 3分,共 18分)
11. 五边形的内角和为 ▲ .
12. 宁波舟山港作为全球货物吞吐量第一大港,其装卸效率至关重要.四个核心作.业.区.(甬
东、甬南、甬西、甬北)在某周工作日的集装箱平均每小时装卸箱数相同.为了评估各作
业区工作效率的稳定性,统计了其装卸效率的方差如下:S2甬东=25,S2 =36,S2 =64,S2 =16,甬南 甬西 甬北
则装卸效率最稳定的作.业.区.是 ▲ .
13. 已知 x=1是关于 x的一元二次方程 x2+kx+1=0的一个根,则实数 k的值为 ▲ .
14. 如图,DE是△ABC的中位线, ACB的角平分线交 DE于点 F ,若 AC=4,BC=8,则 DF
的长为 ▲ .
(第 14题图) (第 15题图) (第 16题图)
15. 如图,矩形 ABCD k的顶点 A、C在双曲线 y k>0 上,顶点 B、D在 x轴上,AD交 y
x
轴于点 E,若 BO=AB,OE=3,则 k= ▲ .
16. 如图,在 ABCD中,点 E为边 CD的中点,将△ADE沿 AE折叠,边 AD 交 BC的延长
线于点 F,连结 EF,若 AD=5,CF=1,AE= 3 EF,则 AB的长为 ▲ .
三、解答题(本大题有 8小题,共 72分)
17.(本题 8分)计算:
1 12 1( ) 8 (2) 5 1 2 2 10
2
18.(本题 8分)解方程:
(1) x2 2x 8 0 (2) x x 2 6 3x
2024 学年第二学期八年级学业质量检测(数学试卷) 第 3 页 共 6 页
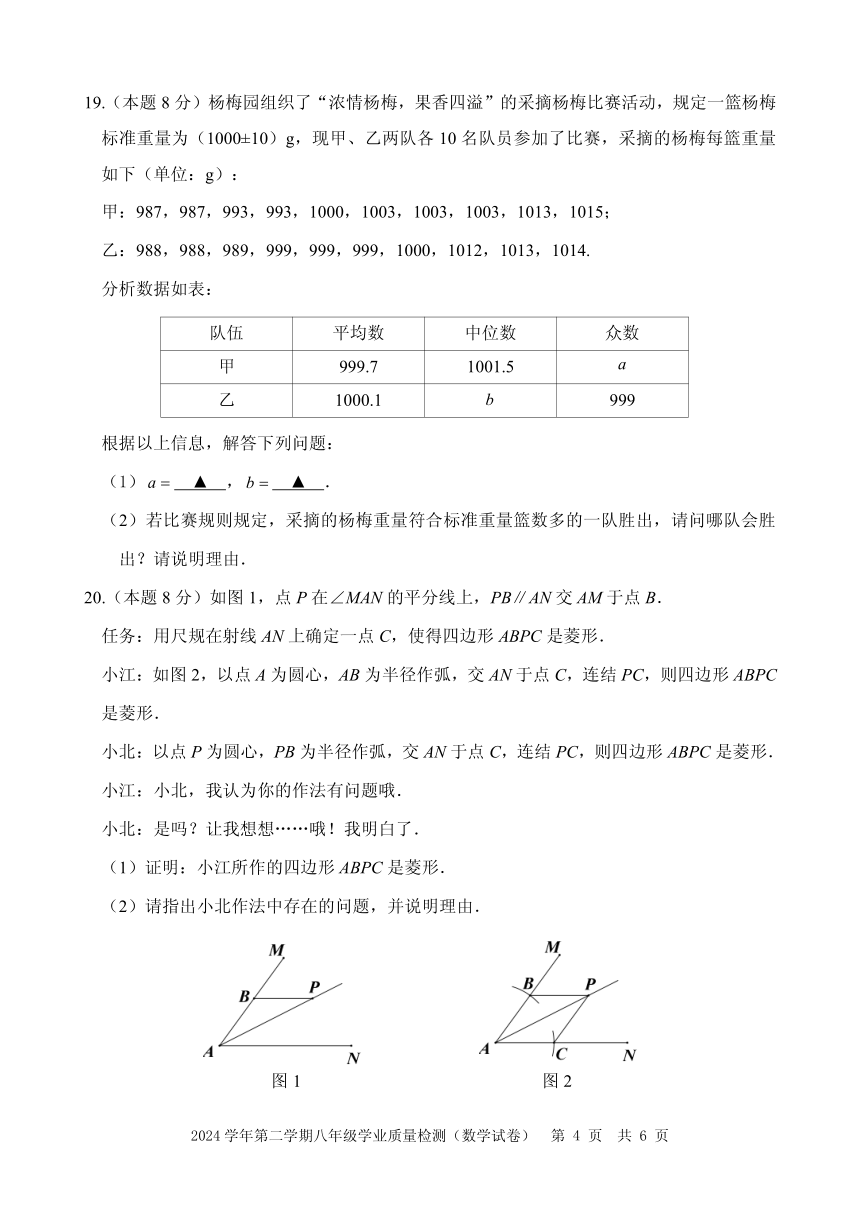
19.(本题 8分)杨梅园组织了“浓情杨梅,果香四溢”的采摘杨梅比赛活动,规定一篮杨梅
标准重量为(1000±10)g,现甲、乙两队各 10名队员参加了比赛,采摘的杨梅每篮重量
如下(单位:g):
甲:987,987,993,993,1000,1003,1003,1003,1013,1015;
乙:988,988,989,999,999,999,1000,1012,1013,1014.
分析数据如表:
队伍 平均数 中位数 众数
甲 999.7 1001.5 a
乙 1000.1 b 999
根据以上信息,解答下列问题:
(1) a ▲ , b ▲ .
(2)若比赛规则规定,采摘的杨梅重量符合标准重量篮数多的一队胜出,请问哪队会胜
出?请说明理由.
20.(本题 8分)如图 1,点 P在∠MAN的平分线上,PB∥AN交 AM于点 B.
任务:用尺规在射线 AN上确定一点 C,使得四边形 ABPC是菱形.
小江:如图 2,以点 A为圆心,AB为半径作弧,交 AN于点 C,连结 PC,则四边形 ABPC
是菱形.
小北:以点 P为圆心,PB为半径作弧,交 AN于点 C,连结 PC,则四边形 ABPC是菱形.
小江:小北,我认为你的作法有问题哦.
小北:是吗?让我想想……哦!我明白了.
(1)证明:小江所作的四边形 ABPC是菱形.
(2)请指出小北作法中存在的问题,并说明理由.
图 1 图 2
2024 学年第二学期八年级学业质量检测(数学试卷) 第 4 页 共 6 页
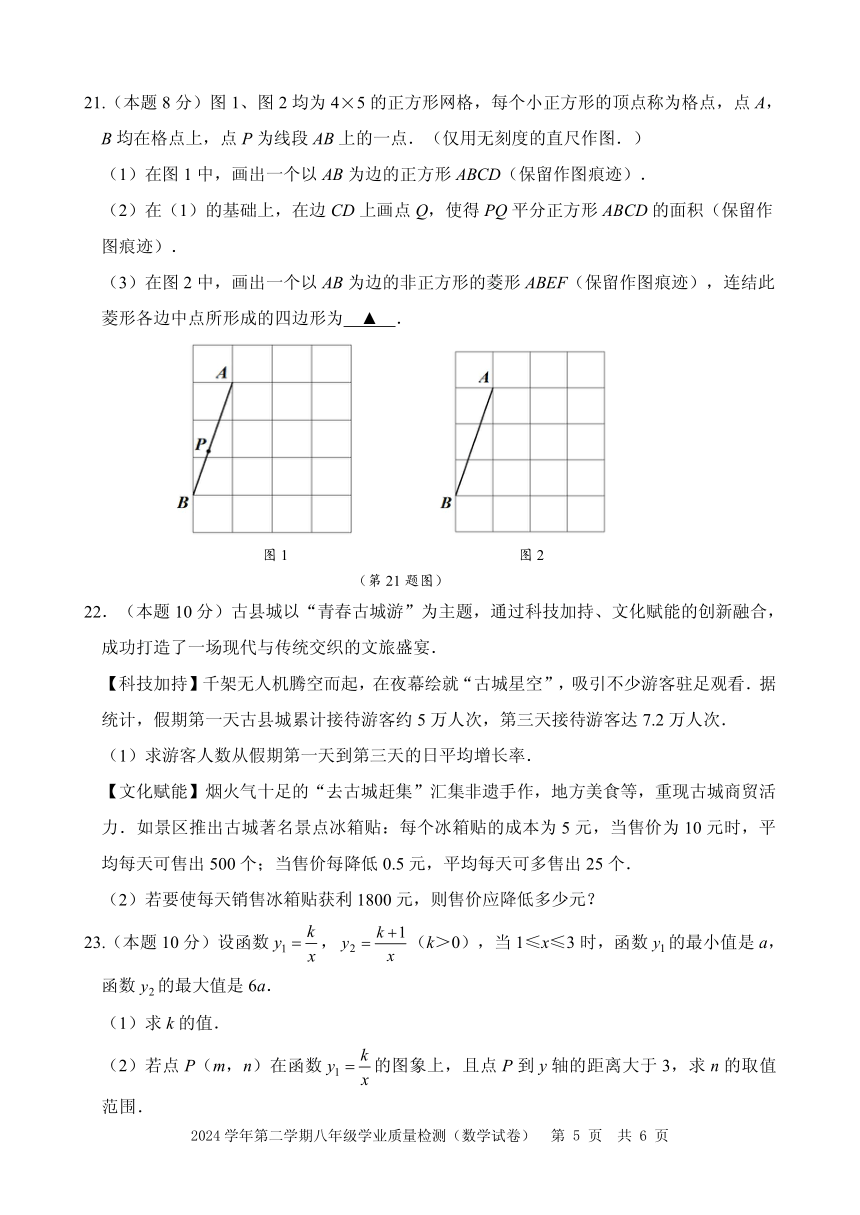
21.(本题 8分)图 1、图 2均为 4×5的正方形网格,每个小正方形的顶点称为格点,点 A,
B均在格点上,点 P为线段 AB上的一点.(仅用无刻度的直尺作图.)
(1)在图 1中,画出一个以 AB为边的正方形 ABCD(保留作图痕迹).
(2)在(1)的基础上,在边 CD上画点 Q,使得 PQ平分正方形 ABCD的面积(保留作
图痕迹).
(3)在图 2中,画出一个以 AB为边的非正方形的菱形 ABEF(保留作图痕迹),连结此
菱形各边中点所形成的四边形为 ▲ .
图 1 图 2
(第 21题图)
22.(本题 10分)古县城以“青春古城游”为主题,通过科技加持、文化赋能的创新融合,
成功打造了一场现代与传统交织的文旅盛宴.
【科技加持】千架无人机腾空而起,在夜幕绘就“古城星空”,吸引不少游客驻足观看.据
统计,假期第一天古县城累计接待游客约 5万人次,第三天接待游客达 7.2万人次.
(1)求游客人数从假期第一天到第三天的日平均增长率.
【文化赋能】烟火气十足的“去古城赶集”汇集非遗手作,地方美食等,重现古城商贸活
力.如景区推出古城著名景点冰箱贴:每个冰箱贴的成本为 5 元,当售价为 10 元时,平
均每天可售出 500个;当售价每降低 0.5元,平均每天可多售出 25个.
(2)若要使每天销售冰箱贴获利 1800元,则售价应降低多少元?
23. 10 k k 1(本题 分)设函数 y1 , y2 (k>0),当 1≤x≤3时,函数 y1的最小值是 a,x x
函数 y2的最大值是 6a.
(1)求 k的值.
(2)若点 P(m k,n)在函数 y1 的图象上,且点 P到 y轴的距离大于 3,求 n的取值x
范围.
2024 学年第二学期八年级学业质量检测(数学试卷) 第 5 页 共 6 页
(3 3 8 k)一次函数 y x 与函数 y1 的图象在第一象限的交点为点 A,且与 x轴交于11 11 x
点 B,点 C k在函数 y1 位于第一象限的图象上,若 S△AOC=S△AOB,直接写出点 C的横坐标.x
(第 23题图)
24.(本题 12分)我国著名的“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼
成一个大正方形.数学兴趣小组的小伙伴们尝试用两对全等的直角三角形与一个矩形拼出
了一个平行四边形.
(1)如图 1,M是 AB的中点,若 ME=DG,AB=6,求 CG的长.
(2)如图 2,M是 AB的中点,连结 HF,EG交于点 O,连结 OM.
①求证:OM∥AD.
②如图 3,若 AH=HE,取 AD的中点 N,连结 ON,NG,MH,若 S NOG 3S MOH ,
HG
求 的值.
DG
图 1 图 2 图 3
(第 24题图)
2024 学年第二学期八年级学业质量检测(数学试卷) 第 6 页 共 6 页
2024 学年第二学期八年级学业质量检测(数学)
参考答案与评分参考
一、选择题(本大题有 10小题,每小题 3分,共 30分,在每小题给出的四个选项中,只有一
项符合题目要求)
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C D D A A D C C
9. ∵点 O到 AB的距离等于点 Q到 AB的距离,∴Q的轨迹为平行于 AB的线段.
过 Q作直线 l∥AB,当 DQ⊥直线 l时 DQ最小,
∵直线 l∥AB ∴ DM⊥AB
在菱形 ABCD中, AD 2 3, BAD 60 ,∴DM=3.
过 O 3作 ON⊥AB,∴ON= ,
2
又∵ON=QM= 3 ,∴DQ= 9 .
2 2
10. 延长 GF交 DC于点 P,连结 PE. 易证△BEH≌△PDF≌△PEF.
∴CE=CP,设 CP=x,∴CE=CP=x,PE=DP= 2x .
2
∴CD=x+ 2x,∴ 2正方形 = 1+ 2 .
在 Rt△DEC中,CE=x,CD=x+ 2x .
∴DE2=(4+2 2 ) 2.
又∵EF= 1 DE,
2
1
2
x2
1 2 正方形 2 2 2
∴ 2 2 2 正方形 = EF DE 1 x . ∴ = = .4 2
2
正方形 1 2 x2 2
二、填空题(本大题有 6小题,每小题 3分,共 18分)
题号 11 12 13 14 15 16
答案 540° 甬北 -2 2 27 3 2 7
4
15. 过点 A,C作 x轴的垂线,交 x轴于点 P,Q. 连结 AO,CO.
∵AB=CD,易证△APB≌△DCQ
∴CQ=AP,DQ=BP
又∵点 A,C在反比例函数图象上 ∴OP=OQ,
∴O为 BD中点,
又∵OB=AB,OA=OB,
∴△OAB为等边三角形,
∴∠AOB=∠BAO=60°, ∴∠EOA=∠EAO=30°
∴EO=AE= 3, ∴AO= 3 3 ,
3 3 9 27 3
∴A( , ) ∴k= .
2 2 4
16. 如图,延长 AE,BC交于点 G.
在 ABCD中,AD=5,AD∥BC
∴∠DAE=∠G,∠D=∠GCE.
∵点 E是 CD中点, ∴CE=DE.
∴△AED≌△GEC(AAS)
∴CG=AD=5,AE=GE.
∵折叠 ∴∠DAE=∠FAE=∠G , ∴AF=GF.
∵AD=5,CF=1,∴AF= GF=CG-CF=AD-CF=4.
∵AE=GE, ∴FE⊥AG
∵AE= 3 EF, ∴设 EF= x,AE= 3x,
在 Rt△AEF中, 42=x2 ( 3x)2, 解得 x=2. ∴∠FAE=∠DAE=30°.
过点 E作 EH⊥AD.
∵AE= 3x = 2 3, ∴EH= 3,AH=3.
∴DH=5-3=2, ∴DE= DH 2 EH 2 = 7 . ∴CD= 2 7 .
三、解答题(本大题有 8个小题,共 72分)
17.(8分)解:
(1) 1原式= 2 3 8 ……………………………2分
2
2 3 2 ……………………………4分
(2)原式=5 2 5 1 2 5 ……………………………6分
=6 …………………………8分
18.(8分)(1) x2 2x 8 0
x 4 x 2 0
x1 2,x2 4 ……………………………4分
(2) x x 2 6 3x
x x 2 3 2 x
x 2 x 3 0
x1 2,x2 3 ……………………………8分
19.(8分)(1)a=1003,b=999 ……………………………4分
(2)甲队有 6人符合标准重量,乙队有 4人符合标准重量,∴甲队胜. …8分
20. (8分) (1)∵AP平分∠MAN, ∴∠MAP=∠NAP.
∵PB∥AN ∴∠APB=∠NAP.
∴∠MAP=∠APB.
∴AB=PB.
∵由作法可知 AB=AC,
∴AC=PB, 图 2
∴四边形 ABPC是平行四边形.
∵AB=AC ∴平行四边形 ABPC是菱形. …………………………4分
(2)以 P为圆心 PB为半径作弧,与 AN可能会有两个交点,其中只有一个是菱形而另一个
不满足要求. (画图举反例也给 4分) ……………………………8分
21. (8分)(1)见下(1)图 ……………………………2分
(2)见下(2)图 ……………………………4分
(3)见下(3)图;矩形
菱形图 2分;答案“矩形”2分,若回答“平行四边形”则给 1分. ………8分
(1)图 (2)图 (3)图
22. (10分)(1)设日平均增长率为 x,
5(1 x)2 7.2 解得 x1 0.2, x2 2.2(舍)
答:日平均增长率为 20%. ……………………………4分
(2)设售价降低 a元,
10 5 a 500 50a 1800,解得 a1=2, a2 7(舍)
答:售价应降低 2元. ……………………………10分
23(1)∵k>0,k+1>0,1≤x≤3,
∴在每一象限内,y1随 x的增大而减小,y2随 x的增大而减小,
∴当 x=3时,y1最小值为 =a,①;3
当 x=1时,y2最大值为 + 1 = 6a,②;
由①,②得:k=1. ……………………………3分
(2)∵P(m,n)到 y轴的距离大于 3,
∴m<-3 或 m>3
∵y1=
1
1 1
∴ - <n<0或 0<n< ……………………………7分
3 3
(3 3 8 k)一次函数 y x 与函数 y1 的图象在第一象限的交点为点 A,且与 x轴交于点11 11 x
B,
8
∴A(1,1),B(- ,0) ∴S 4△AOB= ,3 3
又∵ S△AOC=S
4
△AOB= .3
①当点 C在 A点的右侧
设 C(m 1, ),过 A,C分别关于 x轴作垂线交于点 M、N,
m
∵ S 4△AOC= S直角梯形ACNM = ,3
1
∴ 1 m m 1 4 ,
2 3
1
∴m1 3, m2 (舍).3
①当点 C在 A点的左侧
设 C 1(m, ),过 A,C分别关于 x轴作垂线交于点 M、N,
m
∵ S△AOC= S
4
直角梯形ACNM = ,3
1 1 4
∴ 1 1 m ,
2 m 3
m 3 m 1∴ 1 (舍), 2 3
1
所以点 C的横坐标为 3或 . (写出一个正确答案给 2分) ………………………10分
3
24. (1)∵△ABE是直角三角形,点 M是 AB中点,
∴AM=BM=ME=DG= 1 AB=3.
2
∵△ABE≌△CDG,∴BE=DG=3,
∴∠ABE=60°
∴CG=AE= 3 3 . ……………………………4分
(2)①连结 OB,OD,
∵OE=OG,BE=DG,∠BEO=∠DGO,
∴△BOE≌△DOG,
∴∠BOE=∠DOG,OB=OD,
∴B,O,D三点共线.
∵点 M是 AB中点,
∴OM是△ABD的中位线,
∴OM∥AD. ……………………………8分
②∵AH=HE,M是 AB中点,
∴MH是△ABE的中位线.
∴MH∥BE,BE=2MH.
设 ON与 MD交于点 K,作△MOH的高 h1,△NKG的高 h2 ,
易证 h1= h2 .
S 1∵ △MOH MH h
1
1, S2 △NOG
KG h1 h2 ,2
又∵ S△NOG 3S
MH 2
△MOH ,∴ .KG 3
设 MH=2x,KG=3x,则 BE=DG=2MH=4x,∴KD=KM=7x,∴HK=5x,∴HG=8x,
∴ HG 8x 2 ……………………………12分
DG 4x
考生须知:
1.全卷分试题卷Ⅰ、试题卷Ⅱ和答题卷.试题卷共 6 页,有三个大题,24 个小题.满分
为 120 分,考试时长为 120 分钟.
2.请将姓名、准考证号等信息分别填写在试题卷和答题卷的规定位置上.
3.答题时,请将试题卷 I 的答案在答题卷 I 上对应的选项位置用 2B 铅笔涂黑、涂满.将
试题卷Ⅱ的答案用黑色字迹的钢笔或签字笔书写,答案必须按照题号顺序在答题卷Ⅱ各题目
规定区域内作答,做在试题卷上或超出答题卷区域书写的答案无效.
4.不允许使用计算器,没有近似计算要求的试题,结果都不能用近似数表示.
试 题 卷 Ⅰ
一、选择题(本大题有 10小题,每小题 3分,共 30分,在每小题给出的四个选项中,只有一项
符合题目要求)
1. 二次根式 x 2中字母 x的取值范围是 ( ▲ )
A.x≥2 B.x≤2 C.x>2 D.x<2
2. 在中国的传统文化中,图案纹饰承载着人们对美好生活的期盼和祝福,下列图案纹饰中是
中心对称图形的是 ( ▲ )
A.团花纹 B.山茶纹 C.鱼纹 D.祥云边三兔纹
3.下列计算正确的是 ( ▲ )
A. 2 5 7 B.5 2 2 2 3 C 2 5 10 D 2 2. . 2
4. 用配方法解方程 x2 4x 10 0时,下列配方结果正确的是 ( ▲ )
A. x 2 2 12 B. x 2 2 12 C. x 2 2 14 D. x 2 2 14
5. 牛顿高度评价反证法在数学证明中的关键作用,认为“反证法是数学家最精当的武器之一”.
用反证法证明“在△ABC中,若∠A>∠B>∠C,则∠C<60°”时,应先假设( ▲ )
A.∠C=60° B.∠C>60° C.∠C≠60° D.∠C≥60°
2024 学年第二学期八年级学业质量检测(数学试卷) 第 1 页 共 6 页
6. 已知一组数据:3,3,4,6,若再添加一个数据 4得到一组新数据,则这组新数据的统计
量不会发生变化的是 ( ▲ )
A.平均数 B.众数 C.中位数 D.方差
7. 2已知反比例函数 y ,下列结论正.确.的是 ( ▲ )x
A.图象必经过点(2,1) B.图象在第二、四象限内
C.y随 x的增大而减小 D.若 x>1,则 y>2
8. 如图,在一个对边平行的纸条上有两点 A,B及线段 AB的中点 O,以下操作和判断不.正.
确.的是 ( ▲ )
A.过点 O作任意直线(除直线 AB)交纸条两边于点 C,D,得到平行四边形 ACBD
B.过点 O作 AB的垂线 l交纸条两边于点 C,D,得到菱形 ACBD
C.分别过点 A,B作对边的垂线,交对边于点 C,D,得到矩形 ACBD
D.在点 A,B所在边的对边分别取 C,D两点,使得 AC=BD,得到平行四边形 ACBD
(第 8题图) (第 9题图) (第 10题图)
9. 如图,在菱形 ABCD中,AD 2 3, BAD 60 ,BD与 AC相交于点O,点 P是线段 AB
上的任意点,以 PB为对角线作平行四边形 POBQ,连结DQ,则DQ的最小值是 ( ▲ )
A. 2 3 B.4 C 9. D. 4 3
2
10. 如图,正方形 EFGH的顶点 E在正方形 ABCD上,四边形 FGKD也是正方形,且点 B,
H,K在同一直线上,则正方形 EFGH与正方形 ABCD的面积比为 ( ▲ )
A. 2 B. 2 1 C. 2 2 D. 3 2
2 2 2 2
2024 学年第二学期八年级学业质量检测(数学试卷) 第 2 页 共 6 页
试 题 卷 Ⅱ
二、填空题(本大题有 6小题,每小题 3分,共 18分)
11. 五边形的内角和为 ▲ .
12. 宁波舟山港作为全球货物吞吐量第一大港,其装卸效率至关重要.四个核心作.业.区.(甬
东、甬南、甬西、甬北)在某周工作日的集装箱平均每小时装卸箱数相同.为了评估各作
业区工作效率的稳定性,统计了其装卸效率的方差如下:S2甬东=25,S2 =36,S2 =64,S2 =16,甬南 甬西 甬北
则装卸效率最稳定的作.业.区.是 ▲ .
13. 已知 x=1是关于 x的一元二次方程 x2+kx+1=0的一个根,则实数 k的值为 ▲ .
14. 如图,DE是△ABC的中位线, ACB的角平分线交 DE于点 F ,若 AC=4,BC=8,则 DF
的长为 ▲ .
(第 14题图) (第 15题图) (第 16题图)
15. 如图,矩形 ABCD k的顶点 A、C在双曲线 y k>0 上,顶点 B、D在 x轴上,AD交 y
x
轴于点 E,若 BO=AB,OE=3,则 k= ▲ .
16. 如图,在 ABCD中,点 E为边 CD的中点,将△ADE沿 AE折叠,边 AD 交 BC的延长
线于点 F,连结 EF,若 AD=5,CF=1,AE= 3 EF,则 AB的长为 ▲ .
三、解答题(本大题有 8小题,共 72分)
17.(本题 8分)计算:
1 12 1( ) 8 (2) 5 1 2 2 10
2
18.(本题 8分)解方程:
(1) x2 2x 8 0 (2) x x 2 6 3x
2024 学年第二学期八年级学业质量检测(数学试卷) 第 3 页 共 6 页
19.(本题 8分)杨梅园组织了“浓情杨梅,果香四溢”的采摘杨梅比赛活动,规定一篮杨梅
标准重量为(1000±10)g,现甲、乙两队各 10名队员参加了比赛,采摘的杨梅每篮重量
如下(单位:g):
甲:987,987,993,993,1000,1003,1003,1003,1013,1015;
乙:988,988,989,999,999,999,1000,1012,1013,1014.
分析数据如表:
队伍 平均数 中位数 众数
甲 999.7 1001.5 a
乙 1000.1 b 999
根据以上信息,解答下列问题:
(1) a ▲ , b ▲ .
(2)若比赛规则规定,采摘的杨梅重量符合标准重量篮数多的一队胜出,请问哪队会胜
出?请说明理由.
20.(本题 8分)如图 1,点 P在∠MAN的平分线上,PB∥AN交 AM于点 B.
任务:用尺规在射线 AN上确定一点 C,使得四边形 ABPC是菱形.
小江:如图 2,以点 A为圆心,AB为半径作弧,交 AN于点 C,连结 PC,则四边形 ABPC
是菱形.
小北:以点 P为圆心,PB为半径作弧,交 AN于点 C,连结 PC,则四边形 ABPC是菱形.
小江:小北,我认为你的作法有问题哦.
小北:是吗?让我想想……哦!我明白了.
(1)证明:小江所作的四边形 ABPC是菱形.
(2)请指出小北作法中存在的问题,并说明理由.
图 1 图 2
2024 学年第二学期八年级学业质量检测(数学试卷) 第 4 页 共 6 页
21.(本题 8分)图 1、图 2均为 4×5的正方形网格,每个小正方形的顶点称为格点,点 A,
B均在格点上,点 P为线段 AB上的一点.(仅用无刻度的直尺作图.)
(1)在图 1中,画出一个以 AB为边的正方形 ABCD(保留作图痕迹).
(2)在(1)的基础上,在边 CD上画点 Q,使得 PQ平分正方形 ABCD的面积(保留作
图痕迹).
(3)在图 2中,画出一个以 AB为边的非正方形的菱形 ABEF(保留作图痕迹),连结此
菱形各边中点所形成的四边形为 ▲ .
图 1 图 2
(第 21题图)
22.(本题 10分)古县城以“青春古城游”为主题,通过科技加持、文化赋能的创新融合,
成功打造了一场现代与传统交织的文旅盛宴.
【科技加持】千架无人机腾空而起,在夜幕绘就“古城星空”,吸引不少游客驻足观看.据
统计,假期第一天古县城累计接待游客约 5万人次,第三天接待游客达 7.2万人次.
(1)求游客人数从假期第一天到第三天的日平均增长率.
【文化赋能】烟火气十足的“去古城赶集”汇集非遗手作,地方美食等,重现古城商贸活
力.如景区推出古城著名景点冰箱贴:每个冰箱贴的成本为 5 元,当售价为 10 元时,平
均每天可售出 500个;当售价每降低 0.5元,平均每天可多售出 25个.
(2)若要使每天销售冰箱贴获利 1800元,则售价应降低多少元?
23. 10 k k 1(本题 分)设函数 y1 , y2 (k>0),当 1≤x≤3时,函数 y1的最小值是 a,x x
函数 y2的最大值是 6a.
(1)求 k的值.
(2)若点 P(m k,n)在函数 y1 的图象上,且点 P到 y轴的距离大于 3,求 n的取值x
范围.
2024 学年第二学期八年级学业质量检测(数学试卷) 第 5 页 共 6 页
(3 3 8 k)一次函数 y x 与函数 y1 的图象在第一象限的交点为点 A,且与 x轴交于11 11 x
点 B,点 C k在函数 y1 位于第一象限的图象上,若 S△AOC=S△AOB,直接写出点 C的横坐标.x
(第 23题图)
24.(本题 12分)我国著名的“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼
成一个大正方形.数学兴趣小组的小伙伴们尝试用两对全等的直角三角形与一个矩形拼出
了一个平行四边形.
(1)如图 1,M是 AB的中点,若 ME=DG,AB=6,求 CG的长.
(2)如图 2,M是 AB的中点,连结 HF,EG交于点 O,连结 OM.
①求证:OM∥AD.
②如图 3,若 AH=HE,取 AD的中点 N,连结 ON,NG,MH,若 S NOG 3S MOH ,
HG
求 的值.
DG
图 1 图 2 图 3
(第 24题图)
2024 学年第二学期八年级学业质量检测(数学试卷) 第 6 页 共 6 页
2024 学年第二学期八年级学业质量检测(数学)
参考答案与评分参考
一、选择题(本大题有 10小题,每小题 3分,共 30分,在每小题给出的四个选项中,只有一
项符合题目要求)
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C D D A A D C C
9. ∵点 O到 AB的距离等于点 Q到 AB的距离,∴Q的轨迹为平行于 AB的线段.
过 Q作直线 l∥AB,当 DQ⊥直线 l时 DQ最小,
∵直线 l∥AB ∴ DM⊥AB
在菱形 ABCD中, AD 2 3, BAD 60 ,∴DM=3.
过 O 3作 ON⊥AB,∴ON= ,
2
又∵ON=QM= 3 ,∴DQ= 9 .
2 2
10. 延长 GF交 DC于点 P,连结 PE. 易证△BEH≌△PDF≌△PEF.
∴CE=CP,设 CP=x,∴CE=CP=x,PE=DP= 2x .
2
∴CD=x+ 2x,∴ 2正方形 = 1+ 2 .
在 Rt△DEC中,CE=x,CD=x+ 2x .
∴DE2=(4+2 2 ) 2.
又∵EF= 1 DE,
2
1
2
x2
1 2 正方形 2 2 2
∴ 2 2 2 正方形 = EF DE 1 x . ∴ = = .4 2
2
正方形 1 2 x2 2
二、填空题(本大题有 6小题,每小题 3分,共 18分)
题号 11 12 13 14 15 16
答案 540° 甬北 -2 2 27 3 2 7
4
15. 过点 A,C作 x轴的垂线,交 x轴于点 P,Q. 连结 AO,CO.
∵AB=CD,易证△APB≌△DCQ
∴CQ=AP,DQ=BP
又∵点 A,C在反比例函数图象上 ∴OP=OQ,
∴O为 BD中点,
又∵OB=AB,OA=OB,
∴△OAB为等边三角形,
∴∠AOB=∠BAO=60°, ∴∠EOA=∠EAO=30°
∴EO=AE= 3, ∴AO= 3 3 ,
3 3 9 27 3
∴A( , ) ∴k= .
2 2 4
16. 如图,延长 AE,BC交于点 G.
在 ABCD中,AD=5,AD∥BC
∴∠DAE=∠G,∠D=∠GCE.
∵点 E是 CD中点, ∴CE=DE.
∴△AED≌△GEC(AAS)
∴CG=AD=5,AE=GE.
∵折叠 ∴∠DAE=∠FAE=∠G , ∴AF=GF.
∵AD=5,CF=1,∴AF= GF=CG-CF=AD-CF=4.
∵AE=GE, ∴FE⊥AG
∵AE= 3 EF, ∴设 EF= x,AE= 3x,
在 Rt△AEF中, 42=x2 ( 3x)2, 解得 x=2. ∴∠FAE=∠DAE=30°.
过点 E作 EH⊥AD.
∵AE= 3x = 2 3, ∴EH= 3,AH=3.
∴DH=5-3=2, ∴DE= DH 2 EH 2 = 7 . ∴CD= 2 7 .
三、解答题(本大题有 8个小题,共 72分)
17.(8分)解:
(1) 1原式= 2 3 8 ……………………………2分
2
2 3 2 ……………………………4分
(2)原式=5 2 5 1 2 5 ……………………………6分
=6 …………………………8分
18.(8分)(1) x2 2x 8 0
x 4 x 2 0
x1 2,x2 4 ……………………………4分
(2) x x 2 6 3x
x x 2 3 2 x
x 2 x 3 0
x1 2,x2 3 ……………………………8分
19.(8分)(1)a=1003,b=999 ……………………………4分
(2)甲队有 6人符合标准重量,乙队有 4人符合标准重量,∴甲队胜. …8分
20. (8分) (1)∵AP平分∠MAN, ∴∠MAP=∠NAP.
∵PB∥AN ∴∠APB=∠NAP.
∴∠MAP=∠APB.
∴AB=PB.
∵由作法可知 AB=AC,
∴AC=PB, 图 2
∴四边形 ABPC是平行四边形.
∵AB=AC ∴平行四边形 ABPC是菱形. …………………………4分
(2)以 P为圆心 PB为半径作弧,与 AN可能会有两个交点,其中只有一个是菱形而另一个
不满足要求. (画图举反例也给 4分) ……………………………8分
21. (8分)(1)见下(1)图 ……………………………2分
(2)见下(2)图 ……………………………4分
(3)见下(3)图;矩形
菱形图 2分;答案“矩形”2分,若回答“平行四边形”则给 1分. ………8分
(1)图 (2)图 (3)图
22. (10分)(1)设日平均增长率为 x,
5(1 x)2 7.2 解得 x1 0.2, x2 2.2(舍)
答:日平均增长率为 20%. ……………………………4分
(2)设售价降低 a元,
10 5 a 500 50a 1800,解得 a1=2, a2 7(舍)
答:售价应降低 2元. ……………………………10分
23(1)∵k>0,k+1>0,1≤x≤3,
∴在每一象限内,y1随 x的增大而减小,y2随 x的增大而减小,
∴当 x=3时,y1最小值为 =a,①;3
当 x=1时,y2最大值为 + 1 = 6a,②;
由①,②得:k=1. ……………………………3分
(2)∵P(m,n)到 y轴的距离大于 3,
∴m<-3 或 m>3
∵y1=
1
1 1
∴ - <n<0或 0<n< ……………………………7分
3 3
(3 3 8 k)一次函数 y x 与函数 y1 的图象在第一象限的交点为点 A,且与 x轴交于点11 11 x
B,
8
∴A(1,1),B(- ,0) ∴S 4△AOB= ,3 3
又∵ S△AOC=S
4
△AOB= .3
①当点 C在 A点的右侧
设 C(m 1, ),过 A,C分别关于 x轴作垂线交于点 M、N,
m
∵ S 4△AOC= S直角梯形ACNM = ,3
1
∴ 1 m m 1 4 ,
2 3
1
∴m1 3, m2 (舍).3
①当点 C在 A点的左侧
设 C 1(m, ),过 A,C分别关于 x轴作垂线交于点 M、N,
m
∵ S△AOC= S
4
直角梯形ACNM = ,3
1 1 4
∴ 1 1 m ,
2 m 3
m 3 m 1∴ 1 (舍), 2 3
1
所以点 C的横坐标为 3或 . (写出一个正确答案给 2分) ………………………10分
3
24. (1)∵△ABE是直角三角形,点 M是 AB中点,
∴AM=BM=ME=DG= 1 AB=3.
2
∵△ABE≌△CDG,∴BE=DG=3,
∴∠ABE=60°
∴CG=AE= 3 3 . ……………………………4分
(2)①连结 OB,OD,
∵OE=OG,BE=DG,∠BEO=∠DGO,
∴△BOE≌△DOG,
∴∠BOE=∠DOG,OB=OD,
∴B,O,D三点共线.
∵点 M是 AB中点,
∴OM是△ABD的中位线,
∴OM∥AD. ……………………………8分
②∵AH=HE,M是 AB中点,
∴MH是△ABE的中位线.
∴MH∥BE,BE=2MH.
设 ON与 MD交于点 K,作△MOH的高 h1,△NKG的高 h2 ,
易证 h1= h2 .
S 1∵ △MOH MH h
1
1, S2 △NOG
KG h1 h2 ,2
又∵ S△NOG 3S
MH 2
△MOH ,∴ .KG 3
设 MH=2x,KG=3x,则 BE=DG=2MH=4x,∴KD=KM=7x,∴HK=5x,∴HG=8x,
∴ HG 8x 2 ……………………………12分
DG 4x
同课章节目录
