初中数学北师大版八年级下册 第一章 三角形的证明---三角形全等之半角模型专题复习(无答案)
文档属性
| 名称 | 初中数学北师大版八年级下册 第一章 三角形的证明---三角形全等之半角模型专题复习(无答案) | 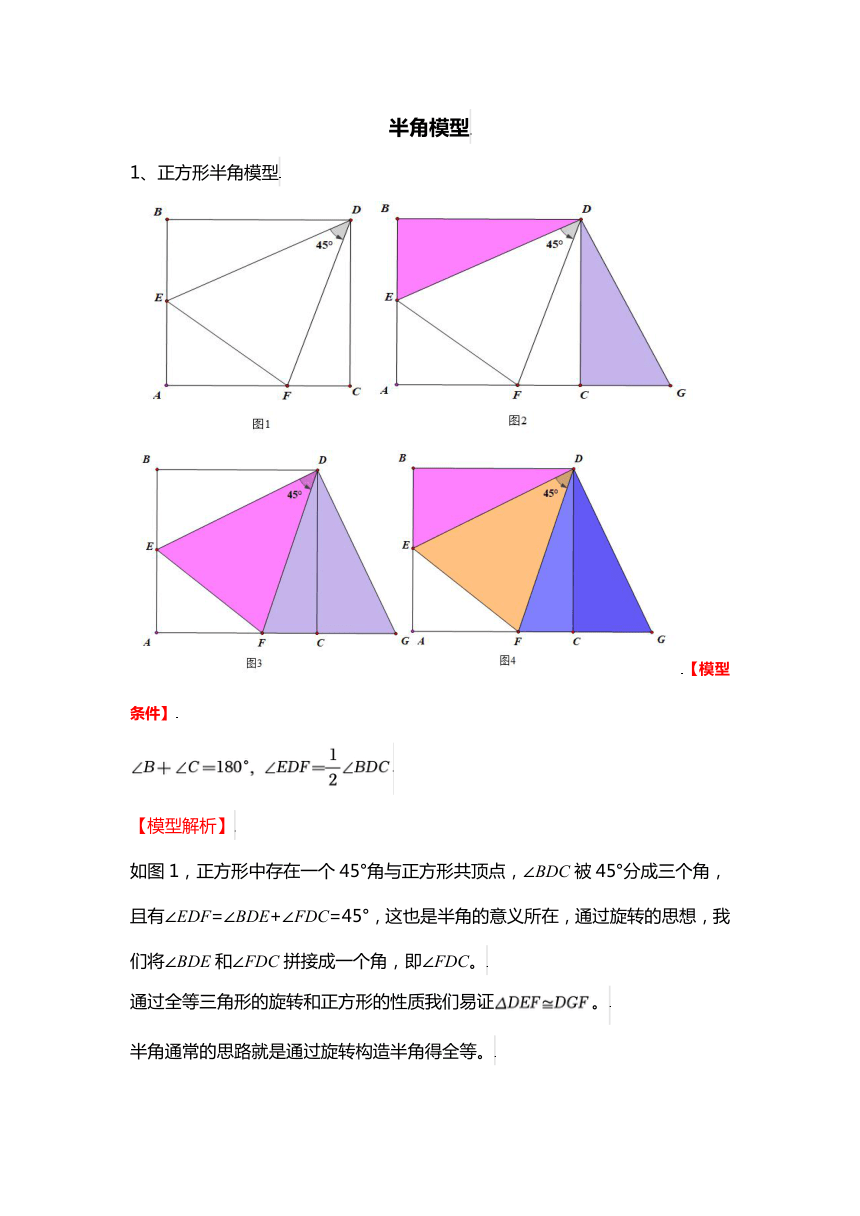 | |
| 格式 | docx | ||
| 文件大小 | 344.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-27 08:44:17 | ||
图片预览


文档简介
半角模型
1、正方形半角模型
【模型条件】
【模型解析】
如图1,正方形中存在一个45°角与正方形共顶点,∠BDC被45°分成三个角,且有∠EDF=∠BDE+∠FDC=45°,这也是半角的意义所在,通过旋转的思想,我们将∠BDE和∠FDC拼接成一个角,即∠FDC。
通过全等三角形的旋转和正方形的性质我们易证。
半角通常的思路就是通过旋转构造半角得全等。
【模型总结】
①;②DF平分∠EAG;③
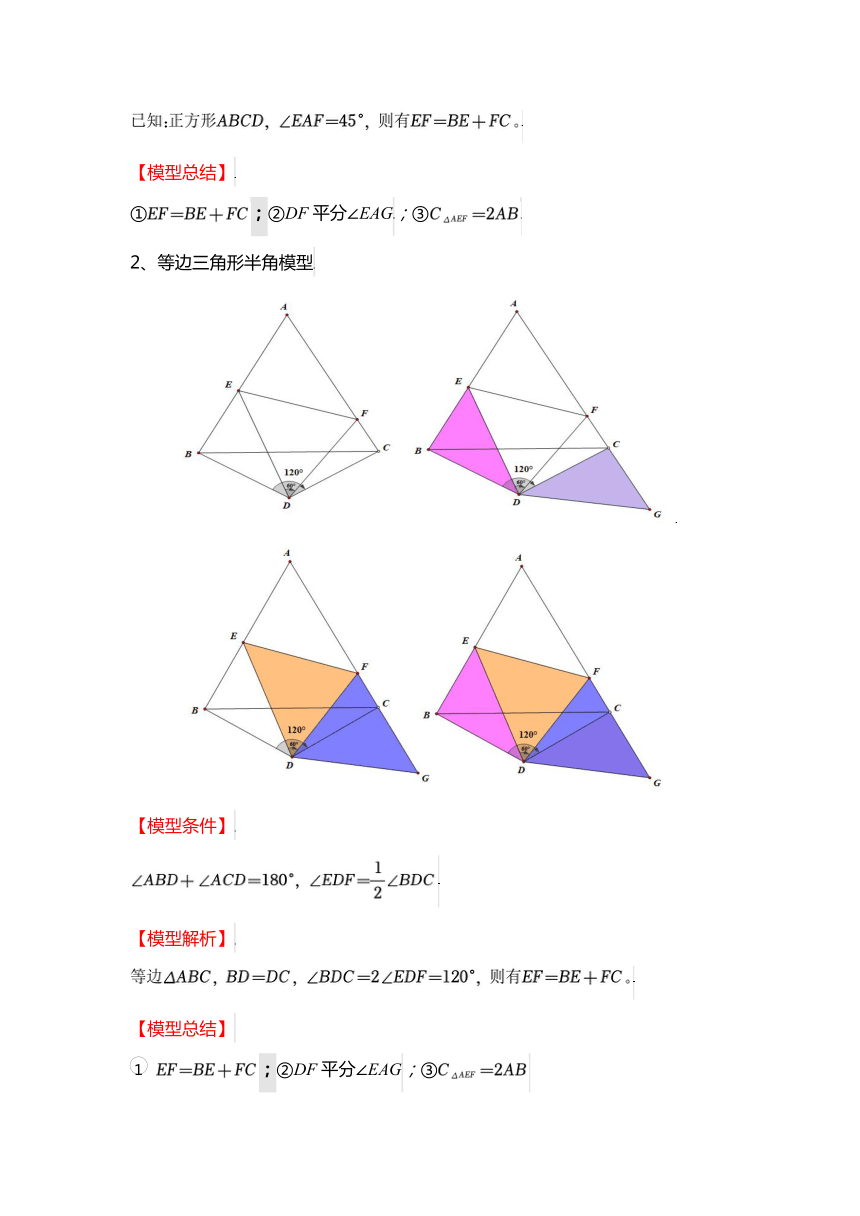
2、等边三角形半角模型
【模型条件】
【模型解析】
【模型总结】
;②DF平分∠EAG;③
【例1】正方形ABCD中,E,F分别是边BC,CD上的点,且∠EAF=45°,将△ABE绕点A逆时针旋转90°,得到△ADG,求证:EF=BE+DF.
【例2】如图,正方形ABCD中,∠EAF的两边分别与边BC、CD交于点E、F,AE、AF分别交BD于点G、H,且∠EAF=45°.
(1)当∠AEB=55°时,求∠DAH的度数;
(2)设∠AEB=α,则∠AFD= (用含α的代数式表示);
(3)求证:∠AEB=∠AEF.
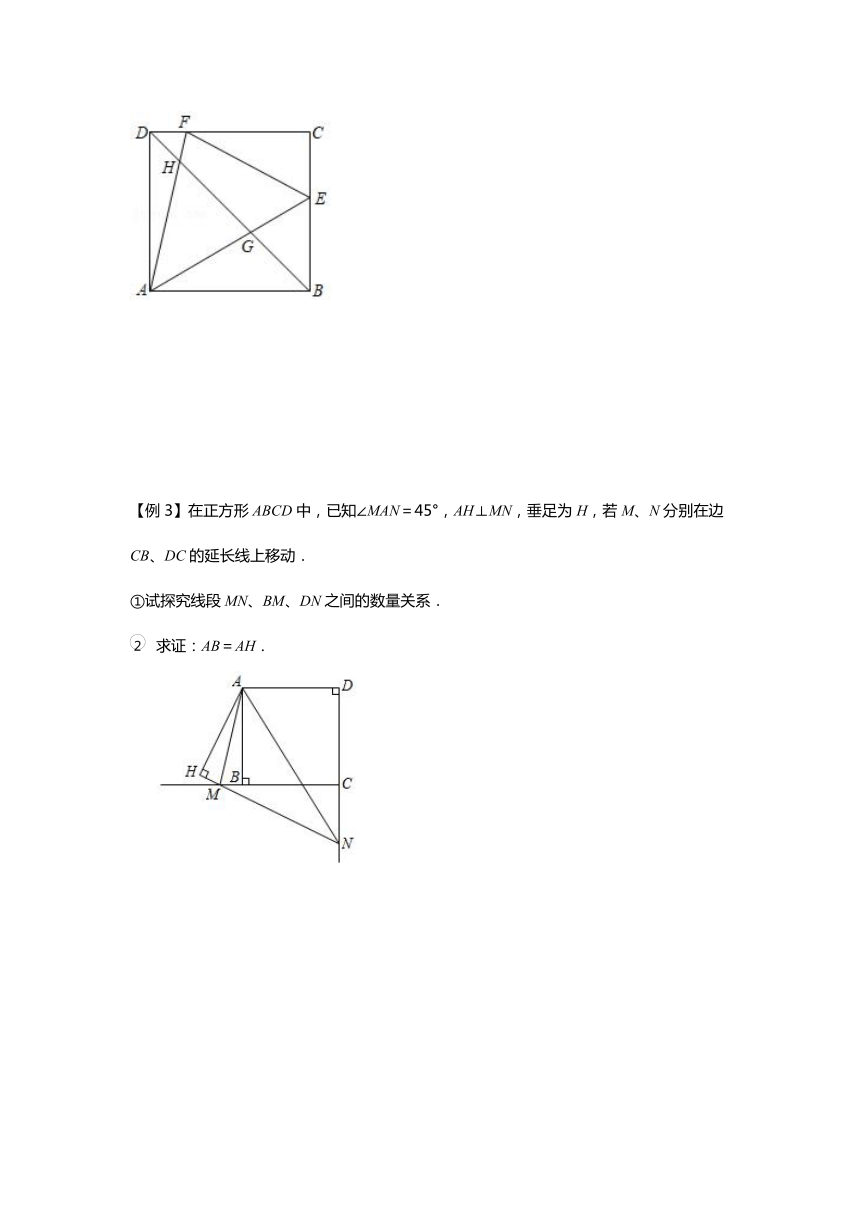
【例3】在正方形ABCD中,已知∠MAN=45°,AH⊥MN,垂足为H,若M、N分别在边CB、DC的延长线上移动.
①试探究线段MN、BM、DN之间的数量关系.
求证:AB=AH.
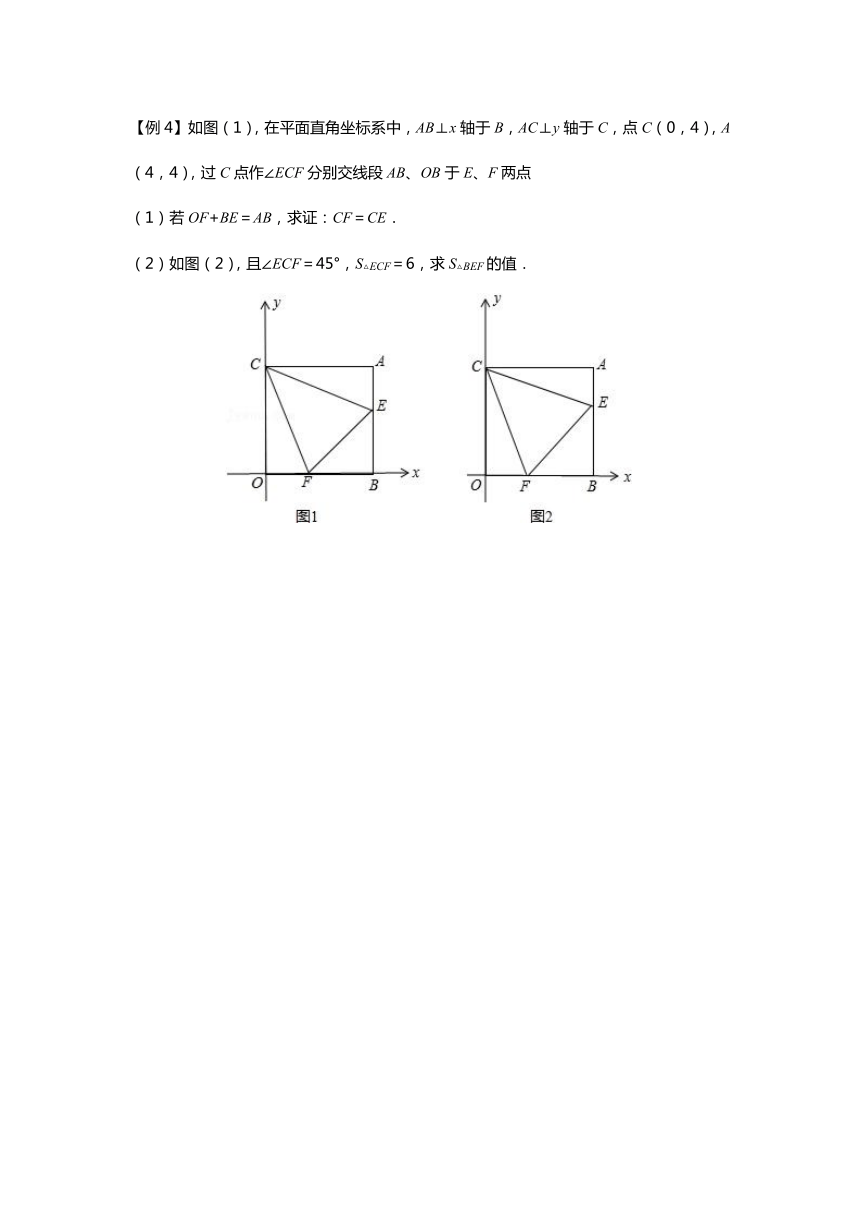
【例4】如图(1),在平面直角坐标系中,AB⊥x轴于B,AC⊥y轴于C,点C(0,4),A(4,4),过C点作∠ECF分别交线段AB、OB于E、F两点
(1)若OF+BE=AB,求证:CF=CE.
(2)如图(2),且∠ECF=45°,S△ECF=6,求S△BEF的值.
【例5】如图,在正方形ABCD中,M、N分别是射线CB和射线DC上的动点,且始终∠MAN=45°.
(1)如图1,当点M、N分别在线段BC、DC上时,请直接写出线段BM、MN、DN之间的数量关系;
(2)如图2,当点M、N分别在CB、DC的延长线上时,(1)中的结论是否仍然成立,若成立,给予证明,若不成立,写出正确的结论,并证明;
(3)如图3,当点M、N分别在CB、DC的延长线上时,若CN=CD=6,设BD与AM的延长线交于点P,交AN于Q,直接写出AQ、AP的长.
【例6】(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD.求证:EF=BE+FD.
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出线段EF、BE、FD它们之间的数量关系,并证明.
(3)如图3,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出线段EF、BE、FD它们之间的数量关系,并证明.
【例7】如图,△ABC与△CDE均为等腰直角三角形,其中∠ACB=∠CDE=90°,AC=BC,CD=DE,且BC=BD,边BD交CE于点F,连接AD.
(1)如图1,连接BE,若AD=4,求BE的长;
(2)如图2,若点F为BD的中点,求证:AD=2EF.
【例8】在等边△ABC的两边AB,AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB,AC上移动时,BM, NC,MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系,
如图1,△ABC是周长为9的等边三角形,则△AMN的周长Q=_______
如图2,当点M,N边AB,AC上,且DM=DN时,BM,NC,MN之间的数量关系是______;=_______点M,N在边AB,AC上,且当DM≠DN时,猜想(2)问的两个结论还成立吗?写出你的猜想并加以证明.
【例9】如图,已知△ABC中,∠BAC=90°,AB=AC,D,E是BC边上的点,将△ABD绕点A旋转,得到△,当∠DAE=45°时,求证:DE=;在(1)的条件下,猜想:有怎样的数量关系?请写出,并说明理由.
1、正方形半角模型
【模型条件】
【模型解析】
如图1,正方形中存在一个45°角与正方形共顶点,∠BDC被45°分成三个角,且有∠EDF=∠BDE+∠FDC=45°,这也是半角的意义所在,通过旋转的思想,我们将∠BDE和∠FDC拼接成一个角,即∠FDC。
通过全等三角形的旋转和正方形的性质我们易证。
半角通常的思路就是通过旋转构造半角得全等。
【模型总结】
①;②DF平分∠EAG;③
2、等边三角形半角模型
【模型条件】
【模型解析】
【模型总结】
;②DF平分∠EAG;③
【例1】正方形ABCD中,E,F分别是边BC,CD上的点,且∠EAF=45°,将△ABE绕点A逆时针旋转90°,得到△ADG,求证:EF=BE+DF.
【例2】如图,正方形ABCD中,∠EAF的两边分别与边BC、CD交于点E、F,AE、AF分别交BD于点G、H,且∠EAF=45°.
(1)当∠AEB=55°时,求∠DAH的度数;
(2)设∠AEB=α,则∠AFD= (用含α的代数式表示);
(3)求证:∠AEB=∠AEF.
【例3】在正方形ABCD中,已知∠MAN=45°,AH⊥MN,垂足为H,若M、N分别在边CB、DC的延长线上移动.
①试探究线段MN、BM、DN之间的数量关系.
求证:AB=AH.
【例4】如图(1),在平面直角坐标系中,AB⊥x轴于B,AC⊥y轴于C,点C(0,4),A(4,4),过C点作∠ECF分别交线段AB、OB于E、F两点
(1)若OF+BE=AB,求证:CF=CE.
(2)如图(2),且∠ECF=45°,S△ECF=6,求S△BEF的值.
【例5】如图,在正方形ABCD中,M、N分别是射线CB和射线DC上的动点,且始终∠MAN=45°.
(1)如图1,当点M、N分别在线段BC、DC上时,请直接写出线段BM、MN、DN之间的数量关系;
(2)如图2,当点M、N分别在CB、DC的延长线上时,(1)中的结论是否仍然成立,若成立,给予证明,若不成立,写出正确的结论,并证明;
(3)如图3,当点M、N分别在CB、DC的延长线上时,若CN=CD=6,设BD与AM的延长线交于点P,交AN于Q,直接写出AQ、AP的长.
【例6】(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD.求证:EF=BE+FD.
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出线段EF、BE、FD它们之间的数量关系,并证明.
(3)如图3,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出线段EF、BE、FD它们之间的数量关系,并证明.
【例7】如图,△ABC与△CDE均为等腰直角三角形,其中∠ACB=∠CDE=90°,AC=BC,CD=DE,且BC=BD,边BD交CE于点F,连接AD.
(1)如图1,连接BE,若AD=4,求BE的长;
(2)如图2,若点F为BD的中点,求证:AD=2EF.
【例8】在等边△ABC的两边AB,AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB,AC上移动时,BM, NC,MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系,
如图1,△ABC是周长为9的等边三角形,则△AMN的周长Q=_______
如图2,当点M,N边AB,AC上,且DM=DN时,BM,NC,MN之间的数量关系是______;=_______点M,N在边AB,AC上,且当DM≠DN时,猜想(2)问的两个结论还成立吗?写出你的猜想并加以证明.
【例9】如图,已知△ABC中,∠BAC=90°,AB=AC,D,E是BC边上的点,将△ABD绕点A旋转,得到△,当∠DAE=45°时,求证:DE=;在(1)的条件下,猜想:有怎样的数量关系?请写出,并说明理由.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
