【暑假专项培优】专题13 数轴与动点行程问题—小升初奥数思维之典型应用题精讲精练讲义(通用版)
文档属性
| 名称 | 【暑假专项培优】专题13 数轴与动点行程问题—小升初奥数思维之典型应用题精讲精练讲义(通用版) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-26 15:30:59 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
小升初奥数思维之典型应用题精讲精练讲义(通用版)
专题13 数轴与动点行程问题
【第一部分:知识归纳】
一、基本概念
1、数轴与动点行程问题是借助数轴研究点的运动规律的行程问题。
2、特点:
(1)直观性强:运动过程可在数轴上清晰展示
(2)方向明确:正方向表示正向运动,负方向表示反向运动
(3)位置精确:点的位置可用具体数值表示
3、核心要素
(1)原点:数轴的基准点(通常记为0)
(2)动点:在数轴上运动的点
(3)运动方向:向右为正方向,向左为负方向
(4)运动速度:单位时间内移动的单位长度
二、基本公式与关系
1. 位置计算公式
t时刻的位置 = 初始位置 ± 速度 × 时间
("+"表示正方向运动,"-"表示负方向运动)
2. 相遇条件
两个动点位置相同:P (t) = P (t)
3. 追及条件
同向运动时,后面的点位置赶上前面的点
三、常见题型与解题方法
1. 单动点基础问题
例题:点A从数轴原点出发,以每秒2个单位的速度向右运动。5秒后A点的位置是多少?
解答:位置 = 0 + 2×5 = 10
2. 双动点相遇问题
例题:点P从+3出发以1单位/秒向左运动,点Q从-5出发以2单位/秒向右运动。它们何时相遇?
解答:设t秒后相遇:
3 - 1t = -5 + 2t
8 = 3t
t = 8/3秒 ≈ 2.67秒
3. 动点往返问题
例题:第一阶段:-2 + 3×4 = 10
第二阶段:10 - 2×3 = 4
最终位置:4
四、解题技巧
1、画数轴示意图:标出初始位置和运动方向
2、建立时间轴:记录各时间段运动情况
3、分段计算:对变速运动分段处理
4、代数方法:设未知数列方程求解
5、单位统一:确保时间和速度单位一致
【第二部分:能力提升】
1.一个圆周长70厘米,甲、乙两只爬虫从同一点同时出发,同向爬行。甲以4厘米/秒的速度不停地爬行,乙爬行15厘米后,立即反向爬行,并且速度增加1倍。如果乙在离出发点10厘米处与甲第一次迎面相遇,则乙爬虫原来的速度是多少厘米/秒
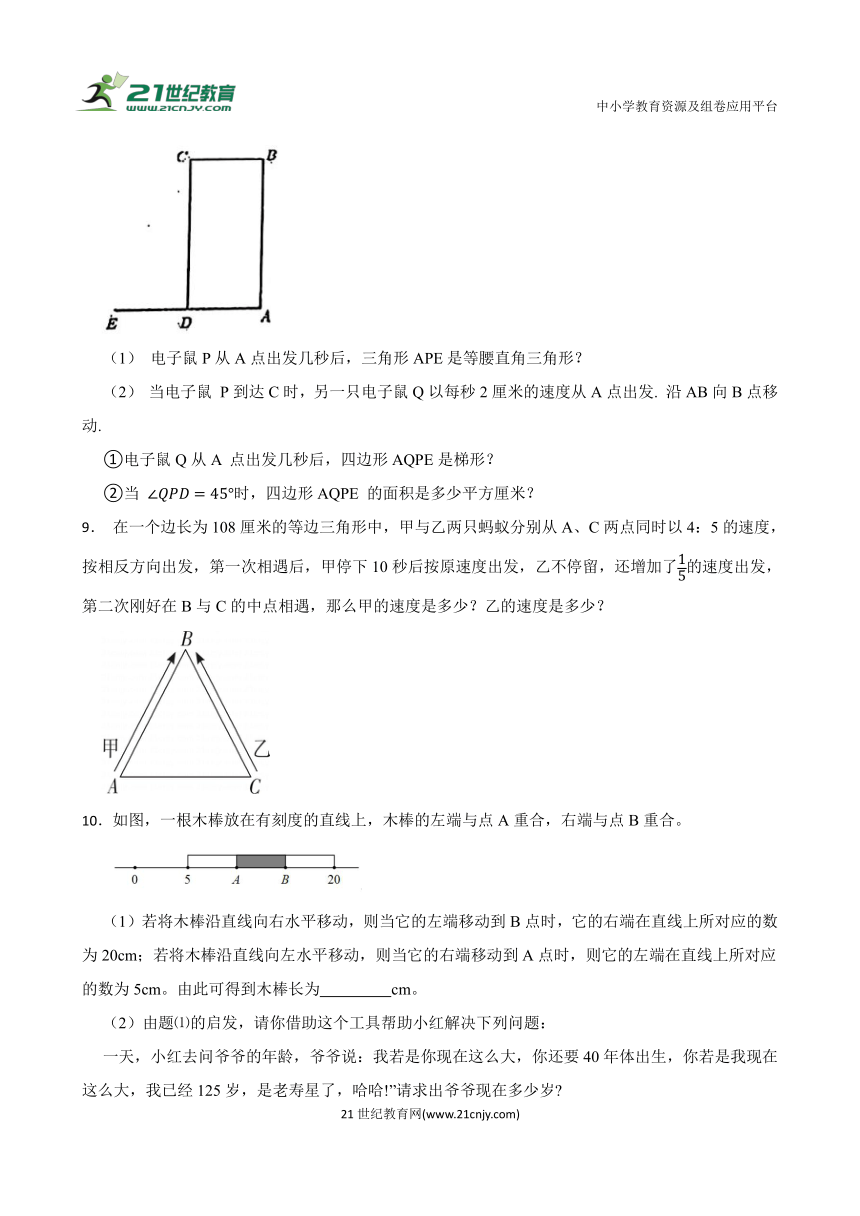
2.学习编程的奇奇最近编写了一套程序.让一只电子鼠P从长方形ABCD的点A出发,沿着长方形的边依次向B,C,D以每秒1厘米的速度移动.已知AB=12厘米,ED=DA=6厘米。
(1)电子RP从A点出发几秒后,三角形APE是等腰直角三角形
(2)当电子鼠P到达C时,另一只电子鼠Q以每秒2厘米的速度从A点出发.沿AB向B点移动.
①电子鼠Q从A点出发几秒后,四边形AQPE是梯形
②当∠QPD=45°时,四边形AQPE的面积是多少平方厘米
3.学习编程的奇奇最近编写了一套程序,让一只电子鼠P从长方形ABCD的点A出发,沿着长方形的边依次向B、C、D以每秒1厘米的速度移动,已知厘米,厘米,
(1)电子鼠P从A点出发几秒后,三角形APE是等腰直角三角形
(2)当电子鼠P到达C时,另一只电子鼠Q以每秒2厘米的速度从A点出发,沿AB向B点移动,
①电子鼠Q从A点出发几秒后,圆边形AQPE是梯形
②当∠QPD=45°时,四边形AQPE的面积是多少平方厘米
4. 两只蚂蚁同时从一个等腰三角形的顶点出发(如右下图),分别沿两腰爬行,一只蚂蚁每分钟爬行0.2米,另一只蚂蚁每分钟爬行0.25米,经过50分钟,在离底边的一端7.5米的地方相遇。这个地方离底边的另一端有多少米?
5.如图,81个边长为1的小正方形组成正方形ABCD,我们把小正方形的顶点都称为格点。
(1)若在正方形ABCD的四个角处都剪掉四个相等的小正方形后,剩余部分恰好能折叠成一个无盖的正方体,求出该正方体的体积。
(2)蚂蚁要沿着小正方形的边从点A出发爬到点C,只能向右或向上爬,速度是每秒钟爬两个单位,请说明:蚂蚁爬达终点的时间是否会随着爬行路径的不同而发生变化?若发生变化,说明理由;若不发生变化,求出这个时间。
(3)真真和诚诚利用该正方形ABCD做游戏,规定从A点出发,每次只能沿小正方形的边向右或向上走,每次只能走1个或两个单位长度,谁先到达C点谁获胜。真真先走,诚诚后走。请问:两个同学中谁有必胜把握?怎样操作才能必胜?
6.如图所示,甲从A点出发,在AD之间不断往返行走。乙从B点出发,沿着B—E—C—B围绕等边三角形BEC不断行走,已知AB=80米,BE=EC=CB=100米,CD=120米,甲的速度是5米/秒,乙的速度是4米/秒,问:甲第一次从背后追上乙的地点离B点多少米?
7.如图, 在长方形 ABCD中, . 点P从点A出发, 沿A—B—C—D路线运动,到D停止:点P的速度为每秒 1cm,a秒时点P的速度变为每秒 bcm,图②是点P出发x秒后。 的面积 与x(秒) 的关系图象;
(1) 根据图像提供的信息, = 。
(2) 点P出发后几秒, 的面积; 是长方形ABCD 面积的四分之一?
8.学习编程的奇奇最近编写了一套程序,让一只电子鼠P从长方形ABCD的点A 出发,沿着长方形的边依次向B,C,D以每秒1厘米的速度移动. 已知 厘米, 厘米.
(1) 电子鼠P从A点出发几秒后,三角形APE是等腰直角三角形?
(2) 当电子鼠 P到达C时,另一只电子鼠Q以每秒2厘米的速度从A点出发. 沿AB向B点移动.
①电子鼠Q从A 点出发几秒后,四边形AQPE是梯形?
②当 时,四边形AQPE 的面积是多少平方厘米?
9. 在一个边长为108厘米的等边三角形中,甲与乙两只蚂蚁分别从A、C两点同时以4:5的速度,按相反方向出发,第一次相遇后,甲停下10秒后按原速度出发,乙不停留,还增加了的速度出发,第二次刚好在B与C的中点相遇,那么甲的速度是多少?乙的速度是多少?
10.如图,一根木棒放在有刻度的直线上,木棒的左端与点A重合,右端与点B重合。
(1)若将木棒沿直线向右水平移动,则当它的左端移动到B点时,它的右端在直线上所对应的数为20cm;若将木棒沿直线向左水平移动,则当它的右端移动到A点时,则它的左端在直线上所对应的数为5cm。由此可得到木棒长为 cm。
(2)由题⑴的启发,请你借助这个工具帮助小红解决下列问题:
一天,小红去问爷爷的年龄,爷爷说:我若是你现在这么大,你还要40年体出生,你若是我现在这么大,我已经125岁,是老寿星了,哈哈!”请求出爷爷现在多少岁
11.如图,在射线OM上有三点A,B,C,满足OA=20cm,AB=60cm,BC=10cm(如图所示),点P从点O出发,沿OM方向以1cm/s的速度匀速运动,点Q从点C出发在线段CO上向点O匀速运动,两点同时出发。
(1)当P在线段AB上,且PA=2PB时,点Q运动到的位置恰好是线段AB的三等分点,求点Q运动的速度;
(2)若点Q运动的速度为3cm/s,经过多长时间P、Q两点相距70cm;
(3)当点P运动到线段AB上时,分别取OP和AB的中点E,F,求的值。
12.点M,N在数轴上分别表示有理数m,n且满足(m+4)2+|n-4|=0。现将数轴在点M,N处剪断,再用绳子将它们连接,就可得到如图所示的“拱形数轴",其中点S为绳子上一点且满足MS=NS,在此数轴上,我们定义任意两点的距离为它们之间折线段的长度之和,如图1,A,两点的距离为线段A的长,记为DAM=AM,记A,B两点的距离为DAB=BN+NS+SM+MA。
(1)请直接写出m= ,n= ;
(2)若MS=6,点B在数轴上表示有理数6,一动点P从点M出发以每秒3个单位长度沿“拱形数轴”
向正方向运动,同时,另一动点Q从点B出发以每秒1个单位长度沿“拱形数轴”向负方向运动,两个点运动到点S处均停止,设运动时间为t秒,请间t取何值时,使得DPN+DQN=DMN-2。
(3)如图2,已知MS=9,动点P从点川出发以每秒2个单位长度沿着“拱形数轴”向正方向运动,同时点Q从点N出发,以每秒1个单位长度沿着“拱形数轴”向负方向运动:两点相遇后,点P速度立即变为原来的一半并沿着“拱形数轴”向负方向运动,同时点Q保持速度不变并沿着“拱形数轴”向正方向运动,设运动时间为t秒,是否存在t使得DPM=3DQN?如果存在,请直接写出出t的值,如果不存在,请说明理由。
13.如图,点M,N分别是边长为4米的正方形ABCD的一组对边AD,BC 的中点,P,Q两个动点同时从M出发,P沿正方形的边逆时针方向运动,速度是1米/秒;Q沿正方形的边顺时针方向运动,速度是2米/秒。求:
(1)第1秒时 的面积;
(2)第15 秒时 的面积;
(3)第2015 秒时 的面积。
14.如图,O是数轴的原点,A、B是数轴上的两个点,A点对应的数是-1,B点对应的数是8,C是线段AB上一点,满足。
(1)求C点对应的数;
(2) 动点M从A点出发,以每秒2个单位长度的速度沿数轴向右匀速运动,当点M到达C点后停留2秒钟,然后继续按原速沿数轴向右匀速运动到B点后停止。在点M从A点出发的同时,动点N从B点出发,以每秒1个单位长度的速度沿数轴匀速向左运动,一直运动到A点后停止.设点N的运动时间为t秒。问当时,求t的值?
15.如图,已知点A、B、C是数轴上三点,点C表示的数为3,BC=2,AB=6.
(1)数轴上点A表示的数为 ,点B表示的数为 ;
(2)动点P、Q分别从点A、C同时出发,点P以每秒2个单位长度的速度沿数轴向右匀速运动,点Q以每秒1个单位长度的速度沿数轴向左匀速运动,M为AP的中点,点N在线段CQ上,且,设运动时间为秒。
①求数轴上M、N表示的数;(用含t的式子表示)
②当t为何值时,原点O恰好是线段PQ的中点
16.如图,在长方形ABCD 中,AB=12cm,AD-=8cm。点P、Q都从点A同时出发,点P向B点运动,点Q向D点运动,且保持,AP=AQ,在这个变化过程中,图中阴影部分的面积液随之变化,当AP由2cm变到8cm时,图中阴影部分的面积是增加了,还是减少了?增加或减少了多少平方厘米?
17. 一点从数轴上表示-2的点开始移动,第一次先向左移动1个单位长度,再向右移动2个单位长度:第二次向左移动2个单位长度,向右移动4个单位长度;第三次先向左移动3个单位长度,再向右移动6个单位长度……求:
(1)写出第一次移动后点在数轴上对应的数;
(2) 写出第二次移动后点在数轴上对应的数:
(3) 写出第三次移动后点在数轴上对应的数;
(4)按上述规律第次移动后点在数轴上对应的数
18.如图,在正方形ABCD中,AB=BC=CD=AD=4cm,动点P从点A出发,以2cm/s速度沿AB—BC—CD—DA的线路运动,同时动点Q从B出发,以1cm/s的速度沿BC—CD的线路运动,设运动的时间为t(s)。()
(1)当点P在AB—BC上运动时,
①用含t的代数式表示线段BP的长度。
②当BQ=2BP时,求t的值。
(2)动点M从D点出发,以每秒4cm/s的速度在线段DC上作往返运动,点M与点P同时出发,当点P停止运动时,点M也停止运动,连接PQ,
③当点P与点M第一次重合时,求t的值,并直接写出此时线段DP的长度。
④当点M落在线段PQ上时,直接写出t的取值范围。
19. 如图①, 在长方形 ABCD中, AB=10cm, BC=8cm, 点P从A出发,沿 A→B→C→D路线运动,到D停止; 点P出发时的速度为每秒1cm,a秒时点P的速度变为每秒 bcm,图②是点 P出发x秒后,△APD的面积S(c㎡) 与x(s) 的函数关系图象.
(1)根据题目中提供的信息,求出图②中a,b,c的值;
(2) 设点P运动的路程为 y(cm)
①7s时, y的值为 cm;
②请写出当点P改变速度后,y与x的函数关系式 ;
(3)当点P出发后几秒时,△APD的面积S是长方形 ABCD面积的 ?
20.如图①,在长方形ABCD中,AB=10cm, BC=8cm, 点P从A出发,沿A、B、C、D路线运动,到D停止;点P的速度为每秒1cm,a秒时点P中的速度变为每秒b厘米;图②是点P出发x秒后,△APD的面积S(Cm2)与×(s)的变化关系图象。根据图②中提供的信息,求a、b及图②中c的值。
21.如图,正方形ABCD的边长为2cm,点E是CD边的中点,正方形ABCD边上的一动点P从点A出发(不与点A重合),沿方向运动(不与点E重合),设点P运动路程为xcm,探究:
(1)当点P运动到与点B重合时,三角形APE的面积为 平方厘米。
(2)在正方形ABCD的边上是否存在点P,使三角形APE的面积为平方厘米?若存在,请求出x的值;若不存在,请说明理由。
22.如图,在直线上有 A、O、B三点,其中 AO=2cm,B0=6cm,若在点O处放一挡板,一小球甲从点A处以1个厘米1秒的速度向左移动:同时另一小球乙从点B处以2厘米/秒的速度也向左移动,在碰到挡板后(忽略球的大小,可看作一点)以原来速度的 1.5倍向相反的方向运动,设运动的时间为t(秒),
(1)当t=10时,求甲,乙两小球到0点的距离;
(2)当t为何值时,甲、乙两小球到0点的距离相等.
23.如图为一个阶梯的纵截面,一只老鼠沿长方形的两边A→B→D路线逃跑,一只猫同时沿阶梯(折线)A→C→D的路线去做捉,结果在距离点C点1.5米的D处,猫捉住了老鼠,已知老鼠的速度是猫的,问阶梯A→C的长度是多少米
24.如图,正方形ABCD的边长为2cm,在对称中心O处有一钉子。动点P、Q同时从点A出发,点P沿A~B~C~D方向以每秒2cm的速度运动,到点D停止:点Q沿A~D方向以每秒1cm的速度运动,到点D停止。P、Q两点用一条可伸缩的细橡皮筋连接,设x秒后橡皮筋扫过的面积为y。
(1)当橡皮筋刚好触及钉子时,求x的位。
(2)当时y的值。
(3)在橡皮筋从触及钉子到运动停止的过程中,直接写出∠POQ为直角时x的数值。
25.如图①,在长方形ABCD中, AB=10cm, BC=8cm,点P从A出发,沿A、B、C、 D路线运动,到D停止;点P的速度为每秒1cm, a秒时点P中的速度变为每秒b厘米;图②是点P出发x秒后,△APD的面积3(cm2 )与x (s)的变化关系图像。根据图②中提供的信息,求a、 b及图②中c的值。
26.8点 10 分, 有甲乙两人以相同的速度分别从相距 60 米的 两地按顺时针方向沿长方形 ARCD的边走向D点, 如下图, 甲 8 点 20 分到 D点后, 丙、丁两人立即以相同速度从D点出发。丙由D点向A点走去, 8 点24分与乙在E点相遇; 丁由D点向C点走去, 8 点 30 分在 F点被乙追上, 求 的面积?
27.阅读理解:线段上的一点把线段分成相等的两部分,这个点叫作线段的中点。如图①,P点是线段MN的中点,则 如图②,B点是线段AD上的一个动点,从A点到D点以2cm/s的速度运动,C点是线段 BD的中点,
(1)当B点的运动时间是x秒时, cm,BD= cm。
(2)B点的运动时间是x秒,当 时, cm。
(3)如图③,在运动过程中,E点是线段AB的中点。下面小凯的说法正确吗? 说一说你的想法。
参考答案及试题解析
1.解:离出发点 10 cm有甲爬行10 cm,70-10=60cm,70+10=80cm 三种情况。
(1)当甲爬行10 cm时,甲所用的时间为
乙在此过程中分为两个阶段,第一阶段乙爬行15 cm,第二阶段爬行:
两段速度比为1∶2
两段路程比为3:1
两段时间比为
第一段乙用时 乙原来速度为
(2)当甲爬行60 厘米时,甲所用时间为
乙在此过程中分为两个阶段,第一阶段乙爬行15 cm,第二阶段爬行
两段速度比为1 :2,两段路程比为:
两段所用时间比 第一阶段乙用
乙原来的速度:
⑶当甲爬行80cm时,甲所用的时间为
乙在此过程中分为两个阶段,第一阶段乙爬行15 cm,第二阶段乙爬行15-10=5(cm)。
两段速度比1:2,路程比为15:5 = 3 :1。
两段所用时间比 第一阶段乙用了
乙原来的速度为
因此,乙爬虫原来的速度为7cm/s或- 或
【解析】为了解决这个问题,我们需要分析甲和乙的爬行过程,特别是在它们第一次相遇时的情况。由于甲和乙的速度不同,以及乙的速度变化和方向改变,我们需要分情况讨论,分别计算在不同情况下乙的原始速度。
2.(1)解:当电子鼠P爬到和B点重合时,AB=12厘米,故此时需要的时间为12秒。
当爬到CD边的中点时AB=12厘米,BC=DA=6厘米,故此时需要的时间为24秒。
答: 从A点出发12;24秒后
(2)解: ①设电子鼠Q从A点出发x秒后四边形AQPE是梯形。因此当P和Q在同一条直线上时,四边形AQPE成为梯形。此时,AP=12-x,AQ=2x,
12-x=2x
解得:x=4
答: 出发4秒后,四边形AQPE是梯形
②当∠QPD=45度时,PF=FQ=DA=6厘米,PC+AQ=6厘米。AQ=2PC。解这个方程,AQ=4厘米。
四边形AQPE可以分割成一个梯形AQPD和一个三角形PDE,其面积分别为42平方厘米和30平方厘米,因此四边形AQPE的面积为72平方厘米。
答: 四边形AQPE的面积是72平方厘米
【解析】(1)首先要理解等腰直角三角形的定义,然后分析出有两种情况:爬到和B点重合;爬到CD边的中点,进行计算即可。
(2)首先,通过解析电子鼠P的移动路径,确定它何时会与长方形的顶点B、C、D重合,从而计算出等腰直角三角形APE的形成时间。对于第二个问题,首先确定电子鼠Q出发的时间,并分析它在移动过程中四边形AQPE何时会变成梯形。最后,利用几何知识计算出四边形AQPE的面积。
3.(1)解:如图
当电子鼠P爬到和B点重合时,三角形APE第一次成为等腰直角三角形,需要:12+1=12 (秒)
当爬到CD边的中点时,三角形APE第二次成为等腰直角三角形,需要: (12+6+6) +1=24+1=24 (秒)
答:电子鼠P从A点出发12秒后,三角形APE第一次成为等腰直角三角形;经过24秒后,三角形APE第二次成为等腰直角三角形。
(2)解:①如图,
设电子鼠Q从A点出发x秒后四边形AQPE是梯形,
12-x=2x
3x=12
x=4
答:电子鼠Q从A点出发4秒后,四边形AQPE是梯形。
② 如图
图中电子鼠Q从A点向上运动,电子鼠P同时从C点向下运动时,当∠QPD=45°时,PF=6cm,PC+AQ=6cm。又因为电子鼠Q的速度是电子鼠P的
2倍,所以电子鼠Q行驶路程也是电子鼠P的2倍,AQ==4 (cm) 。而四边形AQPE为四边形,可以将其分割成一个梯形AQPD和一个三角形PED,分别求出这两个图形面积是: (4+10) x6+2=42(cm2)
6x10+2=30 (cm2)
所以四边形面积为42+30=72 (cm2) 。
答:四边形AQPE的面积是72平方厘米。
【解析】(1) 电子鼠P从A点出发 ,要使三角形APE是等腰直角三角形,需要分情况讨论:①当电子鼠P爬到和B点重合时,三角形APE第一次成为等腰直角三角形; ② 当爬到CD边的中点时,三角形APE第二次成为等腰直角三角形。分别计算出这两种情况时所需的时间即可
(2)①设电子鼠Q从A点出发x秒后四边形AQPE是梯形,按路线画出图形:
根据路线,列出方程:12-x=2x,即可计算
② 如图,
要使∠QPD=45°,需要分别求出梯形AQPD和一个三角形PED的面积,然后将其相加即可求解
4.解:根据题意及图形所示,可得
较快的蚂蚁比较慢的蚂蚁多走:
(0.25-0.2)×50
=0.05×50
=2.5(米)
这个地方离底边的另一端有:
7.5-2.5=5(米)
答:这个地方离底边的另一端有5米
【解析】先求出较快的蚂蚁比较慢的蚂蚁多行驶的路程,7.5米减去多行驶的路程正好是到另一端的距离。
5.(1)解:根据题意,可得
81=9×9
9=3×3
9-3×2=3
3×3×3=27
答:正方体的体积是27。
(2)解:根据题意,可得
(9+9)÷2
=18÷2
=9(秒)
答:爬到终点的时间不发生变化,始终是9秒。
(3)解:根据题意,可得
9+9=18
18÷(2+1)
=18÷3
=6
答:诚诚必胜,真真走1步,诚诚就走2步,真真走2步,诚诚走1步,诚诚每次和真真走的步数和为3,诚诚肯定先走到C点。
【解析】(1)正方形ABCD由81个边长为1的小正方形组成,每个角处剪掉9个相等的正方形。每个角剪掉的正方形边长为3,因9=3×3。剪掉四个角后,剩余部分的面积为81 4×9=81 36=45。剩余部分可以折叠成一个无盖的正方体。正方体的边长为3,因为45=3×3×5。正方体的体积为3×3×3=27。
(2)蚂蚁从点A到点C需要爬行的总距离为9+9=18个单位。蚂蚁的速度是每秒钟爬两个单位,因此蚂蚁爬到终点的时间为18÷2=9(秒),由于蚂蚁只能向右或向上爬,所有路径的总距离都是18个单位,因此蚂蚁爬到终点的时间不会随着爬行路径的不同而发生变化。
(3)从点A到点C需要走的总步数为9+9=18步。真真和诚诚每次只能走1步或2步,且每次只能走一个或两个单位长度。诚诚每次和真真走的步数和为3,即真真走1步,诚诚就走2步;真真走2步,诚诚就走1步。这样诚诚每次都能保证自己走的步数和真真走的步数和为3。
6.解:100x2÷4=50(秒)
100x3÷4=75(秒)
乙在C到B的时间段是:50--75;125--150;200--225等.
甲在由C到B的方向上,到达C的时间是:
(80+40+120x2)-5=84(秒);204;324等
204-200=4(秒)
4x4÷(5-4)= 16(秒)
100-16x5=20(米)
答:甲第一次从背后追上乙的地点离B点20米。
【解析】由已知条件和图形可知:甲要从背后追上乙,必须具备2个条件:一是方向是由C向B;二是在同一时间甲到C点而乙过C点不久。
乙在C到B的时间段是:100x2-4=50(秒)---100x3-4=75(秒);125--150;200--225等等甲在由C到B的方向上,到达C的时间是:(80+40+120x2)-5=84(秒);204;324等.对照可得,符合要求的时间是204秒,即此时乙刚过C点4秒,距C点是4x4=16(米),甲追上乙用时是16÷(5-4)=16(秒),此时甲已离开C的距离是16x5=80米,再求离B距离即可.
7.(1)6
(2)解:∵a=6,b=2,
∴动点P改变速度后y与出发后的运动时间x(秒)的函数关系式为:y=6+2(x﹣6)=2x﹣6
①当0≤x≤6时
AP=x(cm)
S△APD==4x
②当6<x≤8时
AP=6+(x﹣6)×2=2x﹣6
S△APD==8x﹣24
③当x运动到C点时
2x﹣6=18解得:x=12
即:8<x≤12时
S△APD==40
④当12<x≤17时
DP=2DC+BC﹣(2x﹣6)=﹣2x+34
S△APD==﹣8x+136
综上:S△APD=;
S△APD=
①4x=20时,x=5∈[0,6],符合
②2x﹣6=20时,x=13(6,8],舍去
③8<x≤12时,S△APD=40≠24,舍去
④﹣8x+136=20,x=14.5∈(8,12],符合
所以点P出发后5秒或14.5秒,△APD的面积S1是长方形ABCD面积的
【解析】解:根据图象可知
S△APD=
∴a=6
故答案为:6
【分析】(1)根据三角形的面积公式可求a的值;
(2)①P在AB上运动时,S△APD=,AP为运动时间t的一次函数;
②P在BC上运动时S△APD=为定值.
③P在DC段上运动时,S△APD=.DP为P点运动时间的一次函数.
先计算△APD的面积,然后将计算出来的数值代入所求函数的不同分段,解出对应的x的值,若解出的x值在对应的分段区间内,则x的值即为所求的解,反之则不是.
8.(1)解:如图:
当电子鼠P爬到和B点重合时,三角形APE第一次成为等腰直角三角形,
需要:12÷1=12(秒)
当爬到CD边的中点时,三角形APE第二次成为等腰直角三角形,
需要:(12+6+6)÷1
=24÷1
=24(秒)
答:电子鼠P从A点出发12秒后,三角形APE第一次成为等腰直角三角形;经过24秒后,三角形APE第二次成为等腰直角三角形。
(2)解: ①如图:
可设电子鼠Q从A点出发x秒后四边形AQPE是梯形,
12-x=2x
3x=12
x=4
答:电子鼠Q从A点出发4秒后,四边形AQPE是梯形。
②如图:
图中电子鼠Q从A点向上运动,电子鼠P同时从C点向下运动时,当∠QPD=45°时,PF=6cm,PC+AQ=6cm。又因为电子鼠Q的速度是电子鼠P的2倍,所以电子鼠Q行驶路程也是电子鼠P的2倍,AQ= 。而四边形AQPE为四边形,可以将其分割成一个梯形AQPD和一个三角形PED,分别求出这两个图形面积是:(4+10)×6÷2=42(cm2)
6×10÷2=30(cm2)
所以四边形面积为42+30=72(cm2)。
答:四边形AQPE的面积是72平方厘米。
【解析】由图可知:当电子鼠P爬到和B点重合时,三角形APE第一次成为等腰直角三角形;当爬到CD边的中点时,三角形APE第二次成为等腰直角三角形;然后求出A点到B点的距离及A点到CD中点的距离,进而根据:路程÷速度=时间,分别解答即可。
(2)①当DP∥AQ时,AQPE就是梯形,可设电子鼠Q从A点出发x秒后四边形AQPE是梯形,列式为12-x=2x,解答即可。
②当∠QPD=45°时,PF=6cm,PC+AQ=6cm。又因为电子鼠Q的速度是电子鼠P 的2倍,所以电子鼠Q行驶路程也是电子鼠P 的2倍,AQ=,然后将其分割成一个梯形AQPD 和一个三角形PED,分别求出这两个图形面积,进一步解答即可。
9.解:如图
开始时,甲乙蚂蚁的速度比是4:5,则路程比也是4:5
所以,甲蚂蚁爬行的路程为108×2÷(4+5)×4=96(厘米),
乙蚂蚁爬行的路程为108×2 96=120(厘米),由于第二次甲与乙蚂蚁在BC中点相遇,
则由第一次相遇到第二次相遇甲蚂蚁爬行的路程是120 108÷2=66(厘米),
乙蚂蚁爬行的路程是96+108+108÷2=258(厘米).
由于第一次相遇后乙蚂蚁增加了15的速度,所以,相遇后甲乙蚂蚁的速度比为4:(5×15)=2:3,
故甲蚂蚁爬行66厘米路程时,乙蚂蚁爬行的路程是66÷2×3=99(厘米),
则甲蚂蚁停留的10秒钟,乙蚂蚁爬行的距离是258 99=159(厘米),
乙最初的爬行速度是159÷10÷(1+15)=13.25(厘米/秒)
甲的速度是13.25÷5×4=10.6(厘米/秒),
答:甲的速度是10.6厘米/秒,乙的速度是13.25厘米/秒。
【解析】先根据甲乙蚂蚁的速度比求出第一次相遇时,甲乙蚂蚁爬行的路程,再求出第一次相遇后,甲乙蚂蚁的速度比,进而求出甲蚂蚁停留的10秒钟,乙蚂蚁所爬行的路程,即可得出结论.
10.(1)5
(2)解:把小红与爷爷的年龄差看做木棒AB,
类似爷爷比小红大时看做当A点移动到B点时,此时B点所对应的数为-40,
小红比爷爷大时看做当B点移动到A点时,此时A点所对应的数为125,
∴可知爷爷比小红大[125-(-40)]÷3=55,可知爷爷的年龄为125-55=70.
答:爷爷的年龄是70岁.
【解析】(1)解:由数轴观察知三根木棒长是20-5=15(cm),则此木棒长为:15÷3=5cm,
故答案为:5
【分析】(1)此题关键是正确识图,由数轴观察即可得到木棒长。
(2)借助数轴用数形结合的方法求解.类似爷爷比小红大时看做当A点移动到B点时,求出此时B点所对应的数,小红比爷爷大时看做当B点移动到A点时,求出此时A点所对应的数,可知爷爷的年龄.
11.(1)解:当P在线段AB上时,因为P=2PB,AB=60cm
所以PA=60÷(1+2)×2=40(cm)
OP=0A+20=40+20=60(cm),
又因为点P 从点O沿OM 方向以1cm/s 的速度勺速运动,
所以60÷1=60(秒)
即点P 运动时间为 60 秒。
若AQ=AB,则BQ=AB=×60=40(cm),CQ=BC+BQ=10+40=50(cm)
点Q的运动速度为:50÷60=(cm/s)
若BQ=AB=×60=20(cm),CQ=BC+BQ=10+20=30(cm)
点Q的运动速度为:30÷60=(cm/s)
答:当P在线段AB上时,点Q运动的速度是cm/s或cm/s。
(2)解:设运动时间为t秒,则:
t+3t=90+70或t+3t=90-70,
解得:t=40或5
因为点Q运动到点O时没法继续运动,所以点Q最多运动30秒。
即t=40(不合题意,舍去)
所以t=5。
QO=CB+BA+AO=10+60+20=90(cm)
90÷3=30(秒)
即当点Q运动 30秒到点O时,点Q没法运动,P,0距离为70cm,即OP=70cm,
70÷1=70(秒)
即运动时间为 70·秒。
故经过5秒或70秒,两点相距70cm。
答:经过5秒或70 秒时P、Q两点相距70cm。
(3)解:如下图所示:
设OP=xcm
点P在线段AB上,因为OA=20cm,AB=60cm
所以20≤x≤80
OB-AP=OA+AB-(OP-OA)=20+60-(x-20)=100-x
EF=OF-OE=OA+AB-OE=20+×60-x=50-x
所以==2
答:的值是2。
【解析】(1)从题中我们可以看出点P及Q是运动的,当PA=2PB时实际上是P正好到了AB的三等分点上,而且PA=40, PB=20.由速度公式就可求出P点的运动时间,也是点Q的运动时间,点Q运动到的位置恰好是线段AB的三等分点,由此就可求出CQ长和点Q的速度.
(2)若点Q运动速度为5cm/s,经过多长时间P、Q两点相距70cm,这也有两种情况即当它们相向而行时,和它们背向而行时,此题可设运动时间为t秒,列方程就可解了.
(3)此题就可把它当成一个静止的线段问题来解决了,但必须借助图形.
12.(1)-4;4
(2)解:∵n=4,
∴点N在数轴上表示有理数4,
∵点B在数轴上表示有理数6,
∴B点位置如图所示,
∵MS=SN=6,
由题意知,DPN=MS+NS-PM=12-3t,DQN=|6-4-t|=|2-t|,DMN=MS+SM=6+6=12,
∵DPN+DQN=DMN-2,
∴12-3t+|2-t|=12-2,
当t≥2时,12-3t+t-2=12-2,
∴t=0(舍去),
当0<t<2时,12-3t+2-t=12-2,
∴t=1时,使得DPN+DQN=DMN-2;
(3)解:存在t使得DPM=3DQN;理由如下,
∵MS=SN=9,
∴相遇时,两点各自运动的时间为(9+9)÷(2+1)=6(秒),
动点P从点M出发以每秒2个单位长度沿着“拱形数轴”向正方向运动,同时点Q从点N出发,以每秒1个单位长度沿着“拱形数轴”向负方向运动,
∴当0<t<6时,DPM=2t,DQN=t,
∴2t=3t,
∴t=0(舍去),
当t≥6时,DPM=12-(t-6)=18-t,DQN=6-(t-6)=12-t,
∴18-t=3(12-t),
∴t=9,
∴当t=9时,DPM=3DQN.
【解析】解:(1)点M,N在数轴上分别表示有理数m,n且满足(m+4)2+|n-4|=0,
∴m+4=0,n-4=0,
∴m=-4,n=4,
故答案为:-4,4;
【分析】(1)由题中条件,利用平方与绝对值非负性,结合非负式和为0的条件求解即可得到答案;
(2)由含t的代数式表示出DPN,DQN,DMN,再列方程求解即可得到答案;
(3)根据数轴上动点问题,分相遇前0<t<6和相遇后t≥6两种情况列方程求解即可得到答案;
根据题意,数形结合列方程求解是解决问题的关键.
13.(1)解:如图1
(平方米)
(2)解:如图2
(平方米)
(3)解:因为16÷1=16,16÷2=8,
所以每经过16秒,点P和点Q 都回到出发点M。
2015÷16=125……15(秒)
第2015 秒点 P、点Q 的位置与第15秒时相同,△NPQ 的面积是6平方米。
【解析】(1)第1秒时,P点移动1米,位于MD中点;Q点移动2米,恰好移动到D点。此时,△NPQ的底为正方形边长4米,高为3米(即MD的长度减去P点移动的距离),因此△NPQ的面积为:3×4÷2=6平方米。
(2)第15秒时,P点移动了15米,Q点移动了30米。由于正方形的周长为16米,P点会在16秒后回到M点,Q点则在8秒后回到M点。所以,第15秒时,P点位于MD中点,Q点位于A点,即Q点与A点重合。此时,△NPQ的底仍为4米,高为3米(与第1秒时相同),面积为:3×4÷2=6平方米。
(3)第2015秒时,P点和Q点的位置与第15秒时相同。由于2015÷16=125...15,表示P、Q完成了125圈循环后,还额外移动了15秒,即回到与第15秒时相同的位置。所以,第2015秒时,△NPQ的面积同样为6平方米。
14.(1)解:已知A点对应的数是 1,B点对应的数是8。
在数轴上,两点间的距离等于右边的点对应的数减去左边的点对应的数,所以AB=8 ( 1)=8+1=9。
因为BCAC =45 ,且AB=AC+BC=9,
设AC=5x,BC=4x,则5x+4x=9,即9x=9,
解得x=1。
所以AC=5×1=5,
BC=4×1=4。
C点在B点左侧,C点对应的数等于B点对应的数减去BC的长度,即8 BC=8 4=4。
答:C点对应的数是4。
(2)解:当M、N未相遇时
此时M在AC上运动,M运动的速度是每秒2个单位长度,运动时间为t秒,那么M表示的数是起始点A对应的数 1加上运动的距离2t,即 1+2t。
N从B点出发,以每秒1个单位长度的速度沿数轴匀速向左运动,运动时间为t秒,所以N表示的数是B点对应的数8减去运动的距离t,即8 t。
因为MN=4,所以N表示的数减去M表示的数等于4,可列方程:
8 t ( 1+2t)=4
解得,t=
当M、N相遇后
M从A点运动到C点所用时间为:,在C点停留2秒,所以M从A点出发到在BC上运动时,总共用时t秒,此时M表示的数是4+2(t 25 2)=4+2(t 29 )=2t 5。
N表示的数依然是8 t。
因为MN=4,所以M表示的数减去N表示的数等于4,可列方程:
2t 5 (8 t)=4
解得,t=
综上所述,t的值为 或。
【解析】(1)根据已知的A、B两点对应的数以及BCAC 的比例关系,求出AC和BC的长度,进而确定C点对应的数。
(2)需要分M、N未相遇和相遇后两种情况,根据M、N在不同时刻表示的数以及MN=4这个条件列出方程求解。
15.(1)解: 点C表示的数为3,BC=2,AB=6 ,OB=3-2=1;AO=6-1=5所以A表示-5;答: 数轴上点A表示的数为 -5.;解:点C表示的数为3,BC=2,OB=3-2=1,所以 B表示 1;答: 点B表示的数为 1.
(2)解:①由题意得,如图:
t秒后,
点p表示的数为:-5+2t,
点Q表示的数为:3-t,
M为AP的中点 ,所以点M表示的数为:,
因为,所以CN=,
所以点N表示的数为:;
②由题意可,如图:P在左侧,Q在右侧时,
OP=5-2t,OQ=3-t,
原点O恰好是线段PQ的中点 ,所以5-2t=3-t;
解得t=2;
如图:Q在左侧,P在右侧时,
OP=2t-5,OQ=t-3,
原点O恰好是线段PQ的中点 ,所以2t-5=t-3;
解得t=2;
当t=2时,P在左侧,不成立,舍去;
综上,t=2时,原点O恰好是线段PQ的中点。
答:点M表示的数为:,点N表示的数为:;t=2时,原点O恰好是线段PQ的中点。
【解析】(1)根据图片A,B,C点的位置,3-2即为B的位置,6-1即为A的位置,由于A在负半轴,所以A为-5;
(2)①根据题意标出点,点P以每秒2个单位长度的速度沿数轴向右匀速运动,先求出点p表示的数, M为AP的中点 ,即可求出M, 点Q以每秒1个单位长度的速度沿数轴向左匀速运动 ,,先求出点Q表示的数,即可求出点N;
②分点讨论,P在左侧,Q在右侧时,原点O恰好是线段PQ的中点 ,所以5-2t=3-t,解得t=2;Q在左侧,P在右侧时不成立故舍去。
16.解:设AP=AQ=x,阴影部分的面积为S,则S=12×8-12×x2,
即S=96-12x2,
当AP=2cm时,则S=96-12×22=94( cm2),
当AP=8cm时,则S=96-12×82=64( cm2).
所以阴影部分面积减少了94-64=30(cm2).
答: 图中阴影部分的面积是减少了,减少了30平方厘米.
【解析】分析题目,设AP=AQ=x,阴影部分的面积为S,则由图形可知S=12×8-12×x2,即S=96-12x2;
接下来把AP=2和AP=8分别代入关于S的表达式中进行计算,可得对应的S的值;然后将得出的面积相减,即可得到结果.
17.(1)解:-2-1+2
=-3+1
=-1
答:第一次移动后点在数轴上对应的数为-1。
(2)解:-1-2+4
=-3+4
=1
答:第二次移动后点在数轴上对应的数为1。
(3)解:1-3+6
=-2+6
=4
答:第三次移动后点在数轴上对应的数为4。
(4)解:点P在数轴上的数依次是:-2、-1、1、4,
所以第n次移动后点P在数轴上对应的数是-2+=。
【解析】(1)、(2)、(3)根据左减右加,用开始的点减去向左移动的个数再加上向右移动的个数即可。(4)写出前几个点P的位置,发现第一次移动后的点是-2+1,第二次移动后的点是-2+1+2,第三次移动的点是-2+1+2+3,因此,第n次移动后的点就是-2+1+2+3+……n,据此总结规律即可。
18.(1)解:当点P在AB—BC上运动时,
① 当0当2② 当BQ=2BP时,
当0当2综上分析可知,当0(2)解:当点M从D点出发,以每秒4cm/s的速度在线段DC上作往返运动时,
当点P运动到点C时,用的时间为:(4+4)÷2=4(s)
此时点M正好运动到点D,当点M与点Q第一次重合时,有:4(t 4)+(t 4)=4
解得:t=
当点M与点P第二次重合时,有:4(t-5)=2+2(t-5)
解得:t=6
此时点P、M都运动到D处,综上分析可知,
当或时,点M落在线段PQ上。
【解析】(1)分析点P和点Q的运动规律,根据它们的速度和初始位置,可以用含t的代数式表示它们在不同时间段内的位置。
根据题目要求,分别求解当点P在AB—BC上运动时,线段BP的长度表示式以及当BQ=2BP时,t的值。
(2)考虑动点M的运动情况,当点P与点M第一次重合时,我们求解t的值,并直接写出此时线段DP的长度。分析当点M落在线段PQ上时,t的取值范围,通过解方程和不等式,我们得出t的具体取值范围。
19.(1)解:根据图象可知S△APD=AD×AP=×1×a×8=24,
∴a=6
b==2
c=8+(10+8)=17
(2)8;y=2x-6
(3)解:①当0≤x≤6时
AP=x(cm)
S△APD=AD×AP=4x
②当6<x≤8时
AP=6+(x-6)×2=2x-6
S△APD=AD×AP=8x-24
③当x运动到C点时
2x-6=18解得:x=12
即:8<x≤12时
S△APD=AD×AB=40
④当12<x≤17时
DP=2DC+BC-(2x-6)=-2x+34
S△APD=AD×DP=-8x+136
综上:S△APD=
S△APD=s四边形ABCD=AD×AB=20
①4x=20时,x=5∈[0,6],符合
②2x-6=20时,x=13 (6,8],舍去
③8<x≤12时,S△APD=40≠24,舍去
④-8x+136=20,x=14.5∈(8,12],符合
所以点P出发后5秒或14.5秒,△APD的面积S1是长方形ABCD面积的。
【解析】解:(2)因为a=6,b=2,
所以动点P改变速度后y与出发后的运动时间x(秒)的函数关系式为:y=6+2(x-6)=2x-6
当x=7时,y=2×7-6=14-6=8
故答案为:(2)8;y=2x-6。
【分析】 (1)根据三角形的面积公式可求a、b及图②中c的值;
(2)确定y与x的等量关系后列出关系式即可;
(3)①P在AB上运动时,S△APD=AD×AP,AP为运动时间t的一次函数;
②P在BC上运动时S△APD=AD×AB为定值.
③P在DC段上运动时,S△APD=AD×DP.DP为P点运动时间的一次函数.
先计算△APD的面积,然后将计算出来的数值代入所求函数的不同分段,解出对应的x的值,若解出的x值在对应的分段区间内,则x的值即为所求的解,反之则不是.
20.解:由图象可知as时有:
×8× AP=24
4AP=24
AP = 6
又因为P的速度为1,所以a=6÷ 1= 6(s);
当a=8时,S为40,即P点速度变化后到B点用了2s,则
b=(10-6) ÷2
=4÷2
= 2(cm/s)
c=18÷2+8
=9+8
= 17(s)
答: a、b、c的值分别为6、2、17。
【解析】结合图象分析可知APD面积的变化情况:当点P在AB 上运动时,因为三角形高不变,底边增大,所以APD的面积逐渐增大:点P在BC上运动时,因为此时三角形同底等高,所以APD面积不变;点P在CD上运动,因为高不变,底边缩小,所以APD面积逐渐减小。再利用图找出关键点,a秒时,三角形面积是24,即可求出AP长度,a的值可求出;利用动点P改变速度后到B点的时间与路程可求出速度b; c的值为P运动到D点的时间。
21.(1)2
(2)解:存在,有两种情况:
第一种情况:当点P在AB边上时,,
解得:,即
第二种情况:当点 在BC边上时,如图,
设,则,解得:,
所以
答:当x为cm或3cm时,可使三角形APE的面积为。
【解析】解:(1)当点P与点B重合时,如图
即
故答案为:2
【分析】(1)点P运动到点B,连接AE、PE,观察所形成的图形的底边和高与正方形边长的关系,即可求解。
(2)分析题意,要使三角形APE的面积为 ,首先要判断出三角形APE是否为直角三角形,据此可以分两种情况进行讨论:若点P在AB边上时,令△APE的面积为- ,求解即可;若点 在BC边上时,设,令 的面积=,根据关系列方程,即可确定x的值。
22.(1)解:甲小球到原点的距离为:2+1×10=12cm;
乙小球碰到挡板后返回的速度:2×1.5=3(厘米/秒)
乙小球到原点的时间为:10-6÷2=7(秒)
乙小球到原点的距离为:7×3=21cm
答:当t=10时,甲小球到原点的距离为12cm;乙小球到原点的距离为21cm.
(2)解:甲球运动的路程为:1×t=t,
∵OA=2
∴甲球到原点的距离为:t+2;
乙球到原点的距离分两种情况:
当0<t≤3时,乙球运动的路程为:2×t=2t
∵OB=6
∴乙球到原点的距离为:6-2t
由题意得:t+2=6-2t
3t=4
当t>3时,乙球到原点的距离为:2×1.5×﹙t-6÷2﹚=3﹙t-3﹚
由题意得:t+2=3﹙t-3﹚
t+2=3t-9
2t=11
t=5.5
综上所述,当或t=5.5时,甲、乙两小球到0点的距离相等。
【解析】熟知路程、速度、时间三者之间的等量关系是解题关键。路程、速度、时间三者之间的等量关系为:路程=速度×时间;速度=路程÷时间;时间=路程÷速度;
(1)根据”路程=速度×时间“可知:甲球运动的路程为:1×10=10cm,由OA=2cm,可得:甲小球到原点的距离为:2+1×10=12cm;乙小球碰到挡板后返回的速度:2×1.5=3(厘米/秒);乙小球到原点的时间为:10-6÷2=7(秒);乙小球到原点的距离为:7×3=21cm,即可得出答案;
(2)根据乙球的运动轨迹,分0<t≤3和t>3两种情况讨论,由甲球到原点的距离为:t+2;当0<t≤3时,乙球到原点的距离为:6-2t;根据甲、乙两小球到0点的距离相等可列出关于t的一元一次方程,解得t的值;当t>3时,乙球到原点的距离为:2×1.5×﹙t-6÷2﹚=3﹙t-3﹚,根据甲、乙两小球到0点的距离相等可列出关于t的一元一次方程,解得t的值,即可得出答案。
23.解:把楼梯的各条线段进行平移,可得AB+BC=楼梯A→C的总长;
设A→C的路程为x米,则猫行走的路程为x+1.5米,老鼠行走的路程为x-1.5米,
因为猫和老鼠行走的时间相同,且老鼠的速度是猫的,
根据时间一定时,路程与速度成正比的性质可得:
,根据比例的基本性质可得:
解得x=6.5
答:A→C的路程为6.5米.
【解析】 把楼梯的各条线段进行平移,可得到一个长方形ABCE;可得AB+BC=楼梯A→C的总长(即这个长方形周长的一半);猫捉鼠的路程之和为楼梯A→C的总长+线段CD长;老鼠逃窜的路程为AB+BC-线段CD长;根据时间一定时,所行走的路程与速度成正比的性质即可解决问题.
24.(1)解:当时,橡皮筋刚好触及钉子
,
所以,
(2)解:当时
AQ=x,BP=2x-2,OE=1
即
所以,当 时,
(3)解:x=2
【解析】(1)当橡皮筋触及到钉子时,由于Q在边AD上,且速度为1cm,所以在x秒后,Q移动的距离为xcm。由于正方形边长为2cm,所以当橡皮筋触及到钉子时,点Q已经移动了整个边长,即移动了2cm,因此,有等式:,其中,(2x-2)是点P移动的距离,因为点P从点A开始移动了(2x-2)cm到达边BC,解以上方程即可求解
(2)先求出时,x和y之间的关系式:,代入x即可求解。
(3)当橡皮筋刚好触及钉子时,,停止时,,,,所以,,所以,此时x=2
25.解:当点P运动到B点时,S△APD=AB×AD÷2
=8×10÷2
=40(cm2);
所以当点P运动a秒时,点P在AB之间,设该点为E
AE×AD÷2=24,即4AE=24,AE=6;
a=6÷1=6(s);
点P速度变化后到B点用了8-6=2(秒);
b=EB÷2
=(10-6)÷2
=4÷2
=2(cm/s);
c=(BC+CD)÷2+8
=(8+10)÷2+8
=9+8
=17(s)
答: 的值分别为 。
【解析】由图可知,当点P运动到B点时,S△APD=AB×AD÷2=40(cm2),所以当点P运动a秒时,点P在AB之间,设该点为E,根据三角形面积计算公式即可求出AE的长度,再用AE的长度除以点P的速度即可求出a的值。由图象可知,当点P运动8秒时,点P运动到了点B,因此,用8减去a的值求出点P在EB上的运动时间,接着再用EB的长度除以该运动时间即可求出b的值。由图象可知,8到c的这段时间,点P由B点运动到D点,因此,用BC加CD的长度除以b可以求出8到c的这段时间,再加上8即可求出c的值。
26.解:如图,
由题意可知,丙从D到E用4分钟,丁从D到F用10分钟,乙从E经D到F用6分钟,说明甲(或乙)速度是丙(或丁)的:
因为甲走AD用10分钟,所以丙走AD要用,走AE用
因为乙走(BA+AE)用14分钟,所以,丙走AB用
因为AB长60米,所以丙每分钟走
于是求出:
AE=,ED=
DF=,FC=
=
=
=2497.5(平方米)
答: 的面积为2497.5平方米。
【解析】由题意可知,丙从D到E用4分钟,丁从D到F用10分钟,乙从E经D到F用6分钟,说明甲(或乙)速度是丙(或丁)的:
因为甲走AD用10分钟,所以丙走AD要用,走AE用
因为乙走(BA+AE)用14分钟,所以,丙走AB用
因为AB长60米,所以丙每分钟走
于是求出:
AE=,ED=
DF=,FC=
所以,,代入数据即可求出
27.(1)2x;10-2x
(2)3
(3)小凯的说法是错误的,EC的长度不变。因为E点是线段AB 的中点,C点是线段BD的中点,所以AB=2×BE,BD=2×BC,AB+BD=2×(BE+BC)=2×EC=10,所以EC的长度不变,为5cm。
【解析】(1)路程=速度×时间 AB=2x
BD=AD-AB=10-2x
(2)把x=2代入10-2x中,10-2×2=6(cm),BC=BD÷2=6÷2=3(cm)
(3)小凯的说法是错误的,EC的长度不变。因为E点是线段AB 的中点,C点是线段BD的中点,所以AB=2×BE,BD=2×BC,AB+BD=2×(BE+BC)=2×EC=10,所以EC的长度不变,为5cm。
故答案为:(1)2x (2)3
【分析】(1)根据路程=速度x时间,求出AB的长度,然后用AD的长度减去AB的长度就是BD的长度,分别用含有字母x的式子表示即可。(2)把x=2代入式子中,求出BD的长度,再根据C点是线段BD的中点,求出 BC的长度。(3)E点是线段AB的中点,C点是线段BD的中点,所以线段EC的长是AD的一半,EC的长度不变。
21世纪教育网(www.21cnjy.com)
小升初奥数思维之典型应用题精讲精练讲义(通用版)
专题13 数轴与动点行程问题
【第一部分:知识归纳】
一、基本概念
1、数轴与动点行程问题是借助数轴研究点的运动规律的行程问题。
2、特点:
(1)直观性强:运动过程可在数轴上清晰展示
(2)方向明确:正方向表示正向运动,负方向表示反向运动
(3)位置精确:点的位置可用具体数值表示
3、核心要素
(1)原点:数轴的基准点(通常记为0)
(2)动点:在数轴上运动的点
(3)运动方向:向右为正方向,向左为负方向
(4)运动速度:单位时间内移动的单位长度
二、基本公式与关系
1. 位置计算公式
t时刻的位置 = 初始位置 ± 速度 × 时间
("+"表示正方向运动,"-"表示负方向运动)
2. 相遇条件
两个动点位置相同:P (t) = P (t)
3. 追及条件
同向运动时,后面的点位置赶上前面的点
三、常见题型与解题方法
1. 单动点基础问题
例题:点A从数轴原点出发,以每秒2个单位的速度向右运动。5秒后A点的位置是多少?
解答:位置 = 0 + 2×5 = 10
2. 双动点相遇问题
例题:点P从+3出发以1单位/秒向左运动,点Q从-5出发以2单位/秒向右运动。它们何时相遇?
解答:设t秒后相遇:
3 - 1t = -5 + 2t
8 = 3t
t = 8/3秒 ≈ 2.67秒
3. 动点往返问题
例题:第一阶段:-2 + 3×4 = 10
第二阶段:10 - 2×3 = 4
最终位置:4
四、解题技巧
1、画数轴示意图:标出初始位置和运动方向
2、建立时间轴:记录各时间段运动情况
3、分段计算:对变速运动分段处理
4、代数方法:设未知数列方程求解
5、单位统一:确保时间和速度单位一致
【第二部分:能力提升】
1.一个圆周长70厘米,甲、乙两只爬虫从同一点同时出发,同向爬行。甲以4厘米/秒的速度不停地爬行,乙爬行15厘米后,立即反向爬行,并且速度增加1倍。如果乙在离出发点10厘米处与甲第一次迎面相遇,则乙爬虫原来的速度是多少厘米/秒
2.学习编程的奇奇最近编写了一套程序.让一只电子鼠P从长方形ABCD的点A出发,沿着长方形的边依次向B,C,D以每秒1厘米的速度移动.已知AB=12厘米,ED=DA=6厘米。
(1)电子RP从A点出发几秒后,三角形APE是等腰直角三角形
(2)当电子鼠P到达C时,另一只电子鼠Q以每秒2厘米的速度从A点出发.沿AB向B点移动.
①电子鼠Q从A点出发几秒后,四边形AQPE是梯形
②当∠QPD=45°时,四边形AQPE的面积是多少平方厘米
3.学习编程的奇奇最近编写了一套程序,让一只电子鼠P从长方形ABCD的点A出发,沿着长方形的边依次向B、C、D以每秒1厘米的速度移动,已知厘米,厘米,
(1)电子鼠P从A点出发几秒后,三角形APE是等腰直角三角形
(2)当电子鼠P到达C时,另一只电子鼠Q以每秒2厘米的速度从A点出发,沿AB向B点移动,
①电子鼠Q从A点出发几秒后,圆边形AQPE是梯形
②当∠QPD=45°时,四边形AQPE的面积是多少平方厘米
4. 两只蚂蚁同时从一个等腰三角形的顶点出发(如右下图),分别沿两腰爬行,一只蚂蚁每分钟爬行0.2米,另一只蚂蚁每分钟爬行0.25米,经过50分钟,在离底边的一端7.5米的地方相遇。这个地方离底边的另一端有多少米?
5.如图,81个边长为1的小正方形组成正方形ABCD,我们把小正方形的顶点都称为格点。
(1)若在正方形ABCD的四个角处都剪掉四个相等的小正方形后,剩余部分恰好能折叠成一个无盖的正方体,求出该正方体的体积。
(2)蚂蚁要沿着小正方形的边从点A出发爬到点C,只能向右或向上爬,速度是每秒钟爬两个单位,请说明:蚂蚁爬达终点的时间是否会随着爬行路径的不同而发生变化?若发生变化,说明理由;若不发生变化,求出这个时间。
(3)真真和诚诚利用该正方形ABCD做游戏,规定从A点出发,每次只能沿小正方形的边向右或向上走,每次只能走1个或两个单位长度,谁先到达C点谁获胜。真真先走,诚诚后走。请问:两个同学中谁有必胜把握?怎样操作才能必胜?
6.如图所示,甲从A点出发,在AD之间不断往返行走。乙从B点出发,沿着B—E—C—B围绕等边三角形BEC不断行走,已知AB=80米,BE=EC=CB=100米,CD=120米,甲的速度是5米/秒,乙的速度是4米/秒,问:甲第一次从背后追上乙的地点离B点多少米?
7.如图, 在长方形 ABCD中, . 点P从点A出发, 沿A—B—C—D路线运动,到D停止:点P的速度为每秒 1cm,a秒时点P的速度变为每秒 bcm,图②是点P出发x秒后。 的面积 与x(秒) 的关系图象;
(1) 根据图像提供的信息, = 。
(2) 点P出发后几秒, 的面积; 是长方形ABCD 面积的四分之一?
8.学习编程的奇奇最近编写了一套程序,让一只电子鼠P从长方形ABCD的点A 出发,沿着长方形的边依次向B,C,D以每秒1厘米的速度移动. 已知 厘米, 厘米.
(1) 电子鼠P从A点出发几秒后,三角形APE是等腰直角三角形?
(2) 当电子鼠 P到达C时,另一只电子鼠Q以每秒2厘米的速度从A点出发. 沿AB向B点移动.
①电子鼠Q从A 点出发几秒后,四边形AQPE是梯形?
②当 时,四边形AQPE 的面积是多少平方厘米?
9. 在一个边长为108厘米的等边三角形中,甲与乙两只蚂蚁分别从A、C两点同时以4:5的速度,按相反方向出发,第一次相遇后,甲停下10秒后按原速度出发,乙不停留,还增加了的速度出发,第二次刚好在B与C的中点相遇,那么甲的速度是多少?乙的速度是多少?
10.如图,一根木棒放在有刻度的直线上,木棒的左端与点A重合,右端与点B重合。
(1)若将木棒沿直线向右水平移动,则当它的左端移动到B点时,它的右端在直线上所对应的数为20cm;若将木棒沿直线向左水平移动,则当它的右端移动到A点时,则它的左端在直线上所对应的数为5cm。由此可得到木棒长为 cm。
(2)由题⑴的启发,请你借助这个工具帮助小红解决下列问题:
一天,小红去问爷爷的年龄,爷爷说:我若是你现在这么大,你还要40年体出生,你若是我现在这么大,我已经125岁,是老寿星了,哈哈!”请求出爷爷现在多少岁
11.如图,在射线OM上有三点A,B,C,满足OA=20cm,AB=60cm,BC=10cm(如图所示),点P从点O出发,沿OM方向以1cm/s的速度匀速运动,点Q从点C出发在线段CO上向点O匀速运动,两点同时出发。
(1)当P在线段AB上,且PA=2PB时,点Q运动到的位置恰好是线段AB的三等分点,求点Q运动的速度;
(2)若点Q运动的速度为3cm/s,经过多长时间P、Q两点相距70cm;
(3)当点P运动到线段AB上时,分别取OP和AB的中点E,F,求的值。
12.点M,N在数轴上分别表示有理数m,n且满足(m+4)2+|n-4|=0。现将数轴在点M,N处剪断,再用绳子将它们连接,就可得到如图所示的“拱形数轴",其中点S为绳子上一点且满足MS=NS,在此数轴上,我们定义任意两点的距离为它们之间折线段的长度之和,如图1,A,两点的距离为线段A的长,记为DAM=AM,记A,B两点的距离为DAB=BN+NS+SM+MA。
(1)请直接写出m= ,n= ;
(2)若MS=6,点B在数轴上表示有理数6,一动点P从点M出发以每秒3个单位长度沿“拱形数轴”
向正方向运动,同时,另一动点Q从点B出发以每秒1个单位长度沿“拱形数轴”向负方向运动,两个点运动到点S处均停止,设运动时间为t秒,请间t取何值时,使得DPN+DQN=DMN-2。
(3)如图2,已知MS=9,动点P从点川出发以每秒2个单位长度沿着“拱形数轴”向正方向运动,同时点Q从点N出发,以每秒1个单位长度沿着“拱形数轴”向负方向运动:两点相遇后,点P速度立即变为原来的一半并沿着“拱形数轴”向负方向运动,同时点Q保持速度不变并沿着“拱形数轴”向正方向运动,设运动时间为t秒,是否存在t使得DPM=3DQN?如果存在,请直接写出出t的值,如果不存在,请说明理由。
13.如图,点M,N分别是边长为4米的正方形ABCD的一组对边AD,BC 的中点,P,Q两个动点同时从M出发,P沿正方形的边逆时针方向运动,速度是1米/秒;Q沿正方形的边顺时针方向运动,速度是2米/秒。求:
(1)第1秒时 的面积;
(2)第15 秒时 的面积;
(3)第2015 秒时 的面积。
14.如图,O是数轴的原点,A、B是数轴上的两个点,A点对应的数是-1,B点对应的数是8,C是线段AB上一点,满足。
(1)求C点对应的数;
(2) 动点M从A点出发,以每秒2个单位长度的速度沿数轴向右匀速运动,当点M到达C点后停留2秒钟,然后继续按原速沿数轴向右匀速运动到B点后停止。在点M从A点出发的同时,动点N从B点出发,以每秒1个单位长度的速度沿数轴匀速向左运动,一直运动到A点后停止.设点N的运动时间为t秒。问当时,求t的值?
15.如图,已知点A、B、C是数轴上三点,点C表示的数为3,BC=2,AB=6.
(1)数轴上点A表示的数为 ,点B表示的数为 ;
(2)动点P、Q分别从点A、C同时出发,点P以每秒2个单位长度的速度沿数轴向右匀速运动,点Q以每秒1个单位长度的速度沿数轴向左匀速运动,M为AP的中点,点N在线段CQ上,且,设运动时间为秒。
①求数轴上M、N表示的数;(用含t的式子表示)
②当t为何值时,原点O恰好是线段PQ的中点
16.如图,在长方形ABCD 中,AB=12cm,AD-=8cm。点P、Q都从点A同时出发,点P向B点运动,点Q向D点运动,且保持,AP=AQ,在这个变化过程中,图中阴影部分的面积液随之变化,当AP由2cm变到8cm时,图中阴影部分的面积是增加了,还是减少了?增加或减少了多少平方厘米?
17. 一点从数轴上表示-2的点开始移动,第一次先向左移动1个单位长度,再向右移动2个单位长度:第二次向左移动2个单位长度,向右移动4个单位长度;第三次先向左移动3个单位长度,再向右移动6个单位长度……求:
(1)写出第一次移动后点在数轴上对应的数;
(2) 写出第二次移动后点在数轴上对应的数:
(3) 写出第三次移动后点在数轴上对应的数;
(4)按上述规律第次移动后点在数轴上对应的数
18.如图,在正方形ABCD中,AB=BC=CD=AD=4cm,动点P从点A出发,以2cm/s速度沿AB—BC—CD—DA的线路运动,同时动点Q从B出发,以1cm/s的速度沿BC—CD的线路运动,设运动的时间为t(s)。()
(1)当点P在AB—BC上运动时,
①用含t的代数式表示线段BP的长度。
②当BQ=2BP时,求t的值。
(2)动点M从D点出发,以每秒4cm/s的速度在线段DC上作往返运动,点M与点P同时出发,当点P停止运动时,点M也停止运动,连接PQ,
③当点P与点M第一次重合时,求t的值,并直接写出此时线段DP的长度。
④当点M落在线段PQ上时,直接写出t的取值范围。
19. 如图①, 在长方形 ABCD中, AB=10cm, BC=8cm, 点P从A出发,沿 A→B→C→D路线运动,到D停止; 点P出发时的速度为每秒1cm,a秒时点P的速度变为每秒 bcm,图②是点 P出发x秒后,△APD的面积S(c㎡) 与x(s) 的函数关系图象.
(1)根据题目中提供的信息,求出图②中a,b,c的值;
(2) 设点P运动的路程为 y(cm)
①7s时, y的值为 cm;
②请写出当点P改变速度后,y与x的函数关系式 ;
(3)当点P出发后几秒时,△APD的面积S是长方形 ABCD面积的 ?
20.如图①,在长方形ABCD中,AB=10cm, BC=8cm, 点P从A出发,沿A、B、C、D路线运动,到D停止;点P的速度为每秒1cm,a秒时点P中的速度变为每秒b厘米;图②是点P出发x秒后,△APD的面积S(Cm2)与×(s)的变化关系图象。根据图②中提供的信息,求a、b及图②中c的值。
21.如图,正方形ABCD的边长为2cm,点E是CD边的中点,正方形ABCD边上的一动点P从点A出发(不与点A重合),沿方向运动(不与点E重合),设点P运动路程为xcm,探究:
(1)当点P运动到与点B重合时,三角形APE的面积为 平方厘米。
(2)在正方形ABCD的边上是否存在点P,使三角形APE的面积为平方厘米?若存在,请求出x的值;若不存在,请说明理由。
22.如图,在直线上有 A、O、B三点,其中 AO=2cm,B0=6cm,若在点O处放一挡板,一小球甲从点A处以1个厘米1秒的速度向左移动:同时另一小球乙从点B处以2厘米/秒的速度也向左移动,在碰到挡板后(忽略球的大小,可看作一点)以原来速度的 1.5倍向相反的方向运动,设运动的时间为t(秒),
(1)当t=10时,求甲,乙两小球到0点的距离;
(2)当t为何值时,甲、乙两小球到0点的距离相等.
23.如图为一个阶梯的纵截面,一只老鼠沿长方形的两边A→B→D路线逃跑,一只猫同时沿阶梯(折线)A→C→D的路线去做捉,结果在距离点C点1.5米的D处,猫捉住了老鼠,已知老鼠的速度是猫的,问阶梯A→C的长度是多少米
24.如图,正方形ABCD的边长为2cm,在对称中心O处有一钉子。动点P、Q同时从点A出发,点P沿A~B~C~D方向以每秒2cm的速度运动,到点D停止:点Q沿A~D方向以每秒1cm的速度运动,到点D停止。P、Q两点用一条可伸缩的细橡皮筋连接,设x秒后橡皮筋扫过的面积为y。
(1)当橡皮筋刚好触及钉子时,求x的位。
(2)当时y的值。
(3)在橡皮筋从触及钉子到运动停止的过程中,直接写出∠POQ为直角时x的数值。
25.如图①,在长方形ABCD中, AB=10cm, BC=8cm,点P从A出发,沿A、B、C、 D路线运动,到D停止;点P的速度为每秒1cm, a秒时点P中的速度变为每秒b厘米;图②是点P出发x秒后,△APD的面积3(cm2 )与x (s)的变化关系图像。根据图②中提供的信息,求a、 b及图②中c的值。
26.8点 10 分, 有甲乙两人以相同的速度分别从相距 60 米的 两地按顺时针方向沿长方形 ARCD的边走向D点, 如下图, 甲 8 点 20 分到 D点后, 丙、丁两人立即以相同速度从D点出发。丙由D点向A点走去, 8 点24分与乙在E点相遇; 丁由D点向C点走去, 8 点 30 分在 F点被乙追上, 求 的面积?
27.阅读理解:线段上的一点把线段分成相等的两部分,这个点叫作线段的中点。如图①,P点是线段MN的中点,则 如图②,B点是线段AD上的一个动点,从A点到D点以2cm/s的速度运动,C点是线段 BD的中点,
(1)当B点的运动时间是x秒时, cm,BD= cm。
(2)B点的运动时间是x秒,当 时, cm。
(3)如图③,在运动过程中,E点是线段AB的中点。下面小凯的说法正确吗? 说一说你的想法。
参考答案及试题解析
1.解:离出发点 10 cm有甲爬行10 cm,70-10=60cm,70+10=80cm 三种情况。
(1)当甲爬行10 cm时,甲所用的时间为
乙在此过程中分为两个阶段,第一阶段乙爬行15 cm,第二阶段爬行:
两段速度比为1∶2
两段路程比为3:1
两段时间比为
第一段乙用时 乙原来速度为
(2)当甲爬行60 厘米时,甲所用时间为
乙在此过程中分为两个阶段,第一阶段乙爬行15 cm,第二阶段爬行
两段速度比为1 :2,两段路程比为:
两段所用时间比 第一阶段乙用
乙原来的速度:
⑶当甲爬行80cm时,甲所用的时间为
乙在此过程中分为两个阶段,第一阶段乙爬行15 cm,第二阶段乙爬行15-10=5(cm)。
两段速度比1:2,路程比为15:5 = 3 :1。
两段所用时间比 第一阶段乙用了
乙原来的速度为
因此,乙爬虫原来的速度为7cm/s或- 或
【解析】为了解决这个问题,我们需要分析甲和乙的爬行过程,特别是在它们第一次相遇时的情况。由于甲和乙的速度不同,以及乙的速度变化和方向改变,我们需要分情况讨论,分别计算在不同情况下乙的原始速度。
2.(1)解:当电子鼠P爬到和B点重合时,AB=12厘米,故此时需要的时间为12秒。
当爬到CD边的中点时AB=12厘米,BC=DA=6厘米,故此时需要的时间为24秒。
答: 从A点出发12;24秒后
(2)解: ①设电子鼠Q从A点出发x秒后四边形AQPE是梯形。因此当P和Q在同一条直线上时,四边形AQPE成为梯形。此时,AP=12-x,AQ=2x,
12-x=2x
解得:x=4
答: 出发4秒后,四边形AQPE是梯形
②当∠QPD=45度时,PF=FQ=DA=6厘米,PC+AQ=6厘米。AQ=2PC。解这个方程,AQ=4厘米。
四边形AQPE可以分割成一个梯形AQPD和一个三角形PDE,其面积分别为42平方厘米和30平方厘米,因此四边形AQPE的面积为72平方厘米。
答: 四边形AQPE的面积是72平方厘米
【解析】(1)首先要理解等腰直角三角形的定义,然后分析出有两种情况:爬到和B点重合;爬到CD边的中点,进行计算即可。
(2)首先,通过解析电子鼠P的移动路径,确定它何时会与长方形的顶点B、C、D重合,从而计算出等腰直角三角形APE的形成时间。对于第二个问题,首先确定电子鼠Q出发的时间,并分析它在移动过程中四边形AQPE何时会变成梯形。最后,利用几何知识计算出四边形AQPE的面积。
3.(1)解:如图
当电子鼠P爬到和B点重合时,三角形APE第一次成为等腰直角三角形,需要:12+1=12 (秒)
当爬到CD边的中点时,三角形APE第二次成为等腰直角三角形,需要: (12+6+6) +1=24+1=24 (秒)
答:电子鼠P从A点出发12秒后,三角形APE第一次成为等腰直角三角形;经过24秒后,三角形APE第二次成为等腰直角三角形。
(2)解:①如图,
设电子鼠Q从A点出发x秒后四边形AQPE是梯形,
12-x=2x
3x=12
x=4
答:电子鼠Q从A点出发4秒后,四边形AQPE是梯形。
② 如图
图中电子鼠Q从A点向上运动,电子鼠P同时从C点向下运动时,当∠QPD=45°时,PF=6cm,PC+AQ=6cm。又因为电子鼠Q的速度是电子鼠P的
2倍,所以电子鼠Q行驶路程也是电子鼠P的2倍,AQ==4 (cm) 。而四边形AQPE为四边形,可以将其分割成一个梯形AQPD和一个三角形PED,分别求出这两个图形面积是: (4+10) x6+2=42(cm2)
6x10+2=30 (cm2)
所以四边形面积为42+30=72 (cm2) 。
答:四边形AQPE的面积是72平方厘米。
【解析】(1) 电子鼠P从A点出发 ,要使三角形APE是等腰直角三角形,需要分情况讨论:①当电子鼠P爬到和B点重合时,三角形APE第一次成为等腰直角三角形; ② 当爬到CD边的中点时,三角形APE第二次成为等腰直角三角形。分别计算出这两种情况时所需的时间即可
(2)①设电子鼠Q从A点出发x秒后四边形AQPE是梯形,按路线画出图形:
根据路线,列出方程:12-x=2x,即可计算
② 如图,
要使∠QPD=45°,需要分别求出梯形AQPD和一个三角形PED的面积,然后将其相加即可求解
4.解:根据题意及图形所示,可得
较快的蚂蚁比较慢的蚂蚁多走:
(0.25-0.2)×50
=0.05×50
=2.5(米)
这个地方离底边的另一端有:
7.5-2.5=5(米)
答:这个地方离底边的另一端有5米
【解析】先求出较快的蚂蚁比较慢的蚂蚁多行驶的路程,7.5米减去多行驶的路程正好是到另一端的距离。
5.(1)解:根据题意,可得
81=9×9
9=3×3
9-3×2=3
3×3×3=27
答:正方体的体积是27。
(2)解:根据题意,可得
(9+9)÷2
=18÷2
=9(秒)
答:爬到终点的时间不发生变化,始终是9秒。
(3)解:根据题意,可得
9+9=18
18÷(2+1)
=18÷3
=6
答:诚诚必胜,真真走1步,诚诚就走2步,真真走2步,诚诚走1步,诚诚每次和真真走的步数和为3,诚诚肯定先走到C点。
【解析】(1)正方形ABCD由81个边长为1的小正方形组成,每个角处剪掉9个相等的正方形。每个角剪掉的正方形边长为3,因9=3×3。剪掉四个角后,剩余部分的面积为81 4×9=81 36=45。剩余部分可以折叠成一个无盖的正方体。正方体的边长为3,因为45=3×3×5。正方体的体积为3×3×3=27。
(2)蚂蚁从点A到点C需要爬行的总距离为9+9=18个单位。蚂蚁的速度是每秒钟爬两个单位,因此蚂蚁爬到终点的时间为18÷2=9(秒),由于蚂蚁只能向右或向上爬,所有路径的总距离都是18个单位,因此蚂蚁爬到终点的时间不会随着爬行路径的不同而发生变化。
(3)从点A到点C需要走的总步数为9+9=18步。真真和诚诚每次只能走1步或2步,且每次只能走一个或两个单位长度。诚诚每次和真真走的步数和为3,即真真走1步,诚诚就走2步;真真走2步,诚诚就走1步。这样诚诚每次都能保证自己走的步数和真真走的步数和为3。
6.解:100x2÷4=50(秒)
100x3÷4=75(秒)
乙在C到B的时间段是:50--75;125--150;200--225等.
甲在由C到B的方向上,到达C的时间是:
(80+40+120x2)-5=84(秒);204;324等
204-200=4(秒)
4x4÷(5-4)= 16(秒)
100-16x5=20(米)
答:甲第一次从背后追上乙的地点离B点20米。
【解析】由已知条件和图形可知:甲要从背后追上乙,必须具备2个条件:一是方向是由C向B;二是在同一时间甲到C点而乙过C点不久。
乙在C到B的时间段是:100x2-4=50(秒)---100x3-4=75(秒);125--150;200--225等等甲在由C到B的方向上,到达C的时间是:(80+40+120x2)-5=84(秒);204;324等.对照可得,符合要求的时间是204秒,即此时乙刚过C点4秒,距C点是4x4=16(米),甲追上乙用时是16÷(5-4)=16(秒),此时甲已离开C的距离是16x5=80米,再求离B距离即可.
7.(1)6
(2)解:∵a=6,b=2,
∴动点P改变速度后y与出发后的运动时间x(秒)的函数关系式为:y=6+2(x﹣6)=2x﹣6
①当0≤x≤6时
AP=x(cm)
S△APD==4x
②当6<x≤8时
AP=6+(x﹣6)×2=2x﹣6
S△APD==8x﹣24
③当x运动到C点时
2x﹣6=18解得:x=12
即:8<x≤12时
S△APD==40
④当12<x≤17时
DP=2DC+BC﹣(2x﹣6)=﹣2x+34
S△APD==﹣8x+136
综上:S△APD=;
S△APD=
①4x=20时,x=5∈[0,6],符合
②2x﹣6=20时,x=13(6,8],舍去
③8<x≤12时,S△APD=40≠24,舍去
④﹣8x+136=20,x=14.5∈(8,12],符合
所以点P出发后5秒或14.5秒,△APD的面积S1是长方形ABCD面积的
【解析】解:根据图象可知
S△APD=
∴a=6
故答案为:6
【分析】(1)根据三角形的面积公式可求a的值;
(2)①P在AB上运动时,S△APD=,AP为运动时间t的一次函数;
②P在BC上运动时S△APD=为定值.
③P在DC段上运动时,S△APD=.DP为P点运动时间的一次函数.
先计算△APD的面积,然后将计算出来的数值代入所求函数的不同分段,解出对应的x的值,若解出的x值在对应的分段区间内,则x的值即为所求的解,反之则不是.
8.(1)解:如图:
当电子鼠P爬到和B点重合时,三角形APE第一次成为等腰直角三角形,
需要:12÷1=12(秒)
当爬到CD边的中点时,三角形APE第二次成为等腰直角三角形,
需要:(12+6+6)÷1
=24÷1
=24(秒)
答:电子鼠P从A点出发12秒后,三角形APE第一次成为等腰直角三角形;经过24秒后,三角形APE第二次成为等腰直角三角形。
(2)解: ①如图:
可设电子鼠Q从A点出发x秒后四边形AQPE是梯形,
12-x=2x
3x=12
x=4
答:电子鼠Q从A点出发4秒后,四边形AQPE是梯形。
②如图:
图中电子鼠Q从A点向上运动,电子鼠P同时从C点向下运动时,当∠QPD=45°时,PF=6cm,PC+AQ=6cm。又因为电子鼠Q的速度是电子鼠P的2倍,所以电子鼠Q行驶路程也是电子鼠P的2倍,AQ= 。而四边形AQPE为四边形,可以将其分割成一个梯形AQPD和一个三角形PED,分别求出这两个图形面积是:(4+10)×6÷2=42(cm2)
6×10÷2=30(cm2)
所以四边形面积为42+30=72(cm2)。
答:四边形AQPE的面积是72平方厘米。
【解析】由图可知:当电子鼠P爬到和B点重合时,三角形APE第一次成为等腰直角三角形;当爬到CD边的中点时,三角形APE第二次成为等腰直角三角形;然后求出A点到B点的距离及A点到CD中点的距离,进而根据:路程÷速度=时间,分别解答即可。
(2)①当DP∥AQ时,AQPE就是梯形,可设电子鼠Q从A点出发x秒后四边形AQPE是梯形,列式为12-x=2x,解答即可。
②当∠QPD=45°时,PF=6cm,PC+AQ=6cm。又因为电子鼠Q的速度是电子鼠P 的2倍,所以电子鼠Q行驶路程也是电子鼠P 的2倍,AQ=,然后将其分割成一个梯形AQPD 和一个三角形PED,分别求出这两个图形面积,进一步解答即可。
9.解:如图
开始时,甲乙蚂蚁的速度比是4:5,则路程比也是4:5
所以,甲蚂蚁爬行的路程为108×2÷(4+5)×4=96(厘米),
乙蚂蚁爬行的路程为108×2 96=120(厘米),由于第二次甲与乙蚂蚁在BC中点相遇,
则由第一次相遇到第二次相遇甲蚂蚁爬行的路程是120 108÷2=66(厘米),
乙蚂蚁爬行的路程是96+108+108÷2=258(厘米).
由于第一次相遇后乙蚂蚁增加了15的速度,所以,相遇后甲乙蚂蚁的速度比为4:(5×15)=2:3,
故甲蚂蚁爬行66厘米路程时,乙蚂蚁爬行的路程是66÷2×3=99(厘米),
则甲蚂蚁停留的10秒钟,乙蚂蚁爬行的距离是258 99=159(厘米),
乙最初的爬行速度是159÷10÷(1+15)=13.25(厘米/秒)
甲的速度是13.25÷5×4=10.6(厘米/秒),
答:甲的速度是10.6厘米/秒,乙的速度是13.25厘米/秒。
【解析】先根据甲乙蚂蚁的速度比求出第一次相遇时,甲乙蚂蚁爬行的路程,再求出第一次相遇后,甲乙蚂蚁的速度比,进而求出甲蚂蚁停留的10秒钟,乙蚂蚁所爬行的路程,即可得出结论.
10.(1)5
(2)解:把小红与爷爷的年龄差看做木棒AB,
类似爷爷比小红大时看做当A点移动到B点时,此时B点所对应的数为-40,
小红比爷爷大时看做当B点移动到A点时,此时A点所对应的数为125,
∴可知爷爷比小红大[125-(-40)]÷3=55,可知爷爷的年龄为125-55=70.
答:爷爷的年龄是70岁.
【解析】(1)解:由数轴观察知三根木棒长是20-5=15(cm),则此木棒长为:15÷3=5cm,
故答案为:5
【分析】(1)此题关键是正确识图,由数轴观察即可得到木棒长。
(2)借助数轴用数形结合的方法求解.类似爷爷比小红大时看做当A点移动到B点时,求出此时B点所对应的数,小红比爷爷大时看做当B点移动到A点时,求出此时A点所对应的数,可知爷爷的年龄.
11.(1)解:当P在线段AB上时,因为P=2PB,AB=60cm
所以PA=60÷(1+2)×2=40(cm)
OP=0A+20=40+20=60(cm),
又因为点P 从点O沿OM 方向以1cm/s 的速度勺速运动,
所以60÷1=60(秒)
即点P 运动时间为 60 秒。
若AQ=AB,则BQ=AB=×60=40(cm),CQ=BC+BQ=10+40=50(cm)
点Q的运动速度为:50÷60=(cm/s)
若BQ=AB=×60=20(cm),CQ=BC+BQ=10+20=30(cm)
点Q的运动速度为:30÷60=(cm/s)
答:当P在线段AB上时,点Q运动的速度是cm/s或cm/s。
(2)解:设运动时间为t秒,则:
t+3t=90+70或t+3t=90-70,
解得:t=40或5
因为点Q运动到点O时没法继续运动,所以点Q最多运动30秒。
即t=40(不合题意,舍去)
所以t=5。
QO=CB+BA+AO=10+60+20=90(cm)
90÷3=30(秒)
即当点Q运动 30秒到点O时,点Q没法运动,P,0距离为70cm,即OP=70cm,
70÷1=70(秒)
即运动时间为 70·秒。
故经过5秒或70秒,两点相距70cm。
答:经过5秒或70 秒时P、Q两点相距70cm。
(3)解:如下图所示:
设OP=xcm
点P在线段AB上,因为OA=20cm,AB=60cm
所以20≤x≤80
OB-AP=OA+AB-(OP-OA)=20+60-(x-20)=100-x
EF=OF-OE=OA+AB-OE=20+×60-x=50-x
所以==2
答:的值是2。
【解析】(1)从题中我们可以看出点P及Q是运动的,当PA=2PB时实际上是P正好到了AB的三等分点上,而且PA=40, PB=20.由速度公式就可求出P点的运动时间,也是点Q的运动时间,点Q运动到的位置恰好是线段AB的三等分点,由此就可求出CQ长和点Q的速度.
(2)若点Q运动速度为5cm/s,经过多长时间P、Q两点相距70cm,这也有两种情况即当它们相向而行时,和它们背向而行时,此题可设运动时间为t秒,列方程就可解了.
(3)此题就可把它当成一个静止的线段问题来解决了,但必须借助图形.
12.(1)-4;4
(2)解:∵n=4,
∴点N在数轴上表示有理数4,
∵点B在数轴上表示有理数6,
∴B点位置如图所示,
∵MS=SN=6,
由题意知,DPN=MS+NS-PM=12-3t,DQN=|6-4-t|=|2-t|,DMN=MS+SM=6+6=12,
∵DPN+DQN=DMN-2,
∴12-3t+|2-t|=12-2,
当t≥2时,12-3t+t-2=12-2,
∴t=0(舍去),
当0<t<2时,12-3t+2-t=12-2,
∴t=1时,使得DPN+DQN=DMN-2;
(3)解:存在t使得DPM=3DQN;理由如下,
∵MS=SN=9,
∴相遇时,两点各自运动的时间为(9+9)÷(2+1)=6(秒),
动点P从点M出发以每秒2个单位长度沿着“拱形数轴”向正方向运动,同时点Q从点N出发,以每秒1个单位长度沿着“拱形数轴”向负方向运动,
∴当0<t<6时,DPM=2t,DQN=t,
∴2t=3t,
∴t=0(舍去),
当t≥6时,DPM=12-(t-6)=18-t,DQN=6-(t-6)=12-t,
∴18-t=3(12-t),
∴t=9,
∴当t=9时,DPM=3DQN.
【解析】解:(1)点M,N在数轴上分别表示有理数m,n且满足(m+4)2+|n-4|=0,
∴m+4=0,n-4=0,
∴m=-4,n=4,
故答案为:-4,4;
【分析】(1)由题中条件,利用平方与绝对值非负性,结合非负式和为0的条件求解即可得到答案;
(2)由含t的代数式表示出DPN,DQN,DMN,再列方程求解即可得到答案;
(3)根据数轴上动点问题,分相遇前0<t<6和相遇后t≥6两种情况列方程求解即可得到答案;
根据题意,数形结合列方程求解是解决问题的关键.
13.(1)解:如图1
(平方米)
(2)解:如图2
(平方米)
(3)解:因为16÷1=16,16÷2=8,
所以每经过16秒,点P和点Q 都回到出发点M。
2015÷16=125……15(秒)
第2015 秒点 P、点Q 的位置与第15秒时相同,△NPQ 的面积是6平方米。
【解析】(1)第1秒时,P点移动1米,位于MD中点;Q点移动2米,恰好移动到D点。此时,△NPQ的底为正方形边长4米,高为3米(即MD的长度减去P点移动的距离),因此△NPQ的面积为:3×4÷2=6平方米。
(2)第15秒时,P点移动了15米,Q点移动了30米。由于正方形的周长为16米,P点会在16秒后回到M点,Q点则在8秒后回到M点。所以,第15秒时,P点位于MD中点,Q点位于A点,即Q点与A点重合。此时,△NPQ的底仍为4米,高为3米(与第1秒时相同),面积为:3×4÷2=6平方米。
(3)第2015秒时,P点和Q点的位置与第15秒时相同。由于2015÷16=125...15,表示P、Q完成了125圈循环后,还额外移动了15秒,即回到与第15秒时相同的位置。所以,第2015秒时,△NPQ的面积同样为6平方米。
14.(1)解:已知A点对应的数是 1,B点对应的数是8。
在数轴上,两点间的距离等于右边的点对应的数减去左边的点对应的数,所以AB=8 ( 1)=8+1=9。
因为BCAC =45 ,且AB=AC+BC=9,
设AC=5x,BC=4x,则5x+4x=9,即9x=9,
解得x=1。
所以AC=5×1=5,
BC=4×1=4。
C点在B点左侧,C点对应的数等于B点对应的数减去BC的长度,即8 BC=8 4=4。
答:C点对应的数是4。
(2)解:当M、N未相遇时
此时M在AC上运动,M运动的速度是每秒2个单位长度,运动时间为t秒,那么M表示的数是起始点A对应的数 1加上运动的距离2t,即 1+2t。
N从B点出发,以每秒1个单位长度的速度沿数轴匀速向左运动,运动时间为t秒,所以N表示的数是B点对应的数8减去运动的距离t,即8 t。
因为MN=4,所以N表示的数减去M表示的数等于4,可列方程:
8 t ( 1+2t)=4
解得,t=
当M、N相遇后
M从A点运动到C点所用时间为:,在C点停留2秒,所以M从A点出发到在BC上运动时,总共用时t秒,此时M表示的数是4+2(t 25 2)=4+2(t 29 )=2t 5。
N表示的数依然是8 t。
因为MN=4,所以M表示的数减去N表示的数等于4,可列方程:
2t 5 (8 t)=4
解得,t=
综上所述,t的值为 或。
【解析】(1)根据已知的A、B两点对应的数以及BCAC 的比例关系,求出AC和BC的长度,进而确定C点对应的数。
(2)需要分M、N未相遇和相遇后两种情况,根据M、N在不同时刻表示的数以及MN=4这个条件列出方程求解。
15.(1)解: 点C表示的数为3,BC=2,AB=6 ,OB=3-2=1;AO=6-1=5所以A表示-5;答: 数轴上点A表示的数为 -5.;解:点C表示的数为3,BC=2,OB=3-2=1,所以 B表示 1;答: 点B表示的数为 1.
(2)解:①由题意得,如图:
t秒后,
点p表示的数为:-5+2t,
点Q表示的数为:3-t,
M为AP的中点 ,所以点M表示的数为:,
因为,所以CN=,
所以点N表示的数为:;
②由题意可,如图:P在左侧,Q在右侧时,
OP=5-2t,OQ=3-t,
原点O恰好是线段PQ的中点 ,所以5-2t=3-t;
解得t=2;
如图:Q在左侧,P在右侧时,
OP=2t-5,OQ=t-3,
原点O恰好是线段PQ的中点 ,所以2t-5=t-3;
解得t=2;
当t=2时,P在左侧,不成立,舍去;
综上,t=2时,原点O恰好是线段PQ的中点。
答:点M表示的数为:,点N表示的数为:;t=2时,原点O恰好是线段PQ的中点。
【解析】(1)根据图片A,B,C点的位置,3-2即为B的位置,6-1即为A的位置,由于A在负半轴,所以A为-5;
(2)①根据题意标出点,点P以每秒2个单位长度的速度沿数轴向右匀速运动,先求出点p表示的数, M为AP的中点 ,即可求出M, 点Q以每秒1个单位长度的速度沿数轴向左匀速运动 ,,先求出点Q表示的数,即可求出点N;
②分点讨论,P在左侧,Q在右侧时,原点O恰好是线段PQ的中点 ,所以5-2t=3-t,解得t=2;Q在左侧,P在右侧时不成立故舍去。
16.解:设AP=AQ=x,阴影部分的面积为S,则S=12×8-12×x2,
即S=96-12x2,
当AP=2cm时,则S=96-12×22=94( cm2),
当AP=8cm时,则S=96-12×82=64( cm2).
所以阴影部分面积减少了94-64=30(cm2).
答: 图中阴影部分的面积是减少了,减少了30平方厘米.
【解析】分析题目,设AP=AQ=x,阴影部分的面积为S,则由图形可知S=12×8-12×x2,即S=96-12x2;
接下来把AP=2和AP=8分别代入关于S的表达式中进行计算,可得对应的S的值;然后将得出的面积相减,即可得到结果.
17.(1)解:-2-1+2
=-3+1
=-1
答:第一次移动后点在数轴上对应的数为-1。
(2)解:-1-2+4
=-3+4
=1
答:第二次移动后点在数轴上对应的数为1。
(3)解:1-3+6
=-2+6
=4
答:第三次移动后点在数轴上对应的数为4。
(4)解:点P在数轴上的数依次是:-2、-1、1、4,
所以第n次移动后点P在数轴上对应的数是-2+=。
【解析】(1)、(2)、(3)根据左减右加,用开始的点减去向左移动的个数再加上向右移动的个数即可。(4)写出前几个点P的位置,发现第一次移动后的点是-2+1,第二次移动后的点是-2+1+2,第三次移动的点是-2+1+2+3,因此,第n次移动后的点就是-2+1+2+3+……n,据此总结规律即可。
18.(1)解:当点P在AB—BC上运动时,
① 当0
当0
当点P运动到点C时,用的时间为:(4+4)÷2=4(s)
此时点M正好运动到点D,当点M与点Q第一次重合时,有:4(t 4)+(t 4)=4
解得:t=
当点M与点P第二次重合时,有:4(t-5)=2+2(t-5)
解得:t=6
此时点P、M都运动到D处,综上分析可知,
当或时,点M落在线段PQ上。
【解析】(1)分析点P和点Q的运动规律,根据它们的速度和初始位置,可以用含t的代数式表示它们在不同时间段内的位置。
根据题目要求,分别求解当点P在AB—BC上运动时,线段BP的长度表示式以及当BQ=2BP时,t的值。
(2)考虑动点M的运动情况,当点P与点M第一次重合时,我们求解t的值,并直接写出此时线段DP的长度。分析当点M落在线段PQ上时,t的取值范围,通过解方程和不等式,我们得出t的具体取值范围。
19.(1)解:根据图象可知S△APD=AD×AP=×1×a×8=24,
∴a=6
b==2
c=8+(10+8)=17
(2)8;y=2x-6
(3)解:①当0≤x≤6时
AP=x(cm)
S△APD=AD×AP=4x
②当6<x≤8时
AP=6+(x-6)×2=2x-6
S△APD=AD×AP=8x-24
③当x运动到C点时
2x-6=18解得:x=12
即:8<x≤12时
S△APD=AD×AB=40
④当12<x≤17时
DP=2DC+BC-(2x-6)=-2x+34
S△APD=AD×DP=-8x+136
综上:S△APD=
S△APD=s四边形ABCD=AD×AB=20
①4x=20时,x=5∈[0,6],符合
②2x-6=20时,x=13 (6,8],舍去
③8<x≤12时,S△APD=40≠24,舍去
④-8x+136=20,x=14.5∈(8,12],符合
所以点P出发后5秒或14.5秒,△APD的面积S1是长方形ABCD面积的。
【解析】解:(2)因为a=6,b=2,
所以动点P改变速度后y与出发后的运动时间x(秒)的函数关系式为:y=6+2(x-6)=2x-6
当x=7时,y=2×7-6=14-6=8
故答案为:(2)8;y=2x-6。
【分析】 (1)根据三角形的面积公式可求a、b及图②中c的值;
(2)确定y与x的等量关系后列出关系式即可;
(3)①P在AB上运动时,S△APD=AD×AP,AP为运动时间t的一次函数;
②P在BC上运动时S△APD=AD×AB为定值.
③P在DC段上运动时,S△APD=AD×DP.DP为P点运动时间的一次函数.
先计算△APD的面积,然后将计算出来的数值代入所求函数的不同分段,解出对应的x的值,若解出的x值在对应的分段区间内,则x的值即为所求的解,反之则不是.
20.解:由图象可知as时有:
×8× AP=24
4AP=24
AP = 6
又因为P的速度为1,所以a=6÷ 1= 6(s);
当a=8时,S为40,即P点速度变化后到B点用了2s,则
b=(10-6) ÷2
=4÷2
= 2(cm/s)
c=18÷2+8
=9+8
= 17(s)
答: a、b、c的值分别为6、2、17。
【解析】结合图象分析可知APD面积的变化情况:当点P在AB 上运动时,因为三角形高不变,底边增大,所以APD的面积逐渐增大:点P在BC上运动时,因为此时三角形同底等高,所以APD面积不变;点P在CD上运动,因为高不变,底边缩小,所以APD面积逐渐减小。再利用图找出关键点,a秒时,三角形面积是24,即可求出AP长度,a的值可求出;利用动点P改变速度后到B点的时间与路程可求出速度b; c的值为P运动到D点的时间。
21.(1)2
(2)解:存在,有两种情况:
第一种情况:当点P在AB边上时,,
解得:,即
第二种情况:当点 在BC边上时,如图,
设,则,解得:,
所以
答:当x为cm或3cm时,可使三角形APE的面积为。
【解析】解:(1)当点P与点B重合时,如图
即
故答案为:2
【分析】(1)点P运动到点B,连接AE、PE,观察所形成的图形的底边和高与正方形边长的关系,即可求解。
(2)分析题意,要使三角形APE的面积为 ,首先要判断出三角形APE是否为直角三角形,据此可以分两种情况进行讨论:若点P在AB边上时,令△APE的面积为- ,求解即可;若点 在BC边上时,设,令 的面积=,根据关系列方程,即可确定x的值。
22.(1)解:甲小球到原点的距离为:2+1×10=12cm;
乙小球碰到挡板后返回的速度:2×1.5=3(厘米/秒)
乙小球到原点的时间为:10-6÷2=7(秒)
乙小球到原点的距离为:7×3=21cm
答:当t=10时,甲小球到原点的距离为12cm;乙小球到原点的距离为21cm.
(2)解:甲球运动的路程为:1×t=t,
∵OA=2
∴甲球到原点的距离为:t+2;
乙球到原点的距离分两种情况:
当0<t≤3时,乙球运动的路程为:2×t=2t
∵OB=6
∴乙球到原点的距离为:6-2t
由题意得:t+2=6-2t
3t=4
当t>3时,乙球到原点的距离为:2×1.5×﹙t-6÷2﹚=3﹙t-3﹚
由题意得:t+2=3﹙t-3﹚
t+2=3t-9
2t=11
t=5.5
综上所述,当或t=5.5时,甲、乙两小球到0点的距离相等。
【解析】熟知路程、速度、时间三者之间的等量关系是解题关键。路程、速度、时间三者之间的等量关系为:路程=速度×时间;速度=路程÷时间;时间=路程÷速度;
(1)根据”路程=速度×时间“可知:甲球运动的路程为:1×10=10cm,由OA=2cm,可得:甲小球到原点的距离为:2+1×10=12cm;乙小球碰到挡板后返回的速度:2×1.5=3(厘米/秒);乙小球到原点的时间为:10-6÷2=7(秒);乙小球到原点的距离为:7×3=21cm,即可得出答案;
(2)根据乙球的运动轨迹,分0<t≤3和t>3两种情况讨论,由甲球到原点的距离为:t+2;当0<t≤3时,乙球到原点的距离为:6-2t;根据甲、乙两小球到0点的距离相等可列出关于t的一元一次方程,解得t的值;当t>3时,乙球到原点的距离为:2×1.5×﹙t-6÷2﹚=3﹙t-3﹚,根据甲、乙两小球到0点的距离相等可列出关于t的一元一次方程,解得t的值,即可得出答案。
23.解:把楼梯的各条线段进行平移,可得AB+BC=楼梯A→C的总长;
设A→C的路程为x米,则猫行走的路程为x+1.5米,老鼠行走的路程为x-1.5米,
因为猫和老鼠行走的时间相同,且老鼠的速度是猫的,
根据时间一定时,路程与速度成正比的性质可得:
,根据比例的基本性质可得:
解得x=6.5
答:A→C的路程为6.5米.
【解析】 把楼梯的各条线段进行平移,可得到一个长方形ABCE;可得AB+BC=楼梯A→C的总长(即这个长方形周长的一半);猫捉鼠的路程之和为楼梯A→C的总长+线段CD长;老鼠逃窜的路程为AB+BC-线段CD长;根据时间一定时,所行走的路程与速度成正比的性质即可解决问题.
24.(1)解:当时,橡皮筋刚好触及钉子
,
所以,
(2)解:当时
AQ=x,BP=2x-2,OE=1
即
所以,当 时,
(3)解:x=2
【解析】(1)当橡皮筋触及到钉子时,由于Q在边AD上,且速度为1cm,所以在x秒后,Q移动的距离为xcm。由于正方形边长为2cm,所以当橡皮筋触及到钉子时,点Q已经移动了整个边长,即移动了2cm,因此,有等式:,其中,(2x-2)是点P移动的距离,因为点P从点A开始移动了(2x-2)cm到达边BC,解以上方程即可求解
(2)先求出时,x和y之间的关系式:,代入x即可求解。
(3)当橡皮筋刚好触及钉子时,,停止时,,,,所以,,所以,此时x=2
25.解:当点P运动到B点时,S△APD=AB×AD÷2
=8×10÷2
=40(cm2);
所以当点P运动a秒时,点P在AB之间,设该点为E
AE×AD÷2=24,即4AE=24,AE=6;
a=6÷1=6(s);
点P速度变化后到B点用了8-6=2(秒);
b=EB÷2
=(10-6)÷2
=4÷2
=2(cm/s);
c=(BC+CD)÷2+8
=(8+10)÷2+8
=9+8
=17(s)
答: 的值分别为 。
【解析】由图可知,当点P运动到B点时,S△APD=AB×AD÷2=40(cm2),所以当点P运动a秒时,点P在AB之间,设该点为E,根据三角形面积计算公式即可求出AE的长度,再用AE的长度除以点P的速度即可求出a的值。由图象可知,当点P运动8秒时,点P运动到了点B,因此,用8减去a的值求出点P在EB上的运动时间,接着再用EB的长度除以该运动时间即可求出b的值。由图象可知,8到c的这段时间,点P由B点运动到D点,因此,用BC加CD的长度除以b可以求出8到c的这段时间,再加上8即可求出c的值。
26.解:如图,
由题意可知,丙从D到E用4分钟,丁从D到F用10分钟,乙从E经D到F用6分钟,说明甲(或乙)速度是丙(或丁)的:
因为甲走AD用10分钟,所以丙走AD要用,走AE用
因为乙走(BA+AE)用14分钟,所以,丙走AB用
因为AB长60米,所以丙每分钟走
于是求出:
AE=,ED=
DF=,FC=
=
=
=2497.5(平方米)
答: 的面积为2497.5平方米。
【解析】由题意可知,丙从D到E用4分钟,丁从D到F用10分钟,乙从E经D到F用6分钟,说明甲(或乙)速度是丙(或丁)的:
因为甲走AD用10分钟,所以丙走AD要用,走AE用
因为乙走(BA+AE)用14分钟,所以,丙走AB用
因为AB长60米,所以丙每分钟走
于是求出:
AE=,ED=
DF=,FC=
所以,,代入数据即可求出
27.(1)2x;10-2x
(2)3
(3)小凯的说法是错误的,EC的长度不变。因为E点是线段AB 的中点,C点是线段BD的中点,所以AB=2×BE,BD=2×BC,AB+BD=2×(BE+BC)=2×EC=10,所以EC的长度不变,为5cm。
【解析】(1)路程=速度×时间 AB=2x
BD=AD-AB=10-2x
(2)把x=2代入10-2x中,10-2×2=6(cm),BC=BD÷2=6÷2=3(cm)
(3)小凯的说法是错误的,EC的长度不变。因为E点是线段AB 的中点,C点是线段BD的中点,所以AB=2×BE,BD=2×BC,AB+BD=2×(BE+BC)=2×EC=10,所以EC的长度不变,为5cm。
故答案为:(1)2x (2)3
【分析】(1)根据路程=速度x时间,求出AB的长度,然后用AD的长度减去AB的长度就是BD的长度,分别用含有字母x的式子表示即可。(2)把x=2代入式子中,求出BD的长度,再根据C点是线段BD的中点,求出 BC的长度。(3)E点是线段AB的中点,C点是线段BD的中点,所以线段EC的长是AD的一半,EC的长度不变。
21世纪教育网(www.21cnjy.com)
同课章节目录
