2025年北京市高三数学一模试题分类汇编——空间向量与立体几何(含解析)
文档属性
| 名称 | 2025年北京市高三数学一模试题分类汇编——空间向量与立体几何(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-26 16:09:30 | ||
图片预览



文档简介
2025年北京市高三数学一模试题分类汇编——空间向量与立体几何
学校:___________姓名:___________班级:___________
一、单选题(本大题共13小题)
1.[2025北京延庆·一模]某圆锥高为,母线与底面所成的角为,则该圆锥的表面积为( )
A. B. C. D.
2.[2025北京西城·一模]设直线平面,平面平面直线,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.[2025北京丰台·一模]已知,是两条不同的直线,,是两个不同的平面,则下列命题正确的是( )
A.若,,,则 B.若,,则
C.若,,,则 D.若,,,则
4.[2025北京平谷·一模]冰淇淋蛋筒是大家常见的一种食物,有种冰淇淋蛋筒可以看作是由半径为10cm,圆心角为的扇形蛋卷坯卷成的圆锥,假设高出蛋筒部分的奶油和包裹在蛋筒内部的奶油体积相等,则该种冰淇淋中奶油的总体积约为( )(忽略蛋筒厚度)
A. B.
C. D.
5.[2025北京东城·一模]祈年殿(图1)是北京市的标志性建筑之一 距今已有600多年历史.殿内部有垂直于地面的28根木柱,分三圈环形均匀排列.内圈有4根约为19米的龙井柱,寓意一年四季;中圈有12根约为13米的金柱,代表十二个月;外圈有12根约为6米的檐柱,象征十二个时辰.已知由一根龙井柱和两根金柱形成的几何体(图2)中,米,,则平面与平面所成角的正切值约为( )
A. B. C. D.
6.[2025北京石景山·一模]如图,在棱长为2的正方体中,M,N,P分别是,,的中点,Q是线段上的动点(不包含端点),给出下列三个命题:
①对任意点Q,都有;
②存在点Q,使得平面;
③过点Q且与垂直的平面截正方体所得截面面积的最大值为.
其中正确的命题个数是( )
A.0 B.1 C.2 D.3
7.[2025北京门头沟·一模]某纪念塔的一部分建筑结构可抽象为三棱锥,,底面是等腰直角三角形,,顶点到底面的距离为3,则点到平面的距离为( )
A. B. C. D.
8.[2025北京房山·一模]如图,将棱长为2的正方体六个面的中心连线,可得到八面体,为棱上一点,则下列四个结论中错误的是( )
A.平面
B.八面体的体积为
C.的最小值为
D.点到平面的距离为
9.[2025北京丰台·一模]如图,正方体的棱长为2,为的中点,为线段上的动点,给出下列四个结论:
①存在唯一的点,使得,,,四点共面;
②的最小值为;
③存在点,使得;
④有且仅有一个点,使得平面截正方体所得截面的面积为.
其中所有正确结论的个数为( )
A.1 B.2 C.3 D.4
10.[2025北京海淀·一模]已知纸的长宽比约为.现将一张纸卷成一个圆柱的侧面(无重叠部分).当该圆柱的高等于纸的长时,设其体积为,轴截面的面积为;当该圆柱的高等于纸的宽时,设其体积为,轴截面的面积为,则( )
A., B.,
C., D.,
11.[2025北京延庆·一模]已知正方体的棱长为1,若在该正方体的棱上有点M,满足,则点M的个数为( )
A.2 B.4 C.6 D.8
12.[2025全国·一模]已知三棱锥的底面是正三角形,平面,,,,四点都在以为球心的球面上,,则与平面所成角的正切值为( )
A. B. C. D.
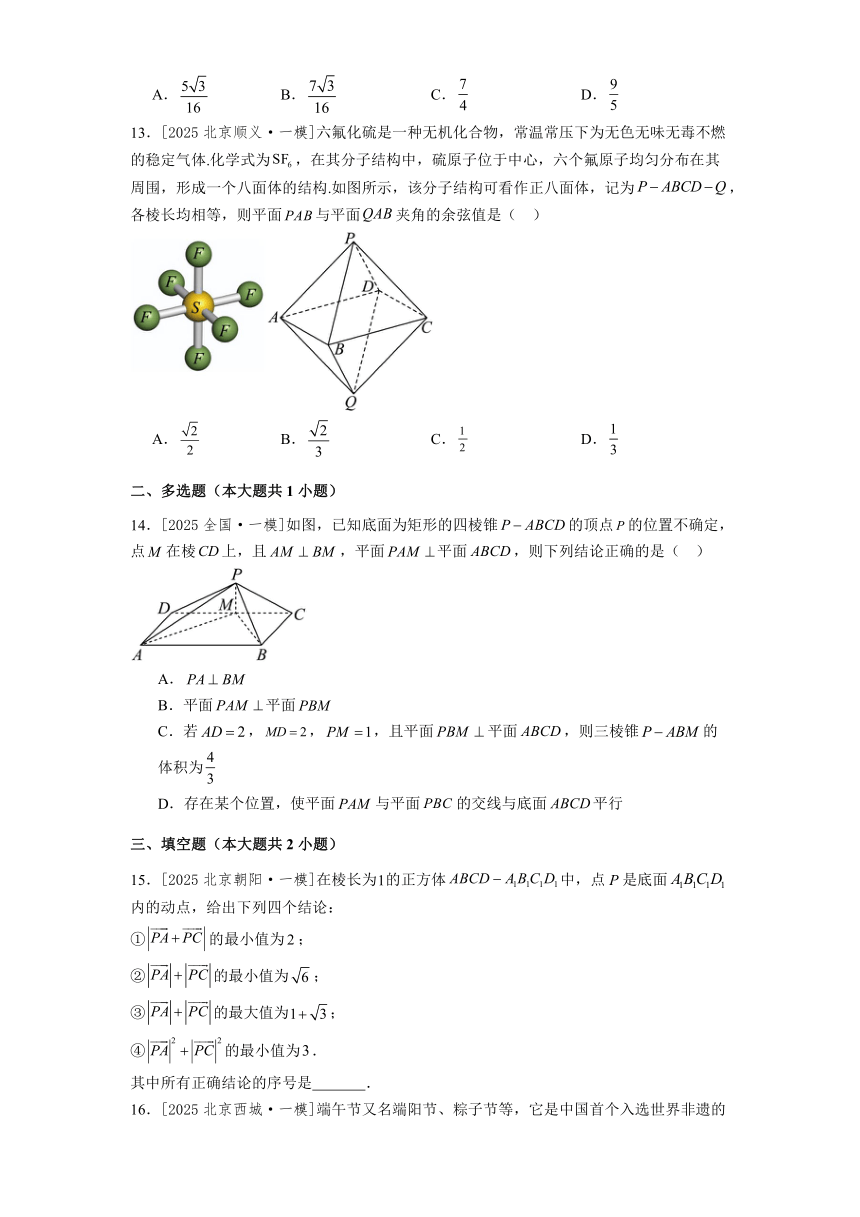
13.[2025北京顺义·一模]六氟化硫是一种无机化合物,常温常压下为无色无味无毒不燃的稳定气体.化学式为,在其分子结构中,硫原子位于中心,六个氟原子均匀分布在其周围,形成一个八面体的结构.如图所示,该分子结构可看作正八面体,记为,各棱长均相等,则平面与平面夹角的余弦值是( )
A. B. C. D.
二、多选题(本大题共1小题)
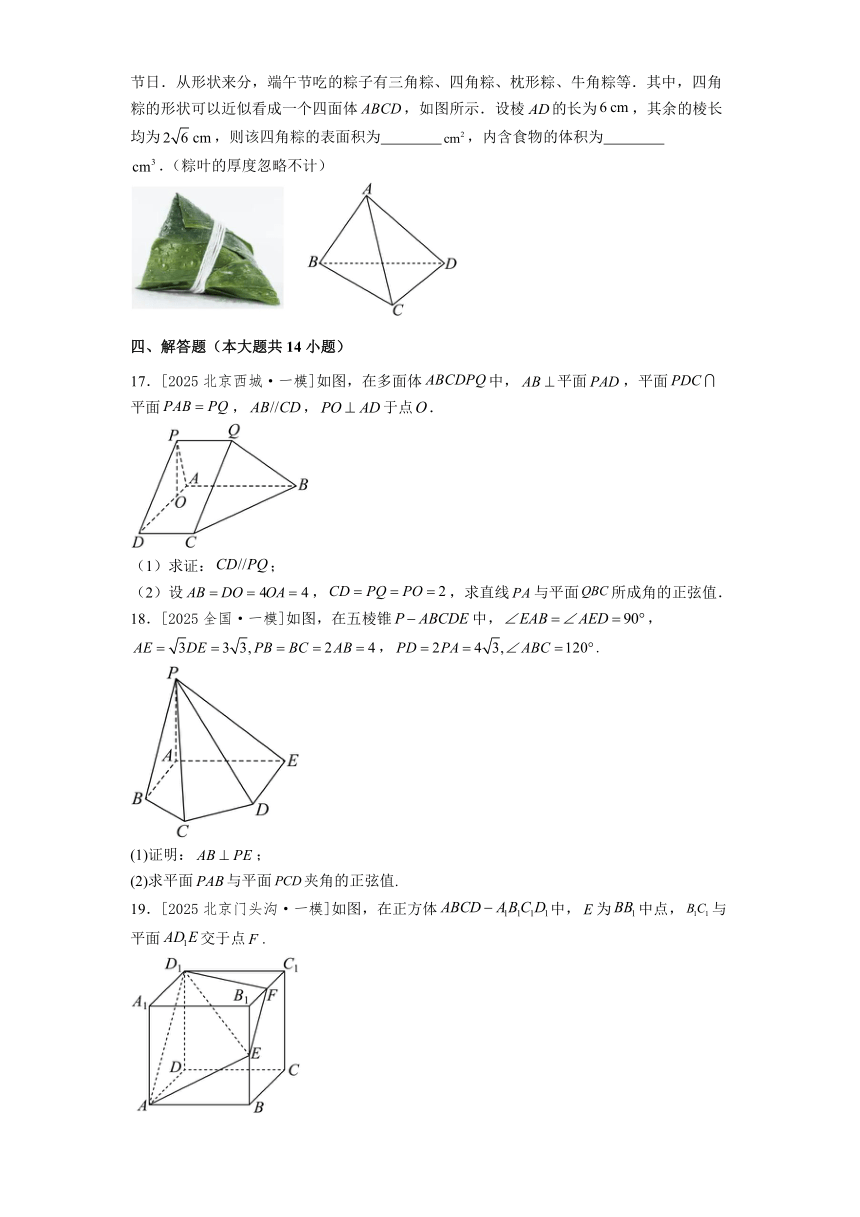
14.[2025全国·一模]如图,已知底面为矩形的四棱锥的顶点的位置不确定,点在棱上,且,平面平面,则下列结论正确的是( )
A.
B.平面平面
C.若,,,且平面平面,则三棱锥的体积为
D.存在某个位置,使平面与平面的交线与底面平行
三、填空题(本大题共2小题)
15.[2025北京朝阳·一模]在棱长为的正方体中,点P是底面内的动点,给出下列四个结论:
①的最小值为;
②的最小值为;
③的最大值为;
④的最小值为.
其中所有正确结论的序号是 .
16.[2025北京西城·一模]端午节又名端阳节、粽子节等,它是中国首个入选世界非遗的节日.从形状来分,端午节吃的粽子有三角粽、四角粽、枕形粽、牛角粽等.其中,四角粽的形状可以近似看成一个四面体,如图所示.设棱的长为,其余的棱长均为,则该四角粽的表面积为 ,内含食物的体积为 .(粽叶的厚度忽略不计)
四、解答题(本大题共14小题)
17.[2025北京西城·一模]如图,在多面体中,平面,平面平面,,于点.
(1)求证:;
(2)设,,求直线与平面所成角的正弦值.
18.[2025全国·一模]如图,在五棱锥中,,,.
(1)证明:;
(2)求平面与平面夹角的正弦值.
19.[2025北京门头沟·一模]如图,在正方体中,为中点,与平面交于点.
(1)求证:为的中点;
(2)求平面与平面夹角的余弦值.
20.[2025北京顺义·一模]如图,在四棱锥中,底面是菱形,,,.
(1)若平面与棱交于点,且平面,求证:是中点;
(2)若是棱上一点,且满足,当时,求与平面所成角的正弦值.
21.[2025北京海淀·一模]如图,五面体中,四边形是正方形.
(1)求证:;
(2)若平面平面,,,求直线与平面所成角的大小.
22.[2025北京延庆·一模]如图,在四棱锥中,底面ABCD是矩形,底面ABCD,且,E是PC的中点,平面ABE与线段PD交于点F.
(1)求证:;
(2)若,求直线BE与平面BCF所成角的正弦值.
23.[2025北京朝阳·一模]如图,在四棱柱中,平面,在四边形中,,为线段的中点.
(1)求证:平面;
(2)若平面平面,,求平面与平面夹角的余弦值.
24.[2025全国·一模]如图,直四棱柱的底面为正方形,点在棱上(包含端点).
(1)证明:平面平面;
(2)已知,求平面与平面所成二面角的正弦值的取值范围.
25.[2025全国·一模]如图,正四棱柱,其侧棱长与底面边长都为2,E,F分别为,的中点,平面与交于点P.
(1)确定点P在线段上的位置;
(2)求平面与平面夹角的余弦值.
26.[2025北京房山·一模]如图,在长方体中,为的中点,与平面交于点.
(1)求证:为的中点;
(2)若二面角的余弦值为,求的长度.
27.[2025北京丰台·一模]如图,在四棱锥中,平面平面,为等边三角形,,,.
(1)求证:平面;
(2)求直线与平面所成角的正弦值.
28.[2025北京平谷·一模]如图,在四棱锥中,平面平面等腰直角三角形,.
(1)点在棱上,若平面,求证:为的中点;
(2)求与平面所成的角.
29.[2025北京石景山·一模]如图,在四棱锥中,平面,,且,,,,,N为的中点.
(1)求证:平面;
(2)求二面角的余弦值;
(3)点M在线段上,直线与平面所成角的正弦值为,求点M到平面的距离.
30.[2025北京东城·一模]如图,在几何体中,四边形为平行四边形,平面平面.
(1)证明:平面;
(2)已知点到平面的距离为,再从条件①、条件②这两个条件中选择一个作为已知,求的长.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
参考答案
1.【答案】A.
【详解】由圆锥高为,母线与底面所成的角为,得圆锥底面圆半径,
母线,所以圆锥的表面积.
故选A.
2.【答案】A
【详解】已知直线平面,平面平面直线,
若,由平面,则;
若,此时得不到,直线可能与平面相交,如下图:
所以“”是“”的充分不必要条件.
故选A.
3.【答案】D
【详解】
如图,在正方体中分析选项A、B、C.
A.平面,平面,平面平面,但,A错误.
B.,平面,但平面,B错误.
C.平面平面,平面,,但平面,C错误.
D.取直线的方向向量,直线的方向向量,
∵,,∴分别为平面的法向量,
∵,∴,∴,D正确.
故选D.
4.【答案】D
【详解】设圆锥底面面积为,
由题意可知,
所以,
设圆锥得高为,则,
所以圆锥的体积为:,
所以该种冰淇淋中奶油的总体积约为,
故选D.
5.【答案】B
【详解】若平面平面,则平面与平面所成角,即为平面与平面所成角,
由题意有,即是等腰三角形,腰长约为8米,,易知,
若是的中点,连接,则,且平面,
由平面,则,都在平面内,
所以平面,则是平面与平面所成角的平面角,
其中,,则.
故选B.
6.【答案】C
【详解】以为原点,以所在直线为轴建立空间直角坐标系,
则,
设,
对于①,,
则,
所以,即,故①正确;
对于②,,
设平面的一个法向量为,
则,取,得,
要使平面,则,
则,即,不符合题意,
所以不存在点Q,使得平面,故②错误;
对于③,如下图,在平面内作⊥,垂足为点,
过点作在平面内作⊥交于,
因为平面平面,平面平面,
且平面,所以平面,
又平面,所以⊥,
因为,、平面,所以平面,
平面截正方体截面为平行四边形,
当与点重合时,为中点,截面面积最大,
此时,,截面面积为,故③对.
故选C.
7.【答案】C
【详解】
因为,且底面是等腰直角三角形,,
所以点在平面上的射影为边的中点,在直角三角形中,由勾股定理得,所以,
又因为底面是等腰直角三角形,,
;
设点到平面的距离为,则
,
所以.
故选C
8.【答案】D
【详解】
在正方体中,连接可知相交于点,且被互相平分,故四边形是平行四边形,
所以,而平面,平面,
所以平面,故A正确;
因为正方体棱长为2,所以四边形是正方形且,
面,,
所以八面体的体积等于棱锥体积的2倍,
而棱锥体积等于,
故八面体的体积为,B正确;
因为为棱上一点,将和展开成一个平面,
由题和均为正三角形,且边长为,
由三角形两边之和大于第三边知最小值为,在中由余弦定理可知,故C正确;
对于D选项:设点到平面的距离为,由等体积法知:
,故错误.
故选D.
9.【答案】B
【详解】对于结论①,取中点为,连接,,,,
因为正方体,为的中点,所以,
所以,,,四点共面,如图确定的平面与线段有且仅有一个交点,
故结论①正确;
对于结论②,因为,求的最小值,即求的最小值,
因为正方体,所以,,,四点共面,
所以与会相交于一点,设为,
此时,
因为,
所以的最小值为错误,
故结论②错误;
对于结论③,取,中点分别为,,连接,设交于点,若平面,
在平面中,易知,
所以,
所以,
所以,所以,
又因为平面,平面,
所以,
,平面,平面,
所以平面,
因为平面,平面,
所以,
所以存在点,使得,
故结论③正确;
对于结论④,当点与点重合时,截面为矩形,截面面积为,
当点为上靠近点的三等分点时,
取中点为,连接,,,,,,
此时四边形即为平面截正方体所得截面,证明如下:
已知平面,求证点为上靠近点的三等分点,
因为,所以,所以点为上靠近点的三等分点,得证,
又因为,且,,所以四边形为等腰梯形,面积为,
所以当点为上靠近点的三等分点时,截面面积为,
当点趋近于点时,截面面积趋近于3,
因为,,点从上靠近点的三等分点向点运动时,截面面积的变化是连续的,
所以点从上靠近点的三等分点向点运动时存在某点,使得截面面积为,
故线段上至少存在两个点使得截面面积为,
故结论④错误.
故选B.
10.【答案】B
【详解】不妨设纸的长宽分别为;
当圆柱的高等于纸的长时,也即圆柱高为时,设其底面圆半径为,则,解得,
故,
此时矩形轴截面的两条边长分别为,故;
当圆柱的高等于纸的宽时,也即圆柱高为时,设其底面圆半径为,则,解得,
故,
此时矩形轴截面的两条边长分别为,故;
综上所述,,.
故选B.
11.【答案】C.
【详解】因为,所以点M不在棱,棱上,
所以当点M在棱上时,设,连接,
在中,,
由余弦定理可得,,
即,可解得,
所以在棱上存在满足题意的一个点M;
由对称性可知在棱,棱,棱上各存在一个点M;
因为,所以点M不在平面内,
所以当点M在棱上时,设,连接,
在直角三角形中,,
所以,即,可解得,
所以在棱上存在满足题意的一个点M;
由对称性可知在棱上也存在一个点M;
综上,满足题意的点M共6个.
故选C.
12.【答案】C
【详解】设是中点,是中点,是正三角形的重心,则是的三等分点,,
由是边长为的正三角形知,,
在平面中,作,作的垂直平分线交于点,
因为平面,,易知四边形是矩形,,.
设与交于点,过作,垂足为,
因为平面,在平面内,
所以,又,为平面内两条相交直线,
所以平面,在平面内,
所以,又为平面内两条相交直线,
所以平面,
所以是与平面所成的角或其补角.
过作直线平行于,交于点,交于点,则,,
把,,,,,,
代入求得,,
在中,,,
在中,,
所以.
故选C.
13.【答案】D
【详解】
设正八面体的棱长为,连接、相较于点,连接,
根据正八面体的性质可知为正方形,,平面,
建立如图所示,以为坐标原点,
分别以、、为、、轴的空间直角坐标系,
,,,,
所以,,
设平面的法向量为,
所以,,令,
则有:,所以,
,,
设平面的法向量为,
所以,,令,
则有:,所以,
设平面与平面夹角为,则,
平面与平面夹角的余弦值为.
故选D.
14.【答案】ABC
【详解】对于A,∵平面平面,平面平面,,平面,∴平面,
又平面,∴,故A正确;
对于B,由A知平面,又平面,∴平面平面,故B正确;
对于C,在中,,,∴,,
∴,∴,
∵平面平面,平面平面,,平面,∴平面,
又平面,∴,同理可证,平面,∴平面,
而,∴三棱锥的体积为,故C正确;
对于D,设平面平面,假设底面,
∵平面平面,平面平面,
∴,,∴,则与重合,则,显然不成立,则假设不成立,故D错误.
故选ABC.
15.【答案】①②④
【详解】设点、、、关于平面的对称点分别为、、、,
设底面、的中心分别为点、,如下图所示:
对于①,易知为的中点,则,可得,
所以,,
当点与点重合时,底面,此时,取最小值,
即的最小值为,①对;
对于④,
,
当点与点重合时,底面,此时,取最小值,
则的最小值为,④对;
对于②,由对称性可知,,
则,
当且仅当点为线段与平面的交点时,取最小值,②对;
对于③,当点与点重合时,,
所以,的最大值不是,③错.
16.【答案】
【详解】,
所以为锐角,所以,
该四角粽的表面积
,
取中点为,连接,
则,
所以,即,
且,平面,
所以平面,
内含食物的体积为.
17.【答案】(1)见详解
(2)
【详解】(1)如图,因为,平面,平面,
所以平面,
又因为平面,平面平面,
所以,
(2)在平面内过点作.
因为平面,所以平面,
因平面,平面,所以,,
因平面,平面,则平面平面,
又因为,平面平面,则平面,
所以,,两两互相垂直.
以为原点,,,所在直线为轴,轴,轴建立空间直角坐标系,则,,,,
,,,,
由题意,得,
设平面的法向量为,
则,即,
令,则,,于是,
所以,
故直线与平面所成角的正弦值为.
18.【答案】(1)证明见解析
(2).
【详解】(1)证明:在中,,所以,
所以,即,
又,所以,
因为,平面,所以平面,
又平面,所以;
(2)连接,在中,,
所以,
在中,,
所以,所以,即,
由(1)知,,又因为,平面,
所以平面.
以A为坐标原点,以所在直线分别为轴建立如图所示的空间直角坐标系,
过点作⊥轴于点,
因为,所以,
又,故,
则,
故,
设平面的法向量为,
则即不妨令,则,
则为平面的一个法向量,
依题意,为平面的一个法向量,
设平面与平面的夹角为,
则,
又因为,
所以平面与平面夹角的正弦值为.
19.【答案】(1)证明见解析;
(2)
【详解】(1)依题意连接,如下图所示:
由正方体性质可得,又平面,平面,
可得平面,
因为与平面交于点,即平面平面,
可得,
因此,又为中点,
可得为的中点;
(2)以为坐标原点,所在直线分别为轴建立空间直角坐标系,如下图所示:
不妨设正方体的棱长为2,
可得,即;
设平面的一个法向量为,
则,令,可得,
即;
显然平面的一个法向量可以为,
因此平面与平面夹角的余弦值为;
可得平面与平面夹角的余弦值.
20.【答案】(1)证明见解析
(2)
【详解】(1)记,连接,如下图:
因为平面,平面,平面平面,所以,
在中,由为的中点,则为的中点.
(2)在菱形中,易知,由,,则,,
因为,,平面,所以平面,
因为平面,所以,由,则,
因为,平面,所以平面,
取的中点为,易知,则平面,则两两垂直,
以为原点,分别以所在直线为轴,建立空间直角坐标系,如下图:
则,,,
可得,,,,
由,则,可得,
设平面的法向量,则
令,则,所以平面的一个法向量,
设与平面所成角为,.
【方法总结】利用空间向量求解立体几何问题的一般步骤
(1)观察图形,建立恰当的空间直角坐标系;
(2)写出相应点的坐标,求出相应直线的方向向量;
(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求
出法向量;
(4)将空间位置关系转化为向量关系;
(5)根据公式求出相应的角或距离.
21.【答案】(1)证明过程见解析;
(2)
【详解】(1)因四边形是正方形,则,
又平面,平面,则平面,
又平面平面,则,故.
(2)因平面平面,,平面平面,
则平面,又平面,平面,
则,,
因,,则,则,
则以为原点,以所在直线为轴,轴,轴建立空间直角坐标系,
则,
则,
设平面的法向量为,
则,令,则,
则,
则直线与平面所成角的正弦值为,
又因其夹角取值范围为,故直线与平面所成角为.
22.【答案】(1)证明见解析;
(2).
【详解】(1)在矩形中,,又平面,平面,
所以平面,又因为平面,且平面平面,
所以.
(2)由(1)可知,又因为E是的中点,所以F是的中点,
因为,即,故.
因为平面平面,所以
又在正方形中,,所以两两垂直.
如图建立空间直角坐标系,
则
所以,
设平面的一个法向量为
由,得,令,得,
设直线与平面所成角为,则
故直线BE与平面BCF所成角的正弦值为.
23.【答案】(1)证明见解析
(2)
【详解】(1)连接.
因为为的中点,
所以.
又,所以四边形为平行四边形.
所以.
又因为,
所以.
所以四边形为平行四边形.
所以.
又因为平面平面,
所以平面.
(2)因为平面,
所以.
又因为平面平面,平面平面,
且平面,
所以平面.
所以.
所以两两垂直.
如图建立空间直角坐标系,
则.
所以.
因为平面,
所以是平面的法向量.
设平面的法向量为,
则,即,
令,则.于是.
设平面与平面夹角为,
则.
24.【答案】(1)证明见解析;
(2).
【详解】(1)证明:由四边形是正方形,得,
因为在直棱柱中平面,平面,所以,
因为,,平面,所以平面,
因为平面,所以平面平面;
(2)以,,所在直线分别为,,轴建立如图所示的空间直角坐标系,
所以,,,,,
设,则,故,,,
设平面的一个法向量为,则,取得,
设平面的一个法向量为,则,取得,
所以,
因为,所以,,,
所以,所以,
即平面与平面所成二面角的正弦值的取值范围是.
25.【答案】(1)点为线段上靠近点的三等分点
(2)
【详解】(1)如图,设的中点为,连接,记,连接,.
由题意知四边形为正方形,又为的中点,∴,,
∴四边形为平行四边形,∴.
又∵平面,平面,∴平面.
∵平面,平面平面,∴,
∴.
又∵为的中点,,∴点为的重心,
∴,∴,
即点为线段上靠近点的三等分点.
(2)以为坐标原点,分别以直线,,为x,y,z轴建立如图所示的空间直角坐标系.
则,,,,,,,
∴,,,,.
设平面的法向量为,
则,即,∴,
令,则,,∴;
设平面的法向量为,
由(1)知,∴,
∴,即,解得,
令,则,,∴.
设平面与平面的夹角为,则
,
即平面与平面夹角的余弦值为.
26.【答案】(1)证明见解析
(2).
【详解】(1)在长方体中,因为平面平面,
平面平面,平面平面,
所以.同理.
所以是平行四边形.所以.
又,
.
所以.
所以为的中点.
(2)在长方体中,建立空间直角坐标系,设,
则.
因此.
设平面的法向量为,
则即
令,则,因此.
易知平面的法向量为,则
.
解得.所以.
27.【答案】(1)证明见详解;
(2)
【详解】(1)∵在中,,,,
∴,故,
∴,∴,
∵平面平面,平面平面,平面,
∴平面;
(2)分别取,中点,连接,,则,,
∵,∴,
∵为等边三角形,∴,故,
∵平面,平面,∴,
∵,∴,故,,两两垂直,
如图,以为原点建立空间直角坐标系,则,,,,
∴,,,,
设平面的一个法向量为,
则即
令,则,,∴,
设直线与平面所成角为,
则,
∴直线与平面所成角的正弦值为.
28.【答案】(1)证明见详解;
(2).
【详解】(1)在中,过点作交于点,连接,
因为,所以,所以四点共面.
因为平面,平面,
平面平面,所以.
所以四边形是平行四边形,
所以,所以为的中点;
(2)过作于,连接.
因为,所以为中点,
,,所以四边形为平行四边形,
又,所以,
又因为平面平面,平面平面,
平面,所以平面.所以,
所以.
如图建立空间直角坐标系.
因为,
由题意得,,
所以.
设平面的法向量为,则即
令,则.所以平面的一个法向量为.
设与平面所成角为,
则,
又,解得.
所以与平面所成的角为
【方法总结】求直线与平面所成角的方法
(1)定义法:①作,在直线上选取恰当的点向平面引垂线,确定垂足的位置是关键;
②证,证明所作的角为直线与平面所成的角,证明的主要依据是直线与平面所成角的概念;
③求,利用解三角形的知识求角.
(2)向量法:sin θ=|cos〈,n〉|=(其中为平面α的斜线AB的方向向量,n为平面α的法向量,θ为斜线AB与平面α所成的角).
29.【答案】(1)证明见详解;
(2);
(3).
【详解】(1)设的中点为,连接,
因为N为的中点,所以,且,
又因为,且,所以,且,
所以四边形为平行四边形,则,
因为平面,平面,
所以平面;
(2)记的中点为,连结,
因为,,,
所以四边形是矩形,则,,
以为原点,以,,所在直线为轴建立空间直角坐标系,
则,,,,
则,,,
设平面的一个法向量为,
所以令,则,
设平面的一个法向量为,
所以令,则,
所以,
由图可知,二面角为锐角,
所以二面角的余弦值为;
(3)依题意,设,则,
又由(2)得平面的一个法向量为,
记直线与平面所成角为,
所以,解得(负值舍去),
所以,则,
由(2)得平面的一个法向量为,
所以点到平面的距离为.
30.【答案】(1)证明见解析;
(2)所选条件见解析,.
【详解】(1)由四边形为平行四边形,则,又,
平面,平面,则平面,同理平面,
由,都在平面内,则平面平面,
平面,则平面;
(2)平面平面,平面平面,平面,
所以平面,平面,则,,
选条件①:,都在平面内,则平面,
平面,则;
选条件②:由,,,
则,又,故,
所以,则,
综上,,,,
以为原点,为的正方向建立空间直角坐标系,
所以,令,则,
故,,
令是平面的一个法向量,则,
取,则,
由题设,可得,
所以.
第 page number 页,共 number of pages 页
学校:___________姓名:___________班级:___________
一、单选题(本大题共13小题)
1.[2025北京延庆·一模]某圆锥高为,母线与底面所成的角为,则该圆锥的表面积为( )
A. B. C. D.
2.[2025北京西城·一模]设直线平面,平面平面直线,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.[2025北京丰台·一模]已知,是两条不同的直线,,是两个不同的平面,则下列命题正确的是( )
A.若,,,则 B.若,,则
C.若,,,则 D.若,,,则
4.[2025北京平谷·一模]冰淇淋蛋筒是大家常见的一种食物,有种冰淇淋蛋筒可以看作是由半径为10cm,圆心角为的扇形蛋卷坯卷成的圆锥,假设高出蛋筒部分的奶油和包裹在蛋筒内部的奶油体积相等,则该种冰淇淋中奶油的总体积约为( )(忽略蛋筒厚度)
A. B.
C. D.
5.[2025北京东城·一模]祈年殿(图1)是北京市的标志性建筑之一 距今已有600多年历史.殿内部有垂直于地面的28根木柱,分三圈环形均匀排列.内圈有4根约为19米的龙井柱,寓意一年四季;中圈有12根约为13米的金柱,代表十二个月;外圈有12根约为6米的檐柱,象征十二个时辰.已知由一根龙井柱和两根金柱形成的几何体(图2)中,米,,则平面与平面所成角的正切值约为( )
A. B. C. D.
6.[2025北京石景山·一模]如图,在棱长为2的正方体中,M,N,P分别是,,的中点,Q是线段上的动点(不包含端点),给出下列三个命题:
①对任意点Q,都有;
②存在点Q,使得平面;
③过点Q且与垂直的平面截正方体所得截面面积的最大值为.
其中正确的命题个数是( )
A.0 B.1 C.2 D.3
7.[2025北京门头沟·一模]某纪念塔的一部分建筑结构可抽象为三棱锥,,底面是等腰直角三角形,,顶点到底面的距离为3,则点到平面的距离为( )
A. B. C. D.
8.[2025北京房山·一模]如图,将棱长为2的正方体六个面的中心连线,可得到八面体,为棱上一点,则下列四个结论中错误的是( )
A.平面
B.八面体的体积为
C.的最小值为
D.点到平面的距离为
9.[2025北京丰台·一模]如图,正方体的棱长为2,为的中点,为线段上的动点,给出下列四个结论:
①存在唯一的点,使得,,,四点共面;
②的最小值为;
③存在点,使得;
④有且仅有一个点,使得平面截正方体所得截面的面积为.
其中所有正确结论的个数为( )
A.1 B.2 C.3 D.4
10.[2025北京海淀·一模]已知纸的长宽比约为.现将一张纸卷成一个圆柱的侧面(无重叠部分).当该圆柱的高等于纸的长时,设其体积为,轴截面的面积为;当该圆柱的高等于纸的宽时,设其体积为,轴截面的面积为,则( )
A., B.,
C., D.,
11.[2025北京延庆·一模]已知正方体的棱长为1,若在该正方体的棱上有点M,满足,则点M的个数为( )
A.2 B.4 C.6 D.8
12.[2025全国·一模]已知三棱锥的底面是正三角形,平面,,,,四点都在以为球心的球面上,,则与平面所成角的正切值为( )
A. B. C. D.
13.[2025北京顺义·一模]六氟化硫是一种无机化合物,常温常压下为无色无味无毒不燃的稳定气体.化学式为,在其分子结构中,硫原子位于中心,六个氟原子均匀分布在其周围,形成一个八面体的结构.如图所示,该分子结构可看作正八面体,记为,各棱长均相等,则平面与平面夹角的余弦值是( )
A. B. C. D.
二、多选题(本大题共1小题)
14.[2025全国·一模]如图,已知底面为矩形的四棱锥的顶点的位置不确定,点在棱上,且,平面平面,则下列结论正确的是( )
A.
B.平面平面
C.若,,,且平面平面,则三棱锥的体积为
D.存在某个位置,使平面与平面的交线与底面平行
三、填空题(本大题共2小题)
15.[2025北京朝阳·一模]在棱长为的正方体中,点P是底面内的动点,给出下列四个结论:
①的最小值为;
②的最小值为;
③的最大值为;
④的最小值为.
其中所有正确结论的序号是 .
16.[2025北京西城·一模]端午节又名端阳节、粽子节等,它是中国首个入选世界非遗的节日.从形状来分,端午节吃的粽子有三角粽、四角粽、枕形粽、牛角粽等.其中,四角粽的形状可以近似看成一个四面体,如图所示.设棱的长为,其余的棱长均为,则该四角粽的表面积为 ,内含食物的体积为 .(粽叶的厚度忽略不计)
四、解答题(本大题共14小题)
17.[2025北京西城·一模]如图,在多面体中,平面,平面平面,,于点.
(1)求证:;
(2)设,,求直线与平面所成角的正弦值.
18.[2025全国·一模]如图,在五棱锥中,,,.
(1)证明:;
(2)求平面与平面夹角的正弦值.
19.[2025北京门头沟·一模]如图,在正方体中,为中点,与平面交于点.
(1)求证:为的中点;
(2)求平面与平面夹角的余弦值.
20.[2025北京顺义·一模]如图,在四棱锥中,底面是菱形,,,.
(1)若平面与棱交于点,且平面,求证:是中点;
(2)若是棱上一点,且满足,当时,求与平面所成角的正弦值.
21.[2025北京海淀·一模]如图,五面体中,四边形是正方形.
(1)求证:;
(2)若平面平面,,,求直线与平面所成角的大小.
22.[2025北京延庆·一模]如图,在四棱锥中,底面ABCD是矩形,底面ABCD,且,E是PC的中点,平面ABE与线段PD交于点F.
(1)求证:;
(2)若,求直线BE与平面BCF所成角的正弦值.
23.[2025北京朝阳·一模]如图,在四棱柱中,平面,在四边形中,,为线段的中点.
(1)求证:平面;
(2)若平面平面,,求平面与平面夹角的余弦值.
24.[2025全国·一模]如图,直四棱柱的底面为正方形,点在棱上(包含端点).
(1)证明:平面平面;
(2)已知,求平面与平面所成二面角的正弦值的取值范围.
25.[2025全国·一模]如图,正四棱柱,其侧棱长与底面边长都为2,E,F分别为,的中点,平面与交于点P.
(1)确定点P在线段上的位置;
(2)求平面与平面夹角的余弦值.
26.[2025北京房山·一模]如图,在长方体中,为的中点,与平面交于点.
(1)求证:为的中点;
(2)若二面角的余弦值为,求的长度.
27.[2025北京丰台·一模]如图,在四棱锥中,平面平面,为等边三角形,,,.
(1)求证:平面;
(2)求直线与平面所成角的正弦值.
28.[2025北京平谷·一模]如图,在四棱锥中,平面平面等腰直角三角形,.
(1)点在棱上,若平面,求证:为的中点;
(2)求与平面所成的角.
29.[2025北京石景山·一模]如图,在四棱锥中,平面,,且,,,,,N为的中点.
(1)求证:平面;
(2)求二面角的余弦值;
(3)点M在线段上,直线与平面所成角的正弦值为,求点M到平面的距离.
30.[2025北京东城·一模]如图,在几何体中,四边形为平行四边形,平面平面.
(1)证明:平面;
(2)已知点到平面的距离为,再从条件①、条件②这两个条件中选择一个作为已知,求的长.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
参考答案
1.【答案】A.
【详解】由圆锥高为,母线与底面所成的角为,得圆锥底面圆半径,
母线,所以圆锥的表面积.
故选A.
2.【答案】A
【详解】已知直线平面,平面平面直线,
若,由平面,则;
若,此时得不到,直线可能与平面相交,如下图:
所以“”是“”的充分不必要条件.
故选A.
3.【答案】D
【详解】
如图,在正方体中分析选项A、B、C.
A.平面,平面,平面平面,但,A错误.
B.,平面,但平面,B错误.
C.平面平面,平面,,但平面,C错误.
D.取直线的方向向量,直线的方向向量,
∵,,∴分别为平面的法向量,
∵,∴,∴,D正确.
故选D.
4.【答案】D
【详解】设圆锥底面面积为,
由题意可知,
所以,
设圆锥得高为,则,
所以圆锥的体积为:,
所以该种冰淇淋中奶油的总体积约为,
故选D.
5.【答案】B
【详解】若平面平面,则平面与平面所成角,即为平面与平面所成角,
由题意有,即是等腰三角形,腰长约为8米,,易知,
若是的中点,连接,则,且平面,
由平面,则,都在平面内,
所以平面,则是平面与平面所成角的平面角,
其中,,则.
故选B.
6.【答案】C
【详解】以为原点,以所在直线为轴建立空间直角坐标系,
则,
设,
对于①,,
则,
所以,即,故①正确;
对于②,,
设平面的一个法向量为,
则,取,得,
要使平面,则,
则,即,不符合题意,
所以不存在点Q,使得平面,故②错误;
对于③,如下图,在平面内作⊥,垂足为点,
过点作在平面内作⊥交于,
因为平面平面,平面平面,
且平面,所以平面,
又平面,所以⊥,
因为,、平面,所以平面,
平面截正方体截面为平行四边形,
当与点重合时,为中点,截面面积最大,
此时,,截面面积为,故③对.
故选C.
7.【答案】C
【详解】
因为,且底面是等腰直角三角形,,
所以点在平面上的射影为边的中点,在直角三角形中,由勾股定理得,所以,
又因为底面是等腰直角三角形,,
;
设点到平面的距离为,则
,
所以.
故选C
8.【答案】D
【详解】
在正方体中,连接可知相交于点,且被互相平分,故四边形是平行四边形,
所以,而平面,平面,
所以平面,故A正确;
因为正方体棱长为2,所以四边形是正方形且,
面,,
所以八面体的体积等于棱锥体积的2倍,
而棱锥体积等于,
故八面体的体积为,B正确;
因为为棱上一点,将和展开成一个平面,
由题和均为正三角形,且边长为,
由三角形两边之和大于第三边知最小值为,在中由余弦定理可知,故C正确;
对于D选项:设点到平面的距离为,由等体积法知:
,故错误.
故选D.
9.【答案】B
【详解】对于结论①,取中点为,连接,,,,
因为正方体,为的中点,所以,
所以,,,四点共面,如图确定的平面与线段有且仅有一个交点,
故结论①正确;
对于结论②,因为,求的最小值,即求的最小值,
因为正方体,所以,,,四点共面,
所以与会相交于一点,设为,
此时,
因为,
所以的最小值为错误,
故结论②错误;
对于结论③,取,中点分别为,,连接,设交于点,若平面,
在平面中,易知,
所以,
所以,
所以,所以,
又因为平面,平面,
所以,
,平面,平面,
所以平面,
因为平面,平面,
所以,
所以存在点,使得,
故结论③正确;
对于结论④,当点与点重合时,截面为矩形,截面面积为,
当点为上靠近点的三等分点时,
取中点为,连接,,,,,,
此时四边形即为平面截正方体所得截面,证明如下:
已知平面,求证点为上靠近点的三等分点,
因为,所以,所以点为上靠近点的三等分点,得证,
又因为,且,,所以四边形为等腰梯形,面积为,
所以当点为上靠近点的三等分点时,截面面积为,
当点趋近于点时,截面面积趋近于3,
因为,,点从上靠近点的三等分点向点运动时,截面面积的变化是连续的,
所以点从上靠近点的三等分点向点运动时存在某点,使得截面面积为,
故线段上至少存在两个点使得截面面积为,
故结论④错误.
故选B.
10.【答案】B
【详解】不妨设纸的长宽分别为;
当圆柱的高等于纸的长时,也即圆柱高为时,设其底面圆半径为,则,解得,
故,
此时矩形轴截面的两条边长分别为,故;
当圆柱的高等于纸的宽时,也即圆柱高为时,设其底面圆半径为,则,解得,
故,
此时矩形轴截面的两条边长分别为,故;
综上所述,,.
故选B.
11.【答案】C.
【详解】因为,所以点M不在棱,棱上,
所以当点M在棱上时,设,连接,
在中,,
由余弦定理可得,,
即,可解得,
所以在棱上存在满足题意的一个点M;
由对称性可知在棱,棱,棱上各存在一个点M;
因为,所以点M不在平面内,
所以当点M在棱上时,设,连接,
在直角三角形中,,
所以,即,可解得,
所以在棱上存在满足题意的一个点M;
由对称性可知在棱上也存在一个点M;
综上,满足题意的点M共6个.
故选C.
12.【答案】C
【详解】设是中点,是中点,是正三角形的重心,则是的三等分点,,
由是边长为的正三角形知,,
在平面中,作,作的垂直平分线交于点,
因为平面,,易知四边形是矩形,,.
设与交于点,过作,垂足为,
因为平面,在平面内,
所以,又,为平面内两条相交直线,
所以平面,在平面内,
所以,又为平面内两条相交直线,
所以平面,
所以是与平面所成的角或其补角.
过作直线平行于,交于点,交于点,则,,
把,,,,,,
代入求得,,
在中,,,
在中,,
所以.
故选C.
13.【答案】D
【详解】
设正八面体的棱长为,连接、相较于点,连接,
根据正八面体的性质可知为正方形,,平面,
建立如图所示,以为坐标原点,
分别以、、为、、轴的空间直角坐标系,
,,,,
所以,,
设平面的法向量为,
所以,,令,
则有:,所以,
,,
设平面的法向量为,
所以,,令,
则有:,所以,
设平面与平面夹角为,则,
平面与平面夹角的余弦值为.
故选D.
14.【答案】ABC
【详解】对于A,∵平面平面,平面平面,,平面,∴平面,
又平面,∴,故A正确;
对于B,由A知平面,又平面,∴平面平面,故B正确;
对于C,在中,,,∴,,
∴,∴,
∵平面平面,平面平面,,平面,∴平面,
又平面,∴,同理可证,平面,∴平面,
而,∴三棱锥的体积为,故C正确;
对于D,设平面平面,假设底面,
∵平面平面,平面平面,
∴,,∴,则与重合,则,显然不成立,则假设不成立,故D错误.
故选ABC.
15.【答案】①②④
【详解】设点、、、关于平面的对称点分别为、、、,
设底面、的中心分别为点、,如下图所示:
对于①,易知为的中点,则,可得,
所以,,
当点与点重合时,底面,此时,取最小值,
即的最小值为,①对;
对于④,
,
当点与点重合时,底面,此时,取最小值,
则的最小值为,④对;
对于②,由对称性可知,,
则,
当且仅当点为线段与平面的交点时,取最小值,②对;
对于③,当点与点重合时,,
所以,的最大值不是,③错.
16.【答案】
【详解】,
所以为锐角,所以,
该四角粽的表面积
,
取中点为,连接,
则,
所以,即,
且,平面,
所以平面,
内含食物的体积为.
17.【答案】(1)见详解
(2)
【详解】(1)如图,因为,平面,平面,
所以平面,
又因为平面,平面平面,
所以,
(2)在平面内过点作.
因为平面,所以平面,
因平面,平面,所以,,
因平面,平面,则平面平面,
又因为,平面平面,则平面,
所以,,两两互相垂直.
以为原点,,,所在直线为轴,轴,轴建立空间直角坐标系,则,,,,
,,,,
由题意,得,
设平面的法向量为,
则,即,
令,则,,于是,
所以,
故直线与平面所成角的正弦值为.
18.【答案】(1)证明见解析
(2).
【详解】(1)证明:在中,,所以,
所以,即,
又,所以,
因为,平面,所以平面,
又平面,所以;
(2)连接,在中,,
所以,
在中,,
所以,所以,即,
由(1)知,,又因为,平面,
所以平面.
以A为坐标原点,以所在直线分别为轴建立如图所示的空间直角坐标系,
过点作⊥轴于点,
因为,所以,
又,故,
则,
故,
设平面的法向量为,
则即不妨令,则,
则为平面的一个法向量,
依题意,为平面的一个法向量,
设平面与平面的夹角为,
则,
又因为,
所以平面与平面夹角的正弦值为.
19.【答案】(1)证明见解析;
(2)
【详解】(1)依题意连接,如下图所示:
由正方体性质可得,又平面,平面,
可得平面,
因为与平面交于点,即平面平面,
可得,
因此,又为中点,
可得为的中点;
(2)以为坐标原点,所在直线分别为轴建立空间直角坐标系,如下图所示:
不妨设正方体的棱长为2,
可得,即;
设平面的一个法向量为,
则,令,可得,
即;
显然平面的一个法向量可以为,
因此平面与平面夹角的余弦值为;
可得平面与平面夹角的余弦值.
20.【答案】(1)证明见解析
(2)
【详解】(1)记,连接,如下图:
因为平面,平面,平面平面,所以,
在中,由为的中点,则为的中点.
(2)在菱形中,易知,由,,则,,
因为,,平面,所以平面,
因为平面,所以,由,则,
因为,平面,所以平面,
取的中点为,易知,则平面,则两两垂直,
以为原点,分别以所在直线为轴,建立空间直角坐标系,如下图:
则,,,
可得,,,,
由,则,可得,
设平面的法向量,则
令,则,所以平面的一个法向量,
设与平面所成角为,.
【方法总结】利用空间向量求解立体几何问题的一般步骤
(1)观察图形,建立恰当的空间直角坐标系;
(2)写出相应点的坐标,求出相应直线的方向向量;
(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求
出法向量;
(4)将空间位置关系转化为向量关系;
(5)根据公式求出相应的角或距离.
21.【答案】(1)证明过程见解析;
(2)
【详解】(1)因四边形是正方形,则,
又平面,平面,则平面,
又平面平面,则,故.
(2)因平面平面,,平面平面,
则平面,又平面,平面,
则,,
因,,则,则,
则以为原点,以所在直线为轴,轴,轴建立空间直角坐标系,
则,
则,
设平面的法向量为,
则,令,则,
则,
则直线与平面所成角的正弦值为,
又因其夹角取值范围为,故直线与平面所成角为.
22.【答案】(1)证明见解析;
(2).
【详解】(1)在矩形中,,又平面,平面,
所以平面,又因为平面,且平面平面,
所以.
(2)由(1)可知,又因为E是的中点,所以F是的中点,
因为,即,故.
因为平面平面,所以
又在正方形中,,所以两两垂直.
如图建立空间直角坐标系,
则
所以,
设平面的一个法向量为
由,得,令,得,
设直线与平面所成角为,则
故直线BE与平面BCF所成角的正弦值为.
23.【答案】(1)证明见解析
(2)
【详解】(1)连接.
因为为的中点,
所以.
又,所以四边形为平行四边形.
所以.
又因为,
所以.
所以四边形为平行四边形.
所以.
又因为平面平面,
所以平面.
(2)因为平面,
所以.
又因为平面平面,平面平面,
且平面,
所以平面.
所以.
所以两两垂直.
如图建立空间直角坐标系,
则.
所以.
因为平面,
所以是平面的法向量.
设平面的法向量为,
则,即,
令,则.于是.
设平面与平面夹角为,
则.
24.【答案】(1)证明见解析;
(2).
【详解】(1)证明:由四边形是正方形,得,
因为在直棱柱中平面,平面,所以,
因为,,平面,所以平面,
因为平面,所以平面平面;
(2)以,,所在直线分别为,,轴建立如图所示的空间直角坐标系,
所以,,,,,
设,则,故,,,
设平面的一个法向量为,则,取得,
设平面的一个法向量为,则,取得,
所以,
因为,所以,,,
所以,所以,
即平面与平面所成二面角的正弦值的取值范围是.
25.【答案】(1)点为线段上靠近点的三等分点
(2)
【详解】(1)如图,设的中点为,连接,记,连接,.
由题意知四边形为正方形,又为的中点,∴,,
∴四边形为平行四边形,∴.
又∵平面,平面,∴平面.
∵平面,平面平面,∴,
∴.
又∵为的中点,,∴点为的重心,
∴,∴,
即点为线段上靠近点的三等分点.
(2)以为坐标原点,分别以直线,,为x,y,z轴建立如图所示的空间直角坐标系.
则,,,,,,,
∴,,,,.
设平面的法向量为,
则,即,∴,
令,则,,∴;
设平面的法向量为,
由(1)知,∴,
∴,即,解得,
令,则,,∴.
设平面与平面的夹角为,则
,
即平面与平面夹角的余弦值为.
26.【答案】(1)证明见解析
(2).
【详解】(1)在长方体中,因为平面平面,
平面平面,平面平面,
所以.同理.
所以是平行四边形.所以.
又,
.
所以.
所以为的中点.
(2)在长方体中,建立空间直角坐标系,设,
则.
因此.
设平面的法向量为,
则即
令,则,因此.
易知平面的法向量为,则
.
解得.所以.
27.【答案】(1)证明见详解;
(2)
【详解】(1)∵在中,,,,
∴,故,
∴,∴,
∵平面平面,平面平面,平面,
∴平面;
(2)分别取,中点,连接,,则,,
∵,∴,
∵为等边三角形,∴,故,
∵平面,平面,∴,
∵,∴,故,,两两垂直,
如图,以为原点建立空间直角坐标系,则,,,,
∴,,,,
设平面的一个法向量为,
则即
令,则,,∴,
设直线与平面所成角为,
则,
∴直线与平面所成角的正弦值为.
28.【答案】(1)证明见详解;
(2).
【详解】(1)在中,过点作交于点,连接,
因为,所以,所以四点共面.
因为平面,平面,
平面平面,所以.
所以四边形是平行四边形,
所以,所以为的中点;
(2)过作于,连接.
因为,所以为中点,
,,所以四边形为平行四边形,
又,所以,
又因为平面平面,平面平面,
平面,所以平面.所以,
所以.
如图建立空间直角坐标系.
因为,
由题意得,,
所以.
设平面的法向量为,则即
令,则.所以平面的一个法向量为.
设与平面所成角为,
则,
又,解得.
所以与平面所成的角为
【方法总结】求直线与平面所成角的方法
(1)定义法:①作,在直线上选取恰当的点向平面引垂线,确定垂足的位置是关键;
②证,证明所作的角为直线与平面所成的角,证明的主要依据是直线与平面所成角的概念;
③求,利用解三角形的知识求角.
(2)向量法:sin θ=|cos〈,n〉|=(其中为平面α的斜线AB的方向向量,n为平面α的法向量,θ为斜线AB与平面α所成的角).
29.【答案】(1)证明见详解;
(2);
(3).
【详解】(1)设的中点为,连接,
因为N为的中点,所以,且,
又因为,且,所以,且,
所以四边形为平行四边形,则,
因为平面,平面,
所以平面;
(2)记的中点为,连结,
因为,,,
所以四边形是矩形,则,,
以为原点,以,,所在直线为轴建立空间直角坐标系,
则,,,,
则,,,
设平面的一个法向量为,
所以令,则,
设平面的一个法向量为,
所以令,则,
所以,
由图可知,二面角为锐角,
所以二面角的余弦值为;
(3)依题意,设,则,
又由(2)得平面的一个法向量为,
记直线与平面所成角为,
所以,解得(负值舍去),
所以,则,
由(2)得平面的一个法向量为,
所以点到平面的距离为.
30.【答案】(1)证明见解析;
(2)所选条件见解析,.
【详解】(1)由四边形为平行四边形,则,又,
平面,平面,则平面,同理平面,
由,都在平面内,则平面平面,
平面,则平面;
(2)平面平面,平面平面,平面,
所以平面,平面,则,,
选条件①:,都在平面内,则平面,
平面,则;
选条件②:由,,,
则,又,故,
所以,则,
综上,,,,
以为原点,为的正方向建立空间直角坐标系,
所以,令,则,
故,,
令是平面的一个法向量,则,
取,则,
由题设,可得,
所以.
第 page number 页,共 number of pages 页
同课章节目录
