2025年云南省昆明市盘龙区中考数学三模试卷(含解析)
文档属性
| 名称 | 2025年云南省昆明市盘龙区中考数学三模试卷(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 248.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-27 00:00:00 | ||
图片预览




文档简介
2025年云南省昆明市盘龙区中考数学三模试卷
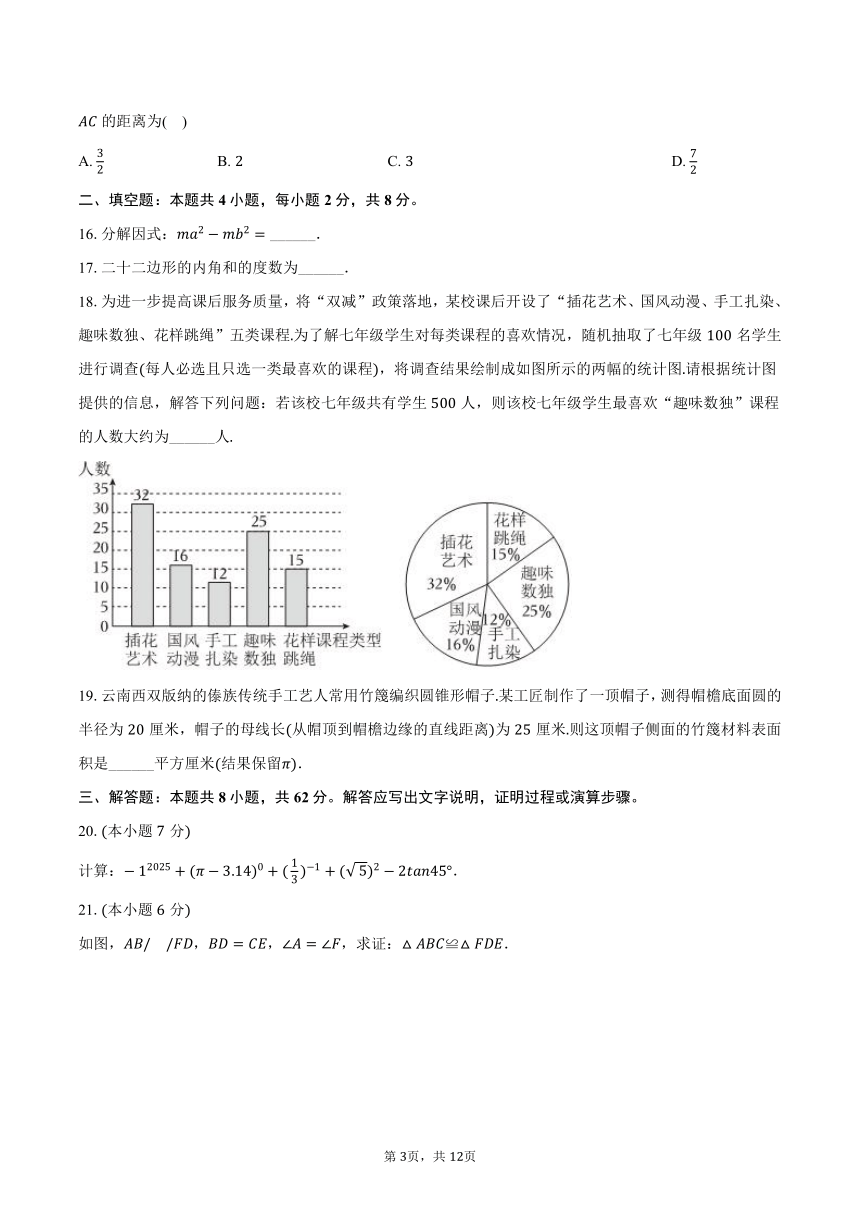
一、选择题:本题共15小题,每小题2分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.我国古代数学名著九章算术中对正负数的概念注有“今两算得失相反,要令正负以名之”若零上记作,则零下应记作( )
A. B. C. D.
2.根据国际能源署年全球可再生能源展望报告,预计年全球太阳能发电总装机容量将达到千瓦下列用科学记数法表示该数据正确的是( )
A. B. C. D.
3.如图,两条直线,被第三条直线所截,若,,则的度数为( )
A.
B.
C.
D.
4.反比例函数的图象一定经过的点是( )
A. B. C. D.
5.下列几何体中,俯视图不是圆的是( )
A. B. C. D.
6.下列运算正确的是( )
A. B.
C. D.
7.如图,在中,点,分别是,的中点,则( )
A.
B.
C.
D.
8.以下是一组按一定规律排列的多项式:,,,,,,则第个多项式是( )
A. B. C. D.
9.云南是我国普洱茶的核心产区,勐海和临沧的茶园因独特气候存在显著差异,某茶叶的品质和口感也深受喝茶人喜爱某茶叶质量检测鉴定中心在两地各选择了一家茶园,统计了近五年“普洱茶”的年产量单位:吨,数据如下:
勐海茶园
临沧茶园
根据上述数据,茶叶的产量更稳定是( )
A. 勐海茶园 B. 临沧茶园 C. 两者稳定性相同 D. 无法判断
10.剪纸是我国最古老的民间艺术之一下列剪纸图案中是中心对称图形的是( )
A. B. C. D.
11.年月日,春节申遗成功伴随着中国春节除夕夜必不可少的春晚,承载了无数家庭的欢乐与记忆据相关统计,年春晚在新媒体端直播规模约亿人次,年约亿人次设这两年春晚在新媒体端直播规模的年平均增长率为,可列方程为( )
A. B. C. D.
12.如图,在中,点是的中点,点在优弧上,若,则的度数为( )
A.
B.
C.
D.
13.估计的值应在( )
A. 到之间 B. 到之间 C. 到之间 D. 到之间
14.已知函数,则在实数范围内自变量的取值范围是( )
A. B. C. D.
15.若是等腰底边上的中线,点到直线的距离为,则点到直线的距离为( )
A. B. C. D.
二、填空题:本题共4小题,每小题2分,共8分。
16.分解因式: ______.
17.二十二边形的内角和的度数为______.
18.为进一步提高课后服务质量,将“双减”政策落地,某校课后开设了“插花艺术、国风动漫、手工扎染、趣味数独、花样跳绳”五类课程为了解七年级学生对每类课程的喜欢情况,随机抽取了七年级名学生进行调查每人必选且只选一类最喜欢的课程,将调查结果绘制成如图所示的两幅的统计图请根据统计图提供的信息,解答下列问题:若该校七年级共有学生人,则该校七年级学生最喜欢“趣味数独”课程的人数大约为______人
19.云南西双版纳的傣族传统手工艺人常用竹篾编织圆锥形帽子某工匠制作了一顶帽子,测得帽檐底面圆的半径为厘米,帽子的母线长从帽顶到帽檐边缘的直线距离为厘米则这顶帽子侧面的竹篾材料表面积是______平方厘米结果保留.
三、解答题:本题共8小题,共62分。解答应写出文字说明,证明过程或演算步骤。
20.本小题分
计算:.
21.本小题分
如图,,,,求证:≌.
22.本小题分
早春三月,草长莺飞,万物复苏,在这春意盎然的季节里,某县开展“植”此青绿,播种希望的义务植树活动该县计划完成总植树任务棵,由于学生志愿者的支援,实际每天植树量比原计划每天多植,结果提前天完成任务,求原计划每天植树多少棵.
23.本小题分
在哪吒之魔童闹海的云南首映式上,主办方设置了一个抽奖环节抽奖规则为:参与者任选一个奖品袋,从中随机抽取一张卡片形状、大小完全相同,记下编号后放回洗匀,再根据所抽卡片上对应的编号领取奖品已知甲奖品袋对应的卡片编号为::哪吒徽章,:敖丙徽章,:申公豹徽章;乙奖品袋对应的卡片编号为::哪吒钥匙扣,:敖丙钥匙扣,:太乙真人钥匙扣两个奖品袋的卡片如图所示
小丽和小颖参加了本次首映式,并分别从甲、乙奖品袋中随机抽取了一个奖品其中,小丽从甲奖品袋中抽取的奖品记为,小颖从乙奖品袋中抽取的奖品记为.
请用列表法或画树状图法中的一种方法,求所有可能出现的结果总数;
求小丽和小颖抽取的奖品所代表的动画人物相同的概率.
24.本小题分
如图,在菱形中,,相交于点,过点作,使,连接.
求证:四边形是矩形;
若四边形的周长为,,求平行线与间的距离.
25.本小题分
曾有言“一剪之趣夺神功,美在民间永不朽”剪纸是中国最古老的民间艺术之一,也是中华民族优秀传统文化的重要载体某校为了让学生感受非遗传承的时代魅力,激发学生的劳动实践能力,计划开展“指尖方寸,非遗传情”的剪纸活动学校决定一次性购进、两种型号的彩纸共件其中,型号彩纸的单价为元,型号彩纸的单价为元,且购进型号彩纸的数量不超过型号彩纸的倍设购进型号彩纸件,、两种型号彩纸的总费用为元.
求与的函数关系式;
在的条件下,请你设计最省钱的购买方案,并求出最少费用.
26.本小题分
已知二次函数的顶点坐标为,且其图象经过点直线:与二次函数图象交于点和点在点的左边,与二次函数的对称轴交于点.
求该二次函数的解析式;
若线段被二次函数的对称轴分成的两条线段的长度比为:,求直线的解析式.
27.本小题分
如图,为的直径,为延长线上的点,,垂足为,连接,,,是线段上一点,若平分,与线段交于点.
若,求的度数;
求证:为的切线;
若,,看一看,想一想,证一证:以下与线段、有关的三个结论:,,,你认为哪个正确?请说明理由.
答案和解析
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】
18.【答案】
19.【答案】
20.【答案】
【解析】解:原式
.
21.【解析】证明:,
,
.
,
.
在和中,
≌.
22.【解析】解:设原计划每天植树棵,则实际每天植树棵,
由题意得:,
解得:,
经检验,是原分式方程的解,且符合题意.
答:原计划每天植树棵.
23.【解析】列表如下:
共有种等可能的结果.
由表格可知,小丽和小颖抽取的奖品所代表的动画人物相同的结果有:,,共种,
小丽和小颖抽取的奖品所代表的动画人物相同的概率为.
24.【解析】证明:四边形是菱形,
,,
,
,
,
,
四边形是平行四边形,
,
四边形是矩形;
解:矩形的周长为,
,
四边形是菱形,,
,,,
,
,
,
,
,
设平行线与间的距离为,
,
,
故平行线与间的距离为.
25.【解析】购进型号彩纸件,
则,
与的函数关系式为.
根据题意,得,
解得,
,
随的减小而减小,
,
当时值最小,,
件.
答:购进型号彩纸件、型号彩纸件最省钱,最少费用为元.
26.【解析】由题意,二次函数图象顶点为,
可设二次函数为.
又图象过,
.
.
二次函数解析式为,即.
由题意,设,,
点在点的左边,
.
.
.
,且,.
线段被直线分成的两条线段长度比为:,
或.
,或,
当时,
,
.
又,
或.
当时,
,
.
又,
.
或.
综上,当时,直线解析式为;
当时,直线解析式为.
27.【解析】解:如图,连接,
,为的直径,
,
,
,
;
证明:,
,
,
∽,
,
,
,
,
,
又为半径,
与相切;
解:正确结论为:.
理由如下:过作于点,
,
,
,
又,
,
又平分,
,
∽,
,,
,
,
,
,
,
,
,
在中,,
,
由勾股定理得:,
,
,
,
.
第9页,共12页
一、选择题:本题共15小题,每小题2分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.我国古代数学名著九章算术中对正负数的概念注有“今两算得失相反,要令正负以名之”若零上记作,则零下应记作( )
A. B. C. D.
2.根据国际能源署年全球可再生能源展望报告,预计年全球太阳能发电总装机容量将达到千瓦下列用科学记数法表示该数据正确的是( )
A. B. C. D.
3.如图,两条直线,被第三条直线所截,若,,则的度数为( )
A.
B.
C.
D.
4.反比例函数的图象一定经过的点是( )
A. B. C. D.
5.下列几何体中,俯视图不是圆的是( )
A. B. C. D.
6.下列运算正确的是( )
A. B.
C. D.
7.如图,在中,点,分别是,的中点,则( )
A.
B.
C.
D.
8.以下是一组按一定规律排列的多项式:,,,,,,则第个多项式是( )
A. B. C. D.
9.云南是我国普洱茶的核心产区,勐海和临沧的茶园因独特气候存在显著差异,某茶叶的品质和口感也深受喝茶人喜爱某茶叶质量检测鉴定中心在两地各选择了一家茶园,统计了近五年“普洱茶”的年产量单位:吨,数据如下:
勐海茶园
临沧茶园
根据上述数据,茶叶的产量更稳定是( )
A. 勐海茶园 B. 临沧茶园 C. 两者稳定性相同 D. 无法判断
10.剪纸是我国最古老的民间艺术之一下列剪纸图案中是中心对称图形的是( )
A. B. C. D.
11.年月日,春节申遗成功伴随着中国春节除夕夜必不可少的春晚,承载了无数家庭的欢乐与记忆据相关统计,年春晚在新媒体端直播规模约亿人次,年约亿人次设这两年春晚在新媒体端直播规模的年平均增长率为,可列方程为( )
A. B. C. D.
12.如图,在中,点是的中点,点在优弧上,若,则的度数为( )
A.
B.
C.
D.
13.估计的值应在( )
A. 到之间 B. 到之间 C. 到之间 D. 到之间
14.已知函数,则在实数范围内自变量的取值范围是( )
A. B. C. D.
15.若是等腰底边上的中线,点到直线的距离为,则点到直线的距离为( )
A. B. C. D.
二、填空题:本题共4小题,每小题2分,共8分。
16.分解因式: ______.
17.二十二边形的内角和的度数为______.
18.为进一步提高课后服务质量,将“双减”政策落地,某校课后开设了“插花艺术、国风动漫、手工扎染、趣味数独、花样跳绳”五类课程为了解七年级学生对每类课程的喜欢情况,随机抽取了七年级名学生进行调查每人必选且只选一类最喜欢的课程,将调查结果绘制成如图所示的两幅的统计图请根据统计图提供的信息,解答下列问题:若该校七年级共有学生人,则该校七年级学生最喜欢“趣味数独”课程的人数大约为______人
19.云南西双版纳的傣族传统手工艺人常用竹篾编织圆锥形帽子某工匠制作了一顶帽子,测得帽檐底面圆的半径为厘米,帽子的母线长从帽顶到帽檐边缘的直线距离为厘米则这顶帽子侧面的竹篾材料表面积是______平方厘米结果保留.
三、解答题:本题共8小题,共62分。解答应写出文字说明,证明过程或演算步骤。
20.本小题分
计算:.
21.本小题分
如图,,,,求证:≌.
22.本小题分
早春三月,草长莺飞,万物复苏,在这春意盎然的季节里,某县开展“植”此青绿,播种希望的义务植树活动该县计划完成总植树任务棵,由于学生志愿者的支援,实际每天植树量比原计划每天多植,结果提前天完成任务,求原计划每天植树多少棵.
23.本小题分
在哪吒之魔童闹海的云南首映式上,主办方设置了一个抽奖环节抽奖规则为:参与者任选一个奖品袋,从中随机抽取一张卡片形状、大小完全相同,记下编号后放回洗匀,再根据所抽卡片上对应的编号领取奖品已知甲奖品袋对应的卡片编号为::哪吒徽章,:敖丙徽章,:申公豹徽章;乙奖品袋对应的卡片编号为::哪吒钥匙扣,:敖丙钥匙扣,:太乙真人钥匙扣两个奖品袋的卡片如图所示
小丽和小颖参加了本次首映式,并分别从甲、乙奖品袋中随机抽取了一个奖品其中,小丽从甲奖品袋中抽取的奖品记为,小颖从乙奖品袋中抽取的奖品记为.
请用列表法或画树状图法中的一种方法,求所有可能出现的结果总数;
求小丽和小颖抽取的奖品所代表的动画人物相同的概率.
24.本小题分
如图,在菱形中,,相交于点,过点作,使,连接.
求证:四边形是矩形;
若四边形的周长为,,求平行线与间的距离.
25.本小题分
曾有言“一剪之趣夺神功,美在民间永不朽”剪纸是中国最古老的民间艺术之一,也是中华民族优秀传统文化的重要载体某校为了让学生感受非遗传承的时代魅力,激发学生的劳动实践能力,计划开展“指尖方寸,非遗传情”的剪纸活动学校决定一次性购进、两种型号的彩纸共件其中,型号彩纸的单价为元,型号彩纸的单价为元,且购进型号彩纸的数量不超过型号彩纸的倍设购进型号彩纸件,、两种型号彩纸的总费用为元.
求与的函数关系式;
在的条件下,请你设计最省钱的购买方案,并求出最少费用.
26.本小题分
已知二次函数的顶点坐标为,且其图象经过点直线:与二次函数图象交于点和点在点的左边,与二次函数的对称轴交于点.
求该二次函数的解析式;
若线段被二次函数的对称轴分成的两条线段的长度比为:,求直线的解析式.
27.本小题分
如图,为的直径,为延长线上的点,,垂足为,连接,,,是线段上一点,若平分,与线段交于点.
若,求的度数;
求证:为的切线;
若,,看一看,想一想,证一证:以下与线段、有关的三个结论:,,,你认为哪个正确?请说明理由.
答案和解析
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】
18.【答案】
19.【答案】
20.【答案】
【解析】解:原式
.
21.【解析】证明:,
,
.
,
.
在和中,
≌.
22.【解析】解:设原计划每天植树棵,则实际每天植树棵,
由题意得:,
解得:,
经检验,是原分式方程的解,且符合题意.
答:原计划每天植树棵.
23.【解析】列表如下:
共有种等可能的结果.
由表格可知,小丽和小颖抽取的奖品所代表的动画人物相同的结果有:,,共种,
小丽和小颖抽取的奖品所代表的动画人物相同的概率为.
24.【解析】证明:四边形是菱形,
,,
,
,
,
,
四边形是平行四边形,
,
四边形是矩形;
解:矩形的周长为,
,
四边形是菱形,,
,,,
,
,
,
,
,
设平行线与间的距离为,
,
,
故平行线与间的距离为.
25.【解析】购进型号彩纸件,
则,
与的函数关系式为.
根据题意,得,
解得,
,
随的减小而减小,
,
当时值最小,,
件.
答:购进型号彩纸件、型号彩纸件最省钱,最少费用为元.
26.【解析】由题意,二次函数图象顶点为,
可设二次函数为.
又图象过,
.
.
二次函数解析式为,即.
由题意,设,,
点在点的左边,
.
.
.
,且,.
线段被直线分成的两条线段长度比为:,
或.
,或,
当时,
,
.
又,
或.
当时,
,
.
又,
.
或.
综上,当时,直线解析式为;
当时,直线解析式为.
27.【解析】解:如图,连接,
,为的直径,
,
,
,
;
证明:,
,
,
∽,
,
,
,
,
,
又为半径,
与相切;
解:正确结论为:.
理由如下:过作于点,
,
,
,
又,
,
又平分,
,
∽,
,,
,
,
,
,
,
,
,
在中,,
,
由勾股定理得:,
,
,
,
.
第9页,共12页
同课章节目录
