北师大版九年级数学下册第二章 二次函数(二次函数中的动点与特殊三角形问题)试题(无答案)
文档属性
| 名称 | 北师大版九年级数学下册第二章 二次函数(二次函数中的动点与特殊三角形问题)试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 524.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-27 14:18:48 | ||
图片预览




文档简介
专题23 二次函数中的动点与特殊三角形问题
【基础训练】
一、解答题
1.如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的解析式.
(2)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.
(3)在y轴上是否存在一点P,使△PBC为等腰三角形?若存在,请直接写出点P的坐标,若不存在请说明理由.
2.如图,已知二次函数的图象过点.
(1)求二次函数的解析式;
(2)请你判断是什么三角形,并说明理由.
(3)若点在第二象限,且是抛物线上的一动点,过点作垂直轴于点,试探究是否存在以、、为顶点的三角形与相似?若存在,求出点的坐标.若不存在,请说明理由.
3.如图,抛物线y=﹣与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)求点A、点B、点C的坐标;
(2)求直线BD的解析式;
(3)当点P在线段OB上运动时,直线l交BD于点M,试探究m为何值时,四边形CQMD是平行四边形;
(4)在点P的运动过程中,是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
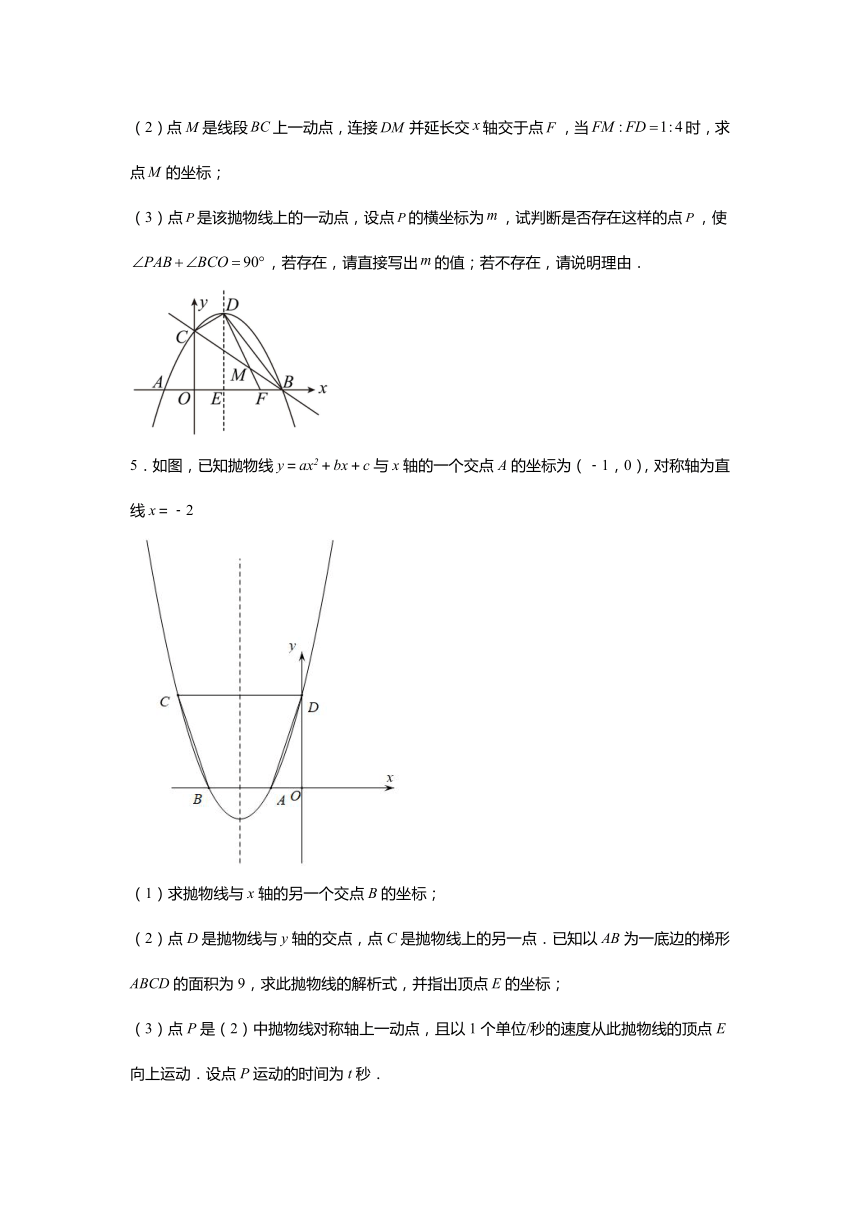
4.综合与探究
如图,直线与轴,轴分别交于,两点,抛物线经过,两点,与轴的另一个交点为(点在点的左侧),抛物线的顶点为点.抛物线的对称轴与轴交于点.
(1)求抛物线的表达式及顶点的坐标;
(2)点M是线段上一动点,连接并延长交轴交于点,当时,求点的坐标;
(3)点是该抛物线上的一动点,设点的横坐标为,试判断是否存在这样的点,使,若存在,请直接写出的值;若不存在,请说明理由.
5.如图,已知抛物线y=ax2+bx+c与x轴的一个交点A的坐标为(﹣1,0),对称轴为直线x=﹣2
(1)求抛物线与x轴的另一个交点B的坐标;
(2)点D是抛物线与y轴的交点,点C是抛物线上的另一点.已知以AB为一底边的梯形ABCD的面积为9,求此抛物线的解析式,并指出顶点E的坐标;
(3)点P是(2)中抛物线对称轴上一动点,且以1个单位/秒的速度从此抛物线的顶点E向上运动.设点P运动的时间为t秒.
①当t为 秒时,△PAD的周长最小?
②当t为 秒时,△PAD是以AD为腰的等腰三角形?(结果保留根号)
6.抛物线与轴交于,两点,与轴交于点,抛物线的对称轴交轴于点,已知,.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点,使是以为腰的等腰三角形?如果存在,求出点的坐标;如果不存在,请说明理由;
(3)点是线段上的一个动点,过点作轴的垂线与抛物线相交于点,当四边形的面积最大时,求点的坐标.
7.如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A,B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).
(1)求二次函数的解析式和直线BD的解析式;
(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
(3)在抛物线上是否存在点Q,且点Q在第一象限,使△BDQ中BD边上的高为?若存在,求出点Q的坐标;若不存在,请说明理由.
8.如图,已知点A的坐标为(-2,0),直线y=-x+3与x轴,y轴分别交于点B和点C,连接AC,顶点为D的抛物线y=ax2+bx+c,过A,B,C三点.
(1)求抛物线的解析式及顶点D的坐标;
(2)设抛物线的对称轴DE交线段BC于点E,P为第一象限内抛物线上一点,过点P作x轴的垂线,交线段BC于点F,若四边形DEFP为平行四边形,求点P的坐标;
(3)设点M是线段BC上的一动点,过点M作MN∥AB,交AC于点N.点Q从点B出发,以每秒1个单位长度的速度沿线段BA向点A运动,运动时间为t(秒).当以MN为直角边的△QMN是等腰直角三角形时,直接写出此时t的取值.
9.如图,抛物线经过A(-1,0)、B(5,6)两点,点是线段上一动点,过点作轴的垂线,交抛物线于点.
(1)求抛物线的解析式;
(2)求线段的最大值;
(3)在抛物线的对称轴上是否存在一个动点,使得是直角三角形?若存在,求出点的坐标;若不存在,请说明理由.
10.如图,已知抛物线与x轴的一个交点为,与y轴的交点为,其顶点为C,对称轴为直线.
(1)求抛物线的函数解析式;
(2)已知点M为y轴上的一个动点,当为等腰三角形时,求点M的坐标.
11.如图1,直线l: y=x+4与x轴,y轴分别交于A、B两点.二次函数y = ax2 - 2ax - 2(a > 0)的图像经过点A,交y轴于点C.
(1)则点C坐标为 _________ ;抛物线对称轴是直线 _________ ;a的值是 _________ ;
(2)已知点M是抛物线上的一个动点,经过点M作x轴的垂线MD,交直线l于点E,过点C作CD⊥MD,垂足为D,连接CM.设点M的横坐标为m.
①当点M位于第一象限的抛物线上,且△CDM是等腰直角三角形时,CM交直线于点F.设点F至直线DM的距离d1,到y轴的距离为d2,求的值.
②如图2,将△CDM绕点C逆时针旋转得到△C,且旋转角∠MC = ∠OAB,当点M的对应点落在y轴上时,请直接写出点M的横坐标m的值.
12.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.
(1)抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求APC的面积的最大值.
(3)在抛物线对称轴上是否存在一点M,使以A,N,M为顶点的三角形是直角三角形?若存在,请直接写出点M的坐标.若不存在,请说明理由.
13.已知二次函数y=x2+bx+c经过A、B两点,BC垂直x轴于点C,且A(﹣1,0),C(4,0),AC=BC.
(1)求抛物线的解析式;
(2)请画出抛物线的图象;
(3)点P是抛物线对称轴上一个动点,是否存在这样的点P,使三角形ABP为直角三角形?若存在,求出P点坐标;若不存在,请说明理由.
14.如图,抛物线与轴相交于A,B两点,与y轴相交于点C,对称轴为直线,项点为D,点B的坐标为.
(1)填空:点A的坐标为_________,点D的坐标为_________,抛物线的解析式为_________;
(2)当二次函数的自变量:满足时,函数y的最小值为,求m的值;
(3)P是抛物线对称轴上一动点,是否存在点P,使是以AC为斜边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
15.如图1,已知抛物线的顶点坐标为(-1,)与y轴交于A(0,3),交直线:x=-2于点B,点C(0,2)在y轴上,连接BC并延长,交抛物线于点D.
(1)求抛物线的表达式;
(2)如图1,E为直线上位于点B下方一动点,连接DE、BD、AD,若,求点E的坐标;
(3)如图2,在(2)的条件下,P为射线EB上一点,作PQ⊥直线DE于点Q,若△APQ为直角三角形,请求出P点的坐标;
16.已知:直线与y轴交于A,与x轴交于D,抛物线y=x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为 (1,0).
(1)求抛物线的解析式;
(2)点P是直线AE下方抛物线上一动点,求△PAE面积的最大值;
(3)动点Q在x轴上移动,当△QAE是直角三角形时,直接写出点Q的坐标;
17.抛物线与轴交于,两点(在左边),与轴交于点.
(1)如图1,若,,求抛物线的解析式;
(2)如图2,为抛物线上一动点(在左边),若,,且.
①求的值;
②如图3,直线,分别与直线交于,两点,于,于.求而的值.
18.如图,已知抛物线与x轴交于A、B两点,与y轴交于C点,其中A(1,0),C(0,3).
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴及点B的坐标;
(3)设点P为该抛物线对称轴上的一个动点,是否存在点P使△BPC为直角三角形,若存在,求出点P的坐标;若不存在,请说明理由.
19.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c为常数a≠0)与x轴,y轴分别交于A,B,C三点,已知A(-1,0),B(3,0),C(0,3),动点E从抛物线的顶点点D出发沿线段DB向终点B运动.
(1)直接写出抛物线解析式和顶点D的坐标;
(2)过点E作EF⊥y轴于点F,交抛物线对称轴左侧的部分于点G,交直线BC于点H,过点H作HP⊥x轴于点P,连接PF,求当线段PF最短时G点的坐标;
(3)在点E运动的同时,另一个动点Q从点B出发沿直线x=3向上运动,点E的速度为每秒个单位长度,点Q速度均为每秒1个单位长度,当点E到达终点B时点Q也随之停止运动,设点E的运动时间为t秒,试问存在几个t值能使△BEQ为等腰三角形?并直接写出相应t值.
20.如图,对称轴为x=1的抛物线经过A(﹣1,0),B(4,5)两点.
(1)求抛物线的解析式;
(2)P为直线AB上的动点,过点P作x轴的垂线交抛物线于点Q.
①当PQ=6时,求点P的坐标;
②是否存在点P,使以A、P、Q为顶点的三角形为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
21.如图,直线y=x+m与抛物线y=x2-2x+l交于不同的两点M、N(点M在点N的左侧).
(1)设抛物线的顶点为B,对称轴l与直线y=x+m的交点为C,连结BM、BN,若S△MBC=S△NBC,求直线MN的解析式;
(2)在(1)条件下,已知点P(t,0)为x轴上的一个动点,
①若△PMN为直角三角形,求点P的坐标.
②若∠MPN>90°,则t的取值范围是 .
22.如图,已知直线y=x+3与x轴交于点B,与y轴交于点C,抛物线y=ax2+bx+3经过B、C两点并与x轴的另一个交点为A,且OC=3OA.
(1)求抛物线的解析式;
(2)点D为直线BC上方对称轴右侧抛物线上一点,当△DBC的面积为时,求D点的坐标;
(3)在(2)的条件下,连接CD,作DE⊥x轴于E,BC、DE交于点H,点P为线段CD上一个动点,过点P作PF∥AC交x轴于点F,连接FH,当∠PFH=45°时,求点F的坐标;
(4)若M(m,n)是直线BC上方抛物线上一点,如果△MBC为锐角三角形,请直接写出点M的横坐标m的取值范围 .
23.如图1,在平面直角坐标系中,直线y=x﹣1与抛物线y=﹣x2+bx+c交于A、B两点,其中A(m,0)、B(4,n),与x轴交于另一点D.
(1)求m、n的值及该抛物线的解析式;
(2)如图2,若点P为线段AD上的一动点(不与A、D重合),分别以AP、DP为斜边,在直线AD的同侧作等腰直角△APM和等腰直角△DPN,连接MN,试确定△MPN面积最大时P点的坐标;
(3)如图3,连接BD、CD,在线段CD上是否存在点Q,使得以A、D、Q为顶点的三角形与△ABD相似若存在,请直接写出点Q的坐标,请说明理由.
24.如图1,抛物线y=x2+bx+c与x轴交于A、B两点,点A、B分别位于原点左、右两侧,且AO=2BO=4,过A点的直线y=kx+c交y轴于点C.
(1)求k、b、c的值;
(2)在抛物线的对称轴上是否存在一点P,使△ACP为直角三角形?若存在,直接写出所有满足条件的点的坐标;若不存在,请说明理由;
(3)如图2,点M为线段AC上一点,连接OM,求AM+OM的最小值.
25.如图,抛物线y=x2﹣x﹣与x轴交于点A和点B,与y轴交于点C,经过点C的直线l与抛物线交于另一点E(4,a),抛物线的顶点为点Q,抛物线的对称轴与x轴交于点D.
(1)求直线CE的解析式.
(2)如图2,P为直线CE下方抛物线上一动点,直线CE与x轴交于点F,连接PF,PC.当△PCF的面积最大时,求点P的坐标及△PCF面积的最大值.
(3)如图3,连接CD,将(1)中抛物线沿射线CD平移得到新抛物线y′,y′经过点D,y′的顶点为点H,在直线QH上是否存在点G,使得△DQG为等腰三角形?若存在,求出点G的坐标.
26.如图,直线与坐标轴交于A,G两点,经过B(2,0)、C(6,0)两点的抛物线y=ax2+bx+2与直线交于A,D两点.
(1)求抛物线的解析式及点D的坐标;
(2)点M是抛物线上位于直线AD下方上的一个动点,当点M运动到什么位置时△MDA的面积最大?最大值是多少?
(3)在x轴上是否存在点P,使以A、P、D为顶点的三角形是直角三角形?若存在,直接写出满足条件的点P的坐标;若不存在,请说明理由.
27.如图,抛物线的图象与x轴分别交于A、B两点,与y轴交于C点,且OC=AB.
(1)求抛物线的解析式.
(2)点D(1,3)在抛物线上,若点P是直线AD上的一个动点,过点P作PQ垂直于x轴,垂足为Q,且以PQ为斜边作等腰直角△PQE.
①当点P与点D重合时,求点E到y轴的距离.
②若点E落在抛物线上,请直接写出E点的坐标.
【基础训练】
一、解答题
1.如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的解析式.
(2)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.
(3)在y轴上是否存在一点P,使△PBC为等腰三角形?若存在,请直接写出点P的坐标,若不存在请说明理由.
2.如图,已知二次函数的图象过点.
(1)求二次函数的解析式;
(2)请你判断是什么三角形,并说明理由.
(3)若点在第二象限,且是抛物线上的一动点,过点作垂直轴于点,试探究是否存在以、、为顶点的三角形与相似?若存在,求出点的坐标.若不存在,请说明理由.
3.如图,抛物线y=﹣与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)求点A、点B、点C的坐标;
(2)求直线BD的解析式;
(3)当点P在线段OB上运动时,直线l交BD于点M,试探究m为何值时,四边形CQMD是平行四边形;
(4)在点P的运动过程中,是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
4.综合与探究
如图,直线与轴,轴分别交于,两点,抛物线经过,两点,与轴的另一个交点为(点在点的左侧),抛物线的顶点为点.抛物线的对称轴与轴交于点.
(1)求抛物线的表达式及顶点的坐标;
(2)点M是线段上一动点,连接并延长交轴交于点,当时,求点的坐标;
(3)点是该抛物线上的一动点,设点的横坐标为,试判断是否存在这样的点,使,若存在,请直接写出的值;若不存在,请说明理由.
5.如图,已知抛物线y=ax2+bx+c与x轴的一个交点A的坐标为(﹣1,0),对称轴为直线x=﹣2
(1)求抛物线与x轴的另一个交点B的坐标;
(2)点D是抛物线与y轴的交点,点C是抛物线上的另一点.已知以AB为一底边的梯形ABCD的面积为9,求此抛物线的解析式,并指出顶点E的坐标;
(3)点P是(2)中抛物线对称轴上一动点,且以1个单位/秒的速度从此抛物线的顶点E向上运动.设点P运动的时间为t秒.
①当t为 秒时,△PAD的周长最小?
②当t为 秒时,△PAD是以AD为腰的等腰三角形?(结果保留根号)
6.抛物线与轴交于,两点,与轴交于点,抛物线的对称轴交轴于点,已知,.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点,使是以为腰的等腰三角形?如果存在,求出点的坐标;如果不存在,请说明理由;
(3)点是线段上的一个动点,过点作轴的垂线与抛物线相交于点,当四边形的面积最大时,求点的坐标.
7.如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A,B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).
(1)求二次函数的解析式和直线BD的解析式;
(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
(3)在抛物线上是否存在点Q,且点Q在第一象限,使△BDQ中BD边上的高为?若存在,求出点Q的坐标;若不存在,请说明理由.
8.如图,已知点A的坐标为(-2,0),直线y=-x+3与x轴,y轴分别交于点B和点C,连接AC,顶点为D的抛物线y=ax2+bx+c,过A,B,C三点.
(1)求抛物线的解析式及顶点D的坐标;
(2)设抛物线的对称轴DE交线段BC于点E,P为第一象限内抛物线上一点,过点P作x轴的垂线,交线段BC于点F,若四边形DEFP为平行四边形,求点P的坐标;
(3)设点M是线段BC上的一动点,过点M作MN∥AB,交AC于点N.点Q从点B出发,以每秒1个单位长度的速度沿线段BA向点A运动,运动时间为t(秒).当以MN为直角边的△QMN是等腰直角三角形时,直接写出此时t的取值.
9.如图,抛物线经过A(-1,0)、B(5,6)两点,点是线段上一动点,过点作轴的垂线,交抛物线于点.
(1)求抛物线的解析式;
(2)求线段的最大值;
(3)在抛物线的对称轴上是否存在一个动点,使得是直角三角形?若存在,求出点的坐标;若不存在,请说明理由.
10.如图,已知抛物线与x轴的一个交点为,与y轴的交点为,其顶点为C,对称轴为直线.
(1)求抛物线的函数解析式;
(2)已知点M为y轴上的一个动点,当为等腰三角形时,求点M的坐标.
11.如图1,直线l: y=x+4与x轴,y轴分别交于A、B两点.二次函数y = ax2 - 2ax - 2(a > 0)的图像经过点A,交y轴于点C.
(1)则点C坐标为 _________ ;抛物线对称轴是直线 _________ ;a的值是 _________ ;
(2)已知点M是抛物线上的一个动点,经过点M作x轴的垂线MD,交直线l于点E,过点C作CD⊥MD,垂足为D,连接CM.设点M的横坐标为m.
①当点M位于第一象限的抛物线上,且△CDM是等腰直角三角形时,CM交直线于点F.设点F至直线DM的距离d1,到y轴的距离为d2,求的值.
②如图2,将△CDM绕点C逆时针旋转得到△C,且旋转角∠MC = ∠OAB,当点M的对应点落在y轴上时,请直接写出点M的横坐标m的值.
12.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.
(1)抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求APC的面积的最大值.
(3)在抛物线对称轴上是否存在一点M,使以A,N,M为顶点的三角形是直角三角形?若存在,请直接写出点M的坐标.若不存在,请说明理由.
13.已知二次函数y=x2+bx+c经过A、B两点,BC垂直x轴于点C,且A(﹣1,0),C(4,0),AC=BC.
(1)求抛物线的解析式;
(2)请画出抛物线的图象;
(3)点P是抛物线对称轴上一个动点,是否存在这样的点P,使三角形ABP为直角三角形?若存在,求出P点坐标;若不存在,请说明理由.
14.如图,抛物线与轴相交于A,B两点,与y轴相交于点C,对称轴为直线,项点为D,点B的坐标为.
(1)填空:点A的坐标为_________,点D的坐标为_________,抛物线的解析式为_________;
(2)当二次函数的自变量:满足时,函数y的最小值为,求m的值;
(3)P是抛物线对称轴上一动点,是否存在点P,使是以AC为斜边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
15.如图1,已知抛物线的顶点坐标为(-1,)与y轴交于A(0,3),交直线:x=-2于点B,点C(0,2)在y轴上,连接BC并延长,交抛物线于点D.
(1)求抛物线的表达式;
(2)如图1,E为直线上位于点B下方一动点,连接DE、BD、AD,若,求点E的坐标;
(3)如图2,在(2)的条件下,P为射线EB上一点,作PQ⊥直线DE于点Q,若△APQ为直角三角形,请求出P点的坐标;
16.已知:直线与y轴交于A,与x轴交于D,抛物线y=x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为 (1,0).
(1)求抛物线的解析式;
(2)点P是直线AE下方抛物线上一动点,求△PAE面积的最大值;
(3)动点Q在x轴上移动,当△QAE是直角三角形时,直接写出点Q的坐标;
17.抛物线与轴交于,两点(在左边),与轴交于点.
(1)如图1,若,,求抛物线的解析式;
(2)如图2,为抛物线上一动点(在左边),若,,且.
①求的值;
②如图3,直线,分别与直线交于,两点,于,于.求而的值.
18.如图,已知抛物线与x轴交于A、B两点,与y轴交于C点,其中A(1,0),C(0,3).
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴及点B的坐标;
(3)设点P为该抛物线对称轴上的一个动点,是否存在点P使△BPC为直角三角形,若存在,求出点P的坐标;若不存在,请说明理由.
19.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c为常数a≠0)与x轴,y轴分别交于A,B,C三点,已知A(-1,0),B(3,0),C(0,3),动点E从抛物线的顶点点D出发沿线段DB向终点B运动.
(1)直接写出抛物线解析式和顶点D的坐标;
(2)过点E作EF⊥y轴于点F,交抛物线对称轴左侧的部分于点G,交直线BC于点H,过点H作HP⊥x轴于点P,连接PF,求当线段PF最短时G点的坐标;
(3)在点E运动的同时,另一个动点Q从点B出发沿直线x=3向上运动,点E的速度为每秒个单位长度,点Q速度均为每秒1个单位长度,当点E到达终点B时点Q也随之停止运动,设点E的运动时间为t秒,试问存在几个t值能使△BEQ为等腰三角形?并直接写出相应t值.
20.如图,对称轴为x=1的抛物线经过A(﹣1,0),B(4,5)两点.
(1)求抛物线的解析式;
(2)P为直线AB上的动点,过点P作x轴的垂线交抛物线于点Q.
①当PQ=6时,求点P的坐标;
②是否存在点P,使以A、P、Q为顶点的三角形为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
21.如图,直线y=x+m与抛物线y=x2-2x+l交于不同的两点M、N(点M在点N的左侧).
(1)设抛物线的顶点为B,对称轴l与直线y=x+m的交点为C,连结BM、BN,若S△MBC=S△NBC,求直线MN的解析式;
(2)在(1)条件下,已知点P(t,0)为x轴上的一个动点,
①若△PMN为直角三角形,求点P的坐标.
②若∠MPN>90°,则t的取值范围是 .
22.如图,已知直线y=x+3与x轴交于点B,与y轴交于点C,抛物线y=ax2+bx+3经过B、C两点并与x轴的另一个交点为A,且OC=3OA.
(1)求抛物线的解析式;
(2)点D为直线BC上方对称轴右侧抛物线上一点,当△DBC的面积为时,求D点的坐标;
(3)在(2)的条件下,连接CD,作DE⊥x轴于E,BC、DE交于点H,点P为线段CD上一个动点,过点P作PF∥AC交x轴于点F,连接FH,当∠PFH=45°时,求点F的坐标;
(4)若M(m,n)是直线BC上方抛物线上一点,如果△MBC为锐角三角形,请直接写出点M的横坐标m的取值范围 .
23.如图1,在平面直角坐标系中,直线y=x﹣1与抛物线y=﹣x2+bx+c交于A、B两点,其中A(m,0)、B(4,n),与x轴交于另一点D.
(1)求m、n的值及该抛物线的解析式;
(2)如图2,若点P为线段AD上的一动点(不与A、D重合),分别以AP、DP为斜边,在直线AD的同侧作等腰直角△APM和等腰直角△DPN,连接MN,试确定△MPN面积最大时P点的坐标;
(3)如图3,连接BD、CD,在线段CD上是否存在点Q,使得以A、D、Q为顶点的三角形与△ABD相似若存在,请直接写出点Q的坐标,请说明理由.
24.如图1,抛物线y=x2+bx+c与x轴交于A、B两点,点A、B分别位于原点左、右两侧,且AO=2BO=4,过A点的直线y=kx+c交y轴于点C.
(1)求k、b、c的值;
(2)在抛物线的对称轴上是否存在一点P,使△ACP为直角三角形?若存在,直接写出所有满足条件的点的坐标;若不存在,请说明理由;
(3)如图2,点M为线段AC上一点,连接OM,求AM+OM的最小值.
25.如图,抛物线y=x2﹣x﹣与x轴交于点A和点B,与y轴交于点C,经过点C的直线l与抛物线交于另一点E(4,a),抛物线的顶点为点Q,抛物线的对称轴与x轴交于点D.
(1)求直线CE的解析式.
(2)如图2,P为直线CE下方抛物线上一动点,直线CE与x轴交于点F,连接PF,PC.当△PCF的面积最大时,求点P的坐标及△PCF面积的最大值.
(3)如图3,连接CD,将(1)中抛物线沿射线CD平移得到新抛物线y′,y′经过点D,y′的顶点为点H,在直线QH上是否存在点G,使得△DQG为等腰三角形?若存在,求出点G的坐标.
26.如图,直线与坐标轴交于A,G两点,经过B(2,0)、C(6,0)两点的抛物线y=ax2+bx+2与直线交于A,D两点.
(1)求抛物线的解析式及点D的坐标;
(2)点M是抛物线上位于直线AD下方上的一个动点,当点M运动到什么位置时△MDA的面积最大?最大值是多少?
(3)在x轴上是否存在点P,使以A、P、D为顶点的三角形是直角三角形?若存在,直接写出满足条件的点P的坐标;若不存在,请说明理由.
27.如图,抛物线的图象与x轴分别交于A、B两点,与y轴交于C点,且OC=AB.
(1)求抛物线的解析式.
(2)点D(1,3)在抛物线上,若点P是直线AD上的一个动点,过点P作PQ垂直于x轴,垂足为Q,且以PQ为斜边作等腰直角△PQE.
①当点P与点D重合时,求点E到y轴的距离.
②若点E落在抛物线上,请直接写出E点的坐标.
