湖南省张家界市桑植县2025届九年级下学期中考三模数学试卷(含解析)
文档属性
| 名称 | 湖南省张家界市桑植县2025届九年级下学期中考三模数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-27 14:03:29 | ||
图片预览



文档简介
2025年湖南省张家界市桑植县中考三模数学试题
一、单选题
1.实数,在数轴上的位置如图所示,则下列式子正确的是( )
A. B. C. D.
2.下列调查样本中最适合用普查的是( )
A.了解一批电视机的使用寿命 B.了解我市居民的年人均收入
C.了解我市学生的视力情况 D.了解某校学生的课外阅读情况
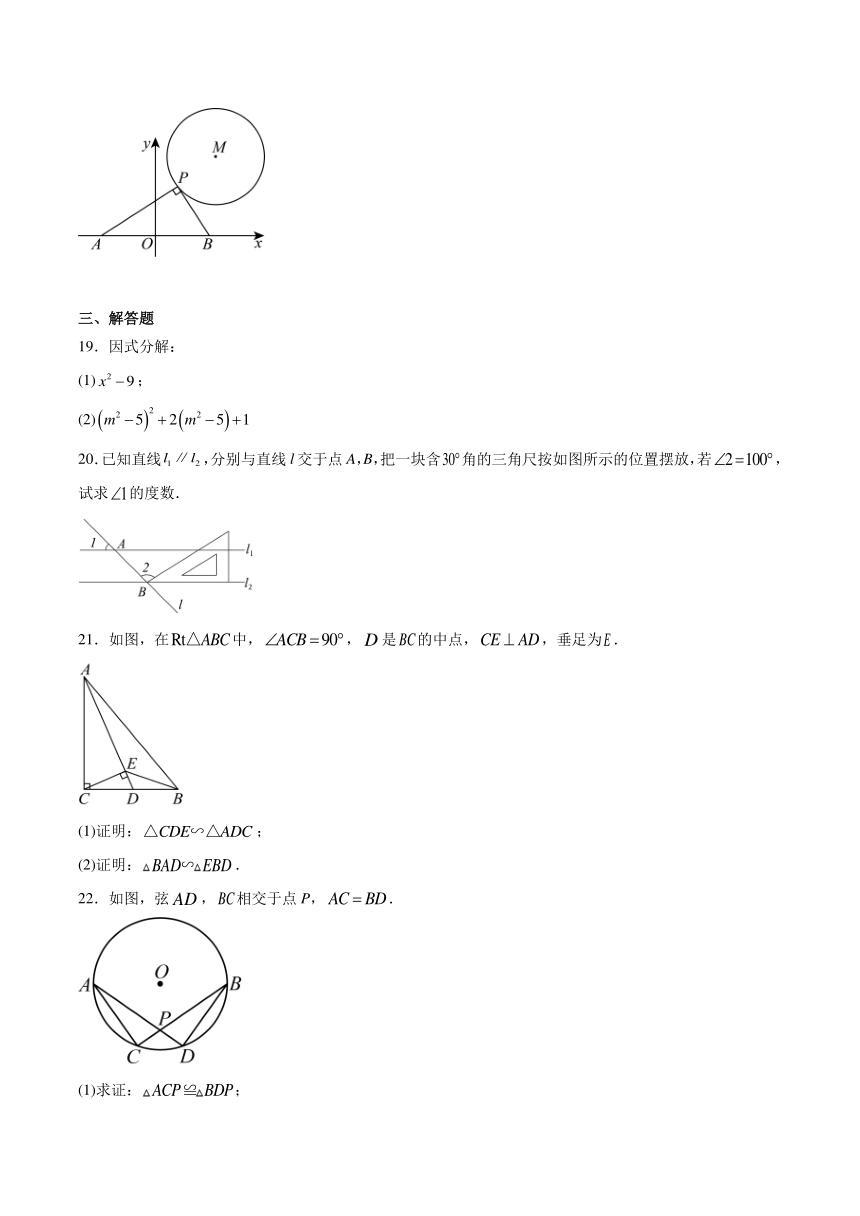
3.下列整数中,与最接近的整数是( )
A.3 B.4 C.5 D.6
4.如图示,,.若,则等于( )
A. B. C. D.
5.按一定规律排列的单项式:.则第7个单项式是( )
A. B. C. D.
6.如图,在平面直角坐标系中,四边形为矩形,点,分别在轴、轴上,且点,为边上一点,将沿所在直线翻折,当点的对应点恰好落在对角线上时,点的坐标为( )
A. B. C. D.
7.如图,在半径为5的圆O中,,是互相垂直的两条弦,垂足为P,且,则的长为( )
A.3 B.4 C. D.
8.若,则的值为( )
A. B. C. D.
9.如图,在中,,和的平分线、相交于点,交于点,交于点,若已知周长为,,,则长为( )
A. B. C. D.4
10.如图,已知抛物线过点与x轴交点的横坐标分别为,,且,,则下列结论:
①;
②方程有两个不相等的实数根;
③;
④;
⑤.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.若,互为相反数,,互为倒数,则 .
12.如图,已知是的直径, ,,那么弧度数等于 .
13.比较下列实数的大小: .
14.如图,在中,过边的中点E作直线交于点D.若,则的长是 .
15.在平面直角坐标系中,已知点,点,则直线与 (填“x”或“y”)轴平行.
16.在一个不透明的口袋里有红、黄、蓝三种颜色的小球,这些球除颜色外完全相同,其中有5个黄球,4个蓝球.若随机摸出一个蓝球的概率为 ,则随机摸出一个红球的概率为 .
17.在解方程组时,甲同学正确解得,乙同学把c看错了,而得到,那么 .
18.如图,圆M的半径为4,圆心M的坐标为,点P是圆M上的任意一点,,且与x轴分别交于A、B两点,若点A、点B关于原点O对称,则的最大值为 .
三、解答题
19.因式分解:
(1);
(2)
20.已知直线,分别与直线l交于点A,B,把一块含角的三角尺按如图所示的位置摆放,若,试求的度数.
21.如图,在中,,是的中点,,垂足为.
(1)证明:;
(2)证明:.
22.如图,弦,相交于点P,.
(1)求证:;
(2)若连接恰是的直径,且,则 .
23.劳动教育必须注重理论联系实际,在实践操作中培养学生的劳动技能.某学校基于这个理念,带领学生到劳动实践基地进行了劳动技能培训活动.为了解培训效果,学校对学生在培训前和培训后各进行了同一项目的劳动技能检测.老师对检测结果的评价为“合格”“良好”“优秀”3个等级,并依次记为分、分、分(比如,某同学检测等级为“优秀”,即得分).学校随机抽取名学生培训前后次的检测等级作为样本,绘制成下面的条形统计图:
请根据所给信息,解答下列问题:
(1)这名学生在培训前得分的中位数对应的等级为 ;(填“合格”“良好”或“优秀”)
(2)求这名学生培训后比培训前的平均分提高了多少.
24.某种新药在试验药效时发现:成人按规定剂量服用后,检测到从第5分钟起每分钟每毫升血液中含药量增加0.1微克,第100分钟达到最高,接着开始衰退,衰退时y与x成反比例函数关系.血液中含药量y(微克)与时间x(分钟)的函数关系如图所示,
(1)求血液中含药量y(微克)与时间x(分钟)的函数表达式;
(2)如果每毫升血液中含药量不低于5微克时是有效的,一次服药后的有效时间能超过130分钟吗?
25.如果两个分式与的和为常数,且为正整数,则称与互为“和整分式”,常数称为“和整值”. 如分式,,,则与互为“和整分式”,“和整值”.
(1)已知分式,互为“和整分式”,则其“和整值”的值为_________;
(2)已知分式,,与互为“和整分式”,且“和整值”,若为正整数,分式的值为正整数.
①求所代表的代数式;②求的值;
(3)在(2)的条件下,已知分式,,且,若该关于的方程无解,求实数的值.
26.【实践探究】
(1)如图1,在中,,且,E是边上一动点,连接,将绕着点C逆时针旋转至,连接交边于点G,连接,证明:.
(2)如图2,在(1)的条件下,连接交于点O,当E在的中点时,求的值.
【拓展应用】
(3)如图3,是等边三角形,E是边上一动点,连接,将绕着点C逆时针旋转至,连接交边于点G,连接交于点O,连接,当E在的中点时,求的值.
参考答案
1.B
解:由数轴可得:,
∴,
∴正确的是B选项;
故选B.
2.D
解:A、调查具有破坏性,适合抽样调查,故不符合题意;
B、人数较多,适合抽样调查,故不符合题意;
C、人数较多,适合抽样调查,故不符合题意;
D、人数不多,容易调查,适合全面调查,故符合题意;
故选:D.
3.A
由于,于是,10与9的距离小于16与10的距离,可得答案.
解:∵,
∴,
10与9的距离小于16与10的距离,
∴与最接近的是3.
故选A.
4.C
解:,,
,
,
,
故选:C
5.B
解:由题意得,第n个单项式为,
∴第7个单项式是,
故选:B.
6.B
解:依题意,,
由折叠的性质,可知,,
.
设,则.在中,由勾股定理,
得,
解得.
点的坐标为,
故选B.
7.D
解:作于M,于N,连接,,
由垂径定理得
勾股定理得:,
弦互相垂直,
,
于M,于N,
四边形是矩形,
,
四边形是正方形,
故选:D.
8.B
解:因为,得.
所以.
故选:.
9.B
解:如图,在上截取,连接,
平分,平分,
,,
,
,
,
,
,
,
,
,
在和中,
,
,
,
,
,
,
,
在和中,
,
,
,
,
周长为,
,
,
,
,
,
,
解得:,
故选:.
10.C
解:①抛物线开口向上,,,
∴当时,,故①不符合题意;
②∵抛物线过点,
∴函数的最小值,
∴有两个不相等的实数根;
∴方程有两个不相等的实数根;故②符合题意;
③∵,,
∴抛物线的对称轴为直线,且,
∴,而,
∴,
∴,故③不符合题意;
④∵抛物线过点,
∴,
∵时,,
即,
当时,,
∴,
∴,
∴,故④符合题意;
⑤∵,,
∴,
由根与系数的关系可得:,,
∴
∴,
∴,故⑤符合题意;
故选:C.
11.
解:∵,互为相反数,,互为倒数,
∴,,
故.
故答案为:.
12./54度
∵
∴,
∴,
∴,
∴弧度数等于.
故答案为:.
13.
解:,,
,
,
故答案为:.
14.4
解:∵,,
∴,
∵是的垂直平分线,
∴,
故答案为:4.
15.x
解:∵点,点,
∴点A和点B的纵坐标相同,
∴直线与x轴平行,
故答案为:x.
16./
解:设红球有个,
随机摸出一个蓝球的概率为 ,
,
解得:,
经检验,是所列方程的解,
∴红球有3个,
∴随机摸出一个红球的概率为:,
故答案为:.
17.7
解:把把代入得:,
得:,
把代入①得:,
把代入得:,
解得:,
,
故答案为:7.
18.28
解:连接,
∵,
∴,
∵点A、点B关于原点O对称,
∴,即点为中点,
∴,
若要使取最大值,则需取最大值,
连接,交于点,
当点P位于点时,取得最小值,
过点M作轴于点Q,圆心M的坐标为,
则,
∴,
又∵,
∴,
∴当点P在的延长线与的交点上时,取最大值,
∴的最大值为,
∴的最大值为.
故答案为:.
19.(1)
(2)
(1)解:.
(2)解:
.
20.
如图所示,,
,
,
,
,
.
答:的度数为.
21.(1)见解析
(2)见解析
(1)∵,
∴
∵
∴;
(2)∵
∴
∵是的中点,
∴
∴
又∵
∴.
22.(1)证明见解析
(2)
(1)证明:∵,,,
∴;
(2)解:如图,连接,
∵为的直径,
∴,
∵,
∴,
∵,
∴,
∴,
∴;
23.(1)合格;
(2)这名学生培训后比培训前的平均分提高了分
(1)解:由题意知,培训前合格的有人,良好的有人,优秀的有人,
∴这名学生在培训前得分的中位数对应的等级为合格,
故答案为:合格.
(2)解:名学生在培训前的平均分为:
(分),
名学生在培训后的平均分为:
(分),
∴这名学生培训后比培训前的平均分提高了:
(分).
24.(1)当时,;当时,
(2)能超过130分钟,见解析
(1)解:从第5分钟起每分钟每毫升血液中含药量增加0.1微克,
∴,
当时,设y与x之间的函数关系式为,
∵经过点,
∴,
解得,
∴;
当时,y与x之间的函数关系式为,
∵经过点,
∴,
解得,即;
(2)解:令,
解得,
令,
解得,
∴一次服药后的有效视角为:(分钟),超过分钟.
25.(1)
(2)①;②的值为1
(3)的值为:1或
(1)解:分式,互为“和整分式”,
,
其“和整值”的值为2;
(2)①,,
,
与互为“和整分式”,且“和整值”,
,
;
②,且分式的值为正整数且为正整数,
或,
或 ,
为正整数,
(舍去),则的值为1 ;
(3)由题意可得:,
,
,
,整理得:,
当,解得:,方程无解,
当,方程无解,则有增根,
将代入得,,解得:,
综上:的值为:1或.
26.(1)见解析;(2);(3)
证明(1)由旋转知,,,
∵,,
∴,
∴,
∴,
∴;
(2)设,
∵,,
∴,
∵,
∴,
∴,
当E在的中点时, ,
∴,,
,
∴,
∴四边形是矩形,
∵,
∴矩形是正方形,
∴,,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∴;
(3)∵是等边三角形,
∴,,
设等边三角形的边长为2,
由旋转知,,,
∴是等边三角形,
∴,
∵,
∴,
∴,
∴,,,
当E在的中点时, ,,,
∴,
∴,,,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
∵,
∴垂直平分,
∴,
∵,
∴,
∴,,
∴.
一、单选题
1.实数,在数轴上的位置如图所示,则下列式子正确的是( )
A. B. C. D.
2.下列调查样本中最适合用普查的是( )
A.了解一批电视机的使用寿命 B.了解我市居民的年人均收入
C.了解我市学生的视力情况 D.了解某校学生的课外阅读情况
3.下列整数中,与最接近的整数是( )
A.3 B.4 C.5 D.6
4.如图示,,.若,则等于( )
A. B. C. D.
5.按一定规律排列的单项式:.则第7个单项式是( )
A. B. C. D.
6.如图,在平面直角坐标系中,四边形为矩形,点,分别在轴、轴上,且点,为边上一点,将沿所在直线翻折,当点的对应点恰好落在对角线上时,点的坐标为( )
A. B. C. D.
7.如图,在半径为5的圆O中,,是互相垂直的两条弦,垂足为P,且,则的长为( )
A.3 B.4 C. D.
8.若,则的值为( )
A. B. C. D.
9.如图,在中,,和的平分线、相交于点,交于点,交于点,若已知周长为,,,则长为( )
A. B. C. D.4
10.如图,已知抛物线过点与x轴交点的横坐标分别为,,且,,则下列结论:
①;
②方程有两个不相等的实数根;
③;
④;
⑤.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.若,互为相反数,,互为倒数,则 .
12.如图,已知是的直径, ,,那么弧度数等于 .
13.比较下列实数的大小: .
14.如图,在中,过边的中点E作直线交于点D.若,则的长是 .
15.在平面直角坐标系中,已知点,点,则直线与 (填“x”或“y”)轴平行.
16.在一个不透明的口袋里有红、黄、蓝三种颜色的小球,这些球除颜色外完全相同,其中有5个黄球,4个蓝球.若随机摸出一个蓝球的概率为 ,则随机摸出一个红球的概率为 .
17.在解方程组时,甲同学正确解得,乙同学把c看错了,而得到,那么 .
18.如图,圆M的半径为4,圆心M的坐标为,点P是圆M上的任意一点,,且与x轴分别交于A、B两点,若点A、点B关于原点O对称,则的最大值为 .
三、解答题
19.因式分解:
(1);
(2)
20.已知直线,分别与直线l交于点A,B,把一块含角的三角尺按如图所示的位置摆放,若,试求的度数.
21.如图,在中,,是的中点,,垂足为.
(1)证明:;
(2)证明:.
22.如图,弦,相交于点P,.
(1)求证:;
(2)若连接恰是的直径,且,则 .
23.劳动教育必须注重理论联系实际,在实践操作中培养学生的劳动技能.某学校基于这个理念,带领学生到劳动实践基地进行了劳动技能培训活动.为了解培训效果,学校对学生在培训前和培训后各进行了同一项目的劳动技能检测.老师对检测结果的评价为“合格”“良好”“优秀”3个等级,并依次记为分、分、分(比如,某同学检测等级为“优秀”,即得分).学校随机抽取名学生培训前后次的检测等级作为样本,绘制成下面的条形统计图:
请根据所给信息,解答下列问题:
(1)这名学生在培训前得分的中位数对应的等级为 ;(填“合格”“良好”或“优秀”)
(2)求这名学生培训后比培训前的平均分提高了多少.
24.某种新药在试验药效时发现:成人按规定剂量服用后,检测到从第5分钟起每分钟每毫升血液中含药量增加0.1微克,第100分钟达到最高,接着开始衰退,衰退时y与x成反比例函数关系.血液中含药量y(微克)与时间x(分钟)的函数关系如图所示,
(1)求血液中含药量y(微克)与时间x(分钟)的函数表达式;
(2)如果每毫升血液中含药量不低于5微克时是有效的,一次服药后的有效时间能超过130分钟吗?
25.如果两个分式与的和为常数,且为正整数,则称与互为“和整分式”,常数称为“和整值”. 如分式,,,则与互为“和整分式”,“和整值”.
(1)已知分式,互为“和整分式”,则其“和整值”的值为_________;
(2)已知分式,,与互为“和整分式”,且“和整值”,若为正整数,分式的值为正整数.
①求所代表的代数式;②求的值;
(3)在(2)的条件下,已知分式,,且,若该关于的方程无解,求实数的值.
26.【实践探究】
(1)如图1,在中,,且,E是边上一动点,连接,将绕着点C逆时针旋转至,连接交边于点G,连接,证明:.
(2)如图2,在(1)的条件下,连接交于点O,当E在的中点时,求的值.
【拓展应用】
(3)如图3,是等边三角形,E是边上一动点,连接,将绕着点C逆时针旋转至,连接交边于点G,连接交于点O,连接,当E在的中点时,求的值.
参考答案
1.B
解:由数轴可得:,
∴,
∴正确的是B选项;
故选B.
2.D
解:A、调查具有破坏性,适合抽样调查,故不符合题意;
B、人数较多,适合抽样调查,故不符合题意;
C、人数较多,适合抽样调查,故不符合题意;
D、人数不多,容易调查,适合全面调查,故符合题意;
故选:D.
3.A
由于,于是,10与9的距离小于16与10的距离,可得答案.
解:∵,
∴,
10与9的距离小于16与10的距离,
∴与最接近的是3.
故选A.
4.C
解:,,
,
,
,
故选:C
5.B
解:由题意得,第n个单项式为,
∴第7个单项式是,
故选:B.
6.B
解:依题意,,
由折叠的性质,可知,,
.
设,则.在中,由勾股定理,
得,
解得.
点的坐标为,
故选B.
7.D
解:作于M,于N,连接,,
由垂径定理得
勾股定理得:,
弦互相垂直,
,
于M,于N,
四边形是矩形,
,
四边形是正方形,
故选:D.
8.B
解:因为,得.
所以.
故选:.
9.B
解:如图,在上截取,连接,
平分,平分,
,,
,
,
,
,
,
,
,
,
在和中,
,
,
,
,
,
,
,
在和中,
,
,
,
,
周长为,
,
,
,
,
,
,
解得:,
故选:.
10.C
解:①抛物线开口向上,,,
∴当时,,故①不符合题意;
②∵抛物线过点,
∴函数的最小值,
∴有两个不相等的实数根;
∴方程有两个不相等的实数根;故②符合题意;
③∵,,
∴抛物线的对称轴为直线,且,
∴,而,
∴,
∴,故③不符合题意;
④∵抛物线过点,
∴,
∵时,,
即,
当时,,
∴,
∴,
∴,故④符合题意;
⑤∵,,
∴,
由根与系数的关系可得:,,
∴
∴,
∴,故⑤符合题意;
故选:C.
11.
解:∵,互为相反数,,互为倒数,
∴,,
故.
故答案为:.
12./54度
∵
∴,
∴,
∴,
∴弧度数等于.
故答案为:.
13.
解:,,
,
,
故答案为:.
14.4
解:∵,,
∴,
∵是的垂直平分线,
∴,
故答案为:4.
15.x
解:∵点,点,
∴点A和点B的纵坐标相同,
∴直线与x轴平行,
故答案为:x.
16./
解:设红球有个,
随机摸出一个蓝球的概率为 ,
,
解得:,
经检验,是所列方程的解,
∴红球有3个,
∴随机摸出一个红球的概率为:,
故答案为:.
17.7
解:把把代入得:,
得:,
把代入①得:,
把代入得:,
解得:,
,
故答案为:7.
18.28
解:连接,
∵,
∴,
∵点A、点B关于原点O对称,
∴,即点为中点,
∴,
若要使取最大值,则需取最大值,
连接,交于点,
当点P位于点时,取得最小值,
过点M作轴于点Q,圆心M的坐标为,
则,
∴,
又∵,
∴,
∴当点P在的延长线与的交点上时,取最大值,
∴的最大值为,
∴的最大值为.
故答案为:.
19.(1)
(2)
(1)解:.
(2)解:
.
20.
如图所示,,
,
,
,
,
.
答:的度数为.
21.(1)见解析
(2)见解析
(1)∵,
∴
∵
∴;
(2)∵
∴
∵是的中点,
∴
∴
又∵
∴.
22.(1)证明见解析
(2)
(1)证明:∵,,,
∴;
(2)解:如图,连接,
∵为的直径,
∴,
∵,
∴,
∵,
∴,
∴,
∴;
23.(1)合格;
(2)这名学生培训后比培训前的平均分提高了分
(1)解:由题意知,培训前合格的有人,良好的有人,优秀的有人,
∴这名学生在培训前得分的中位数对应的等级为合格,
故答案为:合格.
(2)解:名学生在培训前的平均分为:
(分),
名学生在培训后的平均分为:
(分),
∴这名学生培训后比培训前的平均分提高了:
(分).
24.(1)当时,;当时,
(2)能超过130分钟,见解析
(1)解:从第5分钟起每分钟每毫升血液中含药量增加0.1微克,
∴,
当时,设y与x之间的函数关系式为,
∵经过点,
∴,
解得,
∴;
当时,y与x之间的函数关系式为,
∵经过点,
∴,
解得,即;
(2)解:令,
解得,
令,
解得,
∴一次服药后的有效视角为:(分钟),超过分钟.
25.(1)
(2)①;②的值为1
(3)的值为:1或
(1)解:分式,互为“和整分式”,
,
其“和整值”的值为2;
(2)①,,
,
与互为“和整分式”,且“和整值”,
,
;
②,且分式的值为正整数且为正整数,
或,
或 ,
为正整数,
(舍去),则的值为1 ;
(3)由题意可得:,
,
,
,整理得:,
当,解得:,方程无解,
当,方程无解,则有增根,
将代入得,,解得:,
综上:的值为:1或.
26.(1)见解析;(2);(3)
证明(1)由旋转知,,,
∵,,
∴,
∴,
∴,
∴;
(2)设,
∵,,
∴,
∵,
∴,
∴,
当E在的中点时, ,
∴,,
,
∴,
∴四边形是矩形,
∵,
∴矩形是正方形,
∴,,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∴;
(3)∵是等边三角形,
∴,,
设等边三角形的边长为2,
由旋转知,,,
∴是等边三角形,
∴,
∵,
∴,
∴,
∴,,,
当E在的中点时, ,,,
∴,
∴,,,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
∵,
∴垂直平分,
∴,
∵,
∴,
∴,,
∴.
同课章节目录
