2025年浙江省衢州市中考三模数学试卷(含答案)
文档属性
| 名称 | 2025年浙江省衢州市中考三模数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 195.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-27 00:00:00 | ||
图片预览




文档简介
2025年浙江省衢州市中考三模数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在中,负数有个.
A. B. C. D.
2.年世界运动会将于月日至月日在四川省成都市举行,是中国第二次举办世界运动会下列各图都是成都世界运动会的预选图案,其中是轴对称图形的是( )
A. B.
C. D.
3.有一条围巾,两条长边互相平行,按图所示折叠已知,且,则等于( )
A.
B.
C.
D.
4.下列运算正确的是( )
A. B. C. D.
5.在跳绳测试中,某小组位成员每分钟跳绳次数如下:、、、、,这组数据的众数为( )
A. B. C. D.
6.请估计在哪两个整数之间( )
A. 到之间 B. 到之间 C. 到之间 D. 到之间
7.方程组的解为( )
A. B. C. D.
8.如图,已知≌,,,若,则的度数为( )
A.
B.
C.
D.
9.如图,在同一直角坐标系中抛物线与双曲线交于,,三点,则满足的自变量的取值范围是( )
A. 或
B. 或
C. 或或
D. 或或
10.如图,矩形中,为中点,过点的直线分别与、交于点、,连结交于点,连结、若,,则下列结论中正确结论的个数是( )
;四边形是菱形;;::.
A. 个 B. 个 C. 个 D. 个
二、填空题:本题共6小题,每小题3分,共18分。
11.计算: ______.
12.分解因式:______.
13.如图,是的弦,连接,,点在上,若,,则扇形的面积为______.
14.在一个不透明的口袋中,装有红球和蓝球共个,它们除颜色外没有任何区别摇匀后从口袋中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球试验,发规摸到黄球的频率是,则口袋中大约有红球______个
15.已知二次函数,当时,的最大值为,则的值为 .
16.如图,在中,,,,先将沿翻折得到,再将沿翻折得到,过点作交于点垂足为点,则的长为 .
三、计算题:本大题共1小题,共6分。
17.计算:.
四、解答题:本题共7小题,共56分。解答应写出文字说明,证明过程或演算步骤。
18.本小题分
先化简,再求值:,其中.
19.本小题分
如图,在平行四边形中,对角线,交于点,平分,过点作,交的延长线于点连接.
求证:四边形是菱形;
若,,求的长.
20.本小题分
联合国新闻部将中国传统节气“谷雨”这一天定为中文日,以纪念“中华文字始祖”仓颉造字的贡献某校举行了“感受中文魅力,弘扬中华文化”的趣味知识竞赛现从该校七、八年级中各随机抽取名学生的竞赛成绩用表示:百分制分成四组:;;;,将所得数据进行收集、整理、描述和分析:
收集数据:
七年级名学生的竞赛成绩是:,,,,,,,,,,,,,,,,,,,
八年级名学生的竞赛成绩在组中的数据是:,,,,,
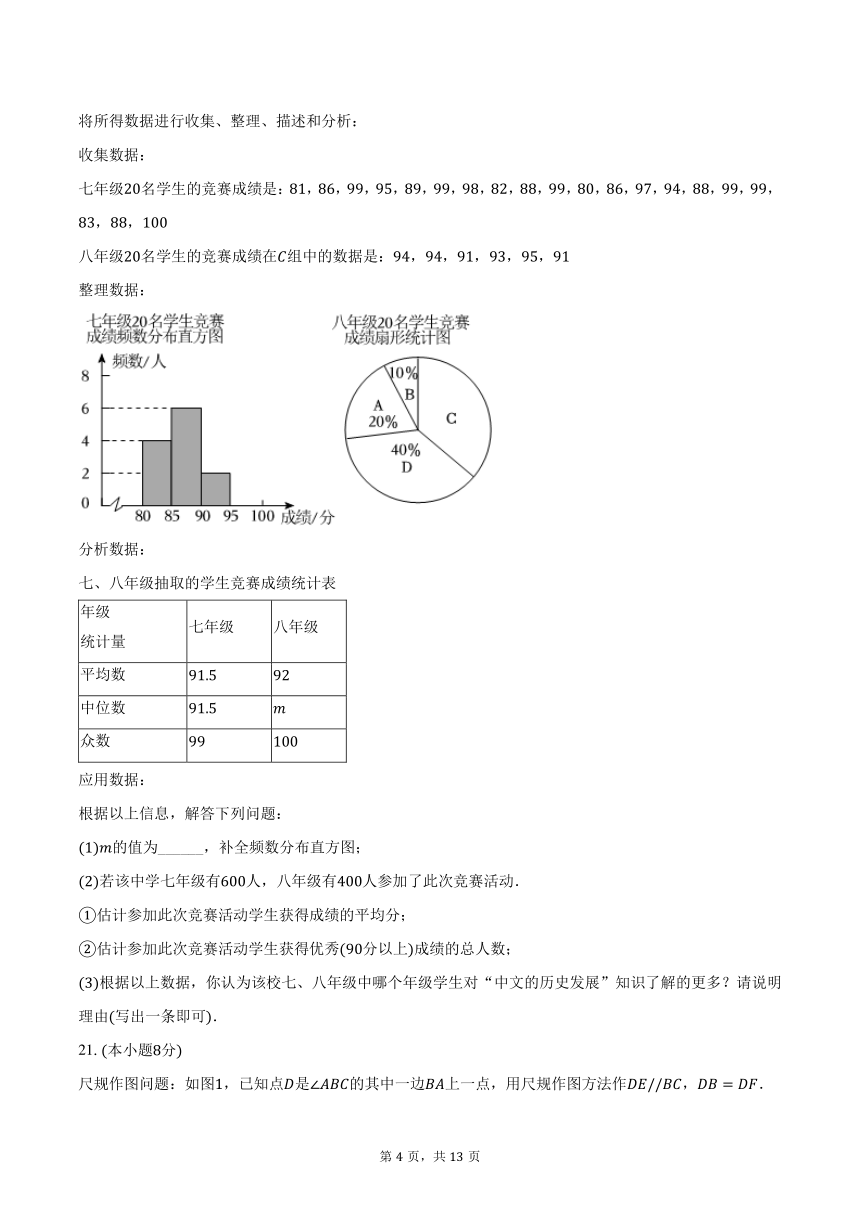
整理数据:
分析数据:
七、八年级抽取的学生竞赛成绩统计表
年级
统计量 七年级 八年级
平均数
中位数
众数
应用数据:
根据以上信息,解答下列问题:
的值为______,补全频数分布直方图;
若该中学七年级有人,八年级有人参加了此次竞赛活动.
估计参加此次竞赛活动学生获得成绩的平均分;
估计参加此次竞赛活动学生获得优秀分以上成绩的总人数;
根据以上数据,你认为该校七、八年级中哪个年级学生对“中文的历史发展”知识了解的更多?请说明理由写出一条即可.
21.本小题分
尺规作图问题:如图,已知点是的其中一边上一点,用尺规作图方法作,.
连接,根据作图痕迹,请说明平分.
如图,用尺规作图法在上确定点画出作图痕迹,使得,连接求证:四边形是菱形.
22.本小题分
一条笔直的路上依次有、、三地,其中、两地相距米.小刚、小欣两人分别从、两地同时出发,匀速而行,分别去往目的地与图中线段、分别表示小刚、小欣两人离地的距离米与行走时间分钟的函数关系图象.
求所在直线的表达式.
出发后小刚行走多少时间,与小欣相遇?
小刚到地后,再经过分钟小欣也到地,求、两地间的距离.
23.本小题分
太阳光线与地面的夹角叫做太阳高度角冬至是北半球各地白昼时间最短、黑夜最长的一天;夏至是北半球各地黑夜时间最短、白昼最长的一天设冬至这天正午时刻太阳高度角为,夏至这天正午时刻太阳高度角为.
厂家设计了可伸缩抛物线型遮阳棚,其侧面示意图如图所示曲线为遮阳棚,为遮阳棚安装在窗户上方的支架,,线段的长度称为遮阳棚的跨度已知遮阳棚所在的抛物线与抛物线的形状相同.
如图,为小明家的朝南窗户,测得,,窗户的高度为米为能最大限度地遮挡夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内,在安装遮阳棚时,需根据实际计算遮阳棚的跨度的长.
求小明家所需的遮阳棚的跨度;
春节前期,小明想在遮阳棚顶部挂一盏高为米的灯笼如图如图,灯笼与窗户的水平距离为米,灯笼的底端点与窗户的上沿点的铅垂高度为米,灯笼顶端点与悬挂点点的距离为米若,,求的最大值.
24.本小题分
如图,已知是的直径,是上的一个动点点与点、不重合,连接,是的中点,作弦,垂直为.
若点和点不重合,连接、和,当是等腰三角形时,求的度数;
若点和点重合,如图,探索与的数量关系并说明理由.
答案和解析
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】解:原式
.
18.【解析】解:
,
当时,原式.
19【解析】证明:在平行四边形中,对角线,交于点,平分,
,,
,
,
,
四边形是菱形;
解:四边形是菱形,
,,,
,
于点,
,
在中,,
,
,
在直角三角形中,由勾股定理得:,
,
,
,
,
20.【解析】人,
则八年级的中位数位于组的第位和位的平均数:
,
七年级组的人数为:人,
故答案为:;
估计参加此次竞赛活动学生获得成绩的平均分为:分;
估计参加此次竞赛活动学生获得优秀分以上成绩的总人数为:
人;
八年级学生对“中文的历史发展”知识了解的更多.
理由:八年级所抽学生的平均成绩大于七年级的平均成绩.答案不唯一.
21.【解析】证明:由作图可知,
,
,
,
,
,
平分;
图形如图所示:
,,
,
,
四边形是平行四边形,
,
四边形是菱形.
22. 解:由题可设所在直线表达式为:,
将点,代入:
可得
解得
所在直线表达式为:.
【小题】
解:由图象可得小刚行驶速度为米分,
小欣行驶速度米分,
两人相遇时间为:分钟
所以,小刚行走分钟后两人相遇.
【小题】
解:设、两地的距离为米.
由题意得,
解得米
答:、两地的距离为米.
23.【解析】由题意,过点作垂线交于点,交于点,如图:
,
,
,
,
,
,
,
,
,
,即,
小明家所需的遮阳棚的跨度长为;
由题意,点坐标为,
将点坐标为代入得,,
令,
,
当时,取最小值,最小值为;当时,取大值,最大值为,
的取值范围,即,
,
当时,.
的最大值为米.
24.【答案】解:连接,
当是等腰三角形时,分两种情况:
当时,如图,
,
设的度数为,则,
,
,为直径,
,
,
是的中点,
,
,
,
,
,
,
,
;
当时,如图,
,
设的度数为,
,
为弦,为半径,
,
,
是的中点,
,
,
,
,
,
,
,
,
,
综上所述,当是等腰三角形时,的度数是或;
,理由是:
如图,点和点重合,
设的度数为,则,
是的中点,
,
,
,
,
,
,
为的直径,
,
.
第11页,共13页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在中,负数有个.
A. B. C. D.
2.年世界运动会将于月日至月日在四川省成都市举行,是中国第二次举办世界运动会下列各图都是成都世界运动会的预选图案,其中是轴对称图形的是( )
A. B.
C. D.
3.有一条围巾,两条长边互相平行,按图所示折叠已知,且,则等于( )
A.
B.
C.
D.
4.下列运算正确的是( )
A. B. C. D.
5.在跳绳测试中,某小组位成员每分钟跳绳次数如下:、、、、,这组数据的众数为( )
A. B. C. D.
6.请估计在哪两个整数之间( )
A. 到之间 B. 到之间 C. 到之间 D. 到之间
7.方程组的解为( )
A. B. C. D.
8.如图,已知≌,,,若,则的度数为( )
A.
B.
C.
D.
9.如图,在同一直角坐标系中抛物线与双曲线交于,,三点,则满足的自变量的取值范围是( )
A. 或
B. 或
C. 或或
D. 或或
10.如图,矩形中,为中点,过点的直线分别与、交于点、,连结交于点,连结、若,,则下列结论中正确结论的个数是( )
;四边形是菱形;;::.
A. 个 B. 个 C. 个 D. 个
二、填空题:本题共6小题,每小题3分,共18分。
11.计算: ______.
12.分解因式:______.
13.如图,是的弦,连接,,点在上,若,,则扇形的面积为______.
14.在一个不透明的口袋中,装有红球和蓝球共个,它们除颜色外没有任何区别摇匀后从口袋中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球试验,发规摸到黄球的频率是,则口袋中大约有红球______个
15.已知二次函数,当时,的最大值为,则的值为 .
16.如图,在中,,,,先将沿翻折得到,再将沿翻折得到,过点作交于点垂足为点,则的长为 .
三、计算题:本大题共1小题,共6分。
17.计算:.
四、解答题:本题共7小题,共56分。解答应写出文字说明,证明过程或演算步骤。
18.本小题分
先化简,再求值:,其中.
19.本小题分
如图,在平行四边形中,对角线,交于点,平分,过点作,交的延长线于点连接.
求证:四边形是菱形;
若,,求的长.
20.本小题分
联合国新闻部将中国传统节气“谷雨”这一天定为中文日,以纪念“中华文字始祖”仓颉造字的贡献某校举行了“感受中文魅力,弘扬中华文化”的趣味知识竞赛现从该校七、八年级中各随机抽取名学生的竞赛成绩用表示:百分制分成四组:;;;,将所得数据进行收集、整理、描述和分析:
收集数据:
七年级名学生的竞赛成绩是:,,,,,,,,,,,,,,,,,,,
八年级名学生的竞赛成绩在组中的数据是:,,,,,
整理数据:
分析数据:
七、八年级抽取的学生竞赛成绩统计表
年级
统计量 七年级 八年级
平均数
中位数
众数
应用数据:
根据以上信息,解答下列问题:
的值为______,补全频数分布直方图;
若该中学七年级有人,八年级有人参加了此次竞赛活动.
估计参加此次竞赛活动学生获得成绩的平均分;
估计参加此次竞赛活动学生获得优秀分以上成绩的总人数;
根据以上数据,你认为该校七、八年级中哪个年级学生对“中文的历史发展”知识了解的更多?请说明理由写出一条即可.
21.本小题分
尺规作图问题:如图,已知点是的其中一边上一点,用尺规作图方法作,.
连接,根据作图痕迹,请说明平分.
如图,用尺规作图法在上确定点画出作图痕迹,使得,连接求证:四边形是菱形.
22.本小题分
一条笔直的路上依次有、、三地,其中、两地相距米.小刚、小欣两人分别从、两地同时出发,匀速而行,分别去往目的地与图中线段、分别表示小刚、小欣两人离地的距离米与行走时间分钟的函数关系图象.
求所在直线的表达式.
出发后小刚行走多少时间,与小欣相遇?
小刚到地后,再经过分钟小欣也到地,求、两地间的距离.
23.本小题分
太阳光线与地面的夹角叫做太阳高度角冬至是北半球各地白昼时间最短、黑夜最长的一天;夏至是北半球各地黑夜时间最短、白昼最长的一天设冬至这天正午时刻太阳高度角为,夏至这天正午时刻太阳高度角为.
厂家设计了可伸缩抛物线型遮阳棚,其侧面示意图如图所示曲线为遮阳棚,为遮阳棚安装在窗户上方的支架,,线段的长度称为遮阳棚的跨度已知遮阳棚所在的抛物线与抛物线的形状相同.
如图,为小明家的朝南窗户,测得,,窗户的高度为米为能最大限度地遮挡夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内,在安装遮阳棚时,需根据实际计算遮阳棚的跨度的长.
求小明家所需的遮阳棚的跨度;
春节前期,小明想在遮阳棚顶部挂一盏高为米的灯笼如图如图,灯笼与窗户的水平距离为米,灯笼的底端点与窗户的上沿点的铅垂高度为米,灯笼顶端点与悬挂点点的距离为米若,,求的最大值.
24.本小题分
如图,已知是的直径,是上的一个动点点与点、不重合,连接,是的中点,作弦,垂直为.
若点和点不重合,连接、和,当是等腰三角形时,求的度数;
若点和点重合,如图,探索与的数量关系并说明理由.
答案和解析
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】解:原式
.
18.【解析】解:
,
当时,原式.
19【解析】证明:在平行四边形中,对角线,交于点,平分,
,,
,
,
,
四边形是菱形;
解:四边形是菱形,
,,,
,
于点,
,
在中,,
,
,
在直角三角形中,由勾股定理得:,
,
,
,
,
20.【解析】人,
则八年级的中位数位于组的第位和位的平均数:
,
七年级组的人数为:人,
故答案为:;
估计参加此次竞赛活动学生获得成绩的平均分为:分;
估计参加此次竞赛活动学生获得优秀分以上成绩的总人数为:
人;
八年级学生对“中文的历史发展”知识了解的更多.
理由:八年级所抽学生的平均成绩大于七年级的平均成绩.答案不唯一.
21.【解析】证明:由作图可知,
,
,
,
,
,
平分;
图形如图所示:
,,
,
,
四边形是平行四边形,
,
四边形是菱形.
22. 解:由题可设所在直线表达式为:,
将点,代入:
可得
解得
所在直线表达式为:.
【小题】
解:由图象可得小刚行驶速度为米分,
小欣行驶速度米分,
两人相遇时间为:分钟
所以,小刚行走分钟后两人相遇.
【小题】
解:设、两地的距离为米.
由题意得,
解得米
答:、两地的距离为米.
23.【解析】由题意,过点作垂线交于点,交于点,如图:
,
,
,
,
,
,
,
,
,
,即,
小明家所需的遮阳棚的跨度长为;
由题意,点坐标为,
将点坐标为代入得,,
令,
,
当时,取最小值,最小值为;当时,取大值,最大值为,
的取值范围,即,
,
当时,.
的最大值为米.
24.【答案】解:连接,
当是等腰三角形时,分两种情况:
当时,如图,
,
设的度数为,则,
,
,为直径,
,
,
是的中点,
,
,
,
,
,
,
,
;
当时,如图,
,
设的度数为,
,
为弦,为半径,
,
,
是的中点,
,
,
,
,
,
,
,
,
,
综上所述,当是等腰三角形时,的度数是或;
,理由是:
如图,点和点重合,
设的度数为,则,
是的中点,
,
,
,
,
,
,
为的直径,
,
.
第11页,共13页
同课章节目录
