2025年浙江省舟山市中考三模数学试卷(含答案)
文档属性
| 名称 | 2025年浙江省舟山市中考三模数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 169.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-27 18:39:51 | ||
图片预览




文档简介
2025年浙江省舟山市中考三模数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在,,,这四个数中,离原点最远的数是( )
A. B. C. D.
2.清朝诗人袁枚在其诗作苔中写道“苔花如米小,也学牡丹开”已知苔花花粉直径约为,数据“”用科学记数法可以表示为( )
A. B. C. D.
3.下列运算正确的是( )
A. B. C. D.
4.在中,,,,则的值为( )
A. B. C. D.
5.在纪录片舌尖上的中国第四季中,西昌火盆烧烤以其独特的风味与文化底蕴,再次展现了西昌这座城市的烟火魅力该片播出后,某西昌火盆烧烤店一周内每天的顾客评分满分分如下:,,,,,,下列说法正确的是( )
A. 平均数为 B. 中位数为 C. 众数为 D. 方差为
6.若关于的一元二次方程有实数根,则字母的取值范围是( )
A. 且 B. C. D. 且
7.如图,在中,,,点为中点,直角绕点旋转,,分别与边,交于,两点,以下五个结论:;≌;是等腰直角三角形;;,其中正确结论的有个.
A. B. C. D.
8.在平面直角坐标系中,将正比例函数的图象向右平移个单位长度得到一次函数的图象,则该一次函数的解析式为( )
A. B. C. D.
9.如图,,,,,是的中点,则长为( )
A. B. C. D.
10.已知点在二次函数的图象上,且点到轴的距离小于,则的取值范围是( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.因式分解:______.
12.中国传统文化中的“四瑞兽”是古代象征样瑞与方位的神兽,分别为:青龙、白虎、朱雀、玄武小王和小李在美术课上都想从“四瑞兽”中随机选择一个瑞兽进行绘画创作,他们所选瑞兽相同的概率是______.
13.用半径为,圆心角为扇形纸片围成一个圆锥的侧面,这个圆锥的高为 .
14.已知,点,,,在上,,过点的切线与的延长线交于点,,,,则的半径为______,的长为______.
15.反比例函数的图象上有,两点,当时, 填“”“”或“”.
16.如图,等边三角形的边在轴上,点在轴上,其中顶点的坐标为若抛物线与等边三角形的边有且只有两个公共点,则的取值范围是______.
三、计算题:本大题共1小题,共6分。
17.计算:;
解不等式组:.
四、解答题:本题共7小题,共56分。解答应写出文字说明,证明过程或演算步骤。
18.本小题分
如图,在边长为个单位长度的小正方形组成的网格中,给出了格点顶点是网格线的交点.
将绕点顺时针旋转得到,画出;
将向下平移个单位长度,再向左平移个单位长度,得到,画出.
借助网格,在上取一点,使得平分的面积保留确定关键点的画法,画出线段.
19.本小题分
“节约用水,从我做起”学校的洗手盆上装有一种抬启式水龙头如图,开启前与水平线平行,完全开启后,把手与水平线的夹角为,此时把手端点、出水口点和落水点在同一直线上洗手盆及水龙头示意图如图,其中,,.
水龙头从闭合到完全开启,求点上升的高度.
求的长结果精确到参考数据:,,,
20.本小题分
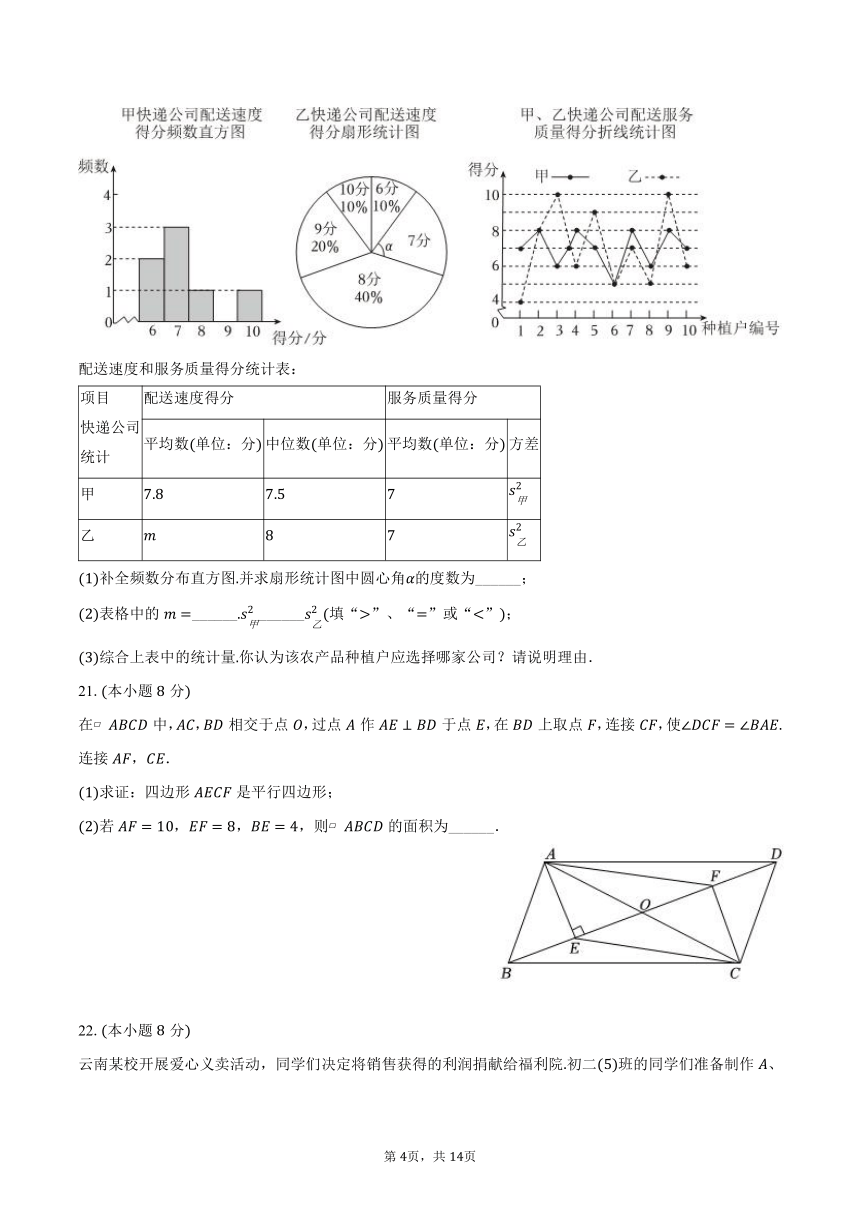
随着快递行业在农村的深入发展,全国各地的特色农产品有了更广阔的销售空间不同的快递公司在配送、服务、收费和投递范围等方面各具优势某农产品种植户经过前期调研打算从甲、乙两家快递公司中选择一家合作为此该种植户收集了家农产品种植户对两家公司的相关评价并整理、描述、分析如下:
配送速度和服务质量得分统计表:
项目
快递公司
统计 配送速度得分 服务质量得分
平均数单位:分 中位数单位:分 平均数单位:分 方差
甲
乙
补全频数分布直方图并求扇形统计图中圆心角的度数为______;
表格中的____________填“”、“”或“”;
综合上表中的统计量你认为该农产品种植户应选择哪家公司?请说明理由.
21.本小题分
在 中,,相交于点,过点作于点,在上取点,连接,使连接,.
求证:四边形是平行四边形;
若,,,则 的面积为______.
22.本小题分
云南某校开展爱心义卖活动,同学们决定将销售获得的利润捐献给福利院初二班的同学们准备制作、两款挂件来进行销售已知制作个款挂件、个款挂件所需成本为元,制作个款挂件、个款挂件所需成本为元已知、两款挂件的售价如下表:
手工制品 款挂件 款挂件
售价元个
求制作一个款挂件、一个款挂件所需的成本分别为多少元?
若该班级共有名学生计划每位同学制作个款挂件或个款挂件,制作的总成本不超过元,且制作款挂件的数量不少于款挂件的倍设安排人制作款挂件,销售的总利润为元请写出元与人之间的函数表达式,求出自变量的取值范围,并说明如何安排,使得总利润最大,最大利润是多少?
23.本小题分
【问题发现】
如图,在中,过点作,垂足为点,且若,则的值为______;
【问题探究】
如图,在中,、的垂直平分线分别交于点、,垂足分别为,,,连接、,求的周长;
【拓展应用】
如图,是一个游乐场的平面示意图,为游乐场大门,其中米,,平分交于点现分别在、上各取一点、,且满足,计划沿、修建两条轨道交通以方便游客游玩,已知两条轨道造价均为每米元,求修建这两条轨道总费用的最小值.
24.本小题分
如图,在平面直角坐标系中,抛物线与轴交于点和点,且点在点的左侧,与轴交于点.
求抛物线的函数表达式;
如图,直线与轴交于点,与轴交于点,点是第一象限内抛物线上的一个动点,设射线与直线交于点,求的最大值,及此时点的坐标;
如图,连接,将原抛物线沿射线方向平移得到新抛物线,使平移后的新抛物线经过点,新抛物线与轴的另一交点为点,在新抛物线上存在一点,使得请直接写出新抛物线的函数表达式及点的坐标.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】或
17.解:
;
,
解不等式得:,
解不等式得:,
综上所述,不等式组的解集为:.
18.【答案】如图,即为所求;
如图,即为所求;
如图,线段即为所求.
19.【解析】如图:过点作,垂足为,
在中,,
,
点上升的高度约为;
延长交于点,则,
由题意得:,,
,
,
在中,,
,
在中,,
,
,
,
的长约为.
20.【解析】甲快递公司配送速度得分为分的有户,
补全频数分布直方图如下:
乙快递公司得分人数所占百分比为,
扇形统计图中圆心角的度数为,
故答案为:;
乙快递公司派送速度的平均数分,
样本中甲快递公司配送速度得分依次为,,,,,,,,,,
乙快递公司配送速度得分依次是,,,,,,,,,,
;
;
,
,
故答案为:,;
选择乙快递公司,
理由:乙快递公司的配送速度得分的平均数,中位数均比甲配送公司的高,
21.【解析】证明:四边形是平行四边形,
,,,,
,
在和中,
,
≌,
,
,
,
又,
四边形是平行四边形;
解:,
,
由得,
在中,由勾股定理得:,即,
,
,
,
,
,
故答案为:.
22.【解析】设制作一个款挂件所需的成本为元,制作一个款挂件所需的成本为元.
根据题意,得,
解得.
答:制作一个款挂件所需的成本为元,制作一个款挂件所需的成本为元.
安排人制作款挂件,
根据题意,得,
解得,
为非负整数,
且为整数,
,
与之间的函数表达式及自变量的取值范围为且为整数,
,
随的增大而增大,
且为整数,
当时值最大,,
人,
安排人制作款挂件、人制作款挂件使得总利润最大,最大利润是元.
23.【解析】,
,
在和中,
,
≌,
,
故答案为:;
、的垂直平分线分别交于点、,
,,
的周长为;
,,
,
平分,
,
如图:作线段,使,,连接,,
,
,,
,
是等边三角形,
,
,
在和中,
,
≌,
,
,
的最小值为,
米,
两条轨道造价均为每米元,
修建这两条轨道总费用的最小值为元.
答:修建这两条轨道总费用的最小值为元.
24.【解析】抛物线,经过点,,
,
解得,
抛物线的解析式为.
如图,过点作交直线于点,
设点,则点,
,
∽,
,
,且,
时,的值最大,最大值为,
把代入,得,
点的坐标为.
直线与轴交于点,与轴交于点,
,,
,
沿着方向平移是一个先向下,再向右平移同样的单位长度的平移变换,
设平移的距离为个单位长度,
,
设,把点代入,
得,
解得舍去或,
,
令,,
解得或,
点,
,,
,
设点,
如图,过点作于点,
∽,
,
即,
解得或舍去,
;
同理可得∽,
,
即,
解得或舍去,
,
综上,点的坐标为或.
第2页,共14页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在,,,这四个数中,离原点最远的数是( )
A. B. C. D.
2.清朝诗人袁枚在其诗作苔中写道“苔花如米小,也学牡丹开”已知苔花花粉直径约为,数据“”用科学记数法可以表示为( )
A. B. C. D.
3.下列运算正确的是( )
A. B. C. D.
4.在中,,,,则的值为( )
A. B. C. D.
5.在纪录片舌尖上的中国第四季中,西昌火盆烧烤以其独特的风味与文化底蕴,再次展现了西昌这座城市的烟火魅力该片播出后,某西昌火盆烧烤店一周内每天的顾客评分满分分如下:,,,,,,下列说法正确的是( )
A. 平均数为 B. 中位数为 C. 众数为 D. 方差为
6.若关于的一元二次方程有实数根,则字母的取值范围是( )
A. 且 B. C. D. 且
7.如图,在中,,,点为中点,直角绕点旋转,,分别与边,交于,两点,以下五个结论:;≌;是等腰直角三角形;;,其中正确结论的有个.
A. B. C. D.
8.在平面直角坐标系中,将正比例函数的图象向右平移个单位长度得到一次函数的图象,则该一次函数的解析式为( )
A. B. C. D.
9.如图,,,,,是的中点,则长为( )
A. B. C. D.
10.已知点在二次函数的图象上,且点到轴的距离小于,则的取值范围是( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.因式分解:______.
12.中国传统文化中的“四瑞兽”是古代象征样瑞与方位的神兽,分别为:青龙、白虎、朱雀、玄武小王和小李在美术课上都想从“四瑞兽”中随机选择一个瑞兽进行绘画创作,他们所选瑞兽相同的概率是______.
13.用半径为,圆心角为扇形纸片围成一个圆锥的侧面,这个圆锥的高为 .
14.已知,点,,,在上,,过点的切线与的延长线交于点,,,,则的半径为______,的长为______.
15.反比例函数的图象上有,两点,当时, 填“”“”或“”.
16.如图,等边三角形的边在轴上,点在轴上,其中顶点的坐标为若抛物线与等边三角形的边有且只有两个公共点,则的取值范围是______.
三、计算题:本大题共1小题,共6分。
17.计算:;
解不等式组:.
四、解答题:本题共7小题,共56分。解答应写出文字说明,证明过程或演算步骤。
18.本小题分
如图,在边长为个单位长度的小正方形组成的网格中,给出了格点顶点是网格线的交点.
将绕点顺时针旋转得到,画出;
将向下平移个单位长度,再向左平移个单位长度,得到,画出.
借助网格,在上取一点,使得平分的面积保留确定关键点的画法,画出线段.
19.本小题分
“节约用水,从我做起”学校的洗手盆上装有一种抬启式水龙头如图,开启前与水平线平行,完全开启后,把手与水平线的夹角为,此时把手端点、出水口点和落水点在同一直线上洗手盆及水龙头示意图如图,其中,,.
水龙头从闭合到完全开启,求点上升的高度.
求的长结果精确到参考数据:,,,
20.本小题分
随着快递行业在农村的深入发展,全国各地的特色农产品有了更广阔的销售空间不同的快递公司在配送、服务、收费和投递范围等方面各具优势某农产品种植户经过前期调研打算从甲、乙两家快递公司中选择一家合作为此该种植户收集了家农产品种植户对两家公司的相关评价并整理、描述、分析如下:
配送速度和服务质量得分统计表:
项目
快递公司
统计 配送速度得分 服务质量得分
平均数单位:分 中位数单位:分 平均数单位:分 方差
甲
乙
补全频数分布直方图并求扇形统计图中圆心角的度数为______;
表格中的____________填“”、“”或“”;
综合上表中的统计量你认为该农产品种植户应选择哪家公司?请说明理由.
21.本小题分
在 中,,相交于点,过点作于点,在上取点,连接,使连接,.
求证:四边形是平行四边形;
若,,,则 的面积为______.
22.本小题分
云南某校开展爱心义卖活动,同学们决定将销售获得的利润捐献给福利院初二班的同学们准备制作、两款挂件来进行销售已知制作个款挂件、个款挂件所需成本为元,制作个款挂件、个款挂件所需成本为元已知、两款挂件的售价如下表:
手工制品 款挂件 款挂件
售价元个
求制作一个款挂件、一个款挂件所需的成本分别为多少元?
若该班级共有名学生计划每位同学制作个款挂件或个款挂件,制作的总成本不超过元,且制作款挂件的数量不少于款挂件的倍设安排人制作款挂件,销售的总利润为元请写出元与人之间的函数表达式,求出自变量的取值范围,并说明如何安排,使得总利润最大,最大利润是多少?
23.本小题分
【问题发现】
如图,在中,过点作,垂足为点,且若,则的值为______;
【问题探究】
如图,在中,、的垂直平分线分别交于点、,垂足分别为,,,连接、,求的周长;
【拓展应用】
如图,是一个游乐场的平面示意图,为游乐场大门,其中米,,平分交于点现分别在、上各取一点、,且满足,计划沿、修建两条轨道交通以方便游客游玩,已知两条轨道造价均为每米元,求修建这两条轨道总费用的最小值.
24.本小题分
如图,在平面直角坐标系中,抛物线与轴交于点和点,且点在点的左侧,与轴交于点.
求抛物线的函数表达式;
如图,直线与轴交于点,与轴交于点,点是第一象限内抛物线上的一个动点,设射线与直线交于点,求的最大值,及此时点的坐标;
如图,连接,将原抛物线沿射线方向平移得到新抛物线,使平移后的新抛物线经过点,新抛物线与轴的另一交点为点,在新抛物线上存在一点,使得请直接写出新抛物线的函数表达式及点的坐标.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】或
17.解:
;
,
解不等式得:,
解不等式得:,
综上所述,不等式组的解集为:.
18.【答案】如图,即为所求;
如图,即为所求;
如图,线段即为所求.
19.【解析】如图:过点作,垂足为,
在中,,
,
点上升的高度约为;
延长交于点,则,
由题意得:,,
,
,
在中,,
,
在中,,
,
,
,
的长约为.
20.【解析】甲快递公司配送速度得分为分的有户,
补全频数分布直方图如下:
乙快递公司得分人数所占百分比为,
扇形统计图中圆心角的度数为,
故答案为:;
乙快递公司派送速度的平均数分,
样本中甲快递公司配送速度得分依次为,,,,,,,,,,
乙快递公司配送速度得分依次是,,,,,,,,,,
;
;
,
,
故答案为:,;
选择乙快递公司,
理由:乙快递公司的配送速度得分的平均数,中位数均比甲配送公司的高,
21.【解析】证明:四边形是平行四边形,
,,,,
,
在和中,
,
≌,
,
,
,
又,
四边形是平行四边形;
解:,
,
由得,
在中,由勾股定理得:,即,
,
,
,
,
,
故答案为:.
22.【解析】设制作一个款挂件所需的成本为元,制作一个款挂件所需的成本为元.
根据题意,得,
解得.
答:制作一个款挂件所需的成本为元,制作一个款挂件所需的成本为元.
安排人制作款挂件,
根据题意,得,
解得,
为非负整数,
且为整数,
,
与之间的函数表达式及自变量的取值范围为且为整数,
,
随的增大而增大,
且为整数,
当时值最大,,
人,
安排人制作款挂件、人制作款挂件使得总利润最大,最大利润是元.
23.【解析】,
,
在和中,
,
≌,
,
故答案为:;
、的垂直平分线分别交于点、,
,,
的周长为;
,,
,
平分,
,
如图:作线段,使,,连接,,
,
,,
,
是等边三角形,
,
,
在和中,
,
≌,
,
,
的最小值为,
米,
两条轨道造价均为每米元,
修建这两条轨道总费用的最小值为元.
答:修建这两条轨道总费用的最小值为元.
24.【解析】抛物线,经过点,,
,
解得,
抛物线的解析式为.
如图,过点作交直线于点,
设点,则点,
,
∽,
,
,且,
时,的值最大,最大值为,
把代入,得,
点的坐标为.
直线与轴交于点,与轴交于点,
,,
,
沿着方向平移是一个先向下,再向右平移同样的单位长度的平移变换,
设平移的距离为个单位长度,
,
设,把点代入,
得,
解得舍去或,
,
令,,
解得或,
点,
,,
,
设点,
如图,过点作于点,
∽,
,
即,
解得或舍去,
;
同理可得∽,
,
即,
解得或舍去,
,
综上,点的坐标为或.
第2页,共14页
同课章节目录
