2025年浙江省温州市中考三模数学试卷(含答案)
文档属性
| 名称 | 2025年浙江省温州市中考三模数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 230.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-27 18:35:48 | ||
图片预览


文档简介
2025年浙江省温州市中考三模数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的相反数是( )
A. B. C. D.
2.如图是发现于甘肃省敦煌藏经洞中的全天星图中的一部分,全天星图中的一种画法便是用直角坐标投影某同学按全天星图的绘图方式将观察到的北斗七星画在如图所示的网格上,建立适当的平面直角坐标系,若表示“摇光”的点坐标为,表示“开阳”的点坐标为,则表示“天权”的点的坐标为( )
A. B. C. D.
3.根据国际能源署年全球可再生能源展望报告,预计年全球太阳能发电总装机容量将达到千瓦下列用科学记数法表示该数据正确的是( )
A. B. C. D.
4.下列计算正确的是( )
A. B. C. D.
5.分式方程解为( )
A. B. C. D.
6.某实验中学迎来年校庆,校史馆要招募一名优秀讲解员,小明经历了笔试、试讲和面试三轮测试终于如愿以偿当选讲解员他的笔试、试讲和面试成绩分别为分、分、分综合成绩中笔试占,试讲占,面试占,那么小明的综合成绩为( )
A. 分 B. 分 C. 分 D. 分
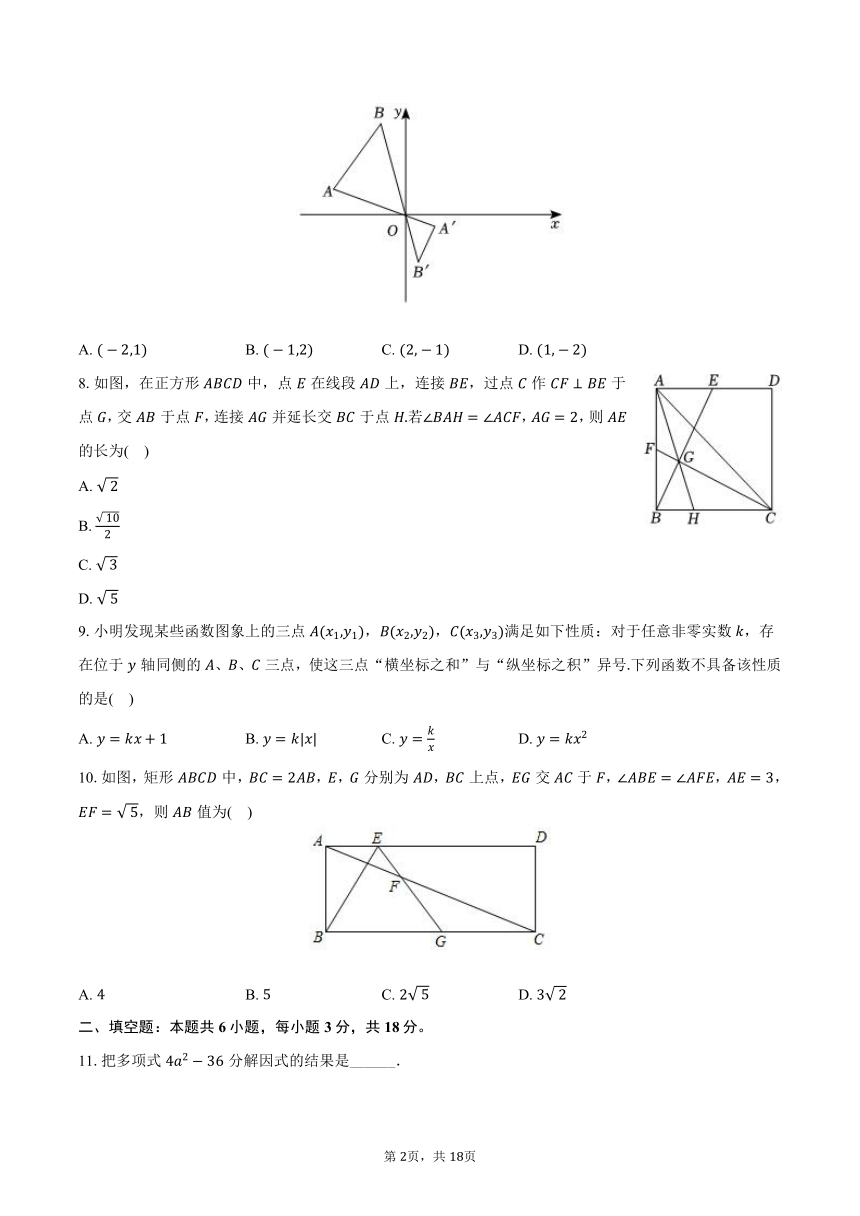
7.如图,在平面直角坐标系中,已知点,的坐标分别为,以点为位似中心,在原点的另一侧按:的相似比将缩小,则点的对应点的坐标是( )
A. B. C. D.
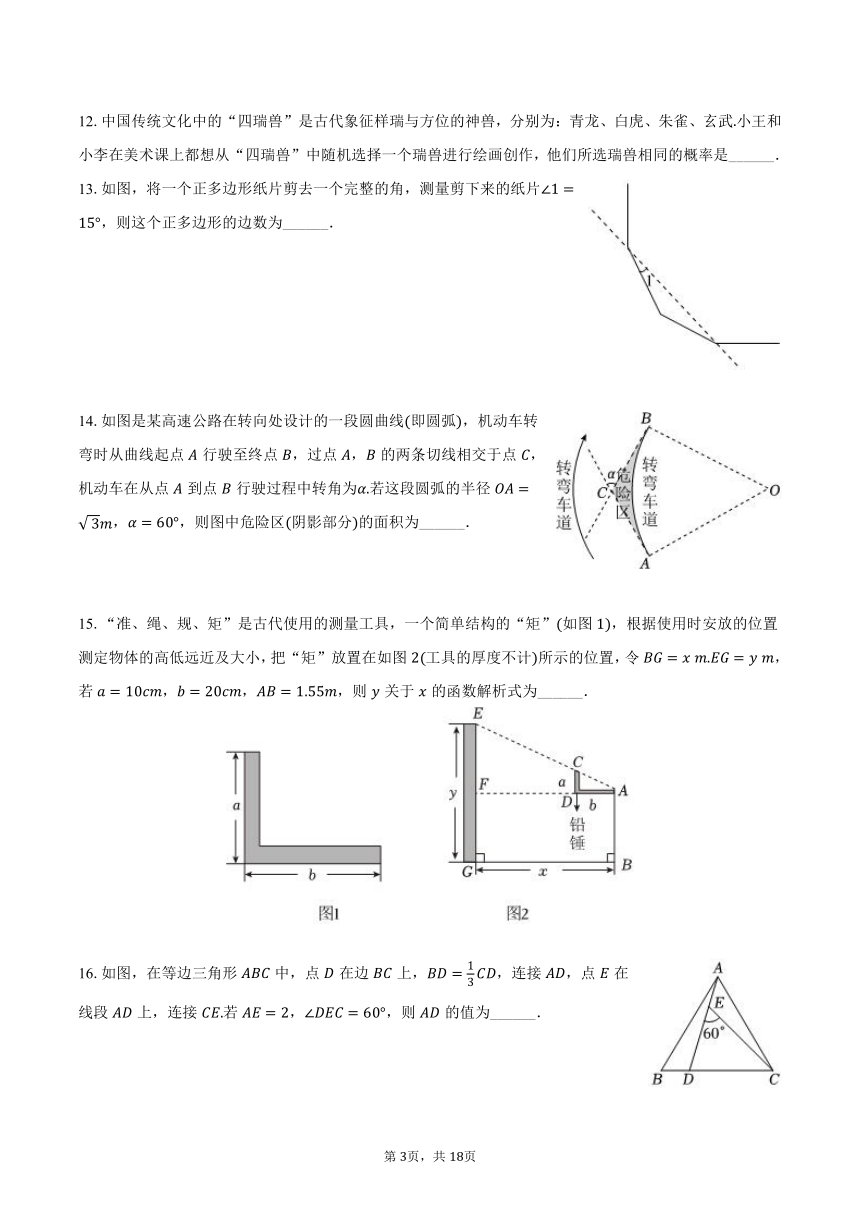
8.如图,在正方形中,点在线段上,连接,过点作于点,交于点,连接并延长交于点若,,则的长为( )
A.
B.
C.
D.
9.小明发现某些函数图象上的三点,,满足如下性质:对于任意非零实数,存在位于轴同侧的、、三点,使这三点“横坐标之和”与“纵坐标之积”异号下列函数不具备该性质的是( )
A. B. C. D.
10.如图,矩形中,,,分别为,上点,交于,,,,则值为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.把多项式分解因式的结果是______.
12.中国传统文化中的“四瑞兽”是古代象征样瑞与方位的神兽,分别为:青龙、白虎、朱雀、玄武小王和小李在美术课上都想从“四瑞兽”中随机选择一个瑞兽进行绘画创作,他们所选瑞兽相同的概率是______.
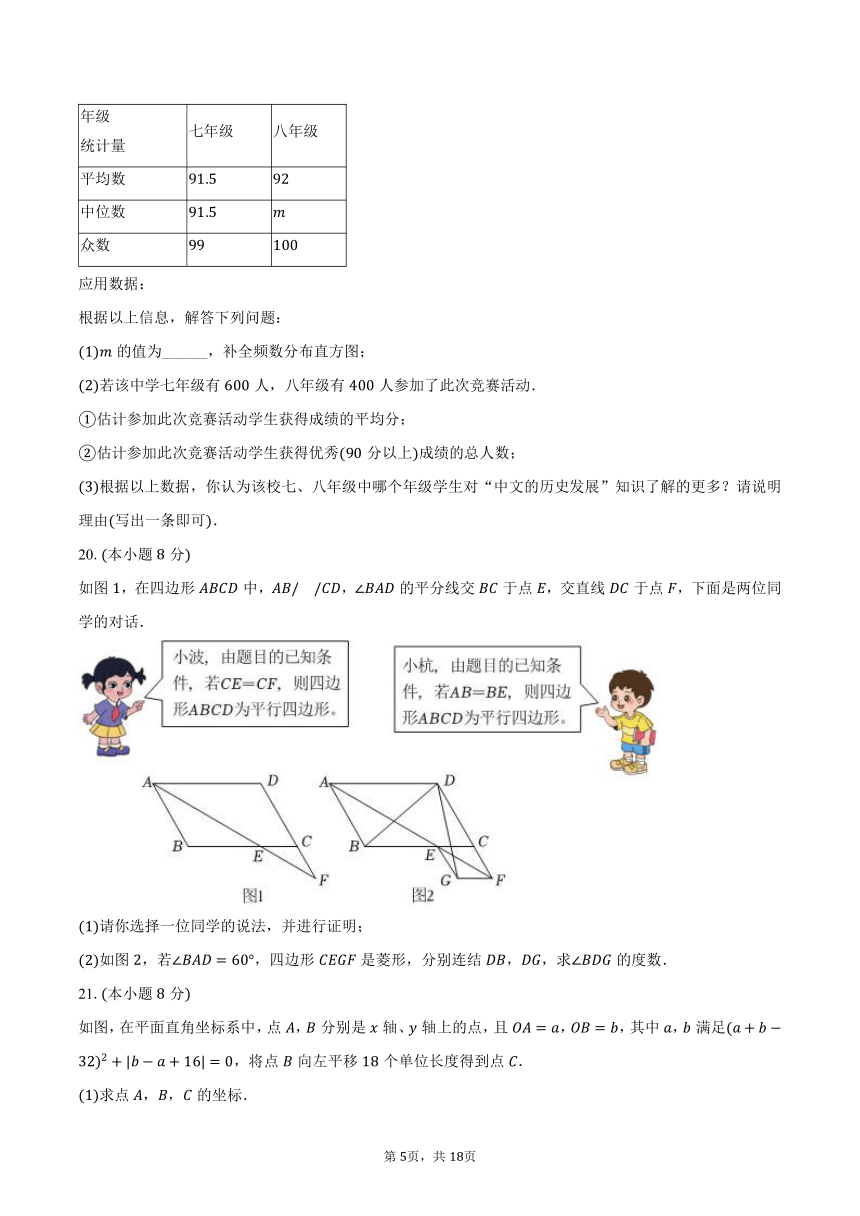
13.如图,将一个正多边形纸片剪去一个完整的角,测量剪下来的纸片,则这个正多边形的边数为______.
14.如图是某高速公路在转向处设计的一段圆曲线即圆弧,机动车转弯时从曲线起点行驶至终点,过点,的两条切线相交于点,机动车在从点到点行驶过程中转角为若这段圆弧的半径,,则图中危险区阴影部分的面积为______.
15.“准、绳、规、矩”是古代使用的测量工具,一个简单结构的“矩”如图,根据使用时安放的位置测定物体的高低远近及大小,把“矩”放置在如图工具的厚度不计所示的位置,令,若,,,则关于的函数解析式为______.
16.如图,在等边三角形中,点在边上,,连接,点在线段上,连接若,,则的值为______.
三、计算题:本大题共1小题,共6分。
17.计算:.
四、解答题:本题共7小题,共56分。解答应写出文字说明,证明过程或演算步骤。
18.本小题分
解不等式组.
19.本小题分
联合国新闻部将中国传统节气“谷雨”这一天定为中文日,以纪念“中华文字始祖”仓颉造字的贡献某校举行了“感受中文魅力,弘扬中华文化”的趣味知识竞赛现从该校七、八年级中各随机抽取名学生的竞赛成绩用表示:百分制分成四组:;;;,将所得数据进行收集、整理、描述和分析:
收集数据:
七年级名学生的竞赛成绩是:,,,,,,,,,,,,,,,,,,,
八年级名学生的竞赛成绩在组中的数据是:,,,,,
整理数据:
分析数据:
七、八年级抽取的学生竞赛成绩统计表
年级
统计量 七年级 八年级
平均数
中位数
众数
应用数据:
根据以上信息,解答下列问题:
的值为______,补全频数分布直方图;
若该中学七年级有人,八年级有人参加了此次竞赛活动.
估计参加此次竞赛活动学生获得成绩的平均分;
估计参加此次竞赛活动学生获得优秀分以上成绩的总人数;
根据以上数据,你认为该校七、八年级中哪个年级学生对“中文的历史发展”知识了解的更多?请说明理由写出一条即可.
20.本小题分
如图,在四边形中,,的平分线交于点,交直线于点,下面是两位同学的对话.
请你选择一位同学的说法,并进行证明;
如图,若,四边形是菱形,分别连结,,求的度数.
21.本小题分
如图,在平面直角坐标系中,点,分别是轴、轴上的点,且,,其中,满足,将点向左平移个单位长度得到点.
求点,,的坐标.
点,分别为线段,上的两个动点,点从点以个单位长度秒的速度向左运动,同时点从点以个单位长度秒的速度向右运动,设运动时间为秒.
当时,求的值.
是否存在一段时间,使得?若存在,求出的取值范围;若不存在,说明理由.
22.本小题分
如图,是的内接三角形,是的直径,点在上,,交于点,延长至点,使得,连接.
求的度数;
求证:是的切线;
过点作于点,若,,求的长.
23.本小题分
如图,抛物线与轴交于,两点,其中,,与轴交于点,抛物线的对称轴交轴于点,直线经过点、,联结.
求抛物线的解析式;
若抛物线上存在一点,使的面积是面积的倍,求点的坐标;
在抛物线的对称轴上是否存在一点,使线段绕点顺时针旋转得到线段,且好落在抛物线上?若存在,求出点的坐标;若不存在,请说明理由.
24.本小题分
问题背景:借助三角形的中位线可构造一组相似三角形,若将它们绕公共顶点旋转,对应顶点连线的长度存在特殊的数量关系,数学小组对此进行了研究如图,在中,,,分别取,的中点,作如图所示,将绕点逆时针旋转,连接,.
探究发现:旋转过程中,线段和的长度存在怎样的数量关系?写出你的猜想,并证明.
性质应用:如图,当所在直线首次经过点时,求的长.
延伸思考:如图,在中,,,,分别取,的中点,作,将绕点逆时针旋转得到,连接,当边平分线段时,求的值.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.解:原式
.
18.【解析】,
解不等式,得,
解不等式组,得,
所以不等式组的解集是.
19.【解析】人,
则八年级的中位数位于组的第位和位的平均数:
,
七年级组的人数为:人,
故答案为:;
估计参加此次竞赛活动学生获得成绩的平均分为:分;
估计参加此次竞赛活动学生获得优秀分以上成绩的总人数为:
人;
八年级学生对“中文的历史发展”知识了解的更多.
理由:八年级所抽学生的平均成绩大于七年级的平均成绩.答案不唯一.
20.【解析】解:选小波,
证明:,
等边对等角,
,
,
的平分线交于点,
,
,
,
四边形为平行四边形;
选小杭,
证明:,
等边对等角,
的平分线交于点,
,
,
,
四边形为平行四边形;
证明:如图,分别连接,,
四边形是平行四边形,
,,,
,,
,
,,
四边形是菱形,
,,
,,
为等边三角形,
,
,
,四边形是菱形,
,
,
,
在和中,
,
≌,
,,
,
是等边三角形,
.
21.【解析】、满足,
,
解得,
,,
,,
,,
将向左平移个单位得到点,
;
由题意知,,
,,
当时,,
;
存在,
,
由知,
,
,.
,
,
,
,
,
.
22.解:是的内接三角形,是的直径,
,
,
;
证明:,
在中,,
,
,
根据圆周角定理得:,
,
,
,
,
,
即,
又是的直径,
是的切线;
过点作于点,如图所示:
,
,
,,
,
是直角三角形,
,
,
在中,,
由勾股定理得:,
由三角形的面积公式得:,
,
在中,由勾股定理得:,
由三角形的面积公式得:,
,
,
是直角三角形,
由勾股定理得:,
,
由可知:,
又,
∽,
,
,
,
设,则,显然,
,,
∽,
,
,
在中,由勾股定理得:,
,
整理得:,
解得:,不合题意,舍去.
的长为.
23.解:抛物线与轴交于,两点,其中,,
把点、点的坐标代入得:
,
解得,
抛物线的解析式为;
如图,连接,
点是抛物线的对称轴与轴的交点,
,
,
,
,
此时,点与点重合,即;
抛物线与轴交于点,
当时,,
,
直线经过点、,把点和点的坐标代入得:
,
解得,
直线的解析式为,
过点作交抛物线于点,
则直线的解析式为,
抛物线的解析式为,
联立解得或,
,
即点的坐标为或;
在抛物线的对称轴上存在一点,使线段绕点顺时针旋转得到线段,且好落在抛物线上;理由如下:
由可知,抛物线解析式为,
把代入直线解析式,得,
与抛物线对称轴的交点,如图:
,
又,
,
则是等腰直角三角形,符合题意,
点即为所求点的一种情况;
当点在轴下方时,
设为,,
线段绕点顺时针旋转得到线段,过作直线的垂线于点,
,,
,,
,
在和中,
,
≌,
,,
,
点恰好落在抛物线上,
,
解得或舍去,
,
综上,在抛物线的对称轴上存在一点,使线段绕点顺时针旋转得到线段,且好落在抛物线上;点坐标为或.
24.证明:,理由如下:
点和点为分别为,中点,
,,
,
,
,,
,
,
根据旋转的性质可得:,
∽,
,即;
由图可知,
点和点为分别为,中点,
,,
∽,
,
当所在直线经过点时,,
根据勾股定理可得:,
由可得,
,
解得;
令,相交于点,过点作于点,如图,
根据题意可得,
,,,
,
,,
边平分线段,,
,
,
∽,
,
,
根据旋转的性质可得:,
,
,,
,,
,
.
第11页,共18页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的相反数是( )
A. B. C. D.
2.如图是发现于甘肃省敦煌藏经洞中的全天星图中的一部分,全天星图中的一种画法便是用直角坐标投影某同学按全天星图的绘图方式将观察到的北斗七星画在如图所示的网格上,建立适当的平面直角坐标系,若表示“摇光”的点坐标为,表示“开阳”的点坐标为,则表示“天权”的点的坐标为( )
A. B. C. D.
3.根据国际能源署年全球可再生能源展望报告,预计年全球太阳能发电总装机容量将达到千瓦下列用科学记数法表示该数据正确的是( )
A. B. C. D.
4.下列计算正确的是( )
A. B. C. D.
5.分式方程解为( )
A. B. C. D.
6.某实验中学迎来年校庆,校史馆要招募一名优秀讲解员,小明经历了笔试、试讲和面试三轮测试终于如愿以偿当选讲解员他的笔试、试讲和面试成绩分别为分、分、分综合成绩中笔试占,试讲占,面试占,那么小明的综合成绩为( )
A. 分 B. 分 C. 分 D. 分
7.如图,在平面直角坐标系中,已知点,的坐标分别为,以点为位似中心,在原点的另一侧按:的相似比将缩小,则点的对应点的坐标是( )
A. B. C. D.
8.如图,在正方形中,点在线段上,连接,过点作于点,交于点,连接并延长交于点若,,则的长为( )
A.
B.
C.
D.
9.小明发现某些函数图象上的三点,,满足如下性质:对于任意非零实数,存在位于轴同侧的、、三点,使这三点“横坐标之和”与“纵坐标之积”异号下列函数不具备该性质的是( )
A. B. C. D.
10.如图,矩形中,,,分别为,上点,交于,,,,则值为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.把多项式分解因式的结果是______.
12.中国传统文化中的“四瑞兽”是古代象征样瑞与方位的神兽,分别为:青龙、白虎、朱雀、玄武小王和小李在美术课上都想从“四瑞兽”中随机选择一个瑞兽进行绘画创作,他们所选瑞兽相同的概率是______.
13.如图,将一个正多边形纸片剪去一个完整的角,测量剪下来的纸片,则这个正多边形的边数为______.
14.如图是某高速公路在转向处设计的一段圆曲线即圆弧,机动车转弯时从曲线起点行驶至终点,过点,的两条切线相交于点,机动车在从点到点行驶过程中转角为若这段圆弧的半径,,则图中危险区阴影部分的面积为______.
15.“准、绳、规、矩”是古代使用的测量工具,一个简单结构的“矩”如图,根据使用时安放的位置测定物体的高低远近及大小,把“矩”放置在如图工具的厚度不计所示的位置,令,若,,,则关于的函数解析式为______.
16.如图,在等边三角形中,点在边上,,连接,点在线段上,连接若,,则的值为______.
三、计算题:本大题共1小题,共6分。
17.计算:.
四、解答题:本题共7小题,共56分。解答应写出文字说明,证明过程或演算步骤。
18.本小题分
解不等式组.
19.本小题分
联合国新闻部将中国传统节气“谷雨”这一天定为中文日,以纪念“中华文字始祖”仓颉造字的贡献某校举行了“感受中文魅力,弘扬中华文化”的趣味知识竞赛现从该校七、八年级中各随机抽取名学生的竞赛成绩用表示:百分制分成四组:;;;,将所得数据进行收集、整理、描述和分析:
收集数据:
七年级名学生的竞赛成绩是:,,,,,,,,,,,,,,,,,,,
八年级名学生的竞赛成绩在组中的数据是:,,,,,
整理数据:
分析数据:
七、八年级抽取的学生竞赛成绩统计表
年级
统计量 七年级 八年级
平均数
中位数
众数
应用数据:
根据以上信息,解答下列问题:
的值为______,补全频数分布直方图;
若该中学七年级有人,八年级有人参加了此次竞赛活动.
估计参加此次竞赛活动学生获得成绩的平均分;
估计参加此次竞赛活动学生获得优秀分以上成绩的总人数;
根据以上数据,你认为该校七、八年级中哪个年级学生对“中文的历史发展”知识了解的更多?请说明理由写出一条即可.
20.本小题分
如图,在四边形中,,的平分线交于点,交直线于点,下面是两位同学的对话.
请你选择一位同学的说法,并进行证明;
如图,若,四边形是菱形,分别连结,,求的度数.
21.本小题分
如图,在平面直角坐标系中,点,分别是轴、轴上的点,且,,其中,满足,将点向左平移个单位长度得到点.
求点,,的坐标.
点,分别为线段,上的两个动点,点从点以个单位长度秒的速度向左运动,同时点从点以个单位长度秒的速度向右运动,设运动时间为秒.
当时,求的值.
是否存在一段时间,使得?若存在,求出的取值范围;若不存在,说明理由.
22.本小题分
如图,是的内接三角形,是的直径,点在上,,交于点,延长至点,使得,连接.
求的度数;
求证:是的切线;
过点作于点,若,,求的长.
23.本小题分
如图,抛物线与轴交于,两点,其中,,与轴交于点,抛物线的对称轴交轴于点,直线经过点、,联结.
求抛物线的解析式;
若抛物线上存在一点,使的面积是面积的倍,求点的坐标;
在抛物线的对称轴上是否存在一点,使线段绕点顺时针旋转得到线段,且好落在抛物线上?若存在,求出点的坐标;若不存在,请说明理由.
24.本小题分
问题背景:借助三角形的中位线可构造一组相似三角形,若将它们绕公共顶点旋转,对应顶点连线的长度存在特殊的数量关系,数学小组对此进行了研究如图,在中,,,分别取,的中点,作如图所示,将绕点逆时针旋转,连接,.
探究发现:旋转过程中,线段和的长度存在怎样的数量关系?写出你的猜想,并证明.
性质应用:如图,当所在直线首次经过点时,求的长.
延伸思考:如图,在中,,,,分别取,的中点,作,将绕点逆时针旋转得到,连接,当边平分线段时,求的值.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.解:原式
.
18.【解析】,
解不等式,得,
解不等式组,得,
所以不等式组的解集是.
19.【解析】人,
则八年级的中位数位于组的第位和位的平均数:
,
七年级组的人数为:人,
故答案为:;
估计参加此次竞赛活动学生获得成绩的平均分为:分;
估计参加此次竞赛活动学生获得优秀分以上成绩的总人数为:
人;
八年级学生对“中文的历史发展”知识了解的更多.
理由:八年级所抽学生的平均成绩大于七年级的平均成绩.答案不唯一.
20.【解析】解:选小波,
证明:,
等边对等角,
,
,
的平分线交于点,
,
,
,
四边形为平行四边形;
选小杭,
证明:,
等边对等角,
的平分线交于点,
,
,
,
四边形为平行四边形;
证明:如图,分别连接,,
四边形是平行四边形,
,,,
,,
,
,,
四边形是菱形,
,,
,,
为等边三角形,
,
,
,四边形是菱形,
,
,
,
在和中,
,
≌,
,,
,
是等边三角形,
.
21.【解析】、满足,
,
解得,
,,
,,
,,
将向左平移个单位得到点,
;
由题意知,,
,,
当时,,
;
存在,
,
由知,
,
,.
,
,
,
,
,
.
22.解:是的内接三角形,是的直径,
,
,
;
证明:,
在中,,
,
,
根据圆周角定理得:,
,
,
,
,
,
即,
又是的直径,
是的切线;
过点作于点,如图所示:
,
,
,,
,
是直角三角形,
,
,
在中,,
由勾股定理得:,
由三角形的面积公式得:,
,
在中,由勾股定理得:,
由三角形的面积公式得:,
,
,
是直角三角形,
由勾股定理得:,
,
由可知:,
又,
∽,
,
,
,
设,则,显然,
,,
∽,
,
,
在中,由勾股定理得:,
,
整理得:,
解得:,不合题意,舍去.
的长为.
23.解:抛物线与轴交于,两点,其中,,
把点、点的坐标代入得:
,
解得,
抛物线的解析式为;
如图,连接,
点是抛物线的对称轴与轴的交点,
,
,
,
,
此时,点与点重合,即;
抛物线与轴交于点,
当时,,
,
直线经过点、,把点和点的坐标代入得:
,
解得,
直线的解析式为,
过点作交抛物线于点,
则直线的解析式为,
抛物线的解析式为,
联立解得或,
,
即点的坐标为或;
在抛物线的对称轴上存在一点,使线段绕点顺时针旋转得到线段,且好落在抛物线上;理由如下:
由可知,抛物线解析式为,
把代入直线解析式,得,
与抛物线对称轴的交点,如图:
,
又,
,
则是等腰直角三角形,符合题意,
点即为所求点的一种情况;
当点在轴下方时,
设为,,
线段绕点顺时针旋转得到线段,过作直线的垂线于点,
,,
,,
,
在和中,
,
≌,
,,
,
点恰好落在抛物线上,
,
解得或舍去,
,
综上,在抛物线的对称轴上存在一点,使线段绕点顺时针旋转得到线段,且好落在抛物线上;点坐标为或.
24.证明:,理由如下:
点和点为分别为,中点,
,,
,
,
,,
,
,
根据旋转的性质可得:,
∽,
,即;
由图可知,
点和点为分别为,中点,
,,
∽,
,
当所在直线经过点时,,
根据勾股定理可得:,
由可得,
,
解得;
令,相交于点,过点作于点,如图,
根据题意可得,
,,,
,
,,
边平分线段,,
,
,
∽,
,
,
根据旋转的性质可得:,
,
,,
,,
,
.
第11页,共18页
同课章节目录
