第5章 函数应用 总结提升--北师大版高中数学必修第一册课件(共43页PPT)
文档属性
| 名称 | 第5章 函数应用 总结提升--北师大版高中数学必修第一册课件(共43页PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 15:15:35 | ||
图片预览











文档简介
(共43张PPT)
第五章
本章总结提升
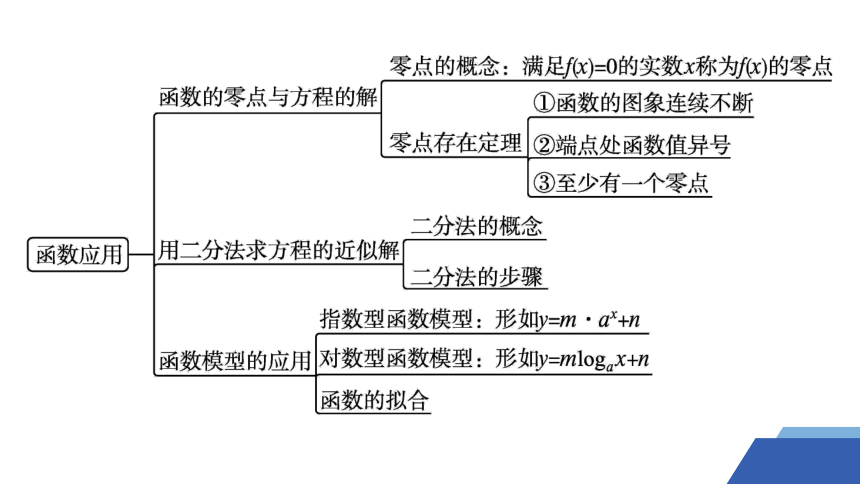
网络构建·归纳整合
专题突破·素养提升
目录索引
易错易混·衔接高考
网络构建·归纳整合
专题突破·素养提升
专题一 利用函数性质判定方程的解
1.一个函数y=f(x)在区间(a,b)内有零点必须同时满足:①函数f(x)在区间[a,b]上的图象是一条连续不断的曲线;②f(a)·f(b)<0.这两个条件缺一不可,否则结论不一定成立,如函数f(x)= ,易知f(-1)·f(1)=-1×1<0,但显然f(x)= 在
(-1,1)内没有零点.
2.若函数f(x)在区间[a,b]上的图象是连续不断的,且在两端点处的函数值f(a),f(b)异号,则函数y=f(x)的图象至少穿过x轴一次,即方程f(x)=0在区间(a,b)内至少有一个实根c.
3.零点存在定理只能判断出零点的存在性,而不能判断出零点的个数.
【例1】 (1)[2024安徽亳州期末]若函数f(x)=2x- +a在区间(1,2)内存在零点,则a的取值范围为 .
★(2)已知二次函数f(x)=ax2+bx-2(a≠0)图象的对称轴为直线x= ,且f(2)=0.
①求函数f(x)的解析式;
②若方程f(x)=m(x+1)的一个根在区间(0,1)内,另一个根在区间(1,2)内,求实数m的取值范围.
变式训练1(1)已知关于x的方程a·4x+b·2x+c=0(a≠0),常数a,b同号,b,c异号,则下列结论中正确的是( )
A.此方程无实根
B.此方程有两个互异的负实根
C.此方程有两个异号实根
D.此方程仅有一个实根
D
解析由常数a,b同号,b,c异号,可得a,c异号,令2x=t,则方程变为at2+bt+c=0, t>0,由于此方程的判别式Δ=b2-4ac>0,故此方程有两个不相等的实数根,且两根之积为 <0,故关于t的方程只有一个实数根,故关于x的方程只有一个实数根.
★(2)函数f(x)=ax2-2x+1,若y=f(x)在区间 内有零点,则实数a的取值范围为 .
(-∞,0]
专题二 二分法求方程的近似解(或函数的零点)
二分法求方程的近似解的步骤:
(1)构造函数,转化为求函数的零点.
(2)明确精确度和函数的零点所在的区间(最好区间左右端点相差1).
(3)利用二分法求函数的零点.
(4)归纳结论.
【例2】 (1)用二分法求方程ln x-2+x=0在区间[1,2]上的近似解,先取区间中点c= ,则下一个含根的区间是 .
★(2)求函数f(x)=x3-x-1在(1,1.5)内的零点(精确度为0.1).
解 f(1)=-1<0,f(1.5)=0.875>0,用二分法逐次计算,列表如下:
区间 中点的值 中点函数近似值
(1,1.5) 1.25 -0.30
(1.25,1.5) 1.375 0.22
(1.25,1.375) 1.312 5 -0.05
(1.312 5,1.375) 1.343 75 0.08
因为|1.375-1.312 5|=0.062 5<0.1,
所以函数的一个近似零点为x=1.312 5.
变式训练2用二分法求方程x2-5=0的一个近似正解(精确度为0.1).
解 令f(x)=x2-5,
因为f(2.2)=-0.16<0,f(2.4)=0.76>0,
所以f(2.2)·f(2.4)<0,说明这个函数在区间(2.2,2.4)内有零点x0.
取区间(2.2,2.4)的中点x1=2.3,f(2.3)=0.29>0,
因为f(2.2)·f(2.3)<0,所以x0∈(2.2,2.3).
再取区间(2.2,2.3)的中点x2=2.25,f(2.25)=0.062 5>0,
因为f(2.2)·f(2.25)<0,所以x0∈(2.2,2.25).
由于|2.25-2.2|=0.05<0.1,
所以原方程的近似正解可取为2.24.
专题三 已知函数模型解决实际问题
解决已给出函数模型的实际应用题,关键要分清函数类型,并要注意相应函数定义域以及实际生活中的自变量取值的限制条件,然后结合所给模型,列出函数关系式,最后结合其实际意义作出解答.
【例3】 某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如表所示.
销售单价/元 6 7 8 9 10 11 12
日均销售量/桶 480 440 400 360 320 280 240
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润
解 由表中数据可知,销售单价每增加1元,日均销售量就减少40桶,设在进价的基础上增加x元后,日均销售利润为y元,在此情况下的日均销售量为480-40(x-1)=(520-40x)(桶).令520-40x>0,则0变式训练3某热力公司每年燃料费约24万元,为了“环评”达标,需要安装一块面积为x(x≥0)(单位:平方米)可用15年的太阳能板,其工本费为 (单位:万元),并与燃料供热互补工作,从此,公司每年的燃料费为 (k为常数)万元,记y为该公司安装太阳能板的费用与15年的燃料费之和.
(1)求k的值,并建立y关于x的函数关系式;
(2)求y的最小值,并求出此时所安装太阳能板的面积.
专题四 用函数模型解决实际问题
解决实际问题的流程
【例4】 某地政府招商引资,为吸引外商,决定第一年产品免税.某外资厂该年A型产品出厂价为每件60元,年销售量为11.8万件,第二年,当地政府开始对该商品征收税率为p%(0(1)将第二年政府对该商品征收的税收y(单位:万元)表示成p的函数,并指出这个函数的定义域.
(2)要使第二年该厂的税收不少于16万元,则p的取值范围是多少
(3)在第二年该厂的税收不少于16万元的前提下,要让厂家获得最大销售金额,则p应为多少
化简得p2-12p+20≤0,
即(p-2)(p-10)≤0,解得2≤p≤10,
故当2≤p≤10时,税收不少于16万元.
变式训练4某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品x(单位:百台),其总成本为G(x)(单位:万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本).销售收入R(x)(单位:万元)满足
假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数y=f(x)的解析式(利润=销售收入-总成本).
(2)要使工厂有盈利,求产量x的取值范围.
(3)工厂生产多少台产品时,可使盈利最多
解 (1)由题意得G(x)=2.8+x.
(2)①当0≤x≤5时,由-0.4x2+3.2x-2.8>0得x2-8x+7<0,
解得1②当x>5时,由8.2-x>0,得x<8.2,
所以5综上,当10.
即当产量x的范围是(1,8.2)(百台)时,能使工厂有盈利.
(3)当0≤x≤5时,函数f(x)=-0.4(x-4)2+3.6,
当x=4时,f(x)有最大值为3.6;
当x>5时,
∵函数f(x)单调递减,
∴f(x)综上,当工厂生产4百台时,可使盈利最多,为3.6万元.
易错易混·衔接高考
1
2
3
4
5
6
1.[2024云南昭阳期末]函数f(x)=3x+2x-7的零点所在的区间是( )
B
1
2
3
4
5
6
B
1
2
3
4
5
6
1
2
3
4
5
6
3.[2024文峰期末](多选题)已知函数 函数
g(x)=[f(x)]2-(m+3)f(x)+3m,则( )
A.函数f(x)的值域为(0,+∞)
B.存在实数m,使得f(m)=f(-m)
C.若g(x)≥-1恒成立,则实数m的取值范围为[1,5]
D.若函数g(x)恰好有5个零点,则函数g(x)的5个零点之积的取值范围是(-∞,0]
BCD
1
2
3
4
5
6
解析 对于A选项,画出函数的大致图象,如图所示,可知函数f(x)的值域为[0,+∞),其中f(1)=|log21|=0,A错误;
1
2
3
4
5
6
对于D选项,∵函数g(x)=[f(x)]2-(m+3)f(x)+3m恰好有5个不同的零点,∴方程[f(x)]2-(m+3)f(x)+3m=0有5个根,可得[f(x)-m][f(x)-3]=0,有f(x)=3或f(x)=m,不妨设x11
2
3
4
5
6
1
2
3
4
5
6
4.[2024云南昭阳期末]已知函数 函数f(x)有________ 个零点;若方程f(x)-k=0有三个不相等的实数根,则k的取值范围是 .
2
(0,4)
解析 画出f(x)的图象,如图所示,由图象可知,f(x)的零点有2个,方程f(x)-k=0有三个不相等的实数根,等价于方程f(x)=k有三个不同的解,即函数f(x)的图象与直线y=k有三个不同的交点,结合函数f(x)的图象,又因为f(2)=4,则k的取值范围是(0,4).
1
2
3
4
5
6
1
2
3
4
5
6
5.[2024福建三明期末]已知函数f(x)=ax2+4x-1,若方程f(x)+|2ax+4|+3=0有2个实数根,则a的取值范围是 .
(-∞,0)∪(0,2)
解析 令g(x)=-|2ax+4|-3,已知函数f(x)=ax2+4x-1,依题意f(x)与g(x)图象有2个不同的交点,当a=0时,g(x)=-7与f(x)=4x-1图象有1个交点,不符合题意,当a<0时,函数f(x)与g(x)的图象如图所示,两个函数图象始终有2个交点,所以a<0符合题意.
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
6.[2024江苏镇江期末]去年某商户销售某品牌服装9 000套,每套服装利润为50元.为提高销售利润,今年计划投入适当的广告费进行产品促销.经市场调研发现,若广告费用为x(单位:万元),则该品牌服装的年销售量将增长
%.请你预算该品牌服装的净利润(净利润为销售利润减去广告费用).
(1)若使得今年净利润比去年至少增长 ,请你预算广告费用的范围
(2)当广告费用为多少万元时,品牌服装的净利润最大
1
2
3
4
5
6
1
2
3
4
5
6
本 课 结 束
第五章
本章总结提升
网络构建·归纳整合
专题突破·素养提升
目录索引
易错易混·衔接高考
网络构建·归纳整合
专题突破·素养提升
专题一 利用函数性质判定方程的解
1.一个函数y=f(x)在区间(a,b)内有零点必须同时满足:①函数f(x)在区间[a,b]上的图象是一条连续不断的曲线;②f(a)·f(b)<0.这两个条件缺一不可,否则结论不一定成立,如函数f(x)= ,易知f(-1)·f(1)=-1×1<0,但显然f(x)= 在
(-1,1)内没有零点.
2.若函数f(x)在区间[a,b]上的图象是连续不断的,且在两端点处的函数值f(a),f(b)异号,则函数y=f(x)的图象至少穿过x轴一次,即方程f(x)=0在区间(a,b)内至少有一个实根c.
3.零点存在定理只能判断出零点的存在性,而不能判断出零点的个数.
【例1】 (1)[2024安徽亳州期末]若函数f(x)=2x- +a在区间(1,2)内存在零点,则a的取值范围为 .
★(2)已知二次函数f(x)=ax2+bx-2(a≠0)图象的对称轴为直线x= ,且f(2)=0.
①求函数f(x)的解析式;
②若方程f(x)=m(x+1)的一个根在区间(0,1)内,另一个根在区间(1,2)内,求实数m的取值范围.
变式训练1(1)已知关于x的方程a·4x+b·2x+c=0(a≠0),常数a,b同号,b,c异号,则下列结论中正确的是( )
A.此方程无实根
B.此方程有两个互异的负实根
C.此方程有两个异号实根
D.此方程仅有一个实根
D
解析由常数a,b同号,b,c异号,可得a,c异号,令2x=t,则方程变为at2+bt+c=0, t>0,由于此方程的判别式Δ=b2-4ac>0,故此方程有两个不相等的实数根,且两根之积为 <0,故关于t的方程只有一个实数根,故关于x的方程只有一个实数根.
★(2)函数f(x)=ax2-2x+1,若y=f(x)在区间 内有零点,则实数a的取值范围为 .
(-∞,0]
专题二 二分法求方程的近似解(或函数的零点)
二分法求方程的近似解的步骤:
(1)构造函数,转化为求函数的零点.
(2)明确精确度和函数的零点所在的区间(最好区间左右端点相差1).
(3)利用二分法求函数的零点.
(4)归纳结论.
【例2】 (1)用二分法求方程ln x-2+x=0在区间[1,2]上的近似解,先取区间中点c= ,则下一个含根的区间是 .
★(2)求函数f(x)=x3-x-1在(1,1.5)内的零点(精确度为0.1).
解 f(1)=-1<0,f(1.5)=0.875>0,用二分法逐次计算,列表如下:
区间 中点的值 中点函数近似值
(1,1.5) 1.25 -0.30
(1.25,1.5) 1.375 0.22
(1.25,1.375) 1.312 5 -0.05
(1.312 5,1.375) 1.343 75 0.08
因为|1.375-1.312 5|=0.062 5<0.1,
所以函数的一个近似零点为x=1.312 5.
变式训练2用二分法求方程x2-5=0的一个近似正解(精确度为0.1).
解 令f(x)=x2-5,
因为f(2.2)=-0.16<0,f(2.4)=0.76>0,
所以f(2.2)·f(2.4)<0,说明这个函数在区间(2.2,2.4)内有零点x0.
取区间(2.2,2.4)的中点x1=2.3,f(2.3)=0.29>0,
因为f(2.2)·f(2.3)<0,所以x0∈(2.2,2.3).
再取区间(2.2,2.3)的中点x2=2.25,f(2.25)=0.062 5>0,
因为f(2.2)·f(2.25)<0,所以x0∈(2.2,2.25).
由于|2.25-2.2|=0.05<0.1,
所以原方程的近似正解可取为2.24.
专题三 已知函数模型解决实际问题
解决已给出函数模型的实际应用题,关键要分清函数类型,并要注意相应函数定义域以及实际生活中的自变量取值的限制条件,然后结合所给模型,列出函数关系式,最后结合其实际意义作出解答.
【例3】 某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如表所示.
销售单价/元 6 7 8 9 10 11 12
日均销售量/桶 480 440 400 360 320 280 240
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润
解 由表中数据可知,销售单价每增加1元,日均销售量就减少40桶,设在进价的基础上增加x元后,日均销售利润为y元,在此情况下的日均销售量为480-40(x-1)=(520-40x)(桶).令520-40x>0,则0
(1)求k的值,并建立y关于x的函数关系式;
(2)求y的最小值,并求出此时所安装太阳能板的面积.
专题四 用函数模型解决实际问题
解决实际问题的流程
【例4】 某地政府招商引资,为吸引外商,决定第一年产品免税.某外资厂该年A型产品出厂价为每件60元,年销售量为11.8万件,第二年,当地政府开始对该商品征收税率为p%(0
(2)要使第二年该厂的税收不少于16万元,则p的取值范围是多少
(3)在第二年该厂的税收不少于16万元的前提下,要让厂家获得最大销售金额,则p应为多少
化简得p2-12p+20≤0,
即(p-2)(p-10)≤0,解得2≤p≤10,
故当2≤p≤10时,税收不少于16万元.
变式训练4某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品x(单位:百台),其总成本为G(x)(单位:万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本).销售收入R(x)(单位:万元)满足
假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数y=f(x)的解析式(利润=销售收入-总成本).
(2)要使工厂有盈利,求产量x的取值范围.
(3)工厂生产多少台产品时,可使盈利最多
解 (1)由题意得G(x)=2.8+x.
(2)①当0≤x≤5时,由-0.4x2+3.2x-2.8>0得x2-8x+7<0,
解得1
所以5
即当产量x的范围是(1,8.2)(百台)时,能使工厂有盈利.
(3)当0≤x≤5时,函数f(x)=-0.4(x-4)2+3.6,
当x=4时,f(x)有最大值为3.6;
当x>5时,
∵函数f(x)单调递减,
∴f(x)
易错易混·衔接高考
1
2
3
4
5
6
1.[2024云南昭阳期末]函数f(x)=3x+2x-7的零点所在的区间是( )
B
1
2
3
4
5
6
B
1
2
3
4
5
6
1
2
3
4
5
6
3.[2024文峰期末](多选题)已知函数 函数
g(x)=[f(x)]2-(m+3)f(x)+3m,则( )
A.函数f(x)的值域为(0,+∞)
B.存在实数m,使得f(m)=f(-m)
C.若g(x)≥-1恒成立,则实数m的取值范围为[1,5]
D.若函数g(x)恰好有5个零点,则函数g(x)的5个零点之积的取值范围是(-∞,0]
BCD
1
2
3
4
5
6
解析 对于A选项,画出函数的大致图象,如图所示,可知函数f(x)的值域为[0,+∞),其中f(1)=|log21|=0,A错误;
1
2
3
4
5
6
对于D选项,∵函数g(x)=[f(x)]2-(m+3)f(x)+3m恰好有5个不同的零点,∴方程[f(x)]2-(m+3)f(x)+3m=0有5个根,可得[f(x)-m][f(x)-3]=0,有f(x)=3或f(x)=m,不妨设x1
2
3
4
5
6
1
2
3
4
5
6
4.[2024云南昭阳期末]已知函数 函数f(x)有________ 个零点;若方程f(x)-k=0有三个不相等的实数根,则k的取值范围是 .
2
(0,4)
解析 画出f(x)的图象,如图所示,由图象可知,f(x)的零点有2个,方程f(x)-k=0有三个不相等的实数根,等价于方程f(x)=k有三个不同的解,即函数f(x)的图象与直线y=k有三个不同的交点,结合函数f(x)的图象,又因为f(2)=4,则k的取值范围是(0,4).
1
2
3
4
5
6
1
2
3
4
5
6
5.[2024福建三明期末]已知函数f(x)=ax2+4x-1,若方程f(x)+|2ax+4|+3=0有2个实数根,则a的取值范围是 .
(-∞,0)∪(0,2)
解析 令g(x)=-|2ax+4|-3,已知函数f(x)=ax2+4x-1,依题意f(x)与g(x)图象有2个不同的交点,当a=0时,g(x)=-7与f(x)=4x-1图象有1个交点,不符合题意,当a<0时,函数f(x)与g(x)的图象如图所示,两个函数图象始终有2个交点,所以a<0符合题意.
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
6.[2024江苏镇江期末]去年某商户销售某品牌服装9 000套,每套服装利润为50元.为提高销售利润,今年计划投入适当的广告费进行产品促销.经市场调研发现,若广告费用为x(单位:万元),则该品牌服装的年销售量将增长
%.请你预算该品牌服装的净利润(净利润为销售利润减去广告费用).
(1)若使得今年净利润比去年至少增长 ,请你预算广告费用的范围
(2)当广告费用为多少万元时,品牌服装的净利润最大
1
2
3
4
5
6
1
2
3
4
5
6
本 课 结 束
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
