第6章 统计 4.1 样本的数字特征 4.2 分层随机抽样的均值与方差 4.3 百分位数--北师大版高中数学必修第一册课件(共54页PPT)
文档属性
| 名称 | 第6章 统计 4.1 样本的数字特征 4.2 分层随机抽样的均值与方差 4.3 百分位数--北师大版高中数学必修第一册课件(共54页PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 15:17:32 | ||
图片预览










文档简介
(共54张PPT)
第六章
4.1 样本的数字特征 4.2 分层随机抽样的均值与方差 4.3 百分位数
基础落实·必备知识一遍过
重难探究·能力素养速提升
目录索引
学以致用·随堂检测促达标
课程标准 1.会求样本的平均数、中位数、众数、百分位数.
2.会求样本的极差、标准差与方差.
3.通过应用相关知识解决实际统计问题,培养数据分析的核心素养.
基础落实·必备知识一遍过
知识点1 样本的数字特征
1.众数、中位数、平均数
众数、中位数、平均数刻画了一组数据的集中趋势.
(1)众数
一组数据中,出现次数最多的数据就是众数.若有两个或几个数据出现的次数相等且都最多,则这些数都是这组数据的众数;若一组数据中,每个数据出现的次数都一样,则这组数据没有众数.
(2)中位数
一般地,将一组数据按从小到大的顺序排列后,“中间”的那个数据为这组数据的中位数.
当数据有奇数个时,位于最中间位置的数就是中位数;当数据有偶数个时,位于最中间的两个数的平均数就是中位数.
(3)平均数
一组数据的平均值,数据x1,x2,…,xn的平均数为 = .
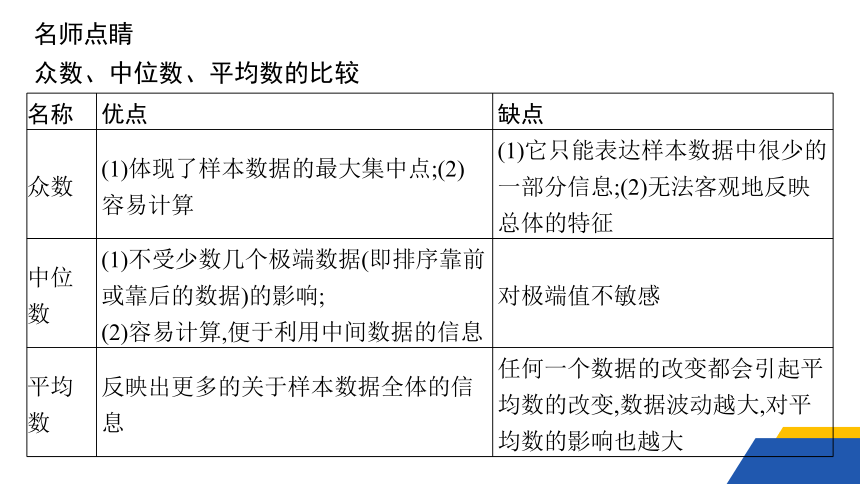
名师点睛
众数、中位数、平均数的比较
名称 优点 缺点
众数 (1)体现了样本数据的最大集中点;(2)容易计算 (1)它只能表达样本数据中很少的一部分信息;(2)无法客观地反映总体的特征
中位数 (1)不受少数几个极端数据(即排序靠前或靠后的数据)的影响; (2)容易计算,便于利用中间数据的信息 对极端值不敏感
平均数 反映出更多的关于样本数据全体的信息 任何一个数据的改变都会引起平均数的改变,数据波动越大,对平均数的影响也越大
2.极差、方差、标准差
极差、方差、标准差刻画了一组数据的 .
(1)极差:数据中 和 的差.
(2)方差:设一组数据为x1,x2,x3,…,xn,其平均数为 ,则方差s2= ,其单位是原始观测数据单位的 ,方差刻画的是数据偏离平均数的离散程度.
离散程度
最大值
最小值
平方
(3)标准差
①定义:它是方差的算术平方根,s=
= ,其单位与原始数据的单位 .
②计算方法:先求出方差s2,再求方差的算术平方根,即得标准差s= .
相同
名师点睛
计算方差、标准差的步骤
计算样本数据x1,x2,…,xn的标准差的算法如下:
第一步:算出样本数据的平均数 ;
第二步:算出每个样本数据与样本平均数的差xi- (i=1,2,…,n);
第三步:算出第二步中xi- (i=1,2,…,n)的平方;
第四步:算出第三步中n个平方数的平均数,即为样本方差;
第五步:算出第四步中平均数的算术平方根,即为样本标准差.
思考辨析
1.一组数据的众数可以有几个 中位数是否也具有相同的结论
提示 一组数据的众数可能有一个,也可能有多个,中位数只有唯一一个.
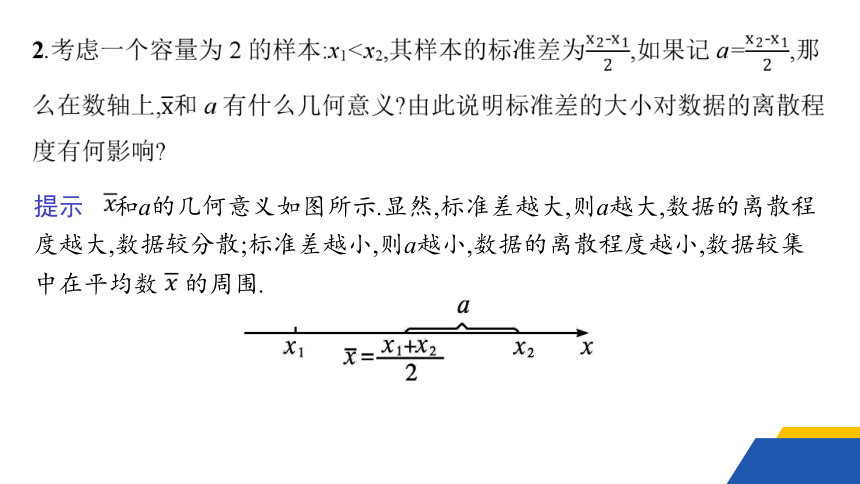
提示 和a的几何意义如图所示.显然,标准差越大,则a越大,数据的离散程度越大,数据较分散;标准差越小,则a越小,数据的离散程度越小,数据较集中在平均数 的周围.
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)频率分布直方图中,平均数左右两边的面积相等.( )
(2)如果一组数中每个数都减去同一个非零常数,则这组数的平均数改变,方差不变.( )
(3)标准差越大,表明各个样本数据在样本平均数周围越集中;标准差越小,表明各个样本数据在样本平均数周围越分散.( )
×
√
×
2.[人教A版教材例题]某学校要定制高一年级的校服,学生根据厂家提供的参考身高选择校服规格.据统计,高一年级女生需要不同规格校服的频数如表所示.
校服规格 155 160 165 170 175 合计
频数 39 64 167 90 26 386
如果用一个量来代表该校高一年级女生所需校服的规格,那么在中位数、平均数和众数中,哪个量比较合适
解 为了更直观地观察数据的特征,我们用条形图来表示表中的数据(图略).可以发现,选择校服规格为“165”的女生的频数最高,所以用众数165作为该校高一年级女生校服的规格比较合适.
知识点2 分层随机抽样的均值与方差
1.分层随机抽样的平均数
(1)定义:一般地,将样本a1,a2,…,am和样本b1,b2,…,bn合并成一个新样本,则这个新样本的平均数为
w1,w2∈[0,1]
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)样本数据分为两层,其中一层的平均数为96,另一层的平均数为98,则样本数据的平均数为 =97.( )
(2)把一个样本分成两层,由每层数据的平均数和方差能求整个样本数据的平均数和方差.( )
×
×
2.[人教A版教材习题]某学校有高中学生500人,其中男生320人,女生180人.有人为了获得该校全体高中学生的身高信息,采用分层随机抽样的方法抽取样本,并观测样本的指标值(单位:cm),计算得男生样本的均值为173.5,方差为17,女生样本的均值为163.83,方差为30.03.
(1)根据以上信息,能够计算出总样本的均值和方差吗 为什么
(2)如果已知男、女生样本量按比例分配,你能计算出总样本的均值和方差各为多少吗
(3)如果已知男、女生的样本量都是25,你能计算出总样本的均值和方差各为多少吗 它们分别作为总体均值和方差的估计合适吗 为什么
解 (1)不能.因为缺少男生样本量和女生样本量.
它们分别作为总体平均数和方差的估计不合适,因为男、女生的身高差异较大,不能等量抽取样本.
知识点3 百分位数
取值连续不断,不能一一列举
1.一般地,当总体是连续变量时,给定一个百分数p∈(0,1),总体的p分位数有这样的特点:总体数据中的任意一个数小于或等于它的可能性是p.
2.计算一组n个数据的p分位数的一般步骤如下:
第一步,按照从小到大排列原始数据;
第二步,计算i=np;
第三步,若i不是整数,大于i的最小整数为j,则p分位数为第j项数据;若i是整数,则p分位数为第i项与第(i+1)项数据的平均数.
思考辨析
1.“某数学测试成绩的70%分位数是85分”这句话是什么意思
2.某班级人数为50,班主任老师说“90%的同学能够考取本科院校”,这里的“90%”是百分位数吗
提示 有70%的同学数学测试成绩小于或等于85分.
提示 不是.是指能够考取本科院校的同学占同学总数的百分比.
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)50%分位数就是中位数.( )
(2)百分位数只能是总体数据中的数.( )
(3)若一组样本数据各不相等,则其75%分位数大于25%分位数.( )
(4)若一组样本数据的10%分位数是23,则在这组数据中有10%的数据大于23.( )
(5)若一组样本数据的24%分位数是24,则在这组数据中至少有76%的数据大于或等于24.( )
√
×
√
×
√
2.[人教B版教材例题]给定甲、乙两组数如下所示,计算其75%分位数.
序号 1 2 3 4 5 6 7 8 9 10
甲组 1 2 2 2 2 3 3 3 5 5
乙组 0 0 0 0 1 1 2 3 4 5
序号 11 12 13 14 15 16 17 18 19 20
甲组 6 6 8 8 9 10 10 12 13 13
乙组 6 6 7 7 10 14 14 14 14 15
重难探究·能力素养速提升
探究点一 平均数、众数、中位数的求法
【例1—1】 某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个,命中个数如下所示:
甲:20,22,27,8,12,13,37,25,24,26
乙:14,9,13,18,19,20,23,21,21,11
则下面结论中正确的是 (填序号).
①甲的极差是29;②乙的众数是21;③甲的平均数为21.4;④甲的中位数是24.
①②③
解析 把两组数据按从小到大的顺序排列,得
甲:8,12,13,20,22,24,25,26,27,37
乙:9,11,13,14,18,19,20,21,21,23
故甲的最大值为37,最小值为8,则极差为29,所以①正确;乙中出现最多的数据是21,所以②正确;甲的平均数为
【例1-2】 在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如表所示.
成绩/m 1.50 1.60 1.65 1.70 1.75 1.80 1.85 1.90
人数 2 3 2 3 4 1 1 1
分别求这些运动员成绩的众数、中位数与平均数.(结果精确到0.01)
解 在17个数据中,1.75出现了4次,出现的次数最多,即这组数据的众数是1.75.题目中表里的17个数据可看成是按从小到大的顺序排列的,其中第9个数据1.70是最中间的一个数据,即这组数据的中位数是1.70.
这组数据的平均数是
所以这17名运动员成绩的众数、中位数、平均数依次为1.75,1.70,1.69.
规律方法 求中位数、众数、平均数的注意事项
求中位数的关键是将数据排序,一般按照从小到大的顺序排列.中位数仅与数据的排列位置有关,某些数据的变动对中位数没有影响.中位数可能在所给数据中,也可能不在所给数据中.当一组数据中的个别数据变动较大时,可用中位数描述数据的集中趋势
确定众数的关键是统计各数据出现的频数,频数最大的数据就是众数.当一组数据中有不少数据多次重复出现时,众数往往更能反映数据的集中趋势
平均数与每一个样本数据都有关,受个别极端数据(比其他数据大很多或小很多的数据)的影响较大,因此若在数据中存在少量极端数据,平均数对总体估计的可靠性较差,这时往往用众数或中位数去估计总体.有时也采用剔除最大值与最小值后所得的平均数去估计总体
变式训练1(1)16位参加百米赛跑半决赛同学的成绩各不相同,按成绩取前8位进入决赛.如果小刘知道了自己的成绩后,要判断能否进入决赛,则其他15位同学成绩的下列数据中,能使他得出结论的是( )
A.平均数 B.极差
C.中位数 D.方差
C
解析 判断能否进入决赛,只要判断是不是前8名,所以只要知道其他15名同学的成绩中是不是有8名高于他,也就是把其他15名同学的成绩排列后看第8名的成绩即可,小刘的成绩高于这个成绩就能进入决赛,低于这个成绩就不能进入决赛,这个第8名的成绩就是这15名同学成绩的中位数.
(2)已知一组数据按从小到大排列为-1,0,4,x,6,15,且这组数据的中位数是5,那么该组数据的众数是 ,平均数是 .
6
5
探究点二 方差和标准差的计算及应用
【例2】 甲、乙两台机床同时加工直径为100 cm的零件,为检验质量,各从中抽取6件测量,数据为:
甲:99,100,98,100,100,103;
乙:99,100,102,99,100,100.
(1)分别计算两组数据的平均数及方差;
(2)根据计算结果判断哪台机床加工零件的质量更稳定.
(2)两台机床所加工零件的直径的平均值相同,又 ,所以乙机床加工零件的质量更稳定.
规律方法 标准差(方差)的两个作用
(1)标准差(方差)越大,数据的离散程度越大;标准差(方差)越小,数据的离散程度越小.
(2)在实际应用中,常常把平均数与标准差结合起来进行决策.在平均值相等的情况下,比较方差或标准差以确定稳定性.
变式训练2已知样本9,10,11,x,y的平均数是10,标准差是 ,则xy= .
96
解析 由题意得9+10+11+x+y=50,
所以x+y=20.
又由(9-10)2+(10-10)2+(11-10)2+(x-10)2+(y-10)2=( )2×5=10,
得x2+y2-20(x+y)=-192,
(x+y)2-2xy-20(x+y)=-192,xy=96.
故填96.
探究点三 求百分位数
【例3—1】 某市3月1日至3月10日的最低气温(单位:℃)折线统计图如图所示,由图可知这10天最低气温的80%分位数是( )
A.-2
B.0
C.1
D.2
D
解析 由折线图可知,这10天的最低气温按照从小到大的排列为
-3,-2,-1,-1,0,0,1,2,2,2.因为共有10个数据,所以10×80%=8,是整数,则这10天最低气温的80%分位数是
★【例3—2】 为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,你能估计一下60株树木的50%分位数和75%分位数吗
解 在[80,90)的频数为60×0.15=9,
在[90,100)的频数为60×0.25=15,
在[100,110)的频数为60×0.3=18,
在[110,120)的频数为60×0.2=12,
在[120,130]的频数为60×0.1=6.
从以上数据可知50%分位数落在区间[100,110)上,
综上可知,50%分位数和75%分位数分别估计为103.3,112.5.
规律方法 计算一组n个数据的p分位数的步骤
第1步,按从小到大排列原始数据.
第2步,计算i=n×p.
第3步,若i不是整数,大于i的最小整数为j,则p分位数为第j项数据;若i是整数,则p分位数为第i项与第(i+1)项数据的平均数.
变式训练3(1)已知100个数据的75%分位数是9.3,则下列说法正确的是( )
A.这100个数据中一定有75个数小于或等于9.3
B.把这100个数据从小到大排列后,9.3是第75个数据
C.把这100个数据从小到大排列后,9.3是第75个数据和第76个数据的平均数
D.把这100个数据从小到大排列后,9.3是第75个数据和第74个数据的平均数
C
解析 因为100×75%=75,为整数,所以第75个数据和第76个数据的平均数为75%分位数,是9.3,故选C.
★(2)从某珍珠公司生产的产品中,任意抽取12颗珍珠,得到它们的质量(单位:g)如下:
7.9,9.0,8.9,8.6,8.4,8.5,8.5,8.5,9.9,7.8,8.3,8.0.
①分别求出这组数据的25%,50%,95%分位数;
②请你找出珍珠质量较小的前15%的珍珠质量;
③若用25%,50%,95%分位数把公司生产的珍珠划分为次品、合格品、优等品和特优品,依照这个样本的数据,给出该公司珍珠等级的划分标准.
解 ①将所有数据从小到大排列,得7.8,7.9,8.0,8.3,8.4,8.5,8.5,8.5,8.6,8.9,9.0,9.9.因为共有12个数据,
所以12×25%=3,12×50%=6,12×95%=11.4,
②因为共有12个数据,所以12×15%=1.8,则15%分位数是7.9 g,即产品质量较小的前15%的产品有2个,它们的质量分别为7.8 g,7.9 g.
③由①可知样本数据的25%分位数是8.15 g,50%分位数为8.5 g,95%分位数是9.9 g,所以质量小于或等于8.15 g的珍珠为次品,质量大于8.15 g且小于或等于8.5 g的珍珠为合格品,质量大于8.5 g且小于或等于9.9 g的珍珠为优等品,质量大于9.9 g的珍珠为特优品.
本节要点归纳
1.知识清单:
(1)众数、中位数、平均数、极差、方差和标准差的意义与计算;
(2)样本数据数字特征的应用;
(3)分层随机抽样的均值与方差;
(4)百分位数.
2.方法归纳:数据分析、统计.
3.常见误区:未对数据排序导致求中位数错误;方差与标准差计算错误;求百分位数时,未排序导致错误.
学以致用·随堂检测促达标
1
2
3
4
5
1.(多选题)下列说法中,正确的是( )
A.数据2,4,6,8的中位数是4,6
B.数据1,2,2,3,4,4的众数是2,4
C.一组数据的平均数、众数、中位数有可能是同一个数据
D.8个数据的平均数为5,另3个数据的平均数为7,则这11个数据的平均数是
BCD
解析 数据2,4,6,8的中位数为 =5,显然A是错误的,B,C,D都是正确的.
1
2
3
4
5
2.已知一组数据:
125,121,123,125,127,129,125,128,130,129,126,124,125,127,126.则这组数据的25%分位数和80%分位数分别是( )
A.125,128 B.124,128 C.125,129 D.125,128.5
D
解析 把这15个数据按从小到大排序,可得121,123,124,125,125,125,125,126,126,127,127,128,129,129,130,由25%×15=3.75,80%C15=12,可知数据的25%分位数为第4项数据为125,80%分位数为第12项与第13项数据的平均数,即 × (128+129)=128.5.
1
2
3
4
5
3.若用分层随机抽样的方法抽得两组数据的平均数分别为8,12,若这两组数据的平均数是10,则这两组数据的权重比值为( )
B
解析 设两组数据的权重分别为w1,w2,由w1×8+w2×12=10.又w1+w2=1,可解得w1=w2= ,所以这两组数据的权重比值为1.
1
2
3
4
5
4.已知一组数据4,2a,3-a,5,6的平均数为4,则a的值是 .
2
解析 由已知,得 × [4+2a+(3-a)+5+6]=4,
解得a=2.
1
2
3
4
5
5.某车间20名工人年龄数据如下表:
年龄/岁 人数
19 1
28 3
29 3
30 5
31 4
32 3
40 1
合计 20
(1)求这20名工人年龄的众数与极差;
(2)求这20名工人年龄的方差s2.
解 (1)这20名工人年龄的众数为30,年龄的极差为40-19=21.
(2)这20名工人年龄的平均数为(19+28×3+29×3+30×5+31×4+32×3+40)÷20=30,
所以这20名工人年龄的方差为
本 课 结 束
第六章
4.1 样本的数字特征 4.2 分层随机抽样的均值与方差 4.3 百分位数
基础落实·必备知识一遍过
重难探究·能力素养速提升
目录索引
学以致用·随堂检测促达标
课程标准 1.会求样本的平均数、中位数、众数、百分位数.
2.会求样本的极差、标准差与方差.
3.通过应用相关知识解决实际统计问题,培养数据分析的核心素养.
基础落实·必备知识一遍过
知识点1 样本的数字特征
1.众数、中位数、平均数
众数、中位数、平均数刻画了一组数据的集中趋势.
(1)众数
一组数据中,出现次数最多的数据就是众数.若有两个或几个数据出现的次数相等且都最多,则这些数都是这组数据的众数;若一组数据中,每个数据出现的次数都一样,则这组数据没有众数.
(2)中位数
一般地,将一组数据按从小到大的顺序排列后,“中间”的那个数据为这组数据的中位数.
当数据有奇数个时,位于最中间位置的数就是中位数;当数据有偶数个时,位于最中间的两个数的平均数就是中位数.
(3)平均数
一组数据的平均值,数据x1,x2,…,xn的平均数为 = .
名师点睛
众数、中位数、平均数的比较
名称 优点 缺点
众数 (1)体现了样本数据的最大集中点;(2)容易计算 (1)它只能表达样本数据中很少的一部分信息;(2)无法客观地反映总体的特征
中位数 (1)不受少数几个极端数据(即排序靠前或靠后的数据)的影响; (2)容易计算,便于利用中间数据的信息 对极端值不敏感
平均数 反映出更多的关于样本数据全体的信息 任何一个数据的改变都会引起平均数的改变,数据波动越大,对平均数的影响也越大
2.极差、方差、标准差
极差、方差、标准差刻画了一组数据的 .
(1)极差:数据中 和 的差.
(2)方差:设一组数据为x1,x2,x3,…,xn,其平均数为 ,则方差s2= ,其单位是原始观测数据单位的 ,方差刻画的是数据偏离平均数的离散程度.
离散程度
最大值
最小值
平方
(3)标准差
①定义:它是方差的算术平方根,s=
= ,其单位与原始数据的单位 .
②计算方法:先求出方差s2,再求方差的算术平方根,即得标准差s= .
相同
名师点睛
计算方差、标准差的步骤
计算样本数据x1,x2,…,xn的标准差的算法如下:
第一步:算出样本数据的平均数 ;
第二步:算出每个样本数据与样本平均数的差xi- (i=1,2,…,n);
第三步:算出第二步中xi- (i=1,2,…,n)的平方;
第四步:算出第三步中n个平方数的平均数,即为样本方差;
第五步:算出第四步中平均数的算术平方根,即为样本标准差.
思考辨析
1.一组数据的众数可以有几个 中位数是否也具有相同的结论
提示 一组数据的众数可能有一个,也可能有多个,中位数只有唯一一个.
提示 和a的几何意义如图所示.显然,标准差越大,则a越大,数据的离散程度越大,数据较分散;标准差越小,则a越小,数据的离散程度越小,数据较集中在平均数 的周围.
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)频率分布直方图中,平均数左右两边的面积相等.( )
(2)如果一组数中每个数都减去同一个非零常数,则这组数的平均数改变,方差不变.( )
(3)标准差越大,表明各个样本数据在样本平均数周围越集中;标准差越小,表明各个样本数据在样本平均数周围越分散.( )
×
√
×
2.[人教A版教材例题]某学校要定制高一年级的校服,学生根据厂家提供的参考身高选择校服规格.据统计,高一年级女生需要不同规格校服的频数如表所示.
校服规格 155 160 165 170 175 合计
频数 39 64 167 90 26 386
如果用一个量来代表该校高一年级女生所需校服的规格,那么在中位数、平均数和众数中,哪个量比较合适
解 为了更直观地观察数据的特征,我们用条形图来表示表中的数据(图略).可以发现,选择校服规格为“165”的女生的频数最高,所以用众数165作为该校高一年级女生校服的规格比较合适.
知识点2 分层随机抽样的均值与方差
1.分层随机抽样的平均数
(1)定义:一般地,将样本a1,a2,…,am和样本b1,b2,…,bn合并成一个新样本,则这个新样本的平均数为
w1,w2∈[0,1]
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)样本数据分为两层,其中一层的平均数为96,另一层的平均数为98,则样本数据的平均数为 =97.( )
(2)把一个样本分成两层,由每层数据的平均数和方差能求整个样本数据的平均数和方差.( )
×
×
2.[人教A版教材习题]某学校有高中学生500人,其中男生320人,女生180人.有人为了获得该校全体高中学生的身高信息,采用分层随机抽样的方法抽取样本,并观测样本的指标值(单位:cm),计算得男生样本的均值为173.5,方差为17,女生样本的均值为163.83,方差为30.03.
(1)根据以上信息,能够计算出总样本的均值和方差吗 为什么
(2)如果已知男、女生样本量按比例分配,你能计算出总样本的均值和方差各为多少吗
(3)如果已知男、女生的样本量都是25,你能计算出总样本的均值和方差各为多少吗 它们分别作为总体均值和方差的估计合适吗 为什么
解 (1)不能.因为缺少男生样本量和女生样本量.
它们分别作为总体平均数和方差的估计不合适,因为男、女生的身高差异较大,不能等量抽取样本.
知识点3 百分位数
取值连续不断,不能一一列举
1.一般地,当总体是连续变量时,给定一个百分数p∈(0,1),总体的p分位数有这样的特点:总体数据中的任意一个数小于或等于它的可能性是p.
2.计算一组n个数据的p分位数的一般步骤如下:
第一步,按照从小到大排列原始数据;
第二步,计算i=np;
第三步,若i不是整数,大于i的最小整数为j,则p分位数为第j项数据;若i是整数,则p分位数为第i项与第(i+1)项数据的平均数.
思考辨析
1.“某数学测试成绩的70%分位数是85分”这句话是什么意思
2.某班级人数为50,班主任老师说“90%的同学能够考取本科院校”,这里的“90%”是百分位数吗
提示 有70%的同学数学测试成绩小于或等于85分.
提示 不是.是指能够考取本科院校的同学占同学总数的百分比.
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)50%分位数就是中位数.( )
(2)百分位数只能是总体数据中的数.( )
(3)若一组样本数据各不相等,则其75%分位数大于25%分位数.( )
(4)若一组样本数据的10%分位数是23,则在这组数据中有10%的数据大于23.( )
(5)若一组样本数据的24%分位数是24,则在这组数据中至少有76%的数据大于或等于24.( )
√
×
√
×
√
2.[人教B版教材例题]给定甲、乙两组数如下所示,计算其75%分位数.
序号 1 2 3 4 5 6 7 8 9 10
甲组 1 2 2 2 2 3 3 3 5 5
乙组 0 0 0 0 1 1 2 3 4 5
序号 11 12 13 14 15 16 17 18 19 20
甲组 6 6 8 8 9 10 10 12 13 13
乙组 6 6 7 7 10 14 14 14 14 15
重难探究·能力素养速提升
探究点一 平均数、众数、中位数的求法
【例1—1】 某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个,命中个数如下所示:
甲:20,22,27,8,12,13,37,25,24,26
乙:14,9,13,18,19,20,23,21,21,11
则下面结论中正确的是 (填序号).
①甲的极差是29;②乙的众数是21;③甲的平均数为21.4;④甲的中位数是24.
①②③
解析 把两组数据按从小到大的顺序排列,得
甲:8,12,13,20,22,24,25,26,27,37
乙:9,11,13,14,18,19,20,21,21,23
故甲的最大值为37,最小值为8,则极差为29,所以①正确;乙中出现最多的数据是21,所以②正确;甲的平均数为
【例1-2】 在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如表所示.
成绩/m 1.50 1.60 1.65 1.70 1.75 1.80 1.85 1.90
人数 2 3 2 3 4 1 1 1
分别求这些运动员成绩的众数、中位数与平均数.(结果精确到0.01)
解 在17个数据中,1.75出现了4次,出现的次数最多,即这组数据的众数是1.75.题目中表里的17个数据可看成是按从小到大的顺序排列的,其中第9个数据1.70是最中间的一个数据,即这组数据的中位数是1.70.
这组数据的平均数是
所以这17名运动员成绩的众数、中位数、平均数依次为1.75,1.70,1.69.
规律方法 求中位数、众数、平均数的注意事项
求中位数的关键是将数据排序,一般按照从小到大的顺序排列.中位数仅与数据的排列位置有关,某些数据的变动对中位数没有影响.中位数可能在所给数据中,也可能不在所给数据中.当一组数据中的个别数据变动较大时,可用中位数描述数据的集中趋势
确定众数的关键是统计各数据出现的频数,频数最大的数据就是众数.当一组数据中有不少数据多次重复出现时,众数往往更能反映数据的集中趋势
平均数与每一个样本数据都有关,受个别极端数据(比其他数据大很多或小很多的数据)的影响较大,因此若在数据中存在少量极端数据,平均数对总体估计的可靠性较差,这时往往用众数或中位数去估计总体.有时也采用剔除最大值与最小值后所得的平均数去估计总体
变式训练1(1)16位参加百米赛跑半决赛同学的成绩各不相同,按成绩取前8位进入决赛.如果小刘知道了自己的成绩后,要判断能否进入决赛,则其他15位同学成绩的下列数据中,能使他得出结论的是( )
A.平均数 B.极差
C.中位数 D.方差
C
解析 判断能否进入决赛,只要判断是不是前8名,所以只要知道其他15名同学的成绩中是不是有8名高于他,也就是把其他15名同学的成绩排列后看第8名的成绩即可,小刘的成绩高于这个成绩就能进入决赛,低于这个成绩就不能进入决赛,这个第8名的成绩就是这15名同学成绩的中位数.
(2)已知一组数据按从小到大排列为-1,0,4,x,6,15,且这组数据的中位数是5,那么该组数据的众数是 ,平均数是 .
6
5
探究点二 方差和标准差的计算及应用
【例2】 甲、乙两台机床同时加工直径为100 cm的零件,为检验质量,各从中抽取6件测量,数据为:
甲:99,100,98,100,100,103;
乙:99,100,102,99,100,100.
(1)分别计算两组数据的平均数及方差;
(2)根据计算结果判断哪台机床加工零件的质量更稳定.
(2)两台机床所加工零件的直径的平均值相同,又 ,所以乙机床加工零件的质量更稳定.
规律方法 标准差(方差)的两个作用
(1)标准差(方差)越大,数据的离散程度越大;标准差(方差)越小,数据的离散程度越小.
(2)在实际应用中,常常把平均数与标准差结合起来进行决策.在平均值相等的情况下,比较方差或标准差以确定稳定性.
变式训练2已知样本9,10,11,x,y的平均数是10,标准差是 ,则xy= .
96
解析 由题意得9+10+11+x+y=50,
所以x+y=20.
又由(9-10)2+(10-10)2+(11-10)2+(x-10)2+(y-10)2=( )2×5=10,
得x2+y2-20(x+y)=-192,
(x+y)2-2xy-20(x+y)=-192,xy=96.
故填96.
探究点三 求百分位数
【例3—1】 某市3月1日至3月10日的最低气温(单位:℃)折线统计图如图所示,由图可知这10天最低气温的80%分位数是( )
A.-2
B.0
C.1
D.2
D
解析 由折线图可知,这10天的最低气温按照从小到大的排列为
-3,-2,-1,-1,0,0,1,2,2,2.因为共有10个数据,所以10×80%=8,是整数,则这10天最低气温的80%分位数是
★【例3—2】 为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,你能估计一下60株树木的50%分位数和75%分位数吗
解 在[80,90)的频数为60×0.15=9,
在[90,100)的频数为60×0.25=15,
在[100,110)的频数为60×0.3=18,
在[110,120)的频数为60×0.2=12,
在[120,130]的频数为60×0.1=6.
从以上数据可知50%分位数落在区间[100,110)上,
综上可知,50%分位数和75%分位数分别估计为103.3,112.5.
规律方法 计算一组n个数据的p分位数的步骤
第1步,按从小到大排列原始数据.
第2步,计算i=n×p.
第3步,若i不是整数,大于i的最小整数为j,则p分位数为第j项数据;若i是整数,则p分位数为第i项与第(i+1)项数据的平均数.
变式训练3(1)已知100个数据的75%分位数是9.3,则下列说法正确的是( )
A.这100个数据中一定有75个数小于或等于9.3
B.把这100个数据从小到大排列后,9.3是第75个数据
C.把这100个数据从小到大排列后,9.3是第75个数据和第76个数据的平均数
D.把这100个数据从小到大排列后,9.3是第75个数据和第74个数据的平均数
C
解析 因为100×75%=75,为整数,所以第75个数据和第76个数据的平均数为75%分位数,是9.3,故选C.
★(2)从某珍珠公司生产的产品中,任意抽取12颗珍珠,得到它们的质量(单位:g)如下:
7.9,9.0,8.9,8.6,8.4,8.5,8.5,8.5,9.9,7.8,8.3,8.0.
①分别求出这组数据的25%,50%,95%分位数;
②请你找出珍珠质量较小的前15%的珍珠质量;
③若用25%,50%,95%分位数把公司生产的珍珠划分为次品、合格品、优等品和特优品,依照这个样本的数据,给出该公司珍珠等级的划分标准.
解 ①将所有数据从小到大排列,得7.8,7.9,8.0,8.3,8.4,8.5,8.5,8.5,8.6,8.9,9.0,9.9.因为共有12个数据,
所以12×25%=3,12×50%=6,12×95%=11.4,
②因为共有12个数据,所以12×15%=1.8,则15%分位数是7.9 g,即产品质量较小的前15%的产品有2个,它们的质量分别为7.8 g,7.9 g.
③由①可知样本数据的25%分位数是8.15 g,50%分位数为8.5 g,95%分位数是9.9 g,所以质量小于或等于8.15 g的珍珠为次品,质量大于8.15 g且小于或等于8.5 g的珍珠为合格品,质量大于8.5 g且小于或等于9.9 g的珍珠为优等品,质量大于9.9 g的珍珠为特优品.
本节要点归纳
1.知识清单:
(1)众数、中位数、平均数、极差、方差和标准差的意义与计算;
(2)样本数据数字特征的应用;
(3)分层随机抽样的均值与方差;
(4)百分位数.
2.方法归纳:数据分析、统计.
3.常见误区:未对数据排序导致求中位数错误;方差与标准差计算错误;求百分位数时,未排序导致错误.
学以致用·随堂检测促达标
1
2
3
4
5
1.(多选题)下列说法中,正确的是( )
A.数据2,4,6,8的中位数是4,6
B.数据1,2,2,3,4,4的众数是2,4
C.一组数据的平均数、众数、中位数有可能是同一个数据
D.8个数据的平均数为5,另3个数据的平均数为7,则这11个数据的平均数是
BCD
解析 数据2,4,6,8的中位数为 =5,显然A是错误的,B,C,D都是正确的.
1
2
3
4
5
2.已知一组数据:
125,121,123,125,127,129,125,128,130,129,126,124,125,127,126.则这组数据的25%分位数和80%分位数分别是( )
A.125,128 B.124,128 C.125,129 D.125,128.5
D
解析 把这15个数据按从小到大排序,可得121,123,124,125,125,125,125,126,126,127,127,128,129,129,130,由25%×15=3.75,80%C15=12,可知数据的25%分位数为第4项数据为125,80%分位数为第12项与第13项数据的平均数,即 × (128+129)=128.5.
1
2
3
4
5
3.若用分层随机抽样的方法抽得两组数据的平均数分别为8,12,若这两组数据的平均数是10,则这两组数据的权重比值为( )
B
解析 设两组数据的权重分别为w1,w2,由w1×8+w2×12=10.又w1+w2=1,可解得w1=w2= ,所以这两组数据的权重比值为1.
1
2
3
4
5
4.已知一组数据4,2a,3-a,5,6的平均数为4,则a的值是 .
2
解析 由已知,得 × [4+2a+(3-a)+5+6]=4,
解得a=2.
1
2
3
4
5
5.某车间20名工人年龄数据如下表:
年龄/岁 人数
19 1
28 3
29 3
30 5
31 4
32 3
40 1
合计 20
(1)求这20名工人年龄的众数与极差;
(2)求这20名工人年龄的方差s2.
解 (1)这20名工人年龄的众数为30,年龄的极差为40-19=21.
(2)这20名工人年龄的平均数为(19+28×3+29×3+30×5+31×4+32×3+40)÷20=30,
所以这20名工人年龄的方差为
本 课 结 束
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
