第6章 统计 总结提升--北师大版高中数学必修第一册课件(共53页PPT)
文档属性
| 名称 | 第6章 统计 总结提升--北师大版高中数学必修第一册课件(共53页PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 15:18:05 | ||
图片预览









文档简介
(共53张PPT)
第六章
本章总结提升
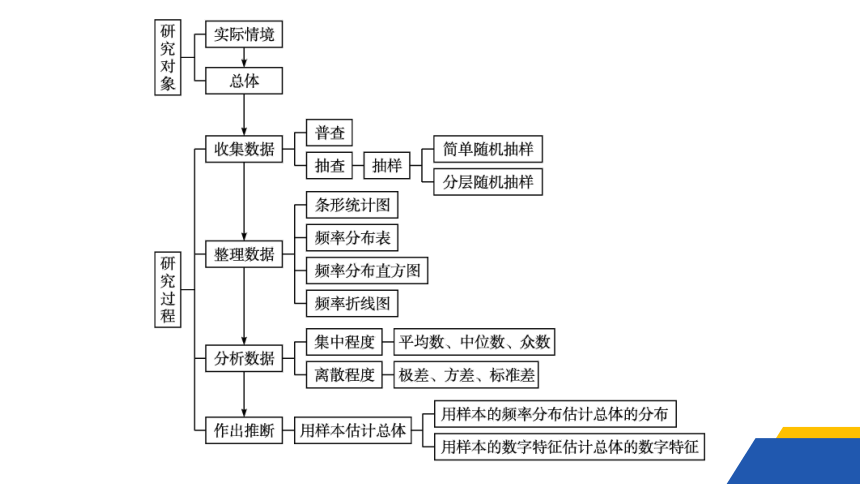
网络构建·归纳整合
专题突破·素养提升
目录索引
易错易混·衔接高考
网络构建·归纳整合
专题突破·素养提升
专题一 抽样的基本方法
1.抽样方法有:简单随机抽样、分层随机抽样.一般地,当总体是由差异明显的几个层组成时选用分层随机抽样,否则考虑用简单随机抽样.选用简单随机抽样时,当总体容量较小时,采用抽签法;当总体容量较大、样本容量较小时,采用随机数法.
2.抽样方法的选择与分层随机抽样中的计算是常考查的知识点,提升数学抽象和数学运算的核心素养.
【例1—1】 某中学组织“党史知识竞赛”活动,已知该校共有高中学生
2 700人,用分层随机抽样的方法从该校高中学生中抽取一个容量为45的样本参加活动,其中高一年级抽取了16人,则该校高一年级学生人数为( )
A.1 680 B.1 020
C.960 D.720
C
解析 设高一学生有x人,则 ,解得x=960,
所以该校高一年级学生人数为960.
【例1—2】 假设要考察某公司生产的袋装牛奶的蛋白质含量,现从800袋牛奶中抽取60袋进行检验,利用随机数表抽取样本时,先将800袋牛奶按000,001,…,799进行编号,如果从随机数表第7行第8列的数开始向右读,则得到的第4个样本个体的编号是 .(下面摘取了随机数表第7行至第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
068
解析 由随机数表可以看出前4个样本的个体的编号是331,572,455,068.于是第4个样本个体的编号是068.
规律方法 应用各种抽样方法抽样时要注意以下问题:
(1)利用抽签法时要注意把号签放在不透明的容器中且搅拌均匀;
(2)利用随机数法时注意编号位数要一致;
(3)在分层随机抽样中,若在某一层抽到的个体数不是整数,应在该层剔除部分个体,使抽取个体数为整数.
变式训练1某校为了了解学生学习的情况,采用分层随机抽样的方法从高一1 000人、高二1 200人、高三n人中抽取81人进行问卷调查,已知高二被抽取的人数为30,那么n=( )
A.860 B.720
C.1 020 D.1 040
D
专题二 用样本的频率分布估计总体分布
1.频率分布直方图的构成及特征
2.掌握频率分布直方图的画法及其应用,重点提升数据分析与逻辑推理的核心素养.
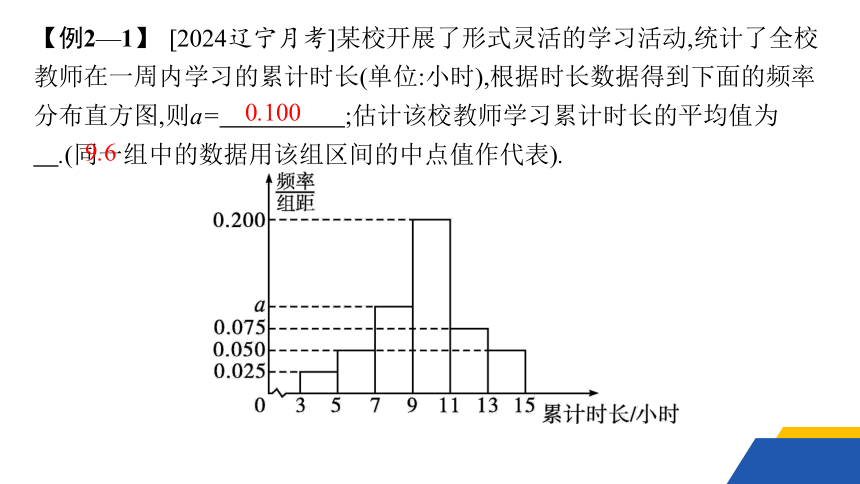
【例2—1】 [2024辽宁月考]某校开展了形式灵活的学习活动,统计了全校教师在一周内学习的累计时长(单位:小时),根据时长数据得到下面的频率分布直方图,则a= ;估计该校教师学习累计时长的平均值为 .(同一组中的数据用该组区间的中点值作代表).
0.100
9.6
解析 由题图可知,2a=1-2×(0.025+0.050×2+0.075+0.200)=0.200,
所以a=0.100,
该校教师学习累计时长的平均值的估计值为
=4×0.025×2+6×0.050×2+8×0.100×2+10×0.200×2+12×0.075×2
+14×0.050×2=9.6.
【例2—2】 从某中学参加2024年全国高中数学联赛预赛的500名同学中,随机抽取若干名同学,将他们的成绩制成频率分布表,下面给出了此表中部分数据.
分组 频数 频率
[70,80) 0.08
[80,90) 0.10
[90,100) ③
[100,110) 16 ①
[110,120) 0.08
[120,130) ② 0.04
[130,140] 0.02
合计 50
(1)根据表中已知数据,分别计算①,②,③处的数值;
(2)补全在区间[70,140]上的频率分布直方图;
(3)若成绩不低于110分的同学能参加决赛,那么可以估计该校大约有多少学生能参加决赛
解 (1)由表中数据知,随机抽取了50人,所以①为 =0.32,②为50×0.04=2,③为1-0.08-0.1-0.32-0.08-0.04-0.02=0.36.
(2)经计算,频率分布表为
分组 频数 频率
[70,80) 4 0.08 0.008
[80,90) 5 0.10 0.010
[90,100) 18 0.36 0.036
[100,110) 16 0.32 0.032
[110,120) 4 0.08 0.008
[120,130) 2 0.04 0.004
[130,140] 1 0.02 0.002
合计 50 1 0.100
根据频率分布表可补全频率分布直方图:
(3)在随机抽取的50名同学中有4+2+1=7(名)同学成绩不低于110分,可以去参加决赛,
故估计参加预赛的同学中能参加决赛的人数大概为
规律方法 与频率分布直方图有关问题的常见类型及解题策略
(1)已知频率分布直方图中的部分数据,求其他数据,可根据频率分布直方图中的数据求出样本与整体的关系,利用频率和等于1可求出其他数据.
(2)已知频率分布直方图,求某种范围内的数据,可利用图形及某范围结合求解.
★变式训练2(1)[2024云南昆明模拟]某大学有男生2 000名.为了解该校男生的身体体重情况,随机抽查了该校100名男生的体重,并将这100名男生的体重(单位:kg)分成以下六组:[54,58),[58,62),[62,66),[66,70),[70,74),[74,78],绘制成如图的频率分布直方图,则该校体重在区间[70,78]上的男生大约有 人.
240
解析 由频率分布直方图可知,该校体重在区间[70,78]上的男生的人数为
2 000×(0.02+0.01)×4=240.
(2)对某校高三年级学生参加社区服务的次数进行统计,随机抽取M名学生,得到这M名学生分别参加社区服务的次数,根据此数据作出了频率分布表和频率分布直方图,如图所示:
分组 频数 频率
[10,15) 10 0.25
[15,20) 24 n
[20,25) m p
[25,30] 2 0.05
合计 M 1.00
①求表中M,p及图中a的值;
②若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数.
②因为该校高三学生有240人,分组[10,15)的频率是0.25,所以估计该校高三学生参加社区服务的次数在区间[10,15)内的人数为240×0.25=60.
专题三 用样本估计总体的数字特征
1.为了从整体上更好地把握总体规律,我们还可以通过样本数据的众数、中位数、平均数估计总体的集中趋势,通过样本数据的方差或标准差估计总体的离散程度.
2.掌握各个数字特征的意义及应用,重点提升数据分析与数学运算的核心素养.
【例3】 某工厂甲、乙两名工人参加操作技能培训.现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,数据如下(单位:分):
甲 95 82 88 81 93 79 84 78
乙 83 75 80 80 90 85 92 95
(1)请你分别计算这两组数据的平均数、中位数.
(2)现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人更合适 请说明理由.
①从平均数看,甲、乙均为85分,平均水平相同;
②从中位数看,乙的中位数大于甲,乙的成绩好于甲;
③从方差来看,因为 ,所以甲的成绩较稳定;
④从数据特点看,获得85分以上(含85分)的次数,甲有3次,而乙有4次,故乙的成绩好些;
⑤从数据的变化趋势看,乙后几次的成绩均高于甲,且呈上升趋势,因此乙更具潜力.
综上分析可知,甲的成绩虽然比乙稳定,但从中位数、获得好成绩的次数及发展势头等方面分析,乙具有明显优势,所以应派乙参赛更有望取得好成绩.
规律方法 用样本的数字特征估计总体的数字特征应注意的问题
(1)中位数用来描述数据的中心位置,众数体现了数据的最大集中点,平均数反映样本数据的总体水平.
(2)标准差(方差)反映了数据的离散与集中、波动与稳定的程度.标准差(方差)较大,数据的离散程度较大;标准差(方差)较小,数据的离散程度较小.
变式训练3某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔一小时抽一包产品,称其质量(单位:克)是否合格,分别记录抽查数据,获得质量数据如下.
甲:107,111,111,113,114,122
乙:108,109,110,112,115,124
(1)写出甲的众数和乙的中位数;
(2)根据样本数据,计算甲、乙两个车间产品质量的平均数与方差,并说明哪个车间的产品的质量相对稳定.
解 (1)甲的众数是111,乙的中位数是111.
专题四 样本的百分位数
1.一般地,当总体是连续变量时,总体的p(02.掌握百分位数的计算及应用,重点提升数据分析与数学运算的核心素养.
【例4—1】 [2024河北廊坊期末]某学校高三12个班级某次朗诵比赛的得分情况如表,则75%分位数是 .
班级得分 9 9.2 9.4 9.6 9.8 10
频数 1 2 2 4 1 2
9.7
解析 将12个班级的得分按照从小到大排序为9,9.2,9.2,9.4,9.4,9.6,9.6,9.6,9.6,9.8,10,10.
因为12×75%=9,可得75%分位数是
★【例4—2】一家保险公司决定对推销员实行目标管理,即给推销员确定一个具体的销售目标.确定的销售目标是否合适,直接影响到公司的经济效益.如果目标定得过高,多数推销员完不成任务,会使推销员失去信心;如果目标定得太低,将不利于挖掘推销员的工作潜力.下面一组数据是部分推销员的月销售额(单位:千元).
19.58 16.11 16.45 20.45 20.24 21.66
22.45 18.22 12.34 19.35 20.55 17.45
18.78 17.96 19.91 18.12 14.65 14.78
16.78 18.78 18.29 18.51 17.86 19.58
19.21 18.55 16.34 15.54 17.55 14.89
18.94 17.43 17.14 18.02 19.98 17.88
17.32 19.35 15.45 19.58 13.45 21.34
14.00 18.42 23.00 17.52 18.51 17.16
24.56 25.14
请根据这组样本数据提出使65%的职工能够完成销售指标的建议.
解 将这50个样本数据按从小到大排序,可得:12.34
13.45 14.00 14.65 14.78 14.89 15.45 15.54 16.11
16.34 16.45 16.78 17.14 17.16 17.32 17.43 17.45
17.52 17.55 17.86 17.88 17.96 18.02 18.12 18.22
18.29 18.42 18.51 18.51 18.55 18.78 18.78 18.94
19.21 19.35 19.35 19.58 19.58 19.58 19.91 19.98
20.24 20.45 20.55 21.34 21.66 22.45 23.00 24.56
25.14
65%的职工能够完成销售指标,那么35%的职工不能完成销售指标.
由50×(1-65%)=17.5可知这组数据的35%分位数为第18项数为17.52.故为使65%的职工能够完成销售指标,该保险公司可将月销售额定为17.52千元.
规律方法 计算一组n个数据的p分位数的一般步骤:
第1步,按从小到大排列原始数据;
第2步,计算i=np;
第3步,若i不是整数,大于i的最小整数为j,则p分位数为第j项数据;若i是整数,则p分位数为第i项与第(i+1)项数据的平均数.
★变式训练4(1)某校高一年级学生打算利用周六休息时间做义工,为了了解高一年级学生做义工时长的情况,随机抽取了高一年级100名学生进行调查,将收集到的做义工时间(单位:小时)数据(时间均在[0,6]内)分成6组: [0,1),[1,2),[2,3),[3,4),[4,5),[5,6],制成如下频率分布直方图.已知该时间数据的70%分位数为3.5,则m,n的值分别为( )
A.0.3,0.35
B.0.4,0.25
C.0.35,0.3
D.0.35,0.25
C
解析 由频率分布直方图可得,
0.05+0.15+m+n+0.11+0.04=1,即m+n=0.65.①
因为时间数据的70%分位数为3.5,
所以0.05+0.15+m+(3.5-3)n=0.7,即m+0.5n=0.5.②
由①②可得,m=0.35,n=0.3.
(2)[2024上海崇明期末]为了解某校高三年级男生的体重,从该校高三年级男生中抽取17名,测得他们的体重数据如下(按从小到大的顺序排列,单位:kg)
56 56 57 58 59 59 61 63 64 65 66 68 69 70 73 74 83
据此估计该校高三年级男生体重的75%分位数为 kg.
69
解析 17×0.75=12.75,数据从小到大第13个数是69,所以75%分位数为69.
易错易混·衔接高考
1
2
3
4
5
6
1.[2024贵州黔东南开学]有一组样本数据都在区间[1,21]内,将其制成如图所示的频率分布直方图,估计该组样本数据的平均数为(同一组中的数据用该组区间的中点值作代表)( )
A.10 B.10.68
C.10.58 D.12
B
解析 由题意,该组样本数据的平均数约为(3×0.02+7×0.08+11×0.09+15×0.02+19×0.04)×4=2.67×4=10.68.
1
2
3
4
5
6
2.[2024安徽蒙城期末]某城市美食节期间,依据小王与小张该月1日至7日每日送外卖的单数(单位:单)数据,整理并绘制的折线图(如图),小王与小张两组数据的平均数分别为 ,标准差分别为s王,s张,则( )
C
解析 根据题意,由折线图可得,小王的总体外卖单数要好于小张的外卖单数,且小张的每日外卖单数波动较大,小王的每日外卖单数较稳定,则有
1
2
3
4
5
6
1
2
3
4
5
6
3.[2024江苏清河期末](多选题)某校1 500名学生参加数学竞赛,随机抽取了40名学生的竞赛成绩(单位:分),成绩的频率分布直方图如图所示,则( )
A.频率分布直方图中a的值为0.005
B.估计这40名学生的竞赛成绩的60%分位数为75
C.估计这40名学生的竞赛成绩的众数为80
D.估计总体中成绩落在[60,70)内的学生人数为225
AD
1
2
3
4
5
6
解析 由10×(2a+3a+7a+6a+2a)=1,可得a=0.005,故A正确;前三个矩形的面积和为10×(2a+3a+7a)=0.6,所以这40名学生的竞赛成绩的60%分位数为80,故B错误;由成绩的频率分布直方图易知,这40名学生的竞赛成绩的众数为75,故C错误;总体中成绩落在[60,70)内的学生人数为
3a×10×1 500=225,故D正确.
1
2
3
4
5
6
4.[2023新高考Ⅰ,9](多选题)有一组样本数据x1,x2,…,x6,其中x1是最小值,x6是最大值,则( )
A.x2,x3,x4,x5的平均数等于x1,x2,…,x6的平均数
B.x2,x3,x4,x5的中位数等于x1,x2,…,x6的中位数
C.x2,x3,x4,x5的标准差不小于x1,x2,…,x6的标准差
D.x2,x3,x4,x5的极差不大于x1,x2,…,x6的极差
BD
1
2
3
4
5
6
1
2
3
4
5
6
5.[2024江西丰城期末]某年级120名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果分成5组:[13,14),[14,15),[15,16),[16,17),[17,18],得到如图所示的频率直方图,如果从左到右的5个小矩形的面积之比为1∶3∶7∶6∶3,那么成绩的70%分位数约为 秒.
16.5
1
2
3
4
5
6
1
2
3
4
5
6
6.[2023全国乙,理17]某厂为比较甲、乙两种工艺对橡胶产品伸缩率的处理效应,进行10次配对试验,每次配对试验选用材质相同的两个橡胶产品,随机地选其中一个用甲工艺处理,另一个用乙工艺处理,测量处理后的橡胶产品的伸缩率,甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为xi,yi(i=1,2,…,10),试验结果如下:
试验序号i 1 2 3 4 5 6 7 8 9 10
伸缩率xi 545 533 551 522 575 544 541 568 596 548
伸缩率yi 536 527 543 530 560 533 522 550 576 536
记zi=xi-yi(i=1,2,…,10),记z1,z2,…,z10的样本平均数为 ,样本方差为s2.
1
2
3
4
5
6
1
2
3
4
5
6
解 (1)∵zi=xi-yi,∴z1=9,z2=6,z3=8,z4=-8,z5=15,z6=11,z7=19,z8=18, z9=20,z10=12,
本 课 结 束
第六章
本章总结提升
网络构建·归纳整合
专题突破·素养提升
目录索引
易错易混·衔接高考
网络构建·归纳整合
专题突破·素养提升
专题一 抽样的基本方法
1.抽样方法有:简单随机抽样、分层随机抽样.一般地,当总体是由差异明显的几个层组成时选用分层随机抽样,否则考虑用简单随机抽样.选用简单随机抽样时,当总体容量较小时,采用抽签法;当总体容量较大、样本容量较小时,采用随机数法.
2.抽样方法的选择与分层随机抽样中的计算是常考查的知识点,提升数学抽象和数学运算的核心素养.
【例1—1】 某中学组织“党史知识竞赛”活动,已知该校共有高中学生
2 700人,用分层随机抽样的方法从该校高中学生中抽取一个容量为45的样本参加活动,其中高一年级抽取了16人,则该校高一年级学生人数为( )
A.1 680 B.1 020
C.960 D.720
C
解析 设高一学生有x人,则 ,解得x=960,
所以该校高一年级学生人数为960.
【例1—2】 假设要考察某公司生产的袋装牛奶的蛋白质含量,现从800袋牛奶中抽取60袋进行检验,利用随机数表抽取样本时,先将800袋牛奶按000,001,…,799进行编号,如果从随机数表第7行第8列的数开始向右读,则得到的第4个样本个体的编号是 .(下面摘取了随机数表第7行至第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
068
解析 由随机数表可以看出前4个样本的个体的编号是331,572,455,068.于是第4个样本个体的编号是068.
规律方法 应用各种抽样方法抽样时要注意以下问题:
(1)利用抽签法时要注意把号签放在不透明的容器中且搅拌均匀;
(2)利用随机数法时注意编号位数要一致;
(3)在分层随机抽样中,若在某一层抽到的个体数不是整数,应在该层剔除部分个体,使抽取个体数为整数.
变式训练1某校为了了解学生学习的情况,采用分层随机抽样的方法从高一1 000人、高二1 200人、高三n人中抽取81人进行问卷调查,已知高二被抽取的人数为30,那么n=( )
A.860 B.720
C.1 020 D.1 040
D
专题二 用样本的频率分布估计总体分布
1.频率分布直方图的构成及特征
2.掌握频率分布直方图的画法及其应用,重点提升数据分析与逻辑推理的核心素养.
【例2—1】 [2024辽宁月考]某校开展了形式灵活的学习活动,统计了全校教师在一周内学习的累计时长(单位:小时),根据时长数据得到下面的频率分布直方图,则a= ;估计该校教师学习累计时长的平均值为 .(同一组中的数据用该组区间的中点值作代表).
0.100
9.6
解析 由题图可知,2a=1-2×(0.025+0.050×2+0.075+0.200)=0.200,
所以a=0.100,
该校教师学习累计时长的平均值的估计值为
=4×0.025×2+6×0.050×2+8×0.100×2+10×0.200×2+12×0.075×2
+14×0.050×2=9.6.
【例2—2】 从某中学参加2024年全国高中数学联赛预赛的500名同学中,随机抽取若干名同学,将他们的成绩制成频率分布表,下面给出了此表中部分数据.
分组 频数 频率
[70,80) 0.08
[80,90) 0.10
[90,100) ③
[100,110) 16 ①
[110,120) 0.08
[120,130) ② 0.04
[130,140] 0.02
合计 50
(1)根据表中已知数据,分别计算①,②,③处的数值;
(2)补全在区间[70,140]上的频率分布直方图;
(3)若成绩不低于110分的同学能参加决赛,那么可以估计该校大约有多少学生能参加决赛
解 (1)由表中数据知,随机抽取了50人,所以①为 =0.32,②为50×0.04=2,③为1-0.08-0.1-0.32-0.08-0.04-0.02=0.36.
(2)经计算,频率分布表为
分组 频数 频率
[70,80) 4 0.08 0.008
[80,90) 5 0.10 0.010
[90,100) 18 0.36 0.036
[100,110) 16 0.32 0.032
[110,120) 4 0.08 0.008
[120,130) 2 0.04 0.004
[130,140] 1 0.02 0.002
合计 50 1 0.100
根据频率分布表可补全频率分布直方图:
(3)在随机抽取的50名同学中有4+2+1=7(名)同学成绩不低于110分,可以去参加决赛,
故估计参加预赛的同学中能参加决赛的人数大概为
规律方法 与频率分布直方图有关问题的常见类型及解题策略
(1)已知频率分布直方图中的部分数据,求其他数据,可根据频率分布直方图中的数据求出样本与整体的关系,利用频率和等于1可求出其他数据.
(2)已知频率分布直方图,求某种范围内的数据,可利用图形及某范围结合求解.
★变式训练2(1)[2024云南昆明模拟]某大学有男生2 000名.为了解该校男生的身体体重情况,随机抽查了该校100名男生的体重,并将这100名男生的体重(单位:kg)分成以下六组:[54,58),[58,62),[62,66),[66,70),[70,74),[74,78],绘制成如图的频率分布直方图,则该校体重在区间[70,78]上的男生大约有 人.
240
解析 由频率分布直方图可知,该校体重在区间[70,78]上的男生的人数为
2 000×(0.02+0.01)×4=240.
(2)对某校高三年级学生参加社区服务的次数进行统计,随机抽取M名学生,得到这M名学生分别参加社区服务的次数,根据此数据作出了频率分布表和频率分布直方图,如图所示:
分组 频数 频率
[10,15) 10 0.25
[15,20) 24 n
[20,25) m p
[25,30] 2 0.05
合计 M 1.00
①求表中M,p及图中a的值;
②若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数.
②因为该校高三学生有240人,分组[10,15)的频率是0.25,所以估计该校高三学生参加社区服务的次数在区间[10,15)内的人数为240×0.25=60.
专题三 用样本估计总体的数字特征
1.为了从整体上更好地把握总体规律,我们还可以通过样本数据的众数、中位数、平均数估计总体的集中趋势,通过样本数据的方差或标准差估计总体的离散程度.
2.掌握各个数字特征的意义及应用,重点提升数据分析与数学运算的核心素养.
【例3】 某工厂甲、乙两名工人参加操作技能培训.现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,数据如下(单位:分):
甲 95 82 88 81 93 79 84 78
乙 83 75 80 80 90 85 92 95
(1)请你分别计算这两组数据的平均数、中位数.
(2)现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人更合适 请说明理由.
①从平均数看,甲、乙均为85分,平均水平相同;
②从中位数看,乙的中位数大于甲,乙的成绩好于甲;
③从方差来看,因为 ,所以甲的成绩较稳定;
④从数据特点看,获得85分以上(含85分)的次数,甲有3次,而乙有4次,故乙的成绩好些;
⑤从数据的变化趋势看,乙后几次的成绩均高于甲,且呈上升趋势,因此乙更具潜力.
综上分析可知,甲的成绩虽然比乙稳定,但从中位数、获得好成绩的次数及发展势头等方面分析,乙具有明显优势,所以应派乙参赛更有望取得好成绩.
规律方法 用样本的数字特征估计总体的数字特征应注意的问题
(1)中位数用来描述数据的中心位置,众数体现了数据的最大集中点,平均数反映样本数据的总体水平.
(2)标准差(方差)反映了数据的离散与集中、波动与稳定的程度.标准差(方差)较大,数据的离散程度较大;标准差(方差)较小,数据的离散程度较小.
变式训练3某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔一小时抽一包产品,称其质量(单位:克)是否合格,分别记录抽查数据,获得质量数据如下.
甲:107,111,111,113,114,122
乙:108,109,110,112,115,124
(1)写出甲的众数和乙的中位数;
(2)根据样本数据,计算甲、乙两个车间产品质量的平均数与方差,并说明哪个车间的产品的质量相对稳定.
解 (1)甲的众数是111,乙的中位数是111.
专题四 样本的百分位数
1.一般地,当总体是连续变量时,总体的p(0
【例4—1】 [2024河北廊坊期末]某学校高三12个班级某次朗诵比赛的得分情况如表,则75%分位数是 .
班级得分 9 9.2 9.4 9.6 9.8 10
频数 1 2 2 4 1 2
9.7
解析 将12个班级的得分按照从小到大排序为9,9.2,9.2,9.4,9.4,9.6,9.6,9.6,9.6,9.8,10,10.
因为12×75%=9,可得75%分位数是
★【例4—2】一家保险公司决定对推销员实行目标管理,即给推销员确定一个具体的销售目标.确定的销售目标是否合适,直接影响到公司的经济效益.如果目标定得过高,多数推销员完不成任务,会使推销员失去信心;如果目标定得太低,将不利于挖掘推销员的工作潜力.下面一组数据是部分推销员的月销售额(单位:千元).
19.58 16.11 16.45 20.45 20.24 21.66
22.45 18.22 12.34 19.35 20.55 17.45
18.78 17.96 19.91 18.12 14.65 14.78
16.78 18.78 18.29 18.51 17.86 19.58
19.21 18.55 16.34 15.54 17.55 14.89
18.94 17.43 17.14 18.02 19.98 17.88
17.32 19.35 15.45 19.58 13.45 21.34
14.00 18.42 23.00 17.52 18.51 17.16
24.56 25.14
请根据这组样本数据提出使65%的职工能够完成销售指标的建议.
解 将这50个样本数据按从小到大排序,可得:12.34
13.45 14.00 14.65 14.78 14.89 15.45 15.54 16.11
16.34 16.45 16.78 17.14 17.16 17.32 17.43 17.45
17.52 17.55 17.86 17.88 17.96 18.02 18.12 18.22
18.29 18.42 18.51 18.51 18.55 18.78 18.78 18.94
19.21 19.35 19.35 19.58 19.58 19.58 19.91 19.98
20.24 20.45 20.55 21.34 21.66 22.45 23.00 24.56
25.14
65%的职工能够完成销售指标,那么35%的职工不能完成销售指标.
由50×(1-65%)=17.5可知这组数据的35%分位数为第18项数为17.52.故为使65%的职工能够完成销售指标,该保险公司可将月销售额定为17.52千元.
规律方法 计算一组n个数据的p分位数的一般步骤:
第1步,按从小到大排列原始数据;
第2步,计算i=np;
第3步,若i不是整数,大于i的最小整数为j,则p分位数为第j项数据;若i是整数,则p分位数为第i项与第(i+1)项数据的平均数.
★变式训练4(1)某校高一年级学生打算利用周六休息时间做义工,为了了解高一年级学生做义工时长的情况,随机抽取了高一年级100名学生进行调查,将收集到的做义工时间(单位:小时)数据(时间均在[0,6]内)分成6组: [0,1),[1,2),[2,3),[3,4),[4,5),[5,6],制成如下频率分布直方图.已知该时间数据的70%分位数为3.5,则m,n的值分别为( )
A.0.3,0.35
B.0.4,0.25
C.0.35,0.3
D.0.35,0.25
C
解析 由频率分布直方图可得,
0.05+0.15+m+n+0.11+0.04=1,即m+n=0.65.①
因为时间数据的70%分位数为3.5,
所以0.05+0.15+m+(3.5-3)n=0.7,即m+0.5n=0.5.②
由①②可得,m=0.35,n=0.3.
(2)[2024上海崇明期末]为了解某校高三年级男生的体重,从该校高三年级男生中抽取17名,测得他们的体重数据如下(按从小到大的顺序排列,单位:kg)
56 56 57 58 59 59 61 63 64 65 66 68 69 70 73 74 83
据此估计该校高三年级男生体重的75%分位数为 kg.
69
解析 17×0.75=12.75,数据从小到大第13个数是69,所以75%分位数为69.
易错易混·衔接高考
1
2
3
4
5
6
1.[2024贵州黔东南开学]有一组样本数据都在区间[1,21]内,将其制成如图所示的频率分布直方图,估计该组样本数据的平均数为(同一组中的数据用该组区间的中点值作代表)( )
A.10 B.10.68
C.10.58 D.12
B
解析 由题意,该组样本数据的平均数约为(3×0.02+7×0.08+11×0.09+15×0.02+19×0.04)×4=2.67×4=10.68.
1
2
3
4
5
6
2.[2024安徽蒙城期末]某城市美食节期间,依据小王与小张该月1日至7日每日送外卖的单数(单位:单)数据,整理并绘制的折线图(如图),小王与小张两组数据的平均数分别为 ,标准差分别为s王,s张,则( )
C
解析 根据题意,由折线图可得,小王的总体外卖单数要好于小张的外卖单数,且小张的每日外卖单数波动较大,小王的每日外卖单数较稳定,则有
1
2
3
4
5
6
1
2
3
4
5
6
3.[2024江苏清河期末](多选题)某校1 500名学生参加数学竞赛,随机抽取了40名学生的竞赛成绩(单位:分),成绩的频率分布直方图如图所示,则( )
A.频率分布直方图中a的值为0.005
B.估计这40名学生的竞赛成绩的60%分位数为75
C.估计这40名学生的竞赛成绩的众数为80
D.估计总体中成绩落在[60,70)内的学生人数为225
AD
1
2
3
4
5
6
解析 由10×(2a+3a+7a+6a+2a)=1,可得a=0.005,故A正确;前三个矩形的面积和为10×(2a+3a+7a)=0.6,所以这40名学生的竞赛成绩的60%分位数为80,故B错误;由成绩的频率分布直方图易知,这40名学生的竞赛成绩的众数为75,故C错误;总体中成绩落在[60,70)内的学生人数为
3a×10×1 500=225,故D正确.
1
2
3
4
5
6
4.[2023新高考Ⅰ,9](多选题)有一组样本数据x1,x2,…,x6,其中x1是最小值,x6是最大值,则( )
A.x2,x3,x4,x5的平均数等于x1,x2,…,x6的平均数
B.x2,x3,x4,x5的中位数等于x1,x2,…,x6的中位数
C.x2,x3,x4,x5的标准差不小于x1,x2,…,x6的标准差
D.x2,x3,x4,x5的极差不大于x1,x2,…,x6的极差
BD
1
2
3
4
5
6
1
2
3
4
5
6
5.[2024江西丰城期末]某年级120名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果分成5组:[13,14),[14,15),[15,16),[16,17),[17,18],得到如图所示的频率直方图,如果从左到右的5个小矩形的面积之比为1∶3∶7∶6∶3,那么成绩的70%分位数约为 秒.
16.5
1
2
3
4
5
6
1
2
3
4
5
6
6.[2023全国乙,理17]某厂为比较甲、乙两种工艺对橡胶产品伸缩率的处理效应,进行10次配对试验,每次配对试验选用材质相同的两个橡胶产品,随机地选其中一个用甲工艺处理,另一个用乙工艺处理,测量处理后的橡胶产品的伸缩率,甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为xi,yi(i=1,2,…,10),试验结果如下:
试验序号i 1 2 3 4 5 6 7 8 9 10
伸缩率xi 545 533 551 522 575 544 541 568 596 548
伸缩率yi 536 527 543 530 560 533 522 550 576 536
记zi=xi-yi(i=1,2,…,10),记z1,z2,…,z10的样本平均数为 ,样本方差为s2.
1
2
3
4
5
6
1
2
3
4
5
6
解 (1)∵zi=xi-yi,∴z1=9,z2=6,z3=8,z4=-8,z5=15,z6=11,z7=19,z8=18, z9=20,z10=12,
本 课 结 束
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
