第7章 概率 2.1-2.2 第1课时 古典概型的概率计算公式及其应用--北师大版高中数学必修第一册课件(共41页PPT)
文档属性
| 名称 | 第7章 概率 2.1-2.2 第1课时 古典概型的概率计算公式及其应用--北师大版高中数学必修第一册课件(共41页PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 15:20:34 | ||
图片预览










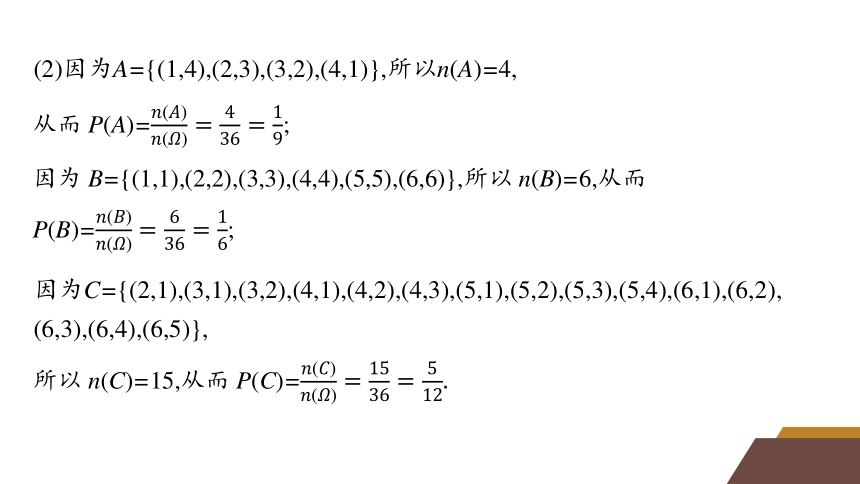

文档简介
(共41张PPT)
第七章
2.1-2.2 第1课时 古典概型的概率计算公式及其应用
基础落实·必备知识一遍过
重难探究·能力素养速提升
目录索引
学以致用·随堂检测促达标
课程标准 1.理解古典概型的定义及两个基本特征.
2.掌握古典概型的概率计算公式,会求古典概型事件的概率.
3.会根据实际问题建立概率模型,并能利用古典概型的概率计算公式进行计算.
基础落实·必备知识一遍过
知识点1 古典概型
当A为必然事件时,P(A)=1;当A为不可能事件时,P(A)=0
1.对于随机事件A,通常用一个数P(A)(0≤P(A)≤1)来表示该事件发生的可能性大小,这个数就称为随机事件A的概率.
2.一般地,若试验E具有如下特征:(1)有限性:试验E的样本空间Ω的样本点总数有限,即样本空间Ω为有限样本空间;(2)等可能性:每次试验中,样本空间Ω的各个样本点出现的可能性相等.
则称这样的试验模型为古典概率概型,简称古典概型.
名师点睛
古典概型的判断标准
一个试验是否为古典概型,在于这个试验是否具有古典概型的两个特点:有限性和等可能性,并不是所有的试验都是古典概型.
下列三类试验不是古典模型:
(1)样本点个数有限,但非等可能;
(2)样本点个数无限,但等可能;
(3)样本点个数无限,也非等可能.
思考辨析
1.若一次试验的结果所包含的样本点的个数是有限个,则该试验是古典概型吗
2.掷一枚不均匀的骰子,求出现点数为偶数点的概率,这个概率模型还是古典概型吗
提示 不一定是,还要看每个样本点发生的可能性是否相同,若相同才是,否则不是.
提示 不是.因为骰子不均匀,所以每个样本点出现的可能性不相等.
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)古典概型的有限性是指样本空间Ω为有限样本空间. ( )
(2)一次试验中样本点总数只有有限个,则这个试验是古典概型.( )
(3)种一粒种子它可能发芽,也可能不发芽是古典概型.( )
√
×
×
2.[人教A版教材例题]抛掷两枚质地均匀的骰子(标记为Ⅰ号和Ⅱ号),观察两枚骰子分别可能出现的基本结果.
(1)写出这个试验的样本空间,并判断这个试验是否为古典概型;
(2)求下列事件的概率:
A=“两个点数之和是5”;
B=“两个点数相等”;
C=“Ⅰ号骰子的点数大于Ⅱ号骰子的点数”.
解 (1)抛掷一枚骰子有6种等可能的结果,Ⅰ号骰子的每一个结果都可与Ⅱ号骰子的任意一个结果配对,组成掷两枚骰子试验的一个结果.用数字m表示Ⅰ号骰子出现的点数是m,数字n表示Ⅱ号骰子出现的点数是n,则数组(m,n)表示这个试验的一个样本点.
因此该试验的样本空间Ω={(m,n)|m,n∈{1,2,3,4,5,6}},其中共有36个样本点.
由于骰子的质地均匀,所以各个样本点出现的可能性相等,因此这个试验是古典概型.
(2)因为A={(1,4),(2,3),(3,2),(4,1)},所以n(A)=4,
因为C={(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),(6,1),(6,2),
(6,3),(6,4),(6,5)},
知识点2 古典概型的概率计算公式
对古典概型来说,如果样本空间Ω包含的样本点总数为n,随机事件A包含的样本点个数为m,那么事件A发生的概率为
名师点睛
使用古典概型概率公式的注意事项
(1)首先判断该模型是不是古典概型;
(2)找出随机事件A所包含的样本点的个数和试验中样本点的总数.
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)古典概型的每个事件发生的可能性相同.( )
(2)古典概型的每个样本点发生的可能性相同.( )
(3)古典概型中样本点的总数为n,随机事件A包含m个样本点,则
×
√
√
2.[2024北京海淀期末]同时抛掷2枚质地均匀的硬币,则“两枚硬币均为正面向上”的概率是( )
A
解析 由题可得,样本空间Ω={正正,正反,反反,反正},共有4个样本点.设事件A表示“两枚硬币均为正面向上”,则A={正正},所以P(A)= .
3.[人教B版教材例题]人的眼皮有单眼皮与双眼皮之分,这是由对应的基因决定的.生物学上已经证明:决定眼皮单双的基因有两种,一种是显性基因(记为B),另一种是隐性基因(记为b);基因总是成对出现(如BB,bB,Bb,bb),而成对的基因中,只要出现了显性基因,那么这个人就一定是双眼皮(也就是说,“单眼皮”的充要条件是“成对的基因是bb”);如果不发生基因突变的话,成对的基因中,一个来自父亲,另一个来自母亲,但父母亲提供基因时都是随机的.有一对夫妻,两人成对的基因都是Bb,不考虑基因突变,求他们的孩子是单眼皮的概率.
解 我们用连着写的两个字母来表示孩子的成对的基因,其中第一个字母表示父亲提供的基因,第二个字母表示母亲提供的基因.
由图所示的树形图可知,样本空间中共含有4个样本点,即Ω={BB,Bb,bB,bb}.
孩子要是单眼皮,成对的基因只能是bb,因此所求概率为 .
重难探究·能力素养速提升
探究点一 古典概型的判断
【例1】 下列概率模型:
①在平面直角坐标系内,从横坐标和纵坐标都是整数的所有点中任取一点;
②某射手射击一次,可能命中0环,1环,2环,…,10环;
③某小组有男生5人,女生3人,从中任选1人做演讲;
④一只使用中的灯泡的寿命长短;
⑤中秋节前夕,某市工商部门调查辖区内某品牌的月饼质量,给该品牌月饼评“优”或“差”.
其中属于古典概型的是 .
③
解析 ①不属于古典概型,原因是所有横坐标和纵坐标都是整数的点有无限多个,不满足有限性;②不属于古典概型,原因是命中0环,1环,…,10环的概率不一定相同,不满足等可能性;③属于古典概型,原因是满足有限性,且任选1人与学生的性别无关,是等可能的;④不属于古典概型,原因是灯泡的寿命是任何一个非负实数,有无限多种可能,不满足有限性;⑤不属于古典概型,原因是该品牌月饼被评为“优”或“差”的概率不一定相同,不满足等可能性.
规律方法 古典概型的判断方法
判断一个试验是不是古典概型,关键看它是否具备古典概型的两个特征:
(1)一次试验中,可能出现的样本点只有有限个,即有限性;(2)每个样本点出现的可能性是均等的,即等可能性.
变式训练1下列试验不是古典概型的是 .(填序号)
①从6名同学中任选4人,参加数学竞赛;
②近三天中有一天降雨;
③从10人中任选两人表演节目.
②
解析 ①③为古典概型,它们符合古典概型的两个特征:有限性和等可能性.②不符合等可能性.
探究点二 古典概型概率的求解
【例2】 袋子中装有除颜色外其他均相同的编号为a,b的2个黑球和编号为c,d,e的3个红球,从中任意摸出2个球,写出试验的样本空间,并求至少摸出1个黑球的概率.
解 试验的样本空间为 Ω={(a,b),(a,c),(a,d),(a,e),(b,c),(b,d),(b,e),(c,d),(c,e),(d,e)},n=10.
记“至少摸出1个黑球”为事件A,则事件A包含7个样本点,∴m=7.
∴P(A)= =0.7.
即至少摸出1个黑球的概率为0.7.
变式探究袋子中有红、白色球各1个,每次任取一个,有放回地摸三次,写出试验的样本空间,并计算下列事件的概率:(1)三次颜色恰有两次同色;(2)三次颜色全相同;(3)三次摸到的红球多于白球.
解 试验的样本空间Ω={(红,红,红),(红,红,白),(红,白,红),(白,红,红),(红,白,白),(白,红,白),(白,白,红),(白,白,白)}.
样本点总数n=8.
(1)记事件A为“三次颜色恰有两次同色”.
∵A中含有的样本点数m1=6,
(2)记事件B为“三次颜色全相同”.
∵B中含有的样本点数m2=2,
(3)记事件C为“三次摸到的红球多于白球”.
∵C中含有的样本点数m3=4,∴P(C)= =0.5.
探究点三 古典概型的综合问题
【例3—1】 [2024陕西西安月考]某创新成果展区分为A区和B区两大板块.A区由最新数据中心产业图谱和国家新型工业化示范基地2个成果组成,B区由算力筑基优秀案例、算力赋能案例、算力网络案例3个成果组成.若从该创新成果展区5个成果中,随机抽取3个成果,则其中恰有2个成果来自B区的概率是( )
D
解析 设A区的2个成果分别记为a,b,B区的3个成果分别记为c,d,e,由题可得,样本空间Ω={abc,abd,abe,bcd,bce,cde,acd,ace,ade,bde},共10个样本空间.设事件A表示“恰有2个成果来自B区”,则A={acd,ade,bcd,bde,ace,bce},共含有6个样本点,则
【例3—2】 编号分别为A1,A2,…,A16的16名篮球运动员在某次训练比赛中的得分记录如下:
运动员编号 A1 A2 A3 A4 A5 A6 A7 A8
得分 15 35 21 28 25 36 18 34
运动员编号 A9 A10 A11 A12 A13 A14 A15 A16
得分 17 26 25 33 22 12 31 38
(1)将得分在对应区间内的人数填入相应的空格:
区间 [10,20) [20,30) [30,40]
人数
(2)从得分在区间[20,30)内的运动员中随机抽取2人,
①用运动员编号列出所有可能的抽取结果;
②求这2人得分之和大于50的概率.
解 (1)由得分记录表,从左到右应填4,6,6.
(2)①得分在区间[20,30)内的运动员编号为A3,A4,A5,A10,A11,A13.从中随机抽取2人,所有的样本点有(A3,A4),(A3,A5),(A3,A10),(A3,A11),(A3,A13),(A4,A5),(A4,A10),(A4,A11),(A4,A13), (A5,A10),(A5,A11),(A5,A13),(A10,A11),(A10,A13),(A11,A13),共15个.
②从得分在区间[20,30)内的运动员中随机抽取2人,将“这2人得分之和大于50”记为事件B,则事件B包含的样本点有(A4,A5),(A4,A10),(A4,A11),(A5,A10),(A10,A11),共5个.所以
规律方法 求解古典概型概率的“四步”法
变式训练2(1)设a,b∈{1,2,3},则函数f(x)=x2+bx+a无零点的概率为 .
解析 由题意知本题是一个古典概型问题,试验的样本点有3×3=9(个).样本点要满足b2-4a<0,即b2<4a.从所给的数据中,当b=1时,a有3种结果;当b=2时,a有2种结果;当b=3时,a有1种结果.
综上所述,共有3+2+1=6(个)样本点,
所以所求概率是
★(2)“渐升数”是指每个数字比其左边的数字大的自然数(如2 578),在两位的“渐升数”中任取一个数比37大的概率是 .
解析 十位是1的“渐升数”有8个,十位是2的“渐升数”有7个,…,十位是8的“渐升数”有1个,所以两位的“渐升数”共有8+7+6+5+4+3+2+1=36(个);
以3为十位数,比37大的“渐升数”有2个,分别以4,5,6,7,8为十位数的“渐升数”均比37大,且共有5+4+3+2+1=15(个),
所以比37大的两位“渐升数”共有2+15=17(个).
故在两位的“渐升数”中任取一个数比37大的概率是
本节要点归纳
1.知识清单:
(1)古典概型的概念;
(2)古典概型的概率公式及应用.
2.方法归纳:列举法、列表法、树状图法.
3.常见误区:因不按照一定的顺序列举,导致漏掉部分样本点;混淆“放回”与“不放回”抽取,导致列举样本点错误.
学以致用·随堂检测促达标
1
2
3
4
1.下列试验中,是古典概型的个数为( )
①种下一粒花生,观察它是否发芽;
②向上抛一枚质地不均匀的硬币,观察正面向上的概率;
③在正方形ABCD内任意一点P,点P恰与点C重合;
④从1,2,3,4四个数中,任取两个数;
⑤在区间[0,5]上任取一点.
A.0 B.1 C.2 D.3
B
解析 只有④是古典概型.
5
1
2
3
4
2.下列说法正确的是( )
A.由生物学知道生男生女的概率约为0.5,一对夫妇先后生两个小孩,则一定为一男一女
B.一次摸奖活动中,中奖概率为0.2,则摸5张票,一定有一张中奖
C.10张票中有1张奖票,10人去摸,谁先摸则谁摸到奖票的可能性大
D.10张票中有1张奖票,10人去摸,无论谁先摸,摸到奖票的概率都是0.1
5
D
1
2
3
4
5
解析 一对夫妇生两个小孩的性别可能是(男,男),(男,女),(女,男),(女,女),所以A不正确;中奖概率为0.2是说中奖的可能性为0.2,当摸5张票时,可能都中奖,也可能中一张、两张、三张、四张,或者都不中奖,所以B不正确;10张票中有1张奖票,10人去摸,每人摸到的可能性是相同的,即无论谁先摸,摸到奖票的概率都是0.1,所以C不正确,D正确.
1
2
3
4
3.抛掷两枚均匀的骰子,则两个都为4点的概率为 ,点数之和为5的概率为 .
解析 样本空间中样本点的总数为36,其中两个都为4点的样本点为(4,4),和为5的是(1,4),(2,3),(3,2),(4,1),故所求的概率分别为
5
1
2
3
4
4.一家保险公司想了解汽车的挡风玻璃破碎的概率,公司收集了20 000部汽车的相关信息,时间是从某年的5月1日到下一年的5月1日,共发现有600部汽车的挡风玻璃破碎,则一部汽车在一年内挡风玻璃破碎的概率近似是 .
5
0.03
1
2
3
4
5.[人教B版教材例题]从含有两件正品a1,a2和一件次品b的3件产品中,按先后顺序任意取出两件产品,每次取出后不放回,求取出的两件产品中恰有一件次品的概率.
5
1
2
3
4
5
解 按照题意,取产品的过程可以用如图所示的树状图直观表示.
因此样本空间可记为Ω={(a1,a2),(a1,b),(a2,a1),(a2,b),(b,a1),(b,a2)},共包含6个样本点.用A表示“取出的两件中,恰好有一件次品”,则A={(a1,b),(a2,b),(b,a1),(b,a2)},A包含的样本点个数为4,所以
本 课 结 束
第七章
2.1-2.2 第1课时 古典概型的概率计算公式及其应用
基础落实·必备知识一遍过
重难探究·能力素养速提升
目录索引
学以致用·随堂检测促达标
课程标准 1.理解古典概型的定义及两个基本特征.
2.掌握古典概型的概率计算公式,会求古典概型事件的概率.
3.会根据实际问题建立概率模型,并能利用古典概型的概率计算公式进行计算.
基础落实·必备知识一遍过
知识点1 古典概型
当A为必然事件时,P(A)=1;当A为不可能事件时,P(A)=0
1.对于随机事件A,通常用一个数P(A)(0≤P(A)≤1)来表示该事件发生的可能性大小,这个数就称为随机事件A的概率.
2.一般地,若试验E具有如下特征:(1)有限性:试验E的样本空间Ω的样本点总数有限,即样本空间Ω为有限样本空间;(2)等可能性:每次试验中,样本空间Ω的各个样本点出现的可能性相等.
则称这样的试验模型为古典概率概型,简称古典概型.
名师点睛
古典概型的判断标准
一个试验是否为古典概型,在于这个试验是否具有古典概型的两个特点:有限性和等可能性,并不是所有的试验都是古典概型.
下列三类试验不是古典模型:
(1)样本点个数有限,但非等可能;
(2)样本点个数无限,但等可能;
(3)样本点个数无限,也非等可能.
思考辨析
1.若一次试验的结果所包含的样本点的个数是有限个,则该试验是古典概型吗
2.掷一枚不均匀的骰子,求出现点数为偶数点的概率,这个概率模型还是古典概型吗
提示 不一定是,还要看每个样本点发生的可能性是否相同,若相同才是,否则不是.
提示 不是.因为骰子不均匀,所以每个样本点出现的可能性不相等.
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)古典概型的有限性是指样本空间Ω为有限样本空间. ( )
(2)一次试验中样本点总数只有有限个,则这个试验是古典概型.( )
(3)种一粒种子它可能发芽,也可能不发芽是古典概型.( )
√
×
×
2.[人教A版教材例题]抛掷两枚质地均匀的骰子(标记为Ⅰ号和Ⅱ号),观察两枚骰子分别可能出现的基本结果.
(1)写出这个试验的样本空间,并判断这个试验是否为古典概型;
(2)求下列事件的概率:
A=“两个点数之和是5”;
B=“两个点数相等”;
C=“Ⅰ号骰子的点数大于Ⅱ号骰子的点数”.
解 (1)抛掷一枚骰子有6种等可能的结果,Ⅰ号骰子的每一个结果都可与Ⅱ号骰子的任意一个结果配对,组成掷两枚骰子试验的一个结果.用数字m表示Ⅰ号骰子出现的点数是m,数字n表示Ⅱ号骰子出现的点数是n,则数组(m,n)表示这个试验的一个样本点.
因此该试验的样本空间Ω={(m,n)|m,n∈{1,2,3,4,5,6}},其中共有36个样本点.
由于骰子的质地均匀,所以各个样本点出现的可能性相等,因此这个试验是古典概型.
(2)因为A={(1,4),(2,3),(3,2),(4,1)},所以n(A)=4,
因为C={(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),(6,1),(6,2),
(6,3),(6,4),(6,5)},
知识点2 古典概型的概率计算公式
对古典概型来说,如果样本空间Ω包含的样本点总数为n,随机事件A包含的样本点个数为m,那么事件A发生的概率为
名师点睛
使用古典概型概率公式的注意事项
(1)首先判断该模型是不是古典概型;
(2)找出随机事件A所包含的样本点的个数和试验中样本点的总数.
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)古典概型的每个事件发生的可能性相同.( )
(2)古典概型的每个样本点发生的可能性相同.( )
(3)古典概型中样本点的总数为n,随机事件A包含m个样本点,则
×
√
√
2.[2024北京海淀期末]同时抛掷2枚质地均匀的硬币,则“两枚硬币均为正面向上”的概率是( )
A
解析 由题可得,样本空间Ω={正正,正反,反反,反正},共有4个样本点.设事件A表示“两枚硬币均为正面向上”,则A={正正},所以P(A)= .
3.[人教B版教材例题]人的眼皮有单眼皮与双眼皮之分,这是由对应的基因决定的.生物学上已经证明:决定眼皮单双的基因有两种,一种是显性基因(记为B),另一种是隐性基因(记为b);基因总是成对出现(如BB,bB,Bb,bb),而成对的基因中,只要出现了显性基因,那么这个人就一定是双眼皮(也就是说,“单眼皮”的充要条件是“成对的基因是bb”);如果不发生基因突变的话,成对的基因中,一个来自父亲,另一个来自母亲,但父母亲提供基因时都是随机的.有一对夫妻,两人成对的基因都是Bb,不考虑基因突变,求他们的孩子是单眼皮的概率.
解 我们用连着写的两个字母来表示孩子的成对的基因,其中第一个字母表示父亲提供的基因,第二个字母表示母亲提供的基因.
由图所示的树形图可知,样本空间中共含有4个样本点,即Ω={BB,Bb,bB,bb}.
孩子要是单眼皮,成对的基因只能是bb,因此所求概率为 .
重难探究·能力素养速提升
探究点一 古典概型的判断
【例1】 下列概率模型:
①在平面直角坐标系内,从横坐标和纵坐标都是整数的所有点中任取一点;
②某射手射击一次,可能命中0环,1环,2环,…,10环;
③某小组有男生5人,女生3人,从中任选1人做演讲;
④一只使用中的灯泡的寿命长短;
⑤中秋节前夕,某市工商部门调查辖区内某品牌的月饼质量,给该品牌月饼评“优”或“差”.
其中属于古典概型的是 .
③
解析 ①不属于古典概型,原因是所有横坐标和纵坐标都是整数的点有无限多个,不满足有限性;②不属于古典概型,原因是命中0环,1环,…,10环的概率不一定相同,不满足等可能性;③属于古典概型,原因是满足有限性,且任选1人与学生的性别无关,是等可能的;④不属于古典概型,原因是灯泡的寿命是任何一个非负实数,有无限多种可能,不满足有限性;⑤不属于古典概型,原因是该品牌月饼被评为“优”或“差”的概率不一定相同,不满足等可能性.
规律方法 古典概型的判断方法
判断一个试验是不是古典概型,关键看它是否具备古典概型的两个特征:
(1)一次试验中,可能出现的样本点只有有限个,即有限性;(2)每个样本点出现的可能性是均等的,即等可能性.
变式训练1下列试验不是古典概型的是 .(填序号)
①从6名同学中任选4人,参加数学竞赛;
②近三天中有一天降雨;
③从10人中任选两人表演节目.
②
解析 ①③为古典概型,它们符合古典概型的两个特征:有限性和等可能性.②不符合等可能性.
探究点二 古典概型概率的求解
【例2】 袋子中装有除颜色外其他均相同的编号为a,b的2个黑球和编号为c,d,e的3个红球,从中任意摸出2个球,写出试验的样本空间,并求至少摸出1个黑球的概率.
解 试验的样本空间为 Ω={(a,b),(a,c),(a,d),(a,e),(b,c),(b,d),(b,e),(c,d),(c,e),(d,e)},n=10.
记“至少摸出1个黑球”为事件A,则事件A包含7个样本点,∴m=7.
∴P(A)= =0.7.
即至少摸出1个黑球的概率为0.7.
变式探究袋子中有红、白色球各1个,每次任取一个,有放回地摸三次,写出试验的样本空间,并计算下列事件的概率:(1)三次颜色恰有两次同色;(2)三次颜色全相同;(3)三次摸到的红球多于白球.
解 试验的样本空间Ω={(红,红,红),(红,红,白),(红,白,红),(白,红,红),(红,白,白),(白,红,白),(白,白,红),(白,白,白)}.
样本点总数n=8.
(1)记事件A为“三次颜色恰有两次同色”.
∵A中含有的样本点数m1=6,
(2)记事件B为“三次颜色全相同”.
∵B中含有的样本点数m2=2,
(3)记事件C为“三次摸到的红球多于白球”.
∵C中含有的样本点数m3=4,∴P(C)= =0.5.
探究点三 古典概型的综合问题
【例3—1】 [2024陕西西安月考]某创新成果展区分为A区和B区两大板块.A区由最新数据中心产业图谱和国家新型工业化示范基地2个成果组成,B区由算力筑基优秀案例、算力赋能案例、算力网络案例3个成果组成.若从该创新成果展区5个成果中,随机抽取3个成果,则其中恰有2个成果来自B区的概率是( )
D
解析 设A区的2个成果分别记为a,b,B区的3个成果分别记为c,d,e,由题可得,样本空间Ω={abc,abd,abe,bcd,bce,cde,acd,ace,ade,bde},共10个样本空间.设事件A表示“恰有2个成果来自B区”,则A={acd,ade,bcd,bde,ace,bce},共含有6个样本点,则
【例3—2】 编号分别为A1,A2,…,A16的16名篮球运动员在某次训练比赛中的得分记录如下:
运动员编号 A1 A2 A3 A4 A5 A6 A7 A8
得分 15 35 21 28 25 36 18 34
运动员编号 A9 A10 A11 A12 A13 A14 A15 A16
得分 17 26 25 33 22 12 31 38
(1)将得分在对应区间内的人数填入相应的空格:
区间 [10,20) [20,30) [30,40]
人数
(2)从得分在区间[20,30)内的运动员中随机抽取2人,
①用运动员编号列出所有可能的抽取结果;
②求这2人得分之和大于50的概率.
解 (1)由得分记录表,从左到右应填4,6,6.
(2)①得分在区间[20,30)内的运动员编号为A3,A4,A5,A10,A11,A13.从中随机抽取2人,所有的样本点有(A3,A4),(A3,A5),(A3,A10),(A3,A11),(A3,A13),(A4,A5),(A4,A10),(A4,A11),(A4,A13), (A5,A10),(A5,A11),(A5,A13),(A10,A11),(A10,A13),(A11,A13),共15个.
②从得分在区间[20,30)内的运动员中随机抽取2人,将“这2人得分之和大于50”记为事件B,则事件B包含的样本点有(A4,A5),(A4,A10),(A4,A11),(A5,A10),(A10,A11),共5个.所以
规律方法 求解古典概型概率的“四步”法
变式训练2(1)设a,b∈{1,2,3},则函数f(x)=x2+bx+a无零点的概率为 .
解析 由题意知本题是一个古典概型问题,试验的样本点有3×3=9(个).样本点要满足b2-4a<0,即b2<4a.从所给的数据中,当b=1时,a有3种结果;当b=2时,a有2种结果;当b=3时,a有1种结果.
综上所述,共有3+2+1=6(个)样本点,
所以所求概率是
★(2)“渐升数”是指每个数字比其左边的数字大的自然数(如2 578),在两位的“渐升数”中任取一个数比37大的概率是 .
解析 十位是1的“渐升数”有8个,十位是2的“渐升数”有7个,…,十位是8的“渐升数”有1个,所以两位的“渐升数”共有8+7+6+5+4+3+2+1=36(个);
以3为十位数,比37大的“渐升数”有2个,分别以4,5,6,7,8为十位数的“渐升数”均比37大,且共有5+4+3+2+1=15(个),
所以比37大的两位“渐升数”共有2+15=17(个).
故在两位的“渐升数”中任取一个数比37大的概率是
本节要点归纳
1.知识清单:
(1)古典概型的概念;
(2)古典概型的概率公式及应用.
2.方法归纳:列举法、列表法、树状图法.
3.常见误区:因不按照一定的顺序列举,导致漏掉部分样本点;混淆“放回”与“不放回”抽取,导致列举样本点错误.
学以致用·随堂检测促达标
1
2
3
4
1.下列试验中,是古典概型的个数为( )
①种下一粒花生,观察它是否发芽;
②向上抛一枚质地不均匀的硬币,观察正面向上的概率;
③在正方形ABCD内任意一点P,点P恰与点C重合;
④从1,2,3,4四个数中,任取两个数;
⑤在区间[0,5]上任取一点.
A.0 B.1 C.2 D.3
B
解析 只有④是古典概型.
5
1
2
3
4
2.下列说法正确的是( )
A.由生物学知道生男生女的概率约为0.5,一对夫妇先后生两个小孩,则一定为一男一女
B.一次摸奖活动中,中奖概率为0.2,则摸5张票,一定有一张中奖
C.10张票中有1张奖票,10人去摸,谁先摸则谁摸到奖票的可能性大
D.10张票中有1张奖票,10人去摸,无论谁先摸,摸到奖票的概率都是0.1
5
D
1
2
3
4
5
解析 一对夫妇生两个小孩的性别可能是(男,男),(男,女),(女,男),(女,女),所以A不正确;中奖概率为0.2是说中奖的可能性为0.2,当摸5张票时,可能都中奖,也可能中一张、两张、三张、四张,或者都不中奖,所以B不正确;10张票中有1张奖票,10人去摸,每人摸到的可能性是相同的,即无论谁先摸,摸到奖票的概率都是0.1,所以C不正确,D正确.
1
2
3
4
3.抛掷两枚均匀的骰子,则两个都为4点的概率为 ,点数之和为5的概率为 .
解析 样本空间中样本点的总数为36,其中两个都为4点的样本点为(4,4),和为5的是(1,4),(2,3),(3,2),(4,1),故所求的概率分别为
5
1
2
3
4
4.一家保险公司想了解汽车的挡风玻璃破碎的概率,公司收集了20 000部汽车的相关信息,时间是从某年的5月1日到下一年的5月1日,共发现有600部汽车的挡风玻璃破碎,则一部汽车在一年内挡风玻璃破碎的概率近似是 .
5
0.03
1
2
3
4
5.[人教B版教材例题]从含有两件正品a1,a2和一件次品b的3件产品中,按先后顺序任意取出两件产品,每次取出后不放回,求取出的两件产品中恰有一件次品的概率.
5
1
2
3
4
5
解 按照题意,取产品的过程可以用如图所示的树状图直观表示.
因此样本空间可记为Ω={(a1,a2),(a1,b),(a2,a1),(a2,b),(b,a1),(b,a2)},共包含6个样本点.用A表示“取出的两件中,恰好有一件次品”,则A={(a1,b),(a2,b),(b,a1),(b,a2)},A包含的样本点个数为4,所以
本 课 结 束
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
