第7章 概率 3 频率与概率--北师大版高中数学必修第一册课件(共36页PPT)
文档属性
| 名称 | 第7章 概率 3 频率与概率--北师大版高中数学必修第一册课件(共36页PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 15:20:50 | ||
图片预览










文档简介
(共36张PPT)
第七章
§3 频率与概率
基础落实·必备知识一遍过
重难探究·能力素养速提升
目录索引
学以致用·随堂检测促达标
课程标准 1.在具体情境中,了解随机事件发生的不确定性和频率的稳定性.
2.正确理解概率的意义,利用概率知识正确理解现实生活中的实际问题.
3.理解概率的意义以及频率与概率的区别.
基础落实·必备知识一遍过
知识点1 概率
该常数是确定的,是一个理论值
在相同条件下,大量重复进行同一试验时,随机事件A发生的频率通常会在某个常数附近摆动,即随机事件A发生的频率具有稳定性.这时,把这个常数叫作随机事件A的概率,记作P(A).
名师点睛
概率的性质
(1)随机事件A的概率P(A)满足0≤P(A)≤1.
(2)当A是必然事件时,P(A)=1;当A是不可能事件时,P(A)=0.
思考辨析
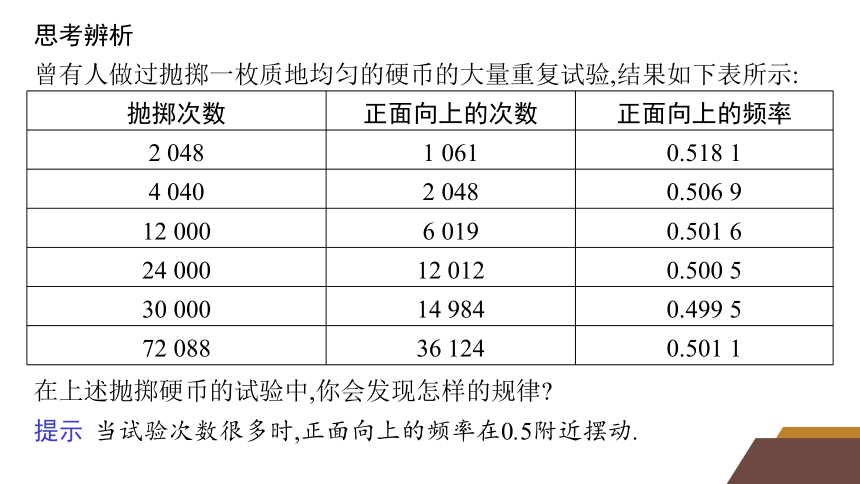
曾有人做过抛掷一枚质地均匀的硬币的大量重复试验,结果如下表所示:
抛掷次数 正面向上的次数 正面向上的频率
2 048 1 061 0.518 1
4 040 2 048 0.506 9
12 000 6 019 0.501 6
24 000 12 012 0.500 5
30 000 14 984 0.499 5
72 088 36 124 0.501 1
在上述抛掷硬币的试验中,你会发现怎样的规律
提示 当试验次数很多时,正面向上的频率在0.5附近摆动.
自主诊断
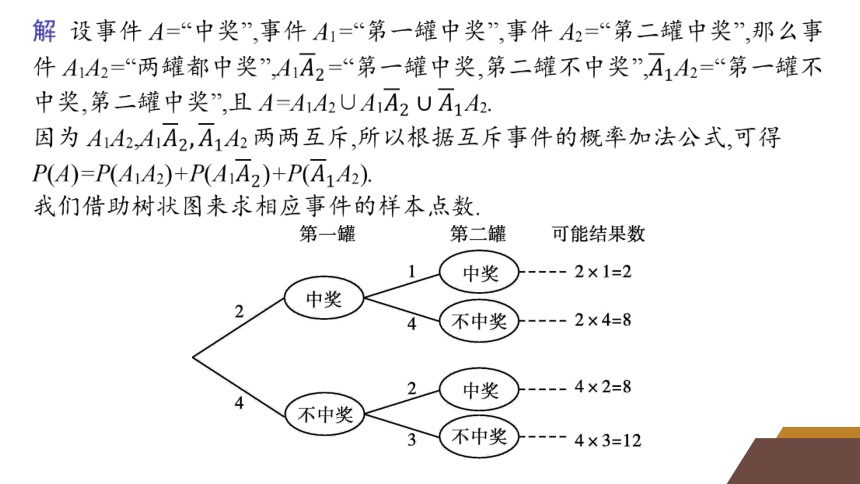
[人教A版教材例题]为了推广一种新饮料,某饮料生产企业开展了有奖促销活动:将6罐这种饮料装一箱,每箱中都放置2罐能够中奖的饮料.若从一箱中随机抽出2罐,能中奖的概率为多少
可以得到,样本空间包含的样本点个数为n(Ω)=6×5=30,且每个样本点都是等可能的.
知识点2 频率与概率之间的关系
1.区别
频率 本身是随机的,在试验之前是无法确定的,做同样次数的重复试验,得到的事件的频率值也可能会不同
概率 本身是一个在[0,1]上的确定值,不随试验结果的改变而改变
2.联系
随机事件的频率是指大量随机试验中,此事件发生的次数与试验次数的比值,它具有一定的稳定性,总是在某一个常数附近摆动,且随着试验次数的不断增加,这种摆动幅度越来越小.我们给这个常数取了一个名字,叫作这个随机事件的概率.概率可看作频率在理论上的期望值,它从数量上反映了随机事件发生的可能性的大小,频率在大量重复试验的前提下可近似地作为这个事件的概率.
名师点睛
频率本身是随机的,在试验前不能确定;概率是一个确定的数,是客观存在的,是事件的固有属性,与每次试验无关.
思考辨析
“某彩票的中奖概率为 ”含义是“买100张彩票能中一次奖”吗
提示 某彩票的中奖概率为 ,意味着中奖的可能性为 ,可能中奖,也可能不中奖,并不一定是买100张彩票能中一次奖.
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)随机事件的频率与概率不可能相等.( )
(2)随机事件A的概率是频率的稳定值,频率是概率的近似值.( )
(3)随机事件发生的概率是随着试验次数的变化而变化的.( )
2.质检部门对世园会所用某种产品进行抽检,得知其合格率为99%,若世园会所需该产品共有20 000件,则其中不合格产品约有 件.
×
√
×
200
解析 不合格产品约有20 000×(1-99%)=200(件).
3.[人教B版教材例题]某女篮运动员统计了她最近几次参加比赛投篮的得分情况,得到的数据如下表所示.
投篮次数 投中两分的次数 投中三分的次数
75 45 12
注:每次投篮,要么得两分,要么得三分,要么没投中.
记该女篮运动员在一次投篮中,投中两分为事件A,投中三分为事件B,没投中为事件C,试估计P(A),P(B),P(C).
重难探究·能力素养速提升
探究点一 概率概念的理解
【例1】问题辨析:
(1)掷一枚均匀的正方体骰子得到6点的概率是 ,是否意味着把它掷6次能得到1次6点
(2)某种病的治愈率是0.3,那么前7个人没有治愈,后3个人一定能治愈吗 如何理解治愈率是0.3
解 (1)把一枚均匀的骰子掷6次相当于做6次试验,因为每次试验的结果都是随机的,所以做6次试验的结果也是随机的.这就是说,每掷一次总是随机地出现一个点数,可以是1点,2点,也可以是其他点数,不一定出现6点.所以掷一枚骰子得到6点的概率是 ,并不意味着把它掷6次能得到1次6点.
(2)如果把治疗一个病人作为一次试验,治愈率是0.3,是指随着试验次数的增加,即治疗病人人数的增加,大约有30%的人能够治愈,对于一次试验来说,其结果是随机的,因此前7个病人没治愈是可能的,对后3个人来说,其结果仍然是随机的,即有可能治愈,也可能没有治愈.
变式探究我们知道,每次抛掷硬币的结果出现正、反的概率都为0.5,则连续抛掷质地均匀的硬币两次,是否一定出现“一次正面向上,一次反面向上”呢
解 不一定.这是因为统计规律不同于确定的数学规律,对于具体的一次试验而言,它带有很大的随机性(即偶然性),通过具体试验可以知道除上述结果外,也可能出现“两次都是正面向上”“两次都是反面向上”.尽管随机事件不像函数关系那样具有确定性,但是如果我们知道某事件发生的概率的大小,也能作出科学的决策.例如:做连续抛掷两枚质地均匀的硬币的试验
1 000次,可以预见:“两个都是正面向上”大约出现250次,“两个都是反面向上”大约出现250次,而“一个正面向上、一个反面向上”大约出现500次.
规律方法 对概率的正确理解
(1)概率是随机事件发生可能性大小的度量,是随机事件的本质属性,大量重复试验中事件A发生的频率是随机事件A发生的概率的近似值.
(2)由概率的定义我们可以知道随机事件A在一次试验中发生与否是随机的,但随机中含有规律性,而概率就是其规律性在数量上的反映.
(3)正确理解概率的意义,要清楚概率与频率的区别与联系.对具体的问题要从全局和整体上去看待,而不是局限于某一次试验或某一个具体的事件.
探究点二 概率与频率的关系及求法
【例2】 某射手在同一条件下进行射击,结果如下表所示:
射击次数n 10 20 50 100 200 500
击中靶心次数m 8 19 44 92 178 455
击中靶心的频率
(1)填写表中击中靶心的频率;
(2)这个射手射击一次,击中靶心的概率约是多少(结果精确到0.01)
解 (1)表中依次填入的数据为0.80,0.95,0.88,0.92,0.89,0.91.
(2)因为频率稳定在常数0.89附近,所以这个射手射击一次,击中靶心的概率约是0.89.
规律方法 概率与频率的解题策略
(1)频率是事件A发生的次数m与试验总次数n的比值,利用此公式可求出它们的频率.频率是变化的,当n很大时,频率总是在一个稳定值附近左右摆动,这个稳定值就是概率.
(2)解此类题目的步骤是:先利用频率的计算公式依次计算频率,然后用频率估计概率.
变式训练1下表是某批乒乓球质量检查结果表:
抽取球数 50 100 200 500 1 000 2 000
优等品数 45 92 194 470 954 1 902
优等品出现的频率
(1)在上表中填上优等品出现的频率.
(2)估计该批乒乓球优等品的概率约是多少(结果精确到0.01)
(3)若抽取乒乓球的数量为1 700只,则优等品的数量大约为多少
解 (1)如下表所示:
抽取球数 50 100 200 500 1 000 2 000
优等品数 45 92 194 470 954 1 902
优等品出现的频率 0.9 0.92 0.97 0.94 0.954 0.951
(2)从表中数据可以看出,这批乒乓球优等品的概率约是0.95.
(3)由优等品的概率约为0.95,则抽取1 700只乒乓球时,优等品数量约为
1 700×0.95=1 615(只).
探究点三 概率的应用
【例3】 为了估计某自然保护区中天鹅的数量,可以使用以下方法:先从该保护区中捕出一定数量的天鹅,例如200只,给每只天鹅做上记号,不影响其存活,然后放回保护区,经过适当的时间,让其和保护区中其余的天鹅充分混合,再从保护区中捕出一定数量的天鹅,例如150只,查看其中有记号的天鹅,设有20只,试根据上述数据,估计该自然保护区中天鹅的数量.
规律方法 概率的实际应用
由于概率体现了随机事件发生的可能性,所以在现实生活中我们可以根据随机事件概率的大小去预测事件能否发生,从而对某些事情作出决策.当某随机事件的概率未知时,可用事件发生的频率去近似估计总体中该事件发生的概率.
变式训练2某中学为了了解初中部学生的佩戴胸卡的情况,在学校随机抽取初中部的150名学生,其中有60名佩戴胸卡.第二次检查,调查了初中部的所有学生,有500名学生佩戴胸卡.据此估计该中学初中部一共有多少名学生.
解 设初中部有n名学生,依题意得 ,解得n=1 250.所以该中学初中部共有学生大约1 250名.
本节要点归纳
1.知识清单:
(1)频率与概率的意义;
(2)用频率估计概率;
(3)概率的应用.
2.方法归纳:数据分析法.
3.常见误区:概率的意义理解错误;不能正确区分频率和概率的含义.
学以致用·随堂检测促达标
1
2
3
4
5
1.对以下命题:
①随机事件的概率与频率一样,与试验重复的次数有关;
②抛掷两枚均匀硬币一次,出现一正一反的概率是 ;
③若一种彩票买一张中奖的概率是 ,则买这种彩票一千张就会中奖;
④“投篮一次,求投中的概率”属于古典概型概率问题.
其中正确的个数是( )
A.0 B.1 C.2 D.3
A
解析 随机事件的概率与频率不一样,与试验重复的次数无关,所以①错误;抛掷两枚均匀硬币一次,包含的样本点是(正,正),(正,反),(反,正),(反,反),所以出现一正一反的概率是 ,所以②错误;若买一张彩票中奖是随机事件,买这种彩票一千张也不一定会中奖,所以③错误;“投篮一次,求投中的概率”,投篮的结果中与不中概率不相等,不属于古典概型概率问题,所以④错误.故选A.
1
2
3
4
5
1
2
3
4
5
2.在一次抛硬币的试验中,同学甲用一枚质地均匀的硬币做了100次试验,发现正面朝上出现了45次,那么出现正面朝上的频率和概率分别为( )
A.0.45,0.45 B.0.5,0.5
C.0.5,0.45 D.0.45,0.5
D
解析 由频率和概率的概念,可知出现正面朝上的频率是 =0.45,而出现正面朝上的概率是0.5.
1
2
3
4
5
3.[2024江苏无锡期中]某中学要在高一二班、三班、四班中任选一个班参加社区服务活动,有人提议用如下方法选班:掷两枚硬币,正面向上记作2点,反面向上记作1点,两枚点数和是几,就选几班,按照这个规则,当选概率最大的是 班.
三
1
2
3
4
5
4.管理人员从一池塘内捞出30条鱼,做上标记后放回池塘,10天后,又从池塘内捞出100条鱼,其中有标记的有2条,根据以上数据可以估计该池塘内共有
条鱼.
1 500
1
2
3
4
5
5.对某产品进行抽样检查,数据如下:
抽查件数 50 100 200 300 500
合格件数 47 92 192 285 475
根据上表中的数据,如果要从该产品中抽到950件合格品,则大约需要抽查
件产品.
1 000
解析 根据题表中数据可知合格品出现的频率为0.94,0.92,0.96,0.95,0.95,因此抽一件产品为合格品的概率约为0.95,因此要抽到950件合格品,大约需要抽查1 000件产品.
本 课 结 束
第七章
§3 频率与概率
基础落实·必备知识一遍过
重难探究·能力素养速提升
目录索引
学以致用·随堂检测促达标
课程标准 1.在具体情境中,了解随机事件发生的不确定性和频率的稳定性.
2.正确理解概率的意义,利用概率知识正确理解现实生活中的实际问题.
3.理解概率的意义以及频率与概率的区别.
基础落实·必备知识一遍过
知识点1 概率
该常数是确定的,是一个理论值
在相同条件下,大量重复进行同一试验时,随机事件A发生的频率通常会在某个常数附近摆动,即随机事件A发生的频率具有稳定性.这时,把这个常数叫作随机事件A的概率,记作P(A).
名师点睛
概率的性质
(1)随机事件A的概率P(A)满足0≤P(A)≤1.
(2)当A是必然事件时,P(A)=1;当A是不可能事件时,P(A)=0.
思考辨析
曾有人做过抛掷一枚质地均匀的硬币的大量重复试验,结果如下表所示:
抛掷次数 正面向上的次数 正面向上的频率
2 048 1 061 0.518 1
4 040 2 048 0.506 9
12 000 6 019 0.501 6
24 000 12 012 0.500 5
30 000 14 984 0.499 5
72 088 36 124 0.501 1
在上述抛掷硬币的试验中,你会发现怎样的规律
提示 当试验次数很多时,正面向上的频率在0.5附近摆动.
自主诊断
[人教A版教材例题]为了推广一种新饮料,某饮料生产企业开展了有奖促销活动:将6罐这种饮料装一箱,每箱中都放置2罐能够中奖的饮料.若从一箱中随机抽出2罐,能中奖的概率为多少
可以得到,样本空间包含的样本点个数为n(Ω)=6×5=30,且每个样本点都是等可能的.
知识点2 频率与概率之间的关系
1.区别
频率 本身是随机的,在试验之前是无法确定的,做同样次数的重复试验,得到的事件的频率值也可能会不同
概率 本身是一个在[0,1]上的确定值,不随试验结果的改变而改变
2.联系
随机事件的频率是指大量随机试验中,此事件发生的次数与试验次数的比值,它具有一定的稳定性,总是在某一个常数附近摆动,且随着试验次数的不断增加,这种摆动幅度越来越小.我们给这个常数取了一个名字,叫作这个随机事件的概率.概率可看作频率在理论上的期望值,它从数量上反映了随机事件发生的可能性的大小,频率在大量重复试验的前提下可近似地作为这个事件的概率.
名师点睛
频率本身是随机的,在试验前不能确定;概率是一个确定的数,是客观存在的,是事件的固有属性,与每次试验无关.
思考辨析
“某彩票的中奖概率为 ”含义是“买100张彩票能中一次奖”吗
提示 某彩票的中奖概率为 ,意味着中奖的可能性为 ,可能中奖,也可能不中奖,并不一定是买100张彩票能中一次奖.
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)随机事件的频率与概率不可能相等.( )
(2)随机事件A的概率是频率的稳定值,频率是概率的近似值.( )
(3)随机事件发生的概率是随着试验次数的变化而变化的.( )
2.质检部门对世园会所用某种产品进行抽检,得知其合格率为99%,若世园会所需该产品共有20 000件,则其中不合格产品约有 件.
×
√
×
200
解析 不合格产品约有20 000×(1-99%)=200(件).
3.[人教B版教材例题]某女篮运动员统计了她最近几次参加比赛投篮的得分情况,得到的数据如下表所示.
投篮次数 投中两分的次数 投中三分的次数
75 45 12
注:每次投篮,要么得两分,要么得三分,要么没投中.
记该女篮运动员在一次投篮中,投中两分为事件A,投中三分为事件B,没投中为事件C,试估计P(A),P(B),P(C).
重难探究·能力素养速提升
探究点一 概率概念的理解
【例1】问题辨析:
(1)掷一枚均匀的正方体骰子得到6点的概率是 ,是否意味着把它掷6次能得到1次6点
(2)某种病的治愈率是0.3,那么前7个人没有治愈,后3个人一定能治愈吗 如何理解治愈率是0.3
解 (1)把一枚均匀的骰子掷6次相当于做6次试验,因为每次试验的结果都是随机的,所以做6次试验的结果也是随机的.这就是说,每掷一次总是随机地出现一个点数,可以是1点,2点,也可以是其他点数,不一定出现6点.所以掷一枚骰子得到6点的概率是 ,并不意味着把它掷6次能得到1次6点.
(2)如果把治疗一个病人作为一次试验,治愈率是0.3,是指随着试验次数的增加,即治疗病人人数的增加,大约有30%的人能够治愈,对于一次试验来说,其结果是随机的,因此前7个病人没治愈是可能的,对后3个人来说,其结果仍然是随机的,即有可能治愈,也可能没有治愈.
变式探究我们知道,每次抛掷硬币的结果出现正、反的概率都为0.5,则连续抛掷质地均匀的硬币两次,是否一定出现“一次正面向上,一次反面向上”呢
解 不一定.这是因为统计规律不同于确定的数学规律,对于具体的一次试验而言,它带有很大的随机性(即偶然性),通过具体试验可以知道除上述结果外,也可能出现“两次都是正面向上”“两次都是反面向上”.尽管随机事件不像函数关系那样具有确定性,但是如果我们知道某事件发生的概率的大小,也能作出科学的决策.例如:做连续抛掷两枚质地均匀的硬币的试验
1 000次,可以预见:“两个都是正面向上”大约出现250次,“两个都是反面向上”大约出现250次,而“一个正面向上、一个反面向上”大约出现500次.
规律方法 对概率的正确理解
(1)概率是随机事件发生可能性大小的度量,是随机事件的本质属性,大量重复试验中事件A发生的频率是随机事件A发生的概率的近似值.
(2)由概率的定义我们可以知道随机事件A在一次试验中发生与否是随机的,但随机中含有规律性,而概率就是其规律性在数量上的反映.
(3)正确理解概率的意义,要清楚概率与频率的区别与联系.对具体的问题要从全局和整体上去看待,而不是局限于某一次试验或某一个具体的事件.
探究点二 概率与频率的关系及求法
【例2】 某射手在同一条件下进行射击,结果如下表所示:
射击次数n 10 20 50 100 200 500
击中靶心次数m 8 19 44 92 178 455
击中靶心的频率
(1)填写表中击中靶心的频率;
(2)这个射手射击一次,击中靶心的概率约是多少(结果精确到0.01)
解 (1)表中依次填入的数据为0.80,0.95,0.88,0.92,0.89,0.91.
(2)因为频率稳定在常数0.89附近,所以这个射手射击一次,击中靶心的概率约是0.89.
规律方法 概率与频率的解题策略
(1)频率是事件A发生的次数m与试验总次数n的比值,利用此公式可求出它们的频率.频率是变化的,当n很大时,频率总是在一个稳定值附近左右摆动,这个稳定值就是概率.
(2)解此类题目的步骤是:先利用频率的计算公式依次计算频率,然后用频率估计概率.
变式训练1下表是某批乒乓球质量检查结果表:
抽取球数 50 100 200 500 1 000 2 000
优等品数 45 92 194 470 954 1 902
优等品出现的频率
(1)在上表中填上优等品出现的频率.
(2)估计该批乒乓球优等品的概率约是多少(结果精确到0.01)
(3)若抽取乒乓球的数量为1 700只,则优等品的数量大约为多少
解 (1)如下表所示:
抽取球数 50 100 200 500 1 000 2 000
优等品数 45 92 194 470 954 1 902
优等品出现的频率 0.9 0.92 0.97 0.94 0.954 0.951
(2)从表中数据可以看出,这批乒乓球优等品的概率约是0.95.
(3)由优等品的概率约为0.95,则抽取1 700只乒乓球时,优等品数量约为
1 700×0.95=1 615(只).
探究点三 概率的应用
【例3】 为了估计某自然保护区中天鹅的数量,可以使用以下方法:先从该保护区中捕出一定数量的天鹅,例如200只,给每只天鹅做上记号,不影响其存活,然后放回保护区,经过适当的时间,让其和保护区中其余的天鹅充分混合,再从保护区中捕出一定数量的天鹅,例如150只,查看其中有记号的天鹅,设有20只,试根据上述数据,估计该自然保护区中天鹅的数量.
规律方法 概率的实际应用
由于概率体现了随机事件发生的可能性,所以在现实生活中我们可以根据随机事件概率的大小去预测事件能否发生,从而对某些事情作出决策.当某随机事件的概率未知时,可用事件发生的频率去近似估计总体中该事件发生的概率.
变式训练2某中学为了了解初中部学生的佩戴胸卡的情况,在学校随机抽取初中部的150名学生,其中有60名佩戴胸卡.第二次检查,调查了初中部的所有学生,有500名学生佩戴胸卡.据此估计该中学初中部一共有多少名学生.
解 设初中部有n名学生,依题意得 ,解得n=1 250.所以该中学初中部共有学生大约1 250名.
本节要点归纳
1.知识清单:
(1)频率与概率的意义;
(2)用频率估计概率;
(3)概率的应用.
2.方法归纳:数据分析法.
3.常见误区:概率的意义理解错误;不能正确区分频率和概率的含义.
学以致用·随堂检测促达标
1
2
3
4
5
1.对以下命题:
①随机事件的概率与频率一样,与试验重复的次数有关;
②抛掷两枚均匀硬币一次,出现一正一反的概率是 ;
③若一种彩票买一张中奖的概率是 ,则买这种彩票一千张就会中奖;
④“投篮一次,求投中的概率”属于古典概型概率问题.
其中正确的个数是( )
A.0 B.1 C.2 D.3
A
解析 随机事件的概率与频率不一样,与试验重复的次数无关,所以①错误;抛掷两枚均匀硬币一次,包含的样本点是(正,正),(正,反),(反,正),(反,反),所以出现一正一反的概率是 ,所以②错误;若买一张彩票中奖是随机事件,买这种彩票一千张也不一定会中奖,所以③错误;“投篮一次,求投中的概率”,投篮的结果中与不中概率不相等,不属于古典概型概率问题,所以④错误.故选A.
1
2
3
4
5
1
2
3
4
5
2.在一次抛硬币的试验中,同学甲用一枚质地均匀的硬币做了100次试验,发现正面朝上出现了45次,那么出现正面朝上的频率和概率分别为( )
A.0.45,0.45 B.0.5,0.5
C.0.5,0.45 D.0.45,0.5
D
解析 由频率和概率的概念,可知出现正面朝上的频率是 =0.45,而出现正面朝上的概率是0.5.
1
2
3
4
5
3.[2024江苏无锡期中]某中学要在高一二班、三班、四班中任选一个班参加社区服务活动,有人提议用如下方法选班:掷两枚硬币,正面向上记作2点,反面向上记作1点,两枚点数和是几,就选几班,按照这个规则,当选概率最大的是 班.
三
1
2
3
4
5
4.管理人员从一池塘内捞出30条鱼,做上标记后放回池塘,10天后,又从池塘内捞出100条鱼,其中有标记的有2条,根据以上数据可以估计该池塘内共有
条鱼.
1 500
1
2
3
4
5
5.对某产品进行抽样检查,数据如下:
抽查件数 50 100 200 300 500
合格件数 47 92 192 285 475
根据上表中的数据,如果要从该产品中抽到950件合格品,则大约需要抽查
件产品.
1 000
解析 根据题表中数据可知合格品出现的频率为0.94,0.92,0.96,0.95,0.95,因此抽一件产品为合格品的概率约为0.95,因此要抽到950件合格品,大约需要抽查1 000件产品.
本 课 结 束
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
