第7章 概率 总结提升--北师大版高中数学必修第一册课件(共47页PPT)
文档属性
| 名称 | 第7章 概率 总结提升--北师大版高中数学必修第一册课件(共47页PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 15:21:35 | ||
图片预览










文档简介
(共47张PPT)
第七章
本章总结提升
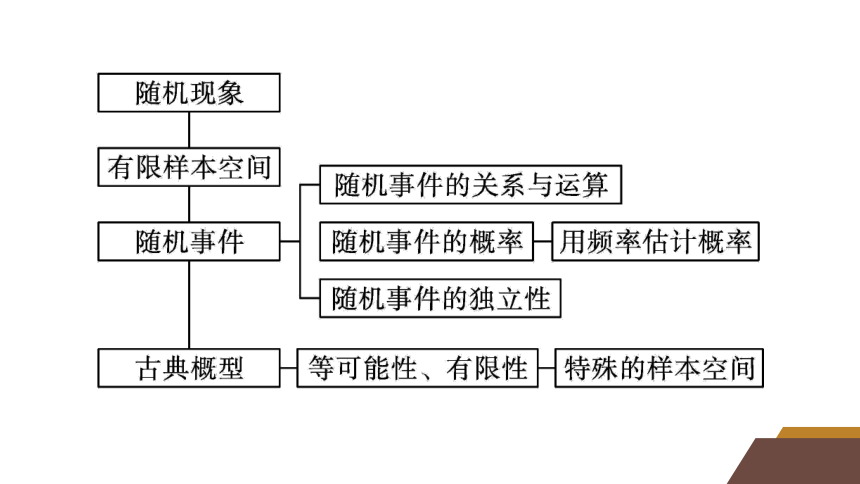
网络构建·归纳整合
专题突破·素养提升
目录索引
易错易混·衔接高考
网络构建·归纳整合
专题突破·素养提升
专题一 频率与概率
频率是概率的近似值,是随机的,随着试验的不同而变化;概率是多次的试验中频率的稳定值,是一个常数,不能用一次或少数次试验中的频率来估计概率.
【例1】 射手甲中靶的概率是0.9,因此我们认为,即使射手甲比较优秀,他射击10发子弹也不可能全中,其中必有一发不中,试判断这种认识正确与否.
解 射手甲射击一次,中靶是随机事件,他射击10次可以看作是重复做了10次试验,而每次试验的结果都是随机的,所以10次的结果也是随机的,这10次射击可能一次也不中,也可能中一次、二次、…、甚至十次都中.
虽然中靶是随机事件,但却具有一定的规律性,概率为0.9,是说在多次的试验中,中靶的可能性稳定在0.9,实际上,他10发子弹全中的概率为0.910≈0.349,这是有可能发生的.
因此题中认识不正确.
规律方法 概率与频率的关系
随机事件的概率是指在相同的条件下,大量重复进行同一试验,随机事件A发生的频率会在某个常数附近摆动,即随机事件A发生的频率具有稳定性.这时,我们把这个常数叫作事件A的概率,记作P(A).它反映的是这个事件发生的可能性的大小.
一个随机事件的发生既有随机性(对单次试验来说),又有规律性(对大量重复试验来说).其概率一般不好求,但可以用频率来估计.
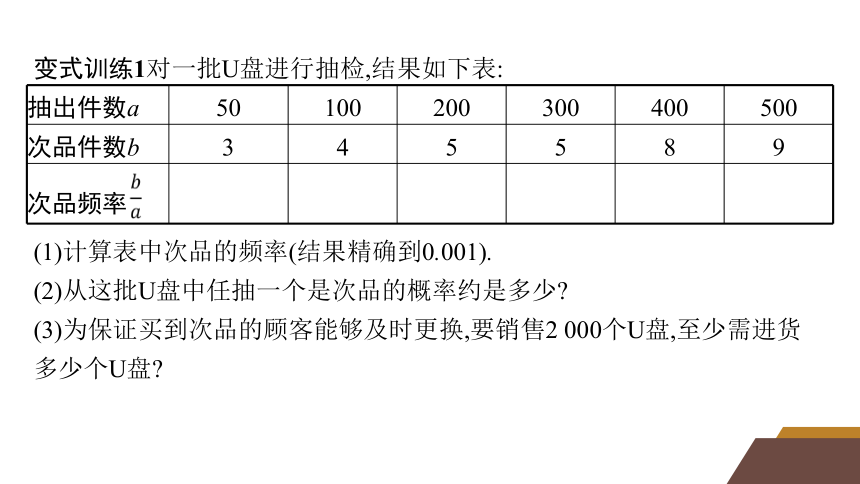
变式训练1对一批U盘进行抽检,结果如下表:
抽出件数a 50 100 200 300 400 500
次品件数b 3 4 5 5 8 9
次品频率
(1)计算表中次品的频率(结果精确到0.001).
(2)从这批U盘中任抽一个是次品的概率约是多少
(3)为保证买到次品的顾客能够及时更换,要销售2 000个U盘,至少需进货多少个U盘
解 (1)表中次品频率从左到右依次为0.06,0.040,0.025,0.017,0.020,0.018.
(2)当抽取件数a越来越大时,出现次品的频率在0.02附近摆动,所以从这批U盘中任抽一个是次品的概率约是0.02.
(3)设需要进货x个U盘,为保证其中有2 000个正品U盘,则x(1-0.020)≥2 000,因为x是正整数,
所以x≥2 041,即至少需进货2 041个U盘.
专题二 互斥事件与对立事件的概率及应用
若事件A1,A2,…,An彼此互斥,则P(A1∪A2∪…∪An)=P(A1)+P(A2)+…+P(An).
设事件A的对立事件是 ,则P(A)=1-P( ).
【例2】 在数学考试中,小王的成绩在90分以上(含90分)的概率是0.18,在[80,90)的概率是0.51,在[70,80)的概率是0.15,在[60,70)的概率是0.09,在60分以下(不含60分)的概率是0.07,此时视为考试不及格.求:
(1)小王在数学考试中取得80分以上(含80分)成绩的概率;
(2)小王数学考试及格的概率.
解 设小王的成绩在90分以上(含90分),在[80,90),在60分以下(不含60分)分别为事件A,B,C,且A,B,C两两互斥.
(1)设小王的成绩在80分以上(含80分)为事件D,则D=A∪B,
所以P(D)=P(A∪B)=P(A)+P(B)=0.18+0.51=0.69.
(2)设小王数学考试及格为事件E,
由于事件E与事件C为对立事件,
所以P(E)=1-P(C)=1-0.07=0.93.
规律方法 互斥事件与对立事件的概率求法
运用互斥事件的概率加法公式时,首先要确定各事件是否彼此互斥,如果彼此互斥,分别求出各事件发生的概率,再求和.求复杂事件的概率通常有两种方法:一是将所求事件转化成彼此互斥的事件的和,运用互斥事件的概率加法公式P(A∪B)=P(A)+P(B)求解;二是先求其对立事件的概率,然后再运用公式P(A)=1-P( )求解.
变式训练2某服务电话,打进的电话响第1声时被接的概率是0.1;响第2声时被接的概率是0.2;响第3声时被接的概率是0.3;响第4声时被接的概率是0.35.
(1)打进的电话在响5声之前被接的概率是多少
(2)打进的电话响4声而不被接的概率是多少
解 (1)设事件“电话响第k声时被接”为Ak(k∈N+),那么事件Ak彼此互斥,设“打进的电话在响5声之前被接”为事件A,根据互斥事件概率加法公式,得P(A)=P(A1∪A2∪A3∪A4)=P(A1)+P(A2)+P(A3)+P(A4)=0.1+0.2+0.3+0.35
=0.95.
(2)由(1)知事件“打进的电话响4声而不被接”是事件“打进的电话在响5声之前被接”的对立事件,记为 根据对立事件的概率公式,得
P( )=1-P(A)=1-0.95=0.05.
专题三 古典概型
古典概型是一种最基本的概率模型,也是学习其他概率模型的基础,在高考题中,经常出现此种概率模型的题目.解题时要紧紧抓住古典概型的两个基本特点,即有限性和等可能性.
【例3—1】 (多选题)随机地排列数字1,2,6得到一个三位数,则( )
A.可以排成6个不同的三位数
AC
【例3—2】 已知函数f(x)=ax2+2bx-1.
(1)若a,b都是从集合{1,2,3}中任取的一个数,求函数f(x)在(-∞,-1)上单调递减的概率;
(2)若a是从集合{1,2,3}中任取的一个数,b是从集合{1,2,3,4}中任取的一个数,求方程f(x)=0在区间(-∞,-3)上有实数根的概率.
解 (1)记“函数f(x)在区间(-∞,-1)上单调递减”为事件A.
由于a,b都是从集合{1,2,3}中任取的一个数,则基本事件有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),共9种,
若函数f(x)在区间(-∞,-1)上单调递减,则有
则事件A包含其中的6个基本事件,
(2)记“方程f(x)=0在区间(-∞,-3)上有实数根”为事件B,由于a是从集合{1,2,3}上任取的一个数,b是从集合{1,2,3,4}上任取的一个数,
则基本事件有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),共12种,
由题意知a>0,f(0)=-1,所以方程f(x)=0在区间(-∞,-3)上有实数根,
则有f(-3)<0,即9a-6b-1<0,
则事件B包含其中的5个基本事件,
所以所求的概率P(B)=
规律方法 古典概型的概率求法
在求古典概型问题的概率时,往往需要我们将所有样本点一一列举出来,以便确定样本点总数及事件所包含的样本点数.这就是我们常说的列举法.在列举时应注意按一定的规律、标准,做到不重不漏.
变式训练3从{1,2,3,4,5}中随机选取一个数为a,从{1,2,3}中随机选取一个数为b,则b>a的概率是( )
D
解析 ∵当b=1时,没有满足条件的a值;
当b=2时,a=1;
当b=3时,a可以是1,可以是2,
∴共3个样本点.
而从{1,2,3,4,5}中随机取一个数a,再从{1,2,3}中随机取一个数b,共有3×5=15个样本点,
专题四 相互独立事件的概率
设A,B为两个事件,如果P(AB)=P(A)P(B),则称事件A与事件B相互独立.如果事件A与B相互独立,那么A与 与B, 也都相互独立.
【例4】 甲、乙两人轮流投篮,每人每次投一球,约定甲先投且先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束,设甲每次投篮投中的概率为 ,乙每次投篮投中的概率为 ,且各自投篮互不影响.
(1)求甲乙各投球一次,比赛结束的概率;
(2)求甲获胜的概率.
解 设事件Ak表示“甲在第k次投篮投中”,其中k=1,2,3,
设事件Bj表示“乙在第j次投篮投中”,其中j=1,2,3,
规律方法 相互独立事件概率的求法
(1)首先要搞清事件间的关系(是否彼此互斥、是否相互独立、是否对立),正确区分“互斥事件”与“对立事件”.当且仅当事件A和事件B相互独立时,才有P(AB)=P(A)P(B).
(2)某些事件若含有较多的互斥事件,可考虑其对立事件的概率,这样可减少运算量,提高准确率.要注意“至多”“至少”等题型的转化.
变式训练4[2024山东济宁期末]一个不透明的箱子中有4个红球、2个蓝球(球除颜色外,没有其他差异).
(1)若从箱子中不放回地随机抽取两球,求两球颜色相同的概率;
(2)若从箱子中有放回地抽取两球,求两球颜色相同的概率.
解 (1)把4个红球标记为A1,A2,A3,A4,2个蓝球标记为B1,B2,从箱子中随机抽取两球的样本空间为Ω={A1A2,A1A3,A1A4,A1B1,A1B2,A2A3,A2A4,A2B1, A2B2,A3A4,A3B1,A3B2,A4B1,A4B2,B1B2},共有15个样本点.设事件E=“从箱子中随机抽取两球且颜色相同”,则事件E={A1A2,A1A3,A1A4,A2A3,A2A4,A3A4,B1B2},包含7个样本点,所以
(2)设事件F=“从箱子中有放回地抽取两球且颜色相同”,
事件M=“从箱子中有放回地抽取两球且两球都为红球”,
事件N=“从箱子中有放回地抽取两球且两球都为蓝球”,
则F=M∪N,且事件M与N互斥,
易错易混·衔接高考
1
2
3
4
5
6
7
1.有50人报名足球俱乐部,60人报名乒乓球俱乐部,70人报名足球或乒乓球俱乐部,若已知某人报足球俱乐部,则其报乒乓球俱乐部的概率为( )
A.0.8 B.0.4 C.0.2 D.0.1
A
解析 50+60-70=40人报名足球和乒乓球俱乐部,因此所求概率为 =0.8,故选A.
1
2
3
4
5
6
7
2.[2024江苏镇江期中]下列说法正确的是( )
①已知a>b,b>c,那么事件“a>c”有可能不发生;
②随机试验的频率与概率相等;
③如果一个事件发生的概率为99.999 9%,那么说明此事件必然发生;
④只有不确定事件有概率;
⑤若事件A发生的概率为P(A),则0≤P(A)≤1.
A.⑤ B.③⑤
C.③④⑤ D.②③④⑤
A
1
2
3
4
5
6
7
解析 对于①,如果a>b,b>c,那么“a>c”是必然事件,故①错误;
对于②,随机试验多次重复发生时,频率会越来越靠近概率,但不一定等于概率,故②错误;
对于③,如果一事件发生的概率为99.999 9%,那么只能说明此事件发生的可能性非常大,不代表一定发生,所以不能说是必然事件,故③错误;
对于④,确定事件也有概率,故④错误;
对于⑤,若事件A发生的概率为P(A),由概率的性质可知0≤P(A)≤1.故⑤正确.
1
2
3
4
5
6
7
3.[2024浙江舟山期末]已知事件A,B,且P(A)=0.6,P(B)=0.7,如果事件A与B互斥,那么P(AB)=p1;如果事件A与B相互独立,那么P(A+ )=p2,则( )
A.p1=0,p2=0.9 B.p1=0.42,p2=0.9
C.p1=0,p2=0.72 D.p1=0.42,p2=0.45
C
1
2
3
4
5
6
7
4.[2024山东日照期末]2023年10月25日,神舟十七号载人飞船在酒泉卫星发射中心成功点火发射.在太空站内有甲、乙、丙三名航天员依次出仓进行同一试验,每次只派一人,每人最多出仓一次.若前一人试验不成功,返仓后派下一人重复进行该试验;若试验成功,终止试验.已知甲、乙、丙各自出仓试验成功的概率分别为 ,每人出仓试验能否成功相互独立,则该项试验最终成功的概率为( )
D
1
2
3
4
5
6
7
1
2
3
4
5
6
7
5.(多选题)如图所示的电路中,5个盒子表示保险匣,设5个盒子分别为A,B,C,D,E.盒中所示数值表示通电时保险丝被切断的概率,下列结论正确的是( )
CD
1
2
3
4
5
6
7
1
2
3
4
5
6
7
6.某产品分甲、乙、丙三级,其中乙、丙两级均属次品,若生产中出现乙级品的概率为0.04,出现丙级品的概率为0.01,则对成品抽查一件抽得正品的概率为 .
0.95
解析 记事件A={抽得甲级品},B={抽得乙级品},C={抽得丙级品},因为事件A,B,C互为互斥事件,且三个事件对立,所以抽得正品即为抽得甲级品的概率为P(A)=1-P(B)-P(C)=0.95.
1
2
3
4
5
6
7
7.(2020全国1,文17)某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元,50元,20元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
甲分厂产品等级
的频数分布表
等级 A B C D
频数 40 20 20 20
乙分厂产品等级的
频数分布表
等级 A B C D
频数 28 17 34 21
1
2
3
4
5
6
7
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务
1
2
3
4
5
6
7
(2)由数据知甲分厂加工出来的100件产品利润的频数分布表为
利润 65 25 -5 -75
频数 40 20 20 20
因此甲分厂加工出来的100件产品的平均利润为
1
2
3
4
5
6
7
由数据知乙分厂加工出来的100件产品利润的频数分布表为
利润 70 30 0 -70
频数 28 17 34 21
本 课 结 束
第七章
本章总结提升
网络构建·归纳整合
专题突破·素养提升
目录索引
易错易混·衔接高考
网络构建·归纳整合
专题突破·素养提升
专题一 频率与概率
频率是概率的近似值,是随机的,随着试验的不同而变化;概率是多次的试验中频率的稳定值,是一个常数,不能用一次或少数次试验中的频率来估计概率.
【例1】 射手甲中靶的概率是0.9,因此我们认为,即使射手甲比较优秀,他射击10发子弹也不可能全中,其中必有一发不中,试判断这种认识正确与否.
解 射手甲射击一次,中靶是随机事件,他射击10次可以看作是重复做了10次试验,而每次试验的结果都是随机的,所以10次的结果也是随机的,这10次射击可能一次也不中,也可能中一次、二次、…、甚至十次都中.
虽然中靶是随机事件,但却具有一定的规律性,概率为0.9,是说在多次的试验中,中靶的可能性稳定在0.9,实际上,他10发子弹全中的概率为0.910≈0.349,这是有可能发生的.
因此题中认识不正确.
规律方法 概率与频率的关系
随机事件的概率是指在相同的条件下,大量重复进行同一试验,随机事件A发生的频率会在某个常数附近摆动,即随机事件A发生的频率具有稳定性.这时,我们把这个常数叫作事件A的概率,记作P(A).它反映的是这个事件发生的可能性的大小.
一个随机事件的发生既有随机性(对单次试验来说),又有规律性(对大量重复试验来说).其概率一般不好求,但可以用频率来估计.
变式训练1对一批U盘进行抽检,结果如下表:
抽出件数a 50 100 200 300 400 500
次品件数b 3 4 5 5 8 9
次品频率
(1)计算表中次品的频率(结果精确到0.001).
(2)从这批U盘中任抽一个是次品的概率约是多少
(3)为保证买到次品的顾客能够及时更换,要销售2 000个U盘,至少需进货多少个U盘
解 (1)表中次品频率从左到右依次为0.06,0.040,0.025,0.017,0.020,0.018.
(2)当抽取件数a越来越大时,出现次品的频率在0.02附近摆动,所以从这批U盘中任抽一个是次品的概率约是0.02.
(3)设需要进货x个U盘,为保证其中有2 000个正品U盘,则x(1-0.020)≥2 000,因为x是正整数,
所以x≥2 041,即至少需进货2 041个U盘.
专题二 互斥事件与对立事件的概率及应用
若事件A1,A2,…,An彼此互斥,则P(A1∪A2∪…∪An)=P(A1)+P(A2)+…+P(An).
设事件A的对立事件是 ,则P(A)=1-P( ).
【例2】 在数学考试中,小王的成绩在90分以上(含90分)的概率是0.18,在[80,90)的概率是0.51,在[70,80)的概率是0.15,在[60,70)的概率是0.09,在60分以下(不含60分)的概率是0.07,此时视为考试不及格.求:
(1)小王在数学考试中取得80分以上(含80分)成绩的概率;
(2)小王数学考试及格的概率.
解 设小王的成绩在90分以上(含90分),在[80,90),在60分以下(不含60分)分别为事件A,B,C,且A,B,C两两互斥.
(1)设小王的成绩在80分以上(含80分)为事件D,则D=A∪B,
所以P(D)=P(A∪B)=P(A)+P(B)=0.18+0.51=0.69.
(2)设小王数学考试及格为事件E,
由于事件E与事件C为对立事件,
所以P(E)=1-P(C)=1-0.07=0.93.
规律方法 互斥事件与对立事件的概率求法
运用互斥事件的概率加法公式时,首先要确定各事件是否彼此互斥,如果彼此互斥,分别求出各事件发生的概率,再求和.求复杂事件的概率通常有两种方法:一是将所求事件转化成彼此互斥的事件的和,运用互斥事件的概率加法公式P(A∪B)=P(A)+P(B)求解;二是先求其对立事件的概率,然后再运用公式P(A)=1-P( )求解.
变式训练2某服务电话,打进的电话响第1声时被接的概率是0.1;响第2声时被接的概率是0.2;响第3声时被接的概率是0.3;响第4声时被接的概率是0.35.
(1)打进的电话在响5声之前被接的概率是多少
(2)打进的电话响4声而不被接的概率是多少
解 (1)设事件“电话响第k声时被接”为Ak(k∈N+),那么事件Ak彼此互斥,设“打进的电话在响5声之前被接”为事件A,根据互斥事件概率加法公式,得P(A)=P(A1∪A2∪A3∪A4)=P(A1)+P(A2)+P(A3)+P(A4)=0.1+0.2+0.3+0.35
=0.95.
(2)由(1)知事件“打进的电话响4声而不被接”是事件“打进的电话在响5声之前被接”的对立事件,记为 根据对立事件的概率公式,得
P( )=1-P(A)=1-0.95=0.05.
专题三 古典概型
古典概型是一种最基本的概率模型,也是学习其他概率模型的基础,在高考题中,经常出现此种概率模型的题目.解题时要紧紧抓住古典概型的两个基本特点,即有限性和等可能性.
【例3—1】 (多选题)随机地排列数字1,2,6得到一个三位数,则( )
A.可以排成6个不同的三位数
AC
【例3—2】 已知函数f(x)=ax2+2bx-1.
(1)若a,b都是从集合{1,2,3}中任取的一个数,求函数f(x)在(-∞,-1)上单调递减的概率;
(2)若a是从集合{1,2,3}中任取的一个数,b是从集合{1,2,3,4}中任取的一个数,求方程f(x)=0在区间(-∞,-3)上有实数根的概率.
解 (1)记“函数f(x)在区间(-∞,-1)上单调递减”为事件A.
由于a,b都是从集合{1,2,3}中任取的一个数,则基本事件有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),共9种,
若函数f(x)在区间(-∞,-1)上单调递减,则有
则事件A包含其中的6个基本事件,
(2)记“方程f(x)=0在区间(-∞,-3)上有实数根”为事件B,由于a是从集合{1,2,3}上任取的一个数,b是从集合{1,2,3,4}上任取的一个数,
则基本事件有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),共12种,
由题意知a>0,f(0)=-1,所以方程f(x)=0在区间(-∞,-3)上有实数根,
则有f(-3)<0,即9a-6b-1<0,
则事件B包含其中的5个基本事件,
所以所求的概率P(B)=
规律方法 古典概型的概率求法
在求古典概型问题的概率时,往往需要我们将所有样本点一一列举出来,以便确定样本点总数及事件所包含的样本点数.这就是我们常说的列举法.在列举时应注意按一定的规律、标准,做到不重不漏.
变式训练3从{1,2,3,4,5}中随机选取一个数为a,从{1,2,3}中随机选取一个数为b,则b>a的概率是( )
D
解析 ∵当b=1时,没有满足条件的a值;
当b=2时,a=1;
当b=3时,a可以是1,可以是2,
∴共3个样本点.
而从{1,2,3,4,5}中随机取一个数a,再从{1,2,3}中随机取一个数b,共有3×5=15个样本点,
专题四 相互独立事件的概率
设A,B为两个事件,如果P(AB)=P(A)P(B),则称事件A与事件B相互独立.如果事件A与B相互独立,那么A与 与B, 也都相互独立.
【例4】 甲、乙两人轮流投篮,每人每次投一球,约定甲先投且先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束,设甲每次投篮投中的概率为 ,乙每次投篮投中的概率为 ,且各自投篮互不影响.
(1)求甲乙各投球一次,比赛结束的概率;
(2)求甲获胜的概率.
解 设事件Ak表示“甲在第k次投篮投中”,其中k=1,2,3,
设事件Bj表示“乙在第j次投篮投中”,其中j=1,2,3,
规律方法 相互独立事件概率的求法
(1)首先要搞清事件间的关系(是否彼此互斥、是否相互独立、是否对立),正确区分“互斥事件”与“对立事件”.当且仅当事件A和事件B相互独立时,才有P(AB)=P(A)P(B).
(2)某些事件若含有较多的互斥事件,可考虑其对立事件的概率,这样可减少运算量,提高准确率.要注意“至多”“至少”等题型的转化.
变式训练4[2024山东济宁期末]一个不透明的箱子中有4个红球、2个蓝球(球除颜色外,没有其他差异).
(1)若从箱子中不放回地随机抽取两球,求两球颜色相同的概率;
(2)若从箱子中有放回地抽取两球,求两球颜色相同的概率.
解 (1)把4个红球标记为A1,A2,A3,A4,2个蓝球标记为B1,B2,从箱子中随机抽取两球的样本空间为Ω={A1A2,A1A3,A1A4,A1B1,A1B2,A2A3,A2A4,A2B1, A2B2,A3A4,A3B1,A3B2,A4B1,A4B2,B1B2},共有15个样本点.设事件E=“从箱子中随机抽取两球且颜色相同”,则事件E={A1A2,A1A3,A1A4,A2A3,A2A4,A3A4,B1B2},包含7个样本点,所以
(2)设事件F=“从箱子中有放回地抽取两球且颜色相同”,
事件M=“从箱子中有放回地抽取两球且两球都为红球”,
事件N=“从箱子中有放回地抽取两球且两球都为蓝球”,
则F=M∪N,且事件M与N互斥,
易错易混·衔接高考
1
2
3
4
5
6
7
1.有50人报名足球俱乐部,60人报名乒乓球俱乐部,70人报名足球或乒乓球俱乐部,若已知某人报足球俱乐部,则其报乒乓球俱乐部的概率为( )
A.0.8 B.0.4 C.0.2 D.0.1
A
解析 50+60-70=40人报名足球和乒乓球俱乐部,因此所求概率为 =0.8,故选A.
1
2
3
4
5
6
7
2.[2024江苏镇江期中]下列说法正确的是( )
①已知a>b,b>c,那么事件“a>c”有可能不发生;
②随机试验的频率与概率相等;
③如果一个事件发生的概率为99.999 9%,那么说明此事件必然发生;
④只有不确定事件有概率;
⑤若事件A发生的概率为P(A),则0≤P(A)≤1.
A.⑤ B.③⑤
C.③④⑤ D.②③④⑤
A
1
2
3
4
5
6
7
解析 对于①,如果a>b,b>c,那么“a>c”是必然事件,故①错误;
对于②,随机试验多次重复发生时,频率会越来越靠近概率,但不一定等于概率,故②错误;
对于③,如果一事件发生的概率为99.999 9%,那么只能说明此事件发生的可能性非常大,不代表一定发生,所以不能说是必然事件,故③错误;
对于④,确定事件也有概率,故④错误;
对于⑤,若事件A发生的概率为P(A),由概率的性质可知0≤P(A)≤1.故⑤正确.
1
2
3
4
5
6
7
3.[2024浙江舟山期末]已知事件A,B,且P(A)=0.6,P(B)=0.7,如果事件A与B互斥,那么P(AB)=p1;如果事件A与B相互独立,那么P(A+ )=p2,则( )
A.p1=0,p2=0.9 B.p1=0.42,p2=0.9
C.p1=0,p2=0.72 D.p1=0.42,p2=0.45
C
1
2
3
4
5
6
7
4.[2024山东日照期末]2023年10月25日,神舟十七号载人飞船在酒泉卫星发射中心成功点火发射.在太空站内有甲、乙、丙三名航天员依次出仓进行同一试验,每次只派一人,每人最多出仓一次.若前一人试验不成功,返仓后派下一人重复进行该试验;若试验成功,终止试验.已知甲、乙、丙各自出仓试验成功的概率分别为 ,每人出仓试验能否成功相互独立,则该项试验最终成功的概率为( )
D
1
2
3
4
5
6
7
1
2
3
4
5
6
7
5.(多选题)如图所示的电路中,5个盒子表示保险匣,设5个盒子分别为A,B,C,D,E.盒中所示数值表示通电时保险丝被切断的概率,下列结论正确的是( )
CD
1
2
3
4
5
6
7
1
2
3
4
5
6
7
6.某产品分甲、乙、丙三级,其中乙、丙两级均属次品,若生产中出现乙级品的概率为0.04,出现丙级品的概率为0.01,则对成品抽查一件抽得正品的概率为 .
0.95
解析 记事件A={抽得甲级品},B={抽得乙级品},C={抽得丙级品},因为事件A,B,C互为互斥事件,且三个事件对立,所以抽得正品即为抽得甲级品的概率为P(A)=1-P(B)-P(C)=0.95.
1
2
3
4
5
6
7
7.(2020全国1,文17)某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元,50元,20元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
甲分厂产品等级
的频数分布表
等级 A B C D
频数 40 20 20 20
乙分厂产品等级的
频数分布表
等级 A B C D
频数 28 17 34 21
1
2
3
4
5
6
7
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务
1
2
3
4
5
6
7
(2)由数据知甲分厂加工出来的100件产品利润的频数分布表为
利润 65 25 -5 -75
频数 40 20 20 20
因此甲分厂加工出来的100件产品的平均利润为
1
2
3
4
5
6
7
由数据知乙分厂加工出来的100件产品利润的频数分布表为
利润 70 30 0 -70
频数 28 17 34 21
本 课 结 束
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
