第1章 1.3 第2课时 全集与补集--北师大版高中数学必修第一册课件(共41页PPT)
文档属性
| 名称 | 第1章 1.3 第2课时 全集与补集--北师大版高中数学必修第一册课件(共41页PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 00:00:00 | ||
图片预览










文档简介
(共41张PPT)
第一章
1.3 第2课时 全集与补集
基础落实·必备知识一遍过
重难探究·能力素养速提升
学以致用·随堂检测促达标
目录索引
课程标准 1.在具体情境中,了解全集的含义.
2.理解在给定集合中一个子集的补集的含义,能求给定子集的补集.
3.能够解决交集、并集、补集的综合运算问题.
基础落实·必备知识一遍过
知识点 全集与补集
1.全集
在研究某些集合的时候,它们往往是某个给定集合的子集,这个给定的集合叫作全集,常用符号U表示.全集包含所要研究的这些集合.
2.补集
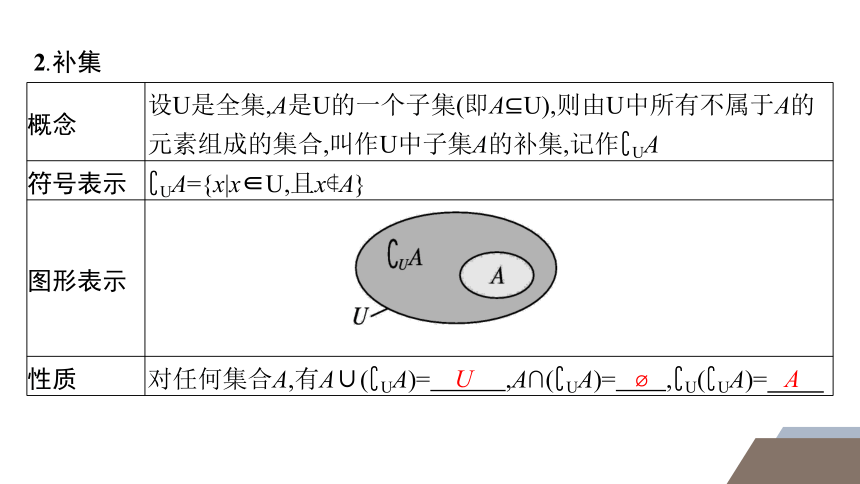
概念 设U是全集,A是U的一个子集(即A U),则由U中所有不属于A的元素组成的集合,叫作U中子集A的补集,记作 UA
符号表示 UA={x|x∈U,且x A}
图形表示
性质 对任何集合A,有A∪( UA)= ,A∩( UA)= , U( UA)=
U
A
名师点睛
1.全集不是固定不变的,它是一个相对概念,是依据具体问题来选择的.
2.补集是相对于全集而言的,它与全集不可分割.一方面,若没有定义全集,则不存在补集的说法;另一方面,补集的元素一定都能在全集中找到.
3.补集既是集合之间的一种关系,也是集合之间的一种运算.求集合A的补集的前提是A为全集U的子集,随着所选全集的不同,得到的补集也是不同的.
4.符号 UA有三层意思:①A是U的一个子集,即A U;② UA表示一个集合,且 UA U;③ UA是由U中不属于A的所有元素组成的集合,即 UA={x|x∈U,且x A}.
5.若x∈U,则x∈A或x∈ UA,二者必居其一.
思考辨析
1.全集一定包含任何元素吗
2.一个确定集合的补集唯一吗
3.一个集合A的补集中的元素具有什么特征
提示 不一定.全集不是固定的,它是相对而言的.只要包含所研究问题中涉及的所有元素即可.
提示 由于补集是相对于某一个全集的补集,因此对于一个确定的集合来说,全集不同时,该集合的补集也不相同.
提示 一个集合A的补集它包含两个方面:一是该集合是全集的子集,二是该集合中的元素属于全集,但是不属于集合A.
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)设集合U={1,2,3,4,5},A={1,2},B={2,3,4},则 U(A∪B)={5}.( )
(2)同一个集合在不同的全集中的补集不同.( )
(3)不同的集合在同一个全集中的补集可能相同.( )
√
√
×
2.若全集U=R,集合A={x|x≥1},则 UA= .
{x|x<1}
解析 由补集的定义可得 UA={x|x<1}.
3.[2024浙江温州高一阶段检测]已知全集U={2,3,a2+2a+2},集合A={2,3}, UA={5},则实数a的值为 .
1或-3
解析 由题可得a2+2a+2=5,解得a=1或a=-3,
所以实数a的值为1或-3.
4.[人教A版教材例题]设全集U={x|x是三角形},A={x|x是锐角三角形},B={x|x是钝角三角形},求A∩B, U(A∪B).
解 根据三角形的分类可知A∩B= ,A∪B={x|x是锐角三角形或钝角三角形}, U(A∪B)={x|x是直角三角形}.
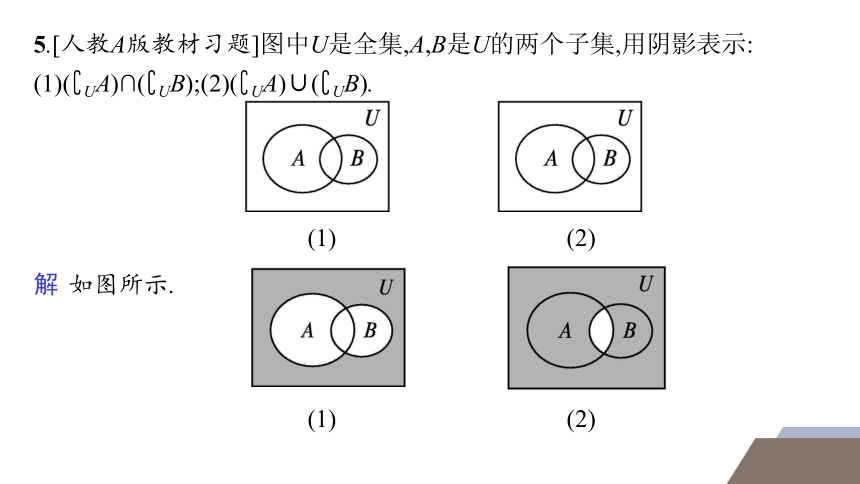
5.[人教A版教材习题]图中U是全集,A,B是U的两个子集,用阴影表示:
(1)( UA)∩( UB);(2)( UA)∪( UB).
(1)
(2)
解 如图所示.
(1)
(2)
重难探究·能力素养速提升
探究点一 补集的基本运算
【例1】 (1)已知全集为U,集合A={1,3,5,7}, UA={2,4,6}, UB={1,4,6},则集合B= .
{2,3,5,7}
解析(方法一)∵A={1,3,5,7}, UA={2,4,6},
∴U={1,2,3,4,5,6,7}.
又 UB={1,4,6},∴B={2,3,5,7}.
(方法二)满足题意的Venn图如图所示.
由图可知B={2,3,5,7}.
(2)已知全集U={x|x≤5},集合A={x|-3≤x<5},则 UA= .
{x|x<-3,或x=5}
解析将全集U和集合A分别表示在数轴上,如图所示.
由补集的定义可知 UA={x|x<-3,或x=5}.
规律方法 求集合的补集的方法
变式训练1(1)[2024河南开封高一月考](多选题)已知全集U=Z,集合A={x∈Z|2x+1≥0},B={-1,0,1,2},则( )
A.A∩B={0,1,2}
B.A∪B={x|x≥0}
C.( UA)∩B={-1}
D.A∩B的真子集个数是7
ACD
★(2)已知全集为U,集合A={x|-3≤x<5}, UA={x|x≥5},B={x|1求 UB.
解 由已知U={x|-3≤x<5}∪{x|x≥5}={x|x≥-3},又B={x|1所以 UB={x|-3≤x≤1或x≥3}.
探究点二 交集、并集与补集的混合运算
【例2】 (1)已知全集U={x∈Z|0A.M∩( UN) B. U(M∩N)
C. U(M∪N) D.( UM)∩N
C
解析 ∵全集U={x∈Z|0(2)已知全集U={x|-5≤x≤3},A={x|-5≤x<-1},B={x|-1≤x<1},求( UA)∩( UB).
解 将集合U,A,B分别表示在数轴上,如图所示,
则 UA={x|-1≤x≤3},
UB={x|-5≤x<-1,或1≤x≤3},
所以( UA)∩( UB)={x|1≤x≤3}.
规律方法 求集合的交、并、补集运算的方法
变式训练2(1)如果全集U=R,M={x|-1A.(-1,1)∪(1,2) B.(-1,2)
C.(-1,1)∪(1,2] D.(-1,2]
C
解析 UN={x|x≠1,且x≠3,且x≠5},
∴M∩( UN)=(-1,1)∪(1,2].
(2)已知全集为R,A={x|3≤x<7},B={x|2解 把集合A,B在数轴上表示如图.
由图知,A∪B={x|2∴ R(A∪B)={x|x≤2,或x≥10}.
∵ RA={x|x<3,或x≥7},
∴( RA)∩B={x|2探究点三 补集性质的应用
【例3】 已知全集为R,集合A={x|x[2,+∞)
解析 ∵B={x|1∴ RB={x|x≤1,或x≥2}.
又A={x|x规律方法 由含补集的运算求参数的取值范围时,常根据补集的定义及集合之间的关系,并借助于数轴列出参数应满足的关系式求解,具体操作时要注意端点值的取舍.
变式训练3已知集合A={x|x2+ax+12b=0}和B={x|x2-ax+b=0},满足B∩( UA)={2},A∩( UB)={4},U=R,求实数a,b的值.
解 ∵B∩( UA)={2},∴2∈B,但2 A.
∵A∩( UB)={4},∴4∈A,但4 B.
探究点四 补集思想的应用
【例4】 已知集合A={x|0≤x≤2},B={x|a≤x≤a+3}.
(1)若( RA)∪B≠R,求实数a的取值范围;
(2)若A∩B≠A,求实数a的取值范围.
解 (1)∵A={x|0≤x≤2},
∴ RA=|x|x<0,或x>2}.
假设( RA)∪B=R,如图所示.
∴a≤0,且a+3≥2,即a≤0,且a≥-1,∴满足( RA)∪B≠R的实数a的取值范围是{a|a<-1,或a>0}.
(2)假设A∩B=A,则A B,又A≠ ,
∴满足A∩B≠A的实数a的取值范围为{a|a<-1,或a>0}.
规律方法 有些数学问题,若直接从正面解决,若解题思路不明朗,或需要考虑的因素太多,可用补集思想考虑其对立面,即从结论的反面去思考,探索已知和未知之间的关系,从而化繁为简,化难为易,开拓解题思路,这就是补集思想的应用.
(1)运用补集思想求参数范围的方法:
①否定已知条件考虑反面问题;
②求解反面问题对应的参数范围;
③将反面问题对应的参数范围取补集,得到原问题的解.
(2)补集思想适用的情况:从正面考虑情况较多、问题较复杂的时候,往往考虑运用补集思想.
变式训练4已知集合A={x|x<-6,或x>3},B={x|k-1≤x-1≤k},若A∩B≠ ,求k的取值范围.
解 由已知可得B={x|k≤x≤k+1},
令P={k|-6≤k≤2},则 RP={k|k<-6,或k>2},
所以满足A∩B≠ 的k的取值范围是{k|k<-6,或k>2}.
本节要点归纳
1.知识清单:
(1)全集和补集的概念及运算;
(2)并、交、补集的混合运算;
(3)与补集有关的参数的求解.
2.方法归纳:正难则反的补集思想、数形结合.
3.常见误区:求补集时忽视全集,运算时易忽视端点的取舍.
学以致用·随堂检测促达标
1
2
3
4
5
1.已知全集U={-1,0,1,3,6},A={0,6},则 UA=( )
A.{-1,3} B.{-1,1,3}
C.{0,1,3} D.{0,3,6}
B
解析 ∵全集U={-1,0,1,3,6},A={0,6},
∴ UA={-1,1,3}.
1
2
3
4
5
2.(多选题)已知全集U=R,集合A={x|1≤x≤3,或4A. UA={x|x<1,或36}
B. UB={x|x<2,或x≥5}
C.A∩( UB)={x|1≤x<2,或5≤x<6}
D.( UA)∪B={x|x<1,或2≤x<5,或x>6}
BC
解析 在数轴上表示出集合A,B,如图,
UA={x|x<1,或3 UB={x|x<2,或x≥5},故B正确;A∩( UB)={x|1≤x<2,或5≤x<6},故C正确; ( UA)∪B={x|x<1,或2≤x<5,或x≥6},故D错误.故选BC.
1
2
3
4
5
1
2
3
4
5
3.[2024江苏南通期中]已知全集U和集合A,B如图所示,则( UA)∩B= .
{5,6}
解析 由题中的Venn图知( UA)∩B={5,6}.
1
2
3
4
5
4.已知全集U=R,A={x|1≤x2
解析 ∵ UA={x|x<1,或x≥2},
∴A={x|1≤x<2}.∴b=2.
1
2
3
4
5
5.已知全集U=R,A={x|-4≤x<2},B={x|-1求A∩B,( UB)∪P,(A∩B)∩( UP).
解 将集合A,B,P分别表示在数轴上,如图所示.
∵A={x|-4≤x<2},B={x|-1∴A∩B={x|-13}.
1
2
3
4
5
本 课 结 束
第一章
1.3 第2课时 全集与补集
基础落实·必备知识一遍过
重难探究·能力素养速提升
学以致用·随堂检测促达标
目录索引
课程标准 1.在具体情境中,了解全集的含义.
2.理解在给定集合中一个子集的补集的含义,能求给定子集的补集.
3.能够解决交集、并集、补集的综合运算问题.
基础落实·必备知识一遍过
知识点 全集与补集
1.全集
在研究某些集合的时候,它们往往是某个给定集合的子集,这个给定的集合叫作全集,常用符号U表示.全集包含所要研究的这些集合.
2.补集
概念 设U是全集,A是U的一个子集(即A U),则由U中所有不属于A的元素组成的集合,叫作U中子集A的补集,记作 UA
符号表示 UA={x|x∈U,且x A}
图形表示
性质 对任何集合A,有A∪( UA)= ,A∩( UA)= , U( UA)=
U
A
名师点睛
1.全集不是固定不变的,它是一个相对概念,是依据具体问题来选择的.
2.补集是相对于全集而言的,它与全集不可分割.一方面,若没有定义全集,则不存在补集的说法;另一方面,补集的元素一定都能在全集中找到.
3.补集既是集合之间的一种关系,也是集合之间的一种运算.求集合A的补集的前提是A为全集U的子集,随着所选全集的不同,得到的补集也是不同的.
4.符号 UA有三层意思:①A是U的一个子集,即A U;② UA表示一个集合,且 UA U;③ UA是由U中不属于A的所有元素组成的集合,即 UA={x|x∈U,且x A}.
5.若x∈U,则x∈A或x∈ UA,二者必居其一.
思考辨析
1.全集一定包含任何元素吗
2.一个确定集合的补集唯一吗
3.一个集合A的补集中的元素具有什么特征
提示 不一定.全集不是固定的,它是相对而言的.只要包含所研究问题中涉及的所有元素即可.
提示 由于补集是相对于某一个全集的补集,因此对于一个确定的集合来说,全集不同时,该集合的补集也不相同.
提示 一个集合A的补集它包含两个方面:一是该集合是全集的子集,二是该集合中的元素属于全集,但是不属于集合A.
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)设集合U={1,2,3,4,5},A={1,2},B={2,3,4},则 U(A∪B)={5}.( )
(2)同一个集合在不同的全集中的补集不同.( )
(3)不同的集合在同一个全集中的补集可能相同.( )
√
√
×
2.若全集U=R,集合A={x|x≥1},则 UA= .
{x|x<1}
解析 由补集的定义可得 UA={x|x<1}.
3.[2024浙江温州高一阶段检测]已知全集U={2,3,a2+2a+2},集合A={2,3}, UA={5},则实数a的值为 .
1或-3
解析 由题可得a2+2a+2=5,解得a=1或a=-3,
所以实数a的值为1或-3.
4.[人教A版教材例题]设全集U={x|x是三角形},A={x|x是锐角三角形},B={x|x是钝角三角形},求A∩B, U(A∪B).
解 根据三角形的分类可知A∩B= ,A∪B={x|x是锐角三角形或钝角三角形}, U(A∪B)={x|x是直角三角形}.
5.[人教A版教材习题]图中U是全集,A,B是U的两个子集,用阴影表示:
(1)( UA)∩( UB);(2)( UA)∪( UB).
(1)
(2)
解 如图所示.
(1)
(2)
重难探究·能力素养速提升
探究点一 补集的基本运算
【例1】 (1)已知全集为U,集合A={1,3,5,7}, UA={2,4,6}, UB={1,4,6},则集合B= .
{2,3,5,7}
解析(方法一)∵A={1,3,5,7}, UA={2,4,6},
∴U={1,2,3,4,5,6,7}.
又 UB={1,4,6},∴B={2,3,5,7}.
(方法二)满足题意的Venn图如图所示.
由图可知B={2,3,5,7}.
(2)已知全集U={x|x≤5},集合A={x|-3≤x<5},则 UA= .
{x|x<-3,或x=5}
解析将全集U和集合A分别表示在数轴上,如图所示.
由补集的定义可知 UA={x|x<-3,或x=5}.
规律方法 求集合的补集的方法
变式训练1(1)[2024河南开封高一月考](多选题)已知全集U=Z,集合A={x∈Z|2x+1≥0},B={-1,0,1,2},则( )
A.A∩B={0,1,2}
B.A∪B={x|x≥0}
C.( UA)∩B={-1}
D.A∩B的真子集个数是7
ACD
★(2)已知全集为U,集合A={x|-3≤x<5}, UA={x|x≥5},B={x|1
解 由已知U={x|-3≤x<5}∪{x|x≥5}={x|x≥-3},又B={x|1
探究点二 交集、并集与补集的混合运算
【例2】 (1)已知全集U={x∈Z|0
C. U(M∪N) D.( UM)∩N
C
解析 ∵全集U={x∈Z|0
解 将集合U,A,B分别表示在数轴上,如图所示,
则 UA={x|-1≤x≤3},
UB={x|-5≤x<-1,或1≤x≤3},
所以( UA)∩( UB)={x|1≤x≤3}.
规律方法 求集合的交、并、补集运算的方法
变式训练2(1)如果全集U=R,M={x|-1
C.(-1,1)∪(1,2] D.(-1,2]
C
解析 UN={x|x≠1,且x≠3,且x≠5},
∴M∩( UN)=(-1,1)∪(1,2].
(2)已知全集为R,A={x|3≤x<7},B={x|2
由图知,A∪B={x|2
∵ RA={x|x<3,或x≥7},
∴( RA)∩B={x|2
【例3】 已知全集为R,集合A={x|x
解析 ∵B={x|1
又A={x|x
变式训练3已知集合A={x|x2+ax+12b=0}和B={x|x2-ax+b=0},满足B∩( UA)={2},A∩( UB)={4},U=R,求实数a,b的值.
解 ∵B∩( UA)={2},∴2∈B,但2 A.
∵A∩( UB)={4},∴4∈A,但4 B.
探究点四 补集思想的应用
【例4】 已知集合A={x|0≤x≤2},B={x|a≤x≤a+3}.
(1)若( RA)∪B≠R,求实数a的取值范围;
(2)若A∩B≠A,求实数a的取值范围.
解 (1)∵A={x|0≤x≤2},
∴ RA=|x|x<0,或x>2}.
假设( RA)∪B=R,如图所示.
∴a≤0,且a+3≥2,即a≤0,且a≥-1,∴满足( RA)∪B≠R的实数a的取值范围是{a|a<-1,或a>0}.
(2)假设A∩B=A,则A B,又A≠ ,
∴满足A∩B≠A的实数a的取值范围为{a|a<-1,或a>0}.
规律方法 有些数学问题,若直接从正面解决,若解题思路不明朗,或需要考虑的因素太多,可用补集思想考虑其对立面,即从结论的反面去思考,探索已知和未知之间的关系,从而化繁为简,化难为易,开拓解题思路,这就是补集思想的应用.
(1)运用补集思想求参数范围的方法:
①否定已知条件考虑反面问题;
②求解反面问题对应的参数范围;
③将反面问题对应的参数范围取补集,得到原问题的解.
(2)补集思想适用的情况:从正面考虑情况较多、问题较复杂的时候,往往考虑运用补集思想.
变式训练4已知集合A={x|x<-6,或x>3},B={x|k-1≤x-1≤k},若A∩B≠ ,求k的取值范围.
解 由已知可得B={x|k≤x≤k+1},
令P={k|-6≤k≤2},则 RP={k|k<-6,或k>2},
所以满足A∩B≠ 的k的取值范围是{k|k<-6,或k>2}.
本节要点归纳
1.知识清单:
(1)全集和补集的概念及运算;
(2)并、交、补集的混合运算;
(3)与补集有关的参数的求解.
2.方法归纳:正难则反的补集思想、数形结合.
3.常见误区:求补集时忽视全集,运算时易忽视端点的取舍.
学以致用·随堂检测促达标
1
2
3
4
5
1.已知全集U={-1,0,1,3,6},A={0,6},则 UA=( )
A.{-1,3} B.{-1,1,3}
C.{0,1,3} D.{0,3,6}
B
解析 ∵全集U={-1,0,1,3,6},A={0,6},
∴ UA={-1,1,3}.
1
2
3
4
5
2.(多选题)已知全集U=R,集合A={x|1≤x≤3,或4
B. UB={x|x<2,或x≥5}
C.A∩( UB)={x|1≤x<2,或5≤x<6}
D.( UA)∪B={x|x<1,或2≤x<5,或x>6}
BC
解析 在数轴上表示出集合A,B,如图,
UA={x|x<1,或3
1
2
3
4
5
1
2
3
4
5
3.[2024江苏南通期中]已知全集U和集合A,B如图所示,则( UA)∩B= .
{5,6}
解析 由题中的Venn图知( UA)∩B={5,6}.
1
2
3
4
5
4.已知全集U=R,A={x|1≤x
解析 ∵ UA={x|x<1,或x≥2},
∴A={x|1≤x<2}.∴b=2.
1
2
3
4
5
5.已知全集U=R,A={x|-4≤x<2},B={x|-1
解 将集合A,B,P分别表示在数轴上,如图所示.
∵A={x|-4≤x<2},B={x|-1
1
2
3
4
5
本 课 结 束
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
