第1章 3.1 不等式的性质--北师大版高中数学必修第一册课件(共37页PPT)
文档属性
| 名称 | 第1章 3.1 不等式的性质--北师大版高中数学必修第一册课件(共37页PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 00:00:00 | ||
图片预览











文档简介
(共37张PPT)
第一章
3.1 不等式的性质
基础落实·必备知识一遍过
重难探究·能力素养速提升
学以致用·随堂检测促达标
目录索引
课程标准 1.能够用作差法比较两个数或式的大小.
2.理解不等式的概念,掌握不等式的性质.
3.会用不等式的性质证明不等式或解决相关问题.
基础落实·必备知识一遍过
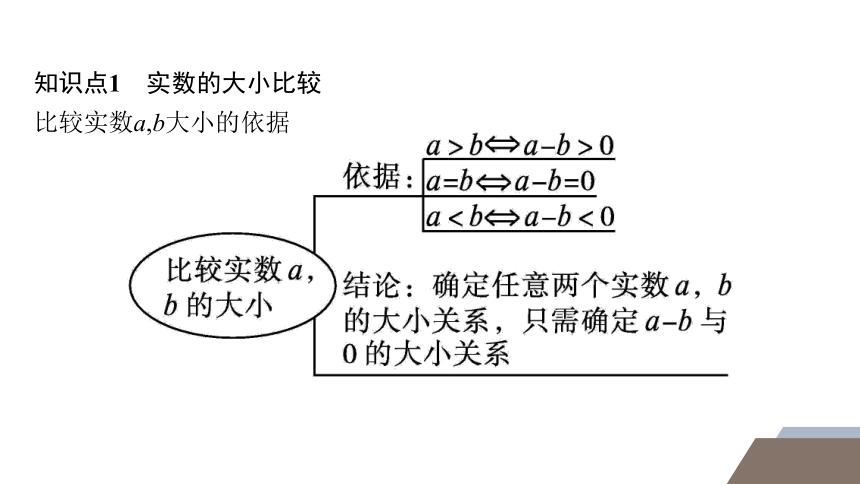
知识点1 实数的大小比较
比较实数a,b大小的依据
思考辨析
如果给定实数a与b,那么如何比较它们的大小呢
提示 通常是通过判断它们的差(a-b)的符号来比较它们的大小.当a与b同号且都不为0时,也可通过它们的商与1的大小关系来比较它们的大小.
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)比较两个代数式的大小只能用作差法.( )
(2)不等式x≥3的含义是指x不小于3.( )
(3)若a2.[人教A版教材习题]比较(x+2)(x+3)和(x+1)(x+4)的大小.
×
√
√
解 因为(x+2)(x+3)-(x+1)(x+4)=(x2+5x+6)-(x2+5x+4)=2>0,
所以(x+2)(x+3)>(x+1)(x+4).
知识点2 不等式的性质
名称 表达式
性质1(传递性) 如果a>b,且b>c,那么a>c
性质2(可加性) 如果a>b,那么a+c>b+c(c∈R)
性质3(乘法法则) 如果a>b,c>0,那么ac>bc;
如果a>b,c<0,那么ac性质4(同向不等式可加性) 如果a>b,c>d,那么a+c>b+d
性质5(不等式的可乘性) 如果a>b>0,c>d>0,那么ac>bd;
如果a>b>0,c乘方法则:当a>b>0时,an>bn,其中n∈N+,n≥2
性质6(开方法则) 当a>b>0时, ,其中n∈N+,n≥2
名师点睛
1.注意“等式”与“不等式”的异同,如:
等式 不等式 说明
a=b b=a a>b ba=b ac=bc(c≠0) a>b ac>bc或ac2.要注意各个不等式成立的前提,如性质4中两个不等式方向要相同,性质3中要按c的正负分情况.
3.由性质2,可得a+b>c a+b+(-b)>c+(-b) a>c-b,即不等式中任何一项可以改变符号后移到不等号的另一边,称为移项法则,在解不等式时经常用到.
4.倒数法则:
如果a>b,ab>0,那么 ,结论成立的条件是a,b要同号.
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)若a>b,则a-c>b-c.( )
(2) >1 a>b.( )
(3)若a>b且c>d,则a-c>b-d.( )
(4)若ac2>bc2,则a>b.( )
√
×
×
√
2.[2024北京丰台高一期末]下列说法正确的是( )
A.若a>b,则ac2>bc2
B.若a>b,c>d,则a+c>b+d
C.若a>b,c>d,则ac>bd
B
解析 当a>b,c=0时,ac2=bc2,故A错误;当a>b,c>d时,a+c>b+d,故B正确;当a=2,b=1,c=-1,d=-2时,a>b,c>d,ac=bd,故C错误;当b=2,a=1,c=1时,
故D错误.故选B.
3.[人教A版教材习题]用不等号“>”或“<”填空:
(1)如果a>b,c(2)如果a>b>0,c>
<
<
<
解析 (1)因为c-d.因为a>b,所以a-c>b-d.
(2)因为c-d>0.
因为a>b>0,所以-ac>-bd,所以ac重难探究·能力素养速提升
探究点一 实数大小的比较
【例1】 比较下列各组中的两个代数式的大小:
(1)2x2+3与x+2,x∈R;
(2)a+2与 ,a∈R,且a≠1.
规律方法 作差法是比较两个代数式大小的基本方法,一般步骤是:(1)作差;(2)变形,变形的常用方法有配方、因式分解、分母有理化等;(3)定号,即确定差的符号;(4)下结论,写出两个代数式的大小关系.
变式训练1[2024广东广州高一期末]求解下列问题:
(1)已知a∈R,比较(a+3)(a+7)和(a+4)(a+6)的大小;
解 (1)因为(a+3)(a+7)-(a+4)(a+6)=a2+10a+21-a2-10a-24=-3<0,
所以(a+3)(a+7)<(a+4)(a+6).
(2)已知x探究点二 不等式基本性质的应用
角度1应用不等式性质判断命题真假
【例2-1】 对于实数a,b,c,判断下列结论是否正确:
(1)若a>b,则ac2>bc2;
(2)若aab>b2;
(3)若c>a>b>0,则
解 (1)当c=0时,有ac2=bc2.故该结论错误.
规律方法 1.解决这类问题时,通常有两种方法:一是直接利用不等式的性质进行推理,看根据条件能否推出相应的不等式;二是采用取特殊值的方法,判断所给的不等式是否成立,尤其是在选择题中经常采用这种办法.
2.注意正确的倒数法则,应该是a>b,ab>0 ,不能误认为是a>b
在应用时不能出错.
变式训练2已知a,b,c满足cC
角度2应用不等式性质证明不等式
【例2-2】 若a>b>0,c∵a>b>0,c0,c+d<0,b-a<0,c-d<0.
∴(a+b)-(c+d)>0,(b-a)+(c-d)<0.
∵e<0,∴e[(a+b)-(c+d)][(b-a)+(c-d)]>0.
(方法二)∵c-d>0,又a>b>0,∴a-c>b-d>0,∴(a-c)2>(b-d)2>0,
规律方法 1.简单不等式的证明可直接由已知条件,利用不等式的性质,通过对不等式变形得证.
2.对于不等式两边都比较复杂的式子,直接利用不等式的性质不易证得,可考虑将不等式两边作差,然后进行变形,根据条件确定每一个因式的符号,利用符号法则判断最终的符号,完成证明.
变式训练3(1)[人教B版教材习题]求证:如果a>b,c<0,那么ac证明 ac-bc=(a-b)c.
因为a>b,所以a-b>0.
又c<0,所以(a-b)c<0,所以ac-bc<0,即ac角度3利用不等式性质求取值范围
【例2-3】 如果3解 因为3所以3+1故a+b的取值范围为(4,17).
又因为9<3a<21,-20<-2b<-2,
所以-11<3a-2b<19.
故3a-2b的取值范围为(-11,19).
规律方法 利用不等式的性质可以解决取值范围问题,当题目中出现两个变量求取值范围时,要注意两个变量是相互制约的,不能分割开来,应建立待求整体与已知变量之间的关系,然后根据不等式的性质求出取值范围.
变式训练4已知-4≤a-b≤-1,-1≤4a-b≤5,求9a-b的取值范围.
解 设9a-b=x(a-b)+y(4a-b),则9a-b=(x+4y)a-(x+y)b,
即-1≤9a-b≤20.故9a-b的取值范围为[-1,20].
本节要点归纳
1.知识清单:
(1)不等式的性质;
(2)不等式的性质的应用.
2.方法归纳:作差法、配方法.
3.常见误区:注意不等式性质的单向性或双向性,即每条性质是否具有可逆性.
学以致用·随堂检测促达标
1
2
3
4
1.(多选题)已知a,b,c∈R,则下列结论不正确的是( )
ABD
1
2
3
4
2.(x+5)(x+7) (x+6)2.(填“>”“<”“≥”或“≤”)
<
解析 (x+5)(x+7)-(x+6)2=x2+12x+35-(x2+12x+36)=-1<0,所以(x+5)(x+7)<(x+6)2.
1
2
3
4
3.已知1≤a≤2,3≤b≤6,则3a-2b的取值范围为 .
[-9,0]
解析 ∵1≤a≤2,3≤b≤6,∴3≤3a≤6,-12≤-2b≤-6,由不等式的性质得-9≤3a-2b≤0,即3a-2b的取值范围为[-9,0].
1
2
3
4
本 课 结 束
第一章
3.1 不等式的性质
基础落实·必备知识一遍过
重难探究·能力素养速提升
学以致用·随堂检测促达标
目录索引
课程标准 1.能够用作差法比较两个数或式的大小.
2.理解不等式的概念,掌握不等式的性质.
3.会用不等式的性质证明不等式或解决相关问题.
基础落实·必备知识一遍过
知识点1 实数的大小比较
比较实数a,b大小的依据
思考辨析
如果给定实数a与b,那么如何比较它们的大小呢
提示 通常是通过判断它们的差(a-b)的符号来比较它们的大小.当a与b同号且都不为0时,也可通过它们的商与1的大小关系来比较它们的大小.
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)比较两个代数式的大小只能用作差法.( )
(2)不等式x≥3的含义是指x不小于3.( )
(3)若a
×
√
√
解 因为(x+2)(x+3)-(x+1)(x+4)=(x2+5x+6)-(x2+5x+4)=2>0,
所以(x+2)(x+3)>(x+1)(x+4).
知识点2 不等式的性质
名称 表达式
性质1(传递性) 如果a>b,且b>c,那么a>c
性质2(可加性) 如果a>b,那么a+c>b+c(c∈R)
性质3(乘法法则) 如果a>b,c>0,那么ac>bc;
如果a>b,c<0,那么ac
性质5(不等式的可乘性) 如果a>b>0,c>d>0,那么ac>bd;
如果a>b>0,c
性质6(开方法则) 当a>b>0时, ,其中n∈N+,n≥2
名师点睛
1.注意“等式”与“不等式”的异同,如:
等式 不等式 说明
a=b b=a a>b ba=b ac=bc(c≠0) a>b ac>bc或ac
3.由性质2,可得a+b>c a+b+(-b)>c+(-b) a>c-b,即不等式中任何一项可以改变符号后移到不等号的另一边,称为移项法则,在解不等式时经常用到.
4.倒数法则:
如果a>b,ab>0,那么 ,结论成立的条件是a,b要同号.
自主诊断
1.判断正误.(正确的画√,错误的画×)
(1)若a>b,则a-c>b-c.( )
(2) >1 a>b.( )
(3)若a>b且c>d,则a-c>b-d.( )
(4)若ac2>bc2,则a>b.( )
√
×
×
√
2.[2024北京丰台高一期末]下列说法正确的是( )
A.若a>b,则ac2>bc2
B.若a>b,c>d,则a+c>b+d
C.若a>b,c>d,则ac>bd
B
解析 当a>b,c=0时,ac2=bc2,故A错误;当a>b,c>d时,a+c>b+d,故B正确;当a=2,b=1,c=-1,d=-2时,a>b,c>d,ac=bd,故C错误;当b=2,a=1,c=1时,
故D错误.故选B.
3.[人教A版教材习题]用不等号“>”或“<”填空:
(1)如果a>b,c
<
<
<
解析 (1)因为c
(2)因为c
因为a>b>0,所以-ac>-bd,所以ac
探究点一 实数大小的比较
【例1】 比较下列各组中的两个代数式的大小:
(1)2x2+3与x+2,x∈R;
(2)a+2与 ,a∈R,且a≠1.
规律方法 作差法是比较两个代数式大小的基本方法,一般步骤是:(1)作差;(2)变形,变形的常用方法有配方、因式分解、分母有理化等;(3)定号,即确定差的符号;(4)下结论,写出两个代数式的大小关系.
变式训练1[2024广东广州高一期末]求解下列问题:
(1)已知a∈R,比较(a+3)(a+7)和(a+4)(a+6)的大小;
解 (1)因为(a+3)(a+7)-(a+4)(a+6)=a2+10a+21-a2-10a-24=-3<0,
所以(a+3)(a+7)<(a+4)(a+6).
(2)已知x
角度1应用不等式性质判断命题真假
【例2-1】 对于实数a,b,c,判断下列结论是否正确:
(1)若a>b,则ac2>bc2;
(2)若a
(3)若c>a>b>0,则
解 (1)当c=0时,有ac2=bc2.故该结论错误.
规律方法 1.解决这类问题时,通常有两种方法:一是直接利用不等式的性质进行推理,看根据条件能否推出相应的不等式;二是采用取特殊值的方法,判断所给的不等式是否成立,尤其是在选择题中经常采用这种办法.
2.注意正确的倒数法则,应该是a>b,ab>0 ,不能误认为是a>b
在应用时不能出错.
变式训练2已知a,b,c满足c
角度2应用不等式性质证明不等式
【例2-2】 若a>b>0,c
∴(a+b)-(c+d)>0,(b-a)+(c-d)<0.
∵e<0,∴e[(a+b)-(c+d)][(b-a)+(c-d)]>0.
(方法二)∵c
规律方法 1.简单不等式的证明可直接由已知条件,利用不等式的性质,通过对不等式变形得证.
2.对于不等式两边都比较复杂的式子,直接利用不等式的性质不易证得,可考虑将不等式两边作差,然后进行变形,根据条件确定每一个因式的符号,利用符号法则判断最终的符号,完成证明.
变式训练3(1)[人教B版教材习题]求证:如果a>b,c<0,那么ac
因为a>b,所以a-b>0.
又c<0,所以(a-b)c<0,所以ac-bc<0,即ac
【例2-3】 如果3
又因为9<3a<21,-20<-2b<-2,
所以-11<3a-2b<19.
故3a-2b的取值范围为(-11,19).
规律方法 利用不等式的性质可以解决取值范围问题,当题目中出现两个变量求取值范围时,要注意两个变量是相互制约的,不能分割开来,应建立待求整体与已知变量之间的关系,然后根据不等式的性质求出取值范围.
变式训练4已知-4≤a-b≤-1,-1≤4a-b≤5,求9a-b的取值范围.
解 设9a-b=x(a-b)+y(4a-b),则9a-b=(x+4y)a-(x+y)b,
即-1≤9a-b≤20.故9a-b的取值范围为[-1,20].
本节要点归纳
1.知识清单:
(1)不等式的性质;
(2)不等式的性质的应用.
2.方法归纳:作差法、配方法.
3.常见误区:注意不等式性质的单向性或双向性,即每条性质是否具有可逆性.
学以致用·随堂检测促达标
1
2
3
4
1.(多选题)已知a,b,c∈R,则下列结论不正确的是( )
ABD
1
2
3
4
2.(x+5)(x+7) (x+6)2.(填“>”“<”“≥”或“≤”)
<
解析 (x+5)(x+7)-(x+6)2=x2+12x+35-(x2+12x+36)=-1<0,所以(x+5)(x+7)<(x+6)2.
1
2
3
4
3.已知1≤a≤2,3≤b≤6,则3a-2b的取值范围为 .
[-9,0]
解析 ∵1≤a≤2,3≤b≤6,∴3≤3a≤6,-12≤-2b≤-6,由不等式的性质得-9≤3a-2b≤0,即3a-2b的取值范围为[-9,0].
1
2
3
4
本 课 结 束
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
