河南省伊川县实验高中人教版高中数学选修2-2学案:1.7.1定积分在几何中的应用(无答案)
文档属性
| 名称 | 河南省伊川县实验高中人教版高中数学选修2-2学案:1.7.1定积分在几何中的应用(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 83.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-29 00:00:00 | ||
图片预览

文档简介
课题
1.7定积分在几何中的简单应用高二数学
李冰锋
课型
新授
教
学
过
程
师
生
活
动
一.知识回顾1、求曲边梯形的思想方法是什么?2、定积分的几何意义是什么?3、微积分基本定理是什么?二.新知探究(一)利用定积分求平面图形的面积例1.计算由两条抛物线和所围成的图形的面积.【分析】两条抛物线所围成的图形的面积,可以由以两条曲线所对应的曲边梯形的面积的差得到。
解:,所以两曲线的交点为(0,0)、(1,1),面积S=,所以=
【点评】在直角坐标系下平面图形的面积的四个步骤:1.作图象;2.求交点;3.用定积分表示所求的面积;4.微积分基本定理求定积分。练习:计算由曲线和所围成的图形的面积.例2.计算由直线,曲线以及x轴所围图形的面积S.分析:首先画出草图,并设法把所求图形的面积问题转化为求曲边梯形的面积问题.与例
1
不同的是,还需把所求图形的面积分成两部分S1和S2.为了确定出被积函数和积分的上、下限,需要求出直线与曲线的交点的横坐标,直线与
x
轴的交点.
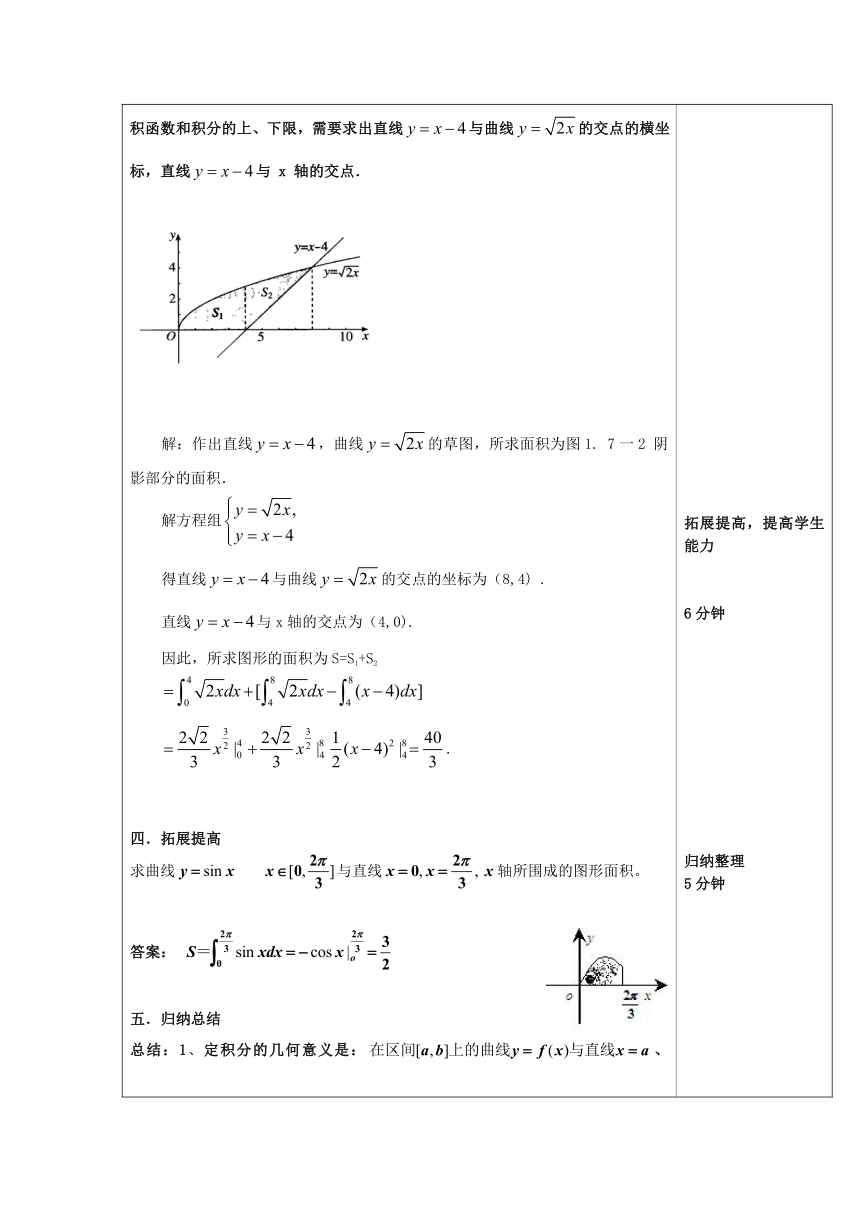
( http: / / www.21cnjy.com )解:作出直线,曲线的草图,所求面积为图1.
7一2
阴影部分的面积.解方程组得直线与曲线的交点的坐标为(8,4)
.
直线与x轴的交点为(4,0).
因此,所求图形的面积为S=S1+S2.四.拓展提高求曲线与直线轴所围成的图形面积。答案:
五.归纳总结总结:1、定积分的几何意义是:、轴所围成的图形的面积的代数和,即.因此求一些曲边图形的面积要可以利用定积分的几何意义以及微积分基本定理,但要特别注意图形面积与定积分不一定相等,如函数的图像与轴围成的图形的面积为4,而其定积分为0.2、求曲边梯形面积的方法与步骤:画图,并将图形分割为若干个曲边梯形;对每个曲边梯形确定其存在的范围,从而确定积分的上、下限;确定被积函数;求出各曲边梯形的面积和,即各积分的绝对值的和。3、几种常见的曲边梯形面积的计算方法:型区域:①由一条曲线与直线以及轴所围成的曲边梯形的面积:(如图(1));②由一条曲线与直线以及轴所围成的曲边梯形的面积:(如图(2));③由两条曲线与直线图(1)
图(2)
图(3)所围成的曲边梯形的面积:(如图(3));六.作业设计1、必做题:P58练习(1)(2);P60A组1;2、选做题:P60B组3。七.精彩一练1、求直线与抛物线所围成的图形面积。2、求由抛物线及其在点M(0,-3)和N(3,0)处的两条切线所围成的图形的面积。
八.学后反思
回顾前面所学知识加深理解3分钟学生自学、探究,分组讨论、交流,归纳几何意义。8分钟5分钟动手实践注意强调用步骤方法。在利用定积分求平面图形的面积时,一般要先画出它的草图,再借助图形直观确定出被积函数以及积分的上、下限10分钟拓展提高,提高学生能力6分钟归纳整理5分钟分层要求8分钟应用整合,强化新知。
板书设计
一、知识回顾
三、求曲边梯形面积的方法与步骤:
二、例题讲解:
四、作业布置
例1:
1、必做题:P58练习(1)(2);P60A组1;
2、选做题:P60B组3。
例2:
A
B
C
D
O
y
a
b
x
y
a
b
x
y
a
b
x
x
y
o
y=-x2+4x-3
1.7定积分在几何中的简单应用高二数学
李冰锋
课型
新授
教
学
过
程
师
生
活
动
一.知识回顾1、求曲边梯形的思想方法是什么?2、定积分的几何意义是什么?3、微积分基本定理是什么?二.新知探究(一)利用定积分求平面图形的面积例1.计算由两条抛物线和所围成的图形的面积.【分析】两条抛物线所围成的图形的面积,可以由以两条曲线所对应的曲边梯形的面积的差得到。
解:,所以两曲线的交点为(0,0)、(1,1),面积S=,所以=
【点评】在直角坐标系下平面图形的面积的四个步骤:1.作图象;2.求交点;3.用定积分表示所求的面积;4.微积分基本定理求定积分。练习:计算由曲线和所围成的图形的面积.例2.计算由直线,曲线以及x轴所围图形的面积S.分析:首先画出草图,并设法把所求图形的面积问题转化为求曲边梯形的面积问题.与例
1
不同的是,还需把所求图形的面积分成两部分S1和S2.为了确定出被积函数和积分的上、下限,需要求出直线与曲线的交点的横坐标,直线与
x
轴的交点.
( http: / / www.21cnjy.com )解:作出直线,曲线的草图,所求面积为图1.
7一2
阴影部分的面积.解方程组得直线与曲线的交点的坐标为(8,4)
.
直线与x轴的交点为(4,0).
因此,所求图形的面积为S=S1+S2.四.拓展提高求曲线与直线轴所围成的图形面积。答案:
五.归纳总结总结:1、定积分的几何意义是:、轴所围成的图形的面积的代数和,即.因此求一些曲边图形的面积要可以利用定积分的几何意义以及微积分基本定理,但要特别注意图形面积与定积分不一定相等,如函数的图像与轴围成的图形的面积为4,而其定积分为0.2、求曲边梯形面积的方法与步骤:画图,并将图形分割为若干个曲边梯形;对每个曲边梯形确定其存在的范围,从而确定积分的上、下限;确定被积函数;求出各曲边梯形的面积和,即各积分的绝对值的和。3、几种常见的曲边梯形面积的计算方法:型区域:①由一条曲线与直线以及轴所围成的曲边梯形的面积:(如图(1));②由一条曲线与直线以及轴所围成的曲边梯形的面积:(如图(2));③由两条曲线与直线图(1)
图(2)
图(3)所围成的曲边梯形的面积:(如图(3));六.作业设计1、必做题:P58练习(1)(2);P60A组1;2、选做题:P60B组3。七.精彩一练1、求直线与抛物线所围成的图形面积。2、求由抛物线及其在点M(0,-3)和N(3,0)处的两条切线所围成的图形的面积。
八.学后反思
回顾前面所学知识加深理解3分钟学生自学、探究,分组讨论、交流,归纳几何意义。8分钟5分钟动手实践注意强调用步骤方法。在利用定积分求平面图形的面积时,一般要先画出它的草图,再借助图形直观确定出被积函数以及积分的上、下限10分钟拓展提高,提高学生能力6分钟归纳整理5分钟分层要求8分钟应用整合,强化新知。
板书设计
一、知识回顾
三、求曲边梯形面积的方法与步骤:
二、例题讲解:
四、作业布置
例1:
1、必做题:P58练习(1)(2);P60A组1;
2、选做题:P60B组3。
例2:
A
B
C
D
O
y
a
b
x
y
a
b
x
y
a
b
x
x
y
o
y=-x2+4x-3
