北师大版五年级上册数学总复习1数与代数(课件)(共26张PPT)
文档属性
| 名称 | 北师大版五年级上册数学总复习1数与代数(课件)(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 776.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-27 07:39:32 | ||
图片预览




文档简介
(共26张PPT)
数与代数
北师大版 数学 五年级上册 总复习
小数除法
倍数和因数
分数的意义
鸡兔同笼
2课时
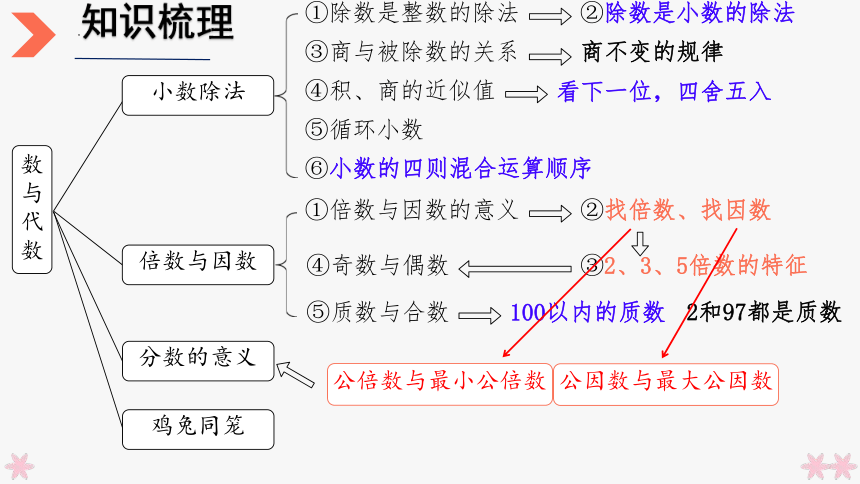
知识梳理
数
与
代
数
小数除法
倍数与因数
分数的意义
鸡兔同笼
①除数是整数的除法
②除数是小数的除法
④积、商的近似值
⑤循环小数
⑥小数的四则混合运算顺序
③商与被除数的关系
商不变的规律
看下一位,四舍五入
①倍数与因数的意义
②找倍数、找因数
③2、3、5倍数的特征
④奇数与偶数
⑤质数与合数
100以内的质数
2和97都是质数
公因数与最大公因数
公倍数与最小公倍数
商不变规律
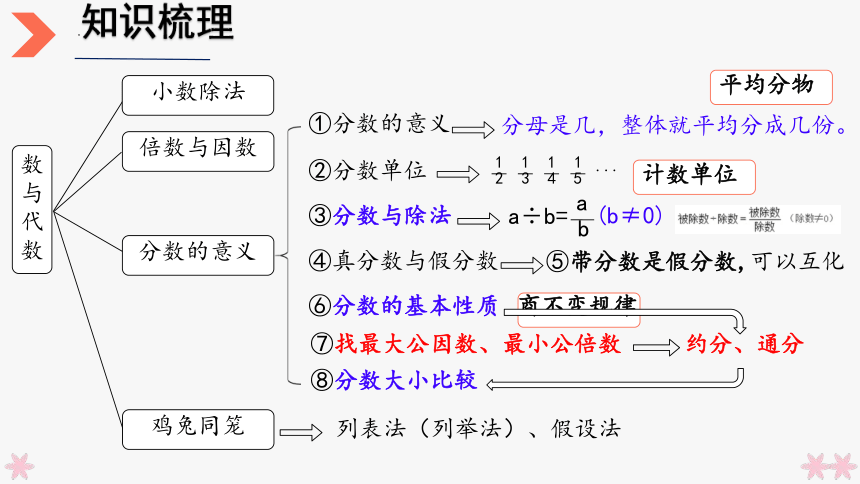
知识梳理
数
与
代
数
小数除法
倍数与因数
分数的意义
鸡兔同笼
①分数的意义
平均分物
分母是几,整体就平均分成几份。
②分数单位
1
2
1
3
1
4
1
5
...
计数单位
③分数与除法
a÷b=
a
b
(b≠0)
④真分数与假分数
⑤带分数是假分数,可以互化
⑥分数的基本性质
约分、通分
⑦找最大公因数、最小公倍数
⑧分数大小比较
列表法(列举法)、假设法
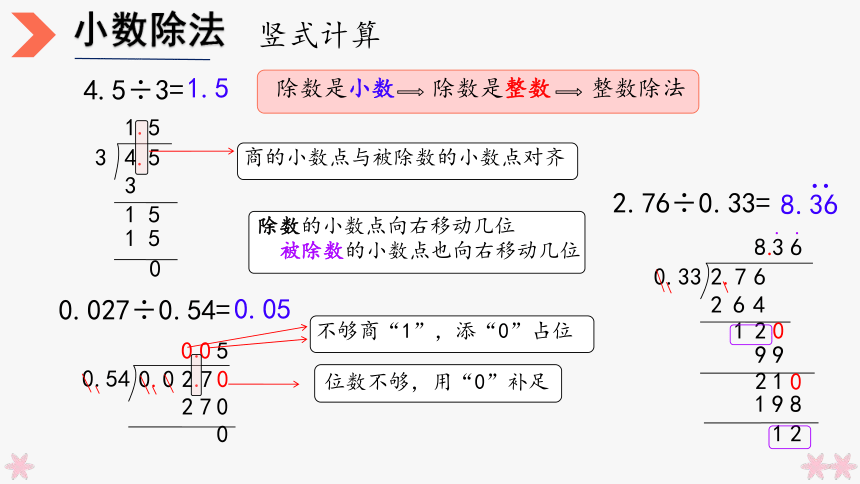
小数除法
竖式计算
4.5÷3=
0.027÷0.54=
2.76÷0.33=
1.5
0.05
8.36
除数是小数
除数是整数
整数除法
4.5
3
1
3
5
.
1
5
1
5
0
商的小数点与被除数的小数点对齐
除数的小数点向右移动几位
被除数的小数点也向右移动几位
位数不够,用“0”补足
0
2
0
.
0
0.0 2 7
0.54
.
0
5
7
0
不够商“1”,添“0”占位
2.7 6
0.33
8
2
3
. .
1
2
1
6
0
6
4
1
9
9
2
1
0
9
8
2
.
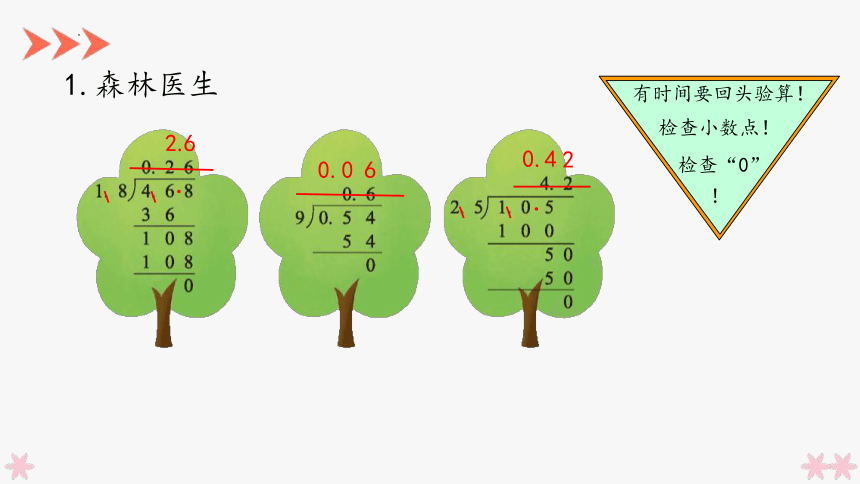
1.森林医生
.
2.
6
0.
0
6
.
0.
4
2
有时间要回头验算!
检查小数点!
检查“0”
!
小数除法
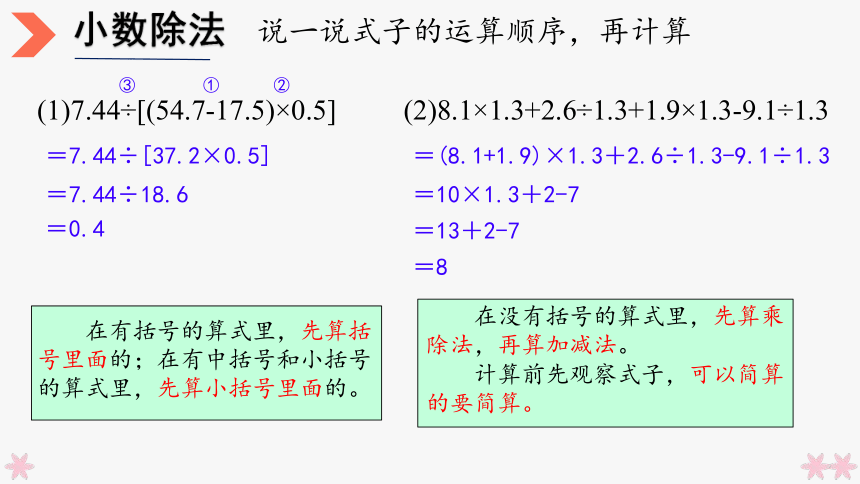
(1)7.44÷[(54.7-17.5)×0.5]
说一说式子的运算顺序,再计算
(2)8.1×1.3+2.6÷1.3+1.9×1.3-9.1÷1.3
①
②
③
=7.44÷[37.2×0.5]
=7.44÷18.6
=0.4
在有括号的算式里,先算括号里面的;在有中括号和小括号的算式里,先算小括号里面的。
在没有括号的算式里,先算乘除法,再算加减法。
计算前先观察式子,可以简算的要简算。
=(8.1+1.9)×1.3+2.6÷1.3-9.1÷1.3
=10×1.3+2-7
=13+2-7
=8
2.脱式计算(易错)
4.8+5.2÷5
78÷0.25÷0.4
=4.8+1.04
=5.84
①
②
=78÷(0.25×0.4)
=78÷0.1
=780
a÷b÷c=a÷(b×c)=a÷c÷b
除法的性质:
一个数连续除以两个数,可以用这个数除以后两个数的积,也可以先除以第二个数,再除以第一个数。
小数除法
商与被除数的关系
关系一:
关系二:
商不变的规律
当除数小于1、等于1、大于1时
当除数<1时,商>被除数
当除数=1时,商=被除数
当除数>1时,商<被除数
填“<”、“=”或“>”
4.8÷0.12( )4.8
4.8÷1.2( )4.8
>
<
被除数和除数同时扩大或缩小相同的倍数,商不变
4.8÷0.12=( )÷1.2
172÷4=1.72÷( )
48
0.04
关系三:
当被除数不变或除数不变时
当被除数不变时,除数变大,商变小;除数变小,商变大。
填“<”、“=”或“>”
4.8÷0.12( )4.8÷1.2
0.66÷3( )6.6÷3
当除数不变时,被除数变大,商也变大;被除数变小,商也变小。
不管是关系几,始终是万变不离其宗:
被除数÷除数=商
>
<
倍数与因数
倍数与因数相互依存,不能单独说一个数是倍数或因数。
易错点1
1.判断
(1)在7×5=35中,35是倍数,7和5是因数。( )
(2)在7×5=35中,35是7和5的倍数,7和5是35的因数。( )
(3)在7×5=35中,35是7的倍数,5是35的因数。( )
×
√
√
要说“谁是谁的倍数,谁是谁的因数”
一个数的倍数是无限的,最小的倍数是这个数本身,没有最大的倍数;
一个数的因数是有限的,最大的因数是这个数本身,最小的因数是1。
易错点2
2.判断
(1)一个数的倍数是有限的。( )
(2)12的最小因数是2。( )
(3)一个数的因数一定比这个数的倍数小。( )
×
×
×
特殊的“0”
易错点3
0是整数;0是最小的自然数;0是偶数。
0既不是正数也不是负数
0和1既不是质数也不是合数
3.判断
一个自然数除以一个小数,所得的商肯定大于这个自然数。( )
在自然数中,既不是质数也不是合数的数只有1。( )
除了2以外,所有的偶数都是合数。( )
×
×
×
易错点4
2是最小的质数,是所有质数中唯一的偶数(偶质数)
91不是质数,97是质数。
4.填空
(1)最小的质数是( ),最小的合数是( )。
(2)在 1~20 各数中,奇数有( )个,偶数有( )个,质 数有( )个,合数有( )个,( )既不是质数也不 是合数。
(3)100以内,大于90的质数有( )个
2
4
10
10
8
12
1
1
2、3、5倍数的特征
2的倍数特征:
个位上是0,2,4,6,8
(偶数)
3的倍数特征:
各个数位上的数相加,它们的和是3的倍数。
14:
1+4=5
5不是3的倍数
→
14不是3的倍数
18:
1+8=9
9是3的倍数
→
18是3的倍数
10086:
1+0+0+8+6=15
1+5=6
→
6是3的倍数
→
10086是3的倍数
5的倍数特征:
个位上是0或5
既是2的倍数也是5的倍数:个位上的数是0
既是2的倍数也是3的倍数:满足3的倍数特征且是偶数
数的奇偶性
偶+偶=偶
奇+奇=偶
偶-偶=偶
奇-奇=偶
偶×奇=偶
偶×偶=偶
偶+奇=奇
偶-奇=奇
奇-偶=奇
奇×奇=奇
了解即可,方便做题
遇到时可以举例验证
→
4-1=3
分数的意义
除法
分数
被除数÷除数=商(除数≠0)
商不变规律
分数的基本性质
被除数和除数同时乘或除以相同的数(0除外)商不变
分子和分母同时乘或除以相同的数(0除外)分数的大小不变
分子÷分母= (分母≠0)
分母
分子
分子
分母
商=
分数的
基本性质
约分
通分
最简分数
24
18
最大公因数
=
24÷6
18÷6
=
4
3
18
24
2
9
12
3
3
4
互质,不能继续分解
18和24的最大公因数:
2×3=6
最小公倍数
分母相同
18
5
12
5
=
18×2
3×2
=
36
6
=
12×3
5×3
=
36
15
18 12
3
6
4
2
3
2
互质,不能继续分解
18和12的最小公倍数:
3×2×3×2=36
分数大小比较
分数大小比较
分数的大小比较
1.分母相同,分子大的分数就大
2.分母不相同,分子相同,分母小的分数就大
3.分母不相同,分子也不同,通分或约分成分母相同
18
5
18
7
7
8
7
4
<
>
分数单位相同
分数单位多的就大
5个
18
1
7个
18
1
8个
7
1
4个
7
1
6
5
8
5
7
4
3
4
4
3
5
4
12
8
18
6
>
<
分子相同,可以直接比较分数单位
分数单位不同,分母小的分数大
<
>
20
15
20
16
3
2
3
1
假分数与带分数互化
7
9
=
7
1×7+2
=
7
7
+
7
2
=
1
7
2
5
11
=
5
2×5+1
=
2
+
5
1
=
2
5
1
3
4
1
=
4
3×4+1
4
13
=
分数分为 和 两类
真分数
假分数
带分数是假分数的特殊形式
带分数>1
假分数≥1
练习巩固
1.(1)写出15,36的全部因数,并找出15和36的最大公因数。
(2)写出50以内3和8的全部倍数,并找出3和8的最小公倍数。
15的因数:1,15,3,5。
36的因数:1,36,2,18,3,12,4,9,6。
15和36的最大公因数:3。
50以内3的倍数:3,6,9,12,15,18,21,24,27,
30,33,36,39,42,45,48
50以内8的倍数:8,16,24,32,40,48。
3和8的最小公倍数:24。
2.把下面的数填入相应的类别。
8
25
28
10
90
45
17
100
97
2的倍数
3的倍数
5的倍数
质数
合数
3.连一连
?
把一个整体平均分成5份,其中的2份。
4.填一填
5
7
3
3
8
25
5.比较大小
<
>
>
<
6.如图,在上面的( )里填上适当的假分数,在下面的( ) 里填上适当的带分数。
5
7
2
5
4
5
11
5
15
3
5
3
5
23
4
5
3
7.(1)长是宽的几倍?
(2)宽是长的几分之几?
120cm
240cm
8.平均分给6个人,每人分到这袋糖果的几分之几?一袋糖果3kg,每人分到多少千克?
240÷120=2
120÷240=
1÷6=
3÷6=
(kg)
8.鸡和兔共有17个头,54只脚。问兔有多少只,鸡有多少只。
列表法:
1
16
2
3
4
5
6
7
15
14
13
12
11
10
66
64
62
60
58
56
54
假设法:
①假设笼子里都是鸡,就有:17×2=34(只)脚,
比实际少54-34=20(只)脚。
②那么需要用兔换鸡,一只兔比一只鸡多 4-2=2(只)脚, 有:20÷2=10(只)兔。
③所以有17-10=7(只)鸡。
数与代数
北师大版 数学 五年级上册 总复习
小数除法
倍数和因数
分数的意义
鸡兔同笼
2课时
知识梳理
数
与
代
数
小数除法
倍数与因数
分数的意义
鸡兔同笼
①除数是整数的除法
②除数是小数的除法
④积、商的近似值
⑤循环小数
⑥小数的四则混合运算顺序
③商与被除数的关系
商不变的规律
看下一位,四舍五入
①倍数与因数的意义
②找倍数、找因数
③2、3、5倍数的特征
④奇数与偶数
⑤质数与合数
100以内的质数
2和97都是质数
公因数与最大公因数
公倍数与最小公倍数
商不变规律
知识梳理
数
与
代
数
小数除法
倍数与因数
分数的意义
鸡兔同笼
①分数的意义
平均分物
分母是几,整体就平均分成几份。
②分数单位
1
2
1
3
1
4
1
5
...
计数单位
③分数与除法
a÷b=
a
b
(b≠0)
④真分数与假分数
⑤带分数是假分数,可以互化
⑥分数的基本性质
约分、通分
⑦找最大公因数、最小公倍数
⑧分数大小比较
列表法(列举法)、假设法
小数除法
竖式计算
4.5÷3=
0.027÷0.54=
2.76÷0.33=
1.5
0.05
8.36
除数是小数
除数是整数
整数除法
4.5
3
1
3
5
.
1
5
1
5
0
商的小数点与被除数的小数点对齐
除数的小数点向右移动几位
被除数的小数点也向右移动几位
位数不够,用“0”补足
0
2
0
.
0
0.0 2 7
0.54
.
0
5
7
0
不够商“1”,添“0”占位
2.7 6
0.33
8
2
3
. .
1
2
1
6
0
6
4
1
9
9
2
1
0
9
8
2
.
1.森林医生
.
2.
6
0.
0
6
.
0.
4
2
有时间要回头验算!
检查小数点!
检查“0”
!
小数除法
(1)7.44÷[(54.7-17.5)×0.5]
说一说式子的运算顺序,再计算
(2)8.1×1.3+2.6÷1.3+1.9×1.3-9.1÷1.3
①
②
③
=7.44÷[37.2×0.5]
=7.44÷18.6
=0.4
在有括号的算式里,先算括号里面的;在有中括号和小括号的算式里,先算小括号里面的。
在没有括号的算式里,先算乘除法,再算加减法。
计算前先观察式子,可以简算的要简算。
=(8.1+1.9)×1.3+2.6÷1.3-9.1÷1.3
=10×1.3+2-7
=13+2-7
=8
2.脱式计算(易错)
4.8+5.2÷5
78÷0.25÷0.4
=4.8+1.04
=5.84
①
②
=78÷(0.25×0.4)
=78÷0.1
=780
a÷b÷c=a÷(b×c)=a÷c÷b
除法的性质:
一个数连续除以两个数,可以用这个数除以后两个数的积,也可以先除以第二个数,再除以第一个数。
小数除法
商与被除数的关系
关系一:
关系二:
商不变的规律
当除数小于1、等于1、大于1时
当除数<1时,商>被除数
当除数=1时,商=被除数
当除数>1时,商<被除数
填“<”、“=”或“>”
4.8÷0.12( )4.8
4.8÷1.2( )4.8
>
<
被除数和除数同时扩大或缩小相同的倍数,商不变
4.8÷0.12=( )÷1.2
172÷4=1.72÷( )
48
0.04
关系三:
当被除数不变或除数不变时
当被除数不变时,除数变大,商变小;除数变小,商变大。
填“<”、“=”或“>”
4.8÷0.12( )4.8÷1.2
0.66÷3( )6.6÷3
当除数不变时,被除数变大,商也变大;被除数变小,商也变小。
不管是关系几,始终是万变不离其宗:
被除数÷除数=商
>
<
倍数与因数
倍数与因数相互依存,不能单独说一个数是倍数或因数。
易错点1
1.判断
(1)在7×5=35中,35是倍数,7和5是因数。( )
(2)在7×5=35中,35是7和5的倍数,7和5是35的因数。( )
(3)在7×5=35中,35是7的倍数,5是35的因数。( )
×
√
√
要说“谁是谁的倍数,谁是谁的因数”
一个数的倍数是无限的,最小的倍数是这个数本身,没有最大的倍数;
一个数的因数是有限的,最大的因数是这个数本身,最小的因数是1。
易错点2
2.判断
(1)一个数的倍数是有限的。( )
(2)12的最小因数是2。( )
(3)一个数的因数一定比这个数的倍数小。( )
×
×
×
特殊的“0”
易错点3
0是整数;0是最小的自然数;0是偶数。
0既不是正数也不是负数
0和1既不是质数也不是合数
3.判断
一个自然数除以一个小数,所得的商肯定大于这个自然数。( )
在自然数中,既不是质数也不是合数的数只有1。( )
除了2以外,所有的偶数都是合数。( )
×
×
×
易错点4
2是最小的质数,是所有质数中唯一的偶数(偶质数)
91不是质数,97是质数。
4.填空
(1)最小的质数是( ),最小的合数是( )。
(2)在 1~20 各数中,奇数有( )个,偶数有( )个,质 数有( )个,合数有( )个,( )既不是质数也不 是合数。
(3)100以内,大于90的质数有( )个
2
4
10
10
8
12
1
1
2、3、5倍数的特征
2的倍数特征:
个位上是0,2,4,6,8
(偶数)
3的倍数特征:
各个数位上的数相加,它们的和是3的倍数。
14:
1+4=5
5不是3的倍数
→
14不是3的倍数
18:
1+8=9
9是3的倍数
→
18是3的倍数
10086:
1+0+0+8+6=15
1+5=6
→
6是3的倍数
→
10086是3的倍数
5的倍数特征:
个位上是0或5
既是2的倍数也是5的倍数:个位上的数是0
既是2的倍数也是3的倍数:满足3的倍数特征且是偶数
数的奇偶性
偶+偶=偶
奇+奇=偶
偶-偶=偶
奇-奇=偶
偶×奇=偶
偶×偶=偶
偶+奇=奇
偶-奇=奇
奇-偶=奇
奇×奇=奇
了解即可,方便做题
遇到时可以举例验证
→
4-1=3
分数的意义
除法
分数
被除数÷除数=商(除数≠0)
商不变规律
分数的基本性质
被除数和除数同时乘或除以相同的数(0除外)商不变
分子和分母同时乘或除以相同的数(0除外)分数的大小不变
分子÷分母= (分母≠0)
分母
分子
分子
分母
商=
分数的
基本性质
约分
通分
最简分数
24
18
最大公因数
=
24÷6
18÷6
=
4
3
18
24
2
9
12
3
3
4
互质,不能继续分解
18和24的最大公因数:
2×3=6
最小公倍数
分母相同
18
5
12
5
=
18×2
3×2
=
36
6
=
12×3
5×3
=
36
15
18 12
3
6
4
2
3
2
互质,不能继续分解
18和12的最小公倍数:
3×2×3×2=36
分数大小比较
分数大小比较
分数的大小比较
1.分母相同,分子大的分数就大
2.分母不相同,分子相同,分母小的分数就大
3.分母不相同,分子也不同,通分或约分成分母相同
18
5
18
7
7
8
7
4
<
>
分数单位相同
分数单位多的就大
5个
18
1
7个
18
1
8个
7
1
4个
7
1
6
5
8
5
7
4
3
4
4
3
5
4
12
8
18
6
>
<
分子相同,可以直接比较分数单位
分数单位不同,分母小的分数大
<
>
20
15
20
16
3
2
3
1
假分数与带分数互化
7
9
=
7
1×7+2
=
7
7
+
7
2
=
1
7
2
5
11
=
5
2×5+1
=
2
+
5
1
=
2
5
1
3
4
1
=
4
3×4+1
4
13
=
分数分为 和 两类
真分数
假分数
带分数是假分数的特殊形式
带分数>1
假分数≥1
练习巩固
1.(1)写出15,36的全部因数,并找出15和36的最大公因数。
(2)写出50以内3和8的全部倍数,并找出3和8的最小公倍数。
15的因数:1,15,3,5。
36的因数:1,36,2,18,3,12,4,9,6。
15和36的最大公因数:3。
50以内3的倍数:3,6,9,12,15,18,21,24,27,
30,33,36,39,42,45,48
50以内8的倍数:8,16,24,32,40,48。
3和8的最小公倍数:24。
2.把下面的数填入相应的类别。
8
25
28
10
90
45
17
100
97
2的倍数
3的倍数
5的倍数
质数
合数
3.连一连
?
把一个整体平均分成5份,其中的2份。
4.填一填
5
7
3
3
8
25
5.比较大小
<
>
>
<
6.如图,在上面的( )里填上适当的假分数,在下面的( ) 里填上适当的带分数。
5
7
2
5
4
5
11
5
15
3
5
3
5
23
4
5
3
7.(1)长是宽的几倍?
(2)宽是长的几分之几?
120cm
240cm
8.平均分给6个人,每人分到这袋糖果的几分之几?一袋糖果3kg,每人分到多少千克?
240÷120=2
120÷240=
1÷6=
3÷6=
(kg)
8.鸡和兔共有17个头,54只脚。问兔有多少只,鸡有多少只。
列表法:
1
16
2
3
4
5
6
7
15
14
13
12
11
10
66
64
62
60
58
56
54
假设法:
①假设笼子里都是鸡,就有:17×2=34(只)脚,
比实际少54-34=20(只)脚。
②那么需要用兔换鸡,一只兔比一只鸡多 4-2=2(只)脚, 有:20÷2=10(只)兔。
③所以有17-10=7(只)鸡。
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
