数学:第二十九章相似形复习课件(冀教版九年级上)
文档属性
| 名称 | 数学:第二十九章相似形复习课件(冀教版九年级上) |  | |
| 格式 | rar | ||
| 文件大小 | 158.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-02-01 20:22:00 | ||
图片预览




文档简介
课件44张PPT。《相似形》复习平行线分线段
成比例定理线段的比成比例线段比例的基本性质推 论 相似三角形相似三角形的判定相似三角形的性质1、若两个三角形相似,对应边3和5, 则它们的相
似比为_______, 对应中线的比为________,
周长比为________.1、若两个三角形相似,对应边3和5, 则它们的相
似比为_______, 对应中线的比为________,
周长比为________.3 : 53 : 53 : 51、若两个三角形相似,对应边3和5, 则它们的相
似比为_______, 对应中线的比为________,
周长比为________.面积比为_________.3 : 53 : 53 : 59 : 25三角形全等 三角形相似ASA
AAS
SAS
SSS
HL两角对应相等.两边对应成比例,
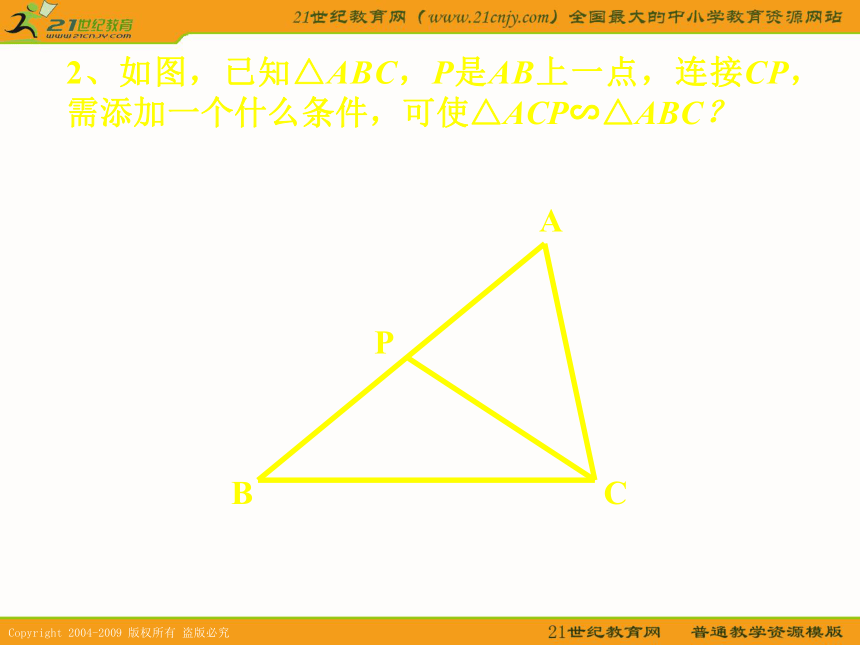
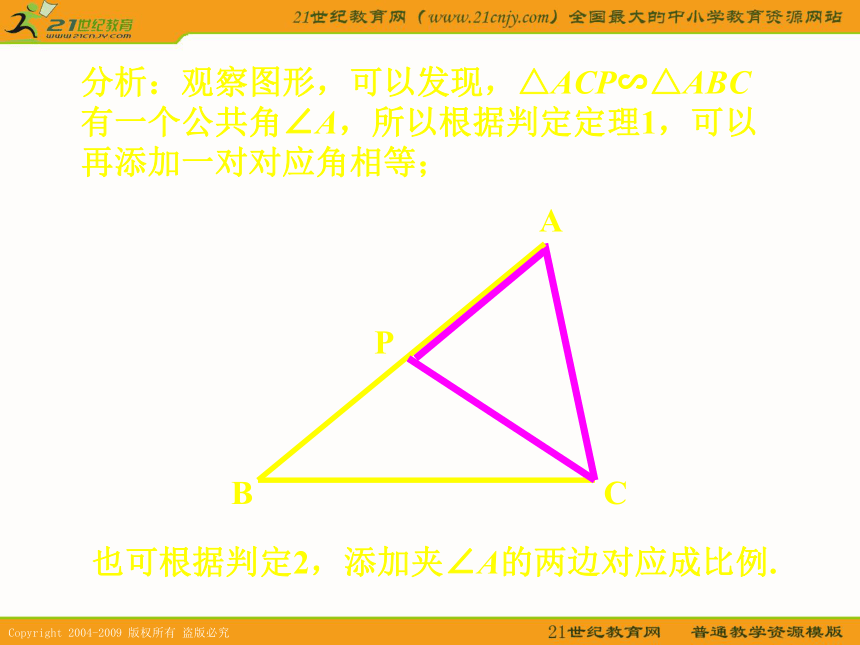
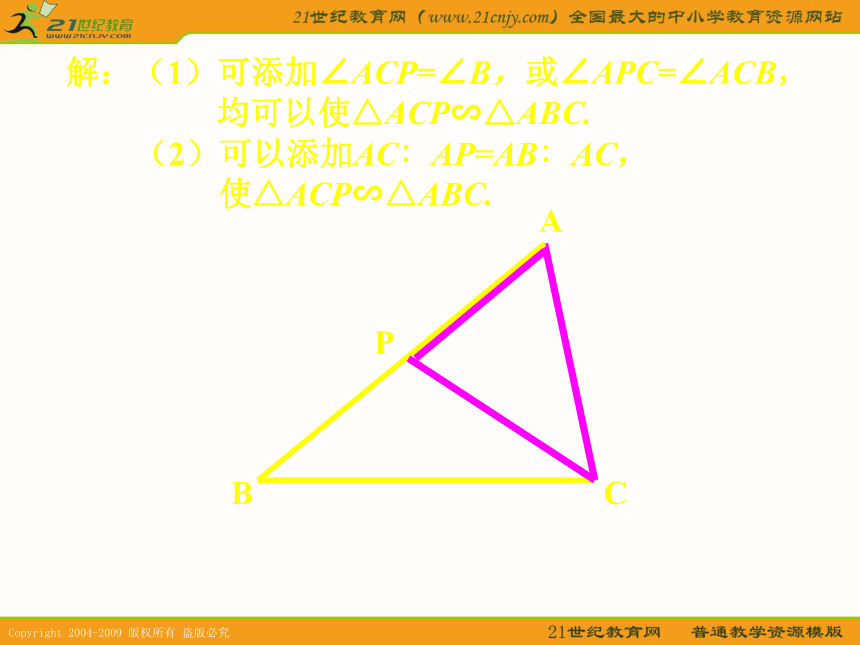
且夹角相等.三边对应成比例.斜边、直角边成比例.2、如图,已知△ABC,P是AB上一点,连接CP,需添加一个什么条件,可使△ACP∽△ABC? BAPCBAPC分析:观察图形,可以发现,△ACP∽△ABC 有一个公共角∠A,所以根据判定定理1,可以再添加一对对应角相等;也可根据判定2,添加夹∠A的两边对应成比例.解:(1)可添加∠ACP=∠B,或∠APC=∠ACB,
均可以使△ACP∽△ABC.
(2)可以添加AC∶AP=AB∶AC,
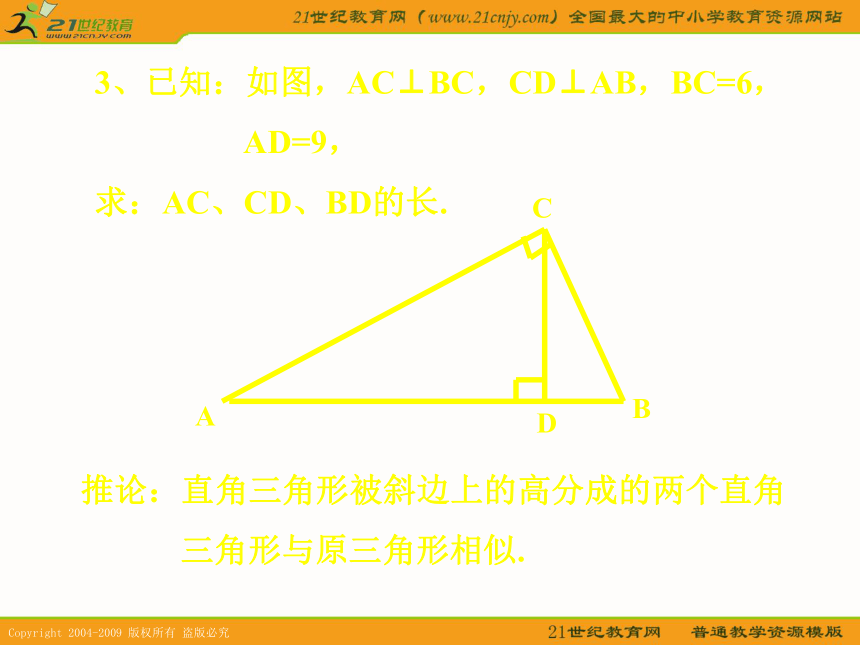
使△ACP∽△ABC.BAPCABCD3、已知:如图,AC⊥BC,CD⊥AB,BC=6,
AD=9,
求:AC、CD、BD的长.推论:直角三角形被斜边上的高分成的两个直角
三角形与原三角形相似.ABCD△ABC∽△ACD.ABCD△ABC ∽△CBD.ABCD△ACD∽△CBD.△ABC∽△ACD∽△CBD.ABCDABCDx6x+9∴△ABC∽△CBD.ABCDx6x+9∴△ABC∽△CBD.ABCDx6x+9∴△ABC∽△CBD.ABCDx6x+9∴△ABC∽△CBD.ABCDx6x+9∴△ABC∽△CBD.ABCDx6x+9∴△ABC∽△CBD.ABCDx6x+9∴△ABC∽△CBD.在△CBD中,
用勾股定理可得ABCDx6x+9∴△ABC∽△CBD.在△CBD中,
用勾股定理可得在△ABC中,用勾股定理可得ABCD∠A=∠1,∠B=∠2.12GABCDE4、已知: 在Rt△ABC中, AB=AC, ∠BAC=90o,
D是AC的中点, AG⊥BD交BC于E,
求证: BE=2EC.???GABCDE???FGABCDE???F需证AC : BF=1 : 2,即证AB : BF=1 : 2.GABCDE???FAD : AB=1 : 2 ,需证AC : BF=1 : 2,即证AB : BF=1 : 2.GABCDE???F证△ABD∽△BFA.GABCDE???F证△ABD∽△BFA.21GABCDE4、已知: 在Rt△ABC中, AB=AC, ∠BAC=90o,
D是AC的中点, AG⊥BD交BC于E,
求证: BE=2EC.???EABCDOEABCDOEABCDOEABCDOEABCDOEABCD5、已知:如图,在锐角△ABC中,AD、EC分别为BC、AB边上的高, △ABC和 △BDE的面积分别等于18和2,DE= ,求点B到直线AC的距离.E先求AC的长,利用面积求高.
先证△ABC∽△DBE.ABCD5、已知:如图,在锐角△ABC中,AD、EC分别为BC、AB边上的高, △ABC和 △BDE的面积分别等于18和2,DE= ,求点B到直线AC的距离.EABCD∵∠BDA=∠BEC,
∠B=∠B,
∴△ADB∽△CEB.
EABCD∵∠BDA=∠BEC,
∠B=∠B,
∴△ADB∽△CEB.
∴又∠B=∠B,
∴△BED∽△BCA.EABCD∵∠BDA=∠BEC,
∠B=∠B,
∴△ADB∽△CEB.
∴又∠B=∠B,
∴△BED∽△BCA. 又ED= ,EABCD∵∠BDA=∠BEC,
∠B=∠B,
∴△ADB∽△CEB.
∴又∠B=∠B,
∴△BED∽△BCA. 又ED= ,∴AC=EABCD∵∠BDA=∠BEC,
∠B=∠B,
∴△ADB∽△CEB.
∴又∠B=∠B,
∴△BED∽△BCA. 又ED= ,∴AC=∴B到AC的距离= 证明线段成比例的基本思考方法:1、观察比例式中的四条线段是否分居于两个三角形中,或是否在“平行线分线段成比例定理及其推论”的基本图形中,若是,则证相似或平行.2、若有三条线段是“1”的情况,则设法把另一条线段等量代换过来. 3、运用等比代换.常辅以等量代换.
若不成,可用“更比性质”.即4、等积代换.
成比例定理线段的比成比例线段比例的基本性质推 论 相似三角形相似三角形的判定相似三角形的性质1、若两个三角形相似,对应边3和5, 则它们的相
似比为_______, 对应中线的比为________,
周长比为________.1、若两个三角形相似,对应边3和5, 则它们的相
似比为_______, 对应中线的比为________,
周长比为________.3 : 53 : 53 : 51、若两个三角形相似,对应边3和5, 则它们的相
似比为_______, 对应中线的比为________,
周长比为________.面积比为_________.3 : 53 : 53 : 59 : 25三角形全等 三角形相似ASA
AAS
SAS
SSS
HL两角对应相等.两边对应成比例,
且夹角相等.三边对应成比例.斜边、直角边成比例.2、如图,已知△ABC,P是AB上一点,连接CP,需添加一个什么条件,可使△ACP∽△ABC? BAPCBAPC分析:观察图形,可以发现,△ACP∽△ABC 有一个公共角∠A,所以根据判定定理1,可以再添加一对对应角相等;也可根据判定2,添加夹∠A的两边对应成比例.解:(1)可添加∠ACP=∠B,或∠APC=∠ACB,
均可以使△ACP∽△ABC.
(2)可以添加AC∶AP=AB∶AC,
使△ACP∽△ABC.BAPCABCD3、已知:如图,AC⊥BC,CD⊥AB,BC=6,
AD=9,
求:AC、CD、BD的长.推论:直角三角形被斜边上的高分成的两个直角
三角形与原三角形相似.ABCD△ABC∽△ACD.ABCD△ABC ∽△CBD.ABCD△ACD∽△CBD.△ABC∽△ACD∽△CBD.ABCDABCDx6x+9∴△ABC∽△CBD.ABCDx6x+9∴△ABC∽△CBD.ABCDx6x+9∴△ABC∽△CBD.ABCDx6x+9∴△ABC∽△CBD.ABCDx6x+9∴△ABC∽△CBD.ABCDx6x+9∴△ABC∽△CBD.ABCDx6x+9∴△ABC∽△CBD.在△CBD中,
用勾股定理可得ABCDx6x+9∴△ABC∽△CBD.在△CBD中,
用勾股定理可得在△ABC中,用勾股定理可得ABCD∠A=∠1,∠B=∠2.12GABCDE4、已知: 在Rt△ABC中, AB=AC, ∠BAC=90o,
D是AC的中点, AG⊥BD交BC于E,
求证: BE=2EC.???GABCDE???FGABCDE???F需证AC : BF=1 : 2,即证AB : BF=1 : 2.GABCDE???FAD : AB=1 : 2 ,需证AC : BF=1 : 2,即证AB : BF=1 : 2.GABCDE???F证△ABD∽△BFA.GABCDE???F证△ABD∽△BFA.21GABCDE4、已知: 在Rt△ABC中, AB=AC, ∠BAC=90o,
D是AC的中点, AG⊥BD交BC于E,
求证: BE=2EC.???EABCDOEABCDOEABCDOEABCDOEABCDOEABCD5、已知:如图,在锐角△ABC中,AD、EC分别为BC、AB边上的高, △ABC和 △BDE的面积分别等于18和2,DE= ,求点B到直线AC的距离.E先求AC的长,利用面积求高.
先证△ABC∽△DBE.ABCD5、已知:如图,在锐角△ABC中,AD、EC分别为BC、AB边上的高, △ABC和 △BDE的面积分别等于18和2,DE= ,求点B到直线AC的距离.EABCD∵∠BDA=∠BEC,
∠B=∠B,
∴△ADB∽△CEB.
EABCD∵∠BDA=∠BEC,
∠B=∠B,
∴△ADB∽△CEB.
∴又∠B=∠B,
∴△BED∽△BCA.EABCD∵∠BDA=∠BEC,
∠B=∠B,
∴△ADB∽△CEB.
∴又∠B=∠B,
∴△BED∽△BCA. 又ED= ,EABCD∵∠BDA=∠BEC,
∠B=∠B,
∴△ADB∽△CEB.
∴又∠B=∠B,
∴△BED∽△BCA. 又ED= ,∴AC=EABCD∵∠BDA=∠BEC,
∠B=∠B,
∴△ADB∽△CEB.
∴又∠B=∠B,
∴△BED∽△BCA. 又ED= ,∴AC=∴B到AC的距离= 证明线段成比例的基本思考方法:1、观察比例式中的四条线段是否分居于两个三角形中,或是否在“平行线分线段成比例定理及其推论”的基本图形中,若是,则证相似或平行.2、若有三条线段是“1”的情况,则设法把另一条线段等量代换过来. 3、运用等比代换.常辅以等量代换.
若不成,可用“更比性质”.即4、等积代换.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
