(进阶篇)2024-2025学年下学期小学数学人教版四年级暑假分层作业3.2乘法运算律(含解析)
文档属性
| 名称 | (进阶篇)2024-2025学年下学期小学数学人教版四年级暑假分层作业3.2乘法运算律(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 256.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-27 00:00:00 | ||
图片预览




文档简介
(进阶篇)2024-2025学年下学期小学数学人教版四年级暑假分层作业3.2乘法运算律
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.小华的计算器上数字键“3”坏了,下面( )算式也可以算出1600÷32的得数。
A.1600÷16×2 B.1600÷8÷4 C.1600÷40-8
2.12×4×125=12×(4×125),应用的是( )。
A.乘法交换律 B.乘法结合律
C.乘法交换律和结合律 D.乘法先结合律后交换律
3.已知△×□=○,下面等式中不正确的是( )。
A.□×△=○ B.○÷△=□ C.○÷□=△ D.□×○=△
4.长城是我国古代劳动人民创造的伟大奇迹,被誉为“世界中古七大奇迹之一”,淡季门票35元/人,某旅行团购买103张门票一共需要多少钱?用算式:103×35解决问题,聪聪想用乘法分配律计算,下面算法正确的是( )。
A.100×35+35×5 B.103×30+35
C.100×35+3×35 D.103×5+103×3
5.小东把30×( +4)算成了30× +4,这样得到的结果与正确结果相比( )。
A.少算了30 B.少算了29 C.少算了29×4
6.不计算,观察下列算式,( )式子的值与963÷18×4的结果不同。
A.963÷(18×4) B.963×4÷18 C.963÷6÷3×4 D.963÷(18÷4)
7.24×25=( )。
A.4×25×6 B.20+4×25 C.24×20+5
二、填空题
8.5×72×20=5×( )×72,这是应用了( )律。
9.两个数相乘,交换两个因数的位置,积不变。这叫作乘法交换律。
用字母表示:a×b= ×
10.交换两个因数的位置( )不变,这叫做乘法( )。字母表示为( )。
11.在里填上合适的数或字母,在里填上合适的运算符号。
(a×b)×c=×(×)
25×13×4=(25×)×
28×21+28×79=28×()
101×18=()×18
(84×25)×8=84()
12.在横线上填上适当的数,并填写所运用的运算律。
(1)48+ =62+
运用了 律
(2)26+( +15)=( +74)+15
运用了 律
(3)25×37×4=25× ×
运用了 律
(4)9×37+9×63= ×( + )
运用了 律
13.根据运算律在横线上填上合适的数。
(1)(42+25)×4= ×4+ ×4
(2)(54+12)×3= × + ×
(3)15×28+15×72= ×(( )+ )
(4)14×10+6×10=(( )+ )×
14.在括号里填上“>”“<”或“=”。
25×(34×40)( )25×34+25×40 (75-20)×8( )75×8-20
99×43( )43×101-43×2 450÷9÷5( )450÷(9×5)
15.分别代表3个数。
=( ),=( ),=( )。
三、判断题
16.35×37+65×37=(35+65)×37。( )
17.(a+b)c=ac+bc,运用了乘法分配律。( )
18.“小马虎”把28×(□+2)错算成28×□+2,结果相差1。( )
19.我们在计算四则混合运算题目时,首先要观察题目的特点,看看能不能用简便方法进行计算,如果不能用,再按四则混合运算的运算顺序去计算。( )
20.420÷7÷5=420÷﹙7÷5﹚。( )
21.算式125×27×8=27×(125×8)只运用了乘法交换律。( )
22.算式104×25进行简便计算时,可以变式为100×25+4。( )
四、计算题
23.计算。
24.你能很快写出得数吗?试一试。
101×55= 101×27= 101×99= 34×101=
五、解答题
25.我们学过哪些运算律?请完成下表。
名称 举例 用字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
四则混合运算,有时可以运用运算律使计算更加简便。
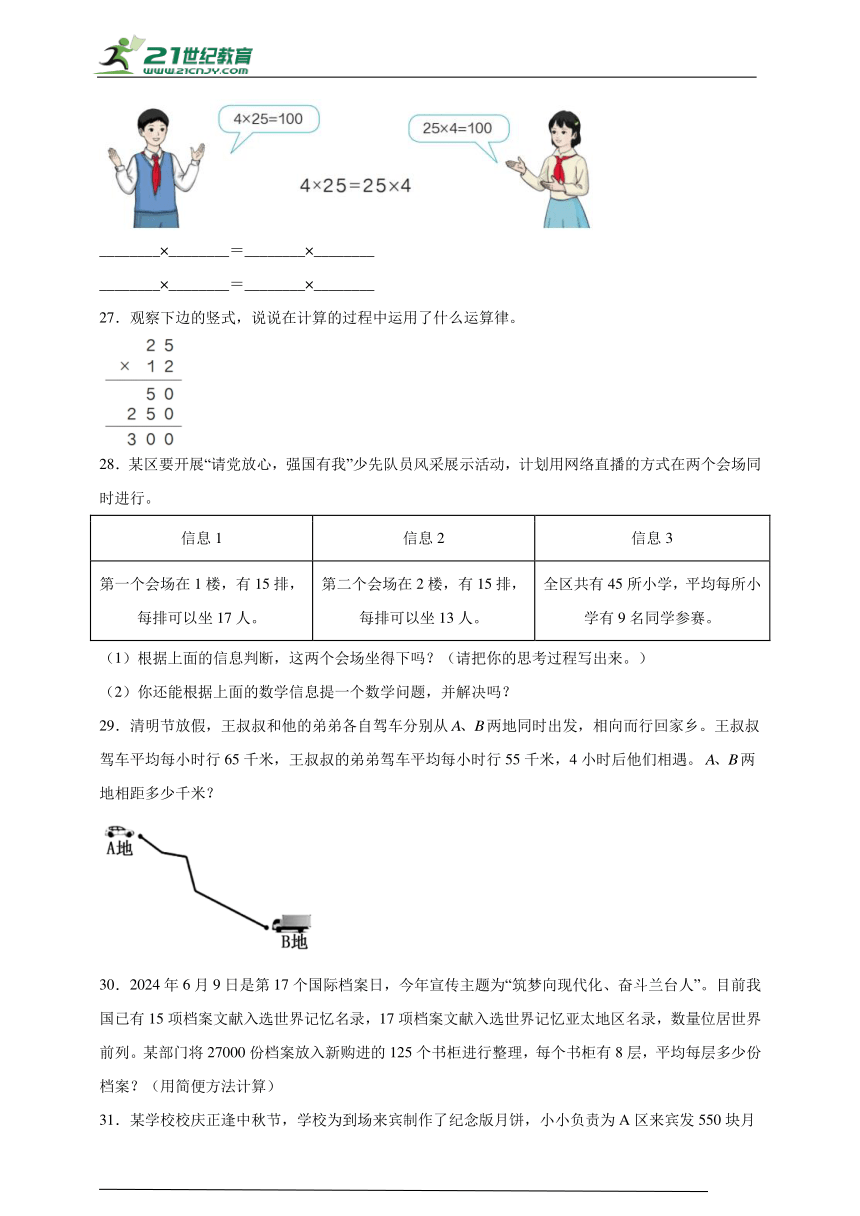
26.你能再写出几个这样的等式吗?你发现了什么?
________×________=________×________
________×________=________×________
27.观察下边的竖式,说说在计算的过程中运用了什么运算律。
28.某区要开展“请党放心,强国有我”少先队员风采展示活动,计划用网络直播的方式在两个会场同时进行。
信息1 信息2 信息3
第一个会场在1楼,有15排,每排可以坐17人。 第二个会场在2楼,有15排,每排可以坐13人。 全区共有45所小学,平均每所小学有9名同学参赛。
(1)根据上面的信息判断,这两个会场坐得下吗?(请把你的思考过程写出来。)
(2)你还能根据上面的数学信息提一个数学问题,并解决吗?
29.清明节放假,王叔叔和他的弟弟各自驾车分别从两地同时出发,相向而行回家乡。王叔叔驾车平均每小时行65千米,王叔叔的弟弟驾车平均每小时行55千米,4小时后他们相遇。两地相距多少千米?
30.2024年6月9日是第17个国际档案日,今年宣传主题为“筑梦向现代化、奋斗兰台人”。目前我国已有15项档案文献入选世界记忆名录,17项档案文献入选世界记忆亚太地区名录,数量位居世界前列。某部门将27000份档案放入新购进的125个书柜进行整理,每个书柜有8层,平均每层多少份档案?(用简便方法计算)
31.某学校校庆正逢中秋节,学校为到场来宾制作了纪念版月饼,小小负责为A区来宾发550块月饼。(列综合算式并用简便方法计算)
(1)他已经发了五仁月饼165块,莲蓉月饼235块,还剩下豆沙月饼没有发。豆沙月饼一共有多少块?
知识链接 中秋节与春节、清明节、端午节并称为中国四大传统节日。中秋节有祭月、赏月、拜月、吃月饼、赏桂花、饮桂花酒等习俗。
(2)B区和C区各有86名来宾,共分发了860块月饼,平均每人分得多少块月饼?
《(进阶篇)2024-2025学年下学期小学数学人教版四年级暑假分层作业3.2乘法运算律》参考答案
题号 1 2 3 4 5 6 7
答案 B B D C C A A
1.B
【分析】本题可以通过把题目条件和选项的结果计算出来,依次进行对比,结果相同的选项即为正确选项,或者运用整数除法的性质,一个数连续除以两个数,等于这个数除以这两个数的乘积,快速选出答案。
【详解】题目中;
A.;
B.;
C.;
故答案为:B
【点睛】本题考查了整数除法的性质以及乘除混合运算、除数是两位数的除法运算。易错点在于计算时,只看除号后面的计算结果是否等于32,忽略了乘除法同级要从左往右依次计算。
2.B
【分析】乘法交换律:两个数相乘,交换两个乘数的位置,积不变;乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积不变。
【详解】12×4×125=12×(4×125),应用的是乘法结合律。
故答案为:B
3.D
【分析】一个因数=积÷另一个因数,乘法交换律:a×b=b×a,据此即可解答。
【详解】A.根据乘法交换律,已知△×□=○,则□×△=△×□=○;
B.根据分析可知,已知△×□=○,则○÷△=□;
C.根据分析可知,已知△×□=○,则○÷□=△
D.根据分析可知,已知△×□=○,则○÷□=△,所以□×○=△不正确。
故答案为:D
4.C
【分析】两个数的和与一个数相乘,可以用这两个数分别和这个数相乘,再把它们的积相加,这叫乘法分配律。可以把103改写成100+3,再运用乘法分配律计算;也可以把35改写成30+5,再运用乘法分配律计算。
【详解】103×35
=(100+3)×35
=100×35+3×35
103×35
=103×(30+5)
=103×30+103×5
A.103×35=100×35+3×35。103×35≠100×35+35×5。
B.103×35=103×30+103×5,103×35≠103×30+35。
C.103×35=100×35+3×35
D.103×35=103×30+103×5,103×35≠103×5+103×3。
算法正确的是103×35=100×35+3×35。
故答案为:C
5.C
【分析】根据乘法分配律,将算式30×( +4)变为30× +30×4,用30× +30×4减去30× +4,即可求出得到的结果与正确结果相比相差多少,据此解答即可。
【详解】30×( +4)
=30× +30×4
30× +30×4-(30× +4)
=30× +30×4-30× -4
=30× -30× +30×4-4
=30×4-4
=(30-1)×4
=29×4
所以小东把30×( +4)算成了30× +4,这样得到的结果与正确结果相比少算了29×4。
故答案为:C
6.A
【分析】(1)根据除法的性质,将算式963÷(18×4)化成963÷18÷4,所以算式963÷(18×4)的值与963÷18×4的结果不同;
(2)根据乘法交换律,把算式963×4÷18化成963÷18×4,因此算式963×4÷18的值与963÷18×4的相同。
(3)根据除法的性质,将算式963÷6÷3×4化成963÷(6×3)×4,即963÷18×4,因此算式963÷6÷3×4的值与963÷18×4的相同。
(4)根据商不变规律,被除数不变,除数除以4,商应乘4,也就是963÷(18÷4)=963÷18×4。
【详解】A.963÷(18×4)=963÷18÷4,所以963÷(18×4) 值与963÷18×4的结果不同;符合题意;
B.963×4÷18=963÷18×4,因此算式963×4÷18的值与963÷18×4的相同。不符合题意;
C.963÷6÷3×4=963÷(6×3)×4=963÷18×4,因此算式963÷6÷3×4的值与963÷18×4的相同。不符合题意;
D.由分析可知,963÷(18÷4)=963÷18×4,因此算式963÷(18÷4)的值与963÷18×4的相同。不符合题意;
故答案为:A
7.A
【分析】简算24×25,可以先把24分解成4×6,再根据乘法交换律,交换25和6的位置,先算4×25,再与6相乘,进行简算。
【详解】由题意得:
24×25
=4×6×25
=4×25×6(与选项A相同)
=100×6
=600
所以24×25=4×25×6。
故答案为:A
8. 20 乘法交换
【分析】乘法交换律是指两个数相乘,交换乘数的位置,它们的积不变。据此解答。
【详解】5×72×20=5×20×72,这是应用了乘法交换律。
9. b a
【分析】根据乘法交换律的特点可知,直接交换a和b的位置即可,依此解答。
【详解】根据分析,乘法交换律用字母表示:a×b=b×a。
10. 积 交换律 a×b=b×a
【详解】交换两个因数的位置,积不变,这叫做乘法交换律。用字母表示为a×b=b×a。
例如:4×25=25×4=100,交换4与25的位置,积不变,运用了乘法交换律;
8×6×125
=8×125×6
=1000×6
=6000
交换6与125的位置,积不变,运用了乘法交换律。
11.a;b;c
4;13
21;+;79
100;+;1
×;25;×;8
【分析】乘法分配律是两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。乘法结合律是三个数相乘,先乘前两个数,或者先乘后两个数,积不变。乘法交换律是指两个数相乘,交换因数的位置,它们的积不变。
【详解】(1)根据乘法结合律可知,计算a、b、c相乘时,先乘a和b,再乘c,或者先乘b和c,再乘a,所以;
(2)根据乘法交换律交换13和4的位置,先计算25乘4进行凑整巧算,然后再乘13,所以;
(3)根据乘法分配律可知,提取相同的因数28,先计算,所以;
(4)把101看成,然后根据乘法分配律进行计算,所以;
(5)根据乘法结合律可知,先计算25乘8进行凑整巧算,然后再乘84,所以。
12.(1) 62 48 加法交换
(2) 74 26 加法结合
(3) 4 37 乘法交换
(4) 9 37 63 乘法分配
【分析】(1)加法交换律:两个数相加,交换加数的位置,和不变;48加62的和等于62加48的和,据此作答;
(2)加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变;26和74能凑出整数,因此可把它们先相加,再与15相加,据此作答;
(3)乘法交换律:两个因数相乘,交换因数的位置,积不变;25乘4能凑成整数,可以交换37和4的位置,先计算25乘4,求出二者的积,再计算积与37相乘,据此作答;
(4)乘法分配率:两个数的和同一个数相乘,等于把两个加数分别同这个数相乘,再把两个积加起来,结果不变;37和63能凑出整数,可以先把它们相加求和,再与9相乘,据此作答。
【详解】(1)48+62
=62+48
=110
所以48+62=62+48,运用了加法交换律。
(2)26+(74+15)
=(26+74)+15
=100+15
=115
所以26+(74+15)=(26+74)+15,运用了加法结合律。
(3)25×37×4
=25×4×37
=100×37
=3700
所以25×37×4=25×4×37,运用了乘法交换律。
(4)9×37+9×63
=9×(37+63)
=9×100
=900
所以9×37+9×63=9×(37+63),运用了乘法分配律。
13.(1) 42 25
(2) 54 3 12 3
(3) 15 28 72
(4) 14 6 10
【分析】根据乘法分配律:(a+b)×c=a×c+b×c或(a-b)×c=a×c-b×c,即可解答。
【详解】(1)(42+25)×4=42×4+25×4
(2)(54+12)×3=54×3+12×3
(3)15×28+15×72=15×(28+72)
(4)14×10+6×10=(14+6)×10
【点睛】本题主要考查乘法运算律的应用,需熟练掌握。
14. > < = =
【详解】(1)运用乘法分配律:a×(b+c)=a×b+a×c,将算式25×34+25×40化简为25×(34+40),再进行比较;
(2)运用乘法分配律:a×(b+c)=a×b+a×c,将算式(75-20)×8化简为75×8-20×8,再进行比较;
(3)运用乘法分配律:a×(b+c)=a×b+a×c,将算式43×101-43×2 化简为43×(101-2),再进行比较;
(4)运用除法的性质:a÷b÷c=a÷(b×c),将算式 450÷9÷5化简为450÷(9×5),再进行比较。
【点睛】根据分析:
(1)25×34+25×40 =25×(34+40),25×(34×40)>25×(34+40),所以25×(34×40)>25×34+25×40 ;
(2)(75-20)×8 =75×8-20×8,75×8-20×8<75×8-20,所以(75-20)×8<75×8-20;
(3)43×101-43×2=43×(101-2)=43×99,所以99×43=43×101-43×2;
(4)450÷9÷5=450÷(9×5),所以450÷9÷5=450÷(9×5)。
15. 150 100 75
【分析】
观察第一行图形,可以得知2个等于3个;由第二行图形可以得知3个等于4个;把第二行的3个用2个替换,可以得知2个等于4个,即1个等于2个;把第三行中的用替换,可以得知:++++=400,即+=400,再把4个用3个替换,即可算出等于多少,再把的数值代入到第二个算式中,即可算出等于多少。据此解答。
【详解】由分析可知:
=+
+++=400
++++=400
+=400
+++=400
=400÷4=100
+100=400
=400-100=300
=300÷4=75
=75+75=150
【点睛】本题主要考查等量代换,解决此题的关键是根据题目信息正确找到三种图形之间的关系。
16.√
【分析】根据乘法分配律的意义,两个数的和同一个数相乘,等于把两个加数分别同这个数相乘,再把两个积加起来,结果不变,用字母表示为:(a+b)×c=a×c+b×c;据此进行判断即可。
【详解】35×37+65×37
=(35+65)×37
=100×37
=3700
所以原题的说法正确。
故答案为:√
【点睛】本题考查了乘法分配律的应用,灵活使用运算律可使计算简便。
17.√
【分析】根据乘法分配律的意义:两个数和一个数相乘,可以先把它们分别与这个数相乘,再将积相加。据此解答。
【详解】(a+b)c=ac+bc,运用了乘法分配律。原题说法正确。
故答案为:√
【点睛】此题考查了乘法分配律。要求熟练掌握并灵活运用。
18.×
【分析】28×(□+2)利用乘法分配律写成28×□+28×2,即28×□+56,“小马虎”把28×(□+2)错算成28×□+2,结果相差56-2=54。
【详解】“小马虎”把28×(□+2)错算成28×□+2,结果相差1。这句话错误,应该相差54。
故答案为:×
19.√
【详解】例如:102×25-2×25观察发现符合乘法分配律的定式,即(a+b)×c=a×c+b×c,使用乘法分配律计算更加简单,所以102×25-2×25就可用简便计算,即102×25-2×25=(102-2)×25=100×25=2500。45×23-15×2观察发现不能使用简便计算,就按照运算顺序计算即可,即45×23-15×2=1035-30=1005。所以原题表述正确。
故答案为:√
20.×
【分析】除法的性质:一个数连续除以两个数,等于除以这两个数的积。据此解答即可。
【详解】420÷7÷5=420÷﹙7×5﹚。原题说法错误。
故答案为:×
21.×
【分析】乘法交换律是指一种计算定律,两个数相乘,交换因数的位置,它们的积不变;乘法结合律是指三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变,据此判断即可。
【详解】125×27×8
=27×125×8
=27×(125×8)
=27×1000
=27000
算式125×27×8=27×(125×8)运用了乘法交换律和乘法结合律,原题说法错误。
故答案为:×
22.×
【分析】乘法分配律:a×(b+c)=a×b+a×c,据此即可解答。
【详解】104×25=(100+4)×25=100×25+4×25,原说法错误。
故答案为:×
【点睛】熟练掌握乘法分配律的计算方法是解答本题的关键。
23.1500
【分析】这道题先利用乘法交换律,交换3与4的位置,再根据乘法结合律,把25与4,3与5结合先乘,再把所得的积相乘。
【详解】
24.5555;2727;9999;3434
【分析】(1)将101看作100和1,先计算出100乘55的结果,再计算出1乘55的结果,最后将这两个结果相加;
(2)将101看作100和1,先计算出100乘27的结果,再计算出1乘27的结果,最后将这两个结果相加;
(3)将101看作100和1,先计算出100乘99的结果,再计算出1乘99的结果,最后将这两个结果相加;
(4)将101看作100和1,先计算出34乘100的结果,再计算出34乘1的结果,最后将这两个结果相加;据此计算。
【详解】(1)101×55
=(100+1)×55
=100×55+1×55
=5500+55
=5555
(2)101×27
=(100+1)×27
=100×27+1×27
=2700+27
=2727
(3)101×99
=(100+1)×99
=100×99+1×99
=9900+99
=9999
(4)34×101
=34×(100+1)
=34×100+34×1
=3400+34
=3434
25.见解析
【分析】两个数相加,交换两个加数的位置,和不变。这叫作加法的交换律。
三个数相加,先把前两个数相加,或者先把后两数相加,和不变。这叫作加法结合律。
两个数相乘,交换两个因数的位置,积不变。这叫作乘法的交换律。
三个数相加乘,先把前两个数相乘,或者先把后两数相乘,积不变。这叫作乘法结合律。
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。这叫作乘法分配律。
【详解】
名称 举例 用字母表示
加法交换律
加法结合律 (15+28)+22=15+(28+22)
乘法交换律 15×28=28×15
乘法结合律 (28×15)×4=28×(15×4)
乘法分配律 25×(4+20)=25×4+25×20
26.150;2;2;150;(算式不唯一)
600;2;2;600;(算式不唯一)
发现:两个数相乘,交换两个因数的位置,积不变。
【分析】先写出一个乘法算式,并计算出积;然后交换两个因数的位置,再计算出它们的积,通过比较即可解答。
【详解】150×2=300,2×150=300,即:150×2=2×150。
600×2=1200,2×600=1200,即:600×2=2×600。(算式不唯一)
我发现:两个数相乘,交换两个因数的位置,积不变。
27.乘法分配律
【分析】观察竖式可知,50代表个位的2乘25的结果,即2×25;250代表十位的1乘25的结果,即10×25;300代表50与250相加;就是把12分解成(10+2),运用了乘法分配律计算,据此解答即可。
【详解】25×12
=25×(10+2)
=25×10+25×2
=250+50
=300
所以,运用了乘法分配律。
28.(1)坐得下;(2)见详解
【分析】(1)把第一个会场的座位和第二个会场的座位数算出来。然后和全区小学参赛的人数比较,可判断。
(2)根据信息一和二可以算出两个会场的总座位数。再根据信息三可以知道参赛的人数,那么就可以提出还剩多少个座位?答案不唯一,合理即可。
【详解】(1)15×17+15×13
=15×(17+13)
=15×30
=450(人)
45×9=405(人)
450>405
答:这两个会场坐得下。
(2)问题:还剩多少个座位?
450-405=45(个)
答:还剩45个座位。
29.480千米
【分析】根据题意可知,两人同时出发,相向而行,两人行驶路程和就是两地的距离。根据路程=速度×时间,分别求出两人行驶的路程,再相加求和。计算时可以根据乘法分配律进行简算。
【详解】65×4+55×4
=(65+55)×4
=120×4
=480(千米)
答:两地相距480千米。
30.27份
【分析】先用27000除以125算出平均每个书柜放多少份档案,再除以8即可算出平均每层放多少份档案。计算时,利用除法的性质:a÷b÷c=a÷(b×c)可使计算简便。据此解答。
【详解】27000÷125÷8
=27000÷(125×8)
=27000÷1000
=27(份)
答:平均每层27份档案。
31.(1)150块;(2)5块
【分析】(1)总共发的月饼块数减去五仁月饼、莲蓉月饼的块数,等于豆沙月饼的块数。
(2)86乘2等于B区和C区的来宾人数和,总共发的月饼块数860除以B区和C区的来宾人数和等于平均每人分得的月饼块数。
【详解】(1)550-165-235
=550-(165+235)
=550-400
=150(块)
答:豆沙月饼一共有150块。
(2)860÷(86×2)
=860÷86÷2
=10÷2
=5(块)
答:平均每人分得5块月饼。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.小华的计算器上数字键“3”坏了,下面( )算式也可以算出1600÷32的得数。
A.1600÷16×2 B.1600÷8÷4 C.1600÷40-8
2.12×4×125=12×(4×125),应用的是( )。
A.乘法交换律 B.乘法结合律
C.乘法交换律和结合律 D.乘法先结合律后交换律
3.已知△×□=○,下面等式中不正确的是( )。
A.□×△=○ B.○÷△=□ C.○÷□=△ D.□×○=△
4.长城是我国古代劳动人民创造的伟大奇迹,被誉为“世界中古七大奇迹之一”,淡季门票35元/人,某旅行团购买103张门票一共需要多少钱?用算式:103×35解决问题,聪聪想用乘法分配律计算,下面算法正确的是( )。
A.100×35+35×5 B.103×30+35
C.100×35+3×35 D.103×5+103×3
5.小东把30×( +4)算成了30× +4,这样得到的结果与正确结果相比( )。
A.少算了30 B.少算了29 C.少算了29×4
6.不计算,观察下列算式,( )式子的值与963÷18×4的结果不同。
A.963÷(18×4) B.963×4÷18 C.963÷6÷3×4 D.963÷(18÷4)
7.24×25=( )。
A.4×25×6 B.20+4×25 C.24×20+5
二、填空题
8.5×72×20=5×( )×72,这是应用了( )律。
9.两个数相乘,交换两个因数的位置,积不变。这叫作乘法交换律。
用字母表示:a×b= ×
10.交换两个因数的位置( )不变,这叫做乘法( )。字母表示为( )。
11.在里填上合适的数或字母,在里填上合适的运算符号。
(a×b)×c=×(×)
25×13×4=(25×)×
28×21+28×79=28×()
101×18=()×18
(84×25)×8=84()
12.在横线上填上适当的数,并填写所运用的运算律。
(1)48+ =62+
运用了 律
(2)26+( +15)=( +74)+15
运用了 律
(3)25×37×4=25× ×
运用了 律
(4)9×37+9×63= ×( + )
运用了 律
13.根据运算律在横线上填上合适的数。
(1)(42+25)×4= ×4+ ×4
(2)(54+12)×3= × + ×
(3)15×28+15×72= ×(( )+ )
(4)14×10+6×10=(( )+ )×
14.在括号里填上“>”“<”或“=”。
25×(34×40)( )25×34+25×40 (75-20)×8( )75×8-20
99×43( )43×101-43×2 450÷9÷5( )450÷(9×5)
15.分别代表3个数。
=( ),=( ),=( )。
三、判断题
16.35×37+65×37=(35+65)×37。( )
17.(a+b)c=ac+bc,运用了乘法分配律。( )
18.“小马虎”把28×(□+2)错算成28×□+2,结果相差1。( )
19.我们在计算四则混合运算题目时,首先要观察题目的特点,看看能不能用简便方法进行计算,如果不能用,再按四则混合运算的运算顺序去计算。( )
20.420÷7÷5=420÷﹙7÷5﹚。( )
21.算式125×27×8=27×(125×8)只运用了乘法交换律。( )
22.算式104×25进行简便计算时,可以变式为100×25+4。( )
四、计算题
23.计算。
24.你能很快写出得数吗?试一试。
101×55= 101×27= 101×99= 34×101=
五、解答题
25.我们学过哪些运算律?请完成下表。
名称 举例 用字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
四则混合运算,有时可以运用运算律使计算更加简便。
26.你能再写出几个这样的等式吗?你发现了什么?
________×________=________×________
________×________=________×________
27.观察下边的竖式,说说在计算的过程中运用了什么运算律。
28.某区要开展“请党放心,强国有我”少先队员风采展示活动,计划用网络直播的方式在两个会场同时进行。
信息1 信息2 信息3
第一个会场在1楼,有15排,每排可以坐17人。 第二个会场在2楼,有15排,每排可以坐13人。 全区共有45所小学,平均每所小学有9名同学参赛。
(1)根据上面的信息判断,这两个会场坐得下吗?(请把你的思考过程写出来。)
(2)你还能根据上面的数学信息提一个数学问题,并解决吗?
29.清明节放假,王叔叔和他的弟弟各自驾车分别从两地同时出发,相向而行回家乡。王叔叔驾车平均每小时行65千米,王叔叔的弟弟驾车平均每小时行55千米,4小时后他们相遇。两地相距多少千米?
30.2024年6月9日是第17个国际档案日,今年宣传主题为“筑梦向现代化、奋斗兰台人”。目前我国已有15项档案文献入选世界记忆名录,17项档案文献入选世界记忆亚太地区名录,数量位居世界前列。某部门将27000份档案放入新购进的125个书柜进行整理,每个书柜有8层,平均每层多少份档案?(用简便方法计算)
31.某学校校庆正逢中秋节,学校为到场来宾制作了纪念版月饼,小小负责为A区来宾发550块月饼。(列综合算式并用简便方法计算)
(1)他已经发了五仁月饼165块,莲蓉月饼235块,还剩下豆沙月饼没有发。豆沙月饼一共有多少块?
知识链接 中秋节与春节、清明节、端午节并称为中国四大传统节日。中秋节有祭月、赏月、拜月、吃月饼、赏桂花、饮桂花酒等习俗。
(2)B区和C区各有86名来宾,共分发了860块月饼,平均每人分得多少块月饼?
《(进阶篇)2024-2025学年下学期小学数学人教版四年级暑假分层作业3.2乘法运算律》参考答案
题号 1 2 3 4 5 6 7
答案 B B D C C A A
1.B
【分析】本题可以通过把题目条件和选项的结果计算出来,依次进行对比,结果相同的选项即为正确选项,或者运用整数除法的性质,一个数连续除以两个数,等于这个数除以这两个数的乘积,快速选出答案。
【详解】题目中;
A.;
B.;
C.;
故答案为:B
【点睛】本题考查了整数除法的性质以及乘除混合运算、除数是两位数的除法运算。易错点在于计算时,只看除号后面的计算结果是否等于32,忽略了乘除法同级要从左往右依次计算。
2.B
【分析】乘法交换律:两个数相乘,交换两个乘数的位置,积不变;乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积不变。
【详解】12×4×125=12×(4×125),应用的是乘法结合律。
故答案为:B
3.D
【分析】一个因数=积÷另一个因数,乘法交换律:a×b=b×a,据此即可解答。
【详解】A.根据乘法交换律,已知△×□=○,则□×△=△×□=○;
B.根据分析可知,已知△×□=○,则○÷△=□;
C.根据分析可知,已知△×□=○,则○÷□=△
D.根据分析可知,已知△×□=○,则○÷□=△,所以□×○=△不正确。
故答案为:D
4.C
【分析】两个数的和与一个数相乘,可以用这两个数分别和这个数相乘,再把它们的积相加,这叫乘法分配律。可以把103改写成100+3,再运用乘法分配律计算;也可以把35改写成30+5,再运用乘法分配律计算。
【详解】103×35
=(100+3)×35
=100×35+3×35
103×35
=103×(30+5)
=103×30+103×5
A.103×35=100×35+3×35。103×35≠100×35+35×5。
B.103×35=103×30+103×5,103×35≠103×30+35。
C.103×35=100×35+3×35
D.103×35=103×30+103×5,103×35≠103×5+103×3。
算法正确的是103×35=100×35+3×35。
故答案为:C
5.C
【分析】根据乘法分配律,将算式30×( +4)变为30× +30×4,用30× +30×4减去30× +4,即可求出得到的结果与正确结果相比相差多少,据此解答即可。
【详解】30×( +4)
=30× +30×4
30× +30×4-(30× +4)
=30× +30×4-30× -4
=30× -30× +30×4-4
=30×4-4
=(30-1)×4
=29×4
所以小东把30×( +4)算成了30× +4,这样得到的结果与正确结果相比少算了29×4。
故答案为:C
6.A
【分析】(1)根据除法的性质,将算式963÷(18×4)化成963÷18÷4,所以算式963÷(18×4)的值与963÷18×4的结果不同;
(2)根据乘法交换律,把算式963×4÷18化成963÷18×4,因此算式963×4÷18的值与963÷18×4的相同。
(3)根据除法的性质,将算式963÷6÷3×4化成963÷(6×3)×4,即963÷18×4,因此算式963÷6÷3×4的值与963÷18×4的相同。
(4)根据商不变规律,被除数不变,除数除以4,商应乘4,也就是963÷(18÷4)=963÷18×4。
【详解】A.963÷(18×4)=963÷18÷4,所以963÷(18×4) 值与963÷18×4的结果不同;符合题意;
B.963×4÷18=963÷18×4,因此算式963×4÷18的值与963÷18×4的相同。不符合题意;
C.963÷6÷3×4=963÷(6×3)×4=963÷18×4,因此算式963÷6÷3×4的值与963÷18×4的相同。不符合题意;
D.由分析可知,963÷(18÷4)=963÷18×4,因此算式963÷(18÷4)的值与963÷18×4的相同。不符合题意;
故答案为:A
7.A
【分析】简算24×25,可以先把24分解成4×6,再根据乘法交换律,交换25和6的位置,先算4×25,再与6相乘,进行简算。
【详解】由题意得:
24×25
=4×6×25
=4×25×6(与选项A相同)
=100×6
=600
所以24×25=4×25×6。
故答案为:A
8. 20 乘法交换
【分析】乘法交换律是指两个数相乘,交换乘数的位置,它们的积不变。据此解答。
【详解】5×72×20=5×20×72,这是应用了乘法交换律。
9. b a
【分析】根据乘法交换律的特点可知,直接交换a和b的位置即可,依此解答。
【详解】根据分析,乘法交换律用字母表示:a×b=b×a。
10. 积 交换律 a×b=b×a
【详解】交换两个因数的位置,积不变,这叫做乘法交换律。用字母表示为a×b=b×a。
例如:4×25=25×4=100,交换4与25的位置,积不变,运用了乘法交换律;
8×6×125
=8×125×6
=1000×6
=6000
交换6与125的位置,积不变,运用了乘法交换律。
11.a;b;c
4;13
21;+;79
100;+;1
×;25;×;8
【分析】乘法分配律是两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。乘法结合律是三个数相乘,先乘前两个数,或者先乘后两个数,积不变。乘法交换律是指两个数相乘,交换因数的位置,它们的积不变。
【详解】(1)根据乘法结合律可知,计算a、b、c相乘时,先乘a和b,再乘c,或者先乘b和c,再乘a,所以;
(2)根据乘法交换律交换13和4的位置,先计算25乘4进行凑整巧算,然后再乘13,所以;
(3)根据乘法分配律可知,提取相同的因数28,先计算,所以;
(4)把101看成,然后根据乘法分配律进行计算,所以;
(5)根据乘法结合律可知,先计算25乘8进行凑整巧算,然后再乘84,所以。
12.(1) 62 48 加法交换
(2) 74 26 加法结合
(3) 4 37 乘法交换
(4) 9 37 63 乘法分配
【分析】(1)加法交换律:两个数相加,交换加数的位置,和不变;48加62的和等于62加48的和,据此作答;
(2)加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变;26和74能凑出整数,因此可把它们先相加,再与15相加,据此作答;
(3)乘法交换律:两个因数相乘,交换因数的位置,积不变;25乘4能凑成整数,可以交换37和4的位置,先计算25乘4,求出二者的积,再计算积与37相乘,据此作答;
(4)乘法分配率:两个数的和同一个数相乘,等于把两个加数分别同这个数相乘,再把两个积加起来,结果不变;37和63能凑出整数,可以先把它们相加求和,再与9相乘,据此作答。
【详解】(1)48+62
=62+48
=110
所以48+62=62+48,运用了加法交换律。
(2)26+(74+15)
=(26+74)+15
=100+15
=115
所以26+(74+15)=(26+74)+15,运用了加法结合律。
(3)25×37×4
=25×4×37
=100×37
=3700
所以25×37×4=25×4×37,运用了乘法交换律。
(4)9×37+9×63
=9×(37+63)
=9×100
=900
所以9×37+9×63=9×(37+63),运用了乘法分配律。
13.(1) 42 25
(2) 54 3 12 3
(3) 15 28 72
(4) 14 6 10
【分析】根据乘法分配律:(a+b)×c=a×c+b×c或(a-b)×c=a×c-b×c,即可解答。
【详解】(1)(42+25)×4=42×4+25×4
(2)(54+12)×3=54×3+12×3
(3)15×28+15×72=15×(28+72)
(4)14×10+6×10=(14+6)×10
【点睛】本题主要考查乘法运算律的应用,需熟练掌握。
14. > < = =
【详解】(1)运用乘法分配律:a×(b+c)=a×b+a×c,将算式25×34+25×40化简为25×(34+40),再进行比较;
(2)运用乘法分配律:a×(b+c)=a×b+a×c,将算式(75-20)×8化简为75×8-20×8,再进行比较;
(3)运用乘法分配律:a×(b+c)=a×b+a×c,将算式43×101-43×2 化简为43×(101-2),再进行比较;
(4)运用除法的性质:a÷b÷c=a÷(b×c),将算式 450÷9÷5化简为450÷(9×5),再进行比较。
【点睛】根据分析:
(1)25×34+25×40 =25×(34+40),25×(34×40)>25×(34+40),所以25×(34×40)>25×34+25×40 ;
(2)(75-20)×8 =75×8-20×8,75×8-20×8<75×8-20,所以(75-20)×8<75×8-20;
(3)43×101-43×2=43×(101-2)=43×99,所以99×43=43×101-43×2;
(4)450÷9÷5=450÷(9×5),所以450÷9÷5=450÷(9×5)。
15. 150 100 75
【分析】
观察第一行图形,可以得知2个等于3个;由第二行图形可以得知3个等于4个;把第二行的3个用2个替换,可以得知2个等于4个,即1个等于2个;把第三行中的用替换,可以得知:++++=400,即+=400,再把4个用3个替换,即可算出等于多少,再把的数值代入到第二个算式中,即可算出等于多少。据此解答。
【详解】由分析可知:
=+
+++=400
++++=400
+=400
+++=400
=400÷4=100
+100=400
=400-100=300
=300÷4=75
=75+75=150
【点睛】本题主要考查等量代换,解决此题的关键是根据题目信息正确找到三种图形之间的关系。
16.√
【分析】根据乘法分配律的意义,两个数的和同一个数相乘,等于把两个加数分别同这个数相乘,再把两个积加起来,结果不变,用字母表示为:(a+b)×c=a×c+b×c;据此进行判断即可。
【详解】35×37+65×37
=(35+65)×37
=100×37
=3700
所以原题的说法正确。
故答案为:√
【点睛】本题考查了乘法分配律的应用,灵活使用运算律可使计算简便。
17.√
【分析】根据乘法分配律的意义:两个数和一个数相乘,可以先把它们分别与这个数相乘,再将积相加。据此解答。
【详解】(a+b)c=ac+bc,运用了乘法分配律。原题说法正确。
故答案为:√
【点睛】此题考查了乘法分配律。要求熟练掌握并灵活运用。
18.×
【分析】28×(□+2)利用乘法分配律写成28×□+28×2,即28×□+56,“小马虎”把28×(□+2)错算成28×□+2,结果相差56-2=54。
【详解】“小马虎”把28×(□+2)错算成28×□+2,结果相差1。这句话错误,应该相差54。
故答案为:×
19.√
【详解】例如:102×25-2×25观察发现符合乘法分配律的定式,即(a+b)×c=a×c+b×c,使用乘法分配律计算更加简单,所以102×25-2×25就可用简便计算,即102×25-2×25=(102-2)×25=100×25=2500。45×23-15×2观察发现不能使用简便计算,就按照运算顺序计算即可,即45×23-15×2=1035-30=1005。所以原题表述正确。
故答案为:√
20.×
【分析】除法的性质:一个数连续除以两个数,等于除以这两个数的积。据此解答即可。
【详解】420÷7÷5=420÷﹙7×5﹚。原题说法错误。
故答案为:×
21.×
【分析】乘法交换律是指一种计算定律,两个数相乘,交换因数的位置,它们的积不变;乘法结合律是指三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变,据此判断即可。
【详解】125×27×8
=27×125×8
=27×(125×8)
=27×1000
=27000
算式125×27×8=27×(125×8)运用了乘法交换律和乘法结合律,原题说法错误。
故答案为:×
22.×
【分析】乘法分配律:a×(b+c)=a×b+a×c,据此即可解答。
【详解】104×25=(100+4)×25=100×25+4×25,原说法错误。
故答案为:×
【点睛】熟练掌握乘法分配律的计算方法是解答本题的关键。
23.1500
【分析】这道题先利用乘法交换律,交换3与4的位置,再根据乘法结合律,把25与4,3与5结合先乘,再把所得的积相乘。
【详解】
24.5555;2727;9999;3434
【分析】(1)将101看作100和1,先计算出100乘55的结果,再计算出1乘55的结果,最后将这两个结果相加;
(2)将101看作100和1,先计算出100乘27的结果,再计算出1乘27的结果,最后将这两个结果相加;
(3)将101看作100和1,先计算出100乘99的结果,再计算出1乘99的结果,最后将这两个结果相加;
(4)将101看作100和1,先计算出34乘100的结果,再计算出34乘1的结果,最后将这两个结果相加;据此计算。
【详解】(1)101×55
=(100+1)×55
=100×55+1×55
=5500+55
=5555
(2)101×27
=(100+1)×27
=100×27+1×27
=2700+27
=2727
(3)101×99
=(100+1)×99
=100×99+1×99
=9900+99
=9999
(4)34×101
=34×(100+1)
=34×100+34×1
=3400+34
=3434
25.见解析
【分析】两个数相加,交换两个加数的位置,和不变。这叫作加法的交换律。
三个数相加,先把前两个数相加,或者先把后两数相加,和不变。这叫作加法结合律。
两个数相乘,交换两个因数的位置,积不变。这叫作乘法的交换律。
三个数相加乘,先把前两个数相乘,或者先把后两数相乘,积不变。这叫作乘法结合律。
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。这叫作乘法分配律。
【详解】
名称 举例 用字母表示
加法交换律
加法结合律 (15+28)+22=15+(28+22)
乘法交换律 15×28=28×15
乘法结合律 (28×15)×4=28×(15×4)
乘法分配律 25×(4+20)=25×4+25×20
26.150;2;2;150;(算式不唯一)
600;2;2;600;(算式不唯一)
发现:两个数相乘,交换两个因数的位置,积不变。
【分析】先写出一个乘法算式,并计算出积;然后交换两个因数的位置,再计算出它们的积,通过比较即可解答。
【详解】150×2=300,2×150=300,即:150×2=2×150。
600×2=1200,2×600=1200,即:600×2=2×600。(算式不唯一)
我发现:两个数相乘,交换两个因数的位置,积不变。
27.乘法分配律
【分析】观察竖式可知,50代表个位的2乘25的结果,即2×25;250代表十位的1乘25的结果,即10×25;300代表50与250相加;就是把12分解成(10+2),运用了乘法分配律计算,据此解答即可。
【详解】25×12
=25×(10+2)
=25×10+25×2
=250+50
=300
所以,运用了乘法分配律。
28.(1)坐得下;(2)见详解
【分析】(1)把第一个会场的座位和第二个会场的座位数算出来。然后和全区小学参赛的人数比较,可判断。
(2)根据信息一和二可以算出两个会场的总座位数。再根据信息三可以知道参赛的人数,那么就可以提出还剩多少个座位?答案不唯一,合理即可。
【详解】(1)15×17+15×13
=15×(17+13)
=15×30
=450(人)
45×9=405(人)
450>405
答:这两个会场坐得下。
(2)问题:还剩多少个座位?
450-405=45(个)
答:还剩45个座位。
29.480千米
【分析】根据题意可知,两人同时出发,相向而行,两人行驶路程和就是两地的距离。根据路程=速度×时间,分别求出两人行驶的路程,再相加求和。计算时可以根据乘法分配律进行简算。
【详解】65×4+55×4
=(65+55)×4
=120×4
=480(千米)
答:两地相距480千米。
30.27份
【分析】先用27000除以125算出平均每个书柜放多少份档案,再除以8即可算出平均每层放多少份档案。计算时,利用除法的性质:a÷b÷c=a÷(b×c)可使计算简便。据此解答。
【详解】27000÷125÷8
=27000÷(125×8)
=27000÷1000
=27(份)
答:平均每层27份档案。
31.(1)150块;(2)5块
【分析】(1)总共发的月饼块数减去五仁月饼、莲蓉月饼的块数,等于豆沙月饼的块数。
(2)86乘2等于B区和C区的来宾人数和,总共发的月饼块数860除以B区和C区的来宾人数和等于平均每人分得的月饼块数。
【详解】(1)550-165-235
=550-(165+235)
=550-400
=150(块)
答:豆沙月饼一共有150块。
(2)860÷(86×2)
=860÷86÷2
=10÷2
=5(块)
答:平均每人分得5块月饼。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
