新课标A版必修2第二章点、直线、平面之间的位置关系单元测试题
文档属性
| 名称 | 新课标A版必修2第二章点、直线、平面之间的位置关系单元测试题 |  | |
| 格式 | rar | ||
| 文件大小 | 132.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-02-04 00:42:00 | ||
图片预览

文档简介
一、选择题
1.若直线a不平行于平面,则下列结论成立的是( )
A. 内所有的直线都与a异面; B. 内不存在与a平行的直线;
C. 内所有的直线都与a相交; D.直线a与平面有公共点.
2.已知两个平面垂直,下列命题
①一个平面内的已知直线必垂直于另一个平面的任意一条直线;
②一个平面内的已知直线必垂直于另一个平面的无数条直线;
③一个平面内的任一条直线必垂直于另一个平面;
④过一个平面内任意一点作交线的垂线,则垂线必垂直于另一个平面.
其中正确的个数是( ) A.3 B.2 C.1 D.0
3.空间四边形ABCD中,若,则与所成角为
A、 B、 C、 D、
4. 给出下列命题:
(1)直线a与平面不平行,则a与平面内的所有直线都不平行;
(2)直线a与平面不垂直,则a与平面内的所有直线都不垂直;
(3)异面直线a、b不垂直,则过a的任何平面与b都不垂直;
(4)若直线a和b共面,直线b和c共面,则a和c共面
其中错误命题的个数为( ) (A)0 (B) 1 (C)2 (D)3
5.正方体ABCD-A1B1C1D1中,与对角线AC1异面的棱有( )条 A 3 B 4 C 6 D 8
6. 点P为ΔABC所在平面外一点,PO⊥平面ABC,垂足为O,若PA=PB=PC,则点O是ΔABC的( ) (A)内心 (B)外心 (C)重心 (D)垂心
7.如图长方体中,AB=AD=2,CC1=,则二面角
C1—BD—C的大小为( )
(A)300 (B)450 (C)600 (D)900
8.直线a,b,c及平面α,β,γ,下列命题正确的是( )
A、若aα,bα,c⊥a, c⊥b 则c⊥α B、若bα, a//b 则 a//α
C、若a//α,α∩β=b 则a//b D、若a⊥α, b⊥α 则a//b
9.平面与平面平行的条件可以是( )
A.内有无穷多条直线与平行; B.直线a//,a//
C.直线a,直线b,且a//,b// D.内的任何直线都与平行
10、 a, b是异面直线,下面四个命题:
①过a至少有一个平面平行于b; ②过a至少有一个平面垂直于b;
③至多有一条直线与a,b都垂直;④至少有一个平面与a,b都平行。
其中正确命题的个数是( )A 0 B 1 C 2 D 3
二、填空题
11.已知直线a//平面,平面//平面,则a与的位置关系为 .
12.已知直线a⊥直线b, a//平面,则b与的位置关系为 .
13如图,ABC是直角三角形,ACB=,PA平面ABC,此图形中有 个直角三角形
14.α、β是两个不同的平面,m、n是平面α及β之外的两条不同直线,
给出四个论断:
① m ( n ②α(β ③ m (β ④ n (α
以其中三个论断作为条件,余下一个论断作为结论,写出你认为
正确的一个命题:______________________________________.
三、解答题
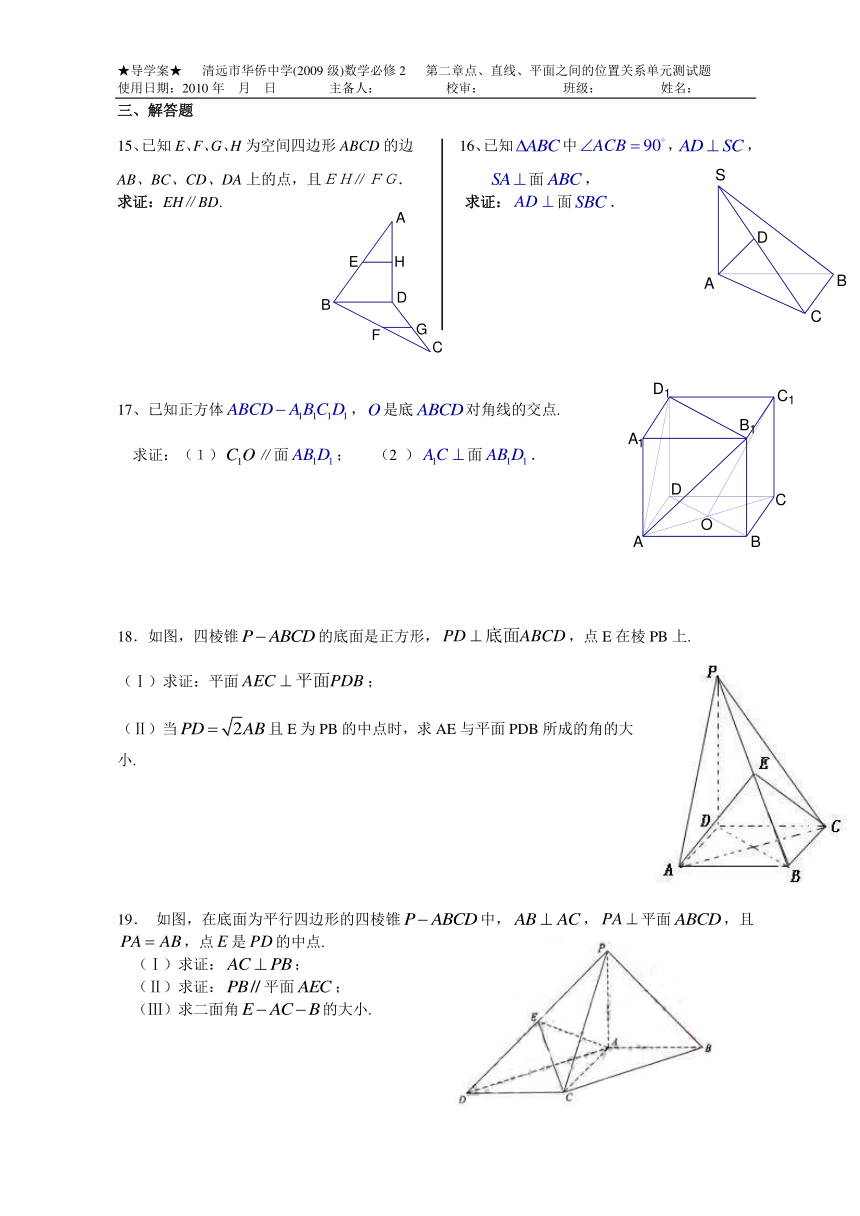
15、已知E、F、G、H为空间四边形ABCD的边 16、已知中,,
AB、BC、CD、DA上的点,且EH∥FG. 面,
求证:EH∥BD. 求证:面.
17、已知正方体,是底对角线的交点.
求证:(1)∥面; (2 )面.
18.如图,四棱锥的底面是正方形,,点E在棱PB上.
(Ⅰ)求证:平面;
(Ⅱ)当且E为PB的中点时,求AE与平面PDB所成的角的大小.
19. 如图,在底面为平行四边形的四棱锥中,,平面,且,点是的中点.
(Ⅰ)求证:;
(Ⅱ)求证:平面;
(Ⅲ)求二面角的大小.
参考答案
1.D;2.C;3.D;4.D;5.C;6.B;7.A;8.D;9.D;10.C
11.平行或在平面内; 12. 平行或在平面内; 13.4; 14.若②③④则①
15、证明:面,面
面
又面,面面,
16、证明:
又面
面
又
面
17、证明:(1)连结,设
连结, 是正方体 是平行四边形
且
又分别是的中点,且
是平行四边形
面,面
面
(2)面
又,
同理可证,
又
面
18、证明:(Ⅰ)∵四边形ABCD是正方形,∴AC⊥BD,
∵,
∴PD⊥AC,∴AC⊥平面PDB,
∴平面.
(Ⅱ)设AC∩BD=O,连接OE,
由(Ⅰ)知AC⊥平面PDB于O,
∴∠AEO为AE与平面PDB所的角,
∴O,E分别为DB、PB的中点,
∴OE//PD,,又∵,
∴OE⊥底面ABCD,OE⊥AO,
在Rt△AOE中,,
∴,即AE与平面PDB所成的角的大小为.
19、【解】
(Ⅰ)PA平面ABCD,
AB是PB在平面ABCD上的射影,
又ABAC,AC平面ABCD,
ACPB.
(Ⅱ)连接BD,与AC相交与O,连接EO,
ABCD是平行四边形 O是BD的中点
又E是PD的中点, EOPB.
又PB平面AEC,EO平面AEC,
PB平面AEC,
(Ⅲ)如图,取AD的中点F,连EF,FO,则
EF是△PAD的中位线, (EFPA又平面, (EF(平面
同理FO是△ADC的中位线,(FOAB(FO(AC由三垂线定理可知((EOF是二面角E-AC-D的平面角. 又FO=AB=PA=EF。
((EOF=45(而二面角与二面角E-AC-D互补,
故所求二面角的大小为135(.
1.若直线a不平行于平面,则下列结论成立的是( )
A. 内所有的直线都与a异面; B. 内不存在与a平行的直线;
C. 内所有的直线都与a相交; D.直线a与平面有公共点.
2.已知两个平面垂直,下列命题
①一个平面内的已知直线必垂直于另一个平面的任意一条直线;
②一个平面内的已知直线必垂直于另一个平面的无数条直线;
③一个平面内的任一条直线必垂直于另一个平面;
④过一个平面内任意一点作交线的垂线,则垂线必垂直于另一个平面.
其中正确的个数是( ) A.3 B.2 C.1 D.0
3.空间四边形ABCD中,若,则与所成角为
A、 B、 C、 D、
4. 给出下列命题:
(1)直线a与平面不平行,则a与平面内的所有直线都不平行;
(2)直线a与平面不垂直,则a与平面内的所有直线都不垂直;
(3)异面直线a、b不垂直,则过a的任何平面与b都不垂直;
(4)若直线a和b共面,直线b和c共面,则a和c共面
其中错误命题的个数为( ) (A)0 (B) 1 (C)2 (D)3
5.正方体ABCD-A1B1C1D1中,与对角线AC1异面的棱有( )条 A 3 B 4 C 6 D 8
6. 点P为ΔABC所在平面外一点,PO⊥平面ABC,垂足为O,若PA=PB=PC,则点O是ΔABC的( ) (A)内心 (B)外心 (C)重心 (D)垂心
7.如图长方体中,AB=AD=2,CC1=,则二面角
C1—BD—C的大小为( )
(A)300 (B)450 (C)600 (D)900
8.直线a,b,c及平面α,β,γ,下列命题正确的是( )
A、若aα,bα,c⊥a, c⊥b 则c⊥α B、若bα, a//b 则 a//α
C、若a//α,α∩β=b 则a//b D、若a⊥α, b⊥α 则a//b
9.平面与平面平行的条件可以是( )
A.内有无穷多条直线与平行; B.直线a//,a//
C.直线a,直线b,且a//,b// D.内的任何直线都与平行
10、 a, b是异面直线,下面四个命题:
①过a至少有一个平面平行于b; ②过a至少有一个平面垂直于b;
③至多有一条直线与a,b都垂直;④至少有一个平面与a,b都平行。
其中正确命题的个数是( )A 0 B 1 C 2 D 3
二、填空题
11.已知直线a//平面,平面//平面,则a与的位置关系为 .
12.已知直线a⊥直线b, a//平面,则b与的位置关系为 .
13如图,ABC是直角三角形,ACB=,PA平面ABC,此图形中有 个直角三角形
14.α、β是两个不同的平面,m、n是平面α及β之外的两条不同直线,
给出四个论断:
① m ( n ②α(β ③ m (β ④ n (α
以其中三个论断作为条件,余下一个论断作为结论,写出你认为
正确的一个命题:______________________________________.
三、解答题
15、已知E、F、G、H为空间四边形ABCD的边 16、已知中,,
AB、BC、CD、DA上的点,且EH∥FG. 面,
求证:EH∥BD. 求证:面.
17、已知正方体,是底对角线的交点.
求证:(1)∥面; (2 )面.
18.如图,四棱锥的底面是正方形,,点E在棱PB上.
(Ⅰ)求证:平面;
(Ⅱ)当且E为PB的中点时,求AE与平面PDB所成的角的大小.
19. 如图,在底面为平行四边形的四棱锥中,,平面,且,点是的中点.
(Ⅰ)求证:;
(Ⅱ)求证:平面;
(Ⅲ)求二面角的大小.
参考答案
1.D;2.C;3.D;4.D;5.C;6.B;7.A;8.D;9.D;10.C
11.平行或在平面内; 12. 平行或在平面内; 13.4; 14.若②③④则①
15、证明:面,面
面
又面,面面,
16、证明:
又面
面
又
面
17、证明:(1)连结,设
连结, 是正方体 是平行四边形
且
又分别是的中点,且
是平行四边形
面,面
面
(2)面
又,
同理可证,
又
面
18、证明:(Ⅰ)∵四边形ABCD是正方形,∴AC⊥BD,
∵,
∴PD⊥AC,∴AC⊥平面PDB,
∴平面.
(Ⅱ)设AC∩BD=O,连接OE,
由(Ⅰ)知AC⊥平面PDB于O,
∴∠AEO为AE与平面PDB所的角,
∴O,E分别为DB、PB的中点,
∴OE//PD,,又∵,
∴OE⊥底面ABCD,OE⊥AO,
在Rt△AOE中,,
∴,即AE与平面PDB所成的角的大小为.
19、【解】
(Ⅰ)PA平面ABCD,
AB是PB在平面ABCD上的射影,
又ABAC,AC平面ABCD,
ACPB.
(Ⅱ)连接BD,与AC相交与O,连接EO,
ABCD是平行四边形 O是BD的中点
又E是PD的中点, EOPB.
又PB平面AEC,EO平面AEC,
PB平面AEC,
(Ⅲ)如图,取AD的中点F,连EF,FO,则
EF是△PAD的中位线, (EFPA又平面, (EF(平面
同理FO是△ADC的中位线,(FOAB(FO(AC由三垂线定理可知((EOF是二面角E-AC-D的平面角. 又FO=AB=PA=EF。
((EOF=45(而二面角与二面角E-AC-D互补,
故所求二面角的大小为135(.
