山东济南天桥区2024-2025学年第二学期八年级数学期末考试试题(含答案)
文档属性
| 名称 | 山东济南天桥区2024-2025学年第二学期八年级数学期末考试试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 343.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-28 18:30:07 | ||
图片预览



文档简介
2024-2025 学年第二学期八年级学业质量监测数学试题
注意事项:
本试题共 6 页,满分为 150 分.考试时间为 120 分钟.
答卷前,请考生务必将自己的姓名、座号和准考证号填写在答题卡上,并同时将考点、姓名、准考证号和座号填写在试卷规定的位置上.
答选择题时,必须使用 2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号;答非选择题时,用 0.5mm 黑色签字笔在答题卡上题号所提示的答题区域作答.答案写在试卷上无效.考试结束后,将本试卷和答题卡一并交回.
第 Ⅰ 卷(选择题共 40 分)
一、选择题(本大题共 10 个小题,每小题 4 分,共 40 分.在每小题给出的四个选项中,只有一项是符合题目要求的).
1.5G 与 AI 时代已经来临,科技全面融入日常生活,推动社会各领域智能化变革,深刻改变人们的生活与工作方式.下列设计的人工智能图标中,是中心对称图形的是( )
A.
2.若 a>b,则下列不等式中成立的是( )
A. a 2 2b D. a+1>b+1
3.下列从左边到右边的变形,是因式分解的是( )
A. m2 3m 4=m(m 3) 4 B. (m+2)(m 2)=m2 4
C. m2 4n2=(m+2n)(m 2n) D. m2 4m 1=(m 2)2 5
4.在平面直角坐标系中,把点 M( 2,1)向左平移 3 个单位长度,再向上平移 2 个单位长度后得到点 N,则 N的坐标为( )
A. ( 4,4) B. ( 5,3) C. (1, 1) D. ( 5, 1)
5.如图,在□ABCD 中,AB = 3,AD = 5,∠ABC 和∠BCD 的角平分线分别交 AD 于点 E 和点 F,则 EF 的值为( )
A.3 B.2 C.2.5 D.1
(第5题图) (第8题图) (第10题图)
6.若关于 x 的一元二次方程 x 2x + m = 0 有实数根,则 m 的值不可能是( )
A.1 B.2 C. 1 D. 2
7.若分式的值为 0,则 x 的值为( )
A.1 B.2 C. 1 D. 2
8.如图,在菱形 ABCD 中,点 E,点 F 分别是 AD,CD 的中点,AB=6,且∠D=60°,则 EF 的长为( )
A.不确定 B.3.5 C.6 D.3
9.下列说法正确的是( )
A.对角线相等的四边形是矩形 B.对角线互相垂直的四边形是菱形
C.对角线相等且互相平分的四边形是矩形 D.对角线互相垂直且相等的四边形是正方形
10.如图,△A1A2A3,△A4A5A6,△A7A8A9,…,△A3n﹣2A3n﹣1A3n(n 为正整数)均为等边三角形,它们的边长依次是 2,4,6,…,2n,顶点 A ,A ,A ,…,A3n均在 y 轴上,点 O 是所有等边三角形的中心(等边三角形各内角角平分线的交点),点 A2024的坐标为( )
A.(675, ) B.(0,) C.(674, ) D.(0, )
第 Ⅱ 卷(非选择题共 110 分)
二、填空题:(本大题共 5 个小题,每小题 4 分,共 20 分.)
11.分解因式:2m2 6m= .
12.计算 的结果是 .
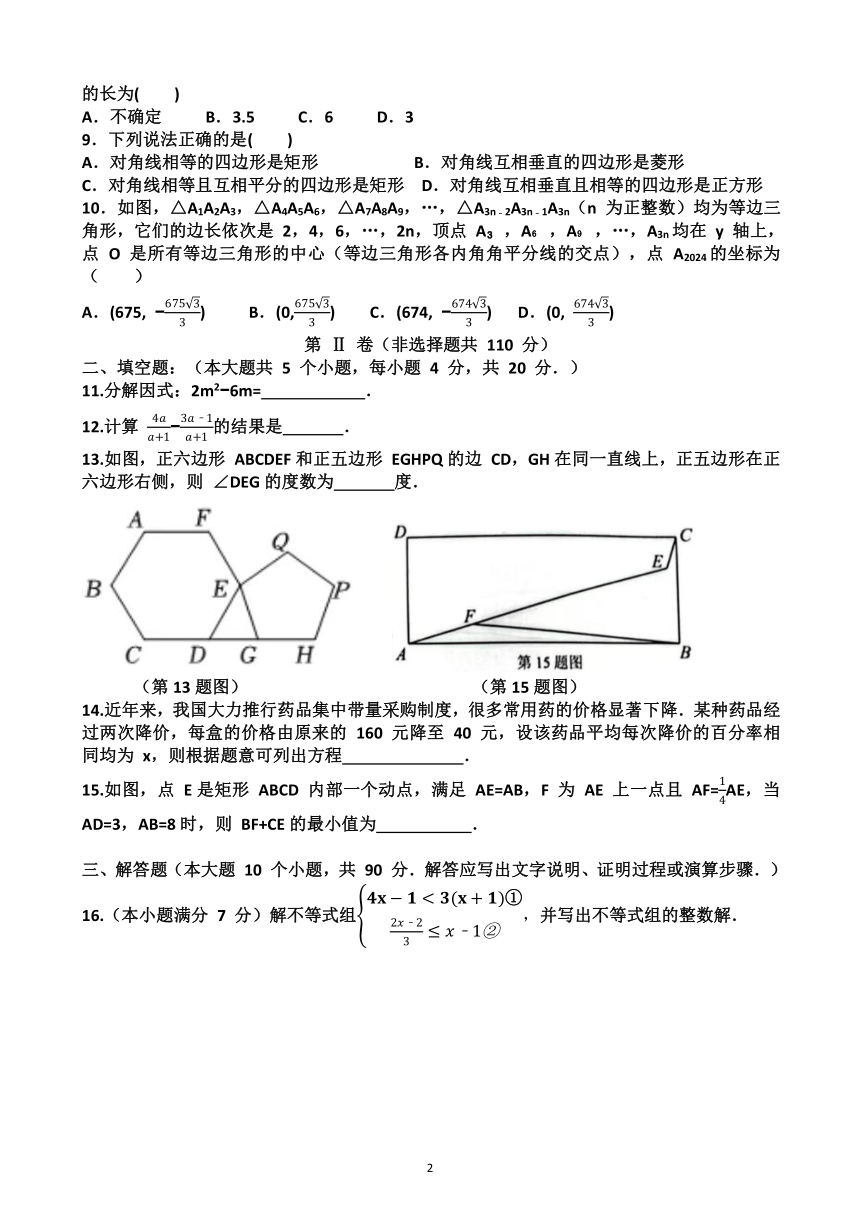
13.如图,正六边形 ABCDEF和正五边形 EGHPQ的边 CD,GH在同一直线上,正五边形在正六边形右侧,则 ∠DEG的度数为 度.
(第13题图) (第15题图)
14.近年来,我国大力推行药品集中带量采购制度,很多常用药的价格显著下降.某种药品经过两次降价,每盒的价格由原来的 160 元降至 40 元,设该药品平均每次降价的百分率相同均为 x,则根据题意可列出方程 .
15.如图,点 E是矩形 ABCD 内部一个动点,满足 AE=AB,F 为 AE 上一点且 AF=AE,当AD=3,AB=8时,则 BF+CE的最小值为 .
三、解答题(本大题 10 个小题,共 90 分.解答应写出文字说明、证明过程或演算步骤.)
16.(本小题满分 7 分)解不等式组,并写出不等式组的整数解.
17.(本小题满分 7 分)先化简,再求值:(1+)·,其中x= .
18.(本小题满分 7 分)如图,E,F是平行四边形ABCD的对角线 AC上两点,且 AE=CF,AC与 BD相交于点 O.求证:BE∥DF.
19.(本小题满分 8 分)(1)因式分解:4x2y 4xy2+y3. (2)解方程:x2+5x+6=0.
20.(本小题满分 8 分)如图,在平面直角坐标系 xOy中,△ABC的顶点坐标分别为 A( 3, 2),B( 1, 1),C(0, 3).
(1)把 △ABC向上平移 5 个单位长度得 △A1B1C1(A,B,C的对应点分别是 A1,B1,C1),请画出 △A1B1C1;
(2)以点 O为旋转中心,将 △ABC逆时针旋转 90 得 △A2B2C2,画出△A2B2C2(A,B,C的对应点分别是 A2,B2,C2);
(3)连接 A1C2与 B1C2,求 △A1B1C2的面积;
21.(本小题满分 9 分)
如图,在四边形 ABCD中,AB∥DC,AB=AD,对角线 AC、BD交于点 O,AC平分 ∠BAD,过点 C作 CE⊥AB,交 AB的延长线于点 E,连接 OE.
(1)求证:四边形 ABCD是菱形.
(2)若 AB=5,BD=6,求 OE的长.
22.(本小题满分 10 分)
2025 年,DeepSeek 掀起全球热潮,其发布的开源大模型堪称 “低成本,高效率” 的典范,为世界贡献了 “中国智慧”.已知某公司拥有甲、乙两个数据中心,甲数据中心通过应用 DeepSeek,使其数据迁移速度提升至乙数据中心的 5 倍,且甲数据中心迁移 100TB 数据比乙数据中心迁移 30TB 数据所需时间少 5 小时.
(1)分别求甲、乙两个数据中心的数据迁移速度(单位:TB / 小时);
(2)现公司要求甲、乙两个数据中心协同完成一项紧急任务,共用 8 小时至少完成 56TB 的数据迁移,且同一时间只能一个数据中心工作,试问:不考虑其他因素,甲数据中心至少需要工作多少小时?
23.(本小题满分 10 分)我国著名的数学家华罗庚先生曾经说过:“数缺形时少直观,形缺数时难入微”,数形结合是数学学习的一种重要的思想方法,借助图的直观性,可以帮助理解数学问题.小明同学在学习了因式分解后,对用图形拼接验证因式分解的方法非常感兴趣,他利用了此方法做了以下研究.
(1)如图 1,大正方形的边长为 a,小明将大正方形拆分为边长为 b的小正方形 A和两个矩形 B,C,然后将矩形 C拼接在了 C′的位置,请写出小明验证的因式分解的公式是 ;
(2)在经过了一些尝试后小明同学又利用图形的拆分和拼接方法验证了多项式:(a+m)(a+n) (b+m)(b+n)的因式分解;那么他是如何验证的呢?在下面的图 2 中画出他拆分和拼接的示意图;并借此因式分解:(a+m)(a+n) (b+m)(b+n);
(3)在对多项式 (a+m)(a+n) (b+m)(b+n)因式分解后,小明还发现了它可以用于巧算这样的计算题:870×830 370×330;小明是怎样巧算的这道题,请写出计算过程.
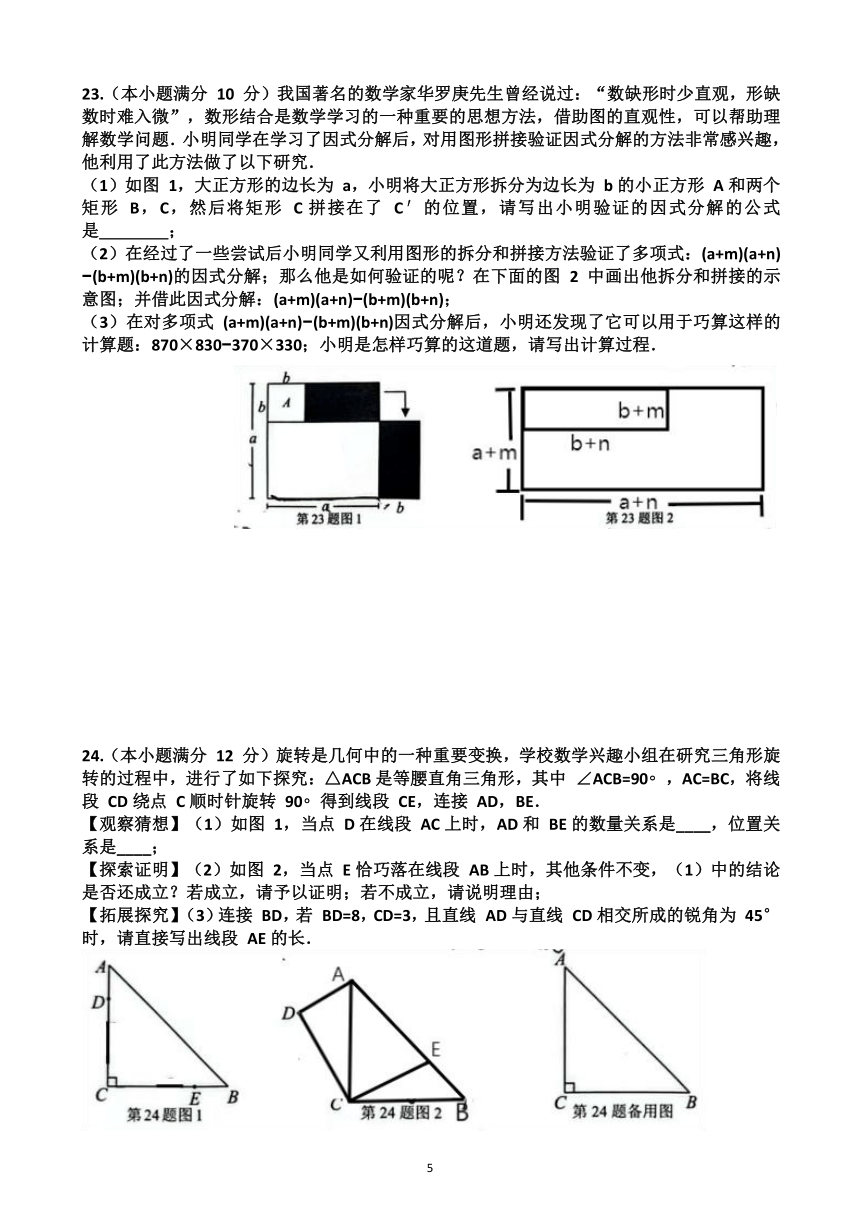
24.(本小题满分 12 分)旋转是几何中的一种重要变换,学校数学兴趣小组在研究三角形旋转的过程中,进行了如下探究:△ACB是等腰直角三角形,其中 ∠ACB=90 ,AC=BC,将线段 CD绕点 C顺时针旋转 90 得到线段 CE,连接 AD,BE.
【观察猜想】(1)如图 1,当点 D在线段 AC上时,AD和 BE的数量关系是____,位置关系是____;
【探索证明】(2)如图 2,当点 E恰巧落在线段 AB上时,其他条件不变,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;
【拓展探究】(3)连接 BD,若 BD=8,CD=3,且直线 AD与直线 CD相交所成的锐角为 45°时,请直接写出线段 AE的长.
25.(本小题满分 12 分)
如图,在平面直角坐标系中,O为坐标原点,矩形 OABC的顶点 A(8,0),C(0,6),将矩形 OABC的一个角沿直线 BD折叠,使得点 A落在对角线 OB上的点 E处,折痕与x轴交于点 D.
(1)线段 OB的长度为 ;
(2)求直线 BD所对应的函数表达式;
(3)求点 E的坐标;
(4)若点 Q在线段 BD上,在线段 BC上是否存在点 P,使以点 D,E,P,Q为顶点的四边形是平行四边形?若存在,请求出点 P的坐标;若不存在,请说明理由.
答案
一、选择题(本大题共 10 个小题,每小题 4 分,共 40 分.在每小题给出的四个选项中,只有一项是符合题目要求的).
1.5G 与 AI 时代已经来临,科技全面融入日常生活,推动社会各领域智能化变革,深刻改变人们的生活与工作方式.下列设计的人工智能图标中,是中心对称图形的是( A )
A.
2.若 a>b,则下列不等式中成立的是( D )
A. a 2 2b D. a+1>b+1
3.下列从左边到右边的变形,是因式分解的是( C )
A. m2 3m 4=m(m 3) 4 B. (m+2)(m 2)=m2 4
C. m2 4n2=(m+2n)(m 2n) D. m2 4m 1=(m 2)2 5
4.在平面直角坐标系中,把点 M( 2,1)向左平移 3 个单位长度,再向上平移 2 个单位长度后得到点 N,则 N的坐标为( B )
A. ( 4,4) B. ( 5,3) C. (1, 1) D. ( 5, 1)
5.如图,在□ABCD 中,AB = 3,AD = 5,∠ABC 和∠BCD 的角平分线分别交 AD 于点 E 和点 F,则 EF 的值为( D )
A.3 B.2 C.2.5 D.1
(第5题图) (第8题图) (第10题图)
6.若关于 x 的一元二次方程 x 2x + m = 0 有实数根,则 m 的值不可能是( B )
A.1 B.2 C. 1 D. 2
7.若分式的值为 0,则 x 的值为( A )
A.1 B.2 C. 1 D. 2
8.如图,在菱形 ABCD 中,点 E,点 F 分别是 AD,CD 的中点,AB=6,且∠D=60°,则 EF 的长为( D )
A.不确定 B.3.5 C.6 D.3
9.下列说法正确的是( C )
A.对角线相等的四边形是矩形 B.对角线互相垂直的四边形是菱形
C.对角线相等且互相平分的四边形是矩形 D.对角线互相垂直且相等的四边形是正方形
10.如图,△A1A2A3,△A4A5A6,△A7A8A9,…,△A3n﹣2A3n﹣1A3n(n 为正整数)均为等边三角形,它们的边长依次是 2,4,6,…,2n,顶点 A ,A ,A ,…,A3n均在 y 轴上,点 O 是所有等边三角形的中心(等边三角形各内角角平分线的交点),点 A2024的坐标为( A )
A.(675, ) B.(0,) C.(674, ) D.(0, )
第 Ⅱ 卷(非选择题共 110 分)
二、填空题:(本大题共 5 个小题,每小题 4 分,共 20 分.)
11.分解因式:2m2 6m= 2m(m﹣3) .
12.计算 的结果是 1 .
13.如图,正六边形 ABCDEF和正五边形 EGHPQ的边 CD,GH在同一直线上,正五边形在正六边形右侧,则 ∠DEG的度数为 48 度.
(第13题图) (第15题图)
14.近年来,我国大力推行药品集中带量采购制度,很多常用药的价格显著下降.某种药品经过两次降价,每盒的价格由原来的 160 元降至 40 元,设该药品平均每次降价的百分率相同均为 x,则根据题意可列出方程 160(1﹣x)2=40 .
15.如图,点 E是矩形 ABCD 内部一个动点,满足 AE=AB,F 为 AE 上一点且 AF=AE,当AD=3,AB=8时,则 BF+CE的最小值为 .
三、解答题(本大题 10 个小题,共 90 分.解答应写出文字说明、证明过程或演算步骤.)
16.(本小题满分 7 分)解不等式组,并写出不等式组的整数解.
解不等式①得x<4
解不等式②得x≥1
不等式组的解集为1≤x<4
整数解有1,2,3
17.(本小题满分 7 分)先化简,再求值:(1+)·,其中x= .
解原式=·
=x+2
将x= 代入得1.5
18.(本小题满分 7 分)如图,E,F是平行四边形ABCD的对角线 AC上两点,且 AE=CF,AC与 BD相交于点 O.求证:BE∥DF.
证明:连接DE,BF
∵O是平行四边形ABCD对角线交点
∴OA=OC,OB=OD
∵AE=CF
∴OA﹣AE=OC﹣CF
∴OE=OF
∴四边形DEBF是平行四边形
∴BE∥DF
19.(本小题满分 8 分)(1)因式分解:4x2y 4xy2+y3. (2)解方程:x2+5x+6=0.
(1)=y(4x2 4xy+y2)
=y(2x﹣y)2
(2)(x+2)(x+3)=0
x1=﹣2,x2=﹣3
20.(本小题满分 8 分)如图,在平面直角坐标系 xOy中,△ABC的顶点坐标分别为 A( 3, 2),B( 1, 1),C(0, 3).
(1)把 △ABC向上平移 5 个单位长度得 △A1B1C1(A,B,C的对应点分别是 A1,B1,C1),请画出 △A1B1C1;
(2)以点 O为旋转中心,将 △ABC逆时针旋转 90 得 △A2B2C2,画出△A2B2C2(A,B,C的对应点分别是 A2,B2,C2);
(3)连接 A1C2与 B1C2,求 △A1B1C2的面积;
(1)(2)略
(3)6
21.(本小题满分 9 分)
如图,在四边形 ABCD中,AB∥DC,AB=AD,对角线 AC、BD交于点 O,AC平分 ∠BAD,过点 C作 CE⊥AB,交 AB的延长线于点 E,连接 OE.
(1)求证:四边形 ABCD是菱形.
(2)若 AB=5,BD=6,求 OE的长.
证明:∵AB // CD
∴∠CAB =∠DCA
∵AC 为 ∠DAB 的平分线
∴∠CAB =∠DAC
∴∠DCA =∠DAC
∴CD = AD
∵AB = AD
∴AB = CD
∵AB // CD
∴四边形 ABCD 是平行四边形,
∵AD = AB ,
平∴行四边形 ACBD 是菱形;
(2)∵四边形 ABCD 是菱形,对角线 AC , BD 交于点O
∴AC⊥BD , OA = OC =AC,OB = OD =BD
∴OB =BD=3,
在 Rt△AOB 中,∠AOB =90°,
∴OA =4
∵CE⊥AB
∴∠AEC =90°
在 Rt△AEC 中,∠AEC =90°, O为 AC 中点
∴OE =AC= OA =4.
22.(本小题满分 10 分)
2025 年,DeepSeek 掀起全球热潮,其发布的开源大模型堪称 “低成本,高效率” 的典范,为世界贡献了 “中国智慧”.已知某公司拥有甲、乙两个数据中心,甲数据中心通过应用 DeepSeek,使其数据迁移速度提升至乙数据中心的 5 倍,且甲数据中心迁移 100TB 数据比乙数据中心迁移 30TB 数据所需时间少 5 小时.
(1)分别求甲、乙两个数据中心的数据迁移速度(单位:TB / 小时);
(2)现公司要求甲、乙两个数据中心协同完成一项紧急任务,共用 8 小时至少完成 56TB 的数据迁移,且同一时间只能一个数据中心工作,试问:不考虑其他因素,甲数据中心至少需要工作多少小时?
(1)设乙数据中心的数据迁移速度为 x TB /小时,则甲数据中心的数据迁移速度为5x TB/小时
由题意得:﹣=5
解得: x =2
经检验, x =2是原方程的解,且符合题意,
∴5x=5x2=10,
答:甲数据中心的数据迁移速度为10TB/小时,乙数据中心的数据迁移速度为2TB/小时;
(2)设甲数据中心工作 y 小时,则乙数据中心工作(8- y )小时,
由题意得:10y+2(8- y )≥56,
解得: y≥5,
答:甲数据中心至少需要工作5小时.
23.(本小题满分 10 分)我国著名的数学家华罗庚先生曾经说过:“数缺形时少直观,形缺数时难入微”,数形结合是数学学习的一种重要的思想方法,借助图的直观性,可以帮助理解数学问题.小明同学在学习了因式分解后,对用图形拼接验证因式分解的方法非常感兴趣,他利用了此方法做了以下研究.
(1)如图 1,大正方形的边长为 a,小明将大正方形拆分为边长为 b的小正方形 A和两个矩形 B,C,然后将矩形 C拼接在了 C′的位置,请写出小明验证的因式分解的公式是 ;
(2)在经过了一些尝试后小明同学又利用图形的拆分和拼接方法验证了多项式:(a+m)(a+n) (b+m)(b+n)的因式分解;那么他是如何验证的呢?在下面的图 2 中画出他拆分和拼接的示意图;并借此因式分解:(a+m)(a+n) (b+m)(b+n);
(3)在对多项式 (a+m)(a+n) (b+m)(b+n)因式分解后,小明还发现了它可以用于巧算这样的计算题:870×830 370×330;小明是怎样巧算的这道题,请写出计算过程.
(1)a2﹣b2=(a+b)(a﹣b)
(2)(a+m)(a+n) (b+m)(b+n)
=a2+an+ma+mn﹣b2﹣bn﹣mb﹣mn
=(a﹣b)(a+b)﹣(a﹣b)(m+n)
=(a﹣b)(a+b﹣m﹣n)
(3)令a=800,m=70,n=30,b=300
a﹣b=500,a+b+m+n=1200
870×830 370×330
=(800+70)(800+30)﹣(300+70)(300+30)
=500×1200
=600000
24.(本小题满分 12 分)旋转是几何中的一种重要变换,学校数学兴趣小组在研究三角形旋转的过程中,进行了如下探究:△ACB是等腰直角三角形,其中 ∠ACB=90 ,AC=BC,将线段 CD绕点 C顺时针旋转 90 得到线段 CE,连接 AD,BE.
【观察猜想】(1)如图 1,当点 D在线段 AC上时,AD和 BE的数量关系是____,位置关系是____;
【探索证明】(2)如图 2,当点 E恰巧落在线段 AB上时,其他条件不变,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;
【拓展探究】(3)连接 BD,若 BD=8,CD=3,且直线 AD与直线 CD相交所成的锐角为 45°时,请直接写出线段 AE的长.
(1)AD=BE AD⊥BE
(2)不变
(3)或
25.(本小题满分 12 分)
如图,在平面直角坐标系中,O为坐标原点,矩形 OABC的顶点 A(8,0),C(0,6),将矩形 OABC的一个角沿直线 BD折叠,使得点 A落在对角线 OB上的点 E处,折痕与x轴交于点 D.
(1)线段 OB的长度为 ;
(2)求直线 BD所对应的函数表达式;
(3)求点 E的坐标;
(4)若点 Q在线段 BD上,在线段 BC上是否存在点 P,使以点 D,E,P,Q为顶点的四边形是平行四边形?若存在,请求出点 P的坐标;若不存在,请说明理由.
(1)由题意,得:点 B 的坐标为(8,6), OA=8,AB = OC =6,
∴OB ==10
(2)设 AD = a ,则 DE = a , OD =8- a,OE = OB - BE =10-6=4
∵OD2= OE2+ DE2 ,即(8- a )2=42+ a2
∴a =3,
∴OD =5,
∴点 D 的坐标为(5,0).
设直线 BD 所对应的函数表达式为y =ka+ b ( k≠0)
将B (8,6), D (5,0)代入 y= ka + b ,得:
解得
∴直线 BD 所对应的函数表达式为 y =2x﹣10
(3)(,)
(4)存在,P(5,6)
注意事项:
本试题共 6 页,满分为 150 分.考试时间为 120 分钟.
答卷前,请考生务必将自己的姓名、座号和准考证号填写在答题卡上,并同时将考点、姓名、准考证号和座号填写在试卷规定的位置上.
答选择题时,必须使用 2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号;答非选择题时,用 0.5mm 黑色签字笔在答题卡上题号所提示的答题区域作答.答案写在试卷上无效.考试结束后,将本试卷和答题卡一并交回.
第 Ⅰ 卷(选择题共 40 分)
一、选择题(本大题共 10 个小题,每小题 4 分,共 40 分.在每小题给出的四个选项中,只有一项是符合题目要求的).
1.5G 与 AI 时代已经来临,科技全面融入日常生活,推动社会各领域智能化变革,深刻改变人们的生活与工作方式.下列设计的人工智能图标中,是中心对称图形的是( )
A.
2.若 a>b,则下列不等式中成立的是( )
A. a 2 2b D. a+1>b+1
3.下列从左边到右边的变形,是因式分解的是( )
A. m2 3m 4=m(m 3) 4 B. (m+2)(m 2)=m2 4
C. m2 4n2=(m+2n)(m 2n) D. m2 4m 1=(m 2)2 5
4.在平面直角坐标系中,把点 M( 2,1)向左平移 3 个单位长度,再向上平移 2 个单位长度后得到点 N,则 N的坐标为( )
A. ( 4,4) B. ( 5,3) C. (1, 1) D. ( 5, 1)
5.如图,在□ABCD 中,AB = 3,AD = 5,∠ABC 和∠BCD 的角平分线分别交 AD 于点 E 和点 F,则 EF 的值为( )
A.3 B.2 C.2.5 D.1
(第5题图) (第8题图) (第10题图)
6.若关于 x 的一元二次方程 x 2x + m = 0 有实数根,则 m 的值不可能是( )
A.1 B.2 C. 1 D. 2
7.若分式的值为 0,则 x 的值为( )
A.1 B.2 C. 1 D. 2
8.如图,在菱形 ABCD 中,点 E,点 F 分别是 AD,CD 的中点,AB=6,且∠D=60°,则 EF 的长为( )
A.不确定 B.3.5 C.6 D.3
9.下列说法正确的是( )
A.对角线相等的四边形是矩形 B.对角线互相垂直的四边形是菱形
C.对角线相等且互相平分的四边形是矩形 D.对角线互相垂直且相等的四边形是正方形
10.如图,△A1A2A3,△A4A5A6,△A7A8A9,…,△A3n﹣2A3n﹣1A3n(n 为正整数)均为等边三角形,它们的边长依次是 2,4,6,…,2n,顶点 A ,A ,A ,…,A3n均在 y 轴上,点 O 是所有等边三角形的中心(等边三角形各内角角平分线的交点),点 A2024的坐标为( )
A.(675, ) B.(0,) C.(674, ) D.(0, )
第 Ⅱ 卷(非选择题共 110 分)
二、填空题:(本大题共 5 个小题,每小题 4 分,共 20 分.)
11.分解因式:2m2 6m= .
12.计算 的结果是 .
13.如图,正六边形 ABCDEF和正五边形 EGHPQ的边 CD,GH在同一直线上,正五边形在正六边形右侧,则 ∠DEG的度数为 度.
(第13题图) (第15题图)
14.近年来,我国大力推行药品集中带量采购制度,很多常用药的价格显著下降.某种药品经过两次降价,每盒的价格由原来的 160 元降至 40 元,设该药品平均每次降价的百分率相同均为 x,则根据题意可列出方程 .
15.如图,点 E是矩形 ABCD 内部一个动点,满足 AE=AB,F 为 AE 上一点且 AF=AE,当AD=3,AB=8时,则 BF+CE的最小值为 .
三、解答题(本大题 10 个小题,共 90 分.解答应写出文字说明、证明过程或演算步骤.)
16.(本小题满分 7 分)解不等式组,并写出不等式组的整数解.
17.(本小题满分 7 分)先化简,再求值:(1+)·,其中x= .
18.(本小题满分 7 分)如图,E,F是平行四边形ABCD的对角线 AC上两点,且 AE=CF,AC与 BD相交于点 O.求证:BE∥DF.
19.(本小题满分 8 分)(1)因式分解:4x2y 4xy2+y3. (2)解方程:x2+5x+6=0.
20.(本小题满分 8 分)如图,在平面直角坐标系 xOy中,△ABC的顶点坐标分别为 A( 3, 2),B( 1, 1),C(0, 3).
(1)把 △ABC向上平移 5 个单位长度得 △A1B1C1(A,B,C的对应点分别是 A1,B1,C1),请画出 △A1B1C1;
(2)以点 O为旋转中心,将 △ABC逆时针旋转 90 得 △A2B2C2,画出△A2B2C2(A,B,C的对应点分别是 A2,B2,C2);
(3)连接 A1C2与 B1C2,求 △A1B1C2的面积;
21.(本小题满分 9 分)
如图,在四边形 ABCD中,AB∥DC,AB=AD,对角线 AC、BD交于点 O,AC平分 ∠BAD,过点 C作 CE⊥AB,交 AB的延长线于点 E,连接 OE.
(1)求证:四边形 ABCD是菱形.
(2)若 AB=5,BD=6,求 OE的长.
22.(本小题满分 10 分)
2025 年,DeepSeek 掀起全球热潮,其发布的开源大模型堪称 “低成本,高效率” 的典范,为世界贡献了 “中国智慧”.已知某公司拥有甲、乙两个数据中心,甲数据中心通过应用 DeepSeek,使其数据迁移速度提升至乙数据中心的 5 倍,且甲数据中心迁移 100TB 数据比乙数据中心迁移 30TB 数据所需时间少 5 小时.
(1)分别求甲、乙两个数据中心的数据迁移速度(单位:TB / 小时);
(2)现公司要求甲、乙两个数据中心协同完成一项紧急任务,共用 8 小时至少完成 56TB 的数据迁移,且同一时间只能一个数据中心工作,试问:不考虑其他因素,甲数据中心至少需要工作多少小时?
23.(本小题满分 10 分)我国著名的数学家华罗庚先生曾经说过:“数缺形时少直观,形缺数时难入微”,数形结合是数学学习的一种重要的思想方法,借助图的直观性,可以帮助理解数学问题.小明同学在学习了因式分解后,对用图形拼接验证因式分解的方法非常感兴趣,他利用了此方法做了以下研究.
(1)如图 1,大正方形的边长为 a,小明将大正方形拆分为边长为 b的小正方形 A和两个矩形 B,C,然后将矩形 C拼接在了 C′的位置,请写出小明验证的因式分解的公式是 ;
(2)在经过了一些尝试后小明同学又利用图形的拆分和拼接方法验证了多项式:(a+m)(a+n) (b+m)(b+n)的因式分解;那么他是如何验证的呢?在下面的图 2 中画出他拆分和拼接的示意图;并借此因式分解:(a+m)(a+n) (b+m)(b+n);
(3)在对多项式 (a+m)(a+n) (b+m)(b+n)因式分解后,小明还发现了它可以用于巧算这样的计算题:870×830 370×330;小明是怎样巧算的这道题,请写出计算过程.
24.(本小题满分 12 分)旋转是几何中的一种重要变换,学校数学兴趣小组在研究三角形旋转的过程中,进行了如下探究:△ACB是等腰直角三角形,其中 ∠ACB=90 ,AC=BC,将线段 CD绕点 C顺时针旋转 90 得到线段 CE,连接 AD,BE.
【观察猜想】(1)如图 1,当点 D在线段 AC上时,AD和 BE的数量关系是____,位置关系是____;
【探索证明】(2)如图 2,当点 E恰巧落在线段 AB上时,其他条件不变,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;
【拓展探究】(3)连接 BD,若 BD=8,CD=3,且直线 AD与直线 CD相交所成的锐角为 45°时,请直接写出线段 AE的长.
25.(本小题满分 12 分)
如图,在平面直角坐标系中,O为坐标原点,矩形 OABC的顶点 A(8,0),C(0,6),将矩形 OABC的一个角沿直线 BD折叠,使得点 A落在对角线 OB上的点 E处,折痕与x轴交于点 D.
(1)线段 OB的长度为 ;
(2)求直线 BD所对应的函数表达式;
(3)求点 E的坐标;
(4)若点 Q在线段 BD上,在线段 BC上是否存在点 P,使以点 D,E,P,Q为顶点的四边形是平行四边形?若存在,请求出点 P的坐标;若不存在,请说明理由.
答案
一、选择题(本大题共 10 个小题,每小题 4 分,共 40 分.在每小题给出的四个选项中,只有一项是符合题目要求的).
1.5G 与 AI 时代已经来临,科技全面融入日常生活,推动社会各领域智能化变革,深刻改变人们的生活与工作方式.下列设计的人工智能图标中,是中心对称图形的是( A )
A.
2.若 a>b,则下列不等式中成立的是( D )
A. a 2 2b D. a+1>b+1
3.下列从左边到右边的变形,是因式分解的是( C )
A. m2 3m 4=m(m 3) 4 B. (m+2)(m 2)=m2 4
C. m2 4n2=(m+2n)(m 2n) D. m2 4m 1=(m 2)2 5
4.在平面直角坐标系中,把点 M( 2,1)向左平移 3 个单位长度,再向上平移 2 个单位长度后得到点 N,则 N的坐标为( B )
A. ( 4,4) B. ( 5,3) C. (1, 1) D. ( 5, 1)
5.如图,在□ABCD 中,AB = 3,AD = 5,∠ABC 和∠BCD 的角平分线分别交 AD 于点 E 和点 F,则 EF 的值为( D )
A.3 B.2 C.2.5 D.1
(第5题图) (第8题图) (第10题图)
6.若关于 x 的一元二次方程 x 2x + m = 0 有实数根,则 m 的值不可能是( B )
A.1 B.2 C. 1 D. 2
7.若分式的值为 0,则 x 的值为( A )
A.1 B.2 C. 1 D. 2
8.如图,在菱形 ABCD 中,点 E,点 F 分别是 AD,CD 的中点,AB=6,且∠D=60°,则 EF 的长为( D )
A.不确定 B.3.5 C.6 D.3
9.下列说法正确的是( C )
A.对角线相等的四边形是矩形 B.对角线互相垂直的四边形是菱形
C.对角线相等且互相平分的四边形是矩形 D.对角线互相垂直且相等的四边形是正方形
10.如图,△A1A2A3,△A4A5A6,△A7A8A9,…,△A3n﹣2A3n﹣1A3n(n 为正整数)均为等边三角形,它们的边长依次是 2,4,6,…,2n,顶点 A ,A ,A ,…,A3n均在 y 轴上,点 O 是所有等边三角形的中心(等边三角形各内角角平分线的交点),点 A2024的坐标为( A )
A.(675, ) B.(0,) C.(674, ) D.(0, )
第 Ⅱ 卷(非选择题共 110 分)
二、填空题:(本大题共 5 个小题,每小题 4 分,共 20 分.)
11.分解因式:2m2 6m= 2m(m﹣3) .
12.计算 的结果是 1 .
13.如图,正六边形 ABCDEF和正五边形 EGHPQ的边 CD,GH在同一直线上,正五边形在正六边形右侧,则 ∠DEG的度数为 48 度.
(第13题图) (第15题图)
14.近年来,我国大力推行药品集中带量采购制度,很多常用药的价格显著下降.某种药品经过两次降价,每盒的价格由原来的 160 元降至 40 元,设该药品平均每次降价的百分率相同均为 x,则根据题意可列出方程 160(1﹣x)2=40 .
15.如图,点 E是矩形 ABCD 内部一个动点,满足 AE=AB,F 为 AE 上一点且 AF=AE,当AD=3,AB=8时,则 BF+CE的最小值为 .
三、解答题(本大题 10 个小题,共 90 分.解答应写出文字说明、证明过程或演算步骤.)
16.(本小题满分 7 分)解不等式组,并写出不等式组的整数解.
解不等式①得x<4
解不等式②得x≥1
不等式组的解集为1≤x<4
整数解有1,2,3
17.(本小题满分 7 分)先化简,再求值:(1+)·,其中x= .
解原式=·
=x+2
将x= 代入得1.5
18.(本小题满分 7 分)如图,E,F是平行四边形ABCD的对角线 AC上两点,且 AE=CF,AC与 BD相交于点 O.求证:BE∥DF.
证明:连接DE,BF
∵O是平行四边形ABCD对角线交点
∴OA=OC,OB=OD
∵AE=CF
∴OA﹣AE=OC﹣CF
∴OE=OF
∴四边形DEBF是平行四边形
∴BE∥DF
19.(本小题满分 8 分)(1)因式分解:4x2y 4xy2+y3. (2)解方程:x2+5x+6=0.
(1)=y(4x2 4xy+y2)
=y(2x﹣y)2
(2)(x+2)(x+3)=0
x1=﹣2,x2=﹣3
20.(本小题满分 8 分)如图,在平面直角坐标系 xOy中,△ABC的顶点坐标分别为 A( 3, 2),B( 1, 1),C(0, 3).
(1)把 △ABC向上平移 5 个单位长度得 △A1B1C1(A,B,C的对应点分别是 A1,B1,C1),请画出 △A1B1C1;
(2)以点 O为旋转中心,将 △ABC逆时针旋转 90 得 △A2B2C2,画出△A2B2C2(A,B,C的对应点分别是 A2,B2,C2);
(3)连接 A1C2与 B1C2,求 △A1B1C2的面积;
(1)(2)略
(3)6
21.(本小题满分 9 分)
如图,在四边形 ABCD中,AB∥DC,AB=AD,对角线 AC、BD交于点 O,AC平分 ∠BAD,过点 C作 CE⊥AB,交 AB的延长线于点 E,连接 OE.
(1)求证:四边形 ABCD是菱形.
(2)若 AB=5,BD=6,求 OE的长.
证明:∵AB // CD
∴∠CAB =∠DCA
∵AC 为 ∠DAB 的平分线
∴∠CAB =∠DAC
∴∠DCA =∠DAC
∴CD = AD
∵AB = AD
∴AB = CD
∵AB // CD
∴四边形 ABCD 是平行四边形,
∵AD = AB ,
平∴行四边形 ACBD 是菱形;
(2)∵四边形 ABCD 是菱形,对角线 AC , BD 交于点O
∴AC⊥BD , OA = OC =AC,OB = OD =BD
∴OB =BD=3,
在 Rt△AOB 中,∠AOB =90°,
∴OA =4
∵CE⊥AB
∴∠AEC =90°
在 Rt△AEC 中,∠AEC =90°, O为 AC 中点
∴OE =AC= OA =4.
22.(本小题满分 10 分)
2025 年,DeepSeek 掀起全球热潮,其发布的开源大模型堪称 “低成本,高效率” 的典范,为世界贡献了 “中国智慧”.已知某公司拥有甲、乙两个数据中心,甲数据中心通过应用 DeepSeek,使其数据迁移速度提升至乙数据中心的 5 倍,且甲数据中心迁移 100TB 数据比乙数据中心迁移 30TB 数据所需时间少 5 小时.
(1)分别求甲、乙两个数据中心的数据迁移速度(单位:TB / 小时);
(2)现公司要求甲、乙两个数据中心协同完成一项紧急任务,共用 8 小时至少完成 56TB 的数据迁移,且同一时间只能一个数据中心工作,试问:不考虑其他因素,甲数据中心至少需要工作多少小时?
(1)设乙数据中心的数据迁移速度为 x TB /小时,则甲数据中心的数据迁移速度为5x TB/小时
由题意得:﹣=5
解得: x =2
经检验, x =2是原方程的解,且符合题意,
∴5x=5x2=10,
答:甲数据中心的数据迁移速度为10TB/小时,乙数据中心的数据迁移速度为2TB/小时;
(2)设甲数据中心工作 y 小时,则乙数据中心工作(8- y )小时,
由题意得:10y+2(8- y )≥56,
解得: y≥5,
答:甲数据中心至少需要工作5小时.
23.(本小题满分 10 分)我国著名的数学家华罗庚先生曾经说过:“数缺形时少直观,形缺数时难入微”,数形结合是数学学习的一种重要的思想方法,借助图的直观性,可以帮助理解数学问题.小明同学在学习了因式分解后,对用图形拼接验证因式分解的方法非常感兴趣,他利用了此方法做了以下研究.
(1)如图 1,大正方形的边长为 a,小明将大正方形拆分为边长为 b的小正方形 A和两个矩形 B,C,然后将矩形 C拼接在了 C′的位置,请写出小明验证的因式分解的公式是 ;
(2)在经过了一些尝试后小明同学又利用图形的拆分和拼接方法验证了多项式:(a+m)(a+n) (b+m)(b+n)的因式分解;那么他是如何验证的呢?在下面的图 2 中画出他拆分和拼接的示意图;并借此因式分解:(a+m)(a+n) (b+m)(b+n);
(3)在对多项式 (a+m)(a+n) (b+m)(b+n)因式分解后,小明还发现了它可以用于巧算这样的计算题:870×830 370×330;小明是怎样巧算的这道题,请写出计算过程.
(1)a2﹣b2=(a+b)(a﹣b)
(2)(a+m)(a+n) (b+m)(b+n)
=a2+an+ma+mn﹣b2﹣bn﹣mb﹣mn
=(a﹣b)(a+b)﹣(a﹣b)(m+n)
=(a﹣b)(a+b﹣m﹣n)
(3)令a=800,m=70,n=30,b=300
a﹣b=500,a+b+m+n=1200
870×830 370×330
=(800+70)(800+30)﹣(300+70)(300+30)
=500×1200
=600000
24.(本小题满分 12 分)旋转是几何中的一种重要变换,学校数学兴趣小组在研究三角形旋转的过程中,进行了如下探究:△ACB是等腰直角三角形,其中 ∠ACB=90 ,AC=BC,将线段 CD绕点 C顺时针旋转 90 得到线段 CE,连接 AD,BE.
【观察猜想】(1)如图 1,当点 D在线段 AC上时,AD和 BE的数量关系是____,位置关系是____;
【探索证明】(2)如图 2,当点 E恰巧落在线段 AB上时,其他条件不变,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;
【拓展探究】(3)连接 BD,若 BD=8,CD=3,且直线 AD与直线 CD相交所成的锐角为 45°时,请直接写出线段 AE的长.
(1)AD=BE AD⊥BE
(2)不变
(3)或
25.(本小题满分 12 分)
如图,在平面直角坐标系中,O为坐标原点,矩形 OABC的顶点 A(8,0),C(0,6),将矩形 OABC的一个角沿直线 BD折叠,使得点 A落在对角线 OB上的点 E处,折痕与x轴交于点 D.
(1)线段 OB的长度为 ;
(2)求直线 BD所对应的函数表达式;
(3)求点 E的坐标;
(4)若点 Q在线段 BD上,在线段 BC上是否存在点 P,使以点 D,E,P,Q为顶点的四边形是平行四边形?若存在,请求出点 P的坐标;若不存在,请说明理由.
(1)由题意,得:点 B 的坐标为(8,6), OA=8,AB = OC =6,
∴OB ==10
(2)设 AD = a ,则 DE = a , OD =8- a,OE = OB - BE =10-6=4
∵OD2= OE2+ DE2 ,即(8- a )2=42+ a2
∴a =3,
∴OD =5,
∴点 D 的坐标为(5,0).
设直线 BD 所对应的函数表达式为y =ka+ b ( k≠0)
将B (8,6), D (5,0)代入 y= ka + b ,得:
解得
∴直线 BD 所对应的函数表达式为 y =2x﹣10
(3)(,)
(4)存在,P(5,6)
同课章节目录
