2025年浙江省温州市中考数学适应性试卷(含答案)
文档属性
| 名称 | 2025年浙江省温州市中考数学适应性试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 132.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-28 19:14:10 | ||
图片预览




文档简介
2025年浙江省温州市中考数学适应性试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列各数中为最小的数是( )
A. B. C. D.
2.红河日报年月日报道,玉河铁路是我州连接越南与玉溪的铁路大通道,也是我州连通国内外市场的便捷桥梁玉河铁路自通车以来,已安全发送旅客万人次,将万用科学记数法表示为( )
A. B. C. D.
3.下列运算正确的是( )
A. B.
C. D.
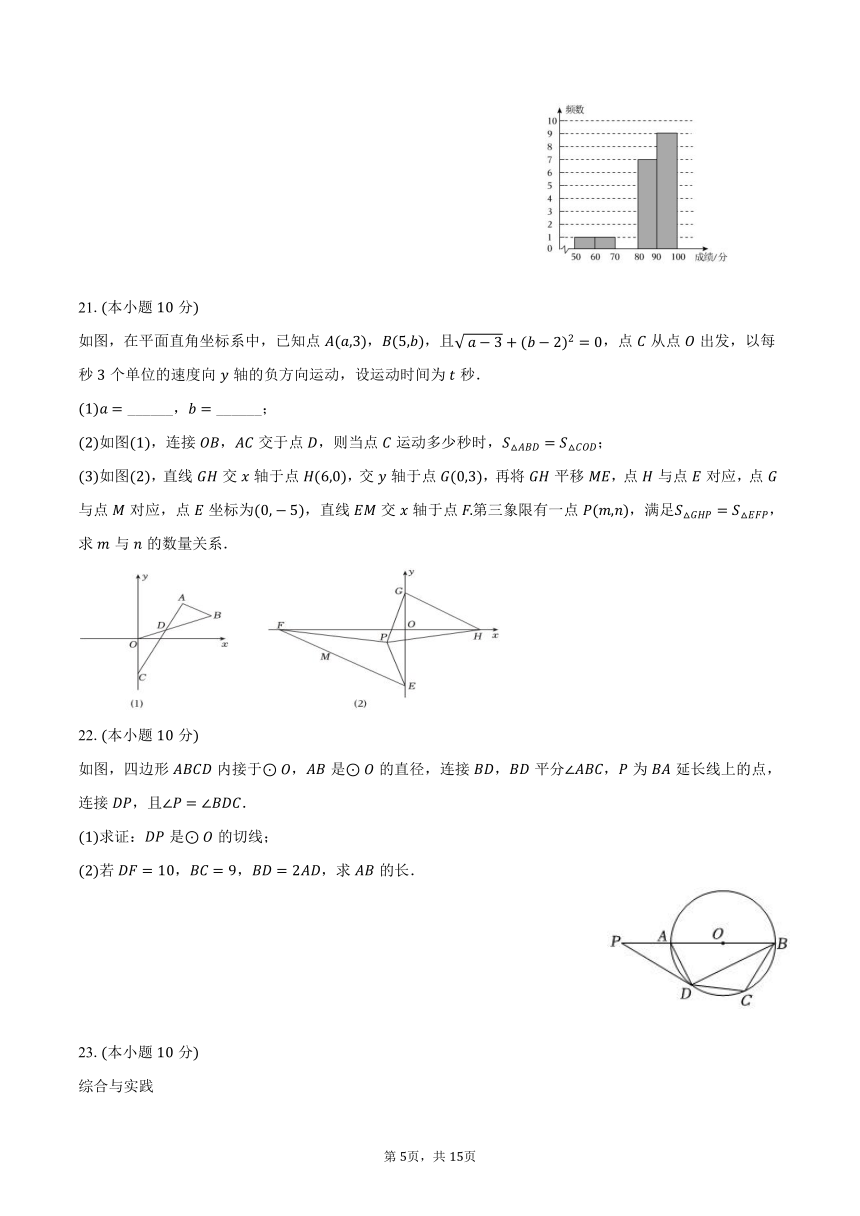
4.“於显乐都,既丽且康陪京之南,居汉之阳,”东汉张衡以一篇南都赋赞颂了家乡南阳地理位置之独特、自然山河之壮美、历史人文之悠远如图是一个正方体的平面展开图,把展开图折叠成正方体后,与“南”字所在面相对的面上的汉字是( )
A. 陪 B. 汉 C. 阳 D. 居
5.某校对七年级学生的体育成绩进行抽样调查,成绩评定采用,,,四个等级,其中,,,分别代表优秀,良好,合格,不合格现对抽取的份数据进行整理与描述,下列结论正确的是( )
A. 本次抽样调查的样本容量是
B. 体育成绩为等级对应的扇形圆心角度数是
C. 体育成绩达到优秀等级的学生人数最多
D. 若该校七年级共有学生人,则估计该校七年级学生体育成绩达到良好及以上的学生有人
6.如图,与是以点为位似中心的图形点,,的对应点分别为点,,若与的周长之比为:,则的值为( )
A.
B.
C.
D.
7.人工智能,是新一轮科技革命和产业变革的重要驱动力量,是研究、开发用于模拟、延伸和扩展人类智能的理论、方法、技术及应用系统的一门新兴的技术科学小明和小丽两位同学计划利用假期,通过智慧课堂学习大数据技术、信息安全和物联网工程三门课程中的任意一门课程,则两人选中信息安全和大数据技术的概率为( )
A. B. C. D.
8.小月同学在手工课上用扇形卡纸制作的简易圆锥形漏斗如图所示,若漏斗的底面圆的直径为,高为,则扇形卡纸的面积是( )
A. B. C. D.
9.已知抛物线:,抛物线与关于轴对称,两抛物线的顶点相距,则的值为( )
A. B. 或 C. D. 或
10.如图,中,,,点是中点,点在上且,将线段绕点顺时针旋转得到线段,连接,则的长为( )
A.
B.
C.
D.
二、填空题:本题共6小题,每小题3分,共18分。
11.分解因式;______.
12.代数式与的差不大于,则的取值范围是______.
13.如图,是的切线,切点为,若,则的度数为______.
14.小怿从科普读物中了解到,光从真空射入介质发生折射时,入射角的正弦值与折射角的正弦值的比值叫做介质的“绝对折射率”,简称“折射率”它表示光在介质中传播时,介质对光作用的一种特征若光从真空射入某介质,入射角为,折射角为,且,,求该介质的折射率______.
15.在平面直角坐标系中,点是反比例函数图象上的一点,如图,将线段向左平移,平移后的对应线段为,点落在反比例函数的图象上,已知线段扫过的面积为,则______.
16.如图,在等边三角形中,点在边上,,连接,点在线段上,连接若,,则的值为______.
三、计算题:本大题共2小题,共12分。
17.计算:.
18.解不等式组:.
四、解答题:本题共6小题,共60分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
如图,中,,将绕点逆时针旋转一定的角度,得到,和分别是和的对应点,延长交于点.
求证:;
连接,若求证:.
20.本小题分
年月日,神舟二十号载人飞船发射取得圆满成功从“东方红一号”到神舟二十号,年间,中国航天书写了从地球走向浩瀚宇宙的壮闹诗篇为了解学生对航空航天知识的掌据情况,某校组织了航天知识竞赛现从七、八年级参赛学生的成绩中各随机抽取个数据,分别对这个数据进行整理,描述和分析,下面给出了部分信息:
信息:七年级参加竞赛的名学生成绩单位:分数据的频数分布直方图如图数据分成组:,,,,;
信息:七年级参加竞赛的名学生成绩数据在这组的是:,,,,,,,且七年级参加竞赛的名学生成绩的众数在这一组;
信息:八年级参加竞赛的名学生成绩的中位数为分.
根据以上信息,解答下列问题:
补全频数分布直方图,七年级参加竞赛的名学生成绩的中位数是______分,七年级参加克赛的名学生成绩的众数是______分;
在这次竞赛中,七年级学生张学与八年级学生李娜的成情都是分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;
已知七年级有名学生参加竞赛,若成绩达到分及以上算作优秀,估计七年级本次竞赛共有多少名学生达到了优秀?
21.本小题分
如图,在平面直角坐标系中,已知点,,且,点从点出发,以每秒个单位的速度向轴的负方向运动,设运动时间为秒.
______, ______;
如图,连接,交于点,则当点运动多少秒时,;
如图,直线交轴于点,交轴于点,再将平移,点与点对应,点与点对应,点坐标为,直线交轴于点第三象限有一点,满足,求与的数量关系.
22.本小题分
如图,四边形内接于,是的直径,连接,平分,为延长线上的点,连接,且.
求证:是的切线;
若,,,求的长.
23.本小题分
综合与实践
如图,投掷铅球时,铅球的飞行路径可以近似看作一条抛物线抛掷铅球时,运动员出球的速度、角度、高度以及空气阻力等是影响抛掷距离的主要因素小明在学校体育场借助红外线检测仪检测三种不同的投掷抛物线,,已知三次抛掷铅球时,出手速度相同,出球角度分别为,,,通过投掷测试,小明希望得到最适合自己的投掷角度.
出球角度 抛物线 相关数据 相关结论
铅球与出球位置的水平距离 的长 运动轨迹的函数解析式
铅球与地面的竖直距离
铅球与地面的竖直距离
铅球与地面的竖直距离
【基础应用】
图中点的坐标为______,的值为______;
【应用与说理】
请判断在,,三个出球角度中,小明以哪一个角度投掷铅球的水平距离最大,并说明理由.
【拓展学习】
根据中的判断结果,小明画出了最大时对应的抛物线,如图已知该抛物线交轴于点,是一个斜坡面,点是抛物线上且在线段上方的一个动点,轴于点,交于点,为点到的铅垂距离,求出的最大值.
24.本小题分
问题背景:借助三角形的中位线可构造一组相似三角形,若将它们绕公共顶点旋转,对应顶点连线的长度存在特殊的数量关系,数学小组对此进行了研究如图,在中,,,分别取,的中点,作如图所示,将绕点逆时针旋转,连接,.
探究发现:旋转过程中,线段和的长度存在怎样的数量关系?写出你的猜想,并证明.
性质应用:如图,当所在直线首次经过点时,求的长.
延伸思考:如图,在中,,,,分别取,的中点,作,将绕点逆时针旋转得到,连接,当边平分线段时,求的值.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】解:原式
.
18.【答案】解:
由得;
由得;
则不等式组的解集为 .
19.【解析】证明:连接,
将绕点逆时针旋转一定的角度,得到,
,,
,
≌,
;
将绕点逆时针旋转一定的角度,得到,
,,
,
,
,
,
,
.
20.【解析】成绩为的学生人数为人,
补全的频数分布直方图如图所示:
将七年级参加知识竞赛活动的名学生成绩按从小到大的顺序排列,中位数是分;
七年级参加克赛的名学生成绩的众数是分;
故答案为:,;
八年级学生李娜排名更靠前,
理由:七年级参加竞赛的名学生成绩的中位数是分,八年级的中位数为分,
又,
八年级学生李娜排名更靠前;
名,
答:估计七年级本次竞赛共有名学生达到了优秀.
21.解:由知,,,
故答案为:,;
由知:,,
如图,连接,过作于,过作轴于,则,,,,
,
,
设运动的时间为秒时,,则,
,
,
,
则;
由点、的坐标得,直线的表达式为:,
过点作的平行线交轴于点,设点,
则,
即,即,则,
设直线交轴于点,则,
即,
则,则,
则,
即.
22.证明:连接,
四边形内接于,
,
,
,
,
,
平分,
,
,
,
,
是的直径,
,
,
,
,
是的半径,
是的切线;
解:,
设,,
,
,,
∽,
,
,
负值舍去,
.
23.解:把代入得,把代入得,,
,,
故答案为:,;
出球角度为时,把代入,
得,
解得舍.
出球角度为时,把代入,
得,
解得,舍.
由表可知,出球角度为时,抛物线对应的长为,
.
小明投掷铅球出球角度为时,抛掷铅球的水平距离最大.
设直线的解析式为,设点的横坐标为.
,
将代入得,
解得,
直线的函数解析式为,
,
.
,
当时,取得最大值,最大值为.
24.证明:,理由如下:
点和点为分别为,中点,
,,
,
,
,,
,
,
根据旋转的性质可得:,
∽,
,即;
由图可知,
点和点为分别为,中点,
,,
∽,
,
当所在直线经过点时,,
根据勾股定理可得:,
由可得,
,
解得;
令,相交于点,过点作于点,如图,
根据题意可得,
,,,
,
,,
边平分线段,,
,
,
∽,
,
,
根据旋转的性质可得:,
,
,,
,,
,
.
第15页,共15页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列各数中为最小的数是( )
A. B. C. D.
2.红河日报年月日报道,玉河铁路是我州连接越南与玉溪的铁路大通道,也是我州连通国内外市场的便捷桥梁玉河铁路自通车以来,已安全发送旅客万人次,将万用科学记数法表示为( )
A. B. C. D.
3.下列运算正确的是( )
A. B.
C. D.
4.“於显乐都,既丽且康陪京之南,居汉之阳,”东汉张衡以一篇南都赋赞颂了家乡南阳地理位置之独特、自然山河之壮美、历史人文之悠远如图是一个正方体的平面展开图,把展开图折叠成正方体后,与“南”字所在面相对的面上的汉字是( )
A. 陪 B. 汉 C. 阳 D. 居
5.某校对七年级学生的体育成绩进行抽样调查,成绩评定采用,,,四个等级,其中,,,分别代表优秀,良好,合格,不合格现对抽取的份数据进行整理与描述,下列结论正确的是( )
A. 本次抽样调查的样本容量是
B. 体育成绩为等级对应的扇形圆心角度数是
C. 体育成绩达到优秀等级的学生人数最多
D. 若该校七年级共有学生人,则估计该校七年级学生体育成绩达到良好及以上的学生有人
6.如图,与是以点为位似中心的图形点,,的对应点分别为点,,若与的周长之比为:,则的值为( )
A.
B.
C.
D.
7.人工智能,是新一轮科技革命和产业变革的重要驱动力量,是研究、开发用于模拟、延伸和扩展人类智能的理论、方法、技术及应用系统的一门新兴的技术科学小明和小丽两位同学计划利用假期,通过智慧课堂学习大数据技术、信息安全和物联网工程三门课程中的任意一门课程,则两人选中信息安全和大数据技术的概率为( )
A. B. C. D.
8.小月同学在手工课上用扇形卡纸制作的简易圆锥形漏斗如图所示,若漏斗的底面圆的直径为,高为,则扇形卡纸的面积是( )
A. B. C. D.
9.已知抛物线:,抛物线与关于轴对称,两抛物线的顶点相距,则的值为( )
A. B. 或 C. D. 或
10.如图,中,,,点是中点,点在上且,将线段绕点顺时针旋转得到线段,连接,则的长为( )
A.
B.
C.
D.
二、填空题:本题共6小题,每小题3分,共18分。
11.分解因式;______.
12.代数式与的差不大于,则的取值范围是______.
13.如图,是的切线,切点为,若,则的度数为______.
14.小怿从科普读物中了解到,光从真空射入介质发生折射时,入射角的正弦值与折射角的正弦值的比值叫做介质的“绝对折射率”,简称“折射率”它表示光在介质中传播时,介质对光作用的一种特征若光从真空射入某介质,入射角为,折射角为,且,,求该介质的折射率______.
15.在平面直角坐标系中,点是反比例函数图象上的一点,如图,将线段向左平移,平移后的对应线段为,点落在反比例函数的图象上,已知线段扫过的面积为,则______.
16.如图,在等边三角形中,点在边上,,连接,点在线段上,连接若,,则的值为______.
三、计算题:本大题共2小题,共12分。
17.计算:.
18.解不等式组:.
四、解答题:本题共6小题,共60分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
如图,中,,将绕点逆时针旋转一定的角度,得到,和分别是和的对应点,延长交于点.
求证:;
连接,若求证:.
20.本小题分
年月日,神舟二十号载人飞船发射取得圆满成功从“东方红一号”到神舟二十号,年间,中国航天书写了从地球走向浩瀚宇宙的壮闹诗篇为了解学生对航空航天知识的掌据情况,某校组织了航天知识竞赛现从七、八年级参赛学生的成绩中各随机抽取个数据,分别对这个数据进行整理,描述和分析,下面给出了部分信息:
信息:七年级参加竞赛的名学生成绩单位:分数据的频数分布直方图如图数据分成组:,,,,;
信息:七年级参加竞赛的名学生成绩数据在这组的是:,,,,,,,且七年级参加竞赛的名学生成绩的众数在这一组;
信息:八年级参加竞赛的名学生成绩的中位数为分.
根据以上信息,解答下列问题:
补全频数分布直方图,七年级参加竞赛的名学生成绩的中位数是______分,七年级参加克赛的名学生成绩的众数是______分;
在这次竞赛中,七年级学生张学与八年级学生李娜的成情都是分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;
已知七年级有名学生参加竞赛,若成绩达到分及以上算作优秀,估计七年级本次竞赛共有多少名学生达到了优秀?
21.本小题分
如图,在平面直角坐标系中,已知点,,且,点从点出发,以每秒个单位的速度向轴的负方向运动,设运动时间为秒.
______, ______;
如图,连接,交于点,则当点运动多少秒时,;
如图,直线交轴于点,交轴于点,再将平移,点与点对应,点与点对应,点坐标为,直线交轴于点第三象限有一点,满足,求与的数量关系.
22.本小题分
如图,四边形内接于,是的直径,连接,平分,为延长线上的点,连接,且.
求证:是的切线;
若,,,求的长.
23.本小题分
综合与实践
如图,投掷铅球时,铅球的飞行路径可以近似看作一条抛物线抛掷铅球时,运动员出球的速度、角度、高度以及空气阻力等是影响抛掷距离的主要因素小明在学校体育场借助红外线检测仪检测三种不同的投掷抛物线,,已知三次抛掷铅球时,出手速度相同,出球角度分别为,,,通过投掷测试,小明希望得到最适合自己的投掷角度.
出球角度 抛物线 相关数据 相关结论
铅球与出球位置的水平距离 的长 运动轨迹的函数解析式
铅球与地面的竖直距离
铅球与地面的竖直距离
铅球与地面的竖直距离
【基础应用】
图中点的坐标为______,的值为______;
【应用与说理】
请判断在,,三个出球角度中,小明以哪一个角度投掷铅球的水平距离最大,并说明理由.
【拓展学习】
根据中的判断结果,小明画出了最大时对应的抛物线,如图已知该抛物线交轴于点,是一个斜坡面,点是抛物线上且在线段上方的一个动点,轴于点,交于点,为点到的铅垂距离,求出的最大值.
24.本小题分
问题背景:借助三角形的中位线可构造一组相似三角形,若将它们绕公共顶点旋转,对应顶点连线的长度存在特殊的数量关系,数学小组对此进行了研究如图,在中,,,分别取,的中点,作如图所示,将绕点逆时针旋转,连接,.
探究发现:旋转过程中,线段和的长度存在怎样的数量关系?写出你的猜想,并证明.
性质应用:如图,当所在直线首次经过点时,求的长.
延伸思考:如图,在中,,,,分别取,的中点,作,将绕点逆时针旋转得到,连接,当边平分线段时,求的值.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】解:原式
.
18.【答案】解:
由得;
由得;
则不等式组的解集为 .
19.【解析】证明:连接,
将绕点逆时针旋转一定的角度,得到,
,,
,
≌,
;
将绕点逆时针旋转一定的角度,得到,
,,
,
,
,
,
,
.
20.【解析】成绩为的学生人数为人,
补全的频数分布直方图如图所示:
将七年级参加知识竞赛活动的名学生成绩按从小到大的顺序排列,中位数是分;
七年级参加克赛的名学生成绩的众数是分;
故答案为:,;
八年级学生李娜排名更靠前,
理由:七年级参加竞赛的名学生成绩的中位数是分,八年级的中位数为分,
又,
八年级学生李娜排名更靠前;
名,
答:估计七年级本次竞赛共有名学生达到了优秀.
21.解:由知,,,
故答案为:,;
由知:,,
如图,连接,过作于,过作轴于,则,,,,
,
,
设运动的时间为秒时,,则,
,
,
,
则;
由点、的坐标得,直线的表达式为:,
过点作的平行线交轴于点,设点,
则,
即,即,则,
设直线交轴于点,则,
即,
则,则,
则,
即.
22.证明:连接,
四边形内接于,
,
,
,
,
,
平分,
,
,
,
,
是的直径,
,
,
,
,
是的半径,
是的切线;
解:,
设,,
,
,,
∽,
,
,
负值舍去,
.
23.解:把代入得,把代入得,,
,,
故答案为:,;
出球角度为时,把代入,
得,
解得舍.
出球角度为时,把代入,
得,
解得,舍.
由表可知,出球角度为时,抛物线对应的长为,
.
小明投掷铅球出球角度为时,抛掷铅球的水平距离最大.
设直线的解析式为,设点的横坐标为.
,
将代入得,
解得,
直线的函数解析式为,
,
.
,
当时,取得最大值,最大值为.
24.证明:,理由如下:
点和点为分别为,中点,
,,
,
,
,,
,
,
根据旋转的性质可得:,
∽,
,即;
由图可知,
点和点为分别为,中点,
,,
∽,
,
当所在直线经过点时,,
根据勾股定理可得:,
由可得,
,
解得;
令,相交于点,过点作于点,如图,
根据题意可得,
,,,
,
,,
边平分线段,,
,
,
∽,
,
,
根据旋转的性质可得:,
,
,,
,,
,
.
第15页,共15页
同课章节目录
